- Преподавателю
- Математика
- Урок Гамильтоновы циклы и задача коммивояжера (9 класс)
Урок Гамильтоновы циклы и задача коммивояжера (9 класс)
| Раздел | Математика |
| Класс | 9 класс |
| Тип | Конспекты |
| Автор | Моторина Е.А. |
| Дата | 09.01.2016 |
| Формат | docx |
| Изображения | Есть |
Урок «Гамильтоновы циклы и задача коммивояжера»
факультативного курса «теория графов и их приложения» (9 класс)
Ранее мы рассмотрели эйлеровы циклы, на этом же занятии - рассмотрим другой вид циклов - гамильтоновы.
Построение эйлерова цикла связано с обходом ребер графа: нам требовалось обойти все ребра графа по одному разу и вернуться в исходную вершину. При этом одни и те же вершины можно было посещать сколь угодно раз. Но существует намного более сложная задача, связанная с обходом вершин. В этой задаче требуется обойти все вершины графа по одному разу и вернуться в исходную вершину. При этом, как и в случае эйлерова цикла по каждому ребру также можно пройти только один раз (учащимся это рекомендуется проверить самостоятельно).
Такой цикл получил название гамильтонова, так как эта задача была предложена выдающимся ирландским математиком Уильямом Гамильтоном. Он предложил совершить «кругосветное» путешествие по графу, имеющему форму додекаэдра. Додекаэдр - это многогранник, гранями которого служат 12 правильных пятиугольников (рисунок 1,а). У него 20 вершин и 30 ребер. В этой задаче вершинам додекаэдра соответствовали известные города, такие как Брюссель, Амстердам, Эдинбург, Пекин, Прага, Дели, Франкфурт и др., а рёбрам соответствовали дороги их соединяющие. Путешественник должен пройти «вокруг света», проложив путь, проходящий через все вершины ровно один раз.
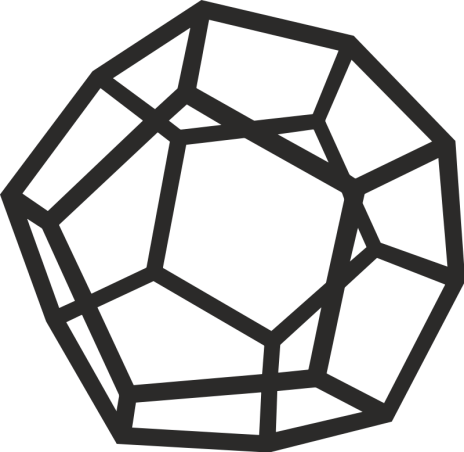
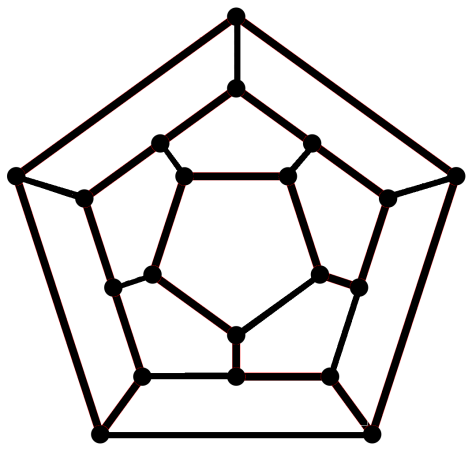
Рисунок 1 - Додекаэдр (а) и плоский граф, ему соответствующий (б)
Для удобства пользования головоломкой, в каждую вершину додекаэдра был вбит гвоздь, и проложенный путь отмечался нитью, которая обматывалась вокруг гвоздя. Но эта конструкция оказалась слишком громоздкой и не практичной, и Гамильтон заменил объемный додекаэдр (рисунок 1,а) изоморфным ему плоским графом (рисунок 1,б).
Известны условия существования гамильтонова цикла в графе.
Необходимое условие довольно очевидно: если неориентированный граф G содержит гамильтонов цикл, тогда в нём не существует ни одной вершины vi с локальной степенью deg(vi) < 2. Это хорошо иллюстрируется рисунком 2 - в графе, изображенном на рисунке 2,а имеется гамильтонов цикл, и все степени его вершин равны 2, а в графе, изображенном на рисунке 2,б - гамильтонова цикла нет, так как в графе есть вершина со степенью меньше 2. Вершина v4 со степенью 1 не дает построить цикл.
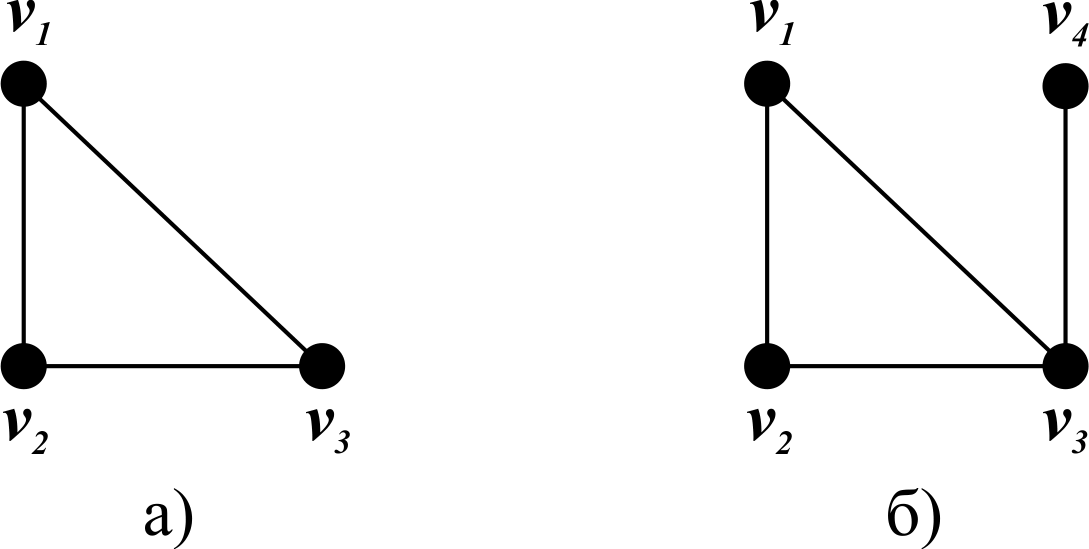
Рисунок 2 - Необходимое условие существования гамильтонова цикла
Достаточных условий на данный момент известно несколько. Рассмотрим два таких утверждения. Утверждение, приведенное ниже, называют теоремой Оре.
Рассмотрим граф G с n≥3 вершинами. Пронумеруем их произвольным образом и выпишем их последовательность (1):
v0, v1, …, vi-1, vi, vi+1,…, vn-1
(1)
В этом случае может оказаться, что некоторые две соседние в данной последовательности вершины, например vk и vk+1, не соединены ребром. Назовем такую ситуацию «разрывом» между вершинами vk и vk+1
Очевидно, что в последовательности v0, v1, …, vi-1, vi не возникнут другие разрывы, если ее записать в обратном порядке, а именно: vi, vi-1, …, v1.
Предположим, что разрыв в последовательности (1) имеется между вершинами v0 и v1 (можно выбрать любые вершины). Предположим также, что vi - вершина графа G, связана ребром с вершиной v0. Очевидно, что число таких вершин vi связанных с v0 равно степени этой вершины: deg(v0).
Пытаясь ликвидировать разрыв в исходной последовательности (1), перепишем ее в таком порядке: v0, vi, vi-1, …, v2,v1, vi+1,…, vn-1. В результате число разрывов уменьшится на единицу в том случае, если между вершинами v1 и vi+1 не возникнет новый разрыв.
Вершину vi среди (n-1) вершин, не совпадающих с v0, всегда можно найти так, чтобы между v1 и vi+1 не возник новый разрыв, если справедливо неравенство (2):
deg(v0) ≥ (n-1) − deg(v1)
(2)
В данном неравенстве справа подсчитывается число разрывов, которые могут возникнуть при всевозможных перестановках последовательности (1).
Теперь необходимо вспомнить, что вершины v0 и v1 были выбраны произвольно; можно было рассмотреть разрыв между любыми другими соседними вершинами в последовательности (1); или даже вершинами vi и vj не стоящими рядом. Лишь необходимо соблюдать неравенство (3):
deg(vi) ≥ (n-1) − deg(vj)
(3)
Заметим, что неравенство (3) симметрично относительно vi и vj, поэтому его можно записать в виде (4):
deg(vi) + deg(vj) ≥ (n-1)
(4)
И тогда в последовательности (1) удастся ликвидировать все разрывы. А это означает, что в графе G найдется гамильтонов путь. Но нас интересует наличие гамильтонова цикла. Покажем, что если для любой пары вершин vi и vj графа G с n вершинами справедливо неравенство (5):
deg(vi) + deg(vj) ≥ n
(5)
то граф G обладает гамильтоновым циклом.
Рассмотрим гамильтонов путь, связывающий вершины vi и vj графа G. Пусть w - одна из вершин графа G, связанная ребром с вершиной vi, Тогда в силу доказанного ранее хотя-бы для одной из таких вершин w найдется в гамильтоновом пути смежная с ней вершина u, такая, которая связана ребром с vj. Добавляя к гамильтонову пути ребра (vi, w) и (u, vj) и удаляя из него ребро (u, w), получим гамильтонов цикл (рисунок 3).
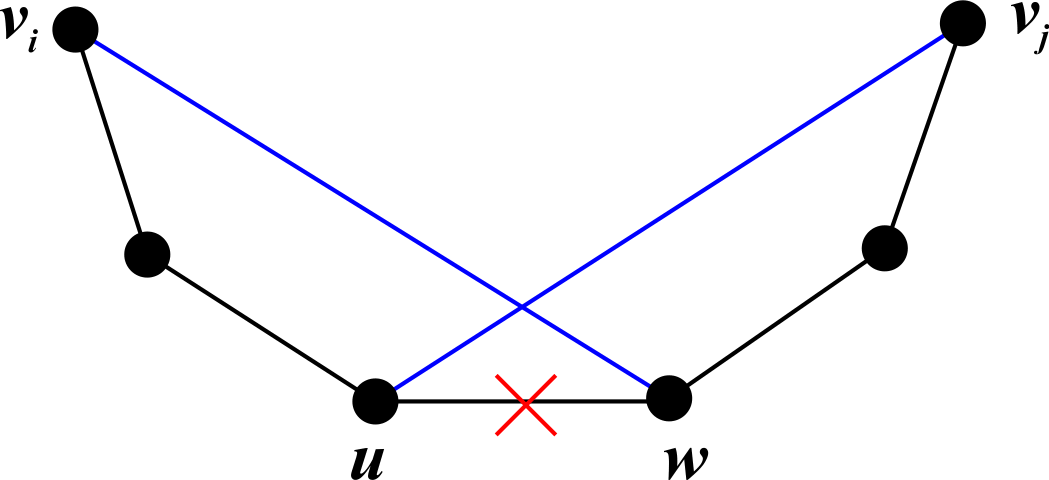
Рисунок 3. Образование гамильтонова цикла из цепи
Второе утверждение называется условием Дирака, оно сформулировано и доказано в 1952 году. Если в графе G, имеющем n вершин, степень каждой вершины не меньше, чем 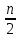 , то граф G - гамильтонов. Зачастую, данное утверждение доказывается на базе предыдущего, но мы приведем здесь независимое доказательство, данное Д.Дж.Ньюманом.
, то граф G - гамильтонов. Зачастую, данное утверждение доказывается на базе предыдущего, но мы приведем здесь независимое доказательство, данное Д.Дж.Ньюманом.
Пусть граф, удовлетворяющий условию Дираку, не гамильтонов. Добавим к исходному графу G новую вершину, соединив ее ребрами со всеми вершинами графа G. Если получившийся граф не является гамильтоновым, добавим еще одну вершину, и также соединим ее ребрами со всеми вершинами графа G, не соединяя, однако с предыдущей добавленной вершиной. Таким образом, мы добавим k новых вершин, причем k - наименьшее число вершин, необходимых для того, чтобы полученный граф G' стал гамильтоновым. Это обязательно произойдет, даже в случае если исходный граф G - пустой, так как в этом случае понадобится добавить n новых вершин. Итак, в новой графе будет (n+k) вершин (рисунок 4).

Рисунок 4. К доказательству условия Дирака
Пусть v→p→w→…→v гамильтонов цикл в получившемся графе G', где v, w - вершины из G, а p - одна из добавленных вершин. Тогда w не является смежной с v, так как в противном случае мы могли бы не использовать вершину p - гамильтонов цикл в графе G уже присутствовал бы, что противоречит минимальности k и начальному преположению. Кроме того, например, вершина, w', смежная с вершиной w, не может непосредственно следовать в выстраиваемом цикле за вершиной v' , смежной вершине v, потому что тогда можно было бы заменить цикл v→p→w→…→v'→w'→…→v циклом v→v'→…→w→w'→…→v, изменив направление обхода между вершинами w и v' b и исключив добавленную вершину p из гамильтонова цикла, а это опять же противоречит минимальности k.
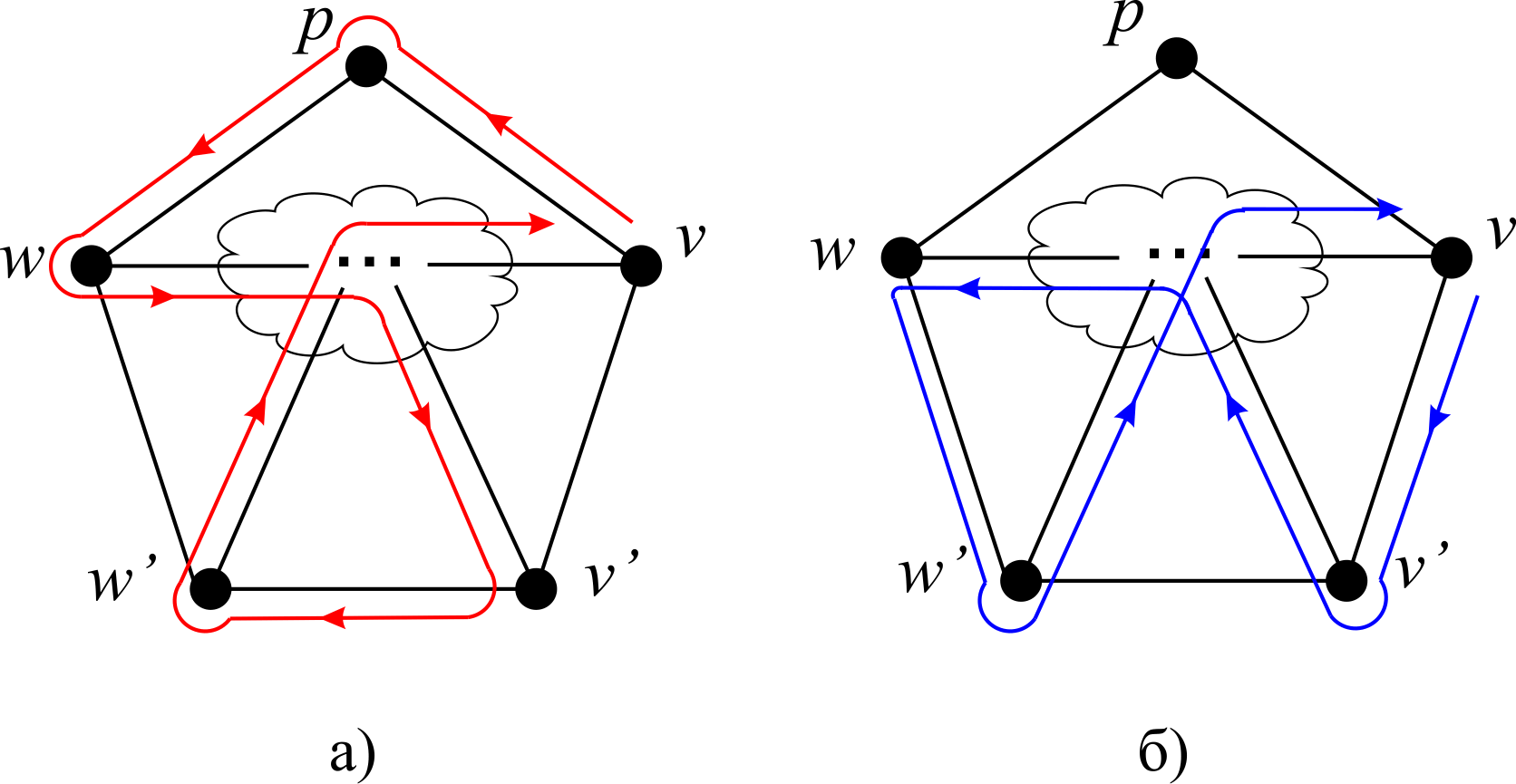
Рисунок 5. К доказательству условия Дирака
Отсюда следует, что число вершин графа G', не являющихся смежными с w, не меньше числа вершин, смежных с v (то есть равно, по меньшей мере, 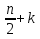 ); с другой стороны, очевидно, что число вершин графа G', смежных с w, тоже равно, по меньшей мере,
); с другой стороны, очевидно, что число вершин графа G', смежных с w, тоже равно, по меньшей мере, 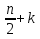 . А так как ни одна вершина графа G' не может быть одновременно смежной и не смежной вершине w, то общее число вершин графа G', равное n+k, не меньше, чем n+2k, что невозможно. Утверждение доказано.
. А так как ни одна вершина графа G' не может быть одновременно смежной и не смежной вершине w, то общее число вершин графа G', равное n+k, не меньше, чем n+2k, что невозможно. Утверждение доказано.
Существуют и другие достаточные условия наличия гамильтонова цикла в графе, например, условие Оре: пусть n - количество вершин в данном графе и n>2 . Если для любой пары несмежных вершин (v, w) выполнено неравенство deg(v)+deg(w)≥n, то данный граф - гамильтонов. Или, формулируя иначе, сумма степеней любых двух несмежных вершин не меньше общего числа вершин в графе.
С построением гамильтонова цикла связана задача коммивояжера. Коммивояжер - торговец, путешествующий по разным городам и предлагающий какие-либо товары (или принимающий заказы по каталогу). Такой способ торговли был популярен в США до широкого распространения интернета. Пусть область, которую должен посетить коммивояжер содержит несколько городов, расстояния (или стоимость проезда) между которыми известны. Требуется найти маршрут, проходящий через все города по одному разу и возвращающийся в исходный пункт. Если таких маршрутов несколько, то необходимо отыскать самый короткий (или самый дешевый).
Напомним, что если ребрам графа приписываются некоторые числовые значения, то такой граф называется взвешенным, а сами эти значения - весами ребер. В качестве веса могут выступать самые разные значения: расстояния, цены, скорости движения по участкам дорог и т.п.
Исходя из этого математическая формулировка задачи коммивояжера такова: требуется найти гамильтонов цикл минимального веса.
К решению задачи коммивояжера сводится, например, следующая. На предприятии, выпускающем электронику, имеется автоматический станок, который должен рассверливать отверстия в печатных платах по заданной программе. Отверстий много и расстояния между ними известны. Необходимо так составить программу обхода этих отверстий, чтобы общее время перемещения между ними было минимальным. Тогда экономия всего нескольких секунд на этой операции при массовом производстве позволит получить существенную экономическую выгоду, увеличив производительность труда.
Задача коммивояжера относится к очень сложным задачам - ее можно решить только перебором всех возможных комбинаций. А количество различных комбинаций при построении оптимального маршрута очень велико. Так, если задача решается для полного неориентированного графа с n вершинами, то число маршрутов, которые надо проанализировать будет равно 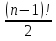 , а для ориентированного еще больше:
, а для ориентированного еще больше: 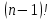 . Например, для полного неориентированного графа с пятью вершинами число возможных маршрутов составит 12, это не очень много. А для неорграфа с 10 вершинами уже порядка 181 тыс. комбинаций.
. Например, для полного неориентированного графа с пятью вершинами число возможных маршрутов составит 12, это не очень много. А для неорграфа с 10 вершинами уже порядка 181 тыс. комбинаций.
Существуют ли какие-либо методы, позволяющие не перебирать все возможные комбинации маршрутов? Да, такие методы есть, но они не гарантируют оптимального решения. Все же, метод, пусть и несовершенный лучше, чем отсутствие метода вообще. Поэтому рассмотрим два наиболее простых метода, облегчающих решение задачи коммивояжера.
Первый метод, который мы рассмотрим на примере задачи - метод ближайшего соседа. Пусть в графе, представленном на рисунке 5,а требуется найти гамильтонов цикл наименьшего веса.
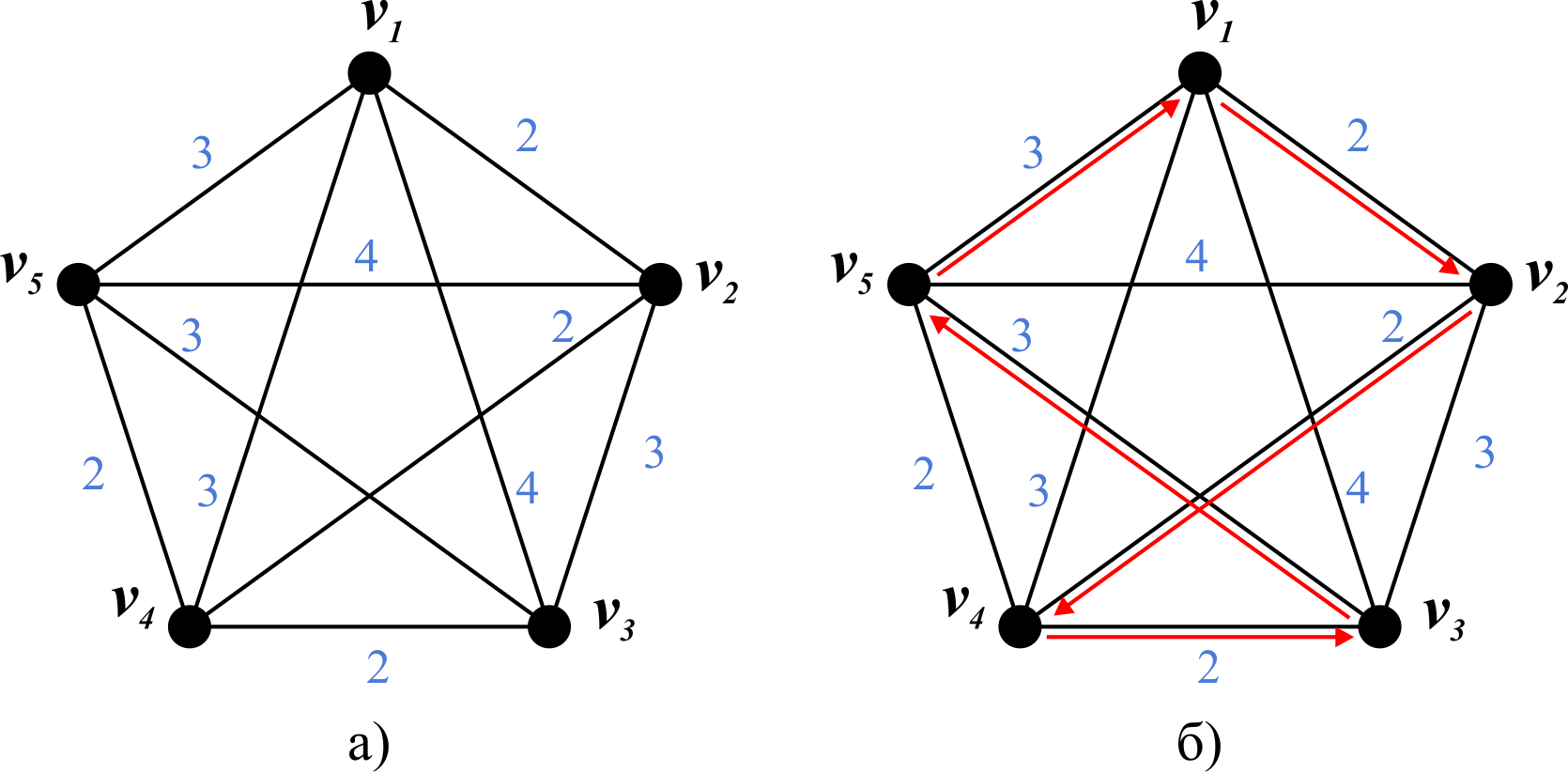
Рисунок 5. Метод ближайшего соседа: исходный граф (а) и построение гамильтонова цикла (б)
Начнем строить гамильтонов цикл, выбрав в качестве начальной любую вершину, например v1. Стоя в вершине v1 просматриваем инцидентные ей ребра, сравнивая их веса. Если имеется несколько ребер с одинаковыми наименьшими весами, можно выбрать любое. Наименьший вес, равный 2, имеет ребро (v1, v2), поэтому следующей вершиной цикла является вершина v2. Повторяя этот шаг и выбирая ребра с наименьшим весом, можно построить гамильтонов цикл: v1→ v2→ v4→ v3→ v5→ v1 с общим весом 12 (рисунок 5,б)
Второй метод построения гамильтонова цикла называют алгоритмом ближайшей вставки. Используем опять в качестве примера граф, изображенный на рисунке. На каждом этапе мы будем строить цикл минимального веса, вставляя в него новые вершины.
Опять начнем строить цикл с вершины v1. Отыщем другую вершину, образующую с v1 цикл минимального веса. Возможны варианты:
-
v1→ v2→ v1 с весом цикла 4;
-
v1→ v3→ v1 с весом цикла 8;
-
v1→ v4→ v1 с весом цикла 6;
-
v1→ v5→ v1 с весом цикла 6;
Выберем цикл с наименьшим весом v1→ v2→ v1 (рисунок 6,а).

Рисунок 6. Метод ближайшей вставки: шаг 1 (а), шаг 2 (б), шаг 3 (в), шаг 4 (г)
Теперь вставим в цикл новую вершину и опять подсчитаем веса циклов. Здесь возможны варианты:
-
v1→ v2→ v3→ v1 с весом цикла 9;
-
v1→ v2→ v4→ v1 с весом цикла 7;
-
v1→ v2→ v5→ v1 с весом цикла 9;
Опять выбираем цикл с наименьшим весом: v1→ v2→ v4→ v1 (рисунок 6, б).
Продолжая алгоритм, вставляем в цикл следующую вершину. Варианты:
-
v1→ v2→ v4→ v3→v1 с весом цикла 10;
-
v1→ v2→ v4→ v5→v1 с весом цикла 9;
Выбираем цикл v1→ v2→ v4→ v5→v1 (рисунок 6, в).
Наконец, вставляем последнюю вершину в цикл и получаем такую последовательность обхода: v1→ v2→ v4→ v5→ v3→v1 с суммарным весом 13 (рисунок 6, г). Этот результат хуже, чем при использовании предыдущего метода.
Как уже говорилось, эти алгоритмы не гарантируют оптимального решения, давая лишь приближенный результат. Качество этого результата, то есть, то насколько он будет близок к наименьшему весу гамильтонова цикла, зависит от выбора начальной вершины обхода и от выбора пути в точках ветвления.
На данный момент всё большую популярность приобретают алгоритмы, использующие некоторые методы искусственного интеллекта - такие как алгоритм муравьиных колоний (иначе, муравьиный алгоритм) или алгоритм отжига и др. Задача коммивояжера всё еще ждет своих исследователей, разрабатывающих эффективные алгоритмы ее решения.
Задачи для самостоятельного решения
-
Система авиасообщения небольшой страны построена так, что каждый город соединен не менее чем с половиной других городов. Можно ли проложить такой маршрут облета городов, который начинается и заканчивается в одном и том же городе и каждый город посещается ровно один раз?
-
На политический саммит собралось четное число глав государств, которые либо находятся в дружественных отношениях, либо враждуют. Оказалось, что у каждого главы государства друзей больше, чем врагов. Можно ли рассадить глав государств за круглым столом так, чтобы справа и слава от каждого из них будут сидеть главы дружественных стран?
-
На рисунке изображена схема торговой сети. На ней отмечено положение склада товаров и сеть магазинов, соединенная дорогами. Проложите возможные маршруты объезда всех магазинов, не подъезжая ни к одному из них более одного раза. Можно ли выполнив такое условие вернуться обратно на склад?
Рекомендуемая литература
-
Березина Л. Ю. Графы и их применение: Пособие для учителей с ил. - М.: Просвещение, 1979. - 143 с.
-
Мельников О.И. Занимательные задачи по теории графов. - Минск: ТетраСистемс, 2001. - 144 с.
-
Мельников О.И. Незнайка в стране графов: Пособие для учащихся. Изд. 3-е, стереотипное. - М.: КомКнига, 2007. - 160 с.
-
Мельников О.И. Теория графов в занимательных задачах. Изд.3, испр. и доп. - М.: Книжный дом «ЛИБРОКОМ», 2009. - 232 с.


