- Преподавателю
- Математика
- Задачи на смеси и сплавы
Задачи на смеси и сплавы
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Дряева М.Г. |
| Дата | 05.12.2014 |
| Формат | docx |
| Изображения | Есть |
Задачи на смеси, сплавы и растворы.
1. Подход к решению задач на смеси.
Человеку часто приходится смешивать различные жидкости, порошки, или твердые вещества, или разбавлять что-либо водой.
Задачи на смеси имеют практическую направленность. Например, мы пьём чай и кладем в чашку столько сахара, чтобы не пересластить (создаём нужную нам концентрацию), а если пересластили, то добавляем воды.
Летом мы ходим за грибами, затем их сушим. И мы понимаем, что чем дольше их сушить, тем меньше в них остается воды, при этом масса сухого вещества не меняется.
Врач выписывает рецепт, и мы покупаем мази, микстуры с определенной концентрацией лекарственных веществ. Решая задачи данного типа, нам нужно будет выделить компоненты, которые изменяются, и те, что остаются неизменными.
Говоря о смесях, растворах и сплавах будем употреблять термин «смесь» независимо от её вида (твердая, жидкая, сыпучая, газообразная). Смесь состоит из основного вещества и примеси. Что такое основное вещество, в каждой задаче определяется отдельно.
Текстовые задачи на смеси, сплавы и растворы входят в различные сборники заданий по математике и химии ОГЭ и ЕГЭ.
При решении любых задач, прежде всего, нужно грамотно прочитать условие, последовательно остановиться на каждой строчке, и попытаться выразить условие в качестве какого-то уравнения.
. Что же отличает задачи на смеси? Уравнение трудно составить, если не знать основную формулу для всех задач на смеси.
В «Занимательной алгебре» Я.И. Перельмана есть любопытная задача под названием: «В парикмахерской»:
Задача: Может ли алгебра понадобиться в парикмахерской? Оказывается, такие случаи бывают. Мне пришлось убедиться в этом, когда однажды в парикмахерской подошел ко мне мастер с неожиданной просьбой:
-Не поможете ли нам разрешить задачу, с которой мы никак не справимся?
- Уж сколько раствора испортили из-за этого!- добавил другой
- В чем задача?
- У нас имеется два раствора перекиси водорода: 30%- ыйи 3 % -ый. Нужно их смешать так, чтобы составился 12% -ый раствор. Не можем подыскать правильной пропорции.
Мне дали бумажку, и требуемая пропорция была найдена.
Она оказалась очень простой. Какой именно?
Решение: Пусть для составления 12%-ной смеси требуется взять x граммов 3%-ного раствора и y граммов 30% -ного раствора. Тогда в первой пропорции содержится 0,03x граммов чистой перекиси водорода, во второй 0,3y, а всего 0,03x + 0,3y
В результате получается (x + y) граммов раствора, в котором чистой перекиси должно быть 0,12 (x + y)
Имеем уравнение: 0,03x + 0,3y=0,12 (x + y)
Из этого уравнения находим x =2y, т.е. 3%-ного раствора надо взять вдвое больше.
Задача, описанная Перельманом, встречается не только в парикмахерских.
Например, для зарядки аккумуляторов бывает необходимо приготовить электролит, который должен содержать 24% серной кислоты из двух растворов с содержанием 92% и 10% серной кислоты.
2. Теоретические основы решения задач на смеси и сплавы.
Задачи на смеси, растворы и сплавы называют еще задачами на процентное содержание или концентрацию. Данный тип задач охватывает большой круг ситуаций - смешение товаров разной цены, жидкостей с различным содержанием соли, кислот различной концентрации, сплавление металлов с различным содержанием некоторого металла и пр. При решении задач данного типа используются следующие допущения:
1. Все получающиеся смеси и сплавы однородны;
2.Всегда выполняется «Закон сохранения объема или массы»:
если два раствора (сплава) соединяют в «новый» раствор (сплав), то выполняются равенства:
V = V1+V2 -сохраняется объем;
m = m1 + m2 - сохраняется масса.
3 Данный закон выполняется и для отдельных составляющих частей (компонентов)сплава (раствора).
Определение. Процентным содержанием (концентрацией или массовой долей) вещества в смеси называется отношение его массы к общей массе всей смеси. Это отношение может быть выражено либо в дробях, либо в процентах.
3.Задачи на смешение растворов разных концентраций.
Решим типовую задачу в общем виде и выведем формулу.
Задача:Имеются два куска сплава меди с цинком. Процентное содержание меди в них p1% иp2 % соответственно. В каком отношении нужно взять массы этих сплавов, чтобы, переплавив взятые куски вместе, получить сплав, содержащий p%меди?
 Решение.Понаблюдаем за содержанием меди.
Решение.Понаблюдаем за содержанием меди.
Исследуем уравнение (*) при условии, что будем брать ненулевые массы сплавов.
I случай. Если p1 ,p2 и p попарно не равны, то получим формулу
m1 (p1 - p) =m2(p - p2) (*)
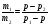
II случай. Возьмём два сплава с одинаковым процентным содержанием меди, т.е. p1=p2 . Решая уравнение (*), получим, что p1=p2=p, т. к. ни большей, ни меньшей концентрации сплав просто не получится, если исходные материалы имеют одинаковую процентную концентрацию меди, каковы бы ни были массы исходных сплавов.
III случай. Если p2 =p, или p1= p ,то вывод тот же.
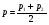 Если взять два сплава, массы которых одинаковы, т.е. m1 = m2 , то
Если взять два сплава, массы которых одинаковы, т.е. m1 = m2 , то
то есть процентное содержание нового сплава станет равно среднему арифметическому процентных концентраций исходных сплавов. А теперь рассмотрим однотипные задачи, решение которых очень удобно по этой формуле:
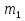
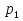
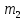
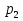
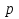

Смешали некоторое количество 11%-го раствора некоторого вещества с таким же количеством 19%-го раствора этого же вещества. Найдите концентрацию раствора.
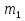
11%
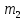
19%
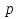
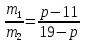
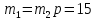
Или т. к. массы исходных растворов равны, то
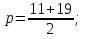

Сколько килограммов 20%-го раствора соли нужно добавить к 1 кг 10%-го раствора, чтобы получить 12%-ый раствор соли?
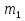
20%
1кг
10%
12%

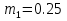
В сосуд, содержащий 13л 18%-го водного раствора некоторого вещества, добавили 5л воды. Найти концентрацию получившегося раствора.
13л
18%
5л
0%
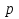 %
%
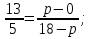
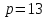
Старинный способ решения задач на смешивание двух веществ.
Предположим, что смешиваются два вещества - первое стоимостью а гривен за фунт и второе стоимостью b гривен за фунт. Желательно получить вещество стоимостью с гривен за фунт. Будем считать, что а<b( если с>b или c<a , то задача неразрешима, ибо, смешивая дешевые вещества, дорогое не получишь). Поэтому можно считать, что a<c<b. Смешиваем один фунт первого вещества и q фунт второго. В результате получится 1+q фунтов вещества стоимостью a+bq гривен. Один фунт смеси должен стоить с гривен. Значит должно выполняться равенство
a+bq=c*(1+q). Отсюда находим q=(c-a)/(b-c) или (b-c):(c-a).
Это соотношение дает старинный способ.
«Правило креста»
При решении задач на смешивание растворов разных концентраций используется «правило креста». В точке пересечения двух прямых обозначают концентрацию смеси. У концов этих прямых слева от точки пересечения указывают концентрации составных частей смеси, а справа - разности концентраций смеси и ее составных частей:
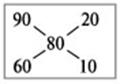
Для приготовления 30 г 80%-го раствора кислоты требуется взять 20 г 90%-го и 10 г 60%-го растворов кислоты.
Задача:У некоторого человека были на продажу масла двух сортов: одно ценою 10 гривен за ведро, другое же 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою 7 гривен за ведро. Какие части этих двух масел нужно взять, чтобы получить ведро масла ценою 7 гривен?
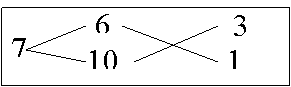
Из схемы делаем заключение, что дешевого масла нужно взять втрое больше, чем дорогого, т.е. для получения одного ведра ценою 7 гривен нужно взять дорогого масла 1/4 ведра, а дешевого масла 3/4.
Способ Л.Ф.Магницкого для трех веществ
Указанный Л. Ф. Магницким способ состоит в следующем. Надо дважды применить способ записи исходных данных и необходимых количеств веществ, причем в первый раз взять вещества с большей и меньшей стоимостью, а во второй раз с наименьшей и средней стоимостью. Повторив действие вычитания и соответствующей записи разности, получим доли, в которых нужно смешивать вещества наибольшей и средней стоимости (на соответствующих строках). Сложив доли дешевого вещества, найденные в первый и во второй раз, получим долю дешевого вещества в общей смеси.
Задача: Некто имеет чай трех сортов - цейлонский по 5 гривен за фунт, индийский по 8 гривен за фунт и китайский по 12 гривен за фунт. В каких долях нужно смешать эти сорта, чтобы получить чай стоимостью 6 гривен за фунт?

Взять 6+2=8 частей чая ценой по 5 гривен и по одной части ценой 8 гривен и 12 гривен за один фунт.
Возьмем 8/10 фунта чая ценой по 5 гривен за фунт и по1/10 фунта чая ценой 8 и 12 гривен за фунт, то получим 1 фунт чая ценой 8/10*5 + 1/10*8 + 1/10*12 = 6 гривен
Ответ: 100 т и 40 т.
4. Задачи на многократные переливания.
Рассмотрим задачи, при решении которых можно выявить общую закономерность изменения концентрации раствора в результате многократно повторяющейся операции.
Решим в общем виде такую задачу:
В сосуде, объём которого равен V0 литров, содержится раствор соли концентрации С0. Из сосуда выливается a литров смеси и доливается a литров воды, после чего раствор тщательно перемешивается. Эта процедура повторяется n раз. Какова станет концентрация соли в растворе после n таких процедур?
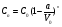 Если в задаче n раз отливают некоторое количество раствора и затем столько же раз приливают такое же количество воды или другого однородного вещества, то для решения задачи пригодится формула:
Если в задаче n раз отливают некоторое количество раствора и затем столько же раз приливают такое же количество воды или другого однородного вещества, то для решения задачи пригодится формула:
Где n- количество шагов, V0- начальный объём, который сохраняют неизменным при каждом шаге Сn- конечная концентрация,C0- начальная концентрация,
a - объём отливаемой каждый раз смеси
Докажем эту формулу:
Последовательность С0, С1, С2, Сn-1, Сn представляет собой убывающую
геометрическую прогрессию концентраций раствора.
Выражение Сn* V0соответствует количеству соли после проведения n-ой процедуры.
Но эта же соль присутствовала в (V0 - a) л предыдущего раствора
в количестве Сn-1 (V0 -a)л Составим уравнение: Сn* V0 = Сn-1 (V0 -a) и разделим обе части на V0 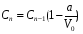 , откуда получаем
, откуда получаем 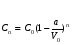 .
.
Однотипные задачи, которые уже легко решить с помощью данной формулы.
С0
V0
a
n
Cn
В сосуде имелось 1250 л 80%-го р-ра к-ты. Из него три раза отливали некоторое кол-во р-ра, добавляя такое же кол-во воды. В результате в сос. осталось 125л чистой к-ты. Какое кол-во р-ра брали изсосуда каждый раз?
Ответ:625 л.
С3=С0(1-a/1250)3
0,1=0,8(1-a/1250)3
0,125=(1-a/1250)3
0,5=1-a/1250
a/1250=0,5
a=625
Сколько литров чистого спирта останется в сосуде, если из 50л 80%-ного раствора 20 раз отливать по 1л раствора, каждый раз добавляя по 1 л воды?
Ответ:26,7 л.
С20=0,8(1-1/50)20
С20=0,534
0,534*50=26,7(л)
Существуют задачи, внешне похожие на применение формулы Сn, но при внимательном чтении оказывается, что цикл переливаний не закончен. В таких случаях надо быть очень внимательным.
Задача:Из сосуда, наполненного кислотой, вылили несколько литров и долили водой; потом опять вылили столько же литров смеси; тогда в сосуде осталось 24 л чистой кислоты. Ёмкость сосуда 54 л. Сколько кислоты вылили в первый раз и второй раз?
Решение: Будем иметь в виду, что на втором шаге воду не доливали.
По условию задачи объём сосуда, наполненного кислотой, 54 л. Её концентрация 100%. Пусть вылили х литров смеси, тогда в сосуде осталось (54-х) литров 100%-ной кислоты. В сосуд доливают хл воды. По определению концентрации надо массу кислоты разделить на массу раствора: (54-х)/54.
Опять выливают х литров смеси, в сосуде остаётся (54-х) л смеси с массовой долей кислоты (54-х)/54.
Чтобы найти массу кислоты в этой оставшейся смеси, надо массу раствора умножить на концентрацию кислоты в этом растворе. По условию масса чистой кислоты в этом растворе стала 24л.
Составим и решим уравнение:
(54-х)* ((54-х)/54) = 24,
(54-х)2= 1296,
зная, что х<54, получим единственное решение: х = 18.
В первый раз вылили 18 литров чистой кислоты. Но во второй раз выливали 18 литров смеси, в ней чистой кислоты было
18* (54-18)/5 =12 (л)
Ответ: 18 л; 12л
Задача: Имеются сплавы золота и серебра. В одном эти металлы находятся в отношении 2: 3, а в другом в отношении 3: 7. Сколько нужно взять от каждого сплава, чтобы получить 1 кг нового, в котором золото и серебро находились бы в отношении 5: 11?

По этой схеме уравнение х + у =1 показывает массу нового сплава.
Определяем массу золота в каждом сплаве и получаем уравнение
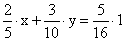
Аналогично определяем массу серебра и получаем уравнение
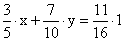
Записываем одну из систем:
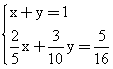
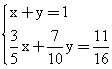
Решая ее, получаем х = 0,125 и у = 0,875
Ответ: 125 г и 875 г.
Есть очень легкий, быстрый и «хитрый» способ решения подобных задач, предложенный американским физиком ( русского происхождения) Алексеем Султановым:
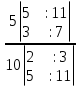 =
= 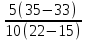 =
=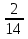 =
=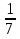
Использованная литература.
-
Алгебра-7:учебник автор: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков,
С.Б. Суворова, Просвещение, 2010
-
Прокопенко Н. И.Задачи на смеси и сплавы. - М.: Чистые пруды, 2010.
-
Под редакцией М.И. Сканави. Сборник задач по математике. Москва, 2002г.
-
И.Н. Сергеев ,С. Н. Олехник. Примени математику. Москва «Наука»,1990 г.
-
Сборник задач по математике. Под редакцией А. И. Прилепко.
Москва «Высшая школа», 1998 г.
-
О. А.Городнова Статья «Учимся решать задачи на«смеси и сплавы»,
г-та«Математика»№36 за 2004 г.
-
А.В. Шевкин Школьные математические олимпиады,
изд-во «Русское слово», 2002г.
8.« Занимательной алгебры» авт. Я.И. Перельман.
1


