- Преподавателю
- Математика
- Статья: Из истории математики Китая и ИНдии
Статья: Из истории математики Китая и ИНдии
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Кравчук Е.В. |
| Дата | 15.08.2015 |
| Формат | doc |
| Изображения | Есть |
Кравчук Е.В.
г. Балашиха Московской области.
Из истории математики Китая и Индии.
Китайский народ имеет богатую много вековую историю. Многие важнейшие открытия в науке и технике, сделанные китайскими учеными вошли в золотой фонд мировой науки и культуры.
Об объеме китайской культуры в древности можно судить хотя бы по китайскому энциклопедическому словарю, составленному в 15в. и состоящему из 11095 книг.
По утверждению китайского историка математики Ли Уня математические познания китайцев восходят к 14в. до н. э. В истории математики Древнего Китая имеются сведения о десятичной системе счисления, специальной иероглифической символике, об оперировании большими числами, наличии вспомогательных счетных устройств (узелки, счетная доска), об использовании циркуля, линейки, угольника и т.д. Древнейшие числовые записи в Китае встречаются на гадательных костях 14-11вв. до н.э., на гончарной или бронзовой утвари и монетах 10-3вв. до н.э. Наибольшее встречающееся здесь число 30000.
Одним из древнейших китайских трактатов по математике, дошедших до нас, является «Математика в девяти книгах» («Цэн чжан суань шу»). Авторство приписывается Чжан Цаню (2в. до н.э.). Произведение неоднократно перерабатывалось. В нем формулировались условия задач (всего 246) и давались ответы к ним. После группы однотипных задач давался алгоритм решения к ним. Вывода и доказательства алгоритма не было.
Первая книга содержит задачи на вычисление площадей полей, имеющих форму прямоугольника, треугольника, трапеции, круга, сектора, сегмента и кольца. Площади прямоугольника, треугольника и трапеции вычислялись по правилам мало отличающимся от современных, но площади круга и элементов круга вычислялись весьма приближенно, т.к. =3. Также первая книга содержит задачи на различные действия с дробями.
Вторая книга рассматривает задачи на «тройное правило», согласно которому по трем заданным величинам находится четвертая пропорциональная.
В третьей книге мы встречаемся с арифметической прогрессией.
Четвертая книга носит трудно переводимое название- «Шао гуан», по-видимому, это специальный термин, по смыслу означающий уменьшение одной из сторон прямоугольника с соответствующим увеличением другой, причем площадь его остается неизменной. Книга начинается с решения задачи на вычисление одной из сторон прямоугольника, если даны другая его сторона и площадь. Кроме того, книга содержит задачи на извлечение квадратного и кубического корней.
Пятая книга посвящена вычислению объемов параллелепипедов, полных и усеченных пирамид, цилиндров, обелисков и некоторых призматических тел.
В шестой книге встречаются элементы приближенных вычислений, основанные на округлении чисел.
Седьмая книга состоит из задач алгебраического содержания, решаемых с помощью уравнений и их систем.
Восьмая книга содержит задачи на решение определенных и неопределенных систем уравнений. В этой книге приводятся правила действий с отрицательными числами и нулем:
(-а)-(-b)= -(а-b), а-(-b)=а+b, (-а)-b= -(а+b), (-а)+(-b)= -(а+b), а+(-b)=а-b,
(-а)+b= -(а-b), 0+(-b)= -b, 0-(-b)=b, 0+b=b, 0-b= -b.
Девятая книга содержит геометрические задачи, решаемые с помощью теоремы Пифагора и свойств подобных прямоугольных треугольников. Приведем одну из подобных задач.
В середине квадратного озера со стороной 10 футов растет тростник, выходящий из воды на 1 фут. Если нагнуть тростник, вершина достигнет берега. Как глубоко озеро?
Пусть х- глубина озера, тогда (х+1)- длина тростника. Учитывая, что тростник растет в середине квадратного озера со стороной 10 футов, получаем, что расстояние от точки выхода тростника из воды до берега равно 10:2=5 футов. Используя теорему Пифагора получаем уравнение:
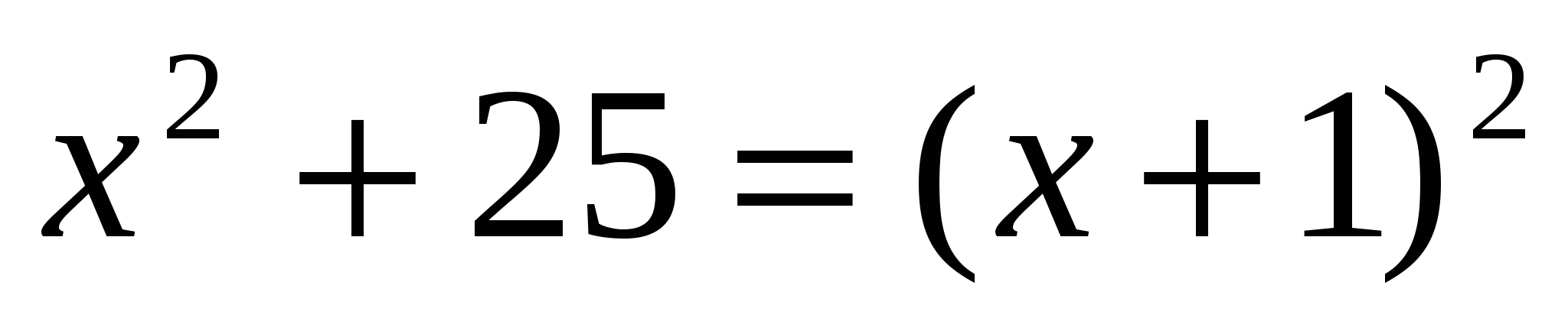 , отсюда
, отсюда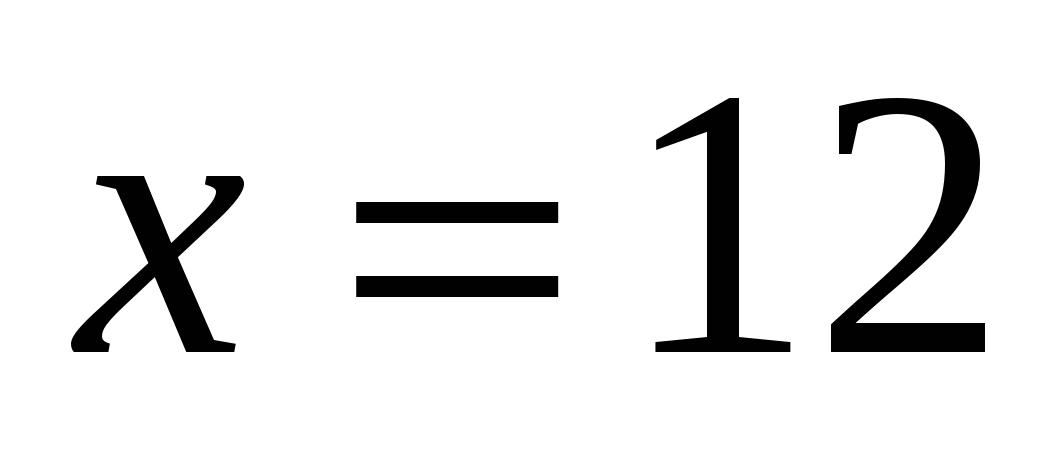 .
.
Итак, глубина озера 12 футов.
Китайские математики 11-14вв. знали свойства биномиальных коэффициентов. Полная таблица биномиальных коэффициентов до восьмой степени встречается у китайского математика Чжу Ци-цзе в 1303г. в его трактате «Зеркало четырех начал». Таблица имела форму:
1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Правило составления данной таблицы было известно задолго до написания трактата, на что указывает сам автор. В Европе она получила широкую известность лишь в 17в. в результате работ Паскаля (почему и носит название треугольника Паскаля).
Необходимо упомянуть еще одно произведение, опубликованное в Китае (1593г.). Это сочинение носит название «Начала искусства вычисления». Важнейшие правила даются в стихотворной форме. Сочинение состоит из 12 книг, много вопросов заимствовано из трактата «Математика в девяти книгах».
Двенадцатая книга этого сочинения посвящена построению магических квадратов. Примером вопросов из этой книги может служить задача Ло-шу: «Заполнить натуральными числами от 1 до 9 квадратную таблицу из девяти клеток так, чтобы суммы чисел по всем строкам, столбцам и диагоналям были равны одному и тому же числу 15».
РЕШЕНИЕ:
-
4
9
2
3
5
7
8
1
6
Приведем еще несколько задач китайских авторов.
Задача Чжан Цю Цзяня (5в.).
Один петух стоит 5 цяней, одна курица стоит 3 цяня, три цыпленка стоят 1 цянь. Всего на 100 цяней купили 100 птиц. Сколько было куплено в отдельности петухов, куриц и цыплят?
РЕШЕНИЕ:
Задачу можно решить двумя способами; либо с помощью системы двух неопределенных уравнений, либо с помощью одного неопределенного уравнения. Пусть К- количество купленных петухов, М- количество куриц, а Н- количество цыплят. Тогда получаем систему уравнений:
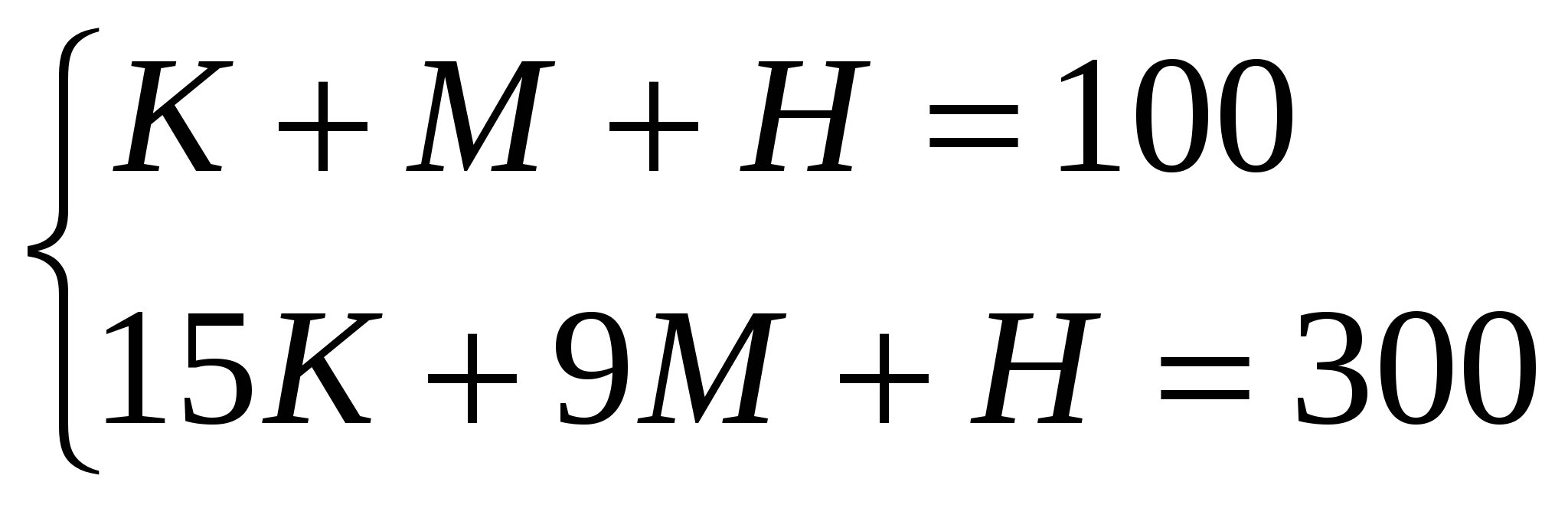
С другой стороны. Пусть х- количество купленных петухов, а у- количество куриц. Тогда количество цыплят 100-х-у. Получаем уравнение:
15х+9у+(100-х-у)=300.
После упрощения получаем уравнение:
7х+4у=100.
Теперь учитывая, что 100 делится на 4 и 4у делится на 4, делаем вывод, что и 7х делится на 4. Тогда сделаем замену х=4к, получаем уравнение 28к+4у=100. Разделив обе части уравнения на 4, имеем
7к+у=25.
Теперь методом подбора решаем это уравнение. Получаем следующую таблицу:
к
0
1
2
3
х
0
4
8
12
у
25
18
11
4
100-х-у
75
78
81
84
Все четыре решения не противоречат условию задачи. Итак были куплены:
-
25 куриц и 75 цыплят;
-
4 петуха, 18 куриц и 78 цыплят;
-
8 петухов, 11 куриц и 81 цыпленок;
-
12 петухов, 4 курицы и 84 цыпленка.
Вообще же подобные задачи были весьма любимы во многих странах мира, далеко за пределами Китая.
Хорошо известна такая задача: «Фазаны и кролики. В клетке 35 голов и 94 ноги. Требуется узнать число фазанов и кроликов в клетке». Эта задача была обнаружена в трактате «Девять отделов искусства счета», подобные ей до сих пор решаются нашими школьниками.
РЕШЕНИЕ:
Пусть х- число кроликов, а у- число фазанов. Тогда имеем систему двух уравнений:
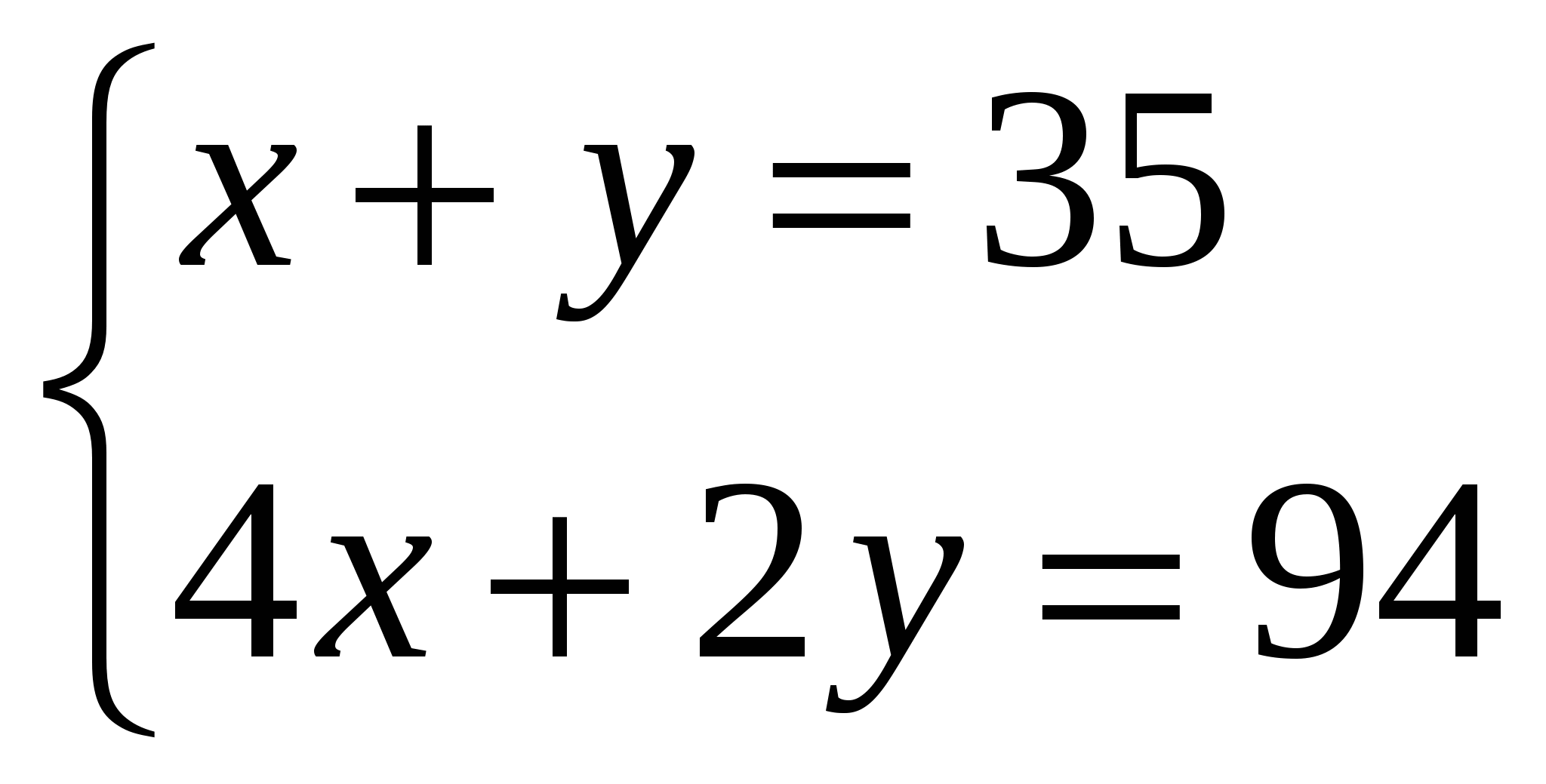 .
.
Решая эту систему, получаем, что в клетке было 12 кроликов и 23 фазана. Легко эту задачу решить с помощью одного уравнения, представив число фазанов как 35-х: 4х+2(35-х)=94.
Приведем еще одну весьма распространенную задачу, появившуюся в 1в н.э.
«Сообща покупают вещь. Если каждый человек внесет по 8, то избыток равен 3. Если каждый человек внесет по 7, то недостаток равен 4. Каково количество человек и какова цена вещи?»
Составив для решения этой задачи систему, и решив ее узнаем, что было 7 человек, а вещь стоила 53.
Начиная с 5 в. центр математической культуры сместился на восток- к индусам и арабам, куда эллинистическое влияние дошло еще во времена Александра Македонского.
Существенное отличие математики индусов от математики греков состоит в том, что она числовая. Строгие доказательства греков индусы заменили наглядностью.
Подобно тому, как эллины считали, что бог геометризует, индийцы считали, что Будда арифметизует. Он будто бы победил женихов своей невесты, определив, сколько атомов уложится на длине одной мили.
Основные достижения индусов в математике следующие: они ввели в обращение цифры, называемые нами арабскими, и позиционную систему записи чисел, отрицательные числа. Обнаружили двойственность корней квадратного уравнения, двузначность квадратного корня. По поводу позиционной системы Лаплас писал: «Мысль выражать все числа десятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за своей простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этому методу, мы видим на примере великих гениев греческой учености Архимеда и Аполлония, от которых эта мысль оказалась скрытой.»
Индусы рассматривали числа и оперировали ими, не прибегая к геометрическому толкованию. При решении задач греки поступали так, чтобы в результате получались положительные числа, если этого не происходило, то менялось условие задачи. Индусы в аналогичных ситуациях либо отбрасывали отрицательные решения, либо истолковывали их как долг. Отсюда был сделан естественный шаг к установлению правил действий над величинами при любом выборе знаков и к установлению двузначности квадратного корня и существованию двух корней квадратного уравнения. Правила действий с именованными величинами впервые ввел Брахмагупта (ок. 598-660). Эти правила выражались словами. В отличии от китайцев математики Индии установили правила для деления и умножения отрицательных чисел.
Но вернемся к самым истокам. Есть основания предполагать, что система счета была изобретена в 1в. н. э., а знак нуля- «сунья» (ничто), стал использоваться во 2в., современный вид индийские цифры приняли в 16в.
Интересны также и арифметические действия индусов. Например, необходимо сложить 3759, 2720 и 1230:
-
7
6 6 0 9
3 7 5 9
2 7 2 0
1 2 3 0
результат 7709.
Индийцы складывали многозначные числа слева направо, «стирая» без труда в числе, написанном в качестве суммы левой колонны, цифру, если нужно было ее увеличить. Сложение слева направо рекомендовалось не раз и в европейской математике (Гаусс). Академик А.Н. Крылов указывает, что профессиональные вычислители всегда складывали числа по два и слева направо: такой способ гарантирует более скорый и более верный путь получения результата.
Результат сложения в Индии писали не под колонками слагаемых, а над ними- прием, который встречается у греков и римлян. Индийский способ сложения усвоил Мухаммед ал-Хорезми в начале IX в. и передал его арабам и через них Европе.
Сакробоско (середина XIII в.), профессор математики и астрономии в Париже, внедряет в Европе через свое руководство правило складывать числа справа налево. С XV в. правила сложения не отличаются уже от современных.
Вычесть 15871 из 34725:
1 8 8
-
9 9 5 4
3 4 7 2 5
1 5 8 7 1
результат 18854.
При выполнении действия вычитания применялись в разные времена два приема: 1) отсчитывание от уменьшаемого единиц вычитаемого, 2) прибавление к вычитаемому такого числа, чтобы в сумме получилось уменьшаемое. Второй прием получил в новое время название австрийского способа.
Первый способ ведет свое начало из Индии, где он выполнялся слева направо, что было практически нетрудно при легкости «стирания» подлежащей изменению цифры при индийском способе письма на посыпанных песком дощечках. При выполнении действия вычитания не на дощечке с песком пришлось ввести неудобный способ перечеркивания и надписывания цифр.
Приведем еще два примера умножения, например, так в 7в. производил умножение Брахмагупта: умножить 325 на 37
-
325
30
9750
325
7
2275
12025
А так производил умножение Бхаскара в 12в.
3 2 5
1
2
4
1
5
3
9
0
6
0
5
17
3
1 2 0
5
2
Здесь приведен пример умножения числа 325 на число 37. При умножении 3 на 7, получается 21. В первой ячейке и записано это число: десятки под чертой и единицы над чертой. Эти действия производятся со всеми цифрами. Цифры произведения получают сложением чисел по наклонным полоскам решетки. Крайняя верхняя полоска дает 5 следующая 12, учитывая это, в следующей полоске получаем 10. В предпоследней будет 12, и в крайней нижней- 1. Результатом умножения будет число 12025.
При решении задач использовалось правило обращения. Суть этого правила состоит в следующем; если нужно найти число, которое после ряда арифметических операций принимает некоторое известное значение, то с этим известным значением проделываются все противоположные операции в обратном порядке. Таким методом решается задача Бхаскары, но при этом метод решения называется методом инверсии. «Прекрасная дева с блестящими очами, ты, которая знаешь как правильно применять метод инверсии, скажи мне величину такого числа, которое будучи умножено на 3, затем увеличено на три четверти числа после умножения, разделено на 7, уменьшено на треть частного, умножено само на себя, уменьшено на 52, после извлечения квадратного корня, прибавления 8 и деления на 10, дает число 2.»
РЕШЕНИЕ:
-
Умножим число 2 на 10, получаем 20.
-
Из 20 вычтем 8, в результате имеем 12.
-
12 возведем в квадрат, получим 144.
-
К 144 прибавим 52, результат равен 196.
-
Извлекая квадратный корень из 196, получаем 14.
-
14 умножаем на 1,5- результат 21.
-
21 умножим на 7, получим 147.
-
147 умножим на четыре седьмых, в результате имеем 84.
-
84 делим на 3 и получаем искомое число 28.
Бхаскара привел отрывок из недошедшего до нас сочинения Шридхары (9-10вв.), содержащий способ решения полного квадратного уравнения: «Умножь обе стороны уравнения на учетверенный коэффициент при квадрате неизвестного, а затем прибавь к обоим частям квадрат первоначального коэффициента при неизвестном в первой степени, затем извлеки из обоих частей квадратный корень.» Это совпадает с тем способом, которым получают решение квадратного уравнения в школе.
Бхаскара изучал уравнения и более высоких степеней, к которым можно применить искусственные приемы решения. Примером тому может служить следующая задача: «Назови, о знающий, число, которое, будучи умножено на 12 и увеличено на куб самого себя, равно сумме квадрата этого числа, умноженного на 6 и 35». Эта задача приводит к кубическому уравнению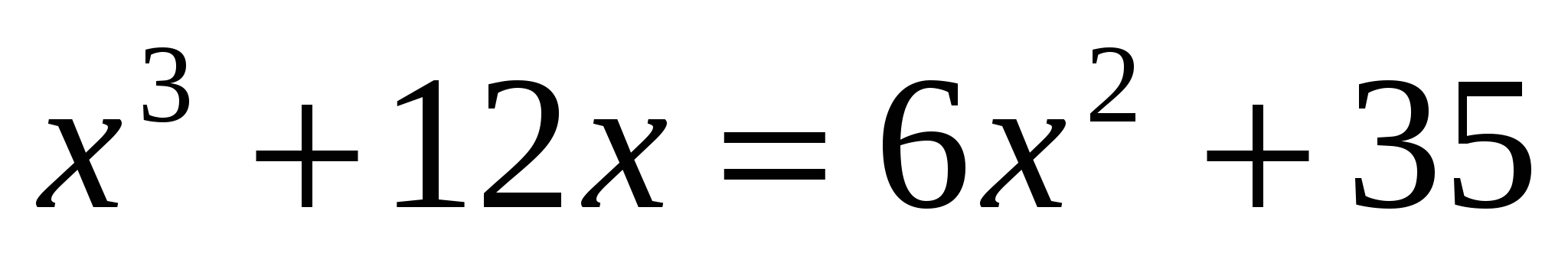 . Если из обеих частей вычесть 8 и переместить
. Если из обеих частей вычесть 8 и переместить 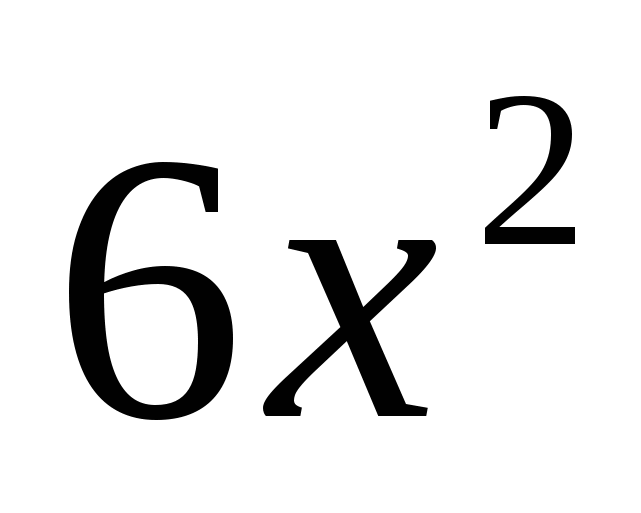 в левую часть, то получим полные кубы
в левую часть, то получим полные кубы 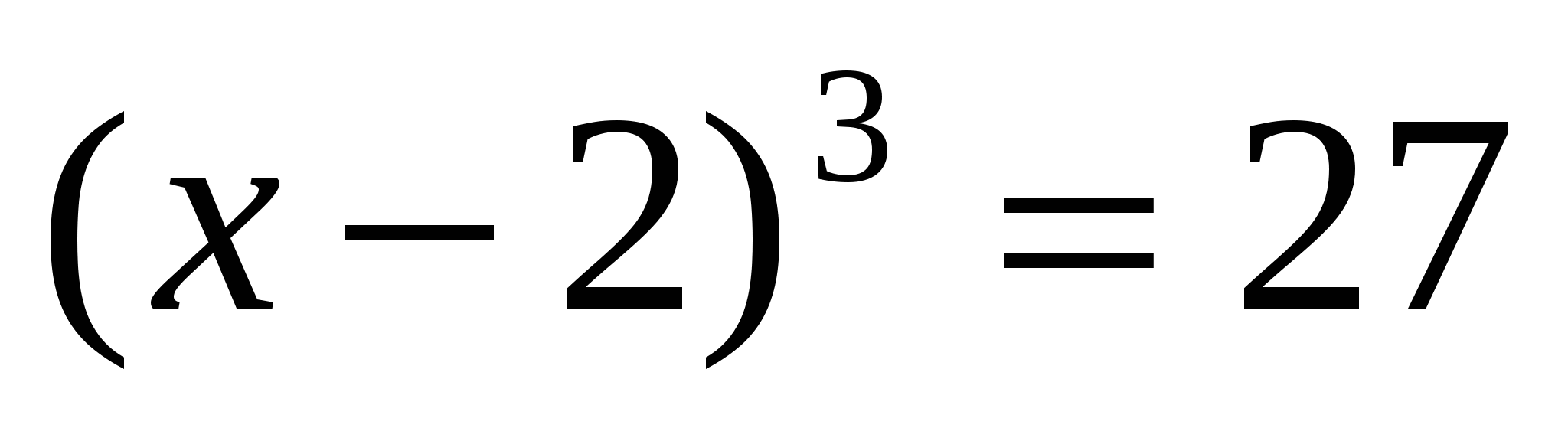 , отсюда х=5. Весьма схожим образом решается задача того же автора. «Если из четвертой степени числа вычесть удвоенную сумму квадрата числа и числа, умноженного на 200, то получим десять тысяч без единицы. Найти это число». Эта задача приводит к уравнениб четвертой степени:
, отсюда х=5. Весьма схожим образом решается задача того же автора. «Если из четвертой степени числа вычесть удвоенную сумму квадрата числа и числа, умноженного на 200, то получим десять тысяч без единицы. Найти это число». Эта задача приводит к уравнениб четвертой степени:
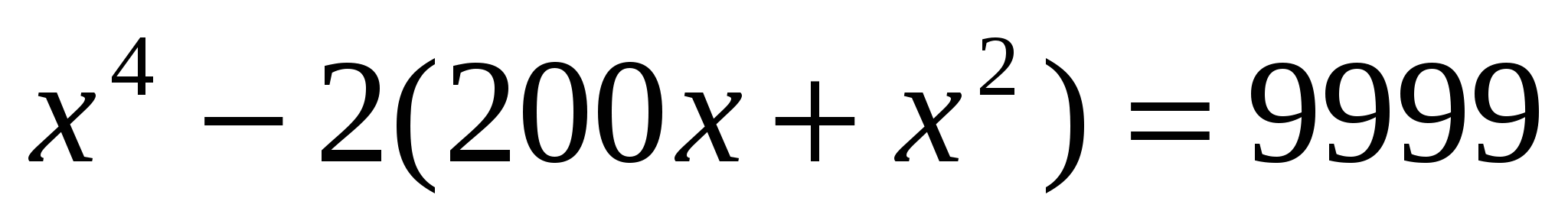 .
.
Прибавив к обеим частям уравнения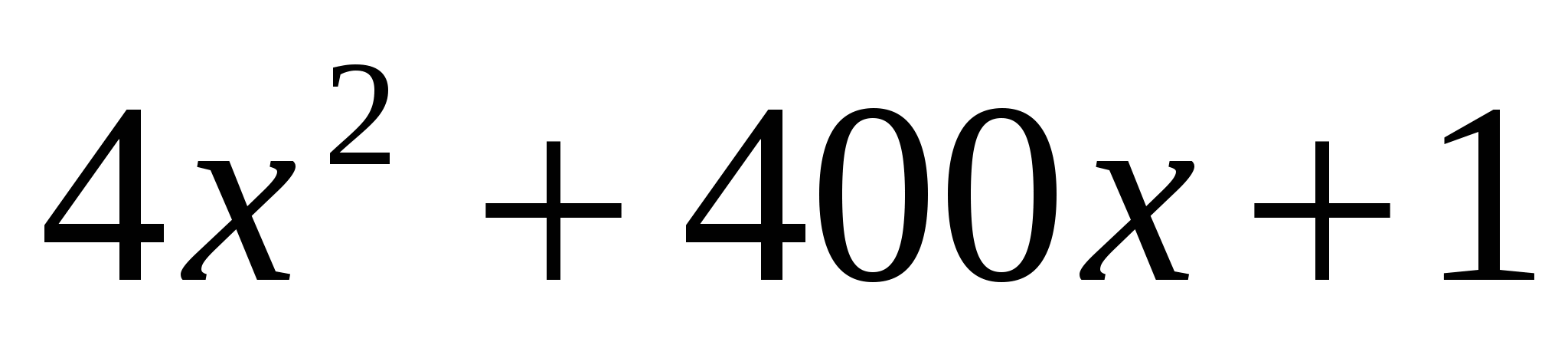 , получим
, получим 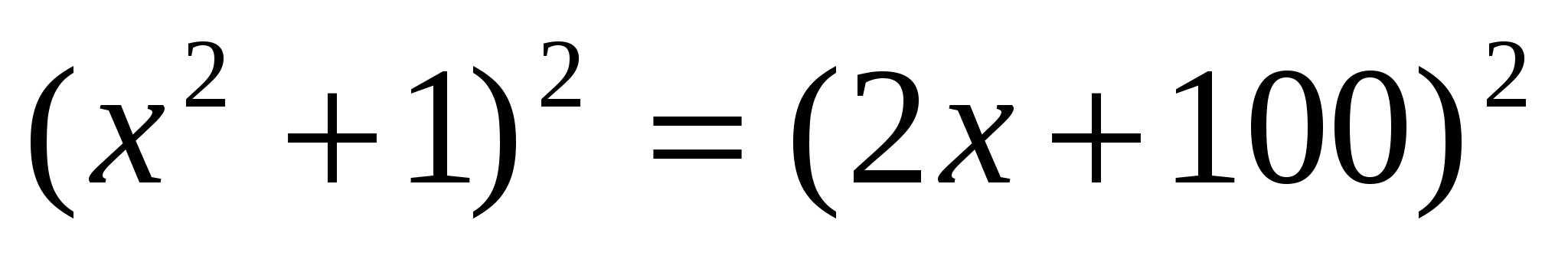 , отсюда х=11. Итак, искомое число 11.
, отсюда х=11. Итак, искомое число 11.
У индусов мы также встречаем действия с иррациональными числами, например, Бхаскара доказал следующие тождества:
1) 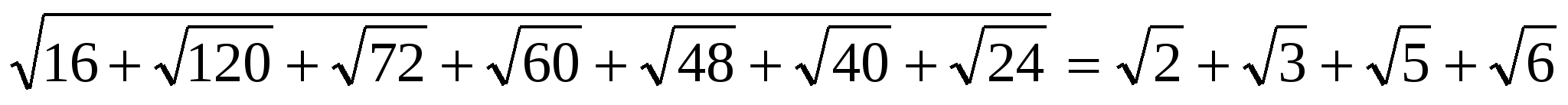 ,
,
2) 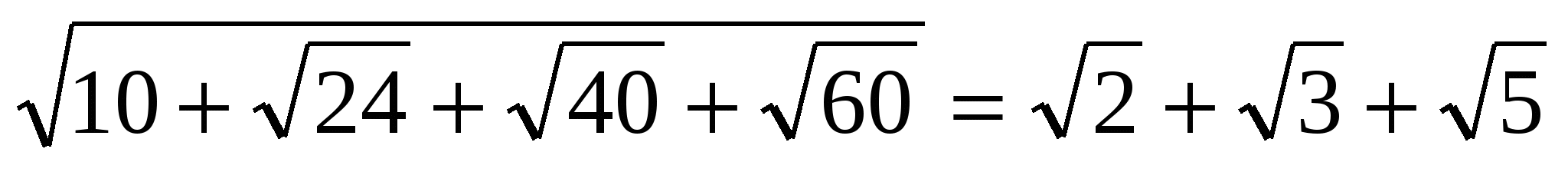
Вероятно, доказательство сводилось к следующему
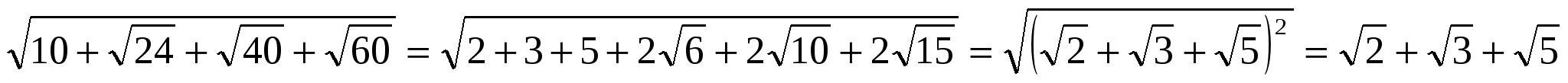
Аналогично и в первом случае.
Приведем задачу из Бахшалийской рукописи: «Найти число, которое от прибавления 5 или отнятия 11 обращается в полный квадрат».
РЕШЕНИЕ:
Пусть Х- искомое число, тогда условие задачи можно записать с помощью системы уравнений:
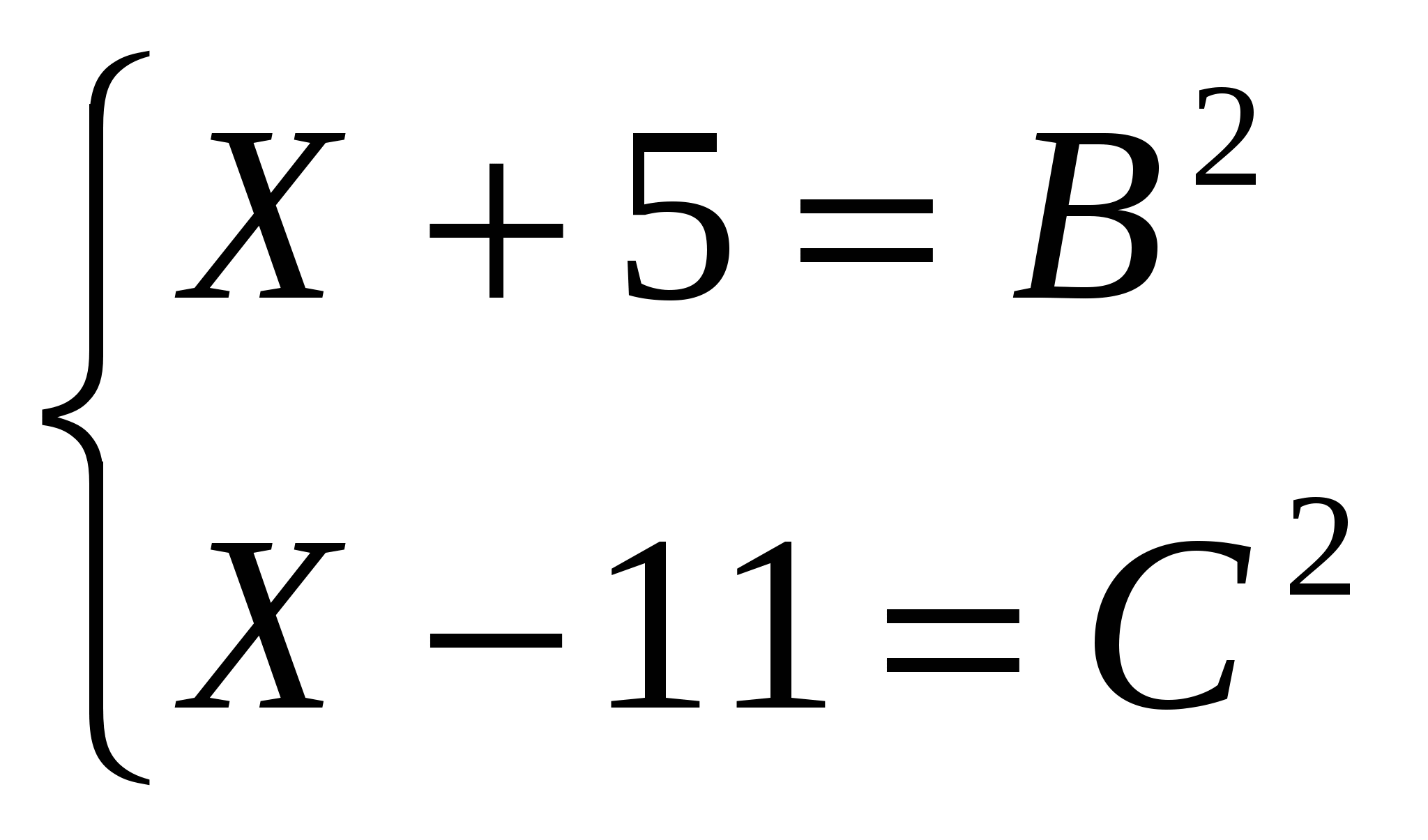
Вычитая из первого уравнения второе, получаем
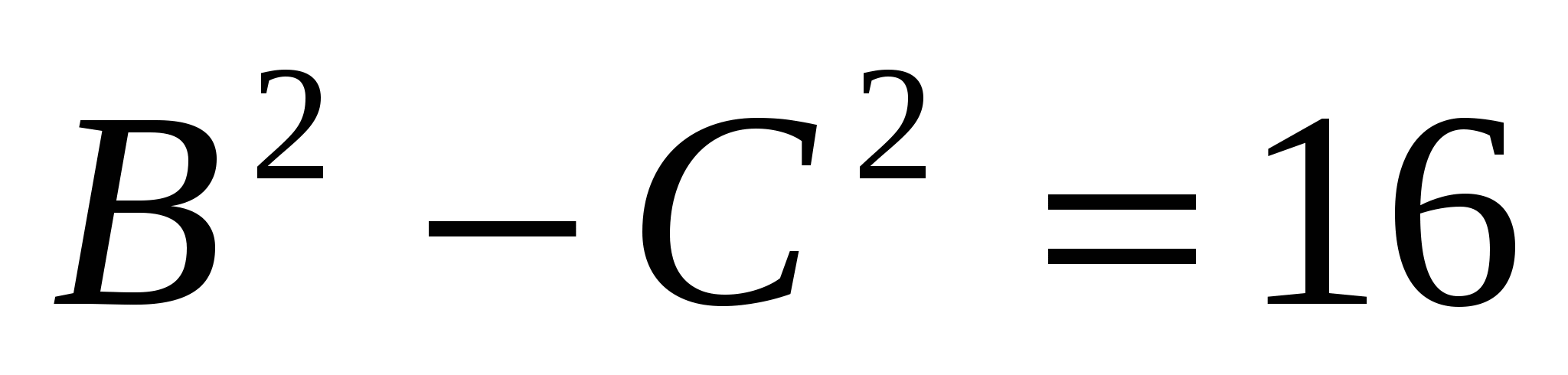 или
или 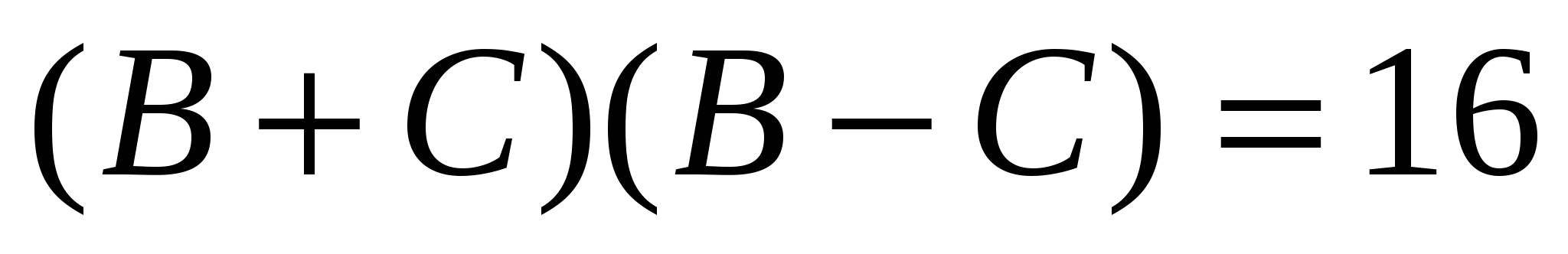
Учитывая разложение на множители числа16 и то, что оба множителя различны получаем системы уравнений:
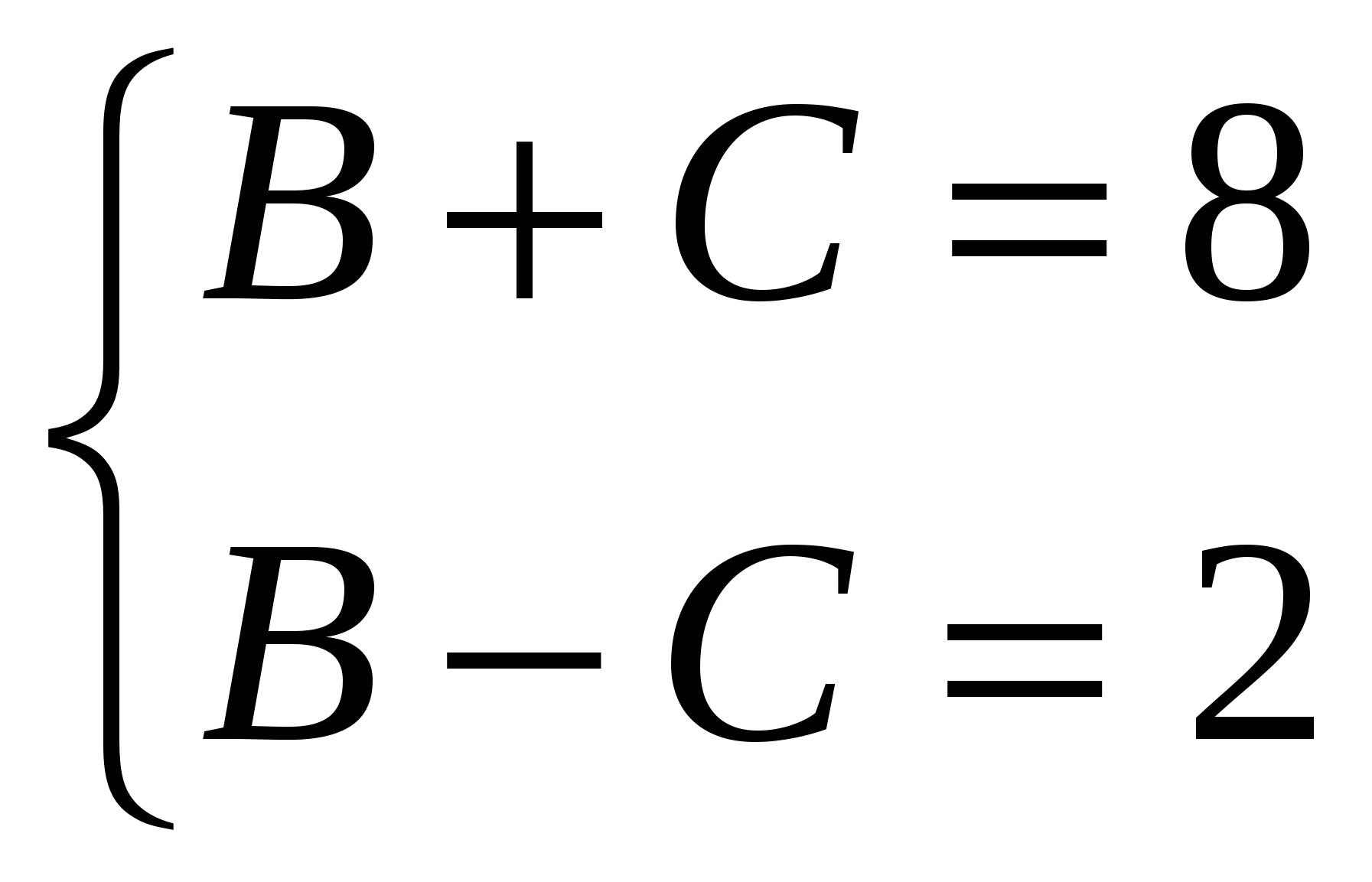 и
и 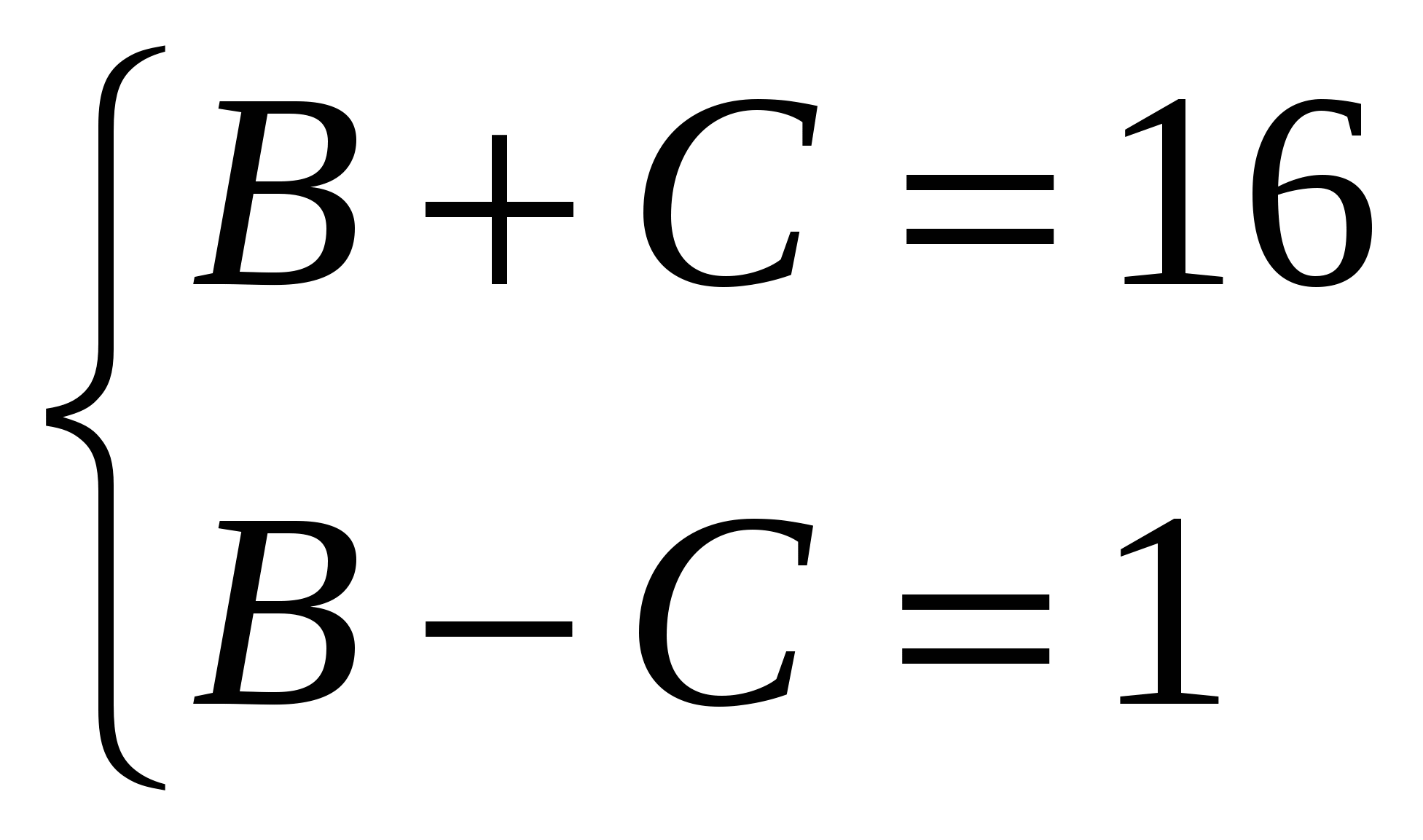
Получаем два числа удовлетворяющих условию задачи, а именно 20 и 67,25.
Индийская математика оказала влияние на математиков стран Ближнего, Среднего Востока и Средней Азии. При посредничестве ученых стран ислама достижения индийских математиков стали известны в Западной Европе и вошли составной частью в сокровищницу мировой науки.
ЛИТЕРАТУРА:
-
Баврин И.И., Фрибус Е.А. «Старинные задачи»-М. «Просвещение»,1994г.
-
Березкина Э.И. «Математика древнего Китая»- М. «Наука», 1980г.
-
Володарский А.И. «Очерки истории средневековой индийской математики»- М. «Наука», 1977г.
-
Депман И.Я. «История арифметики»- М. «Просвещение», 1965г.
-
Никифоровский В.А. «В мире уравнений»- М. «Наука»,1987г.
-
Попов Г.Н. «Исторические задачи по элементарной математике»- М.-Л. ГТТИ, 1932г.
-
Чистяков В.Д. «Материалы по истории математики в Китае и Индии»- М. УЧПЕДГИЗ, 1960г.
-
Шевкин А.В. «Текстовые задачи»- М. «Просвещение», 1997г.


