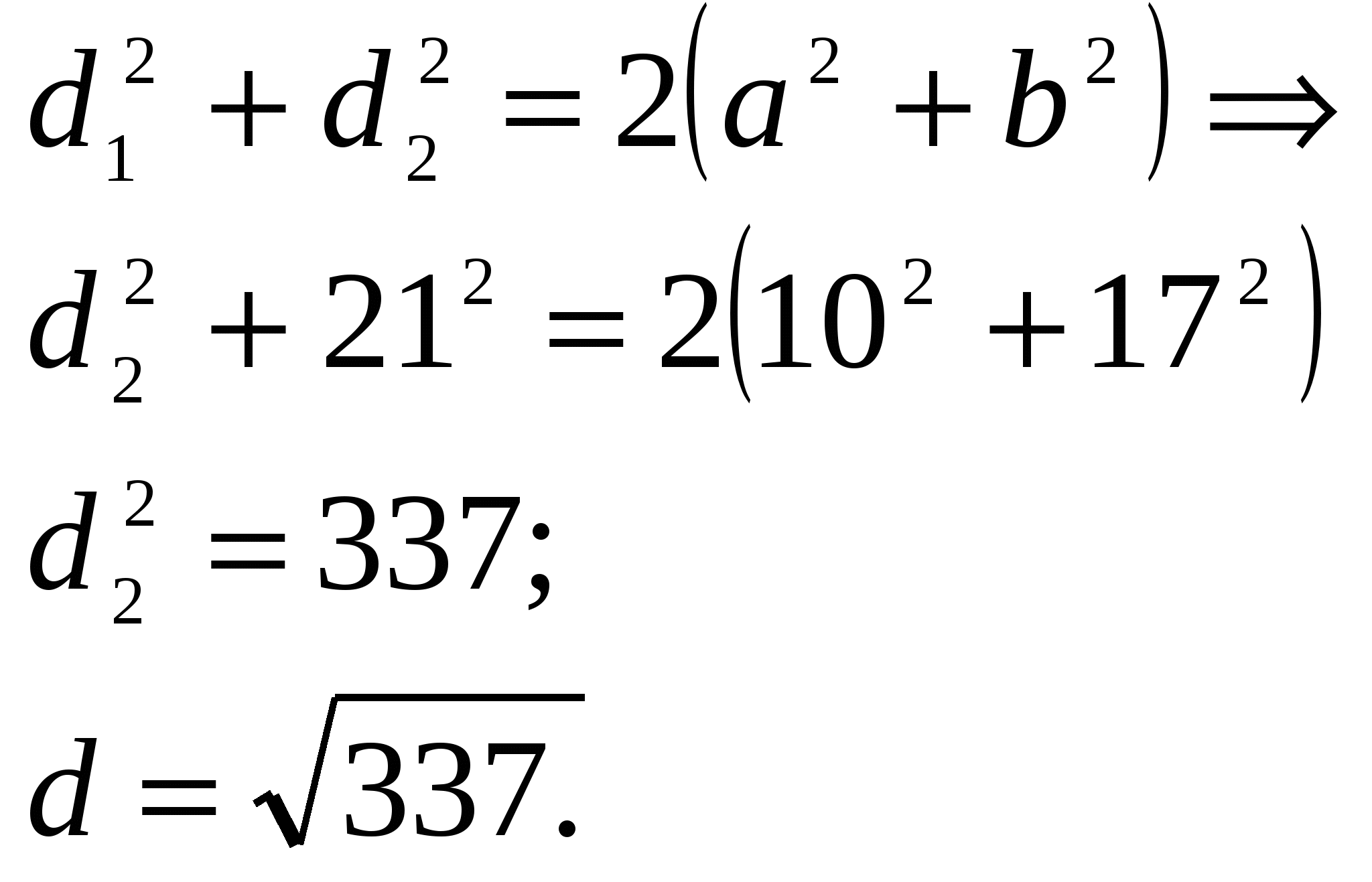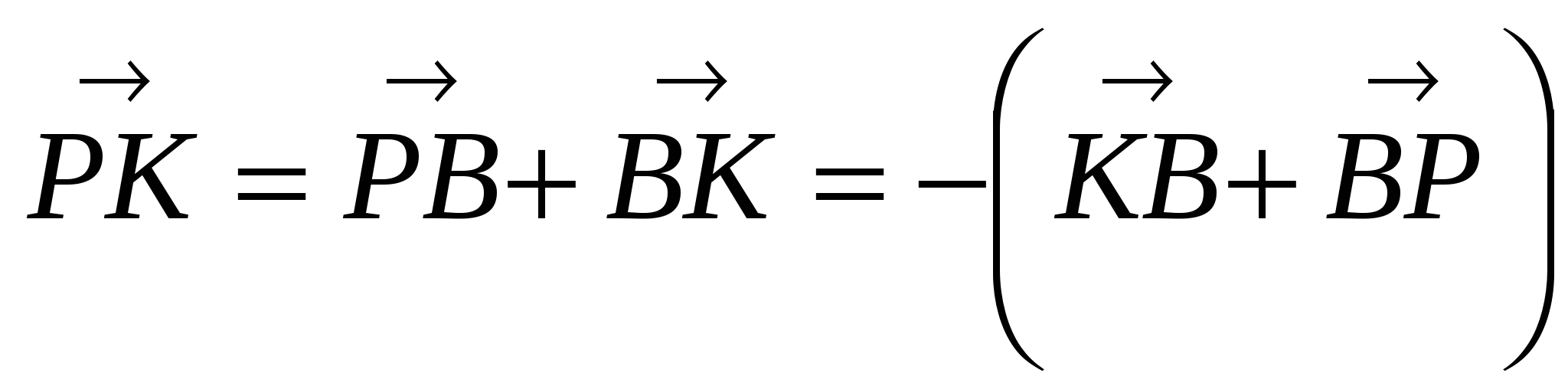- Преподавателю
- Математика
- Методы решения геометрических задач
Методы решения геометрических задач
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Радионова Е.А. |
| Дата | 04.11.2015 |
| Формат | doc |
| Изображения | Есть |
ОГЛАВЛЕНИЕ
1.1. Алгебраический метод5Вводные замечания
4
I. Общие методы решения геометрических задач5
1.2. Векторный метод
8
1.3. Координатный метод
17
1.4. Векторно-координатный метод
22
1.5. Метод геометрических преобразований
27
II. Решение задач различными методами
31
III. Задачи для самостоятельного решения
41
3.1. Векторный метод
41
3.2. Координатный метод
43
3.3. Векторно-координатный метод
44
3.4. Метод геометрических преобразований
46
Библиография
49
Приложение
50
Вводные замечания
Решение задач по геометрии имеет большое общеобразовательное и воспитательное значение, является важным средством развития логического мышления, строгости суждений и математической культуры. Говоря о методах решения геометрических задач, следует отметить их специфические особенности: большое разнообразие, взаимозаменяемость, трудность формального описания, отсутствие четких границ области применения, комбинирование нескольких методов и приемов. В процессе их решения обычно используются три основных метода:
-
геометрический (требуемое утверждение выводится с помощью логических утверждений из ряда геометрических теорем);
-
алгебраический (доказательство утверждения или необходимые искомые величины получаются прямым счетом на основании различных зависимостей между геометрическими величинами или с помощью составления уравнений, систем уравнений);
-
комбинированный (на некоторых этапах решение ведется геометрическим методом, на других - алгебраическим).
Подробная классификация методов решения геометрических задач представлена схемой (Приложение). Содержание работы строится на основании этой схемы.
При составлении рекомендаций были использованы задачи из разных книг, журналов, пособий.
Данная работа окажет существенную методическую помощь для организации занятий по элементарной математике студентов ФМФ. Она является справочной базой для уже используемых в учебном процессе методических рекомендаций по решению планиметрических и стереометрических задач [5, 6].
I. Общие методы решения
ГЕОМЕТРических задач
1.1. Алгебраический метод
Говоря об алгебраическом методе решения геометрических задач, выделим две его разновидности:
а) метод поэтапного решения;
б) метод составления уравнений, систем уравнений.
Сущность поэтапного решения состоит в следующем. Величины, заданные в условии задачи и те, которые нужно найти, связываются цепочкой промежуточных величин, каждая из которых последовательно определяется через предыдущие.
Наиболее распространённым путём получения уравнения является выражение какой-либо величины двумя независимыми способами. Такую величину называют опорным элементом, а алгебраический метод - методом опорного элемента. В качестве опорного элемента могут быть использованы длина отрезка (или квадрат длины отрезка, или сумма отрезков), площадь фигуры, объём фигуры. Если опорным элементом является площадь, то говорят, что применяется метод площадей.
Метод опорного элемента
Задача 1 (метод площадей). Доказать свойство биссектрисы внутреннего угла треугольника.
Д ано: ∆АВС,
ано: ∆АВС,
BD - биссектриса.
Доказать: 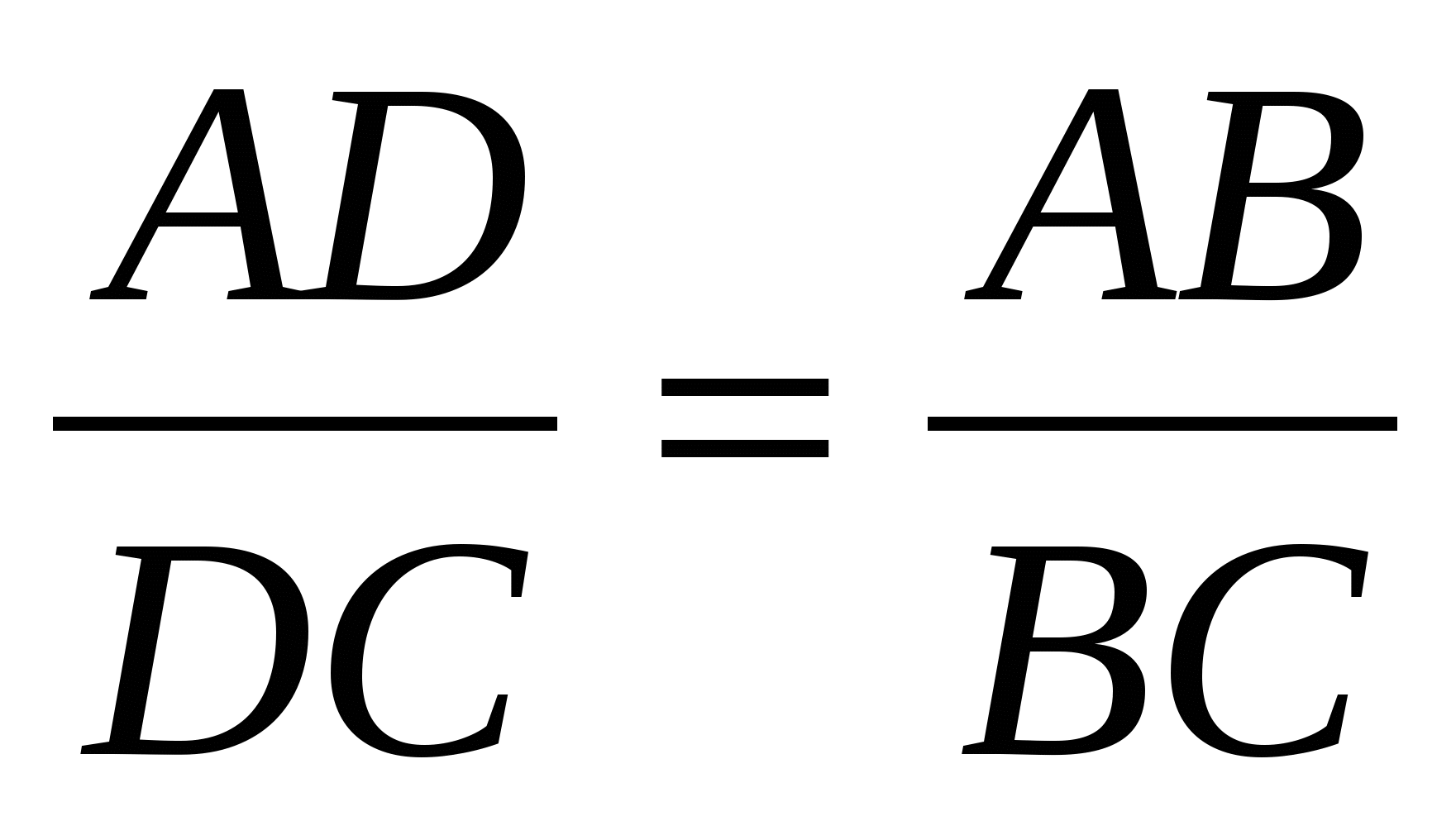 .
.
Доказательство: 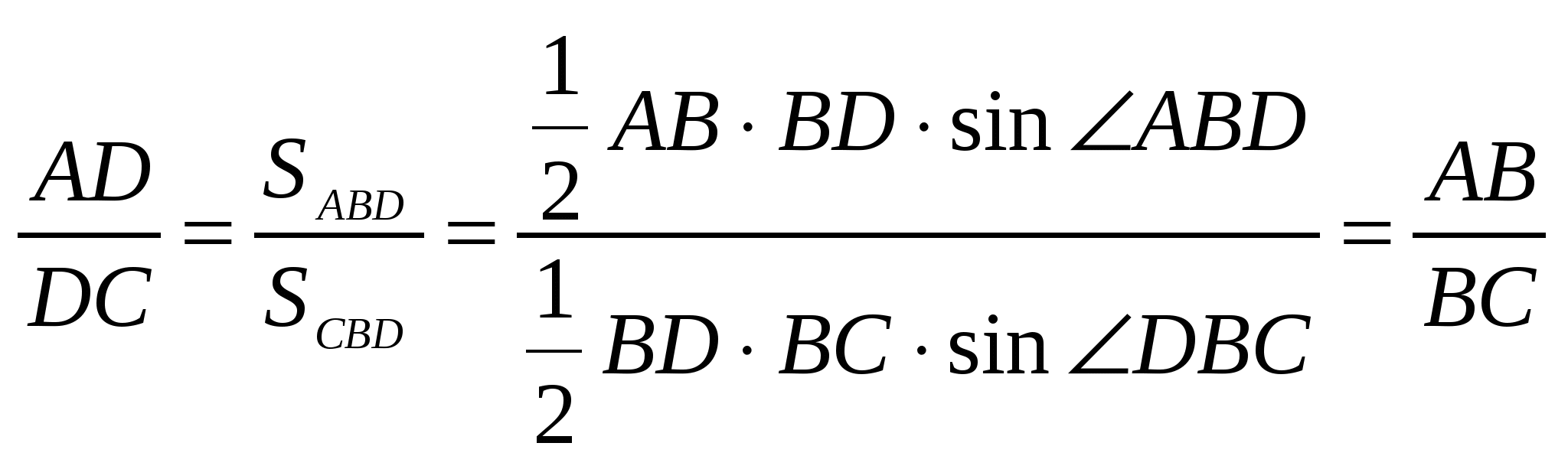
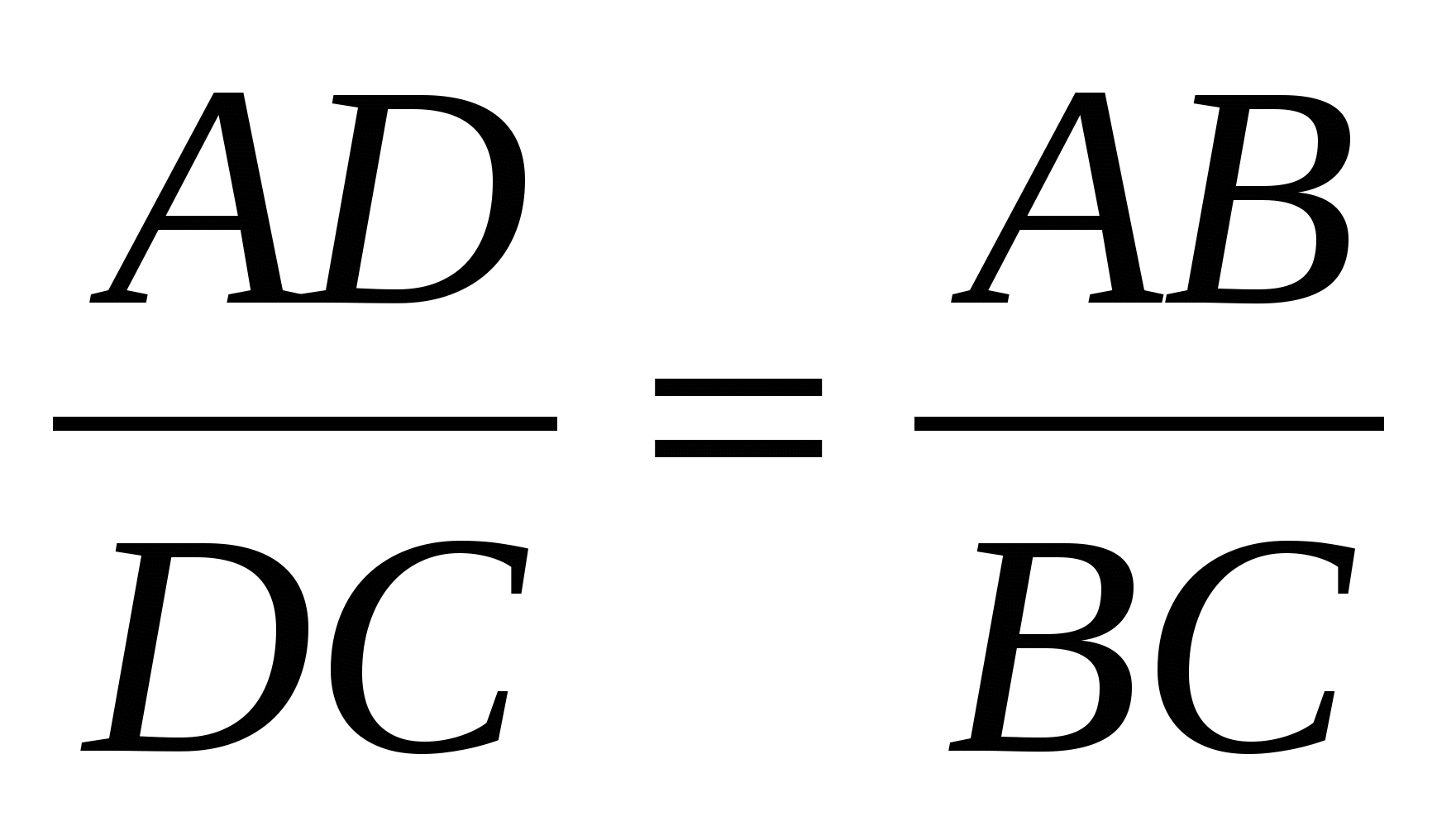 .
.
З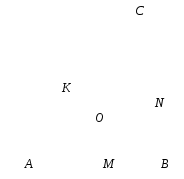 адача 2 (метод площадей).
адача 2 (метод площадей).
Около окружности радиуса 5 описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки 12 и 7,5.
АМ = 12; МВ = 7,5;
ОK = ОМ = ON = r = 5.
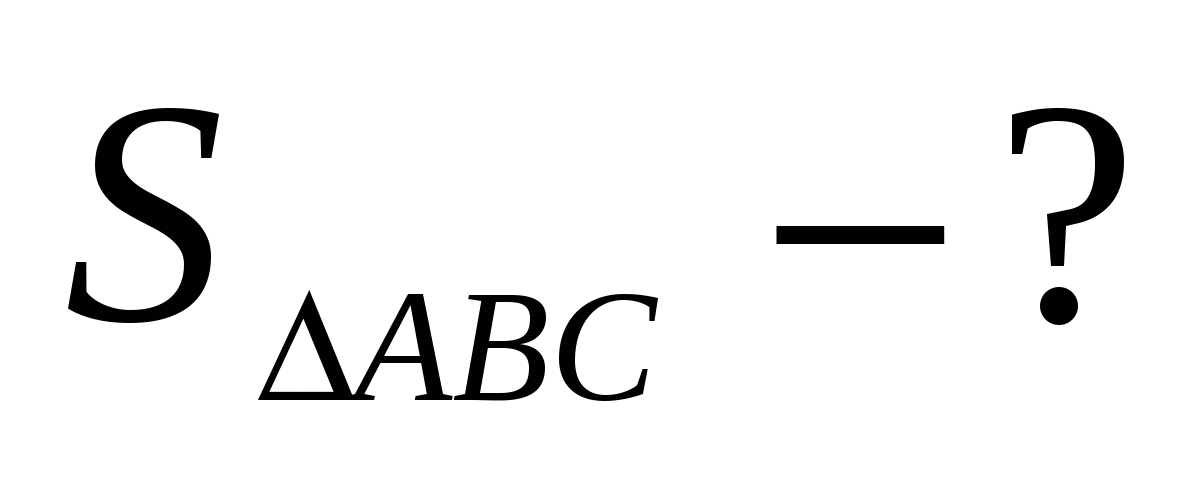
Схема решения:
-
АМ = АK = 12; МВ = NB = 7,5; CK = CN = x.
-
р = 12 + 7,5 + x = 19,5 + x - полупериметр ∆АВС.
-
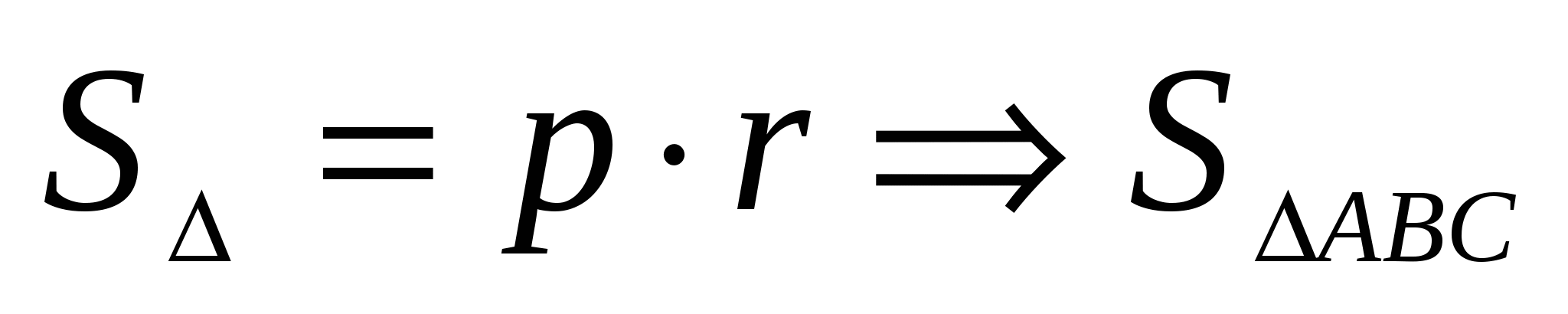 = (19,5 + x)ּ5.
= (19,5 + x)ּ5. -
∆MOB:
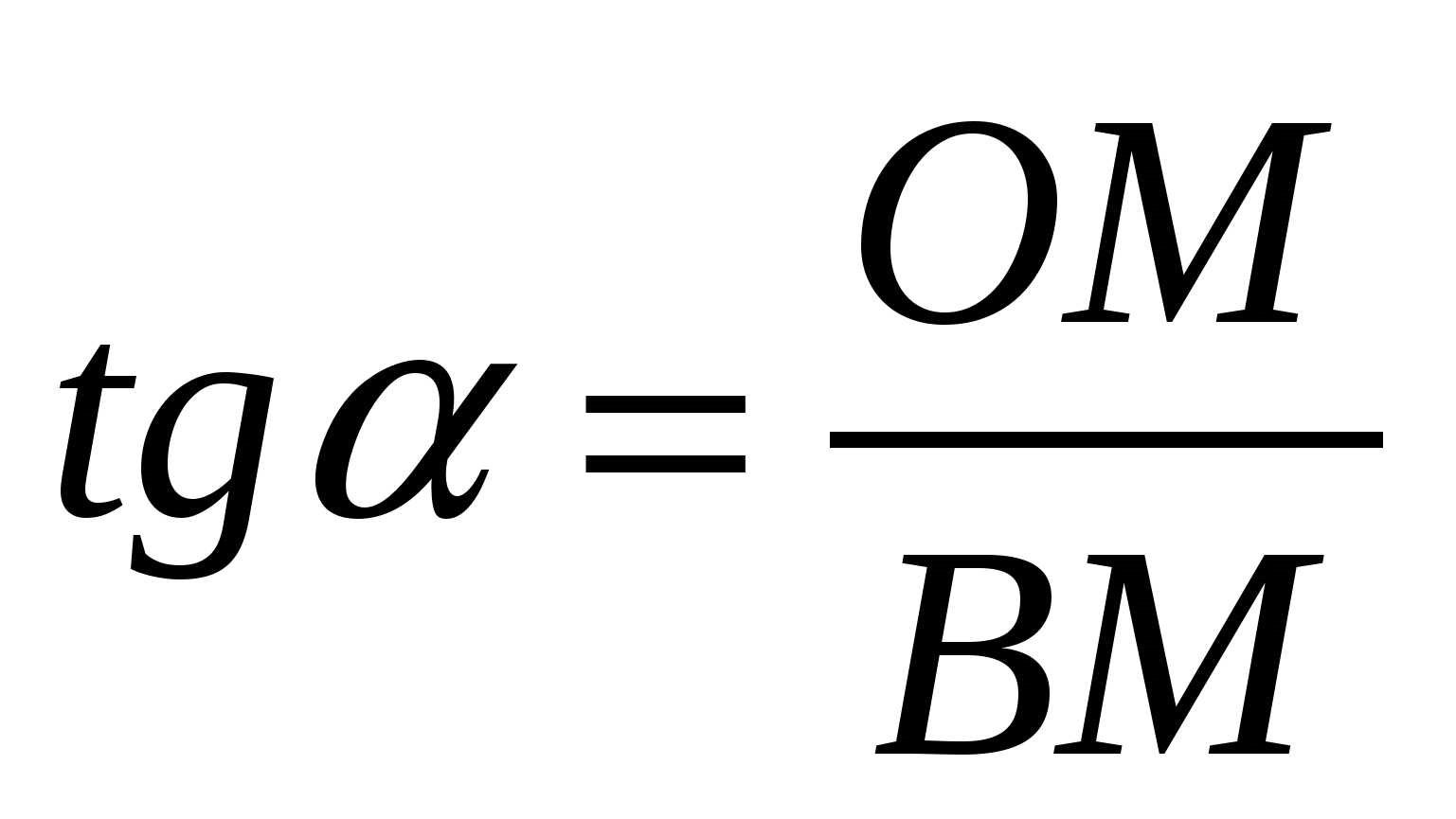
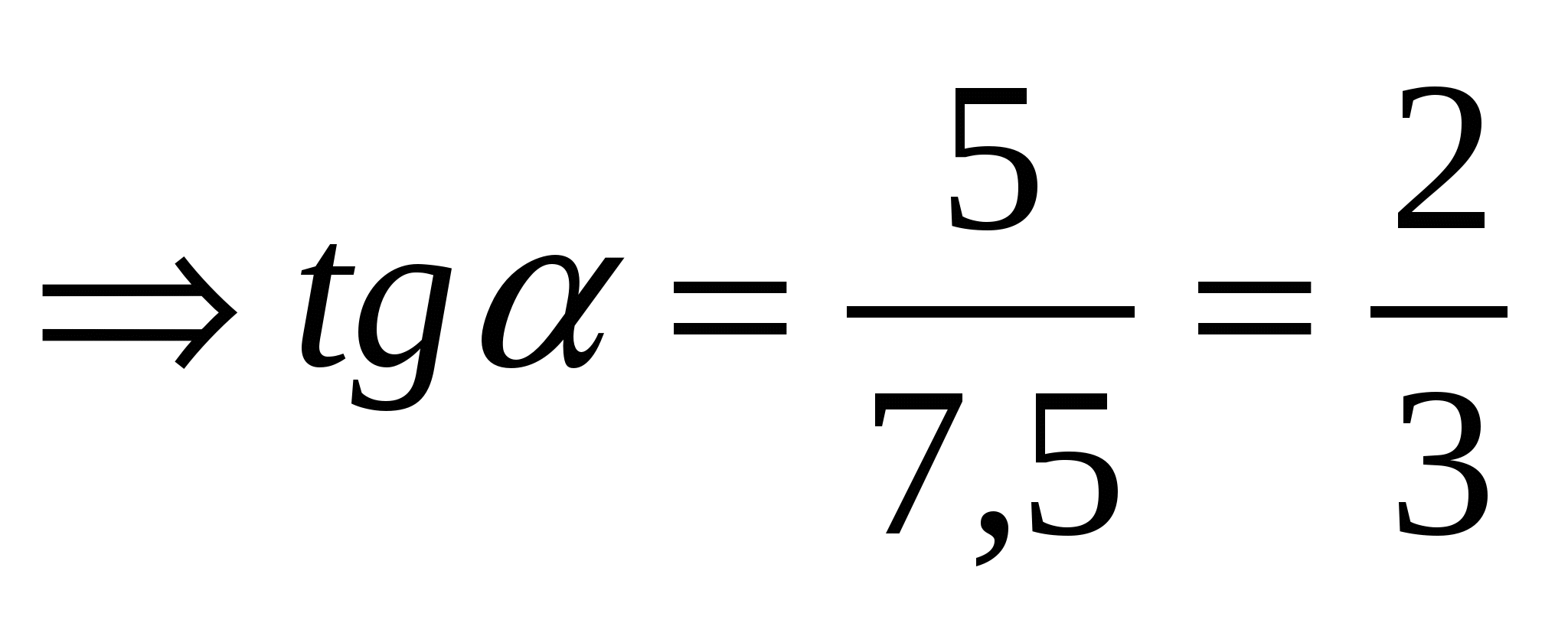 .
. -
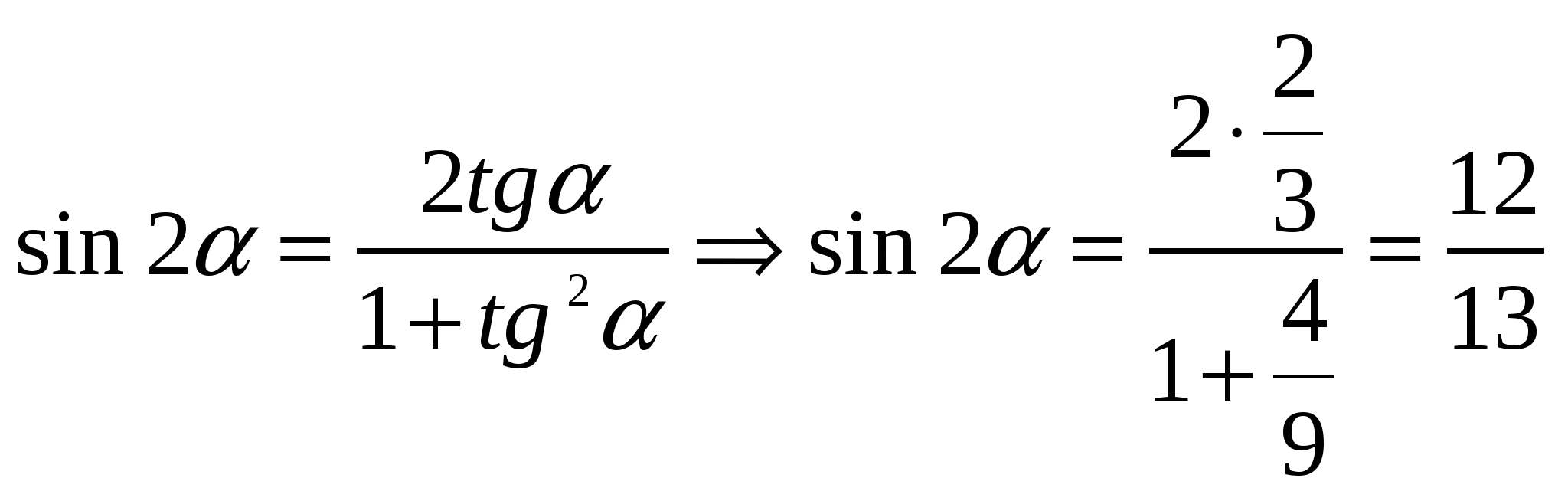 .
. -
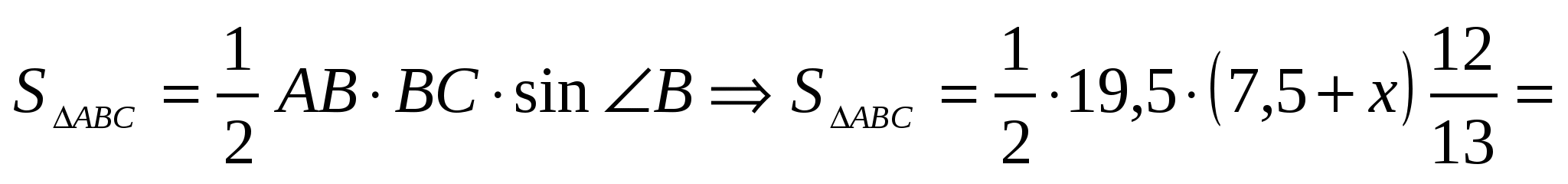
=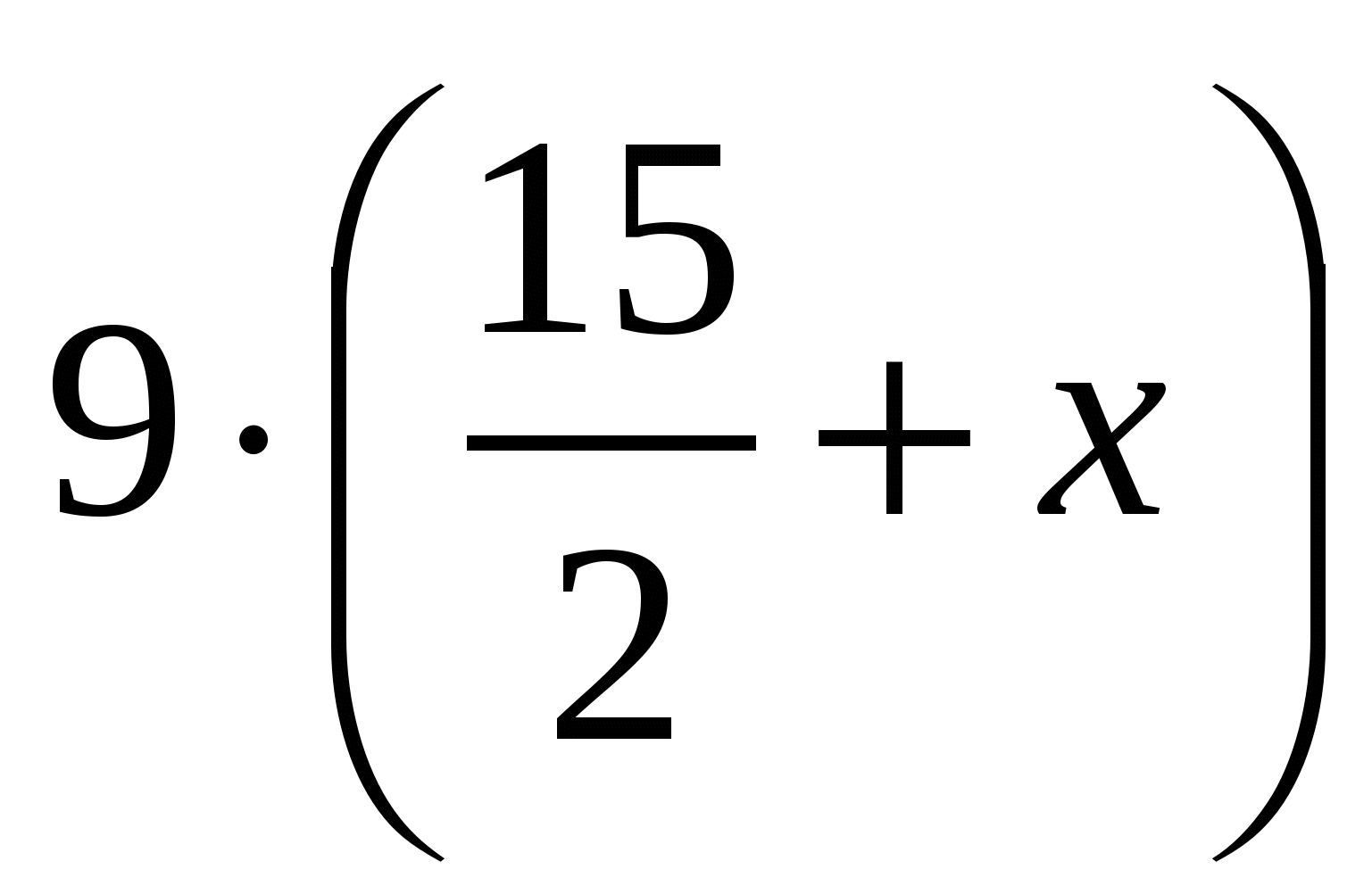
-
Из 3) и 6) получаем уравнение
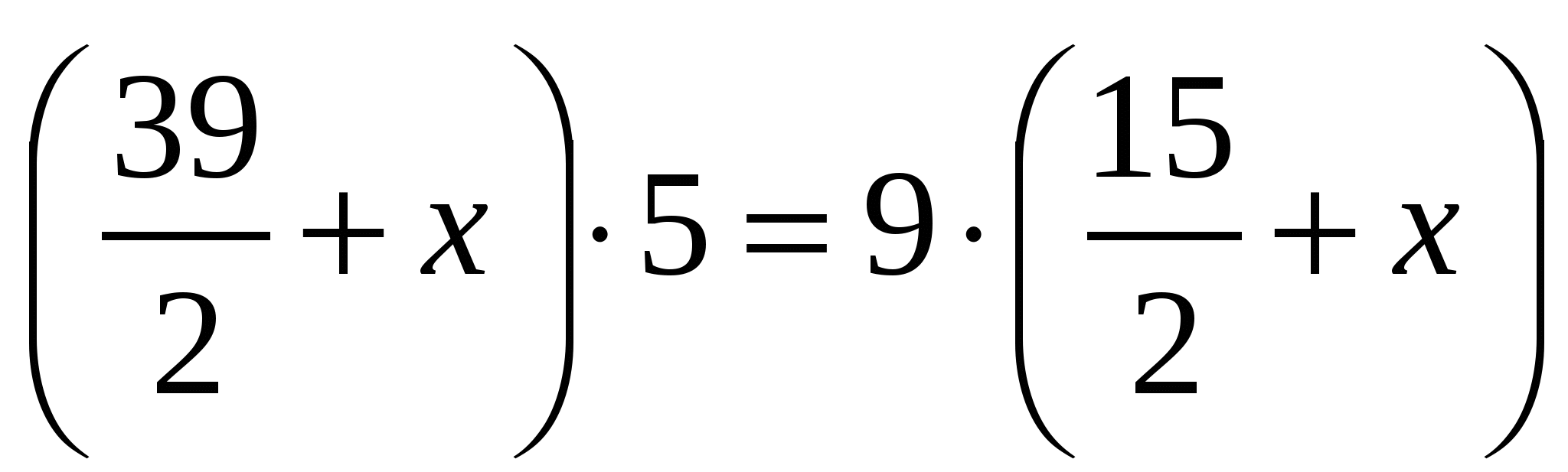 .
.
Решая его, получим: 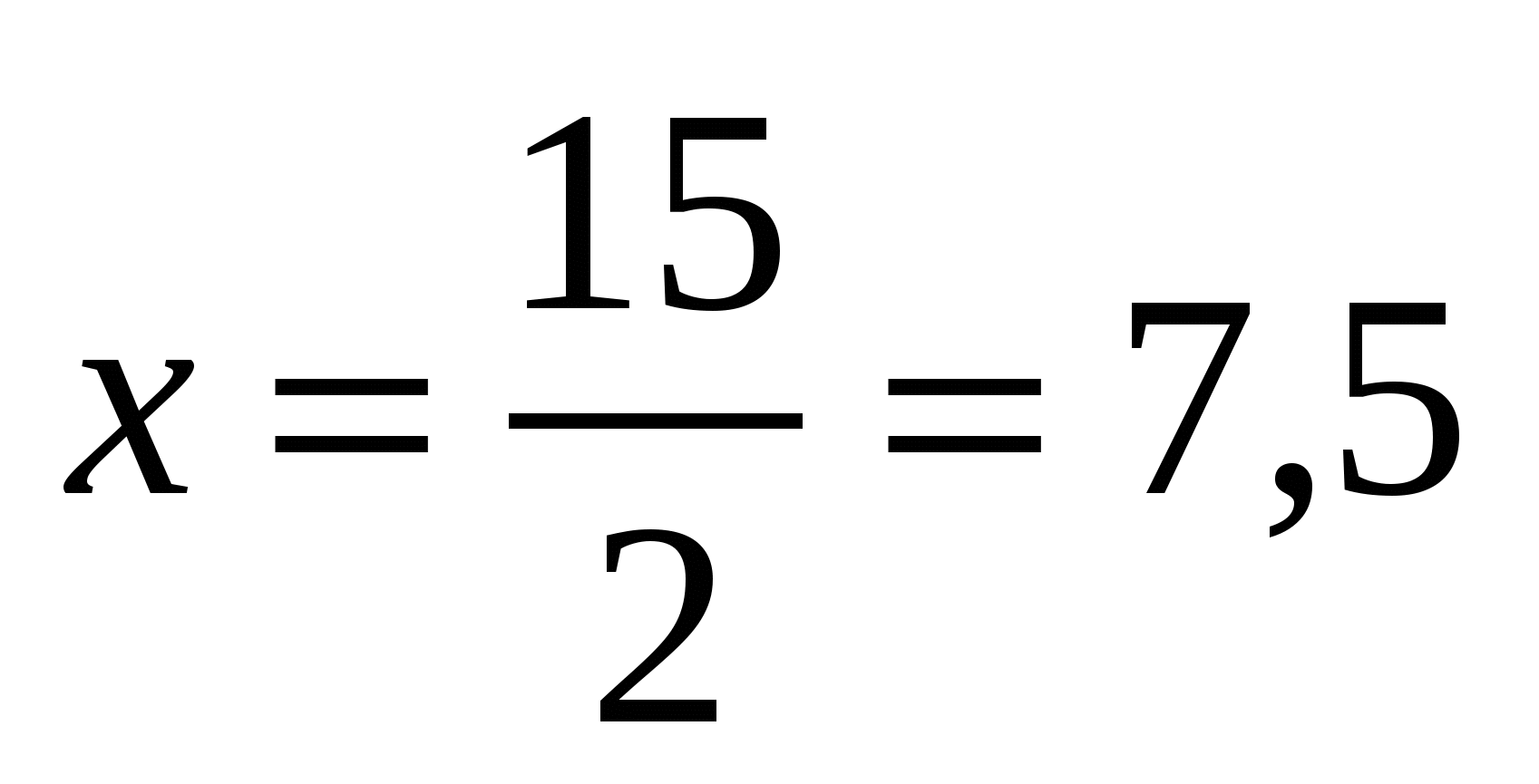 .
.
8) 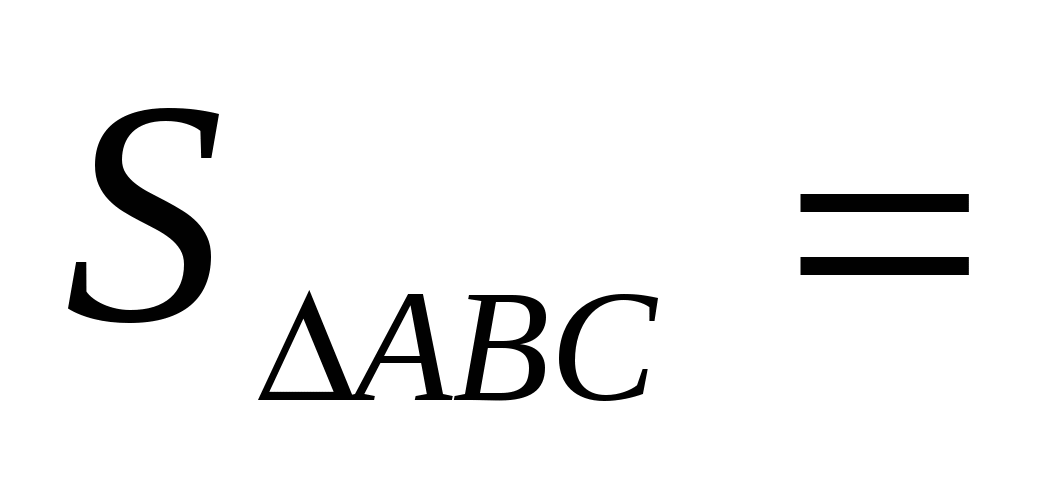 (19,5 + 7,5)ּ5 = 27ּ5 = 135.
(19,5 + 7,5)ּ5 = 27ּ5 = 135.
Ответ: 135.
Задача 3 (Метод опорного элемента «h»). Перпендикуляр, опущенный из вершины параллелограмма на диагональ, делит диагональ на отрезки 6 и 15. Найти стороны и диагонали параллелограмма, если разность сторон равна 7.
АН = 6, НС = 15, АD - АВ = 7. AD, АВ, АС, BD - ?
С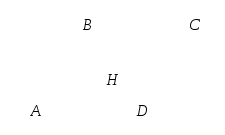 хема решения:
хема решения:
1) 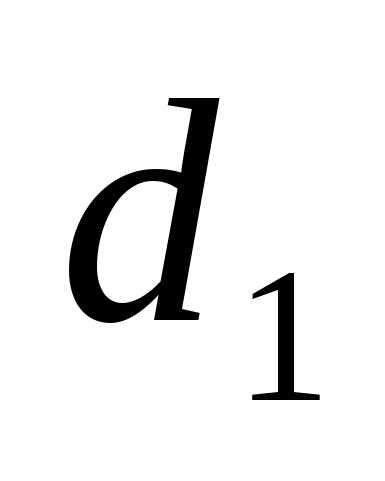 = АН + НС =>
= АН + НС =>
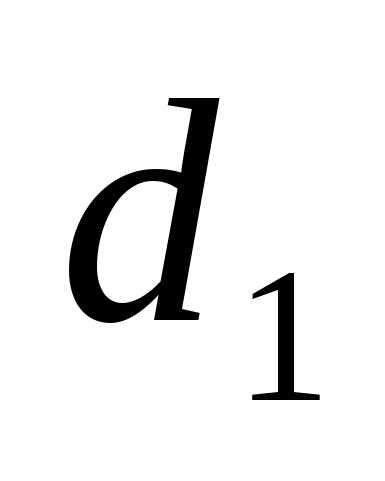 = АС = 6 + 15 = 21,
= АС = 6 + 15 = 21,
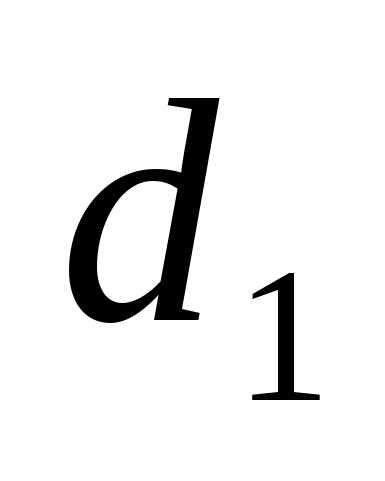 =21.
=21.
2) AD = a, AB = b => a - b = 7.
3) ∆ABH:
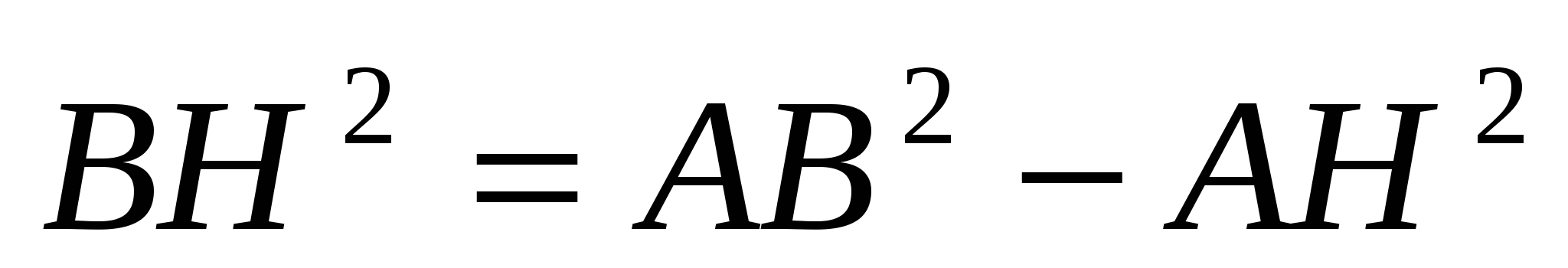 = b2 - 62,
= b2 - 62,
∆CBH:
BH2 = BC2 - HC2 = a2 - 152,
b2 - 62 = a2 - 152.
-
Получаем систему:
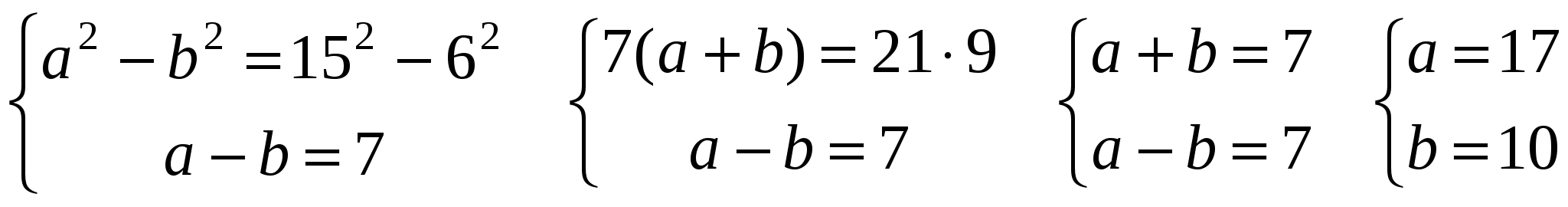
Ответ: 17; 10; 21; 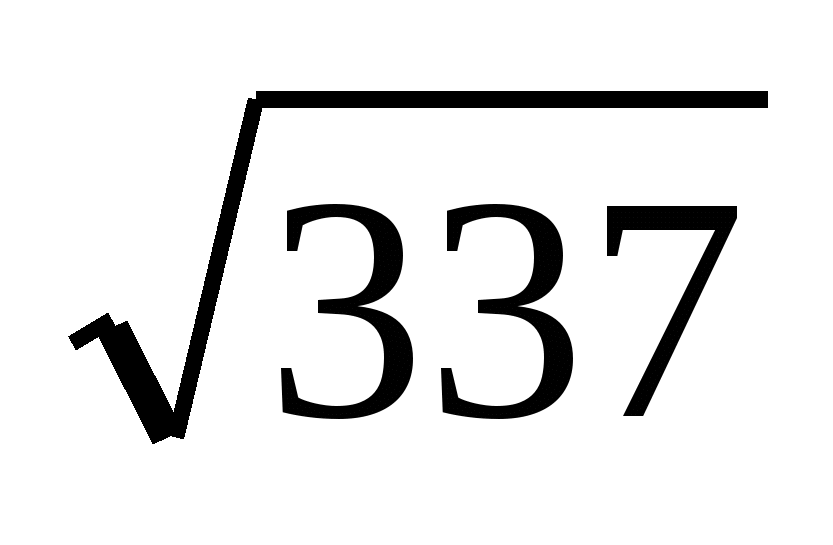 .
.
З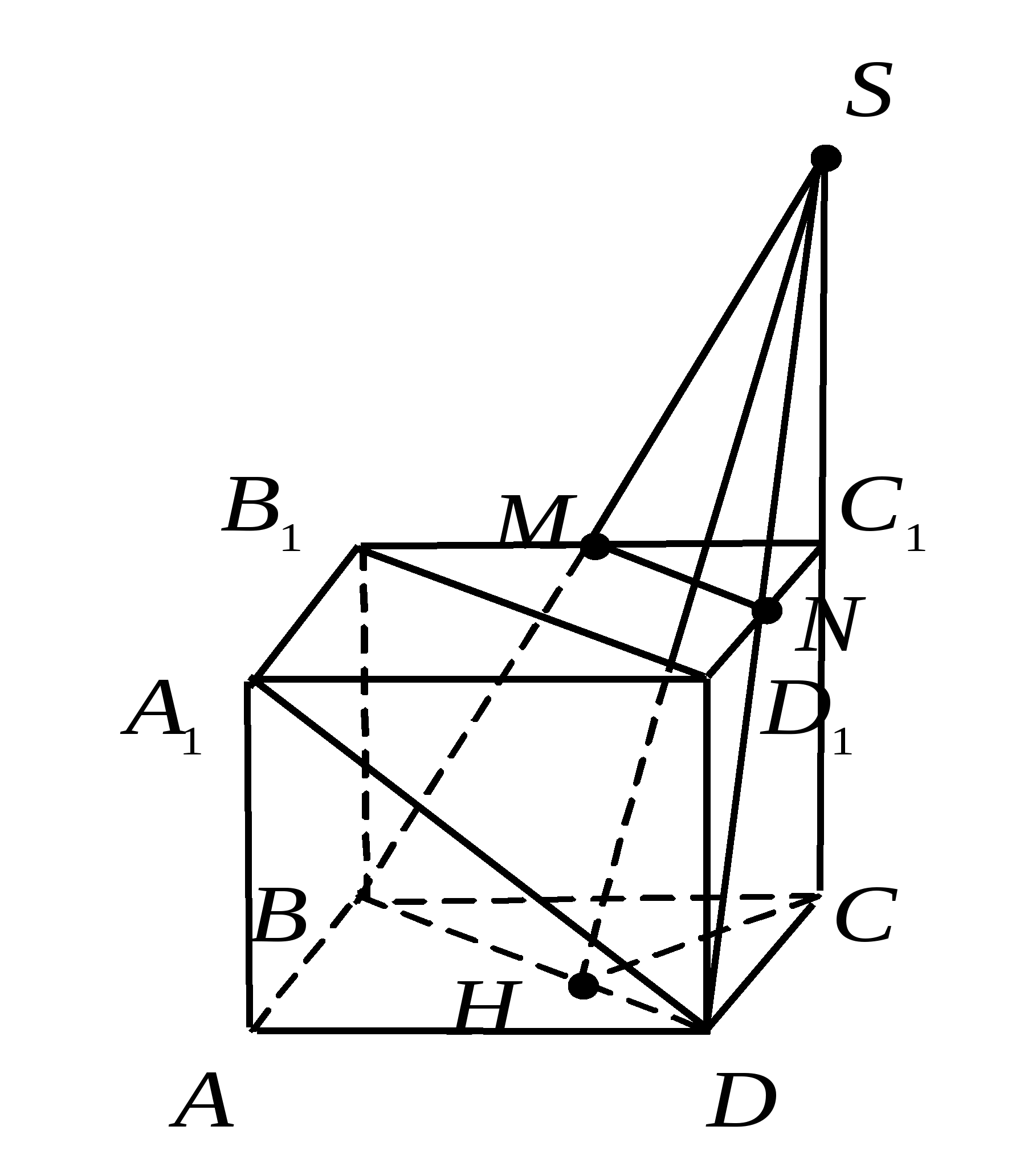 адача 4 (Метод опорного элемента «V»).
адача 4 (Метод опорного элемента «V»).
В прямой призме АВСDА1В1С1D1 в основании лежит прямоугольник АВСD со сторонами АВ = а, ВС = 2а. Высота призмы равна b. Найти расстояние от точки С до плоскости, проходящей через диагональ ВD и середины рёбер В1С1 и С1D1.
Схема решения:
1)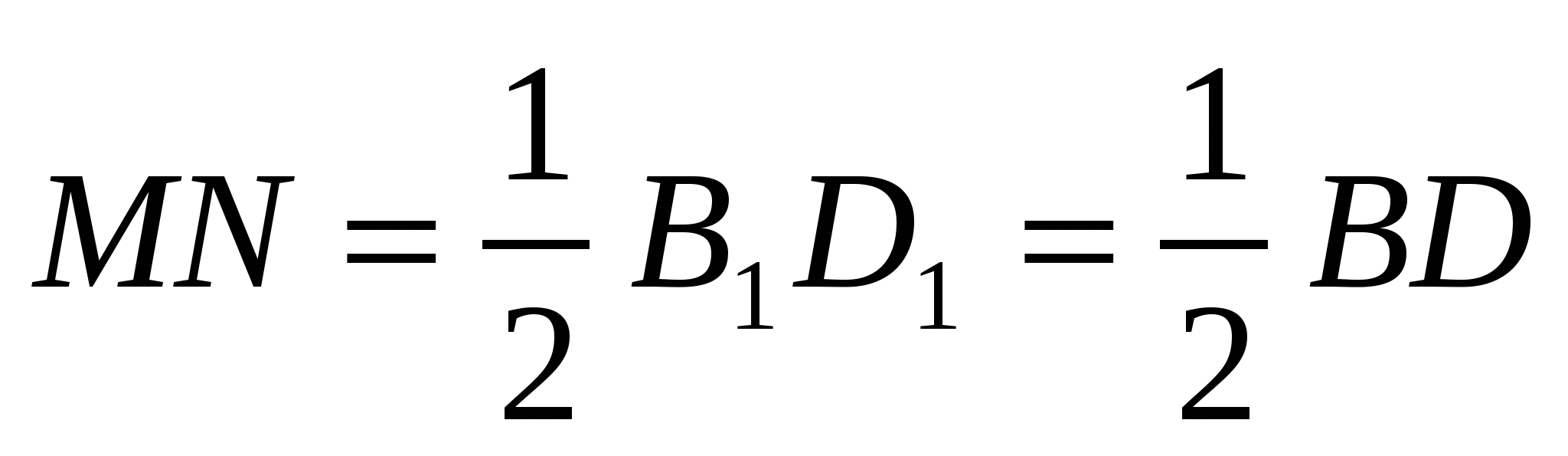 , т.е.
, т.е. 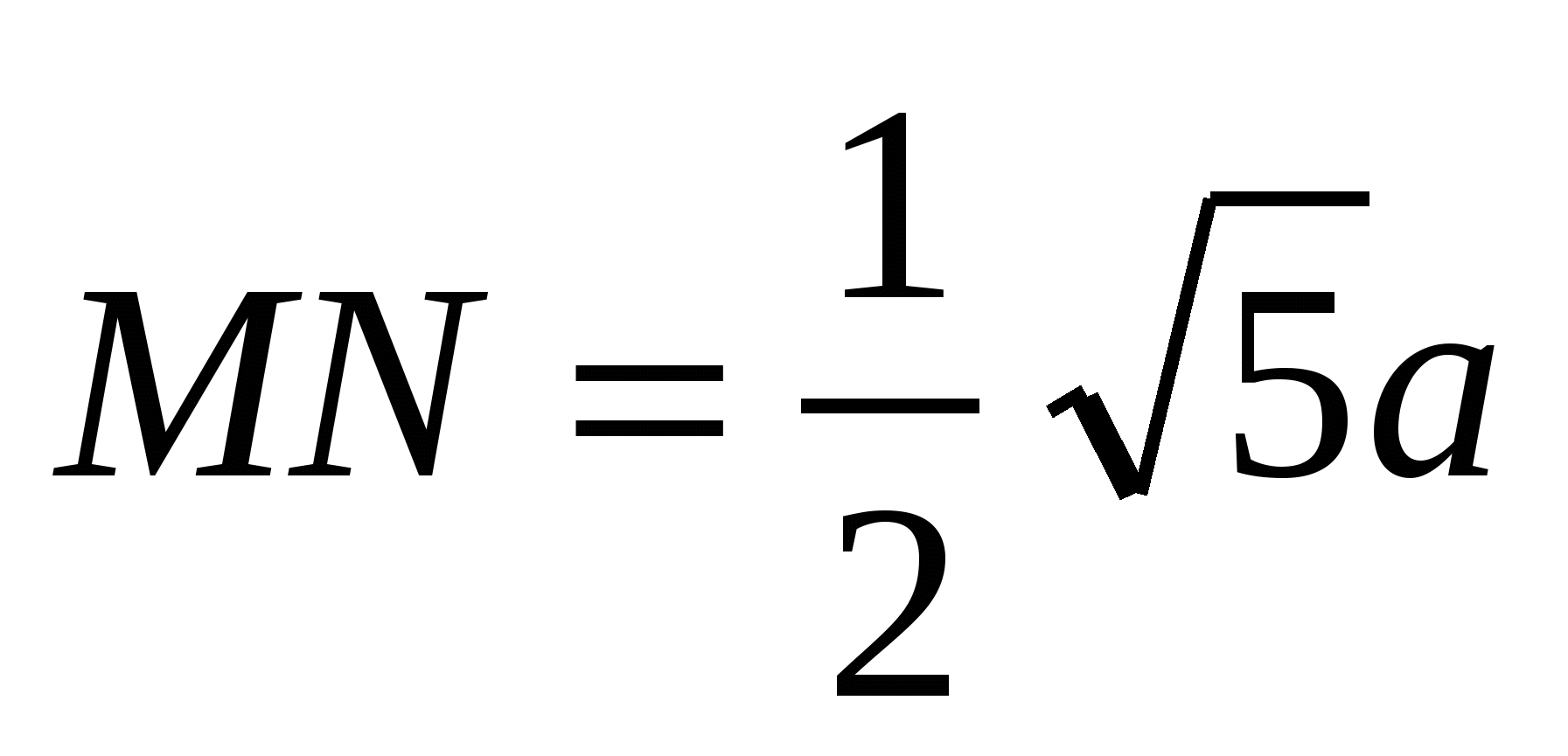 .
.
2) 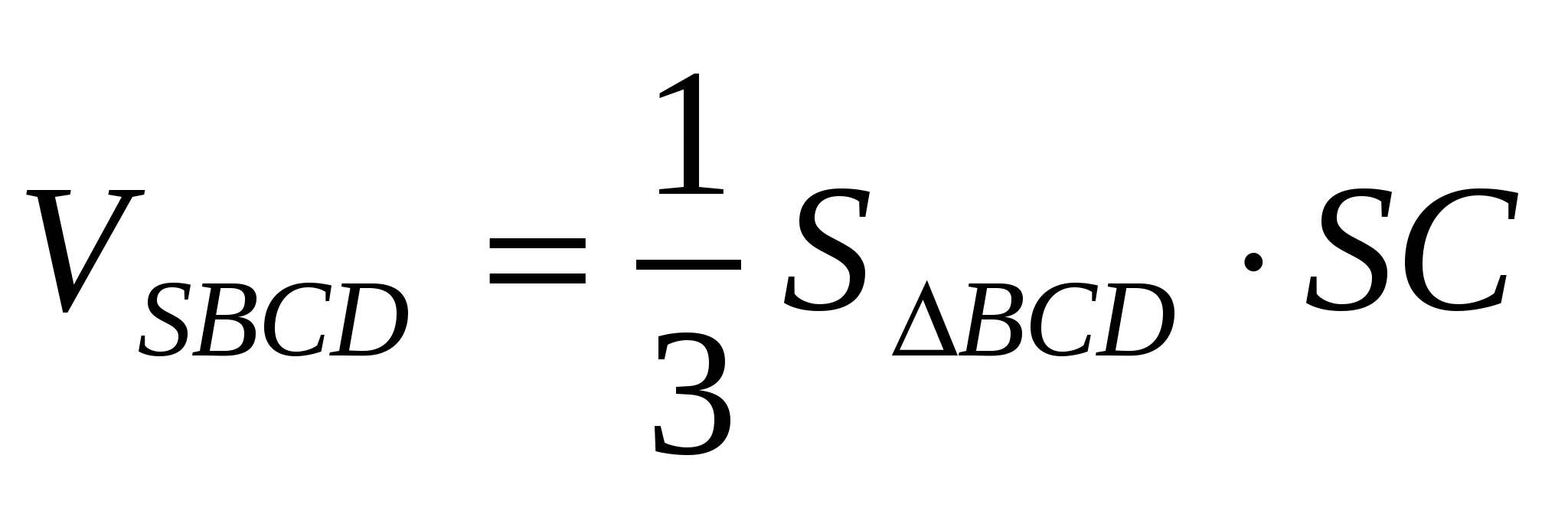 , т.е.
, т.е. 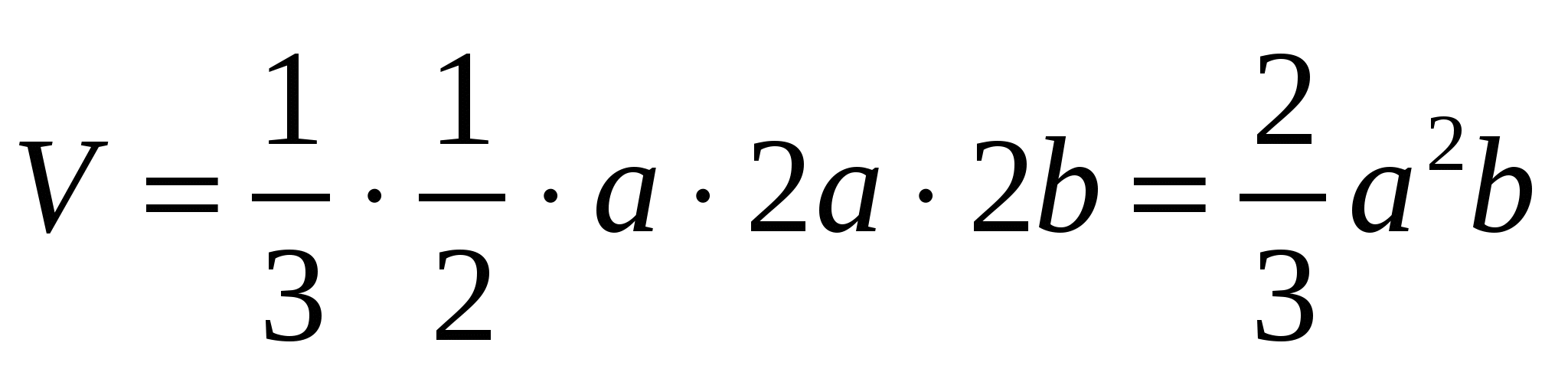 .
.
3) CH - высота ∆BCD, следовательно, BD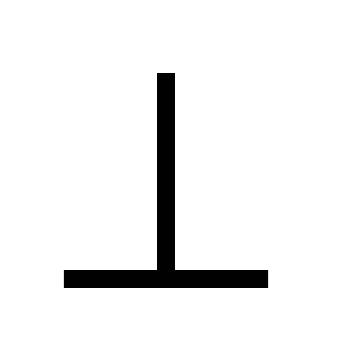 SH (по теореме о трёх перпендикулярах).
SH (по теореме о трёх перпендикулярах).
S∆BDC = a2.
S∆BCD = 
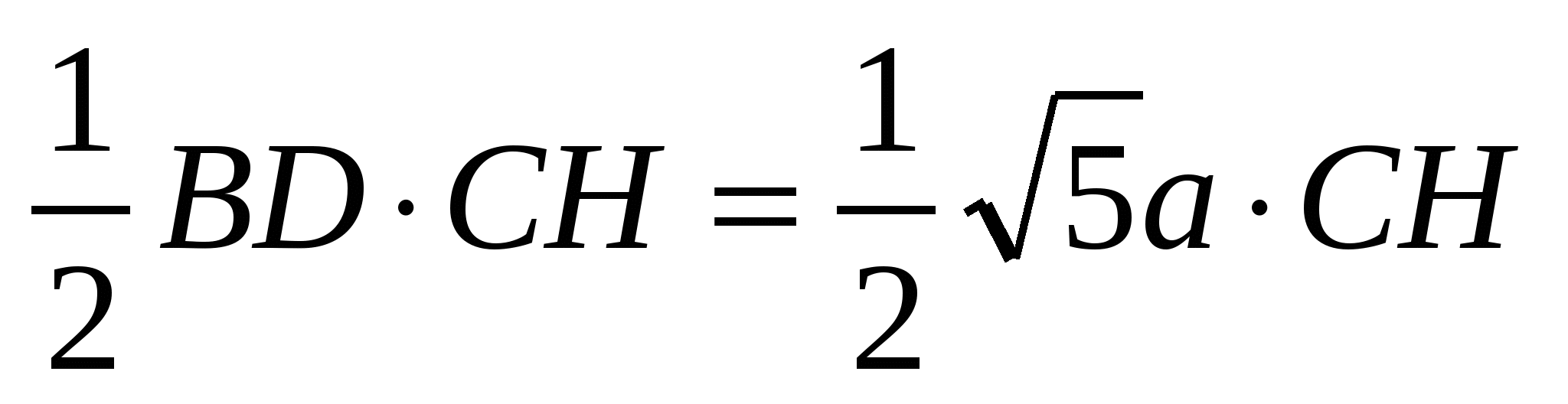 , отсюда получаем:
, отсюда получаем: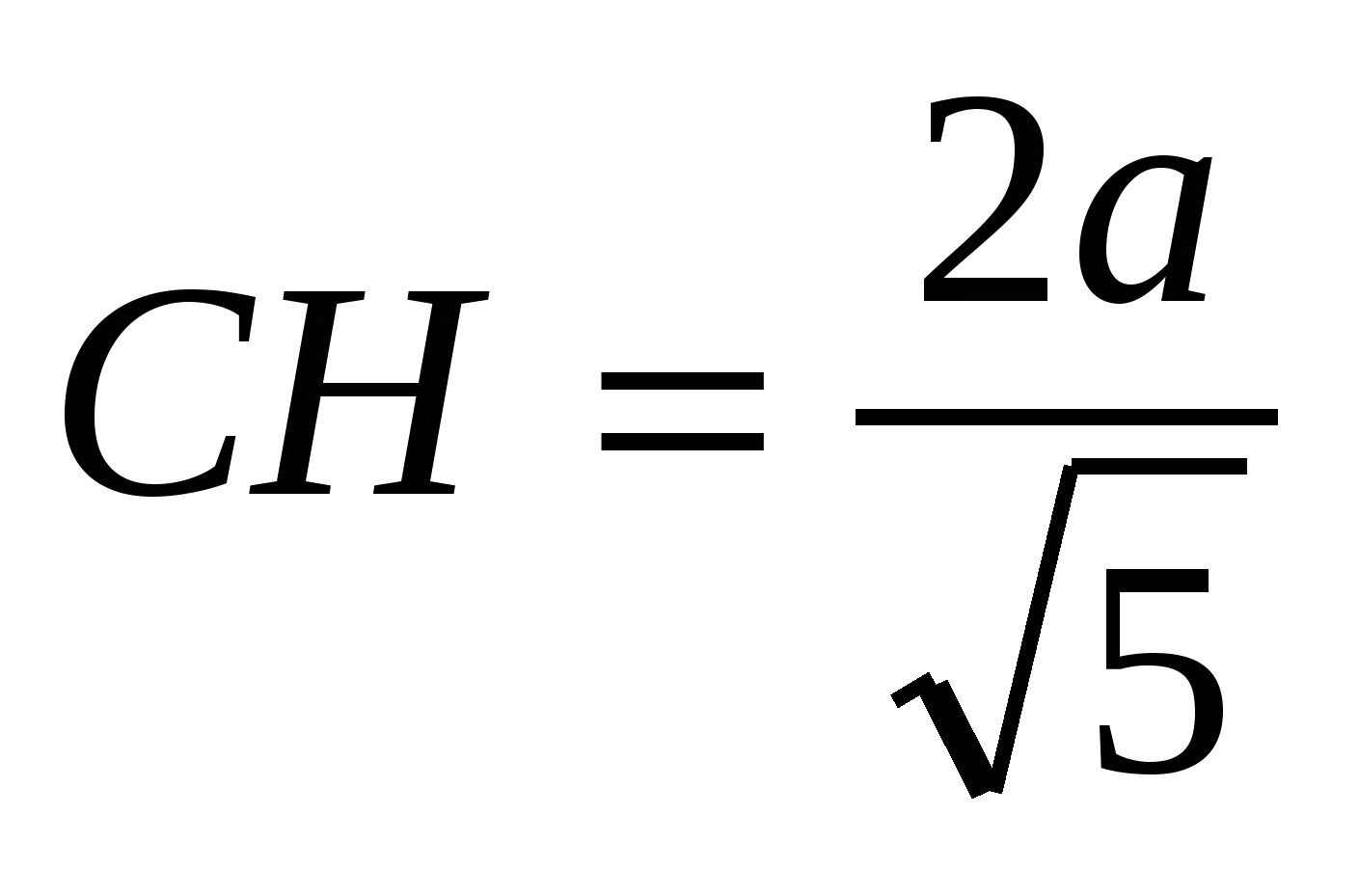 .
.
4) ∆SHC: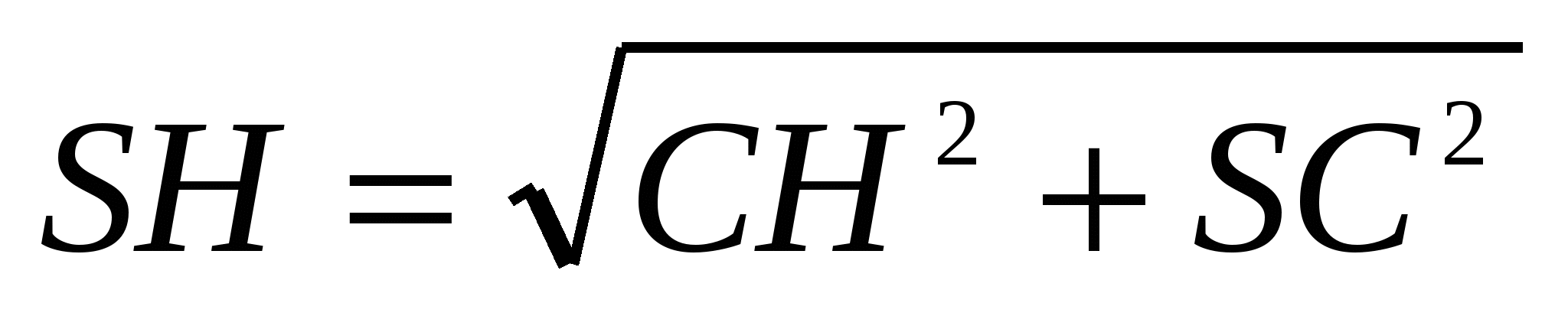 ;
; 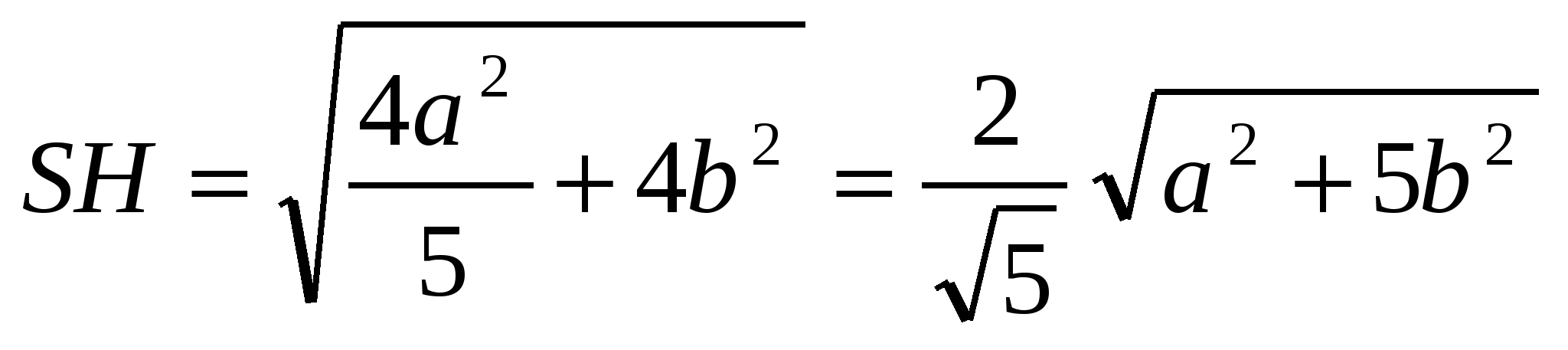 .
.
5) 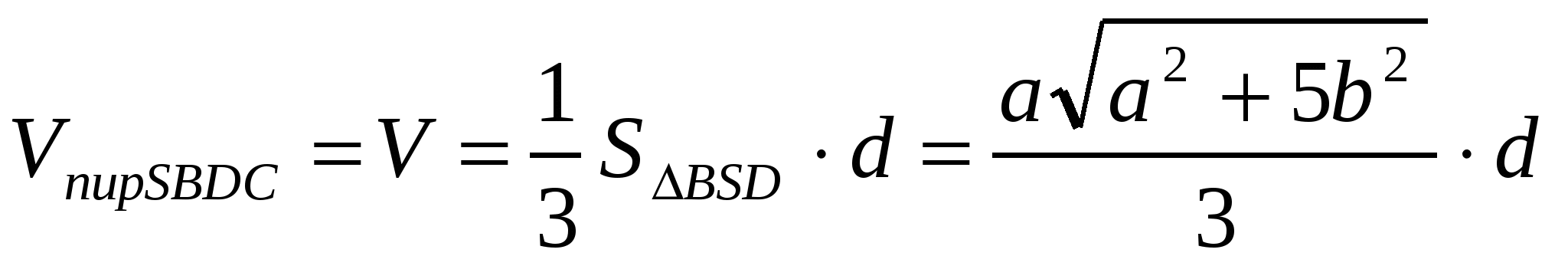 ,
,
где d - искомое расстояние.
6) С другой стороны, 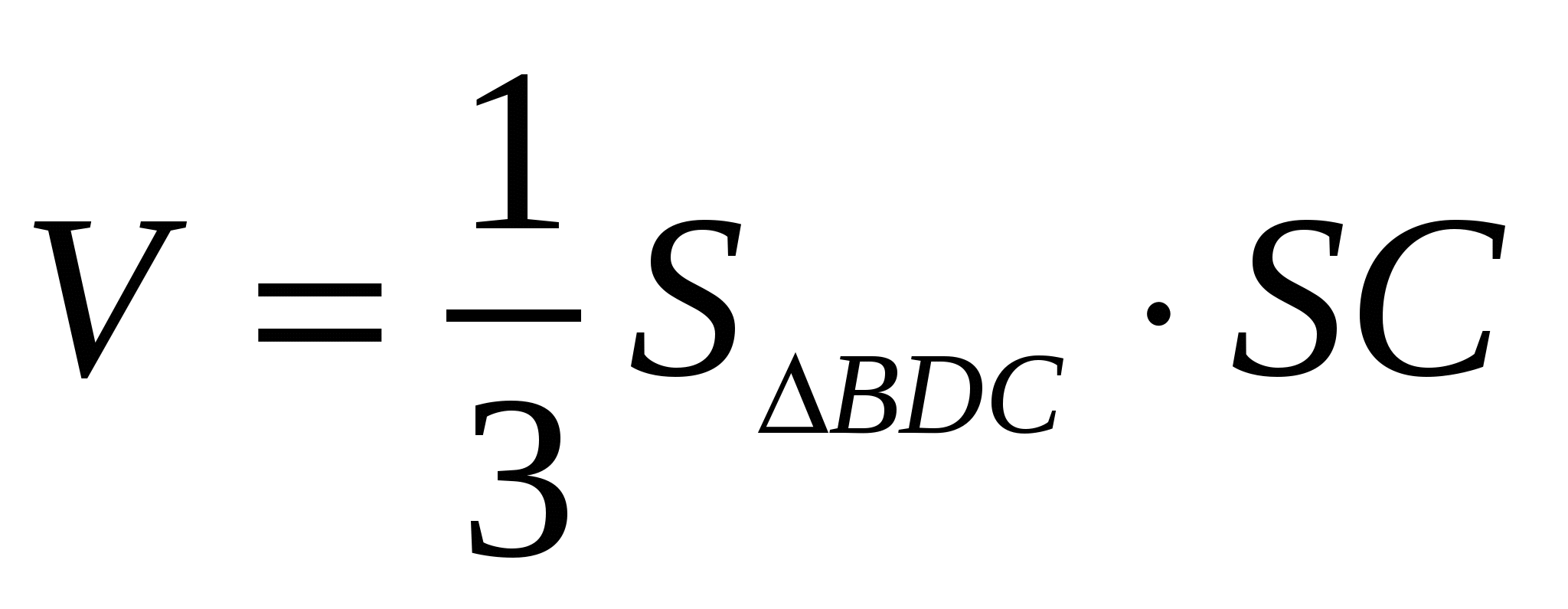 , т.е.
, т.е. 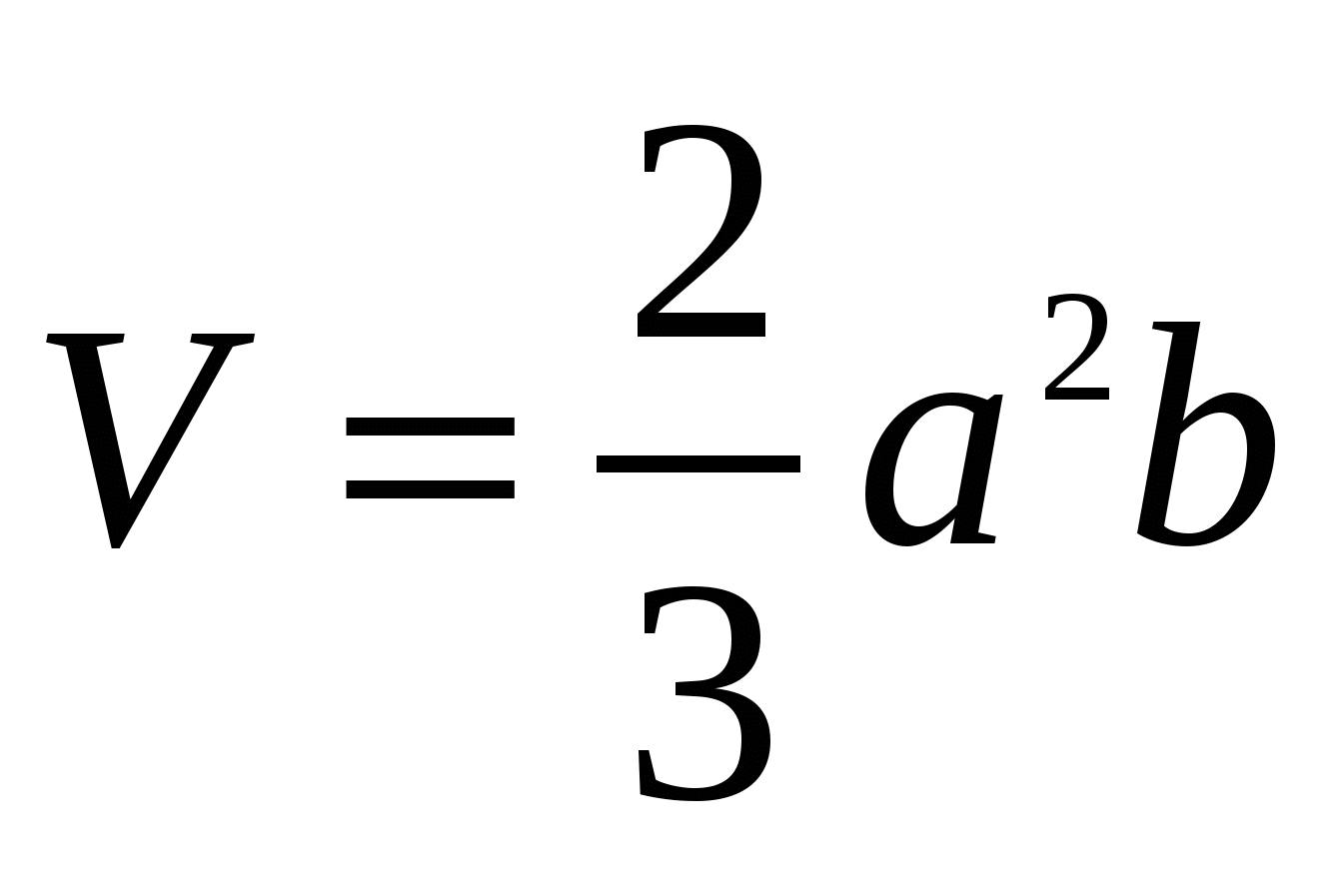 .
.
7) Из 5), 6) получаем: 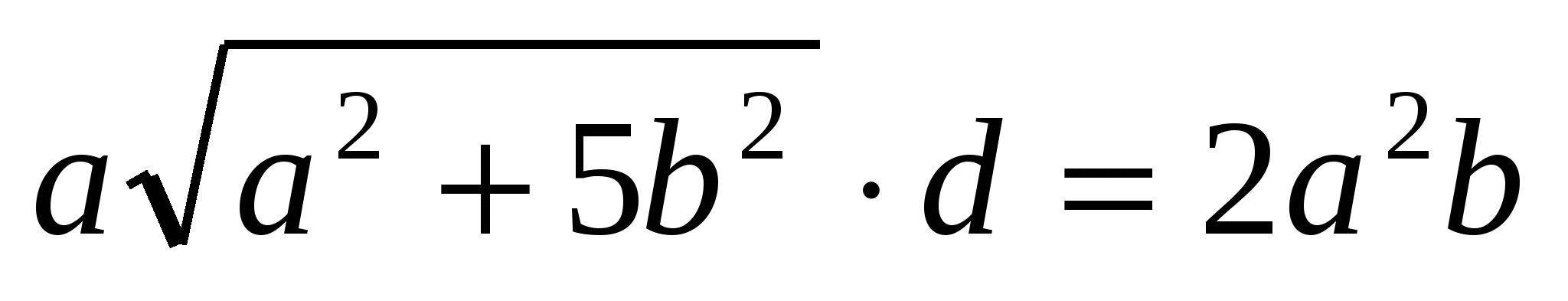 ,
, 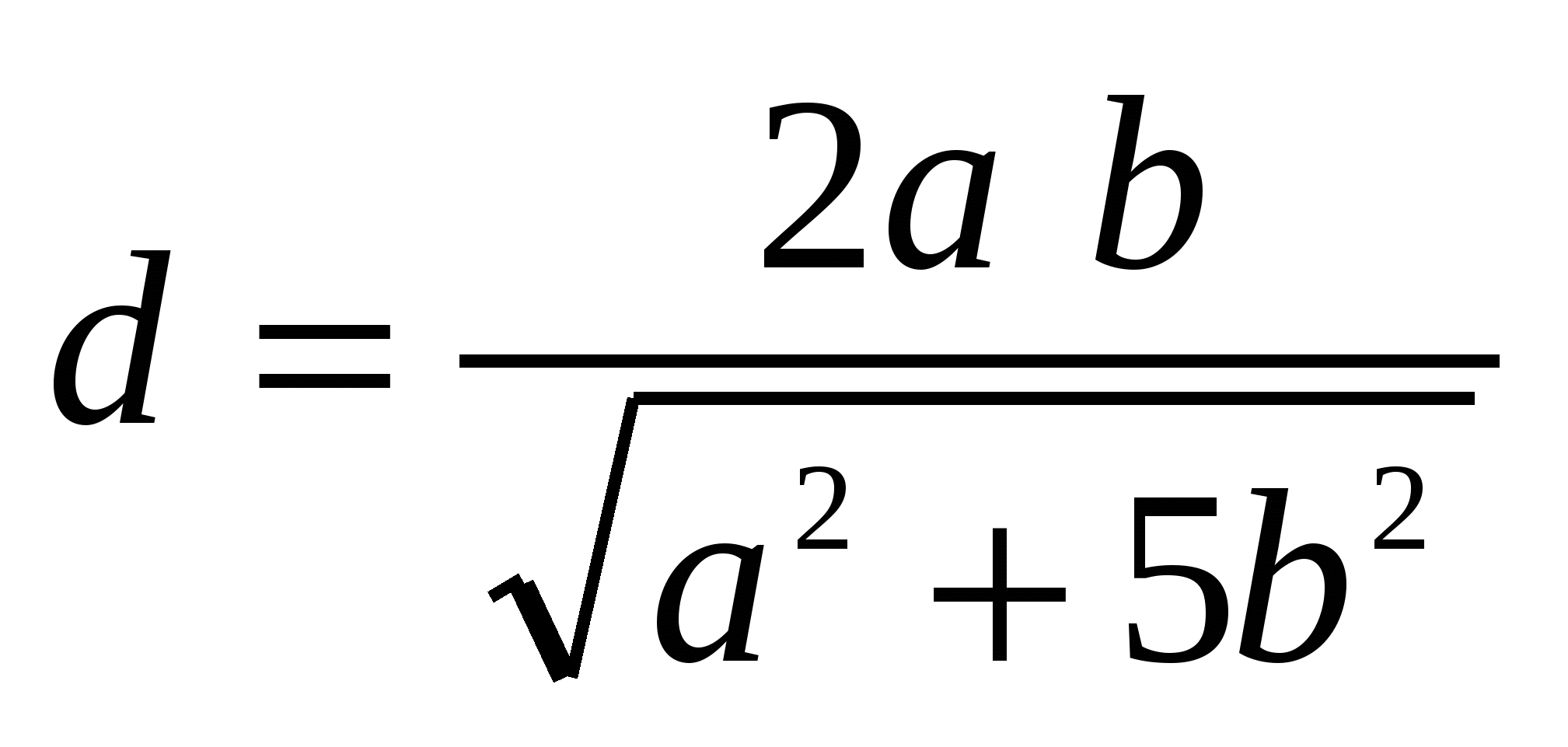 .
.
Ответ: 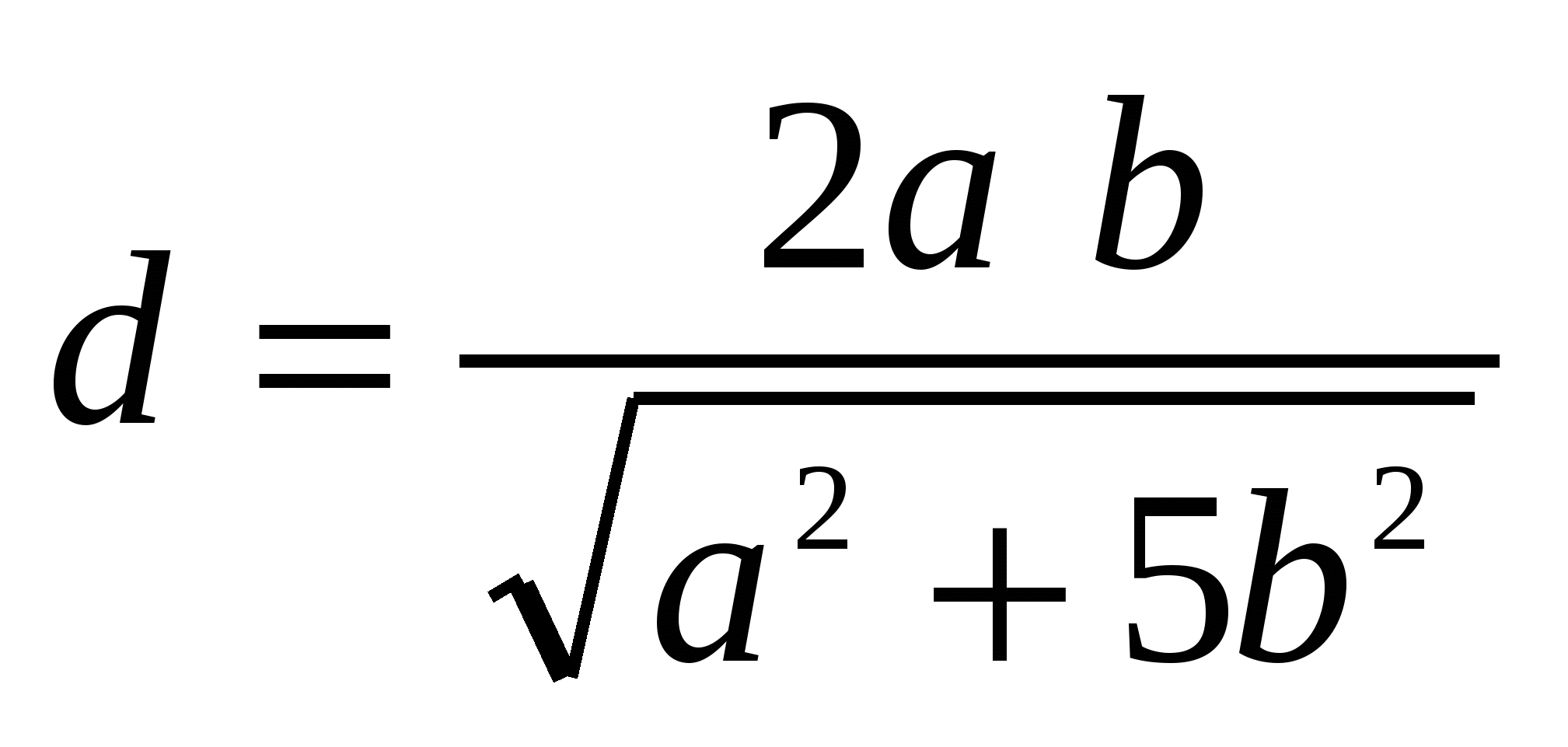 .
.
1.2. Векторный метод
Аппарат векторной алгебры позволил создать особый метод решения геометрических задач. Сущность векторного метода заключается в следующем. Сначала геометрическую задачу переводят на векторный язык, затем решают задачу, используя операции над векторами, опорные задачи векторного метода. Далее полученный результат в векторной форме переводят обратно на геометрический язык.
Основные определения и теоремы векторной алгебры
Вектором называется направленный отрезок.
У нулевого вектора начало совпадает с его концом, т.е. любая точка плоскости является вектором.
Длиной вектора 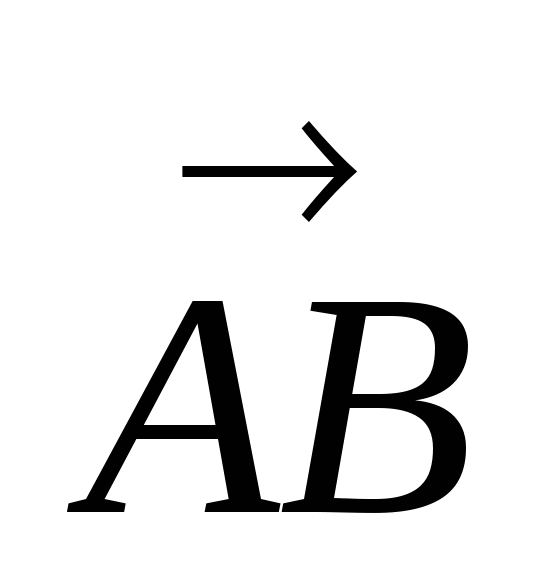 называется длина отрезка АВ.
называется длина отрезка АВ.
Обозначается:  .
.
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Два коллинеарных вектора могут быть одинаково направленными, т.е. сонаправленными, либо противоположно направленными.
Любой вектор можно разложить по двум неколлинеарным векторам: 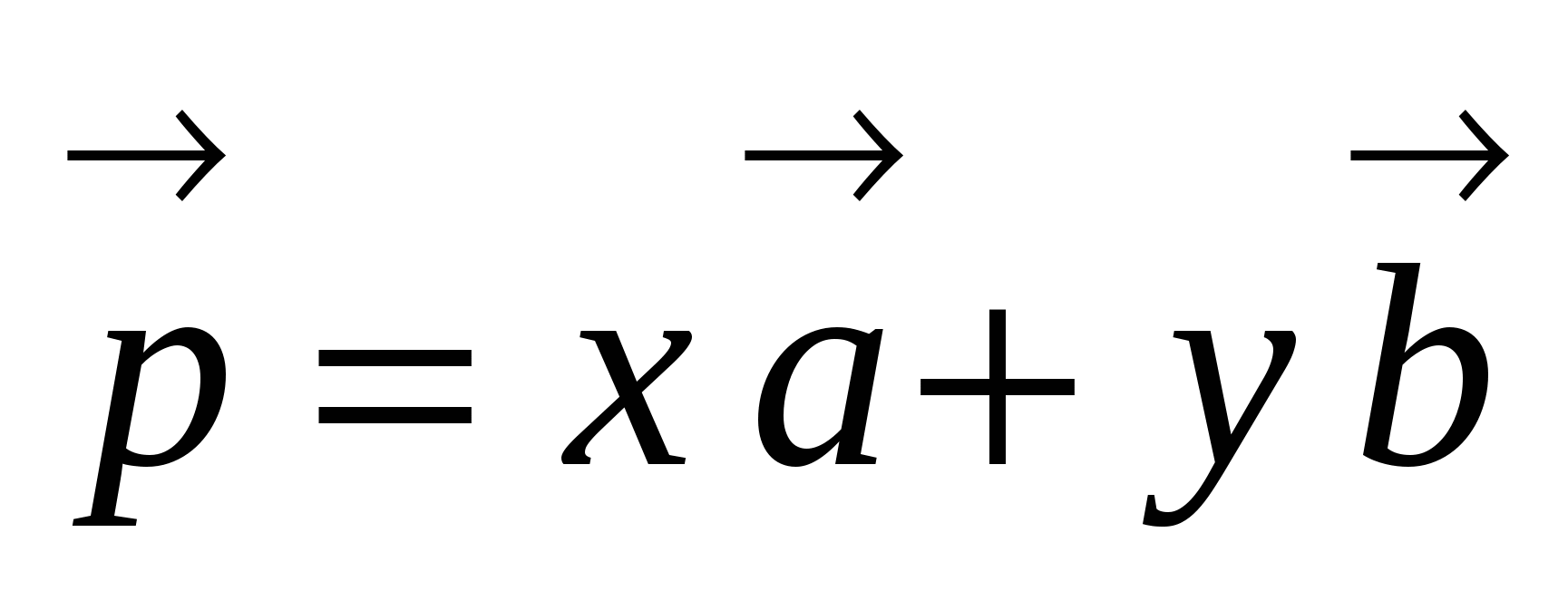 , где х, у - коэффициенты, определяющиеся единственным образом.
, где х, у - коэффициенты, определяющиеся единственным образом.
Векторы называют компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Любой вектор можно разложить по трем некомпланарным векторам:
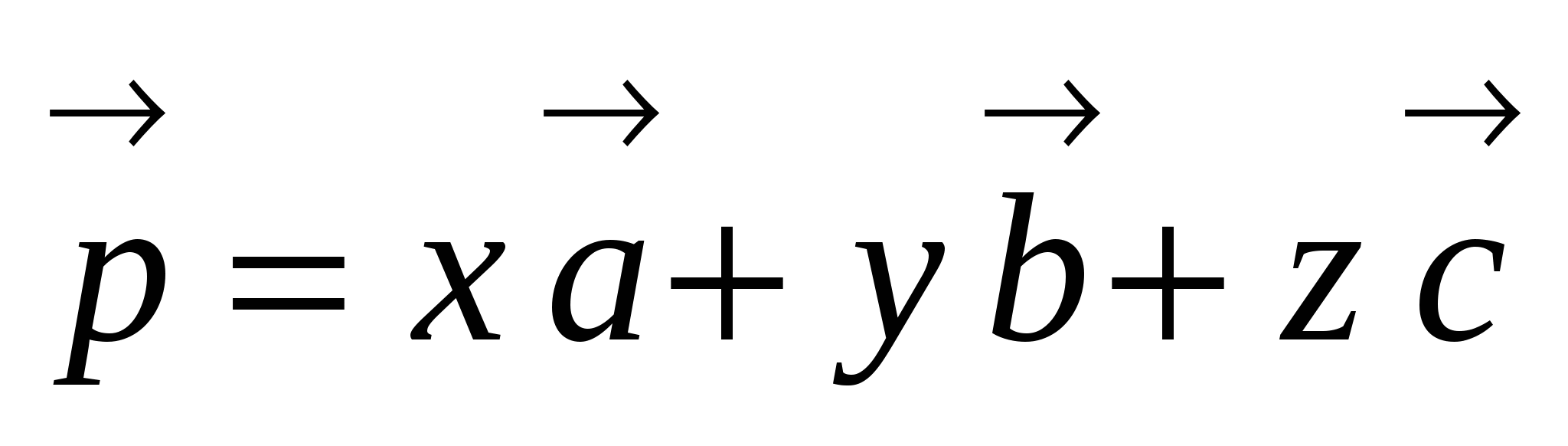 , где х, у, z - коэффициенты разложения, определяющиеся единственным образом.
, где х, у, z - коэффициенты разложения, определяющиеся единственным образом.
Сложение векторов
1) Правило треугольника
Для любых трех точек А, В, С справедливо равенство: 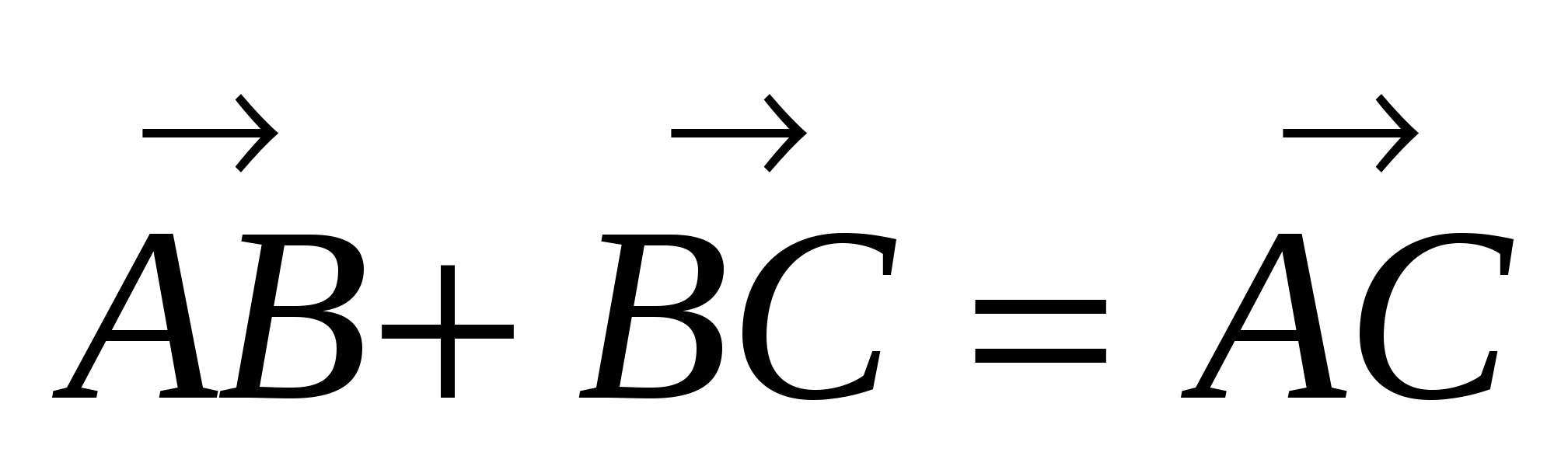 .
.

2) Правило параллелограмма
Если АВСD - параллелограмм, то 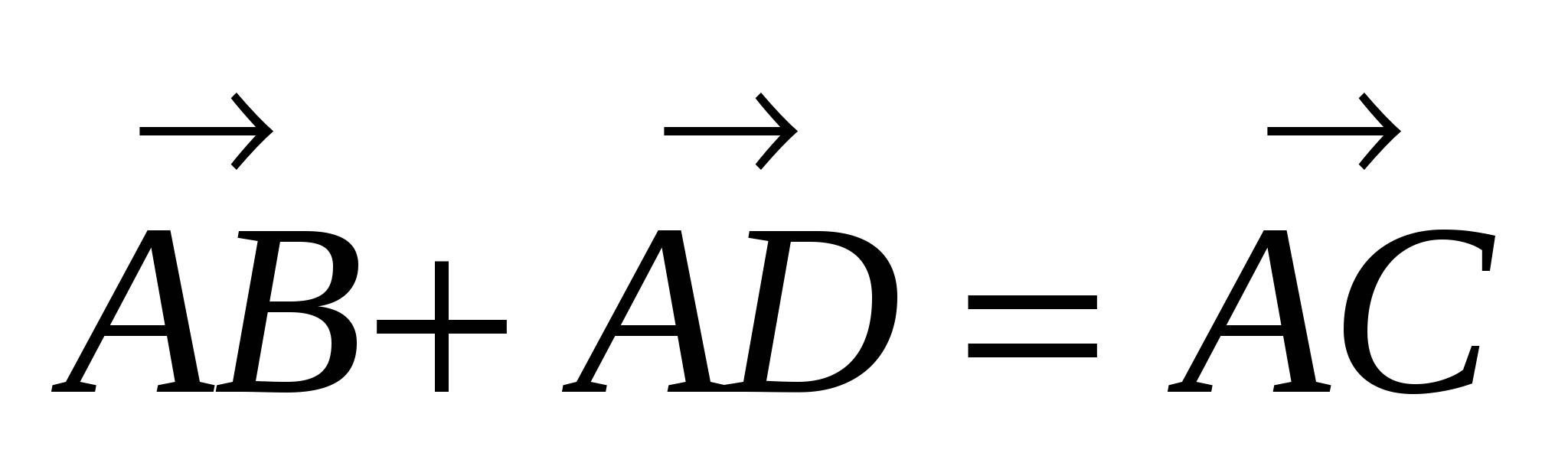 .
.

3) Правило многоугольника
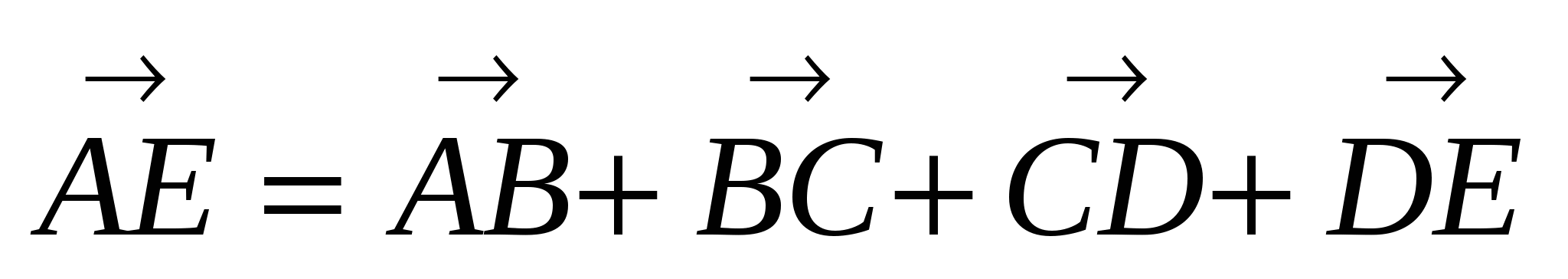 .
.

4) Правило параллелепипеда

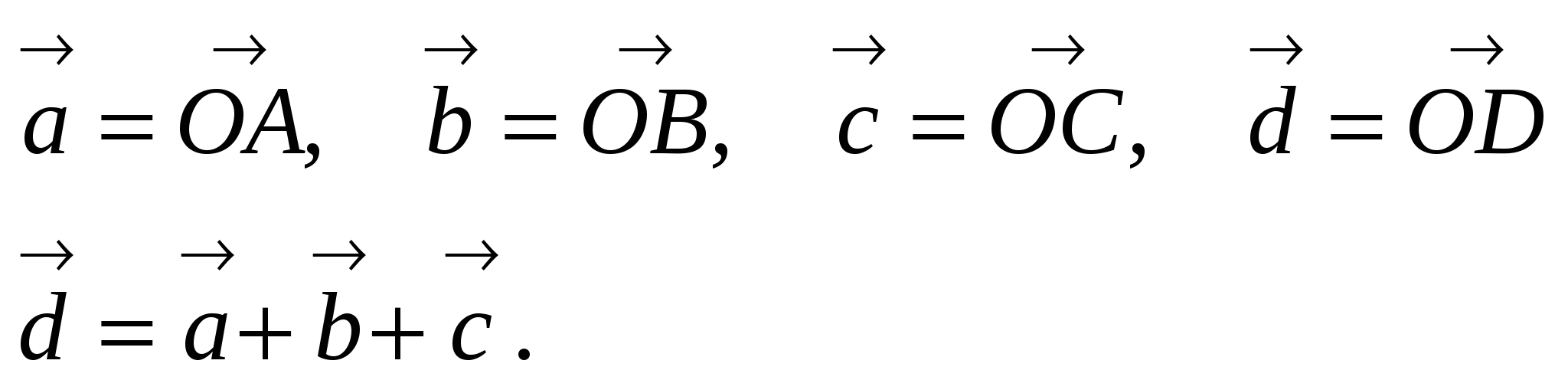
Умножение вектора на число
Произведением вектора 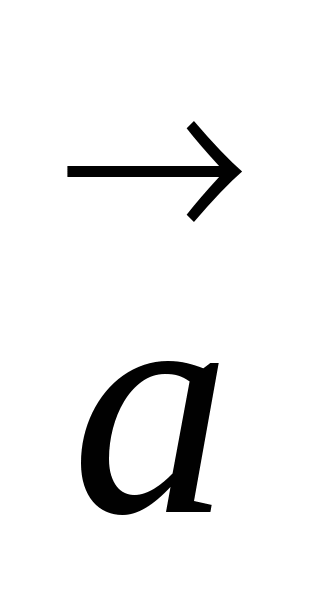 на число k, называется такой вектор
на число k, называется такой вектор 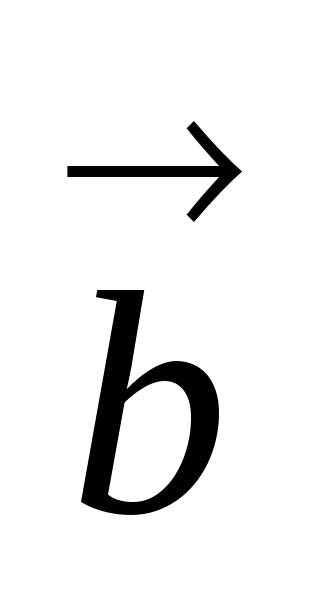 , длина которого равна
, длина которого равна 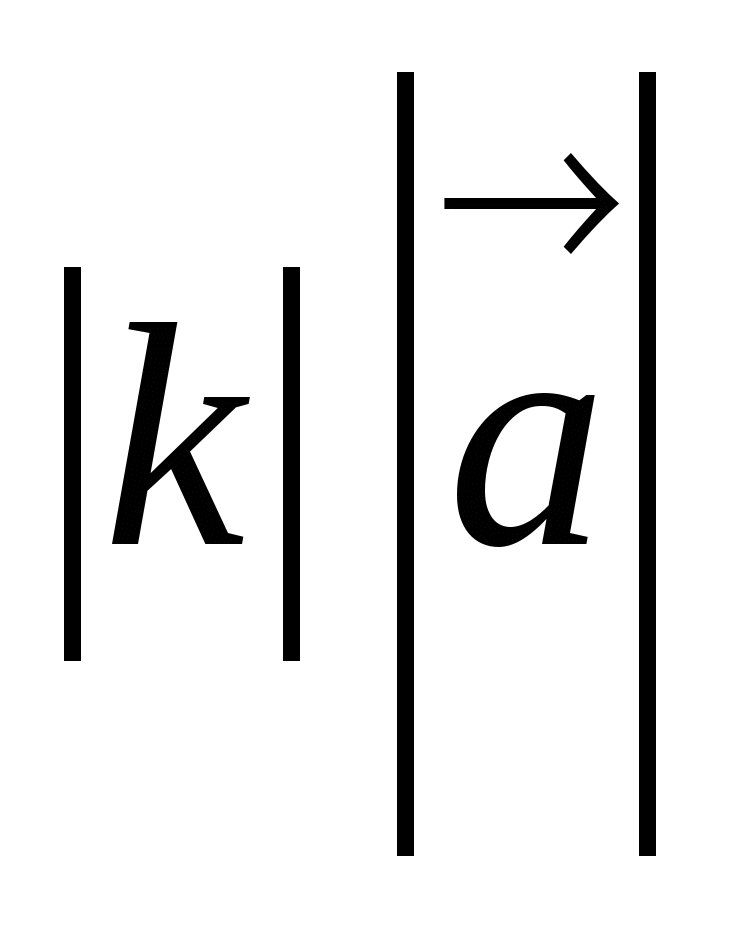 , причем
, причем 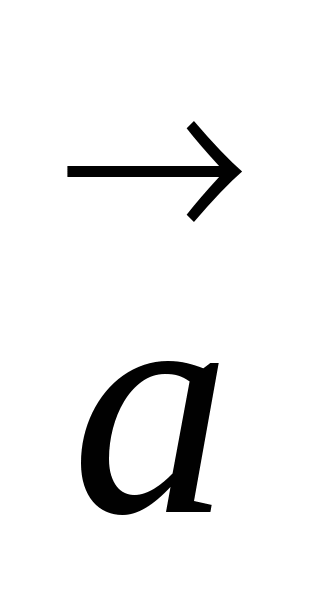 и
и 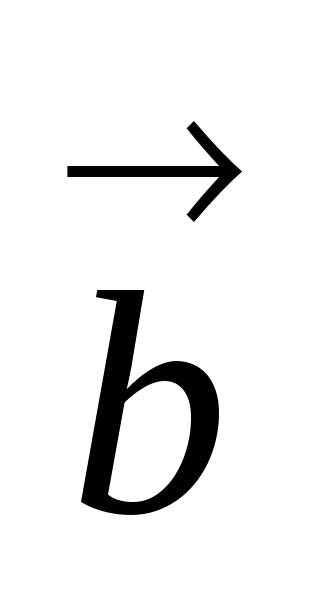 сонаправлены, если
сонаправлены, если 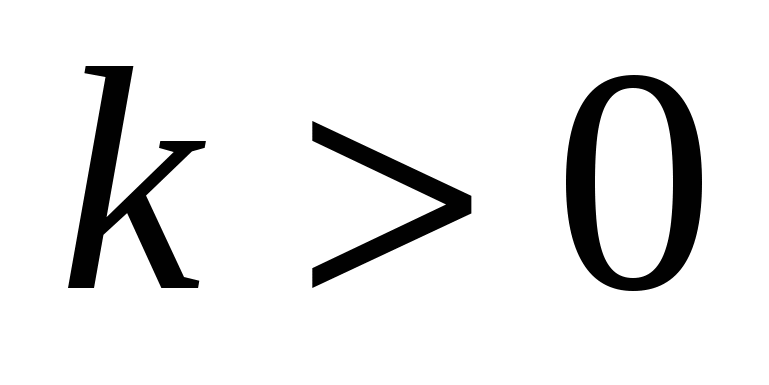 и противоположно направлены, если
и противоположно направлены, если 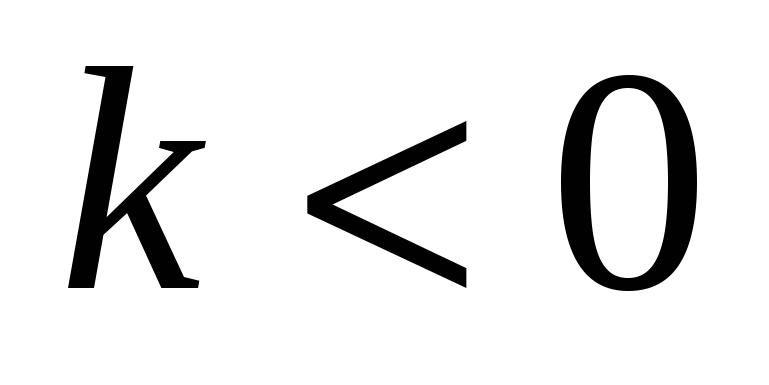 . Обозначается
. Обозначается 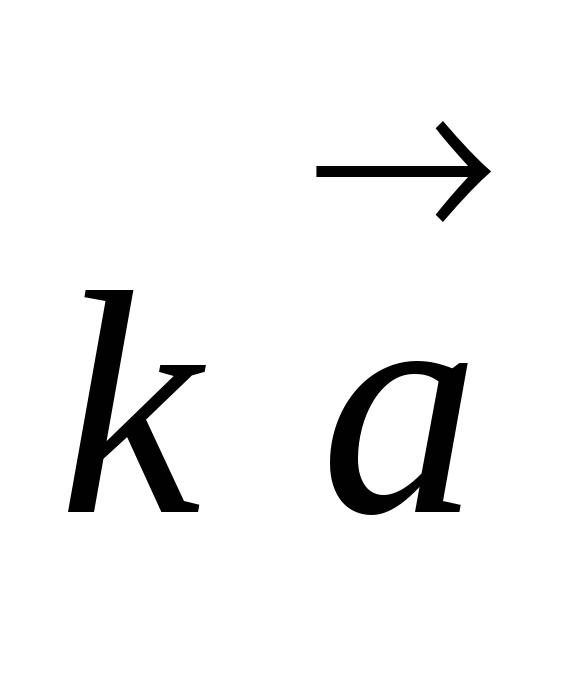 .
.
Свойства умножения вектора на число
1. 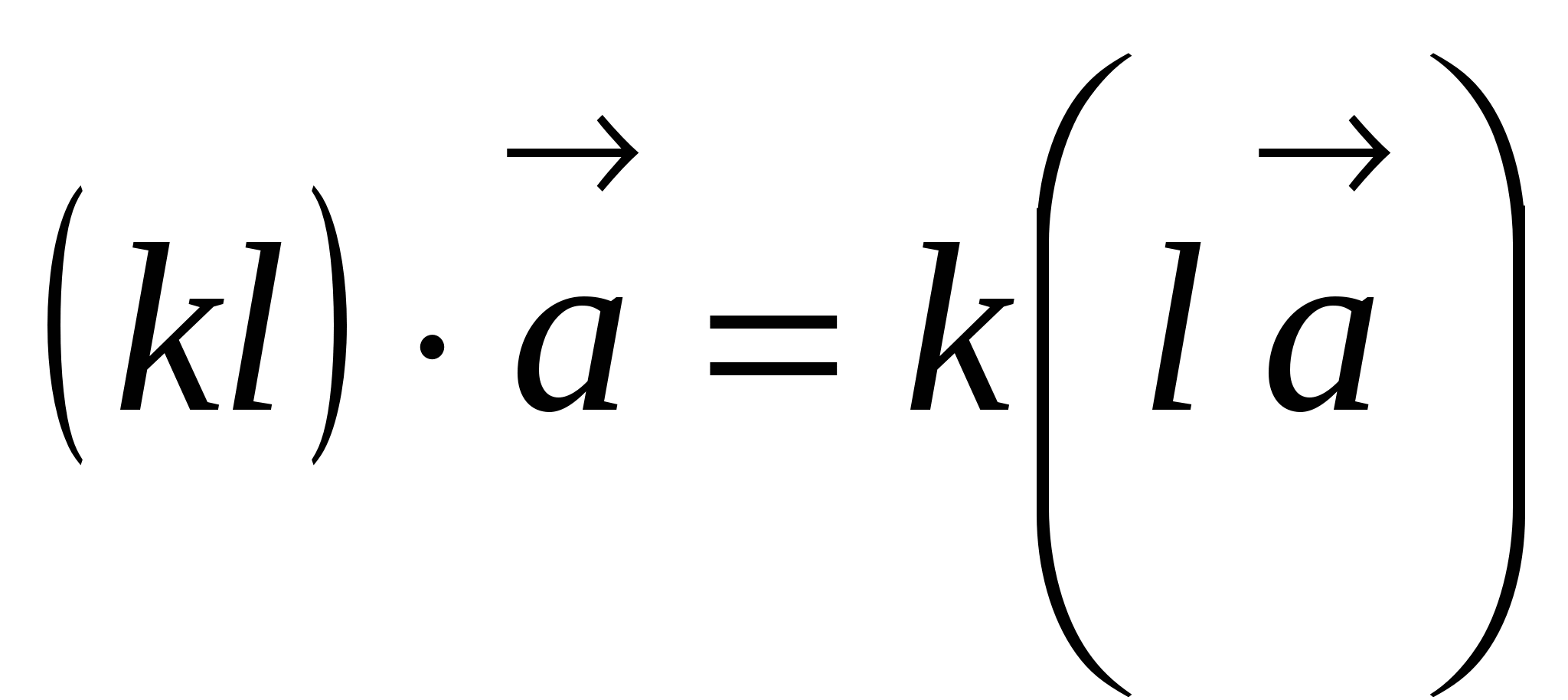 .
.
2. 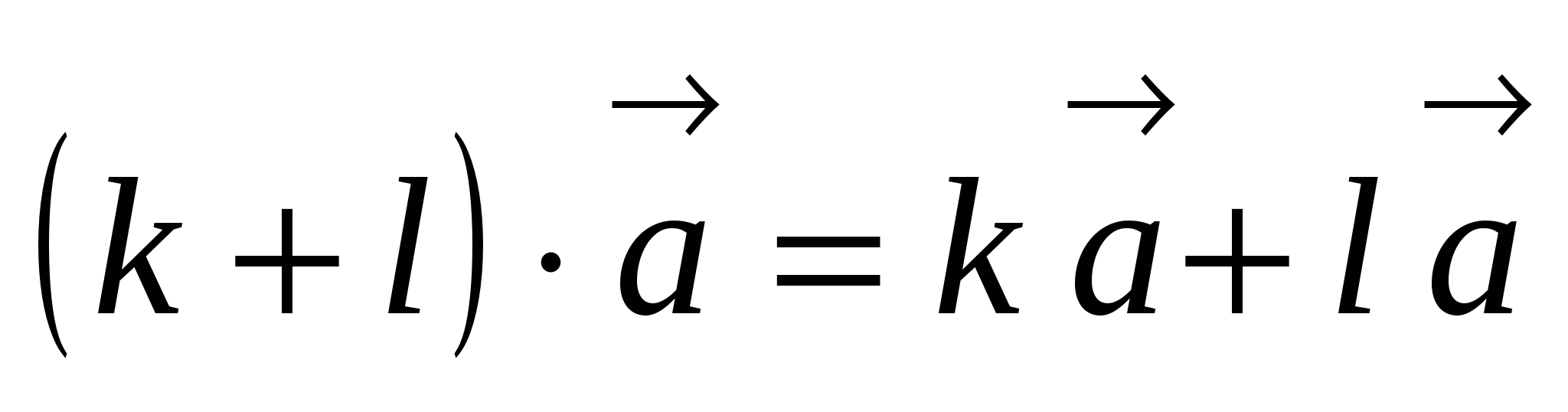 .
.
3. 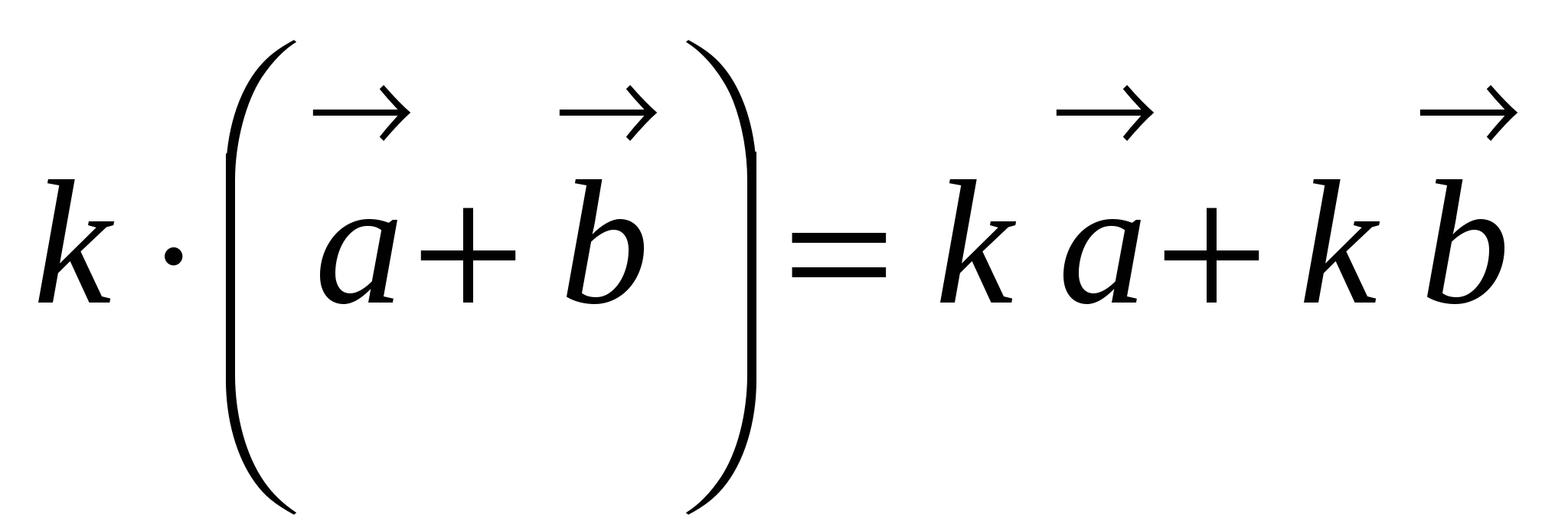 .
.
Угол между ненулевыми векторами
Углом между векторами 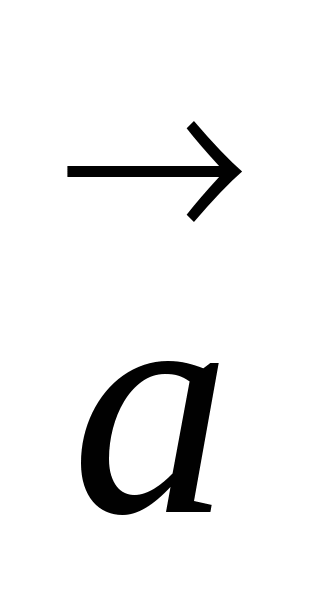 и
и 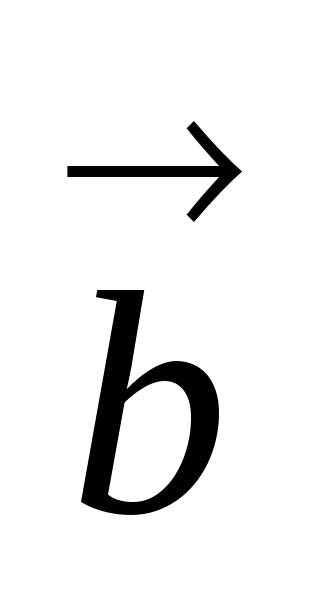 называется наименьший угол
называется наименьший угол 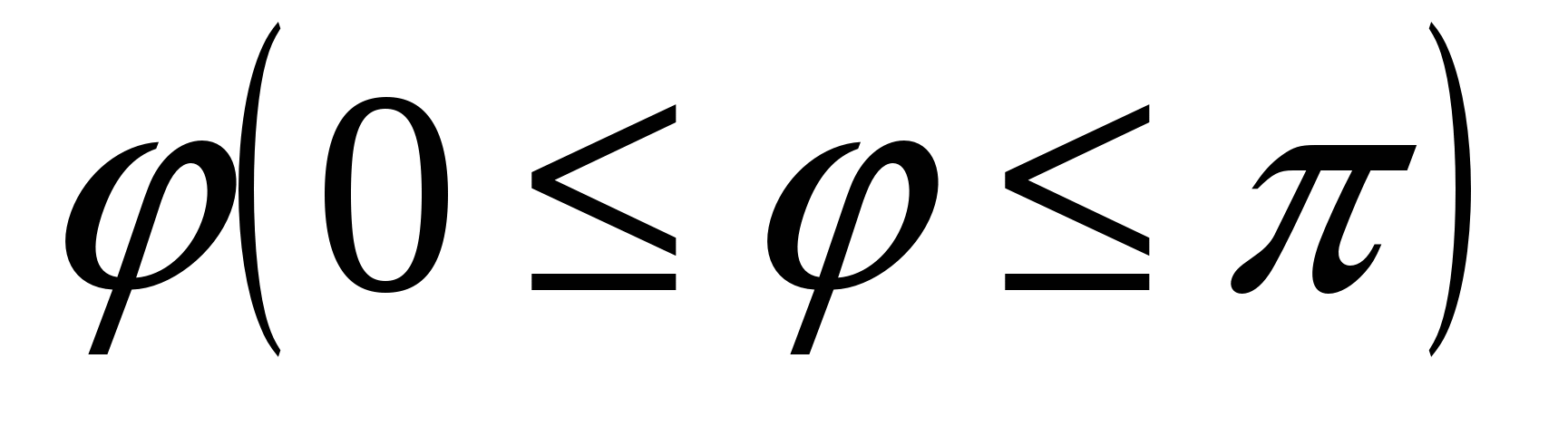 , на который нужно повернуть один из векторов до его совпадения со вторым после приведения этих векторов к общему началу.
, на который нужно повернуть один из векторов до его совпадения со вторым после приведения этих векторов к общему началу.
Скалярное произведение векторов
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
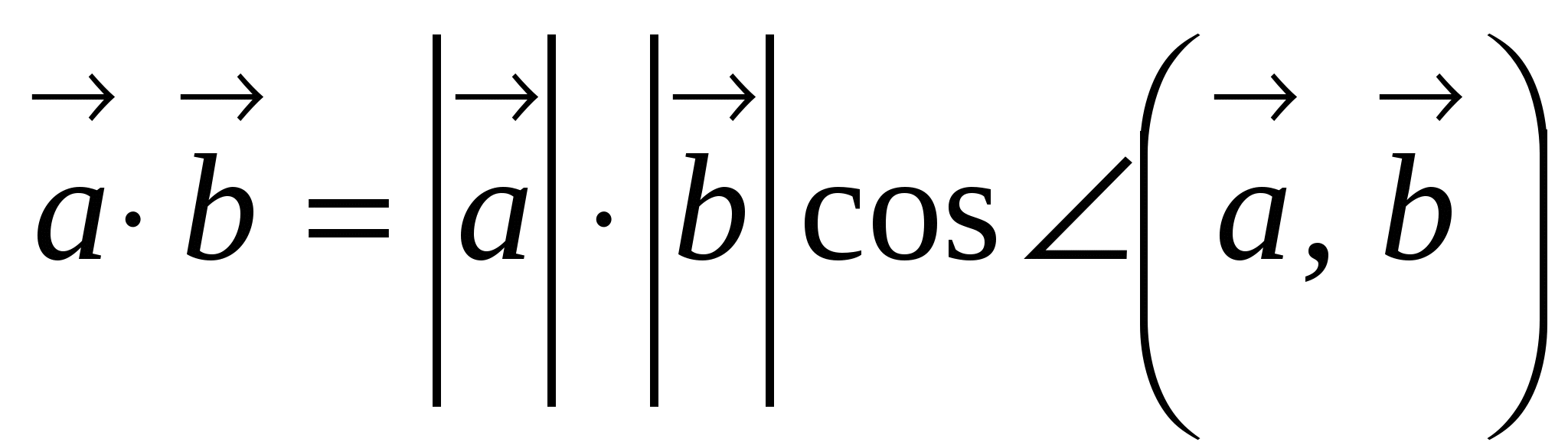
Замечания:
-
Если
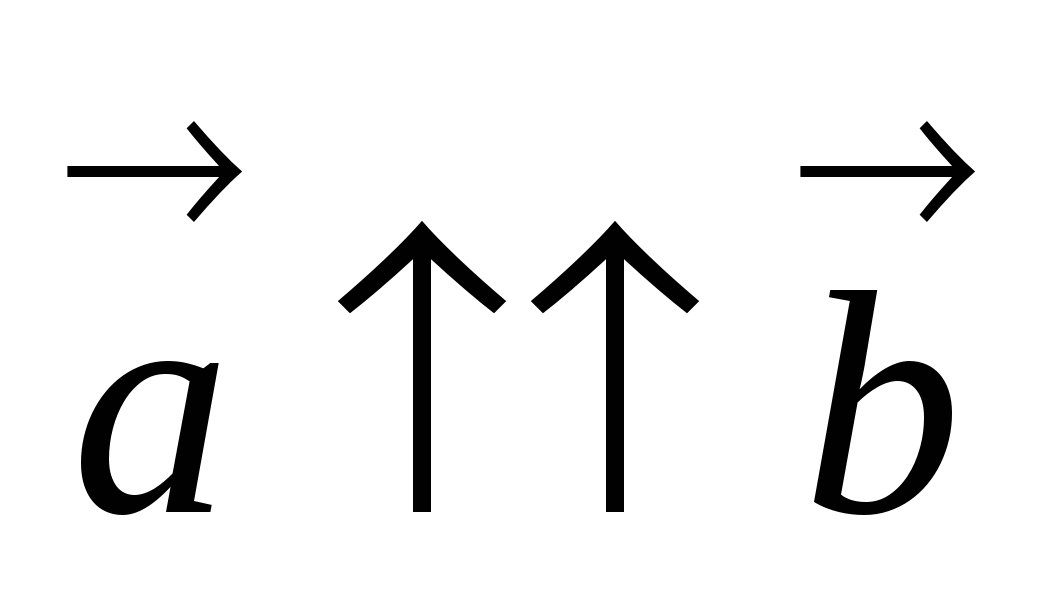 , то
, то 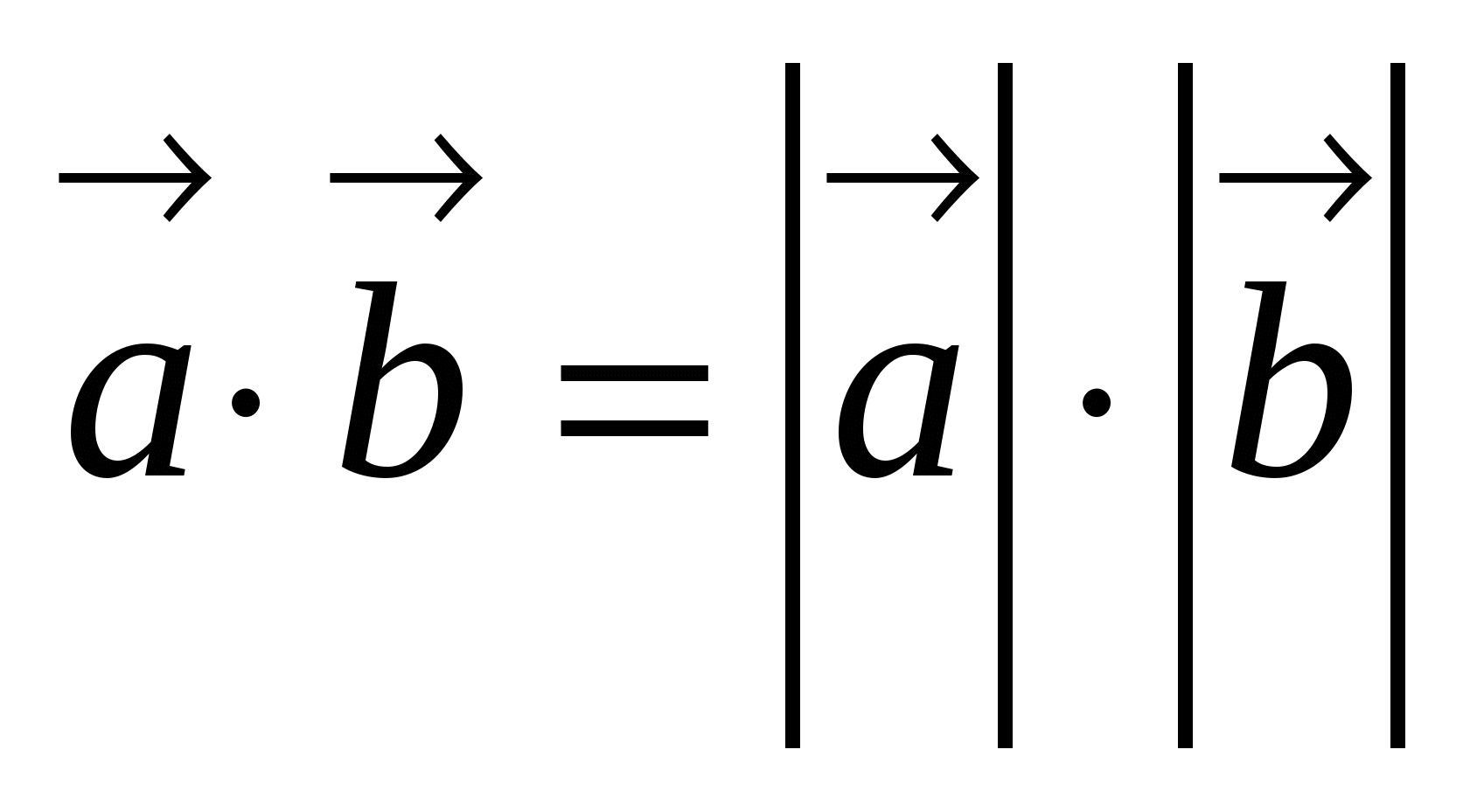 . В частности,
. В частности, 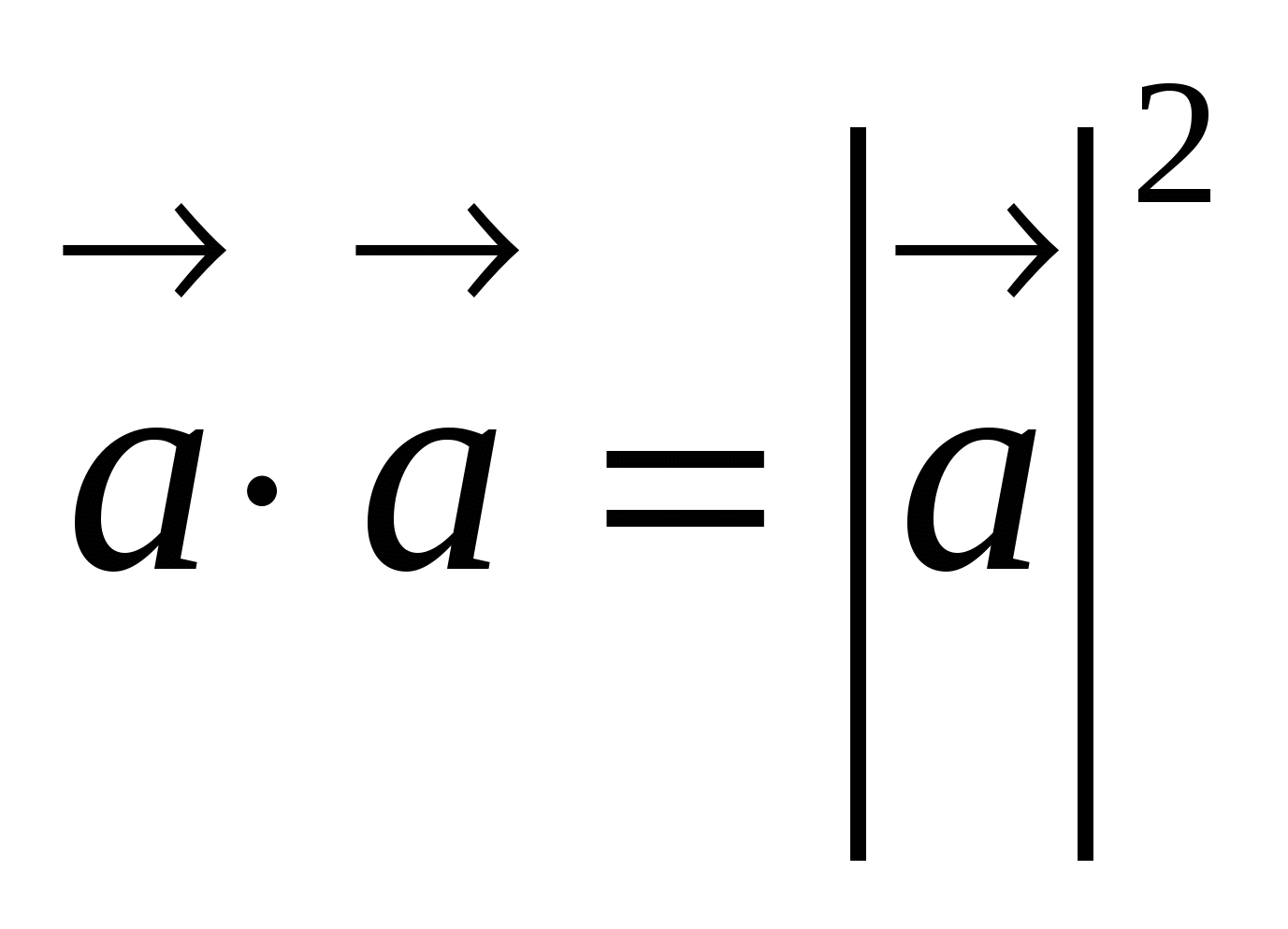 .
.
Скалярное произведение 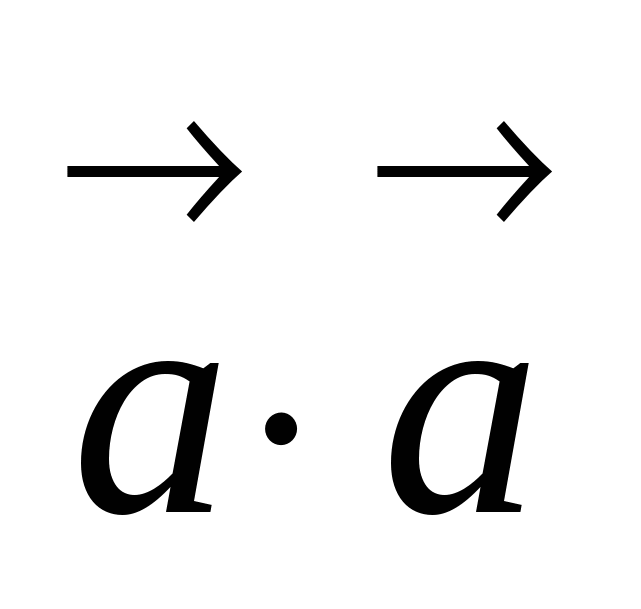 называется скалярным квадратом
называется скалярным квадратом ![]() и обозначается
и обозначается 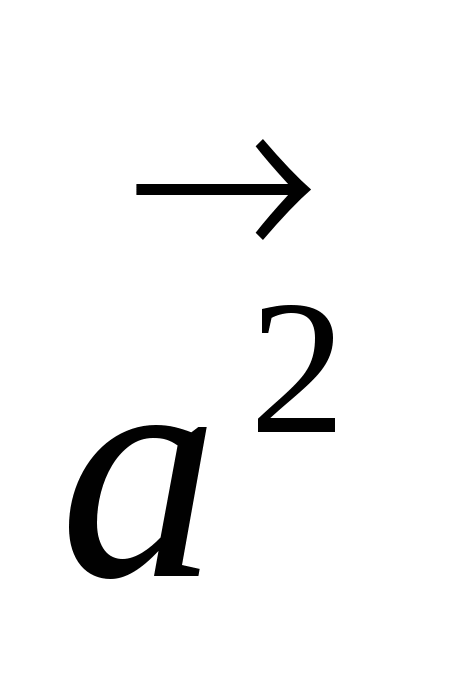 . Таким образом, имеем:
. Таким образом, имеем:
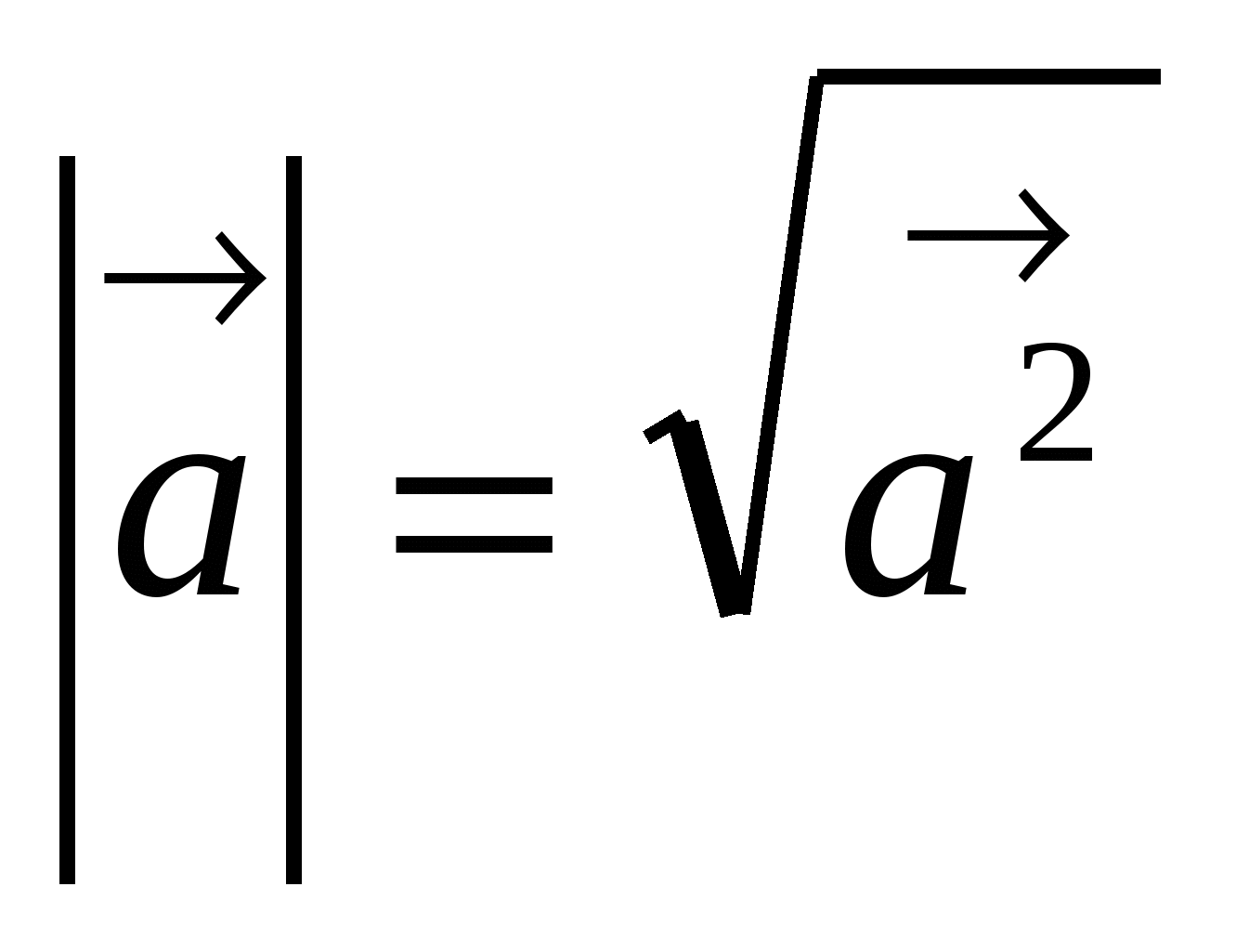 .
.
2. Если ![]() , то
, то 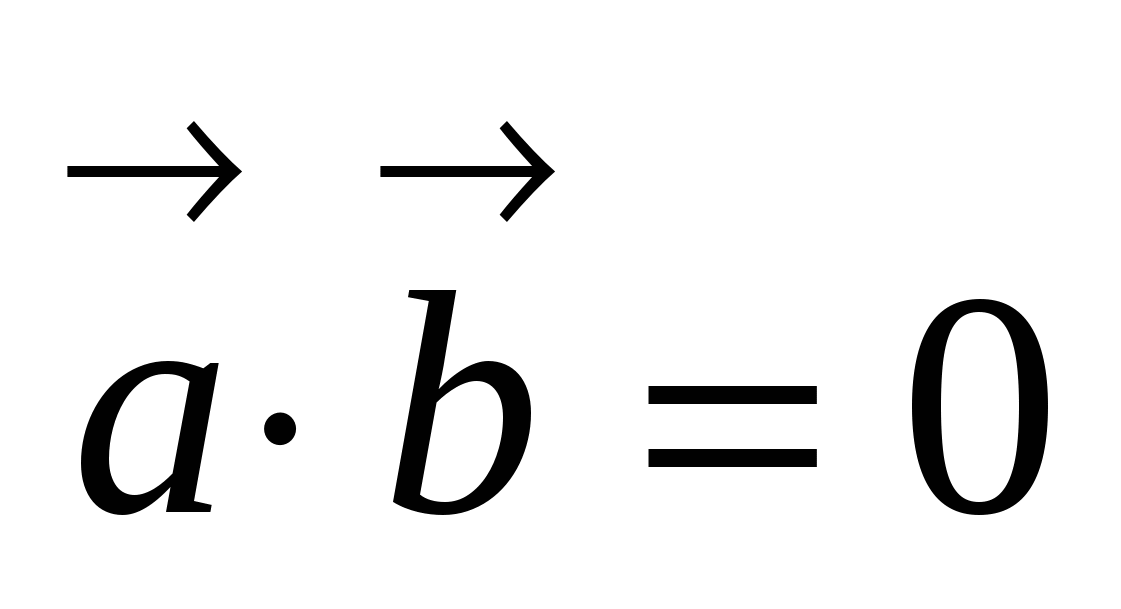 .
.
Свойства скалярного произведения
10. 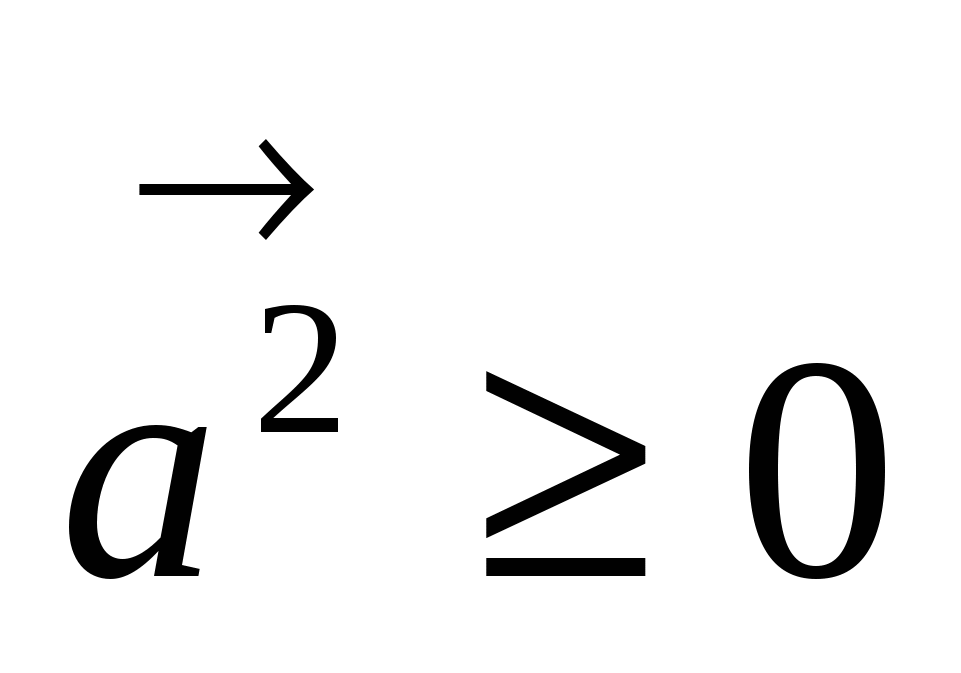 , причем
, причем 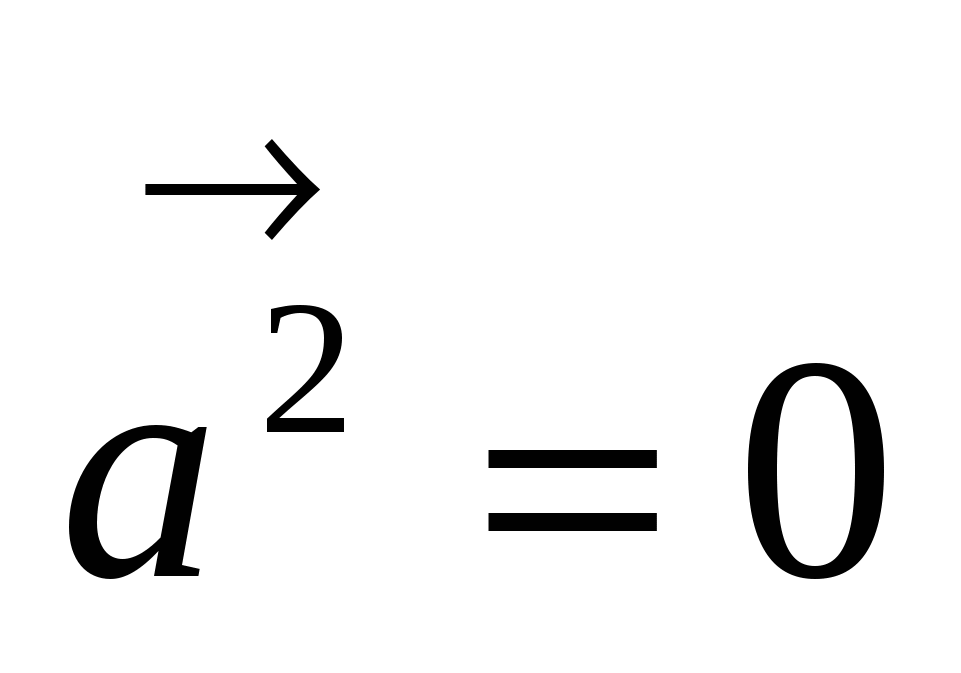 тогда и только тогда, когда
тогда и только тогда, когда 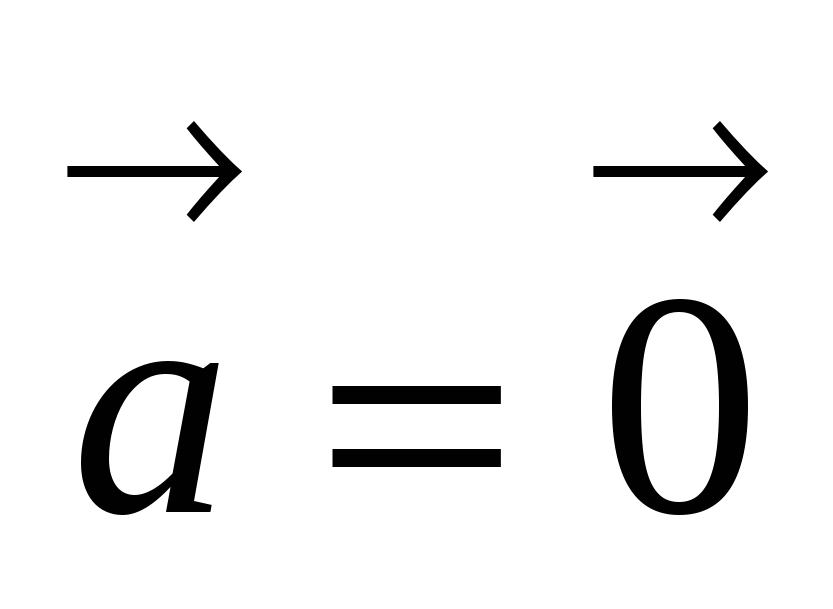 .
.
20. 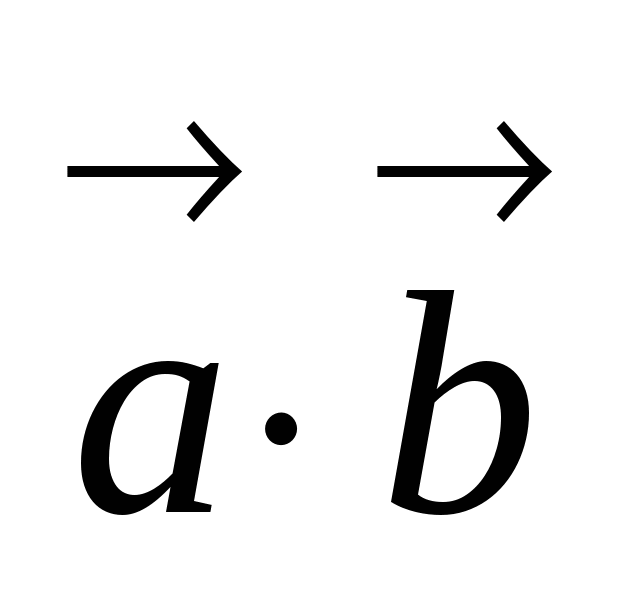 =
= 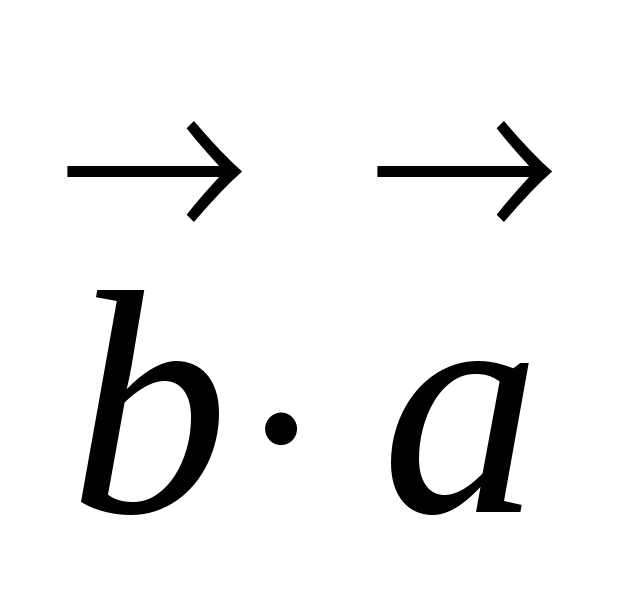 .
.
30. 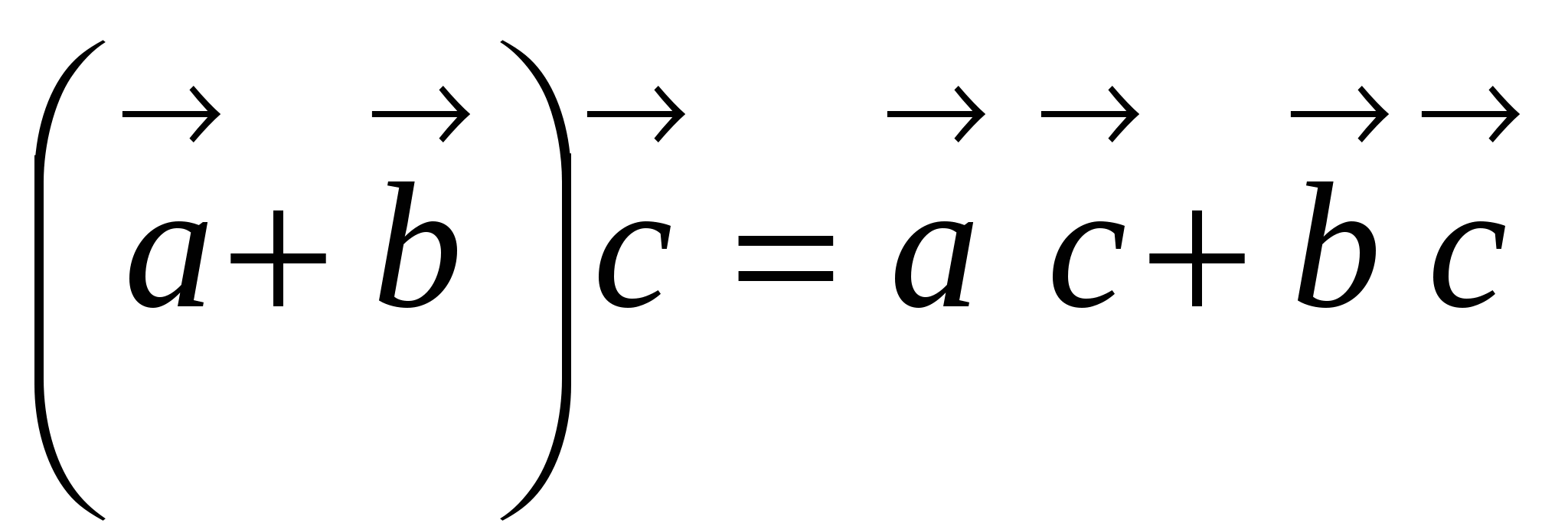 Это свойство имеет место для любого числа слагаемых.
Это свойство имеет место для любого числа слагаемых.
40. 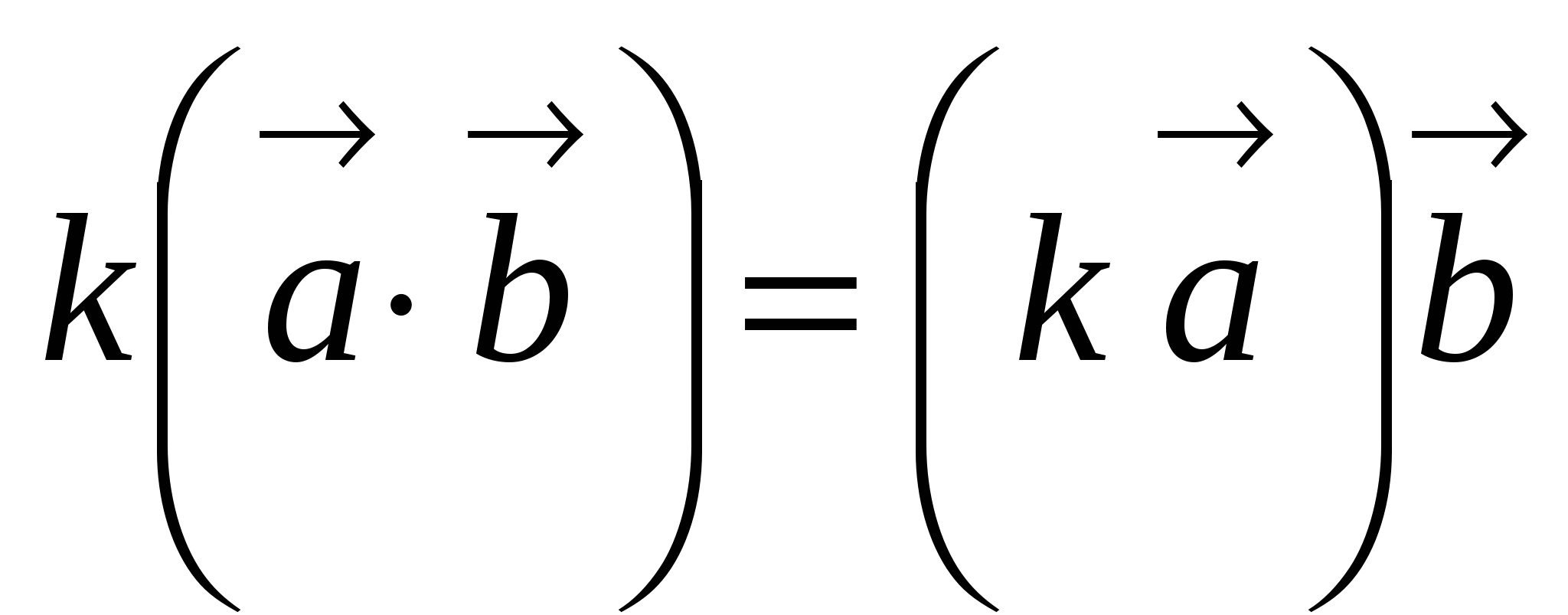 .
.
В следующей таблице приводятся примеры использования векторного языка для формулировки и доказательства некоторых геометрических утверждений или вычисления геометрических величин.
Что требуется
доказать
(на геометрическом языке)
Что достаточно доказать
(на векторном языке)
1) 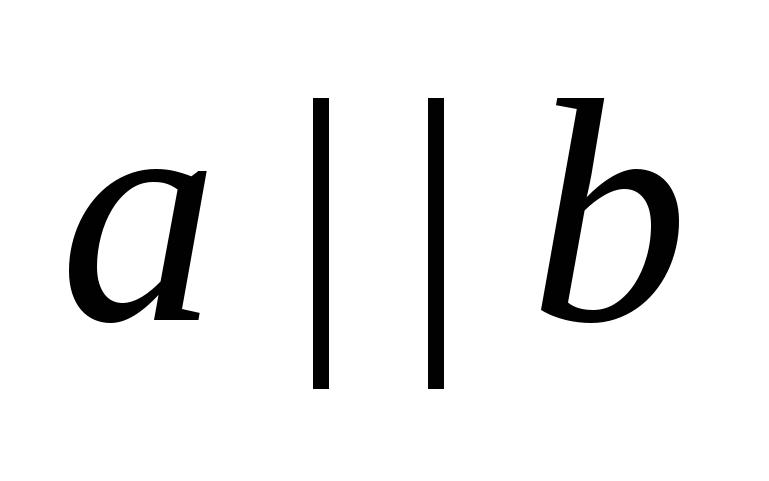
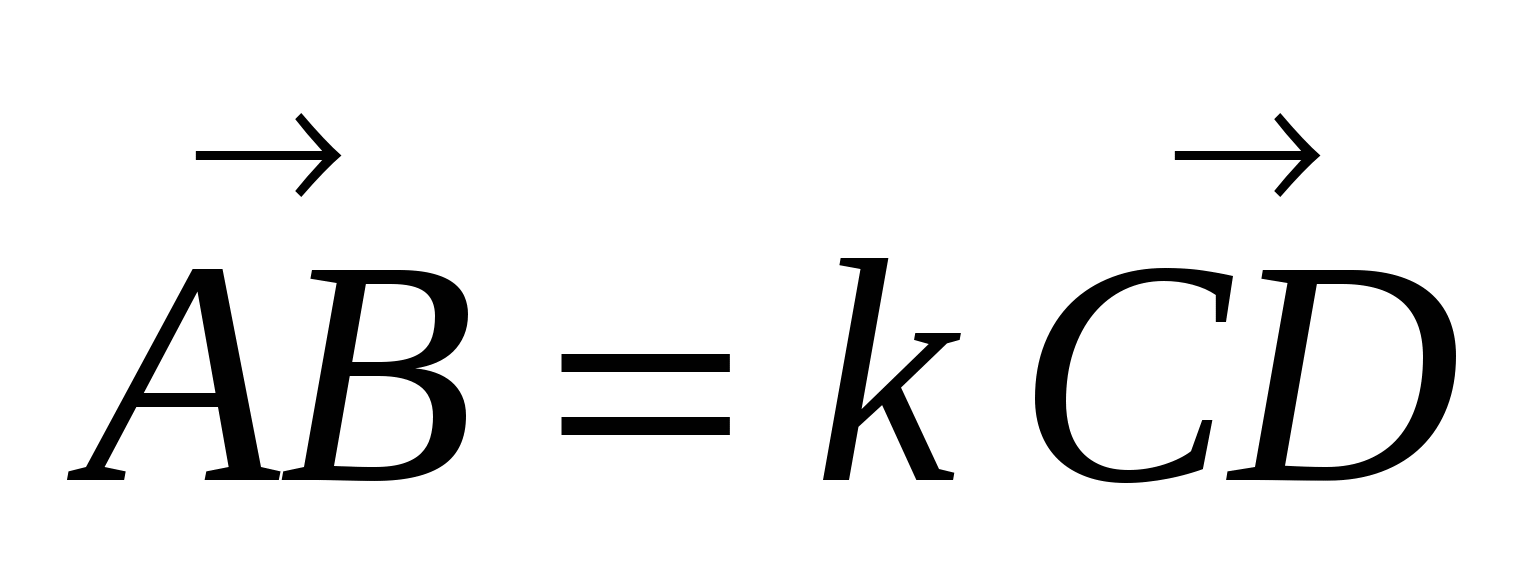 , где отрезки АВ и СD принадлежат соответственно прямым а и b, k - число. В зависимости от выбора АВ и СD возникают различные векторные соотношения, среди которых выбираются подходящие.
, где отрезки АВ и СD принадлежат соответственно прямым а и b, k - число. В зависимости от выбора АВ и СD возникают различные векторные соотношения, среди которых выбираются подходящие.
2) Точки А, В и С принадлежат
прямой а.
а) Установить справедливость одного из следующих равенств: 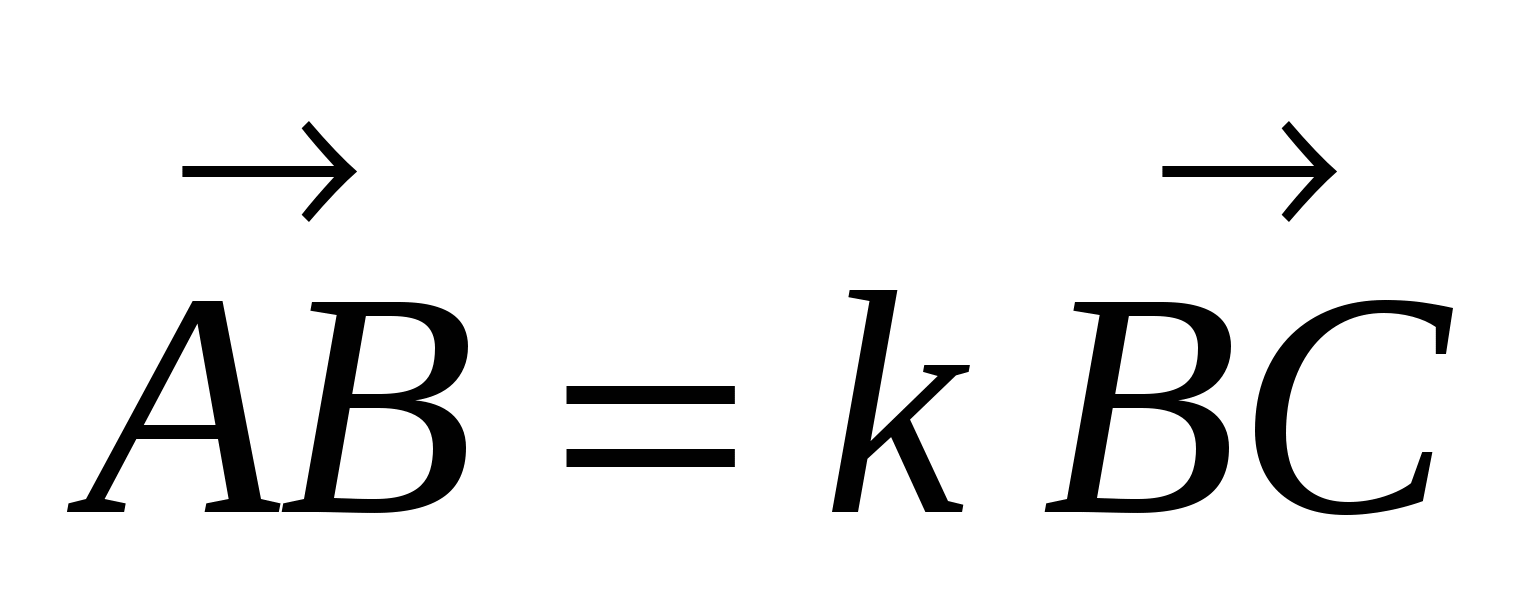 , или
, или 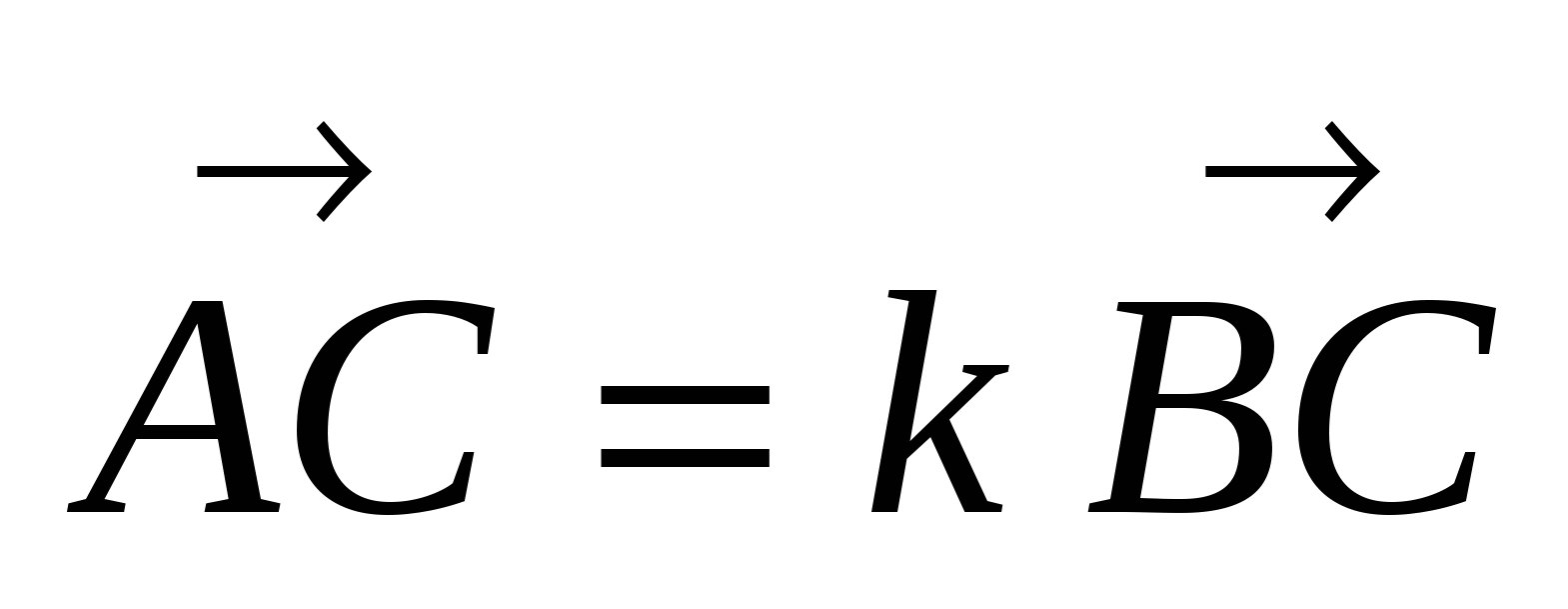 , или
, или 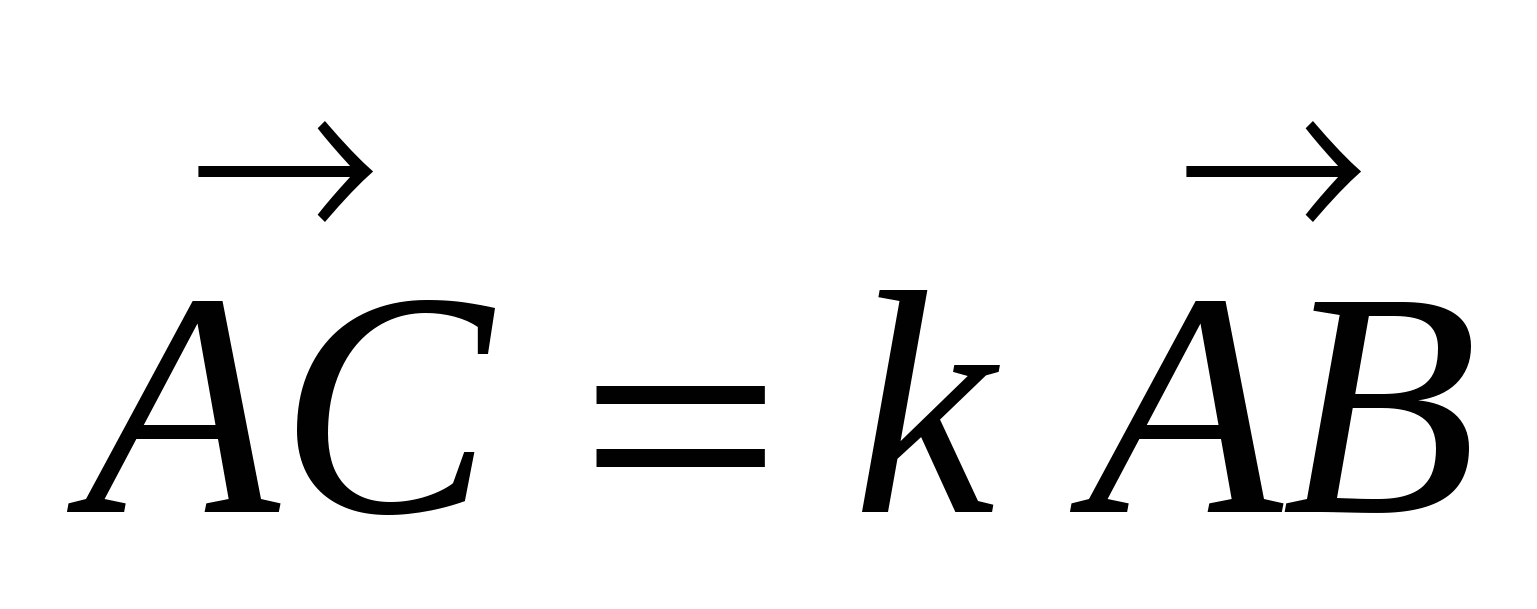 .
.
б) Доказать равенство 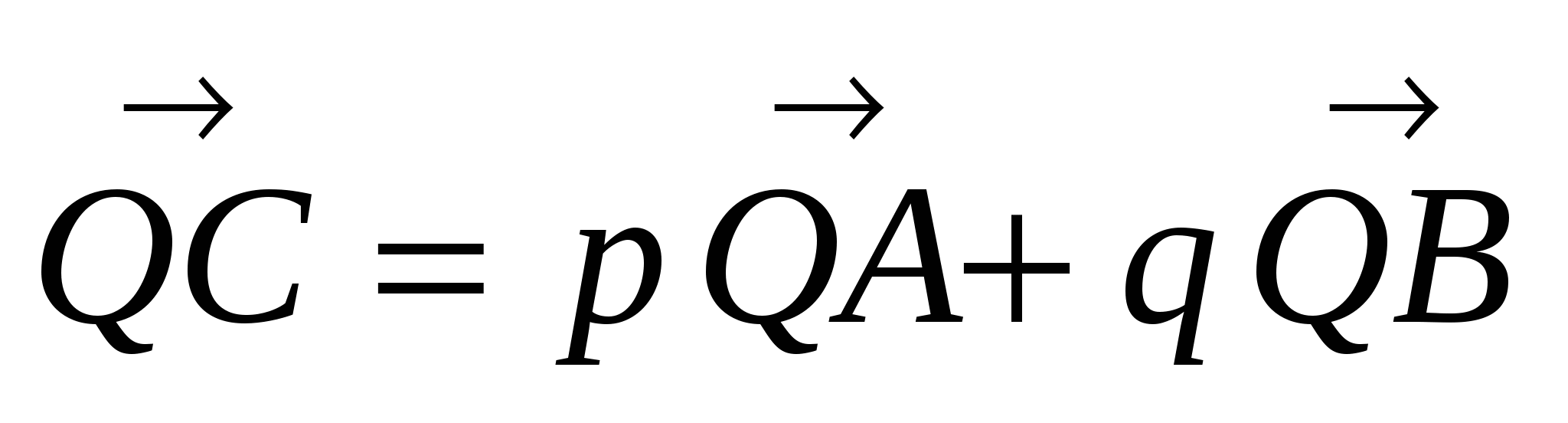 ,
,
где 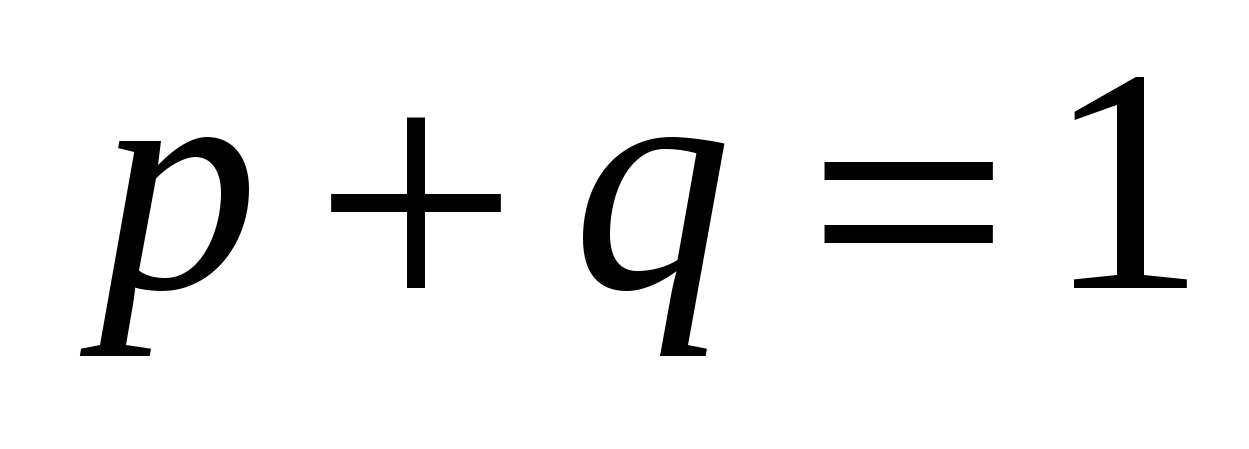 и Q - произвольная точка.
и Q - произвольная точка.
в) Доказать равенство 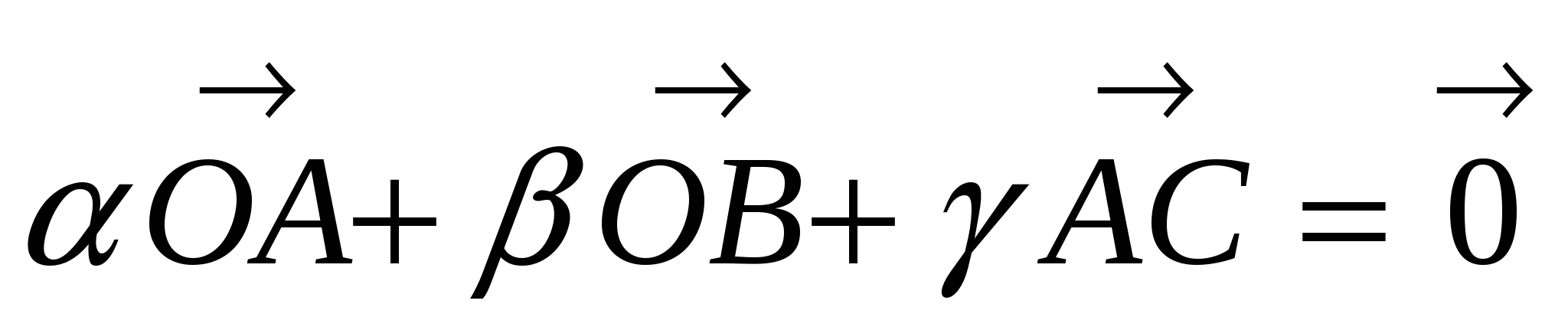 ,
,
где 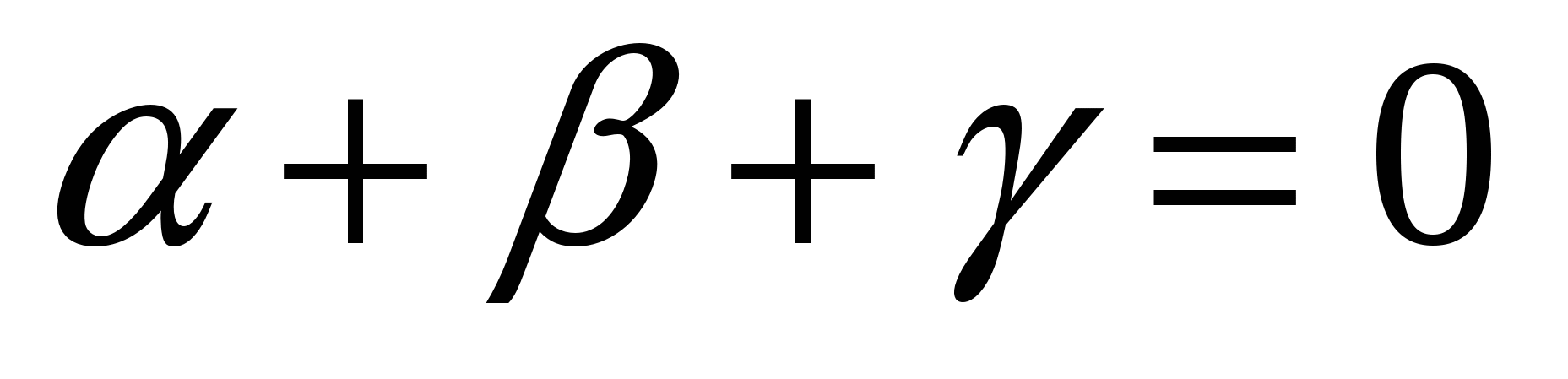 и Q - произвольная точка.
и Q - произвольная точка.
3) Точка С принадлежит отрезку АВ, где 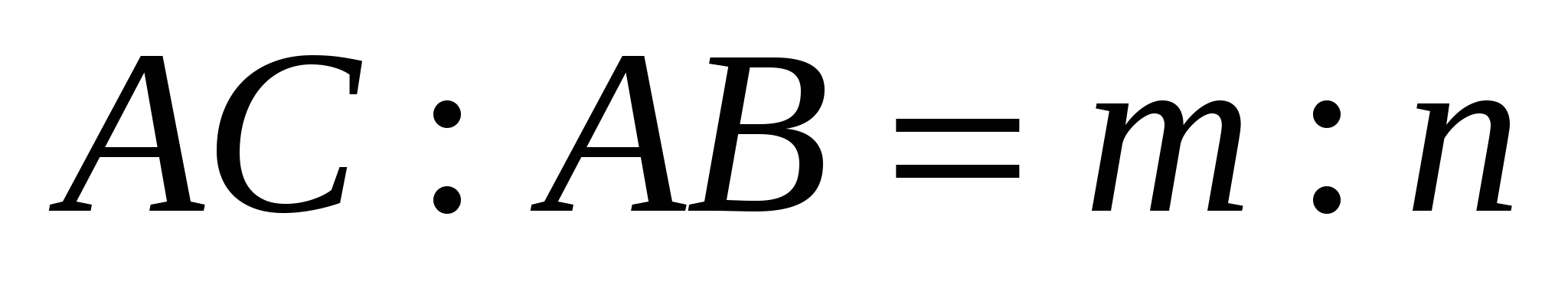 (деление отрезка в данном отношении).
(деление отрезка в данном отношении).
![]() или
или 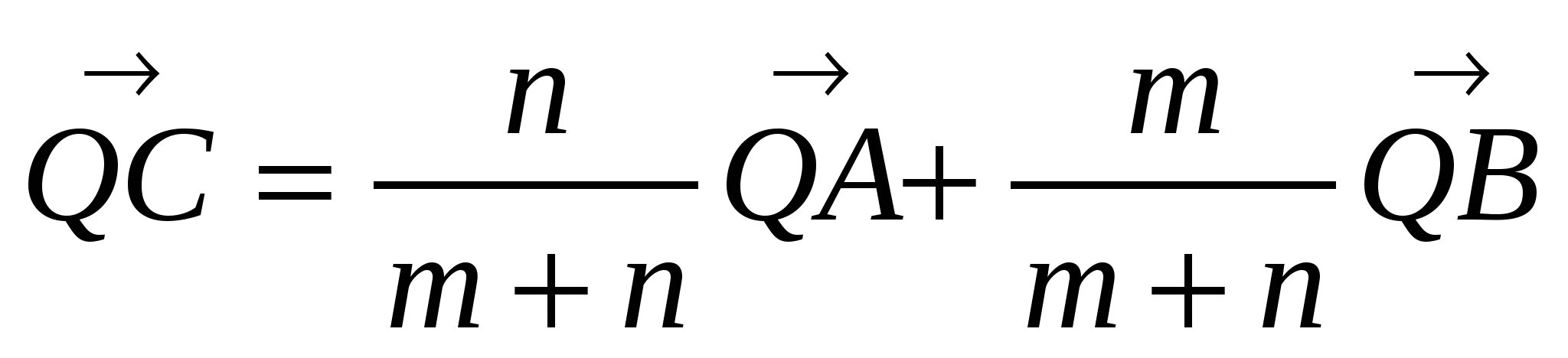
для некоторой точки Q.
4) 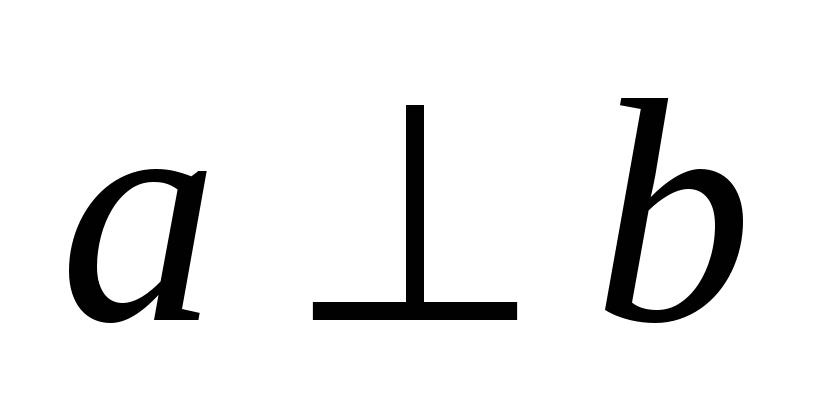
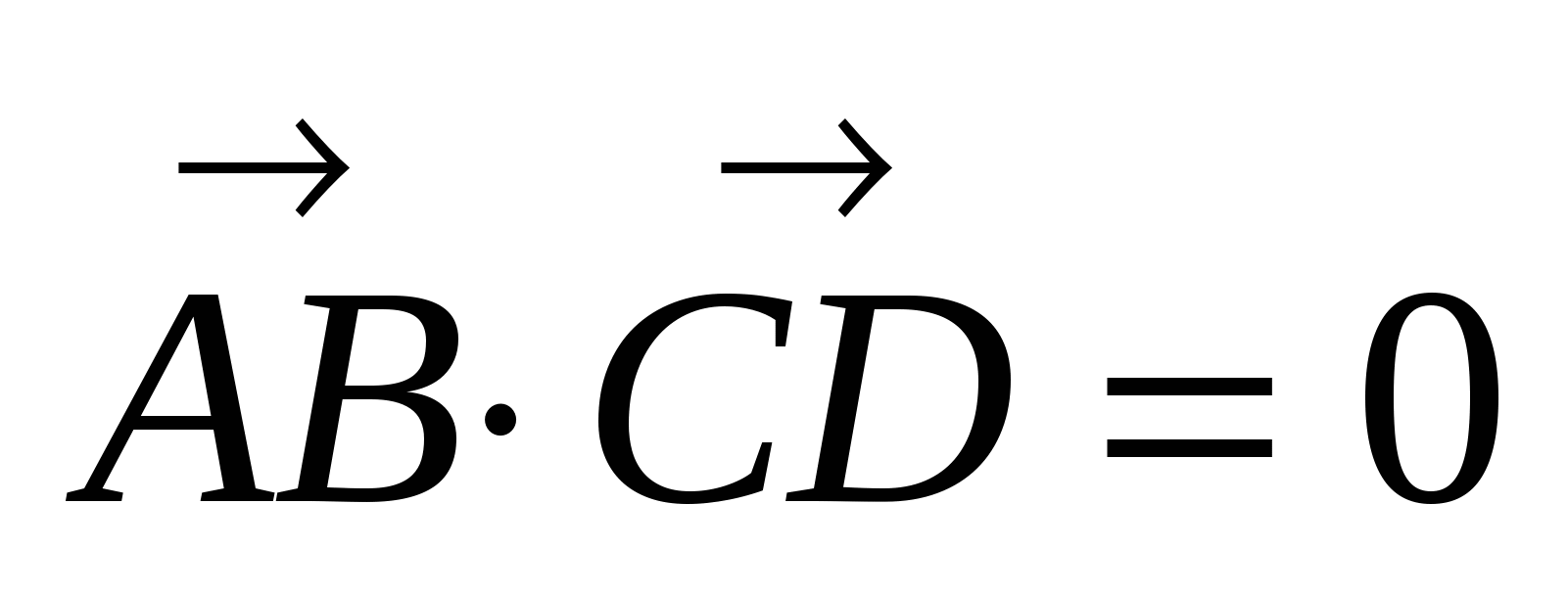 , где точки А и В принадлежат прямой а, точки С и D - прямой b.
, где точки А и В принадлежат прямой а, точки С и D - прямой b.
5) Вычислить
длину отрезка
а) Выбрать два неколлинеарных базисных вектора (или три некомпланарных), у которых известны длины и угол между ними.
б) Разложить по ним вектор, длина которого вычисляется.
в) Найти скалярный квадрат этого вектора, используя формулу ![]() .
.
6) Вычислить
величину угла
а) Выбрать два неколлинеарных базисных вектора, для которых известны отношение длин и углы между ними.
б) Выбрать векторы, задающие искомый угол, и разложить их по базисным векторам.
в) Вычислить 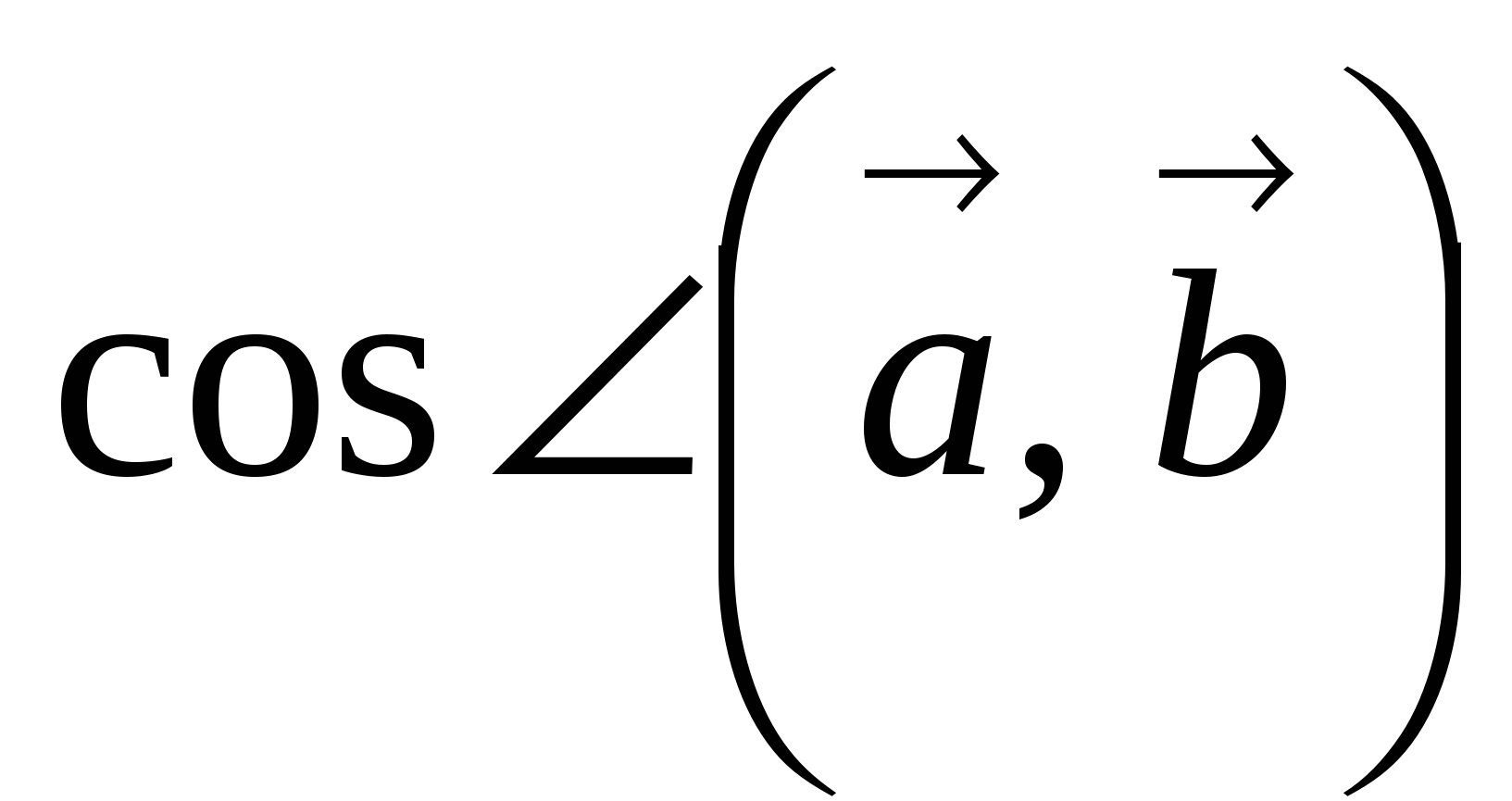
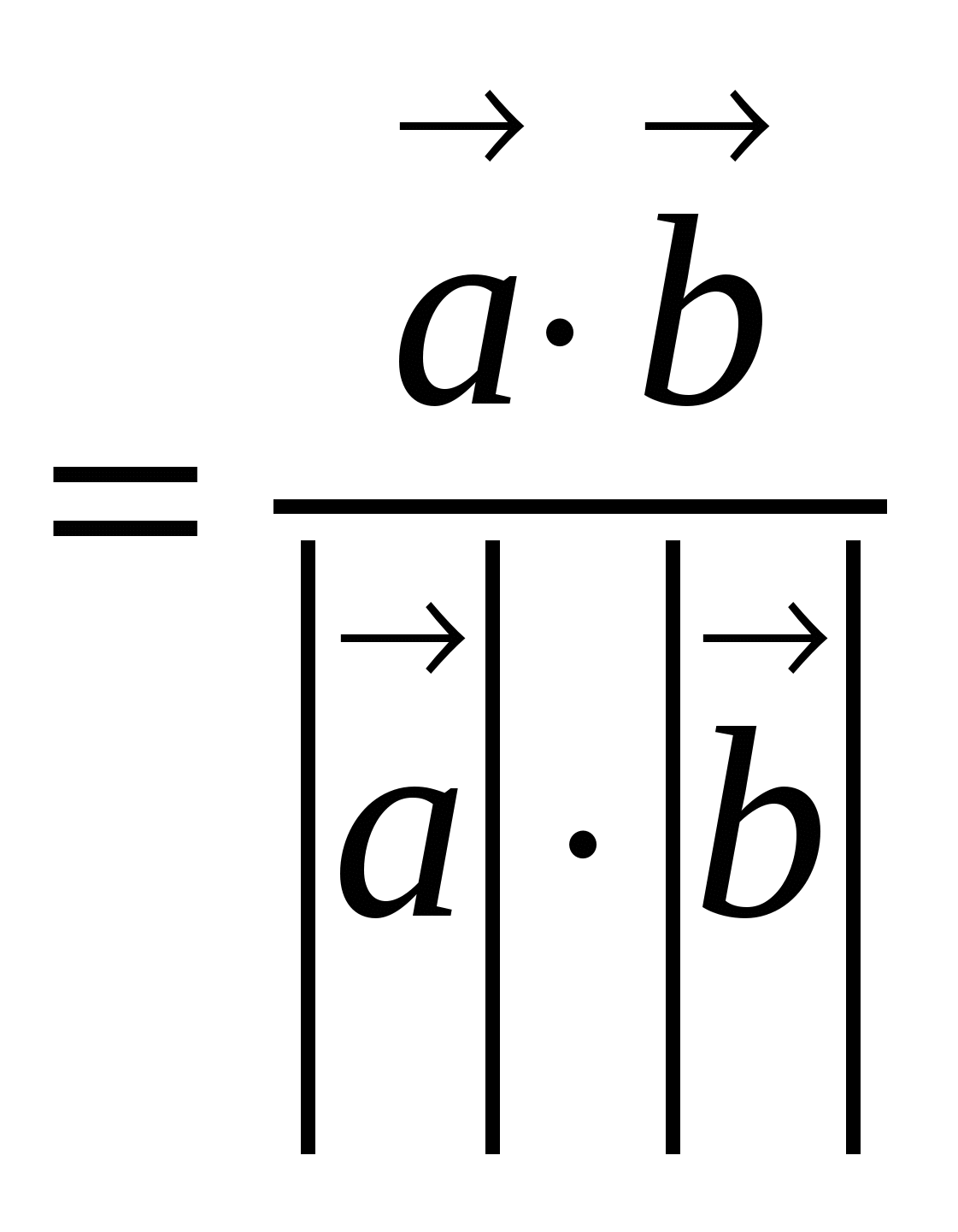 .
.
Задача 1. Найти скалярное произведение векторов 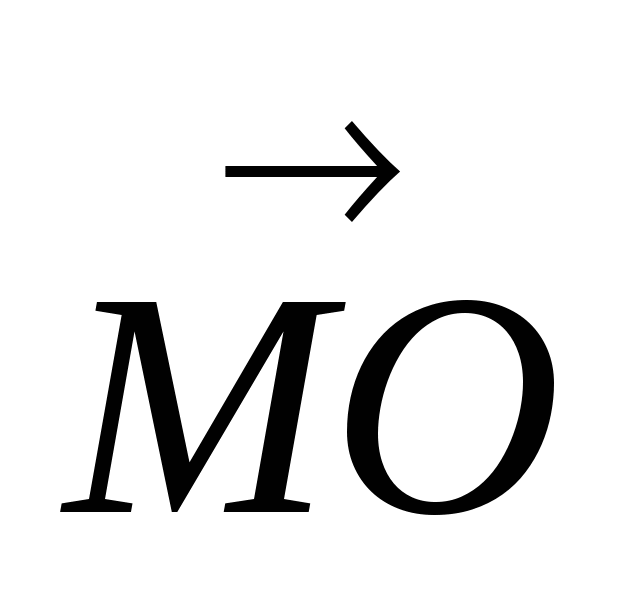 и
и 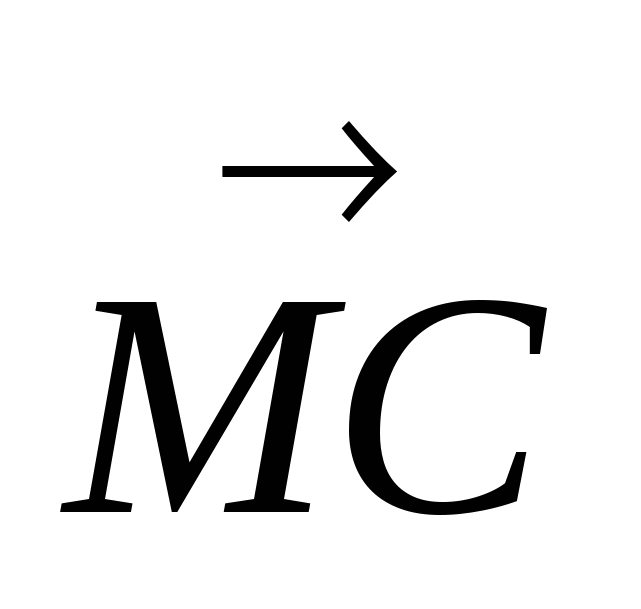 , если высота МО правильной четырёхугольной пирамиды МАВСD равна 7, а боковое ребро равно 14.
, если высота МО правильной четырёхугольной пирамиды МАВСD равна 7, а боковое ребро равно 14.
Схема решения:
1) Из ∆МОС:
ОМС = φ; ![]() =
= 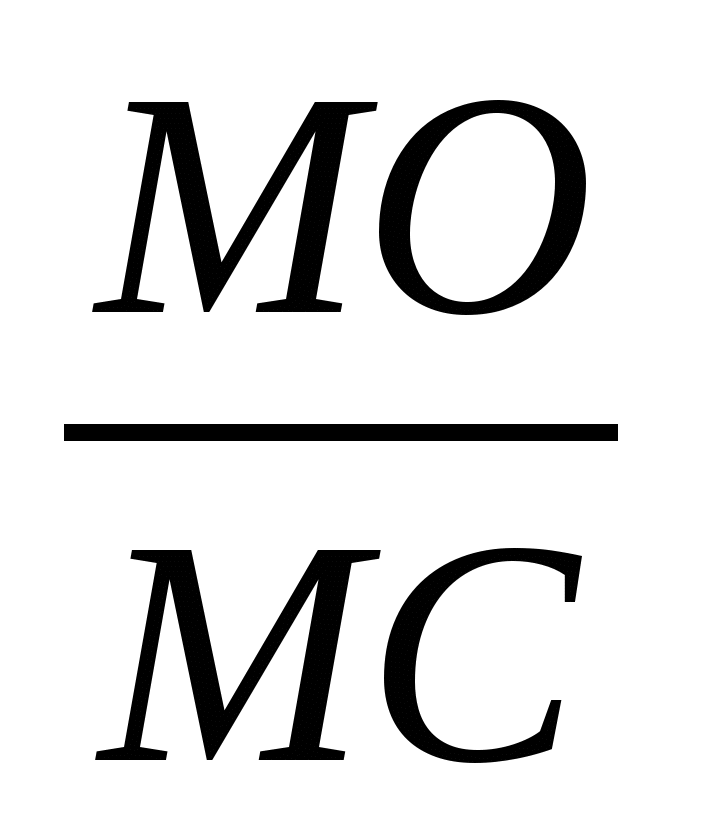 =>
=> 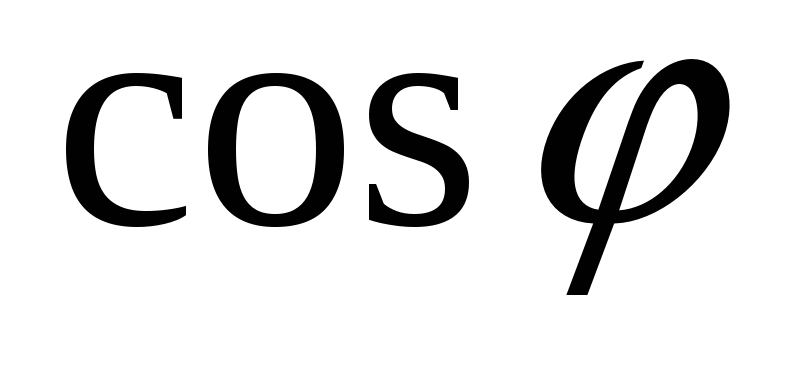 =
= 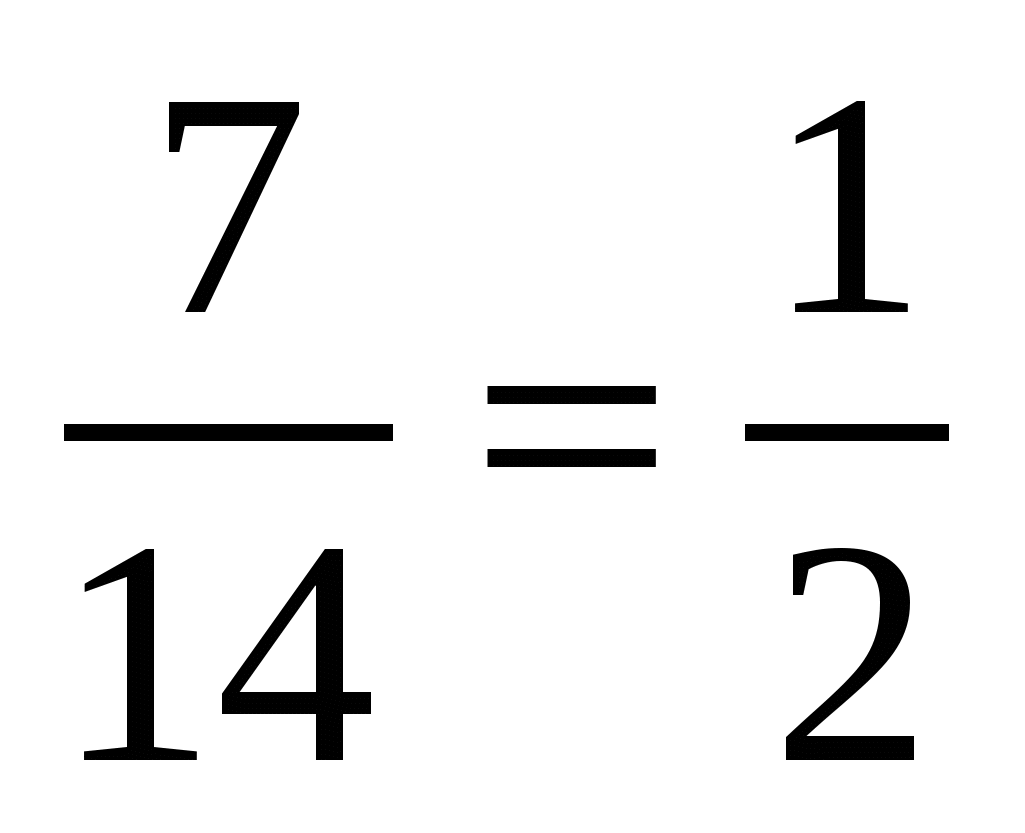 .
.
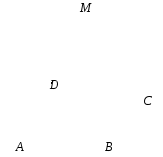
2)  ,
,
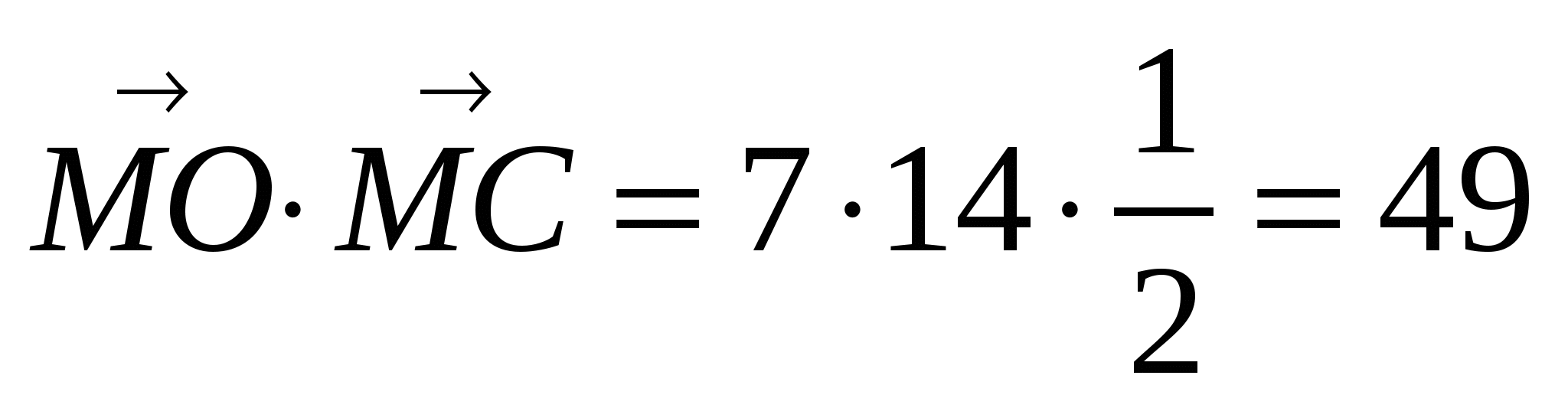 .
.
Ответ: 49.
Задача 2. На окружности с центром в точке О взяты точки А, В, С. Найти угол АОВ, если известно, что ![]() .
.

Схема решения:
1 способ. Точки А, В, С принадлежат окружности, следовательно, 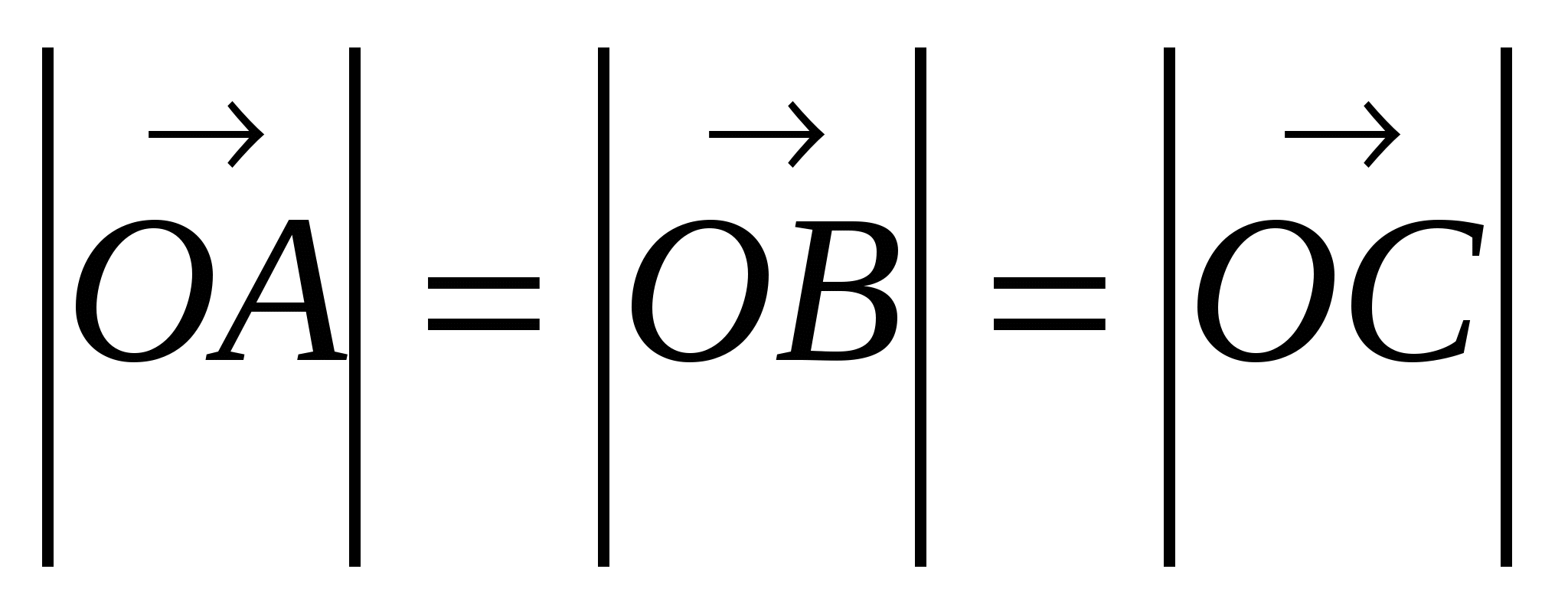 = R, где R - радиус окружности.
= R, где R - радиус окружности.
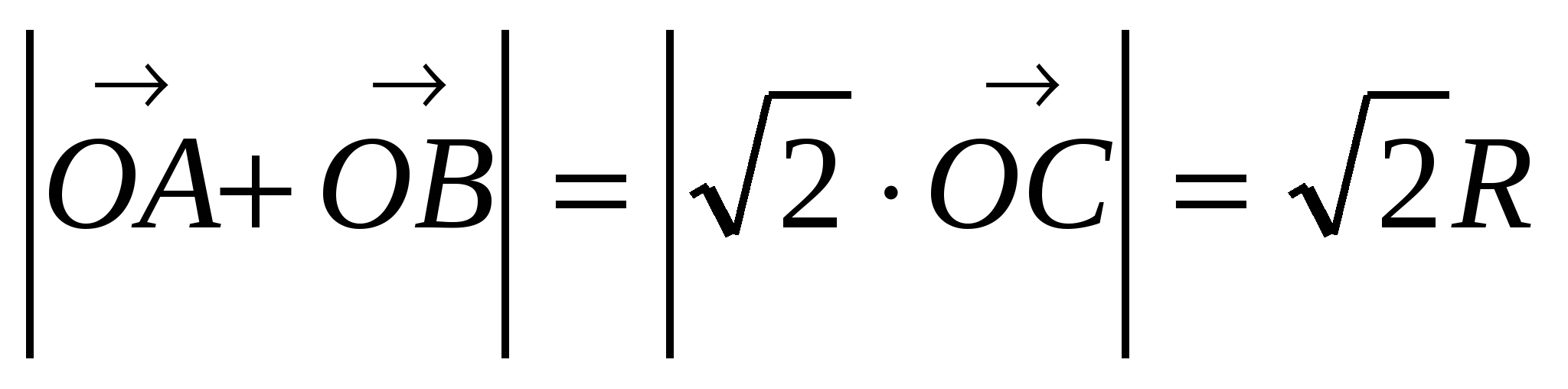 .
.
Если сложить векторы 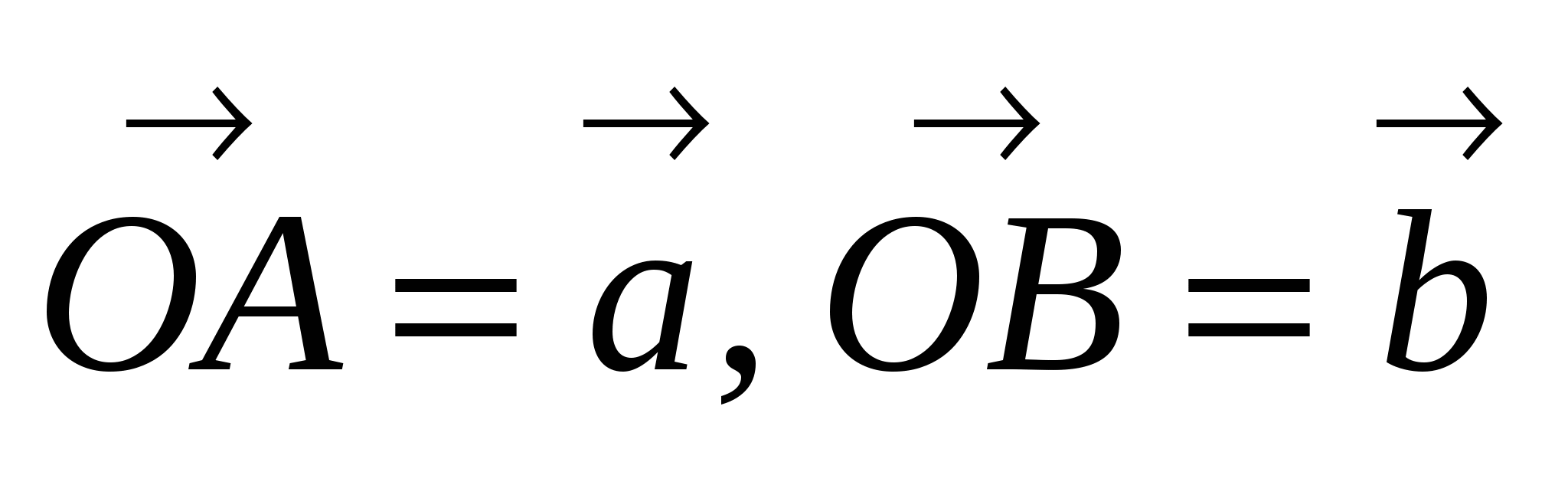 по правилу треугольника, то в этом треугольнике для сторон справедливо соотношение, обратное теореме Пифагора, следовательно,
по правилу треугольника, то в этом треугольнике для сторон справедливо соотношение, обратное теореме Пифагора, следовательно, 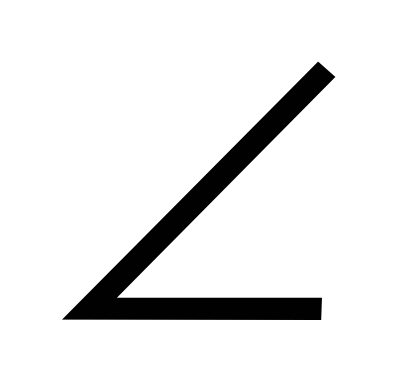 АОВ = 90.
АОВ = 90.
2 способ. Найдём скалярный квадрат (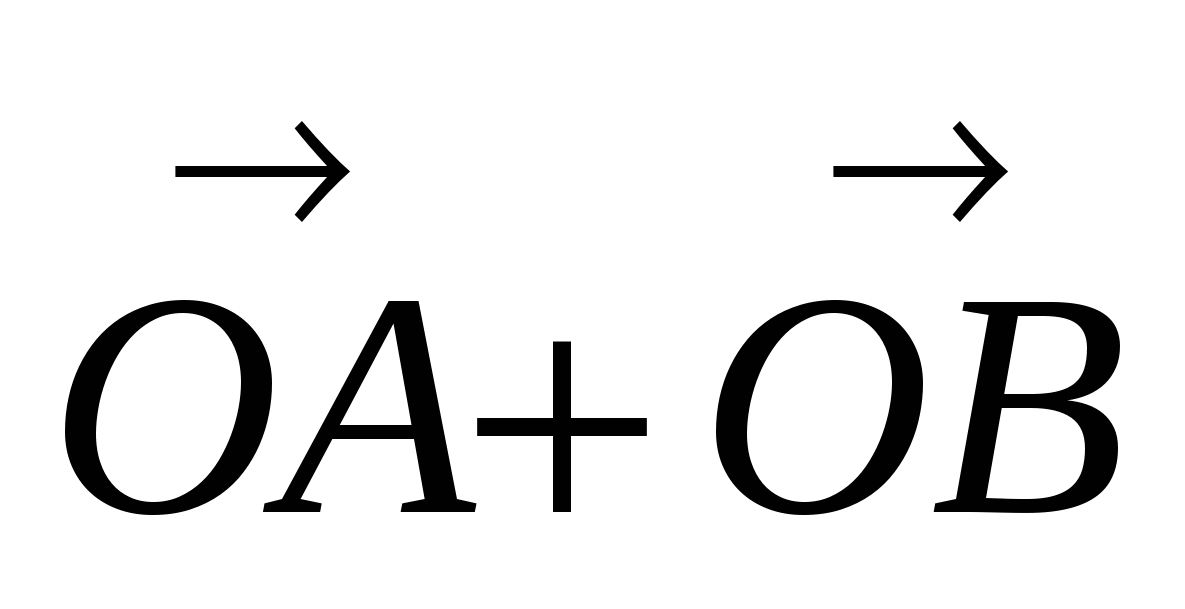 )2 =
)2 =
= 2 +
2 + 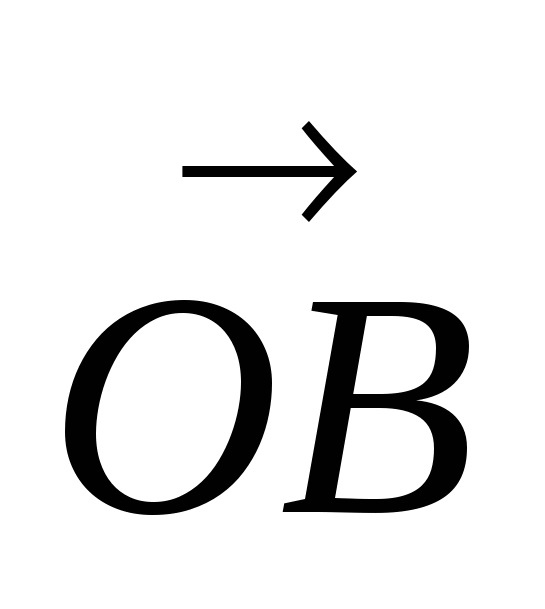 2 +
2 + 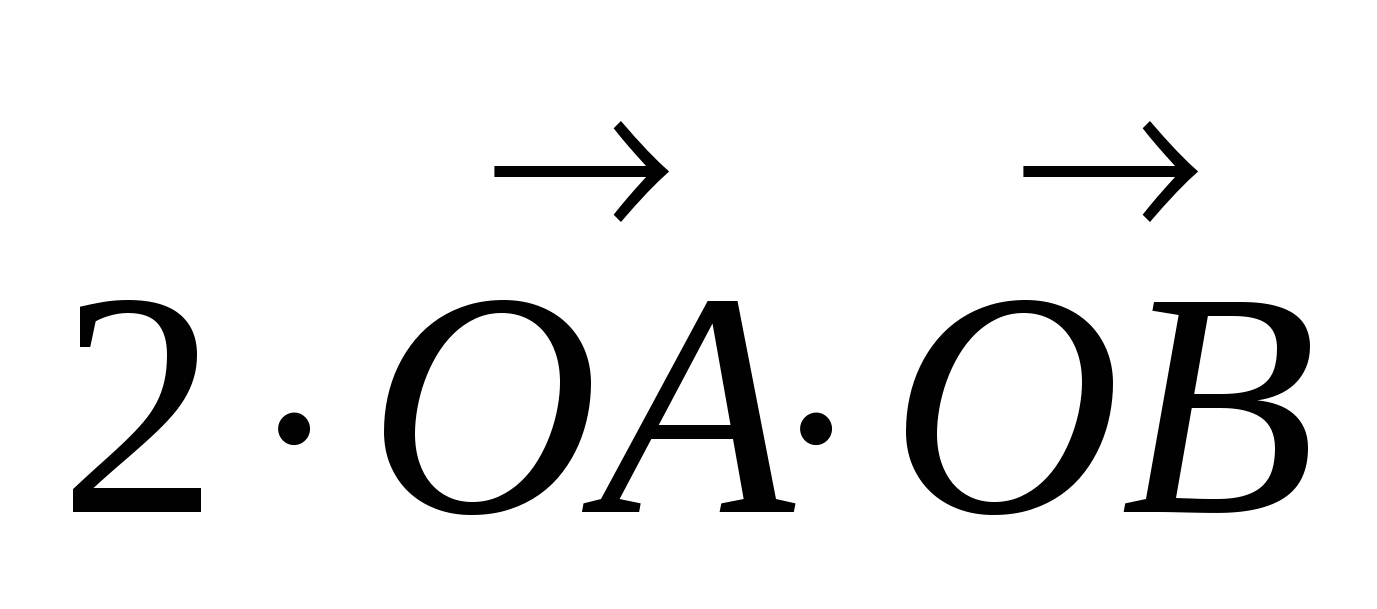 = |
= | |2 + |
|2 + |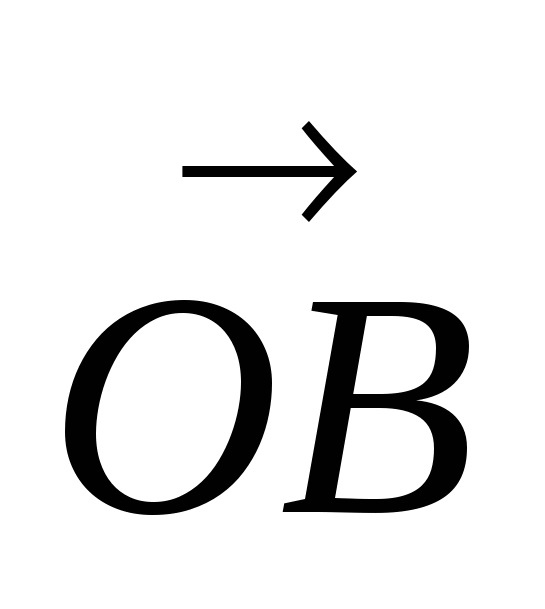 |2 + 2|
|2 + 2| | |
| |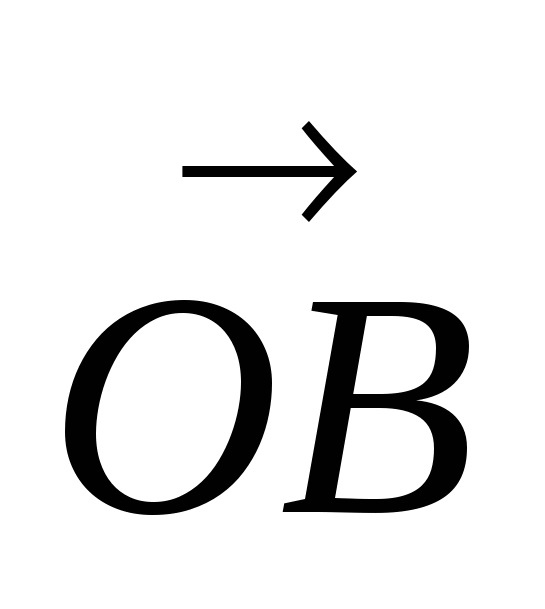 |
| 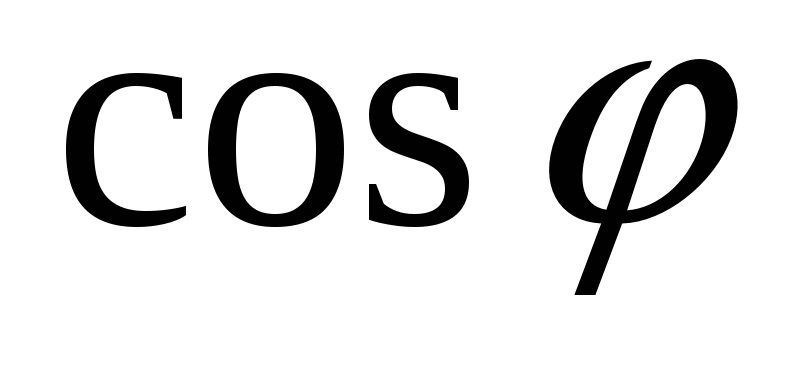 =
=
=R2 + R2 + 2R2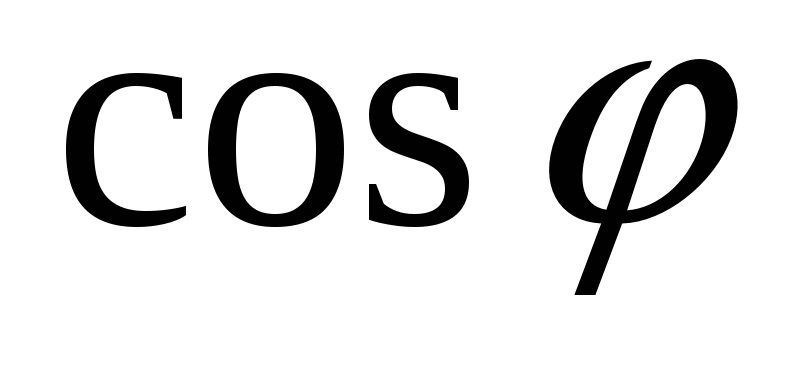 = 2R2 + 2R2
= 2R2 + 2R2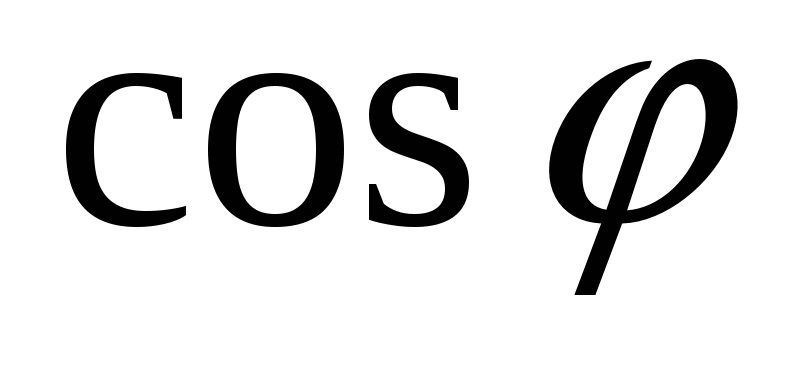 .
.
С другой стороны,
(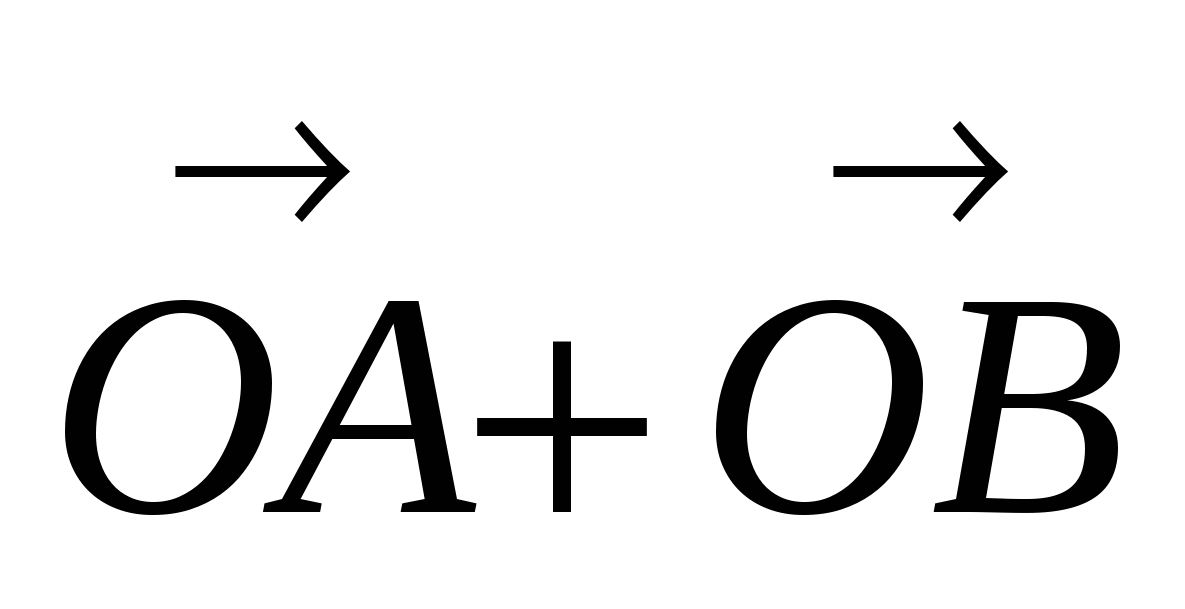 )2 = (
)2 = (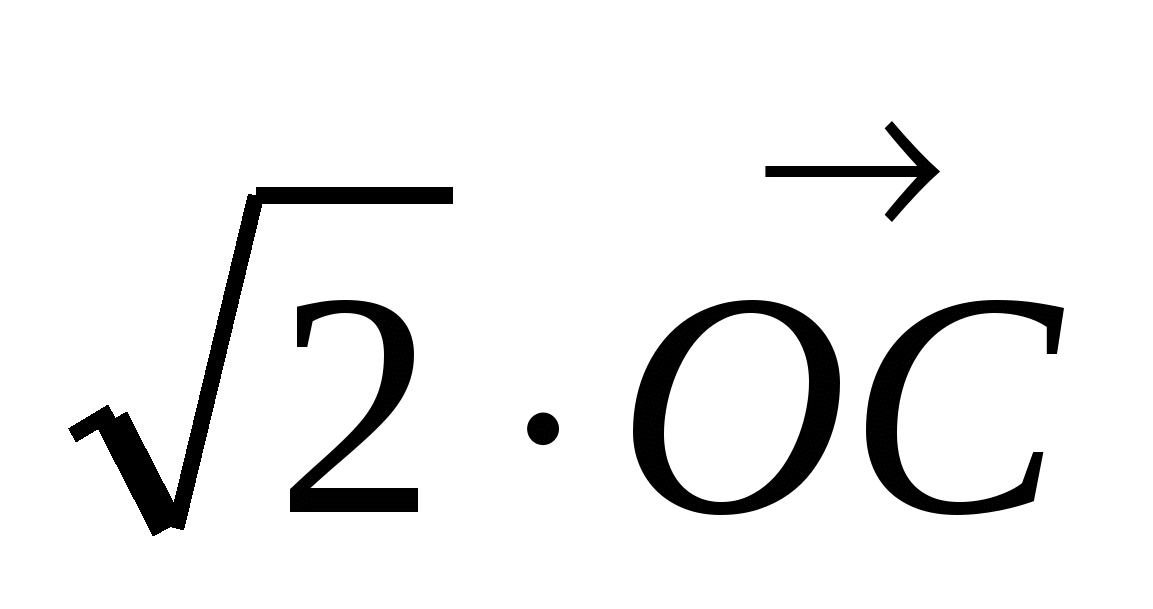 )2 = 2|
)2 = 2|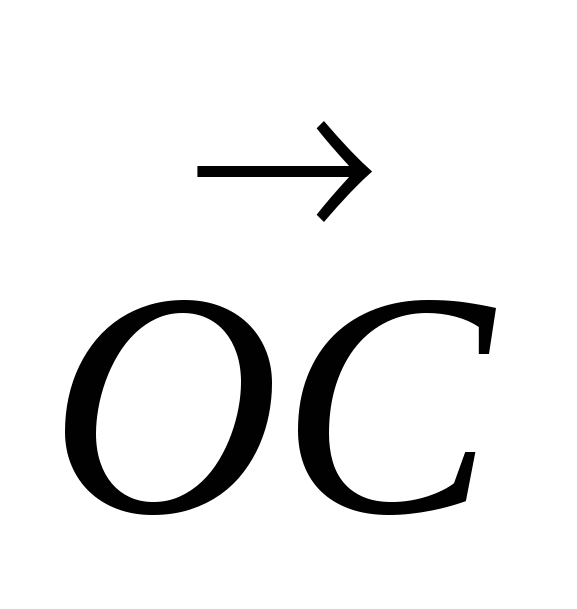 |2 = 2R2.
|2 = 2R2.
Имеем:
2R2 + 2R2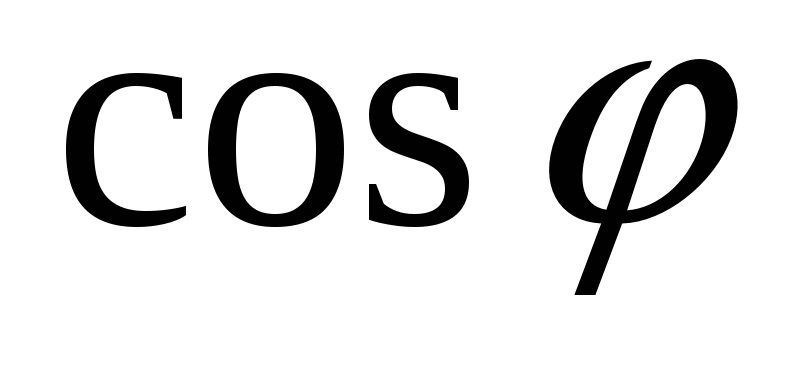 = 2R2,
= 2R2,
2R2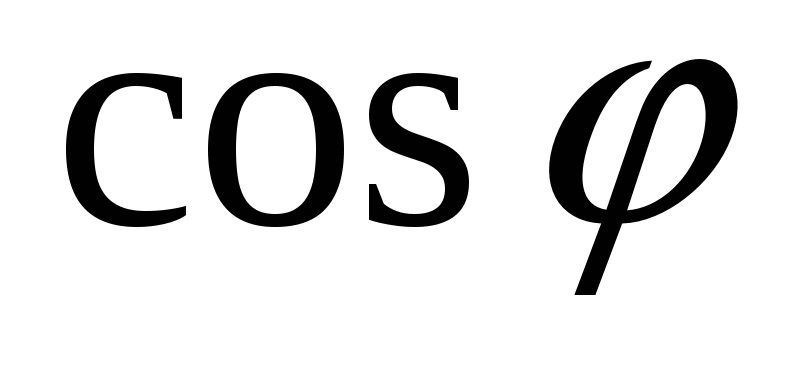 = 0, но R ≠ 0, следовательно,
= 0, но R ≠ 0, следовательно, 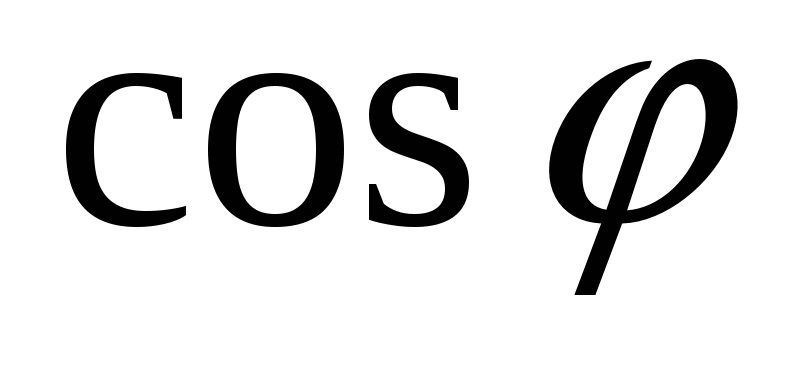 = 0, т.е. φ = 90,
= 0, т.е. φ = 90,
АОВ = 90.
Ответ: 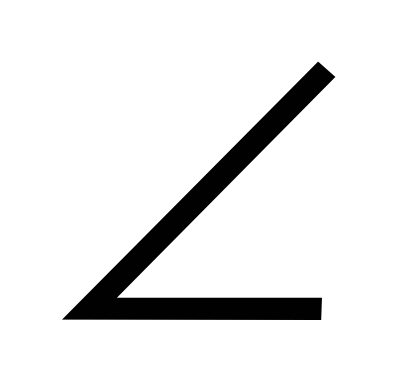 АОВ = 90.
АОВ = 90.
Задача 3. На окружности с центром в точке О взяты точки А,В,С. Найти косинус половины угла ОАВ, если известно, что 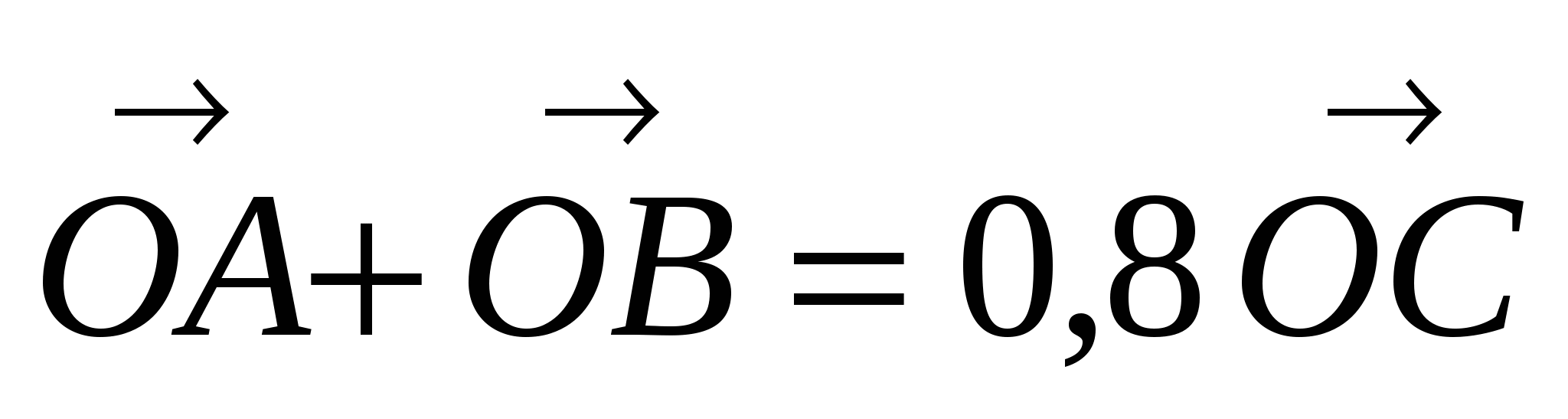 = 0,8
= 0,8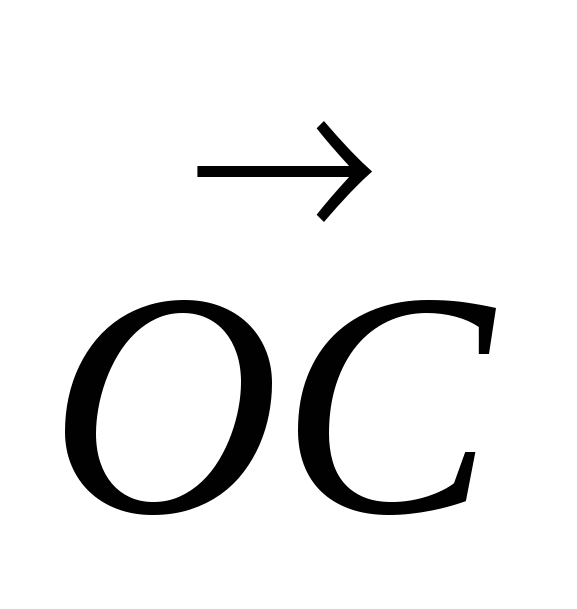 .
.
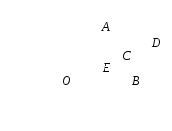
Схема решения:
Сумму векторов  и
и 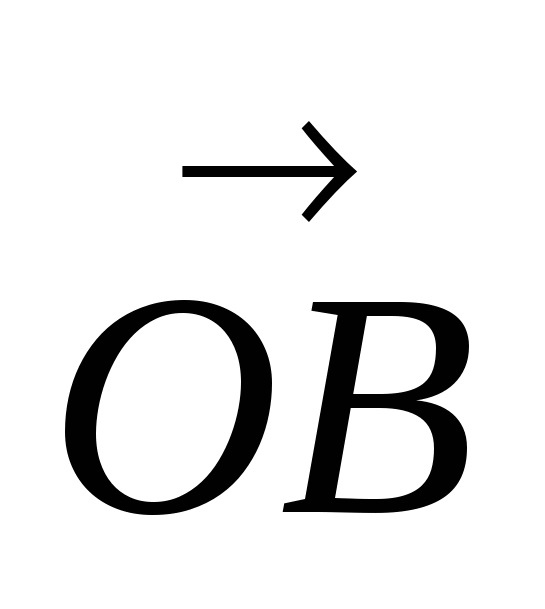 найдём по правилу параллелограмма, получаем вектор
найдём по правилу параллелограмма, получаем вектор 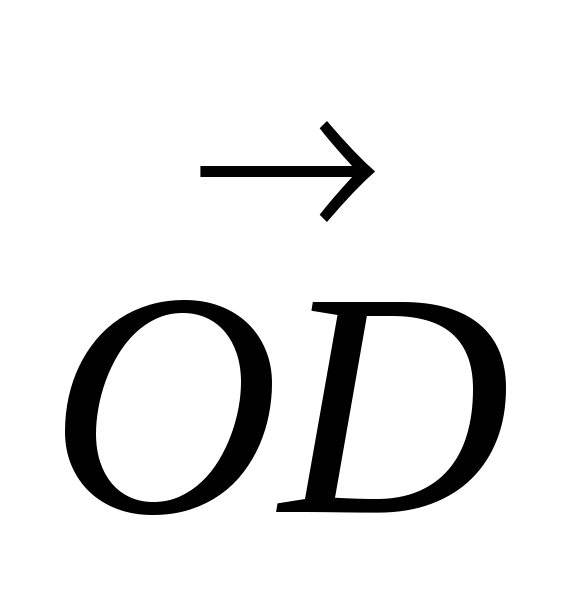 .
.
| | = |
| = |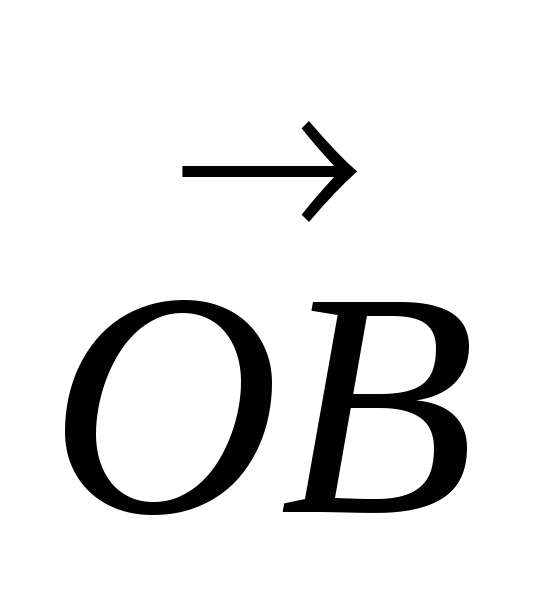 | = |
| = |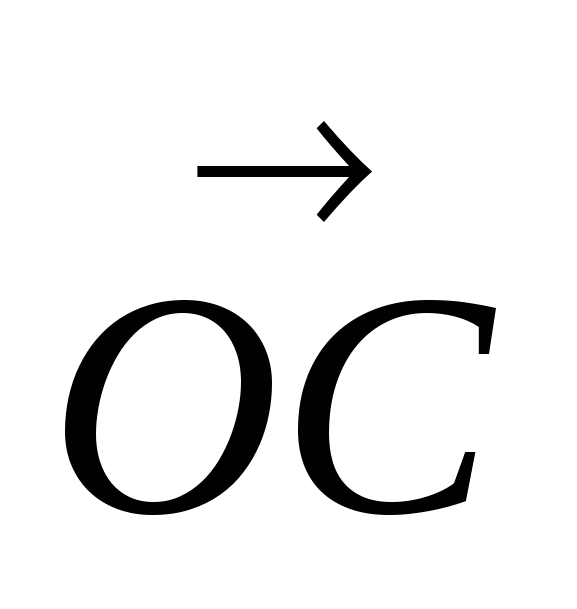 | = R, где R - радиус окружности.
| = R, где R - радиус окружности.
Следовательно, ОАDВ - ромб, диагонали которого перпендикулярны. Так как |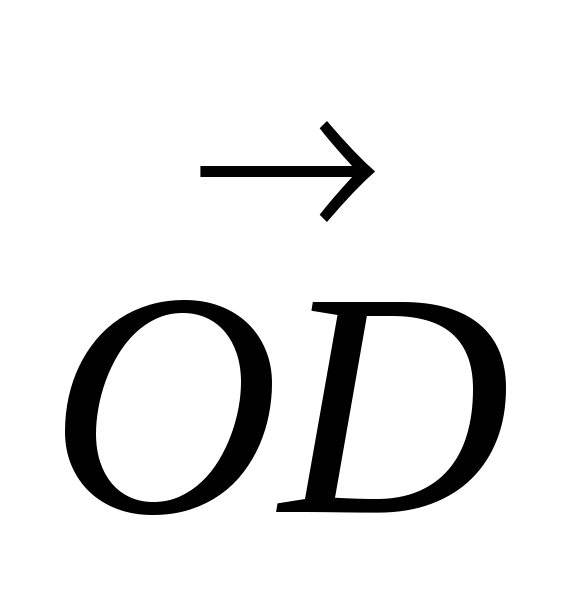 | = |
| = |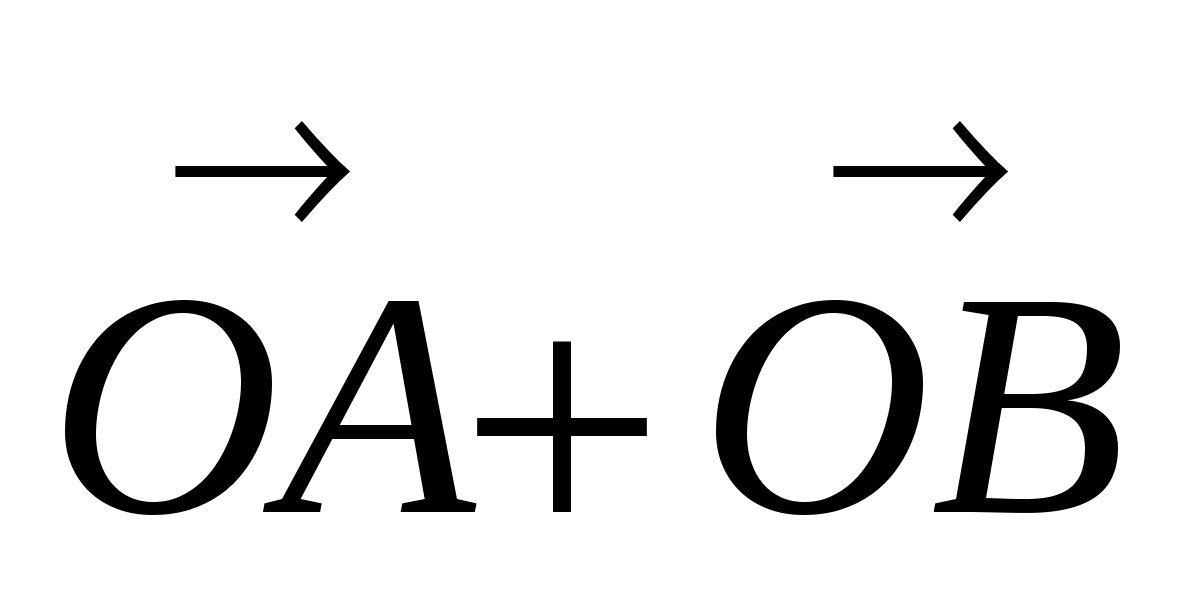 | = | 0,8
| = | 0,8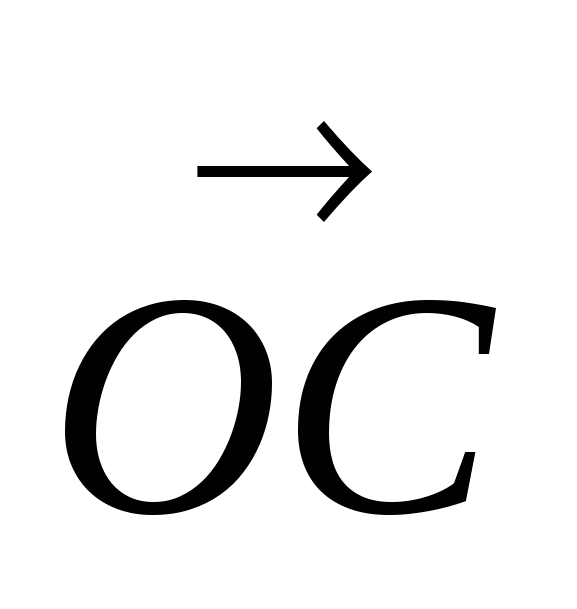 | = 0,8R, то
| = 0,8R, то
|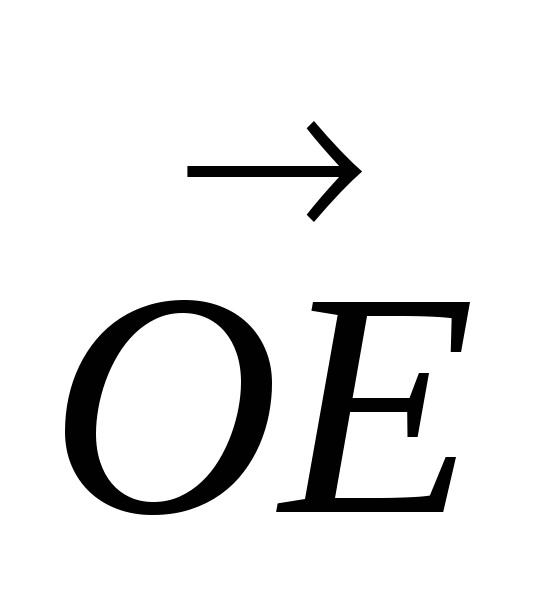 | =
| = 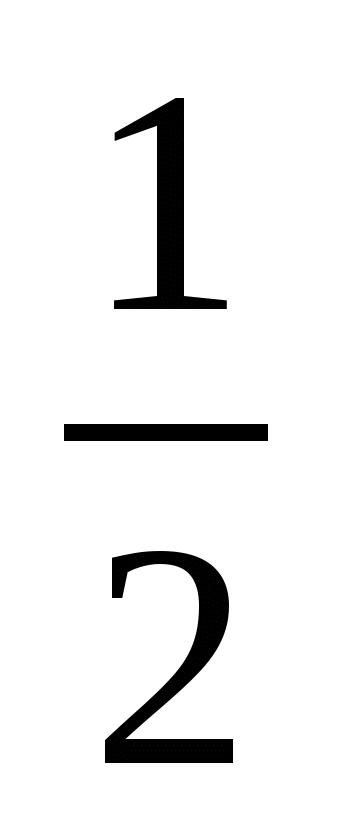 |
|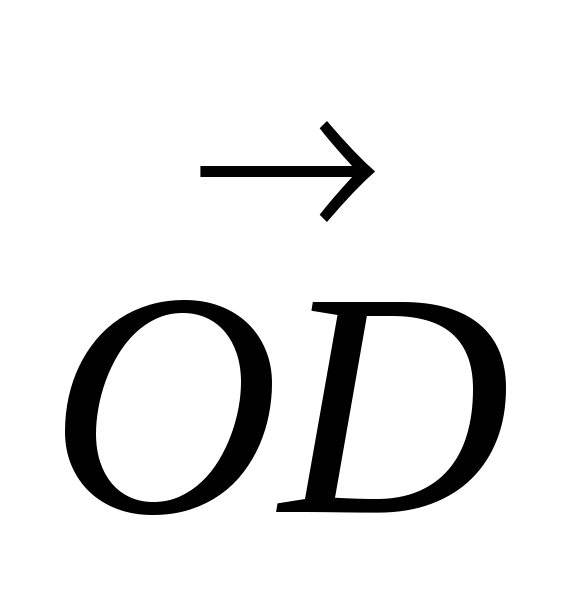 | = 0,4R. Из ∆ОАЕ:
| = 0,4R. Из ∆ОАЕ: 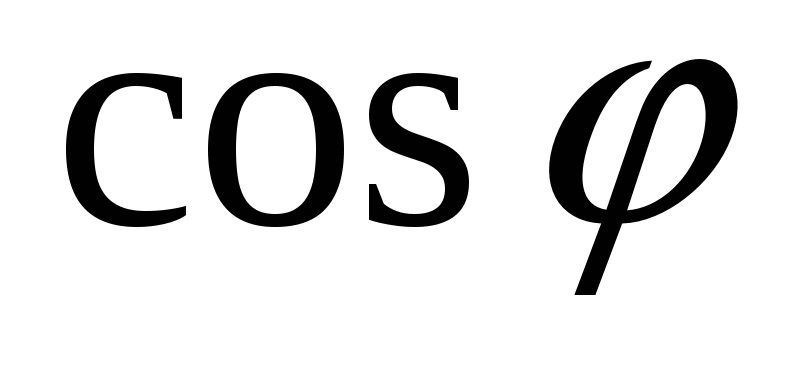 =
= 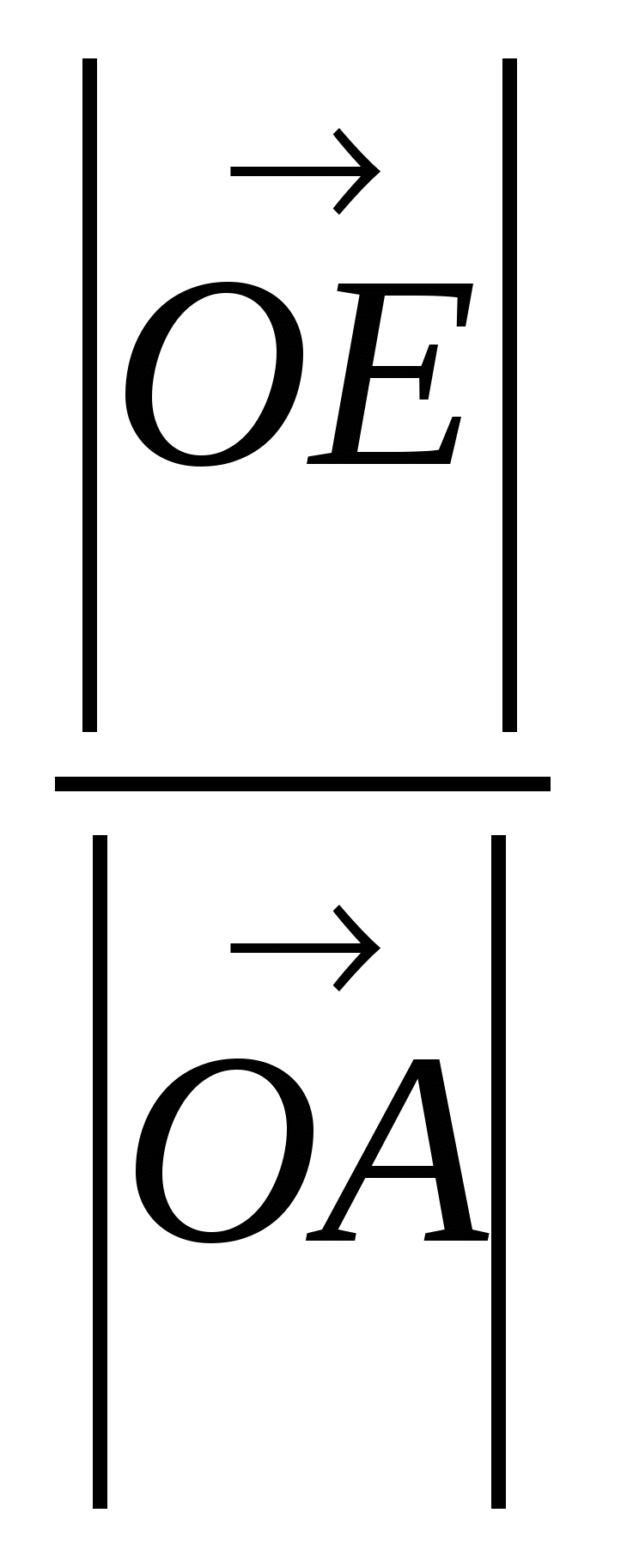 =
= 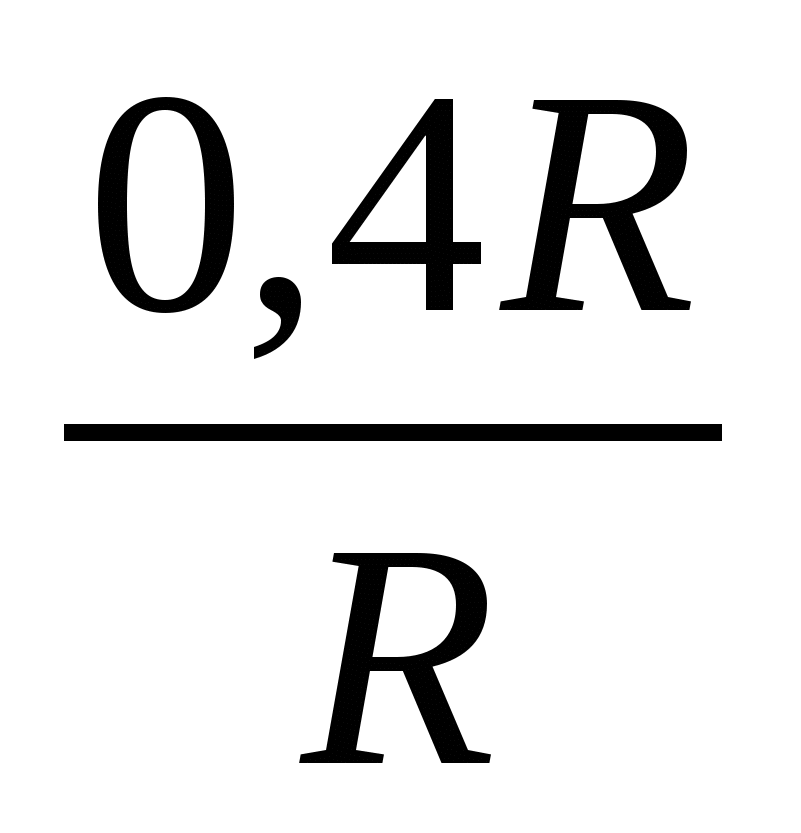 = 0,4.
= 0,4.
Ответ: 0,4.
Задача 4. Все рёбра тетраэдра SABC равны между собой. Точки P и Q - середины рёбер SB и SC соответственно. Найти угол между прямыми AP и BQ.
С хема решения:
хема решения:
![]() ,
,
![]() ,
,
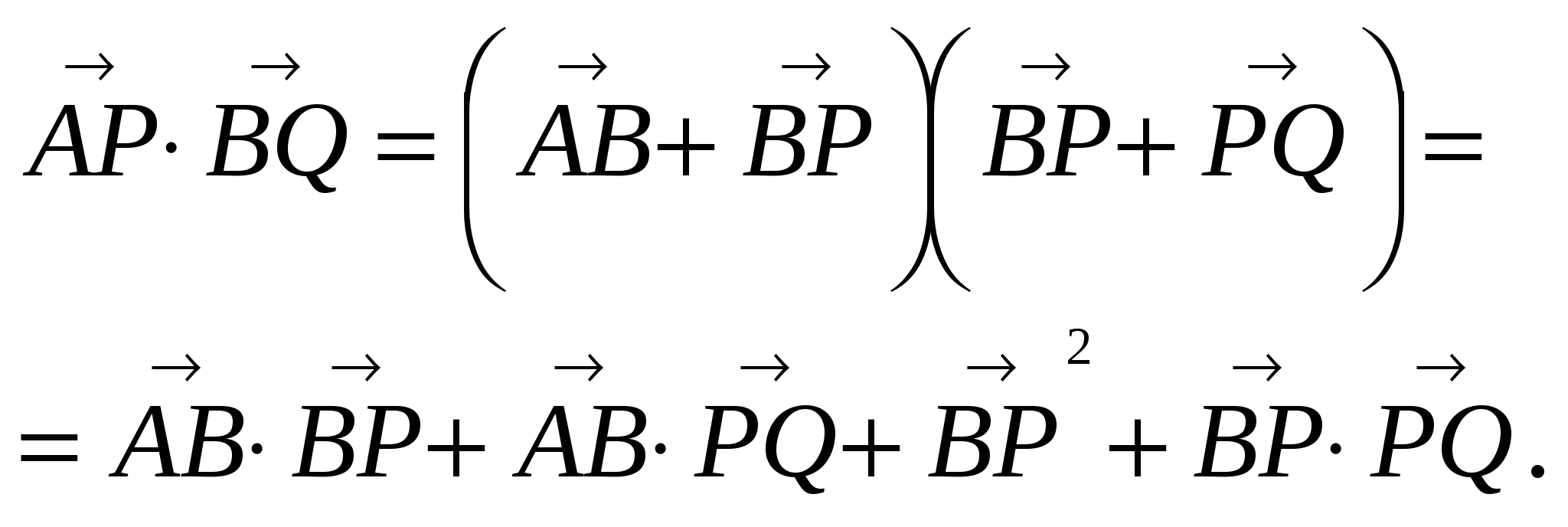
Обозначим длину ребра тетраэдра через а, тогда
AP = 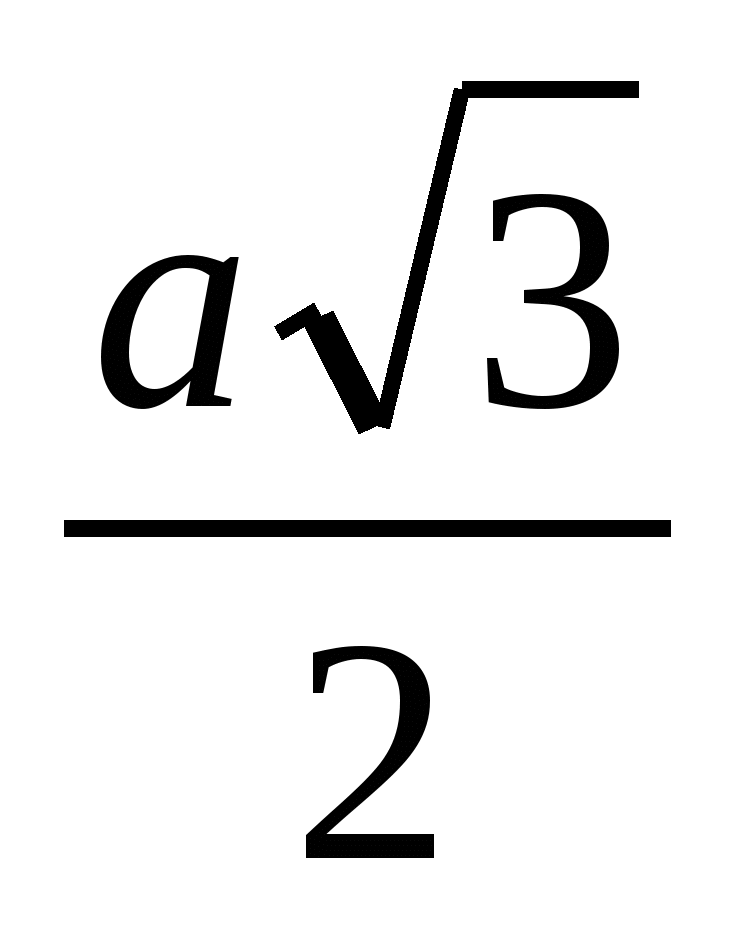 , как высота равностороннего треугольника. Используя формулу для скалярного произведения векторов, имеем:
, как высота равностороннего треугольника. Используя формулу для скалярного произведения векторов, имеем:
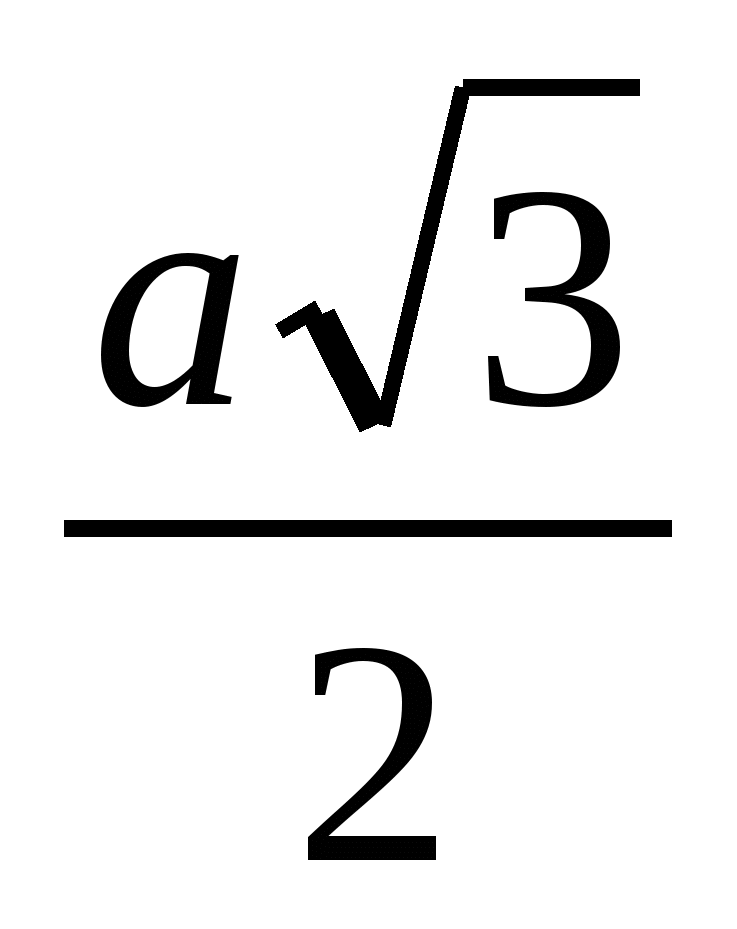
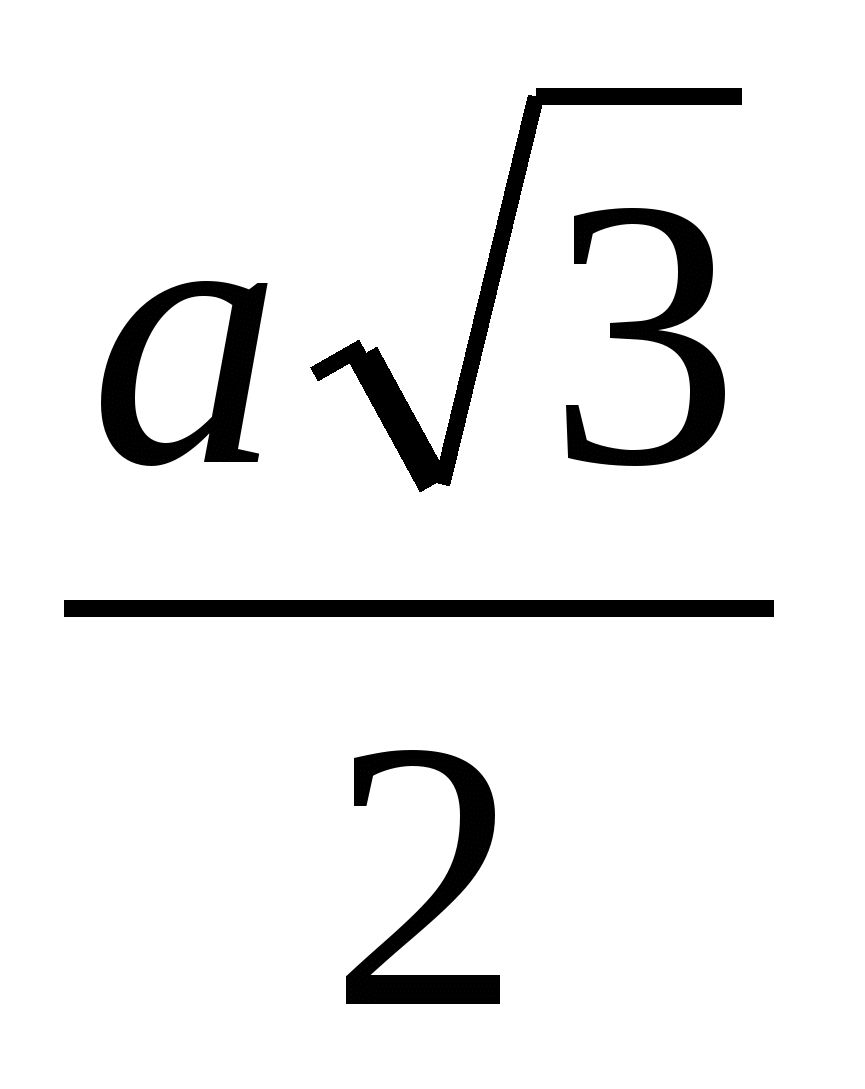
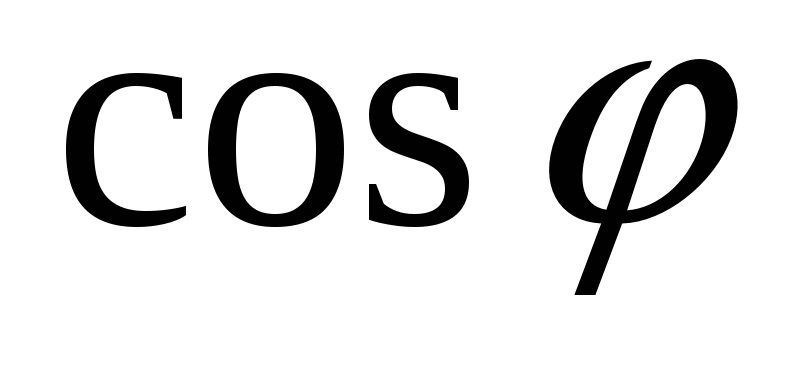 =
= 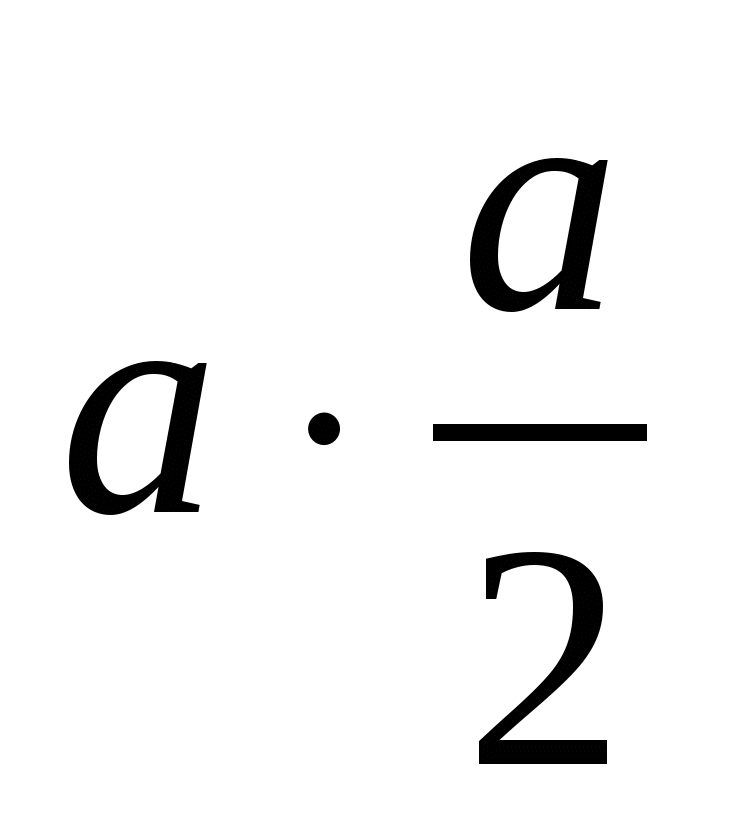
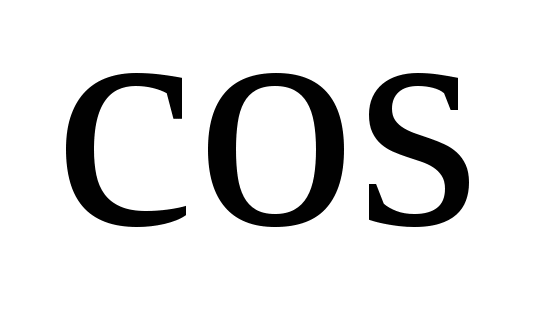 120+
120+ 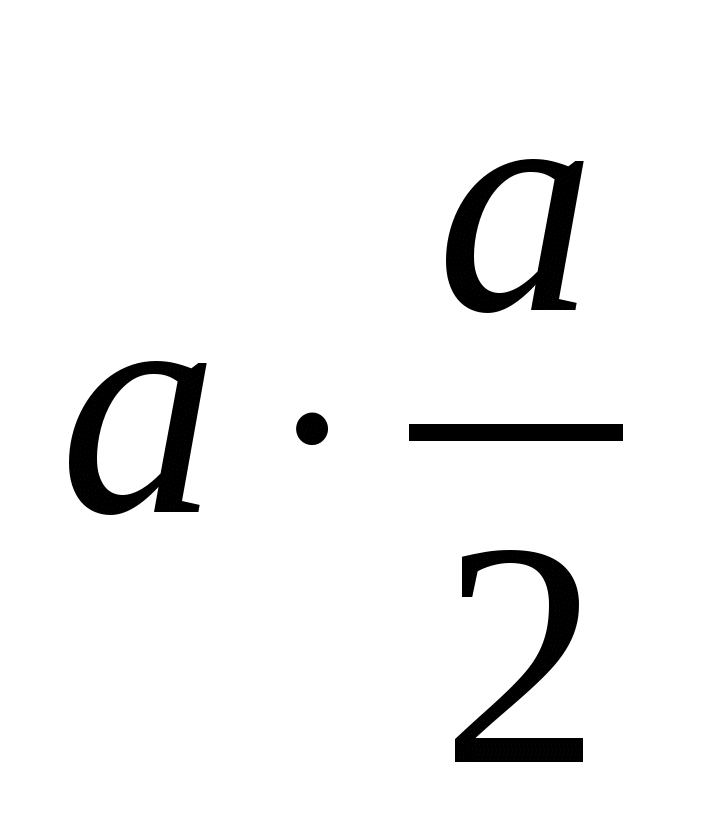
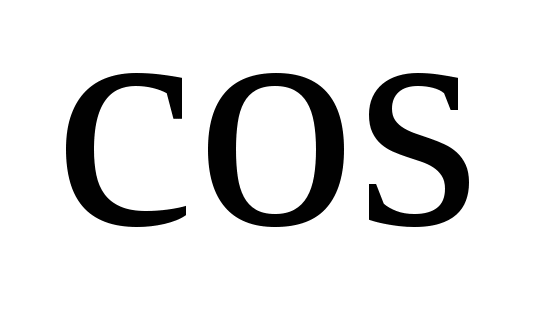 120 +
120 + 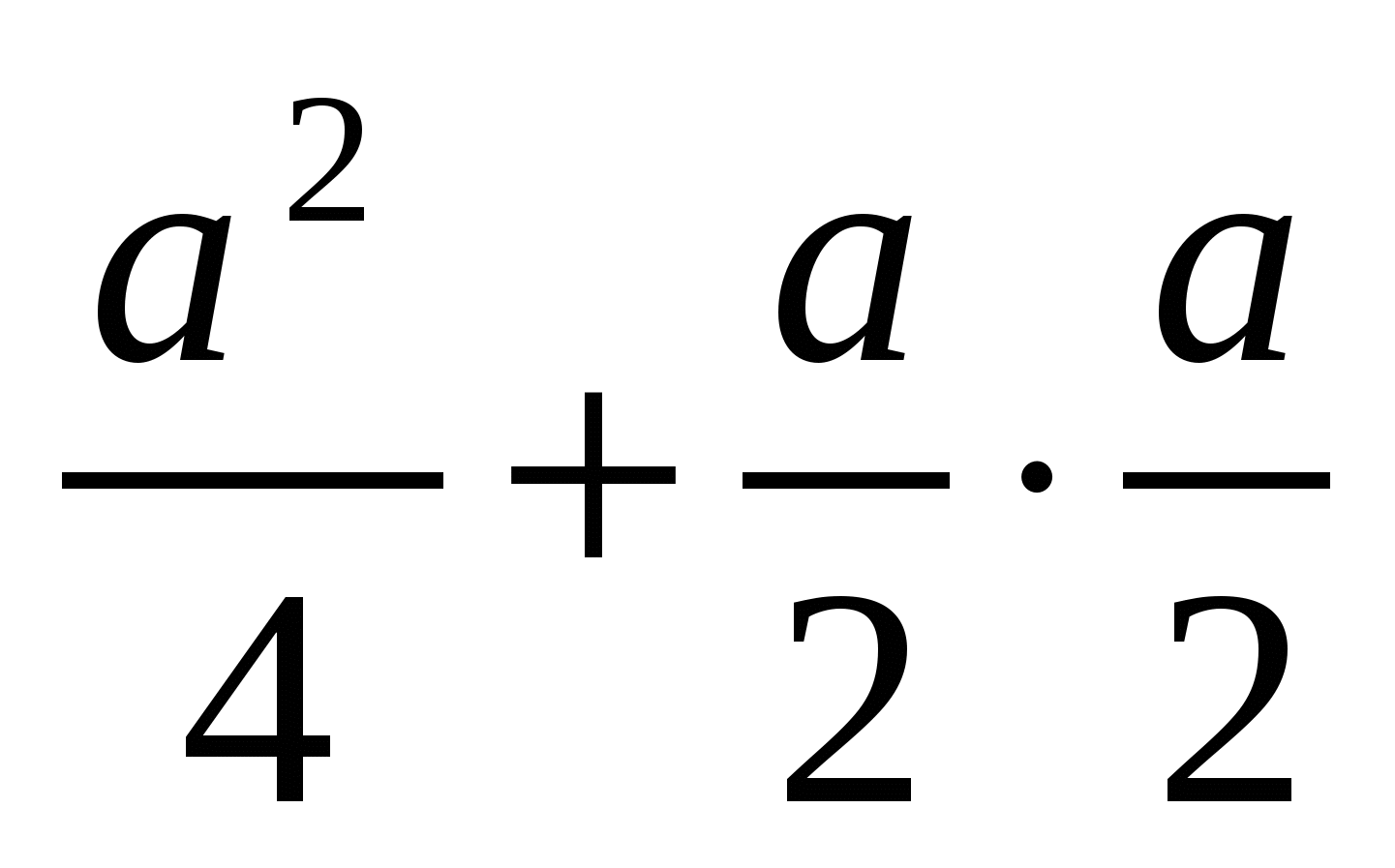
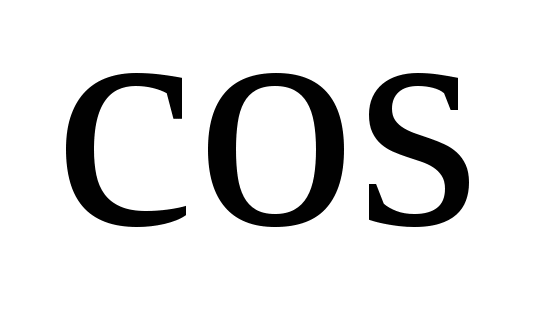 60;
60;
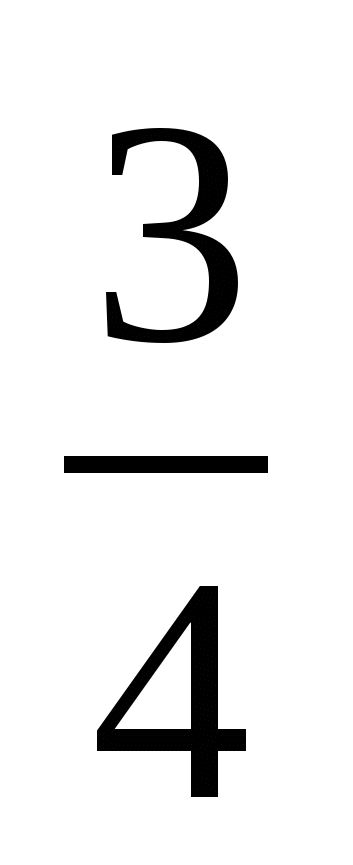
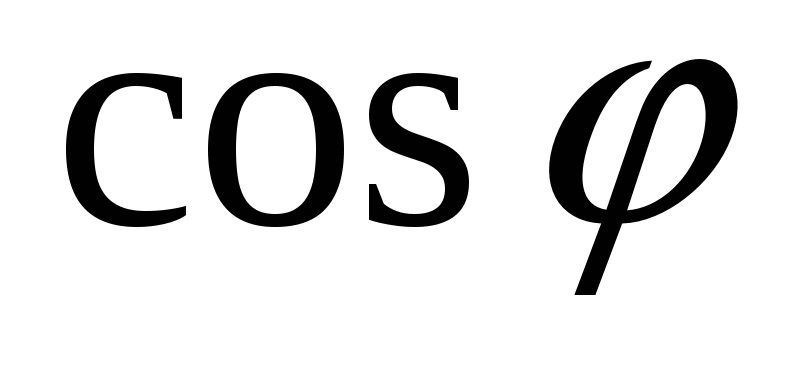 =
=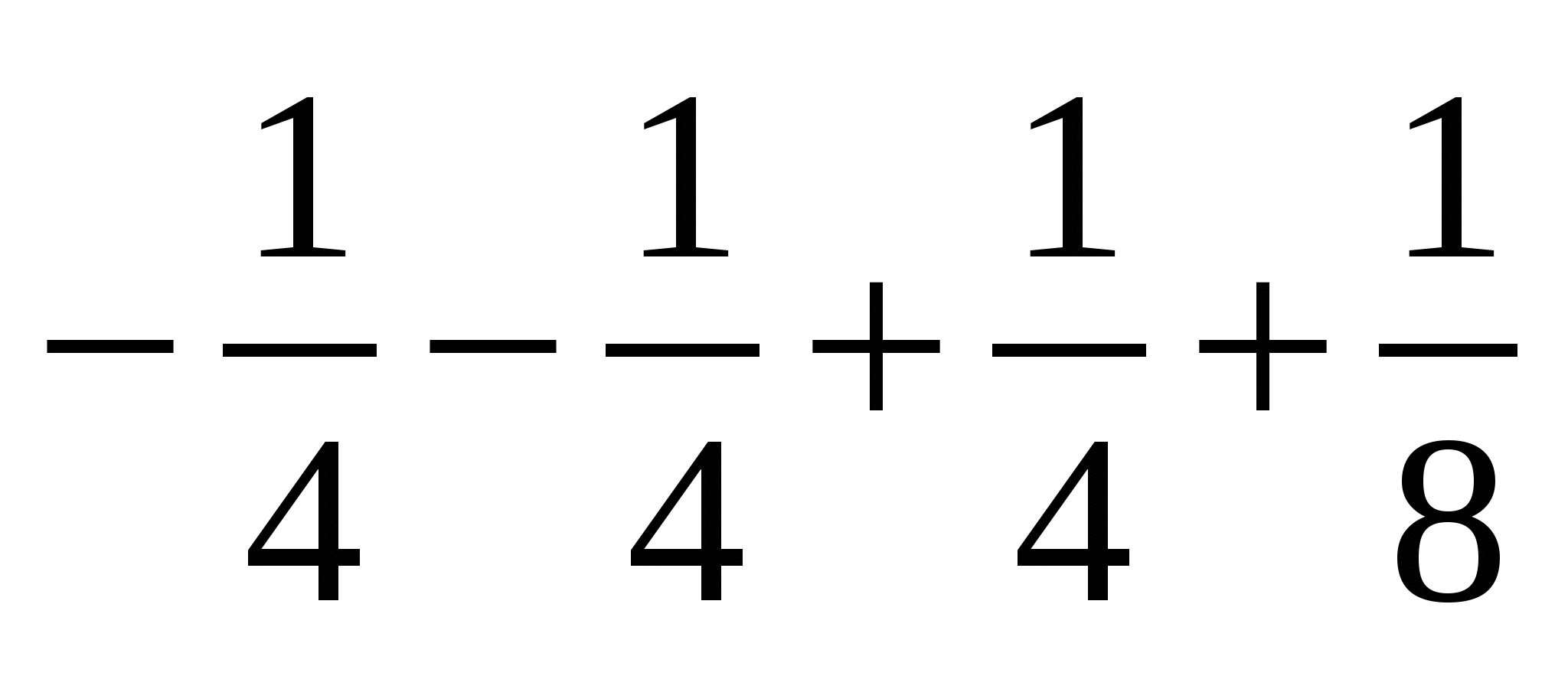 ;
;
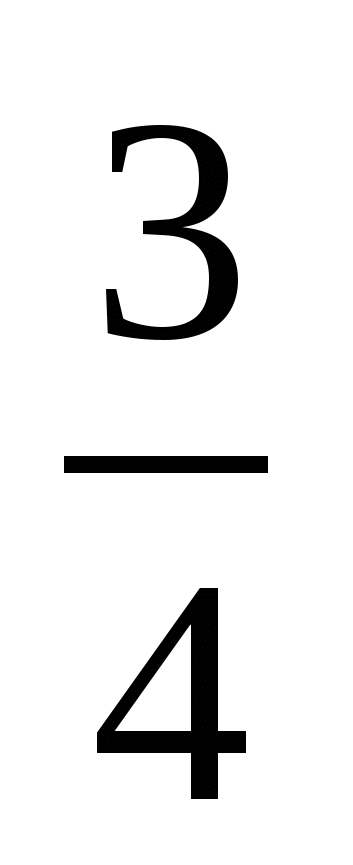
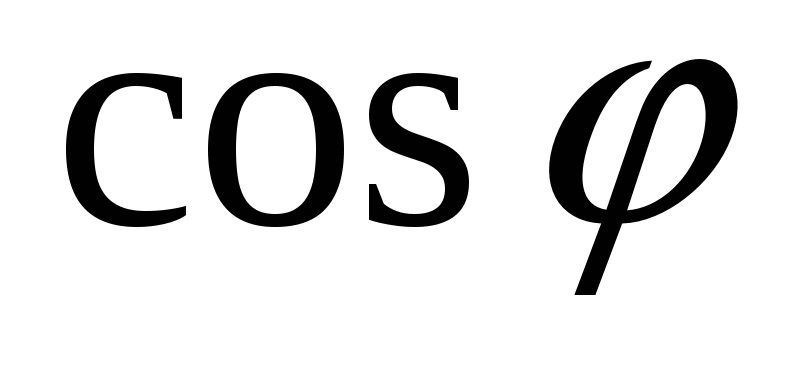 =
= 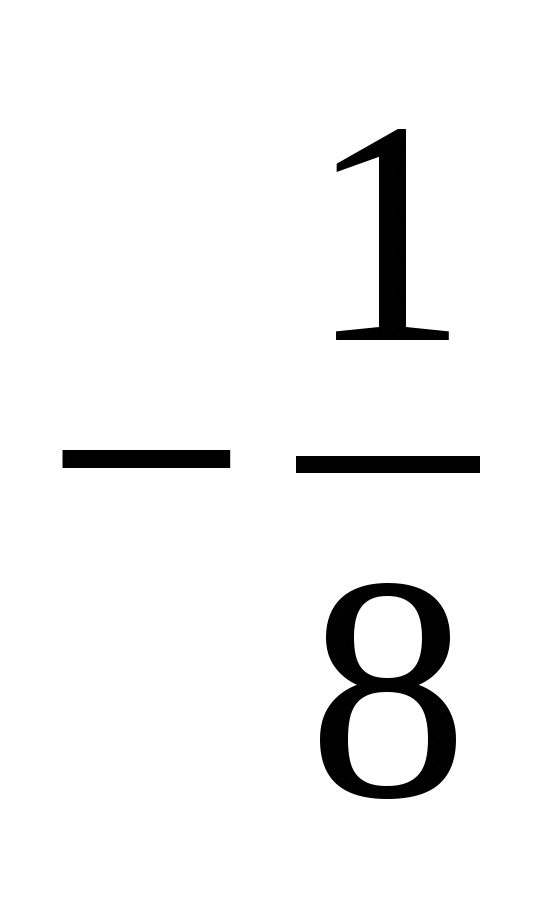 =>
=> 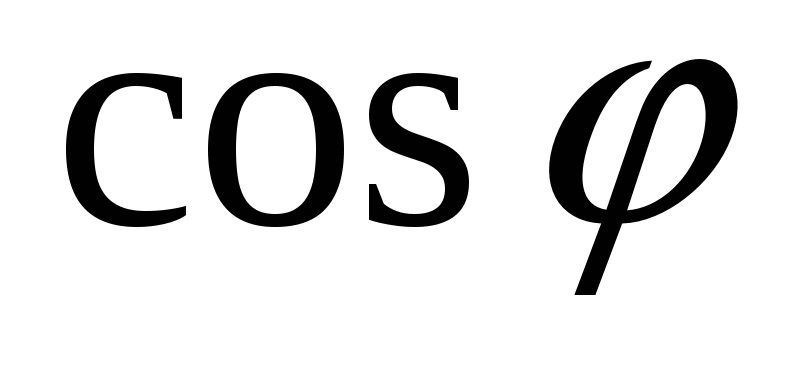 =
= 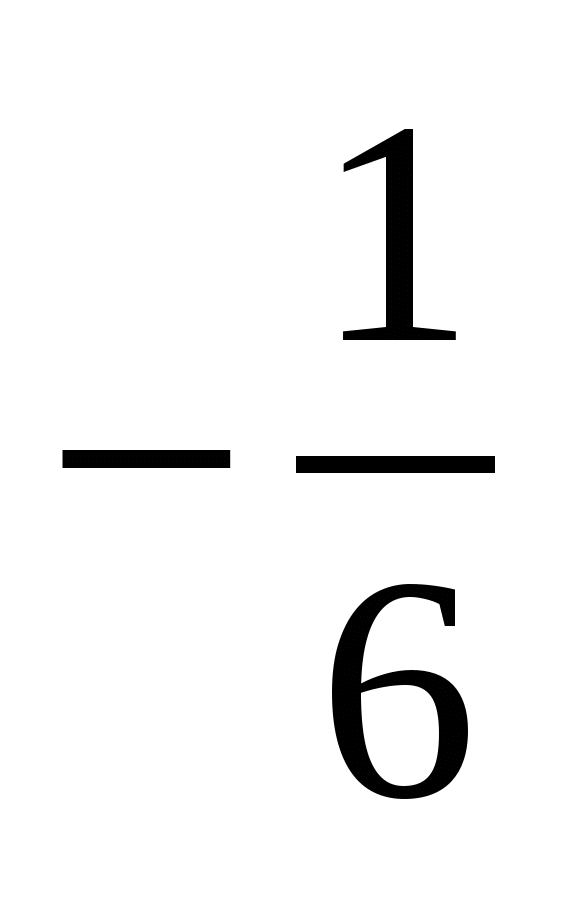 .
.
Ответ:  = arccos
= arccos 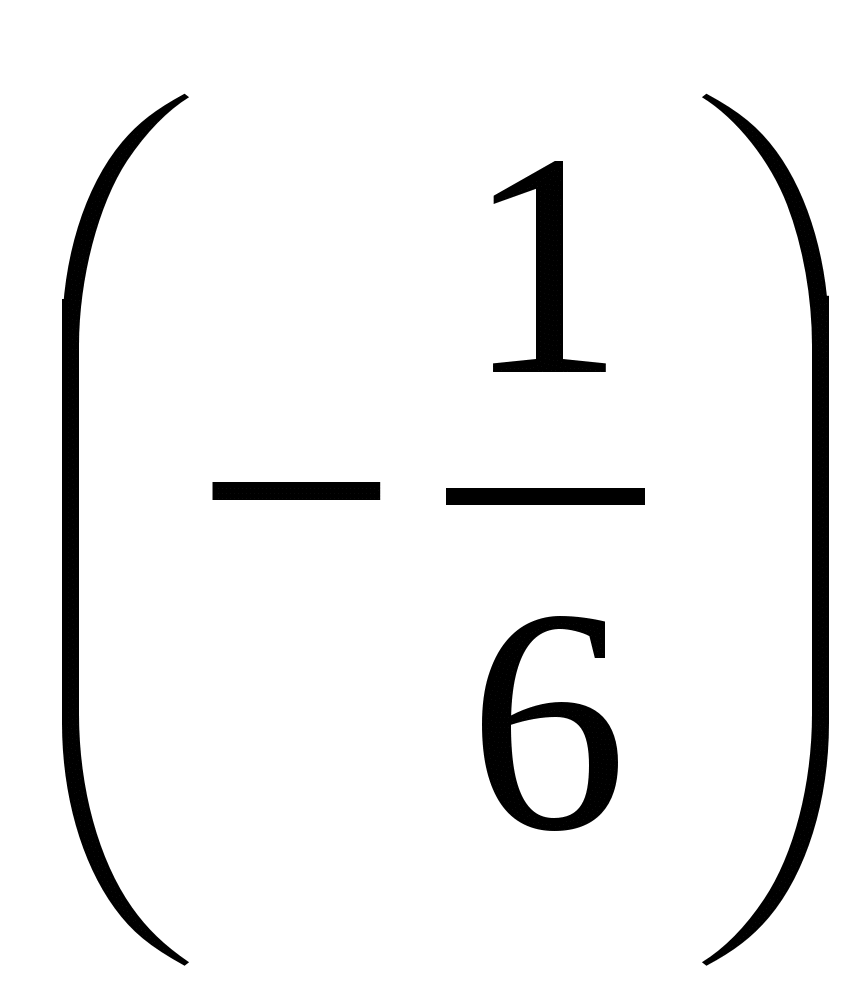 .
.
Задача 5. DАВС - тетраэдр. Медианы ∆DBC пересекаются в точке Р, K - середина АВ. Выразить РK через 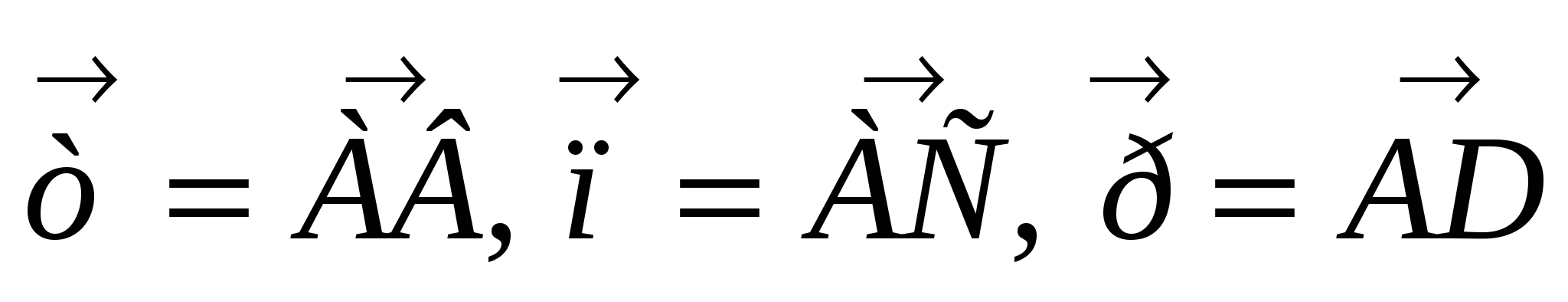 .
.
С хема решения:
хема решения:
Найдём векторы 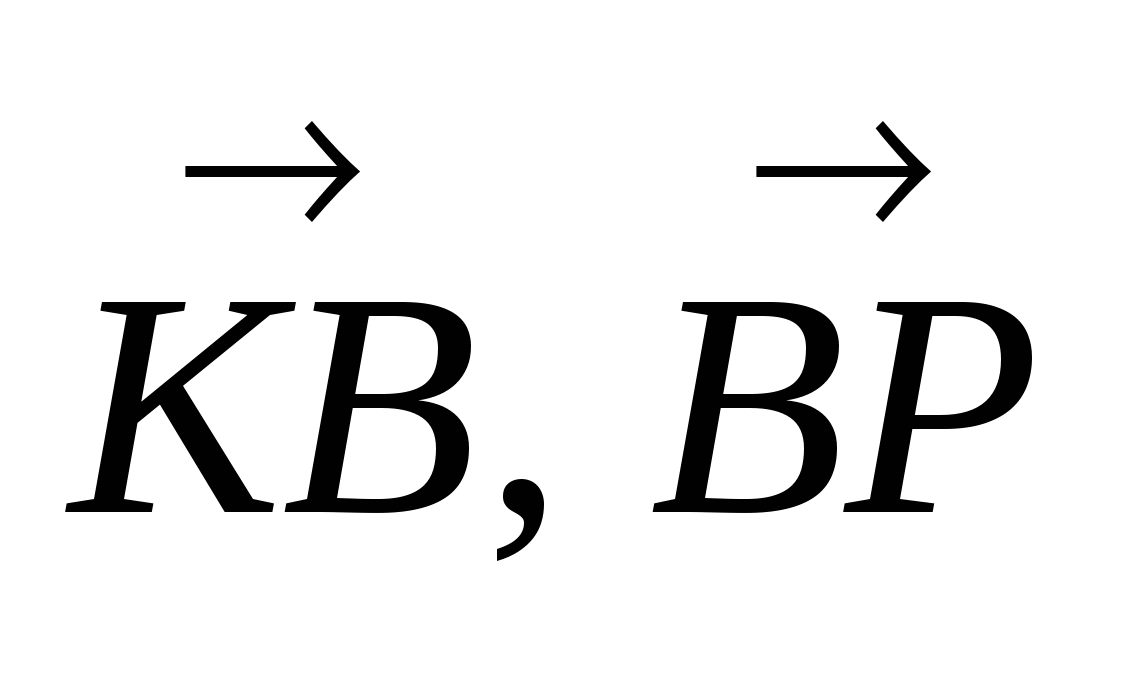 .
.
1) 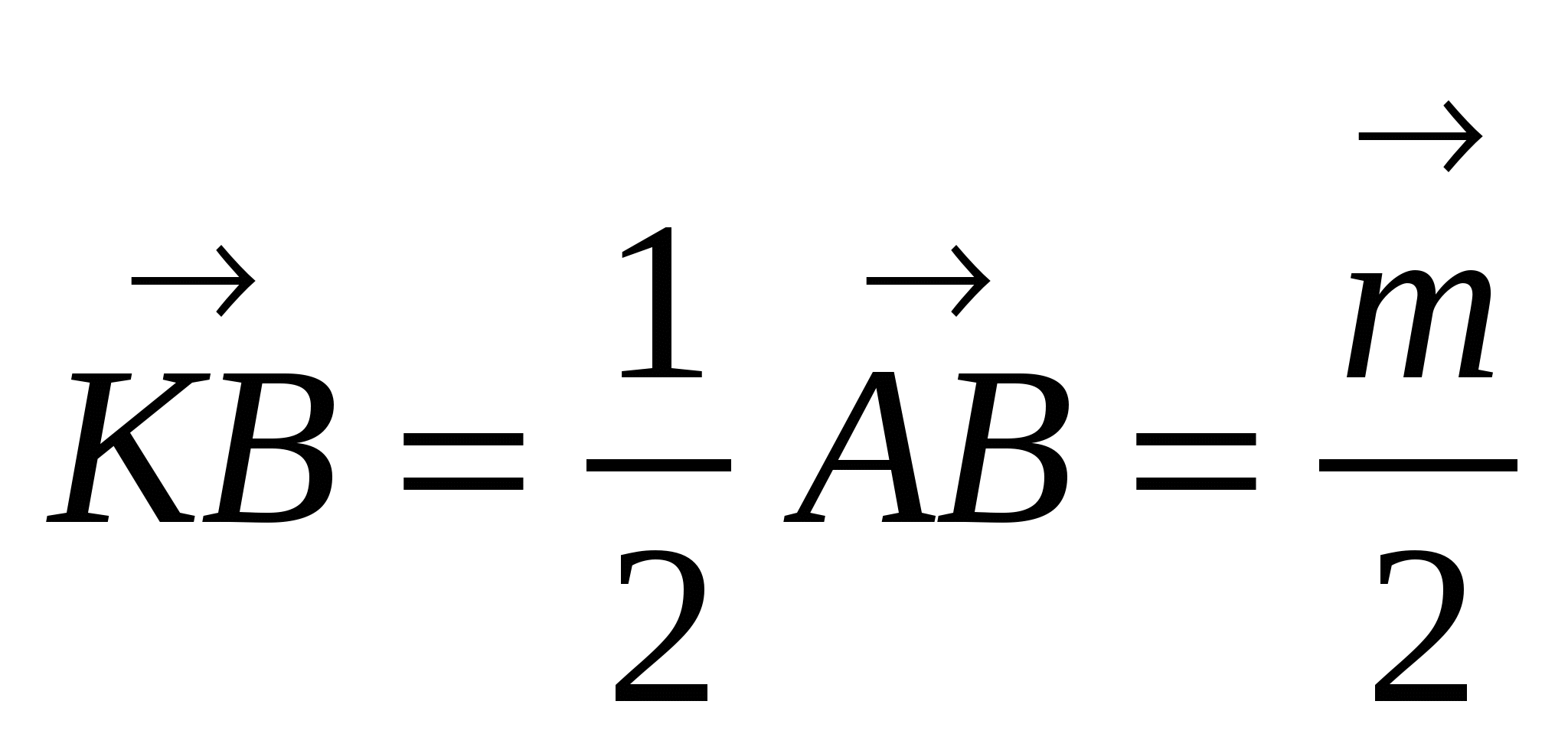
2) 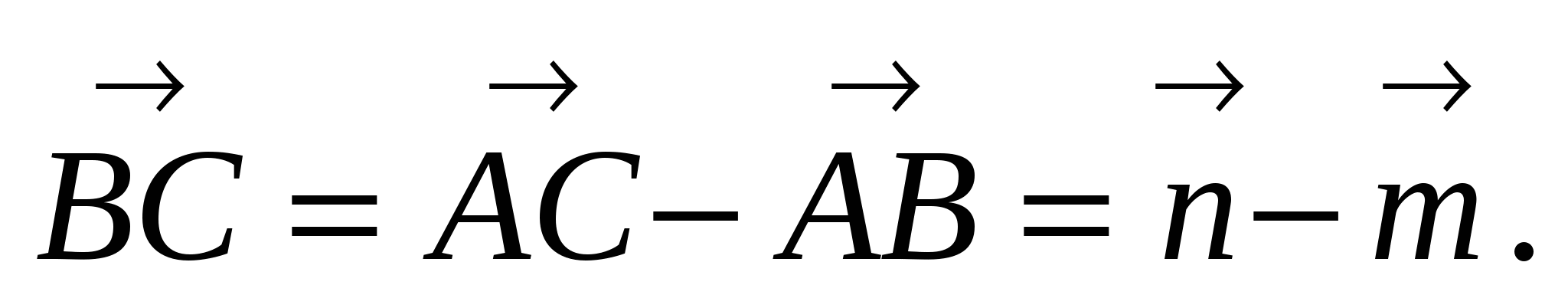
3) 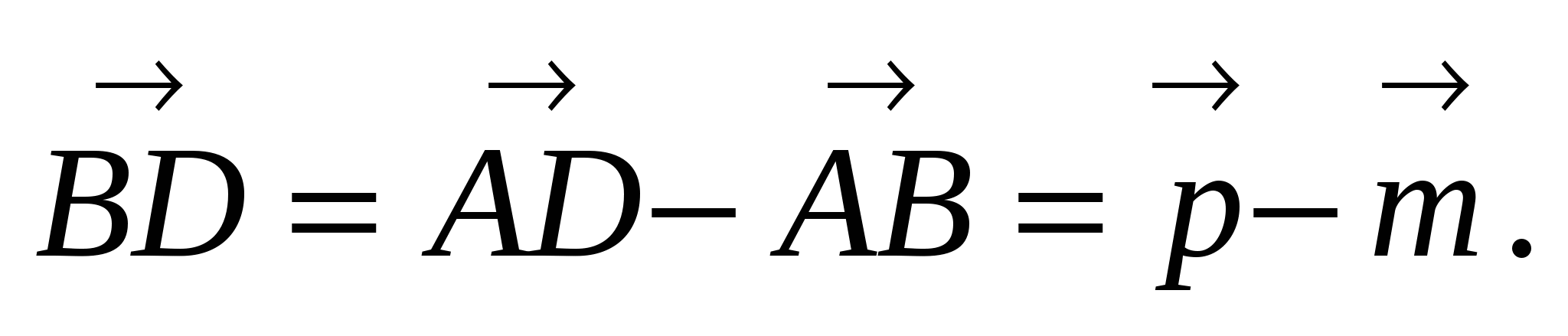
4) 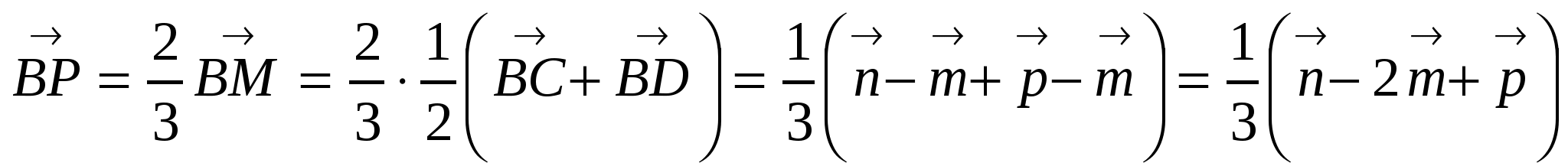 .
.
5) 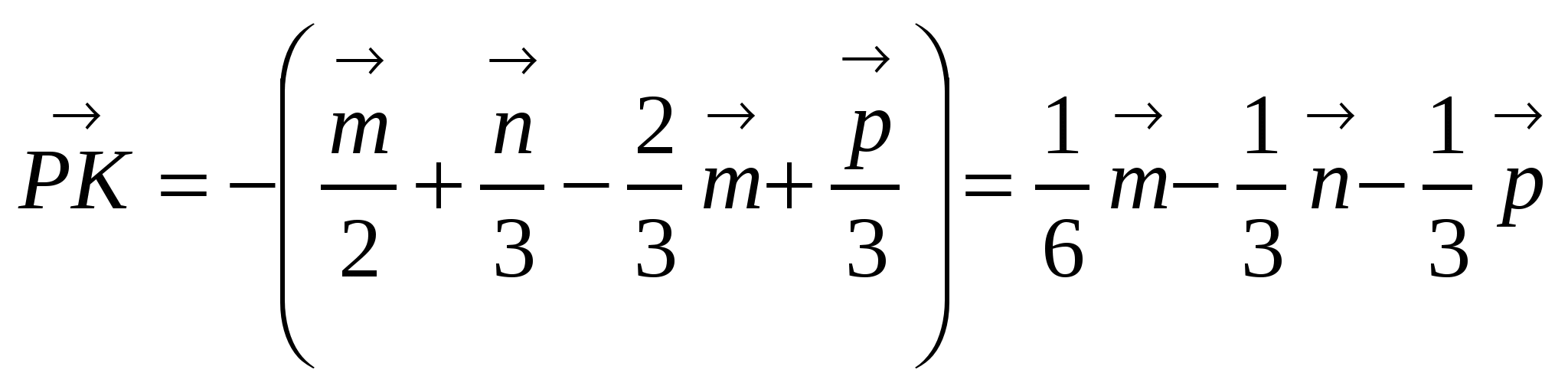 .
.
1.3. Координатный метод
Сущность метода координат состоит в следующем. Задавая фигуры уравнениями (неравенствами) и выражая в координатах различные геометрические соотношения, мы применяем алгебру и анализ к решению геометрических задач, к доказательству теорем. С этой целью нужно ввести прямоугольную систему координат на плоскости или в пространстве и записать условие задачи в координатах.
После этого решение задачи проводится с помощью алгебраических вычислений.
Приведем основные теоретические сведения, используемые при решении задач координатным методом.
Требуется найти
На плоскости
В пространстве
1.
Расстояние
между
двумя
точками
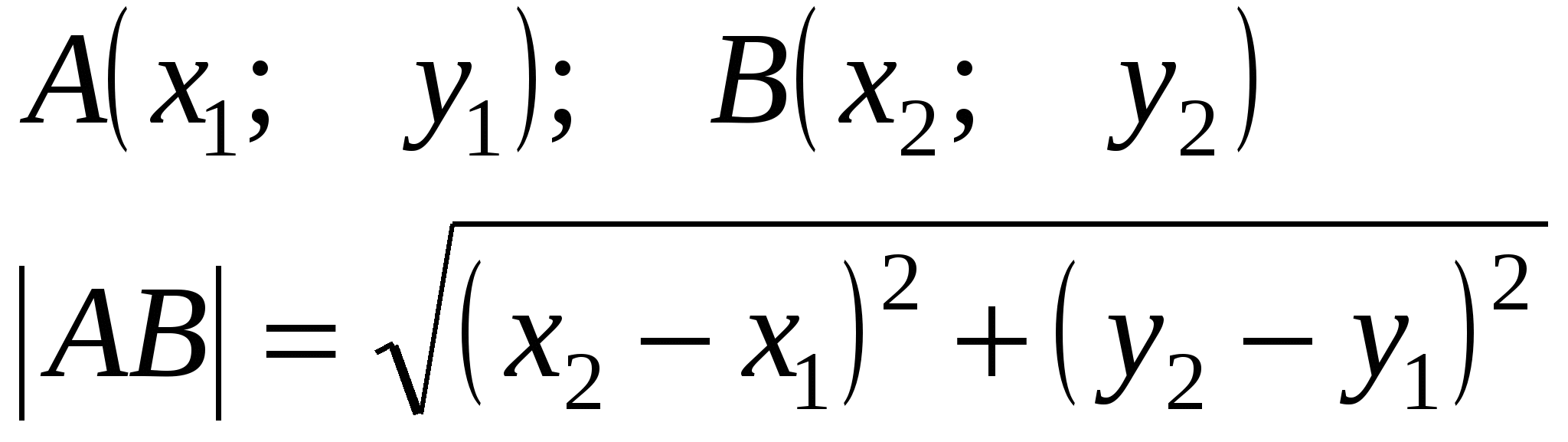
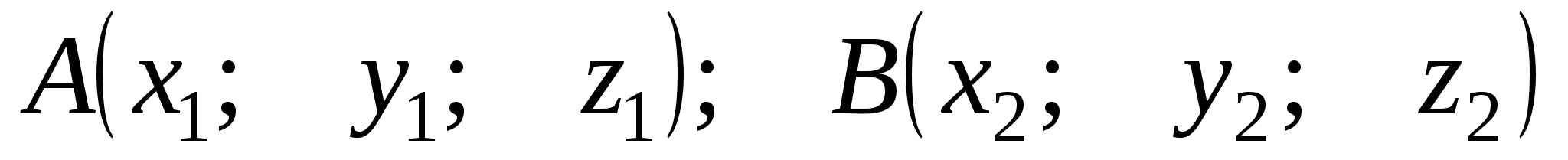
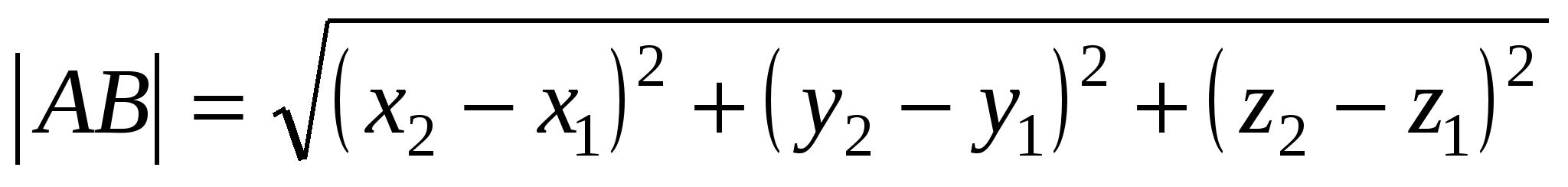
2.
Координаты точки,
делящей отрезок
в данном отношении
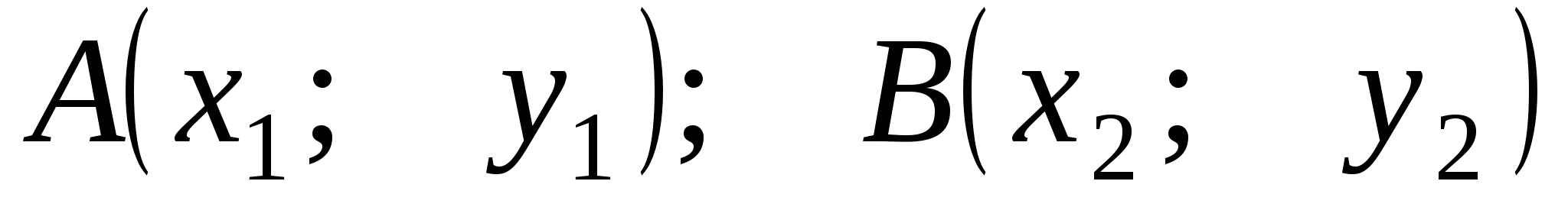
Точка 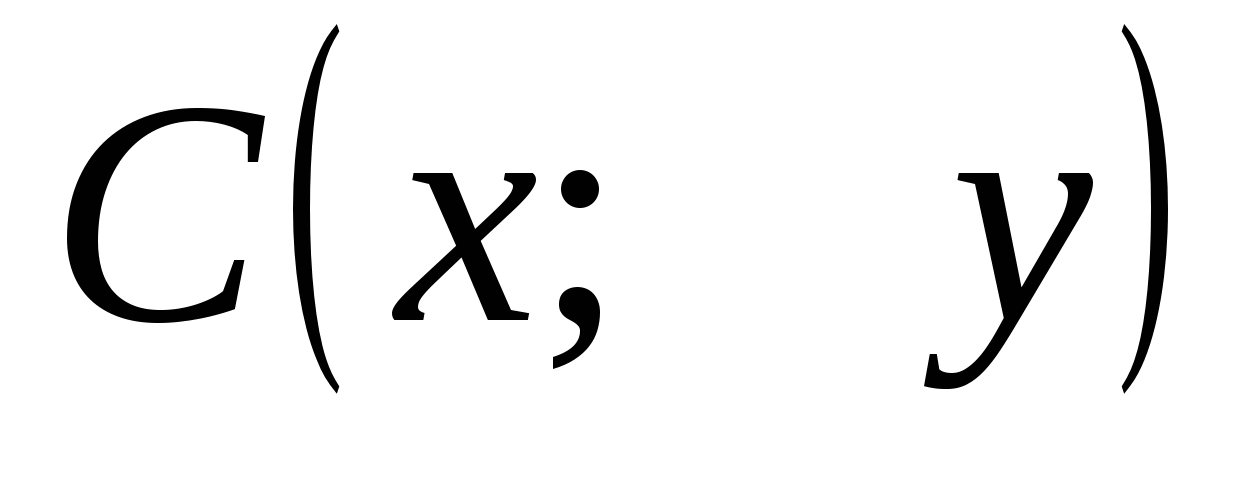 делит
делит
в отношении п отрезок АВ
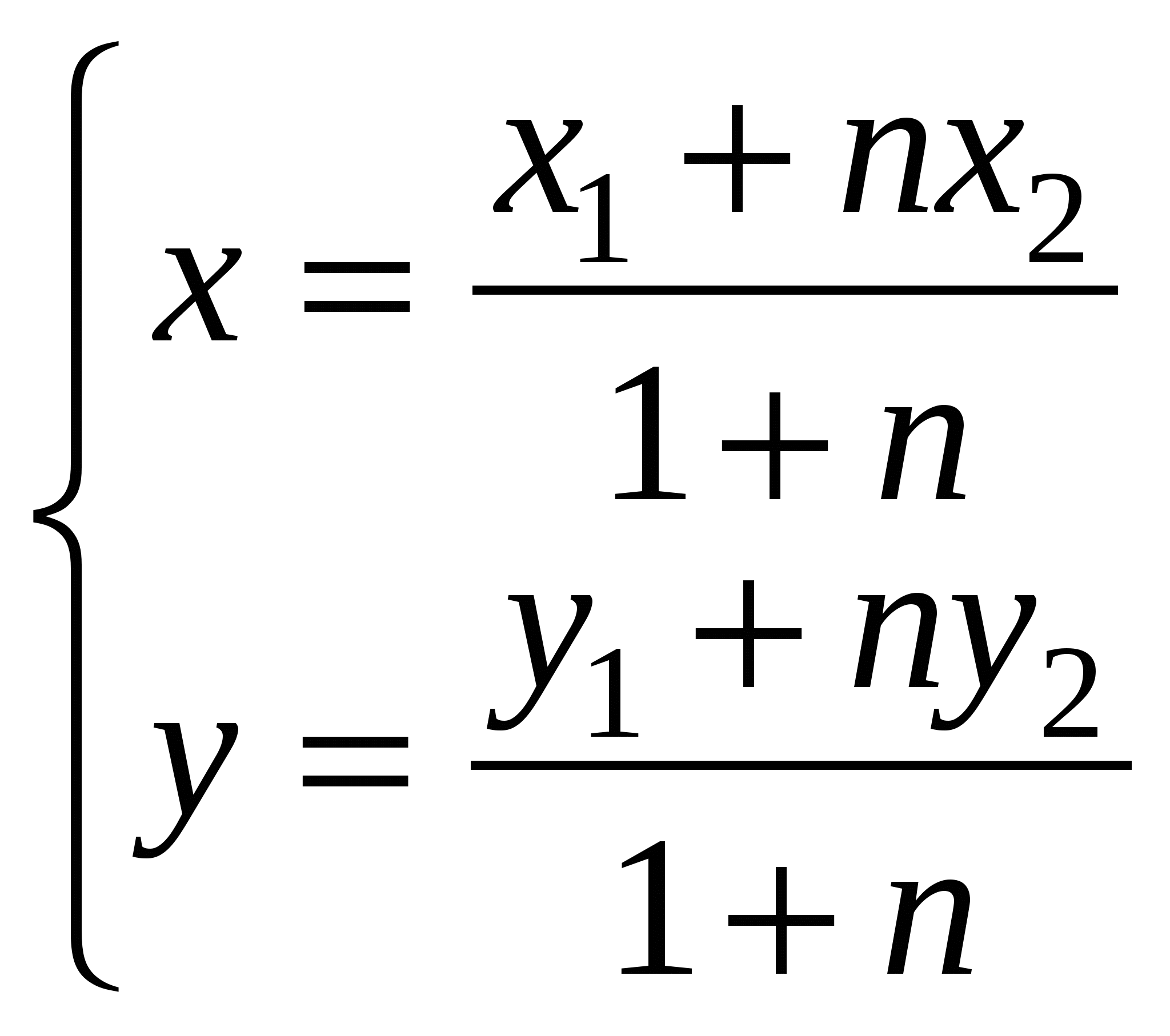
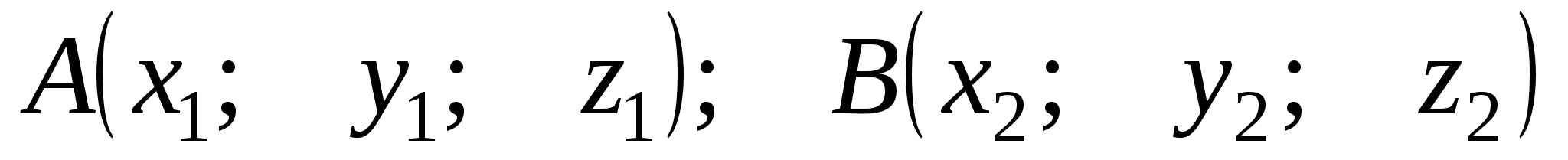
и 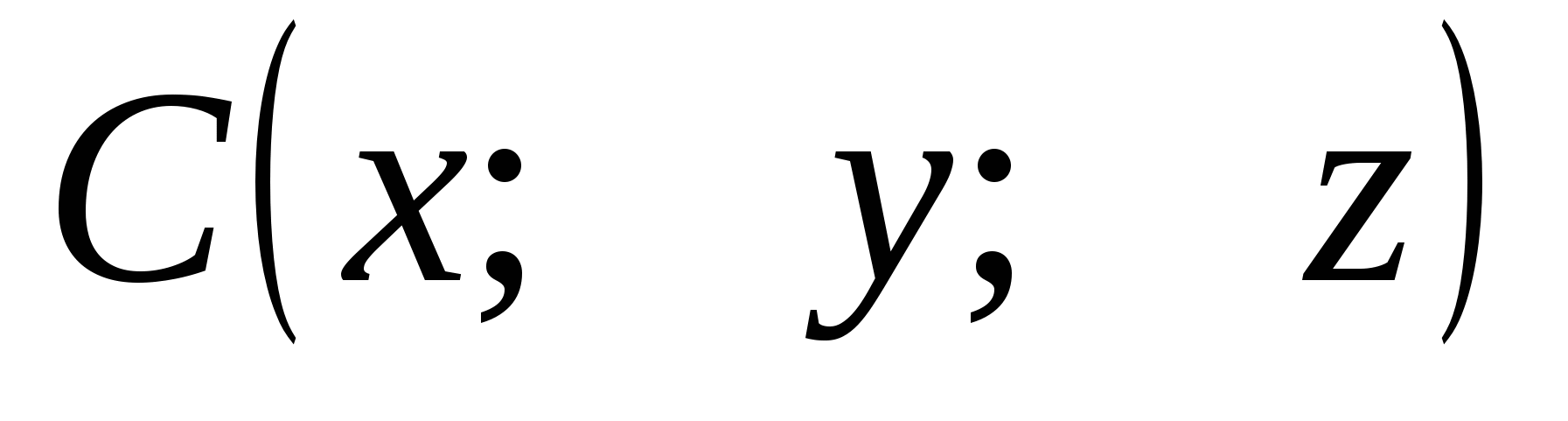 делит в отношении п отрезок АВ
делит в отношении п отрезок АВ
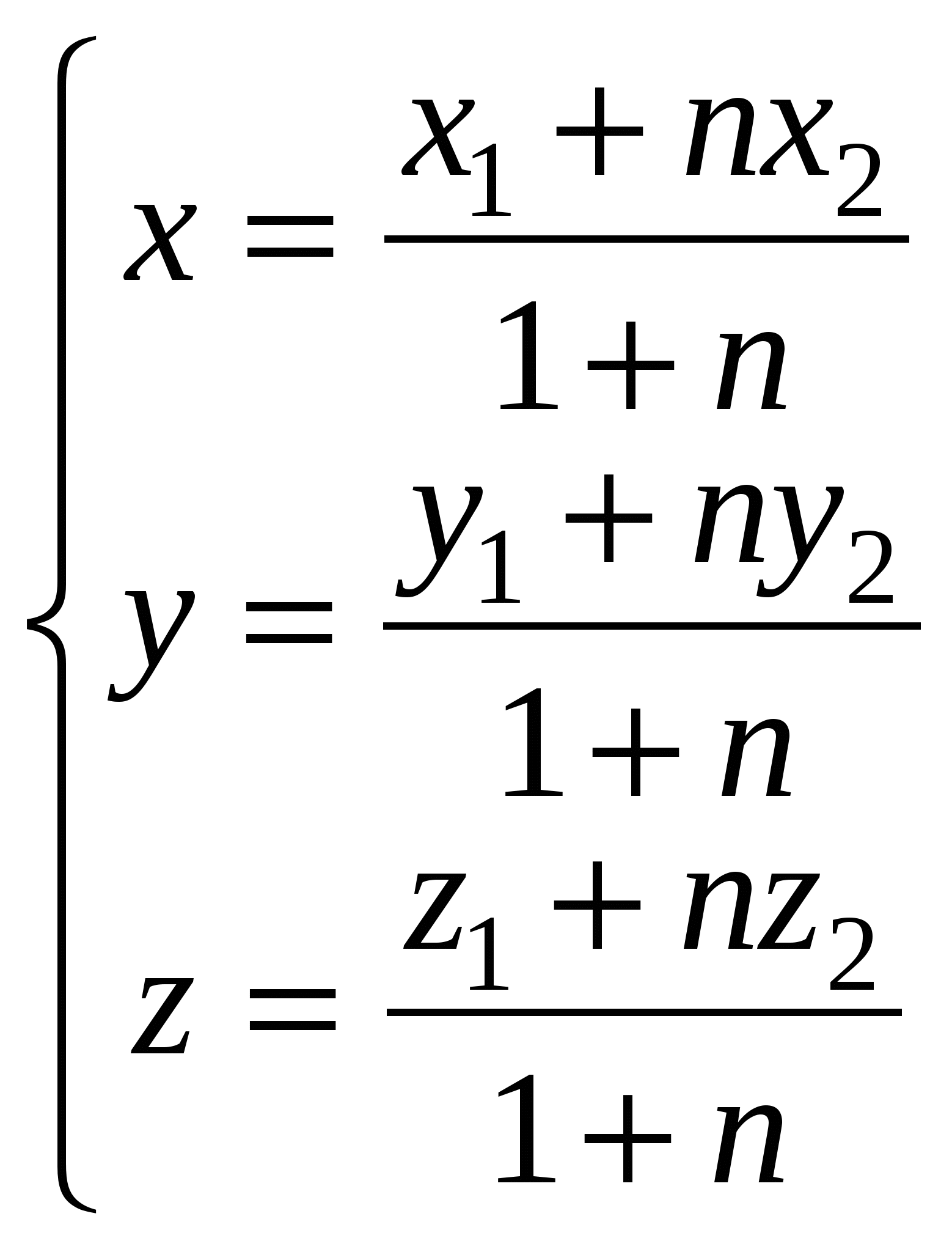
3.
Координаты середины отрезка АВ
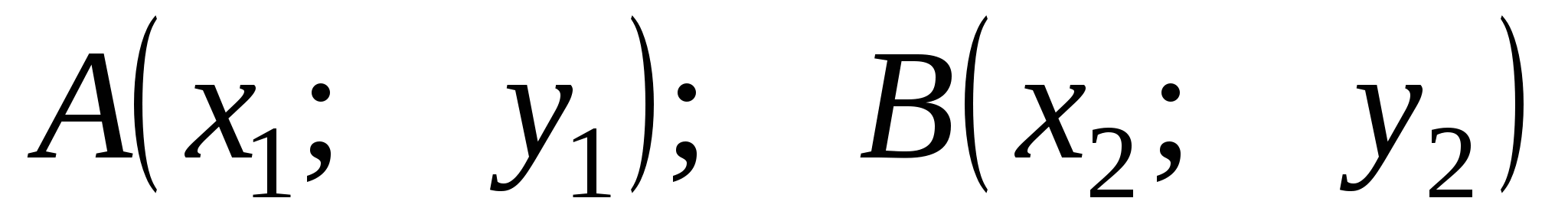
С - середина отрезка АВ
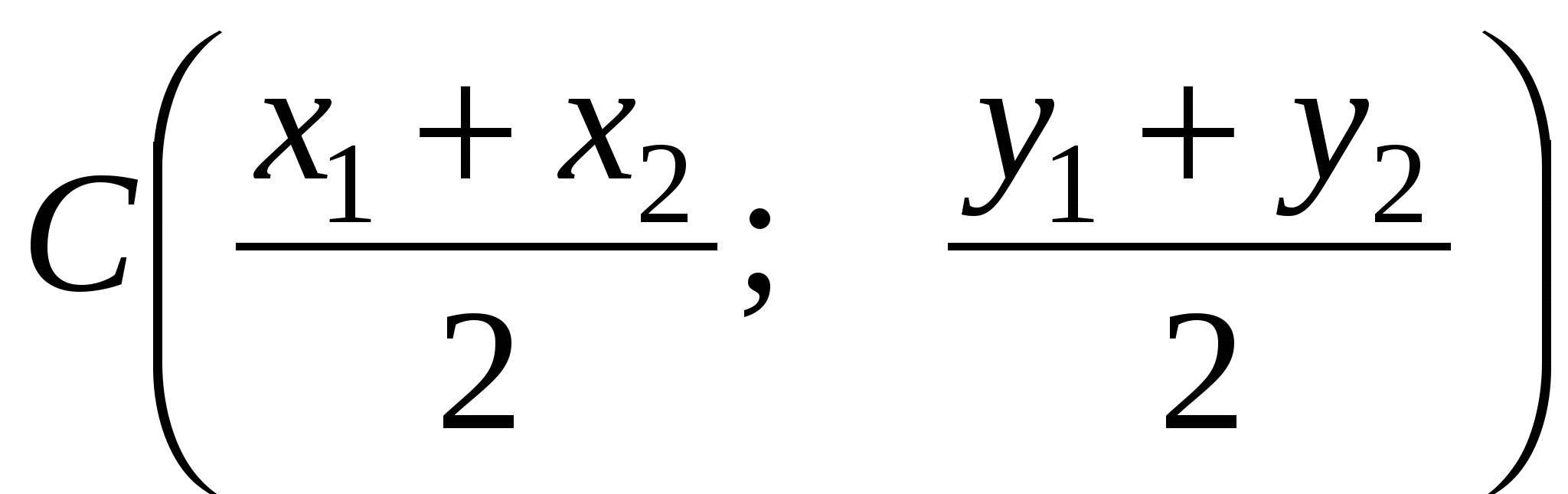
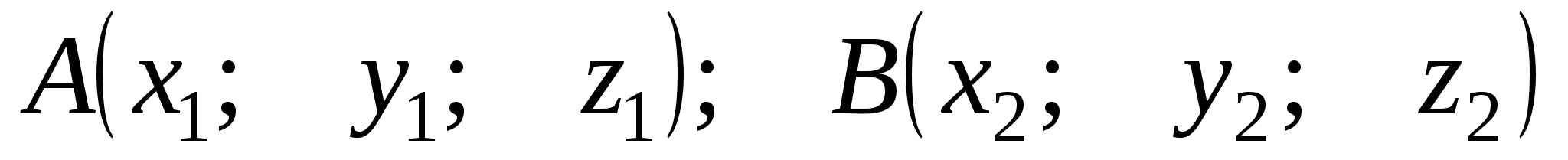 С - середина отрезка АВ
С - середина отрезка АВ
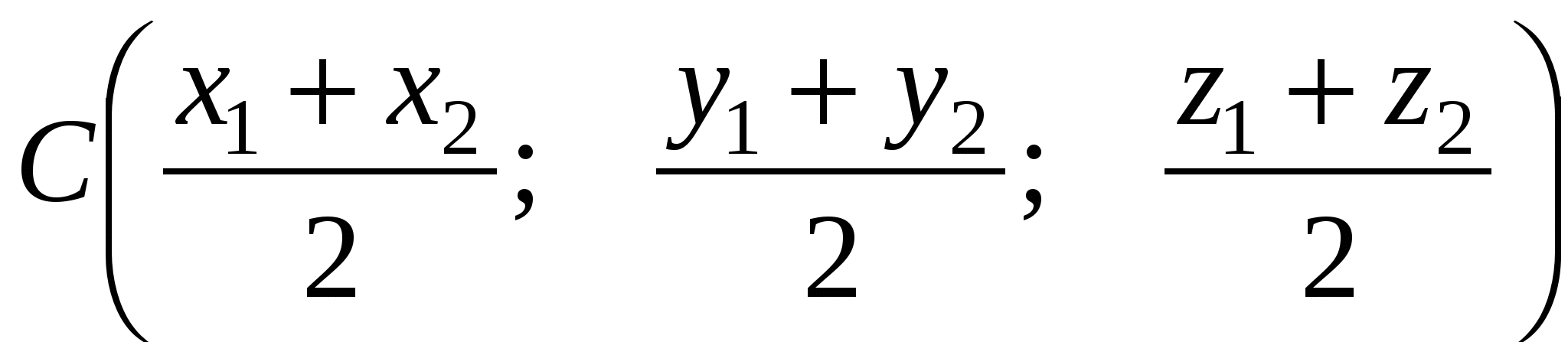
4.
Координаты
точки
пересечения медиан
треугольника АВС
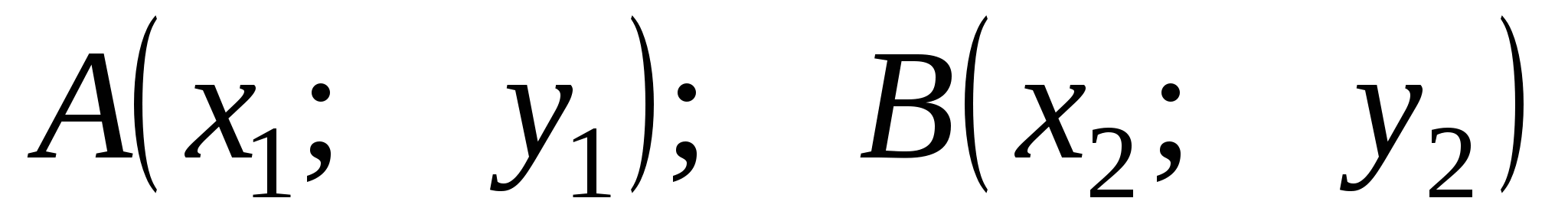 ;
; 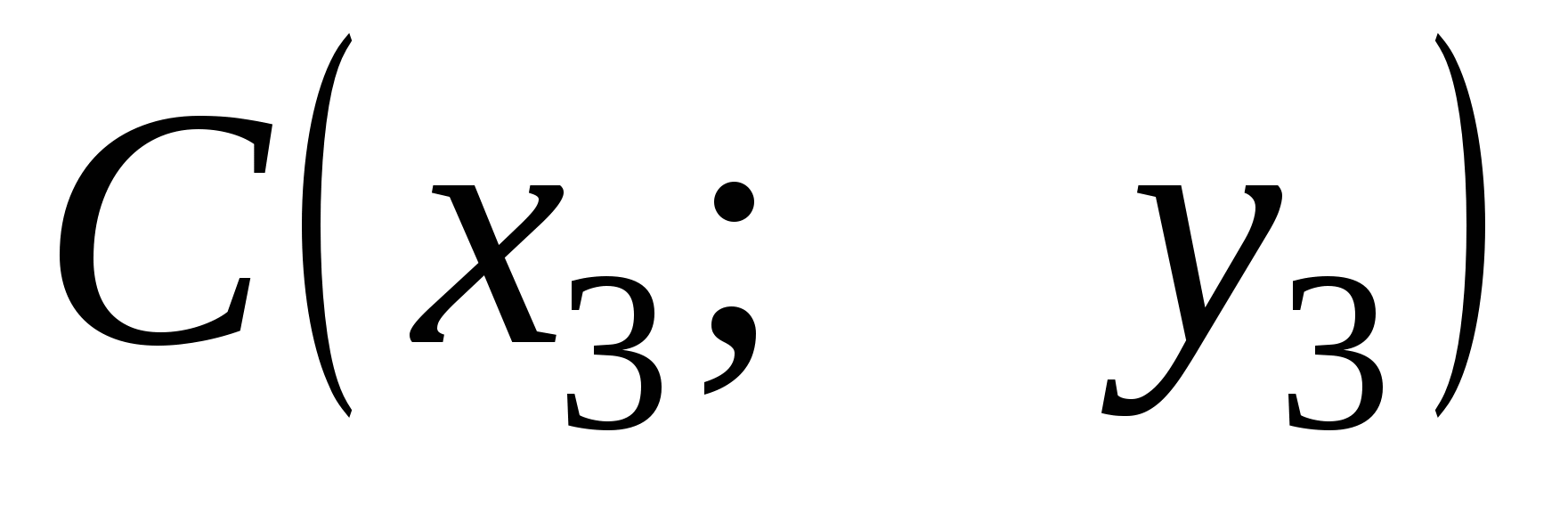
М - точка пересечения
медиан треугольника АВС
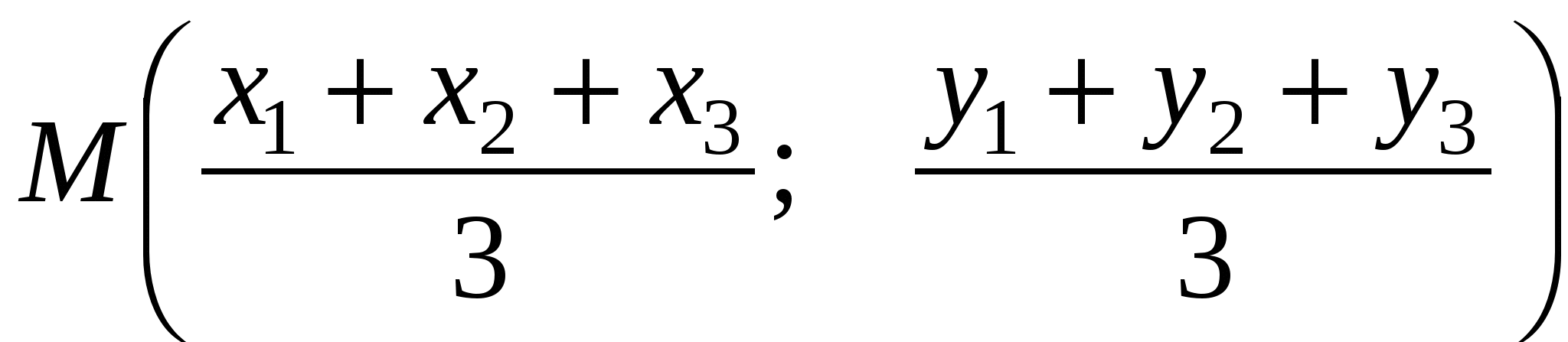
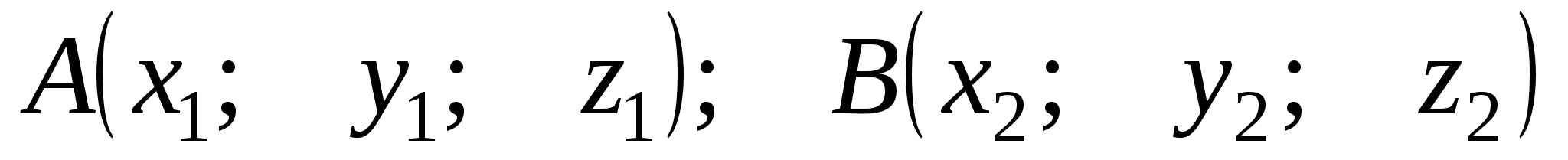
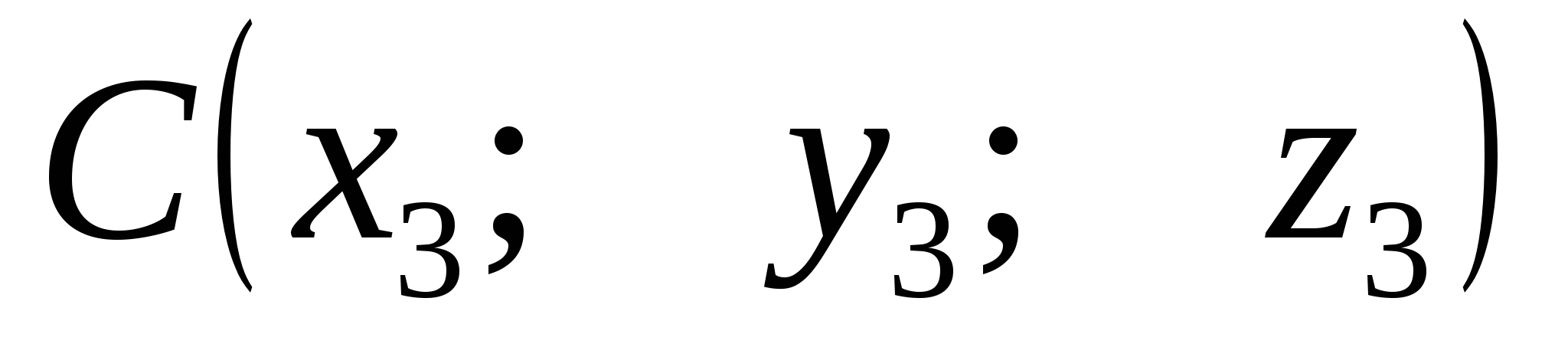
М - точка пересечения
медиан треугольника АВС
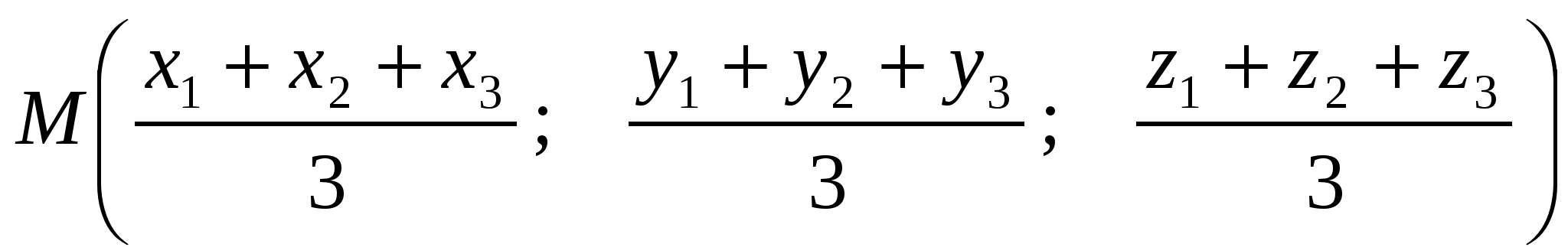
1. Прямая на плоскости.
Уравнение прямой
в общем виде
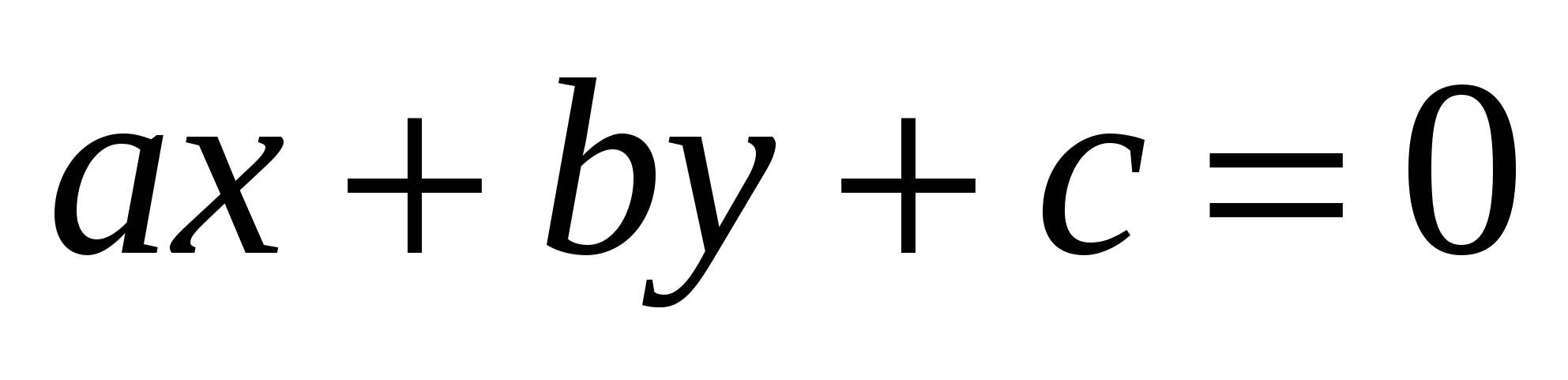 ,
,
где 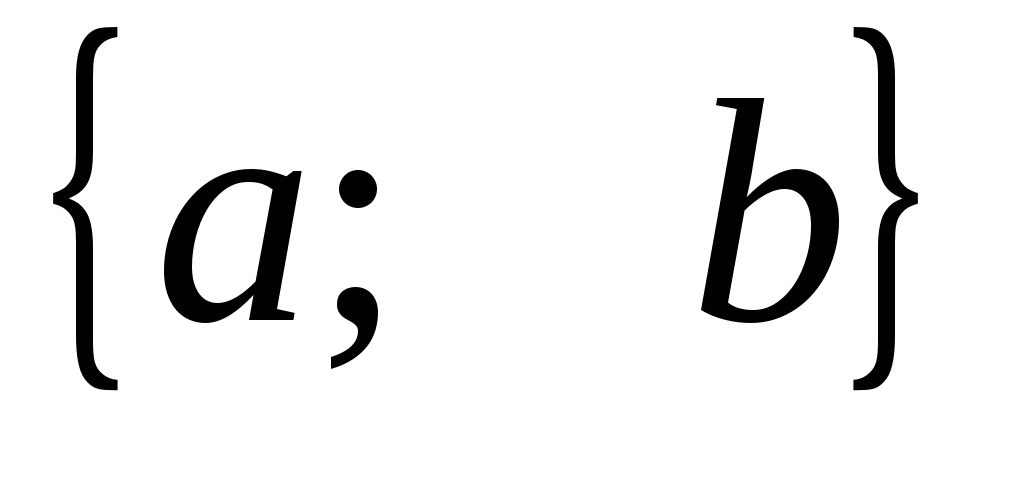 - координаты вектора, перпендикулярного прямой
- координаты вектора, перпендикулярного прямой
Уравнение прямой
с угловым коэффициентом
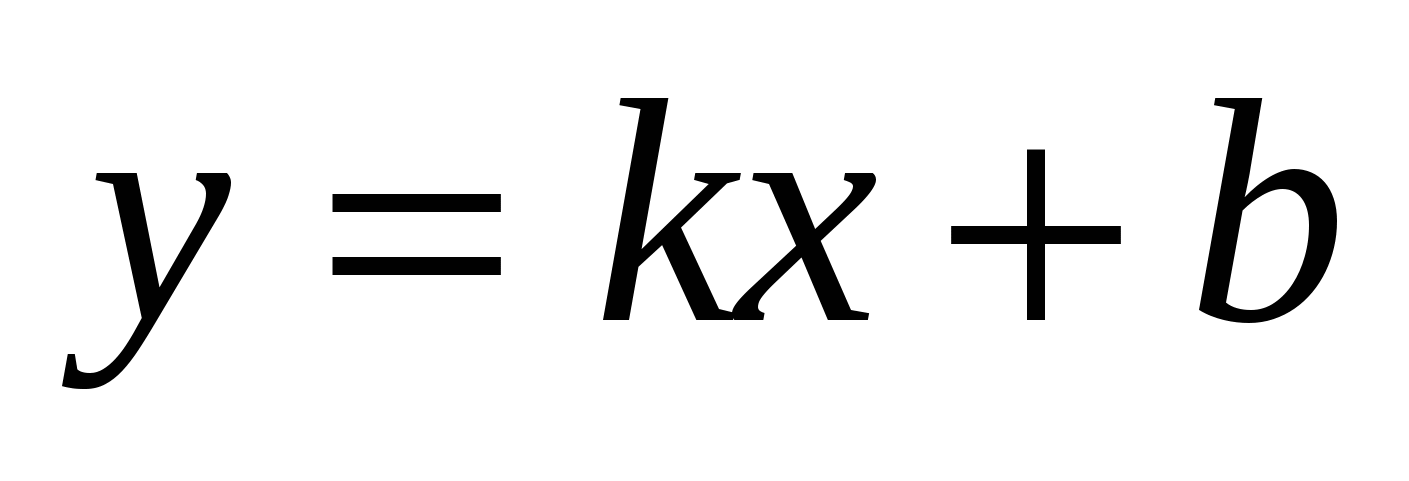
Условие параллельности
прямых
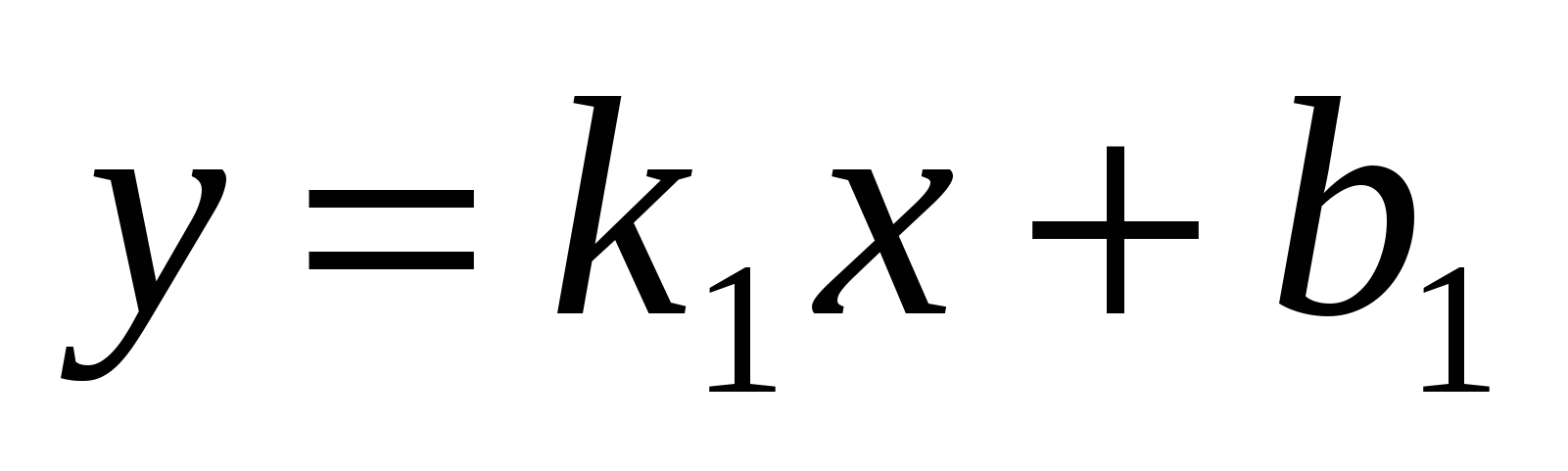 и
и 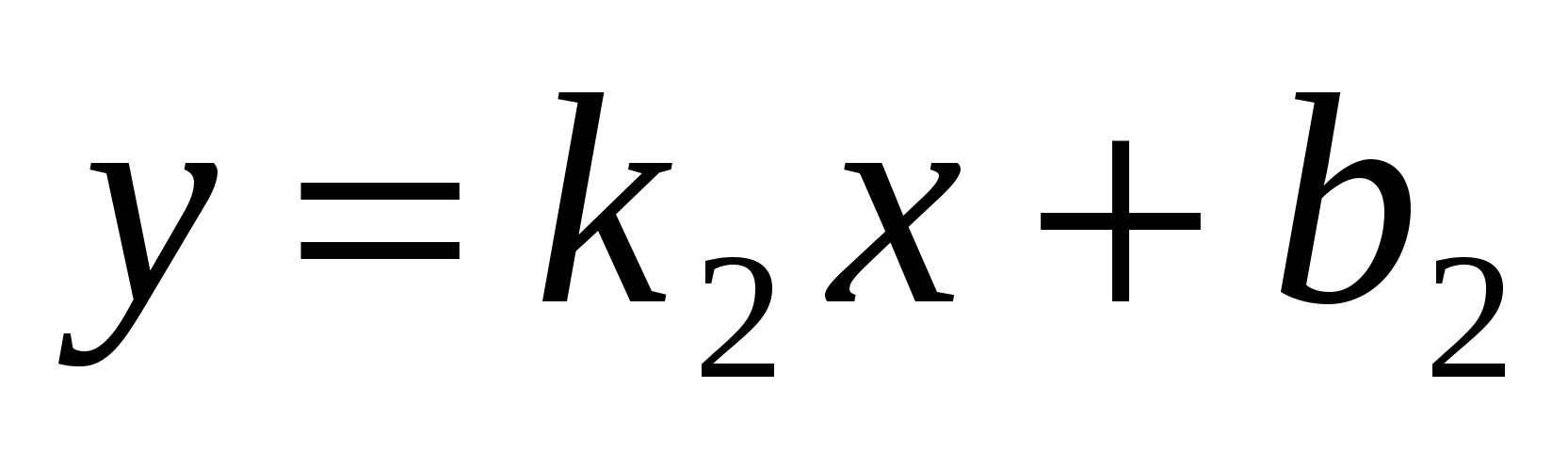
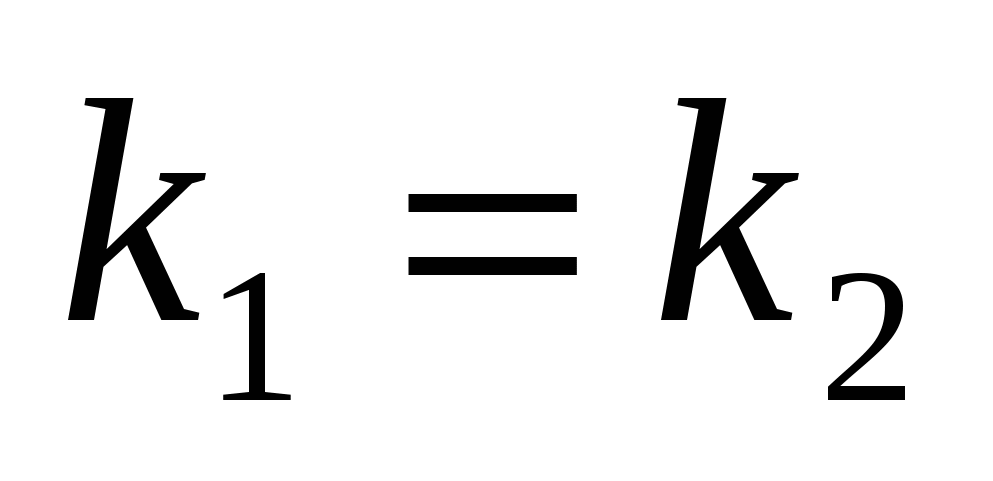
Условие перпендикулярности
прямых
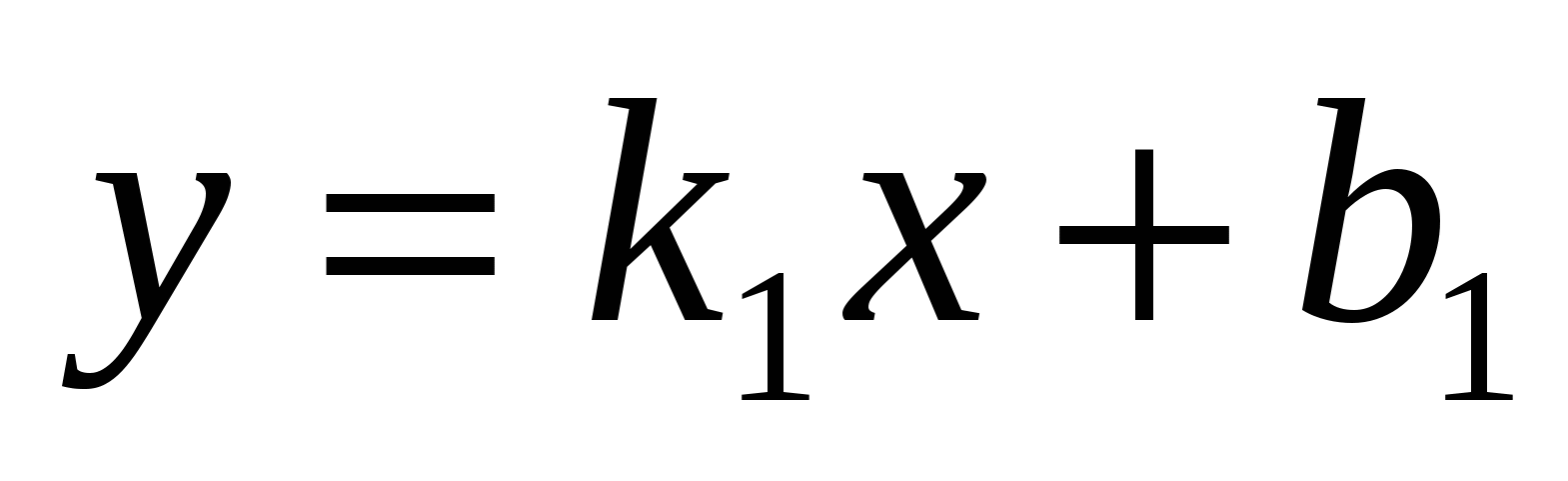 и
и 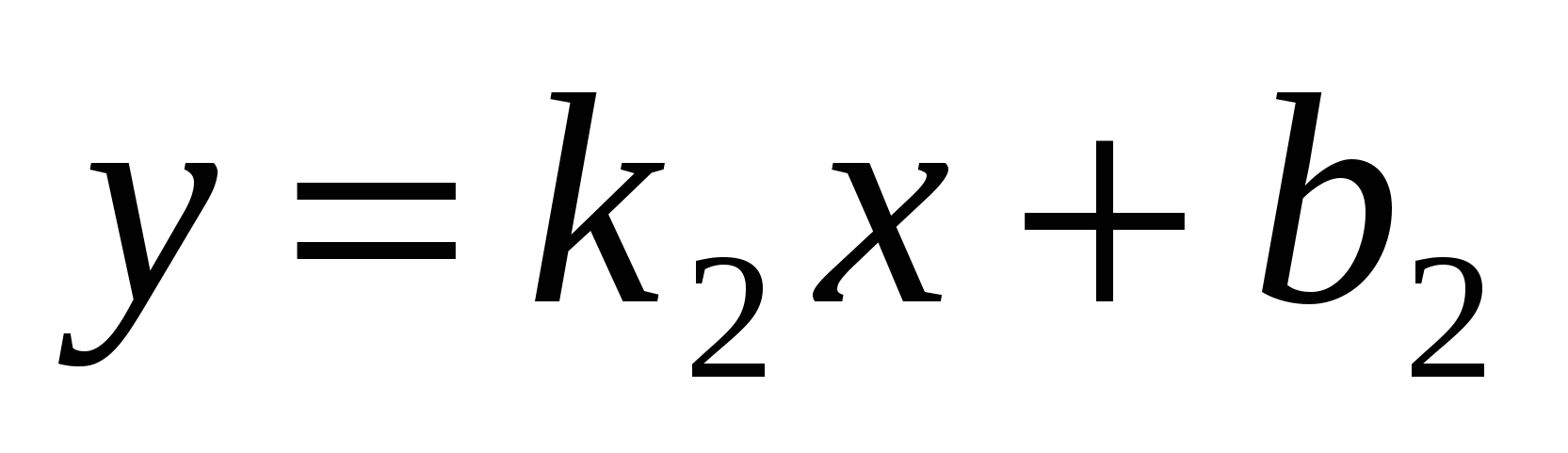
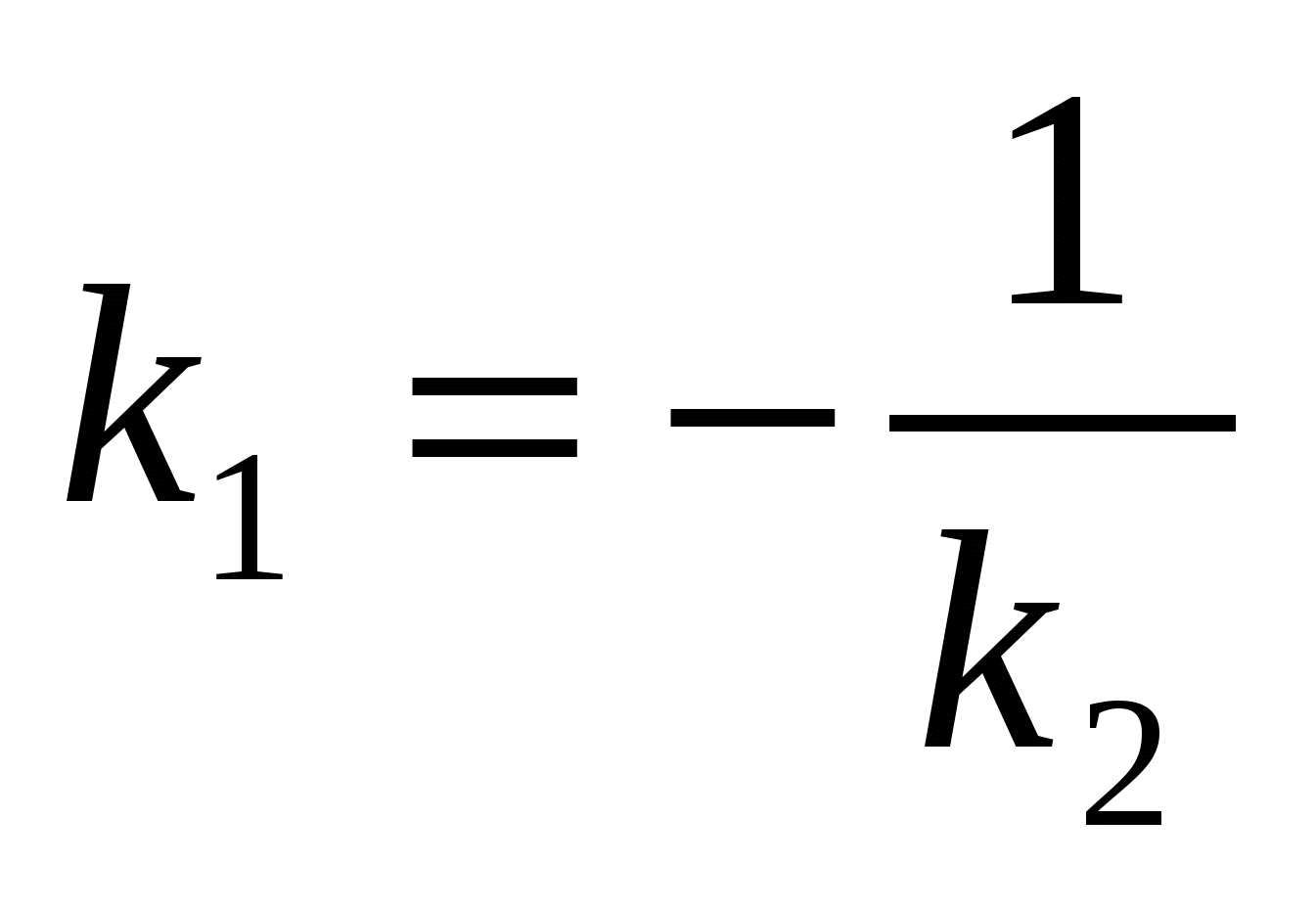
Уравнение прямой
по двум точкам
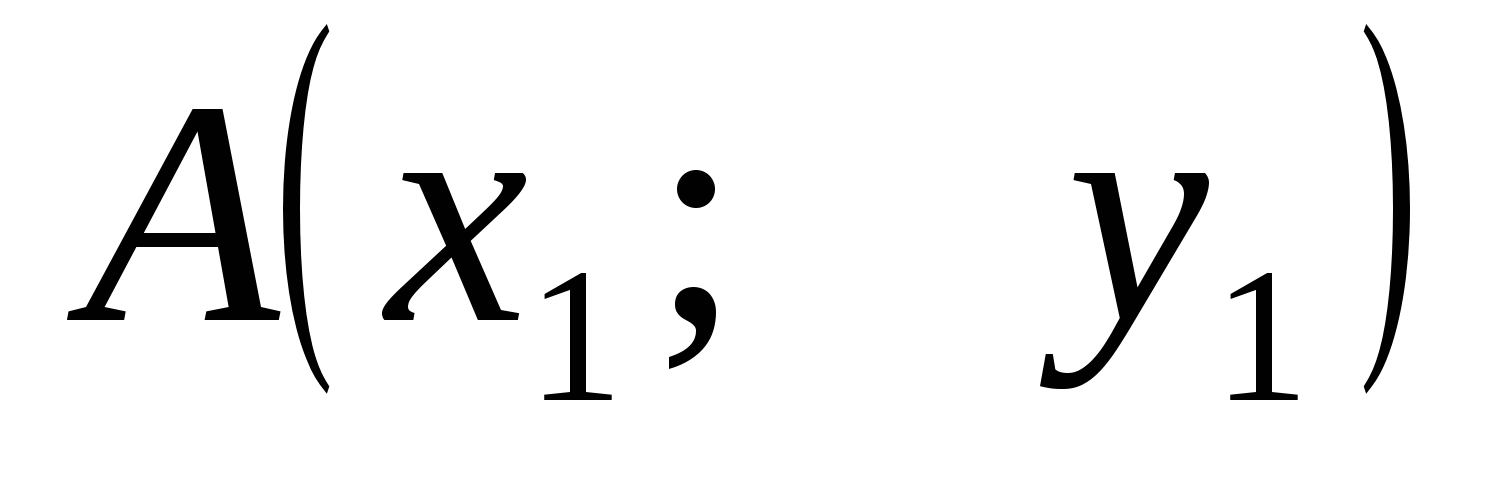 и
и 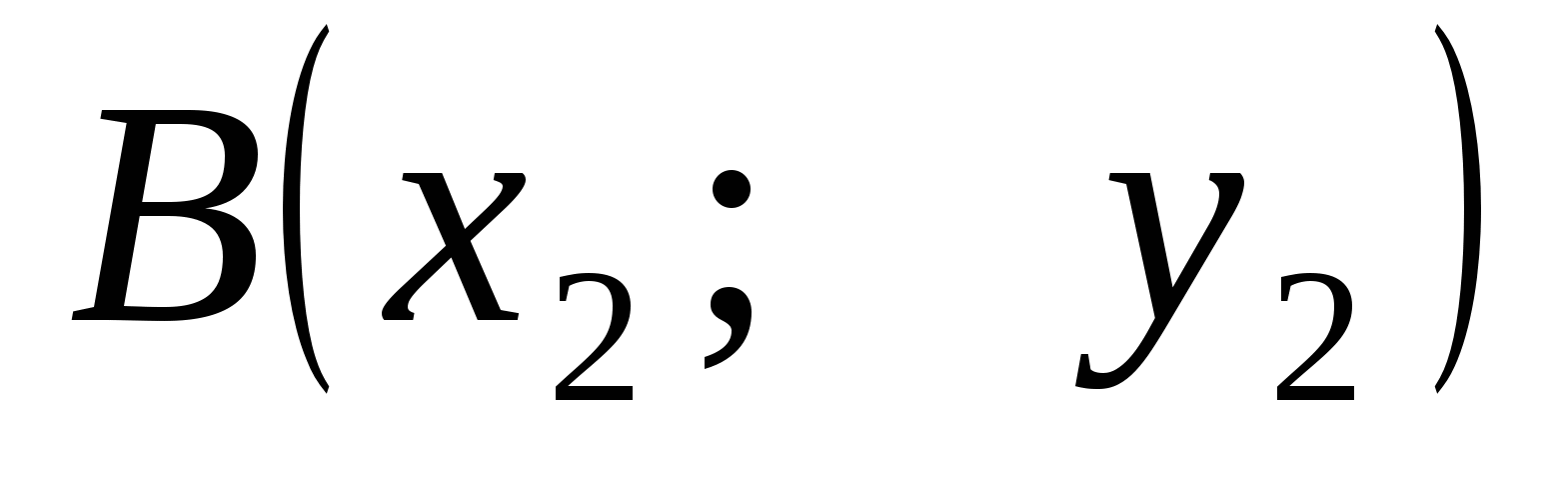
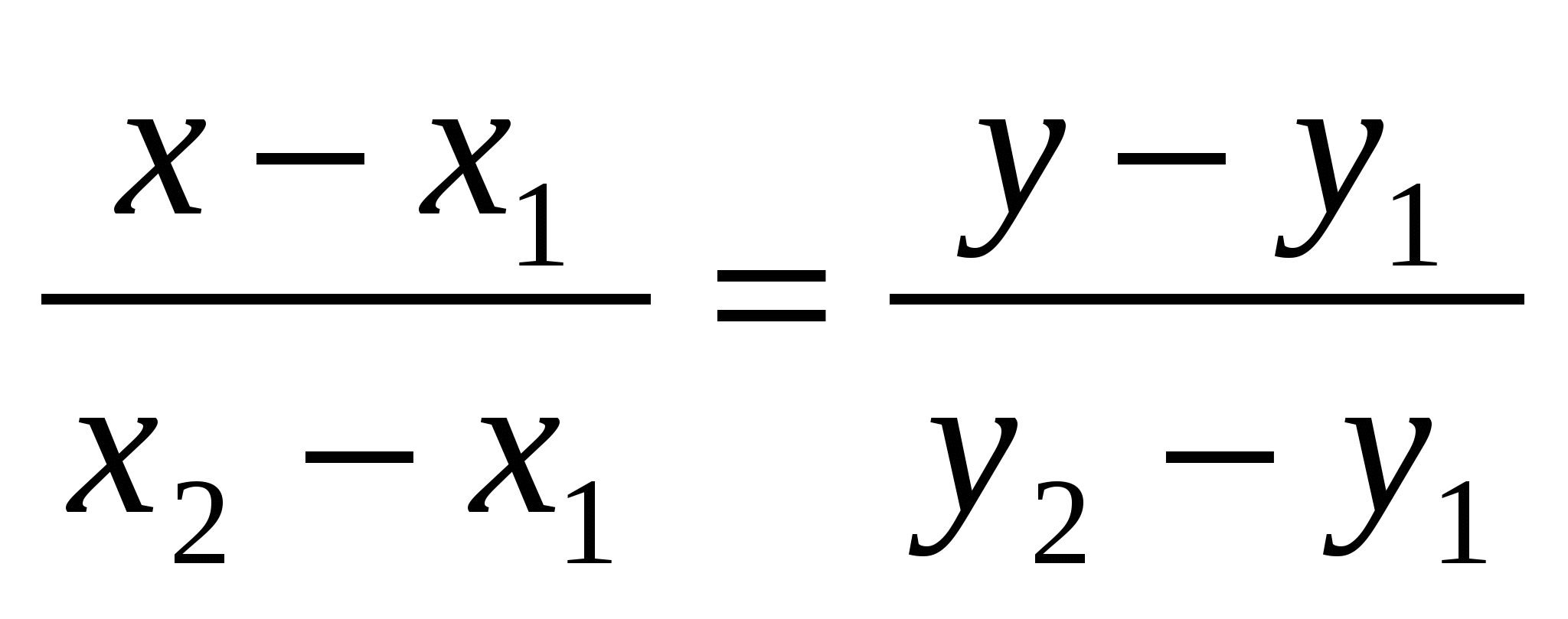
2. Уравнения прямой
в пространстве,
проходящей через точку
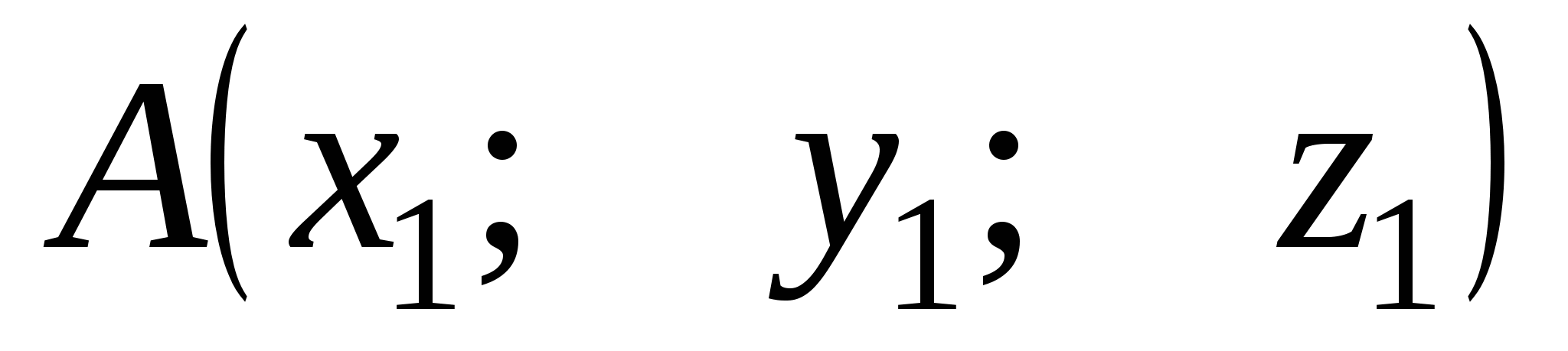 и имеющей
и имеющей
направляющий вектор 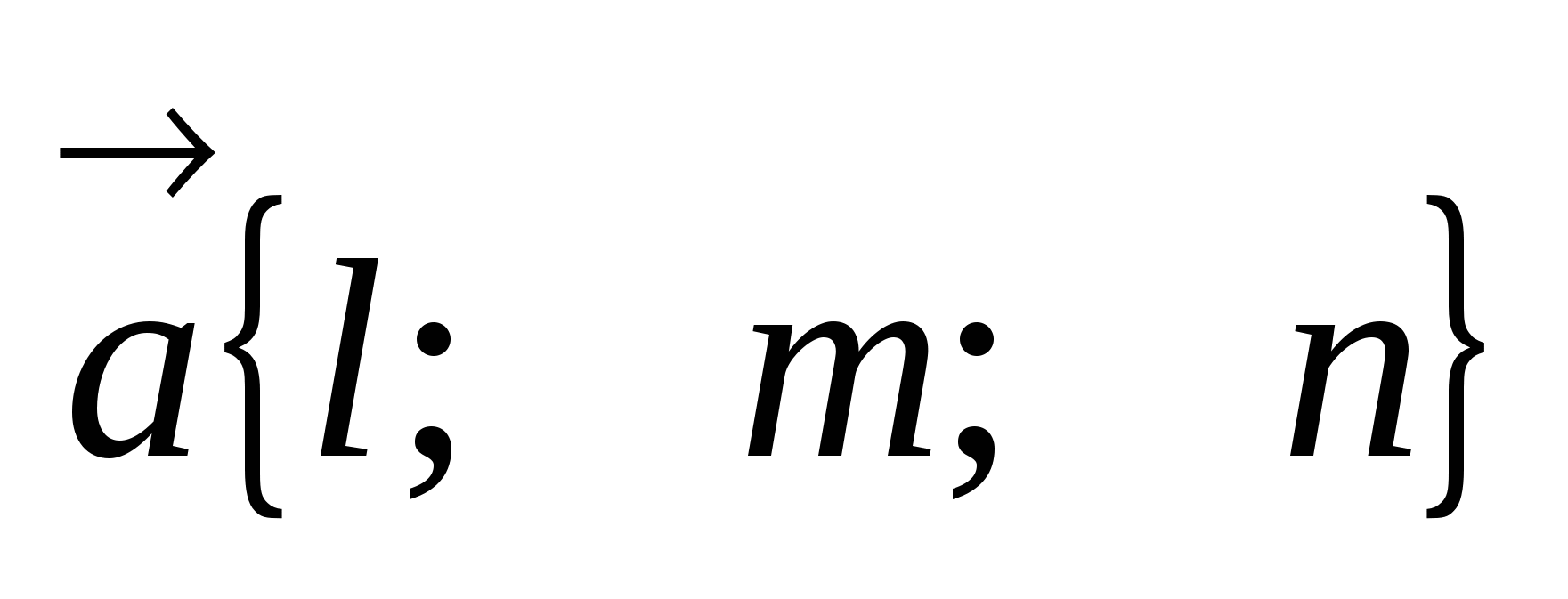
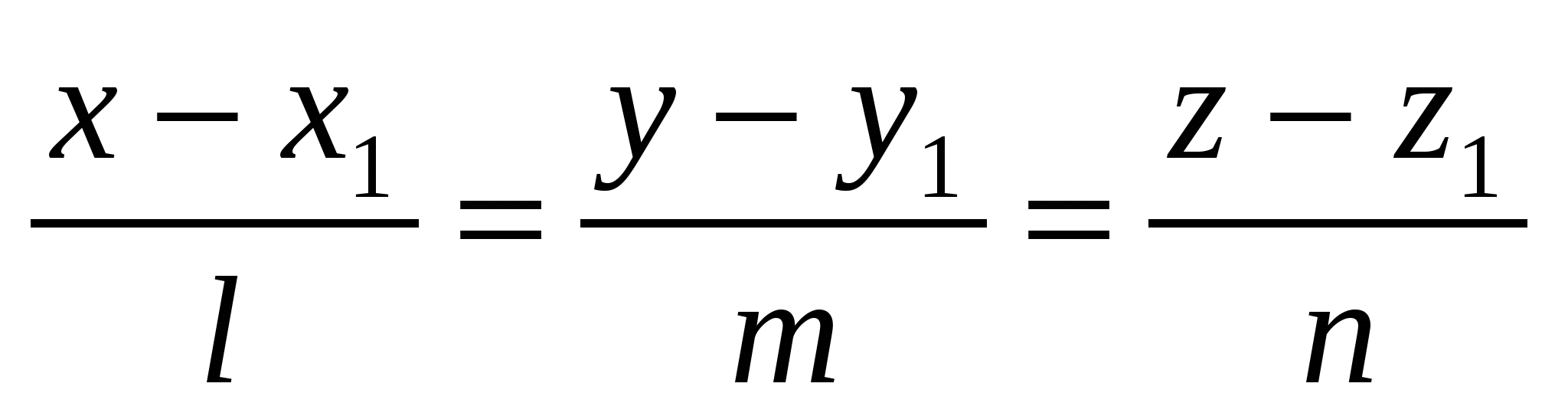
3. Уравнение плоскости
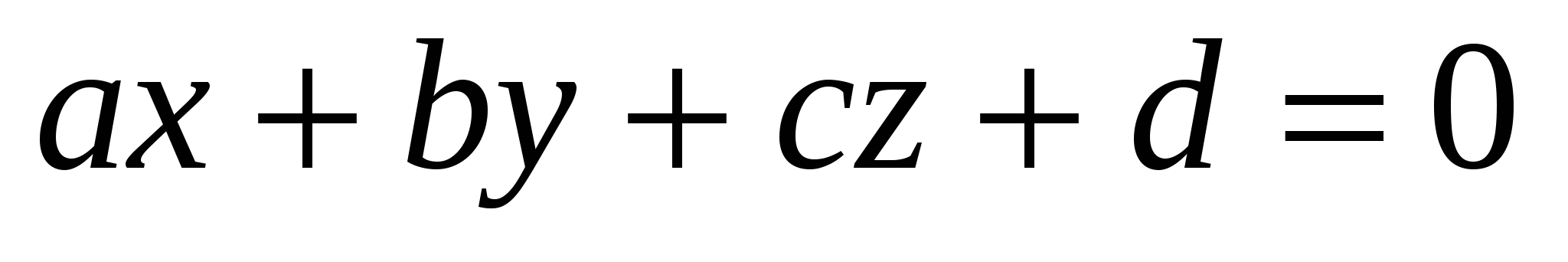 ,
,
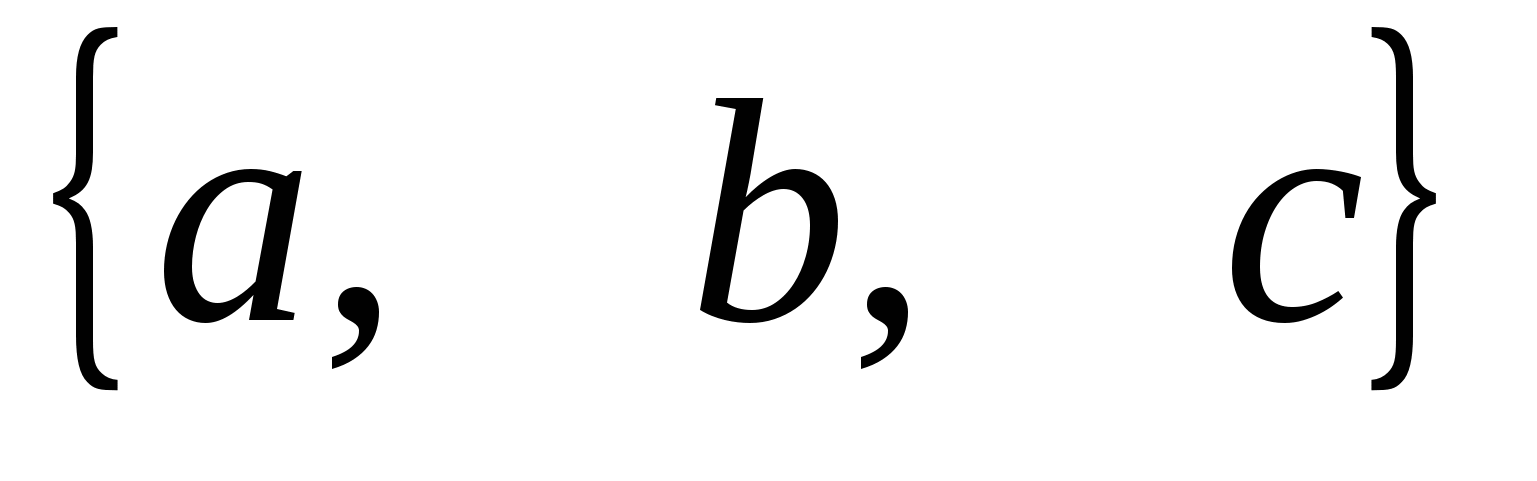 - координаты вектора,
- координаты вектора,
перпендикулярного плоскости
4. Уравнение окружности
(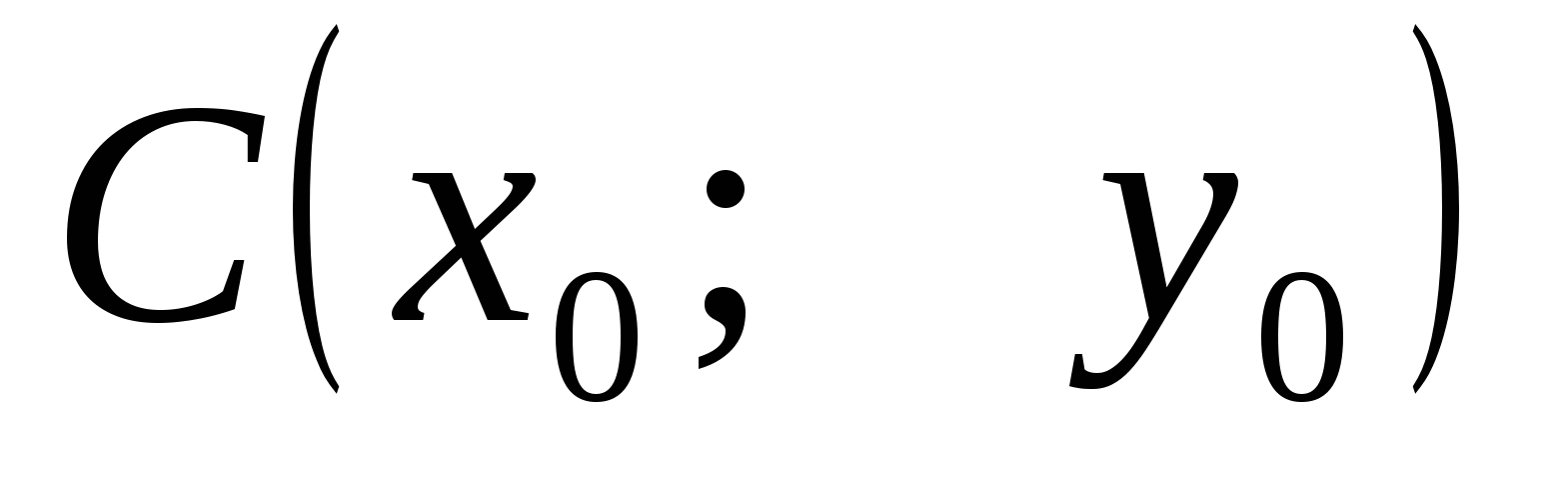 - центр окружности)
- центр окружности)
Уравнение окружности
с центром в начале координат
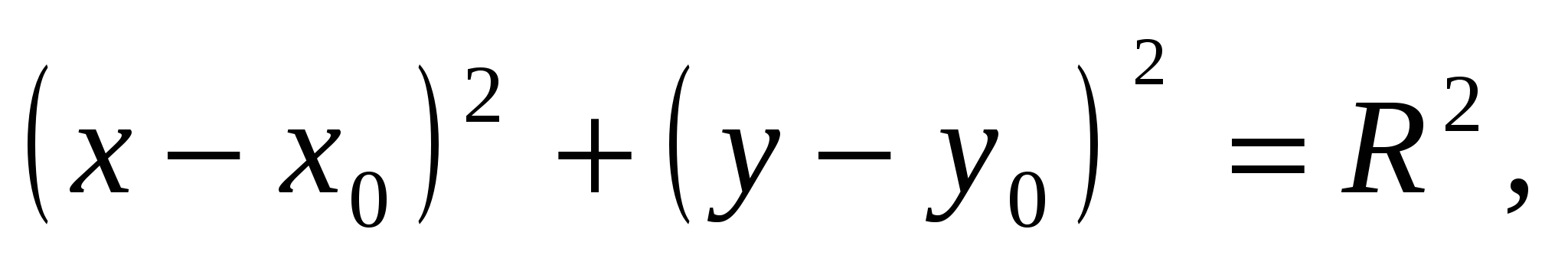
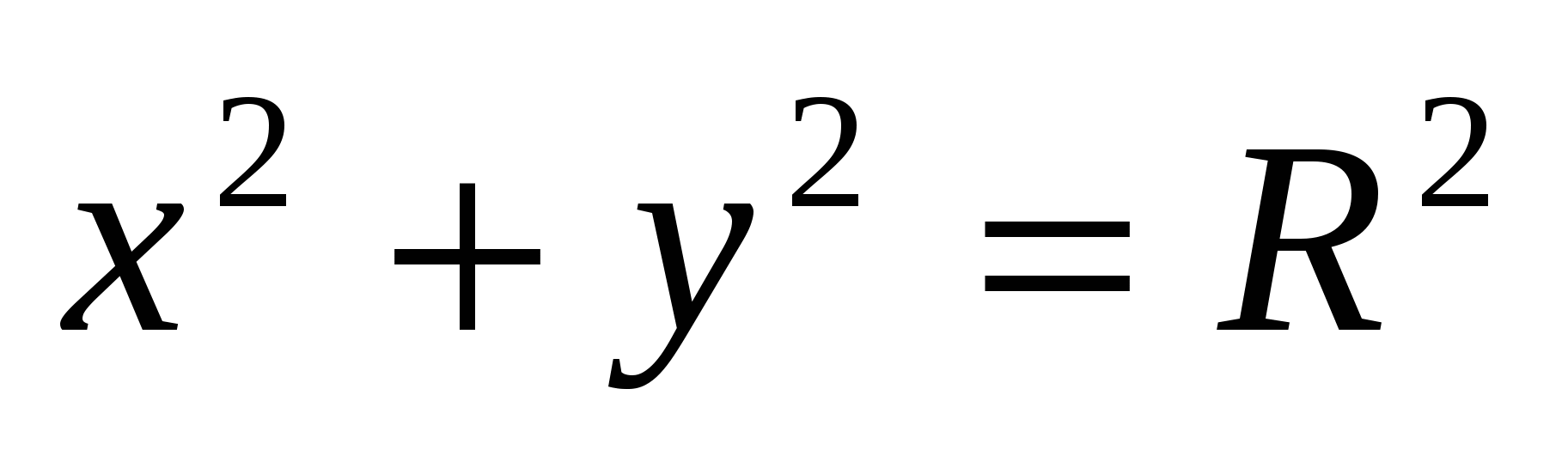
5. Уравнение сферы
(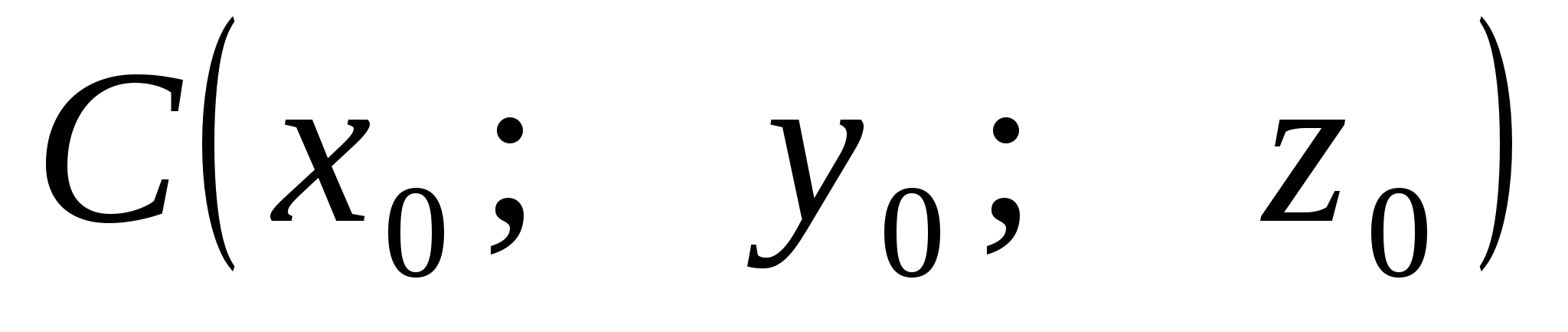 - центр сферы)
- центр сферы)
Уравнение сферы
с центром в начале координат
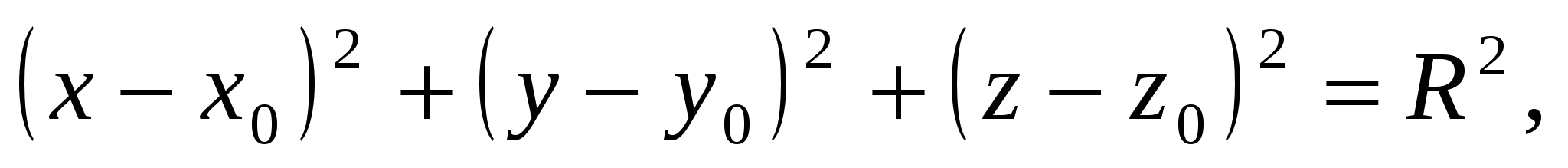
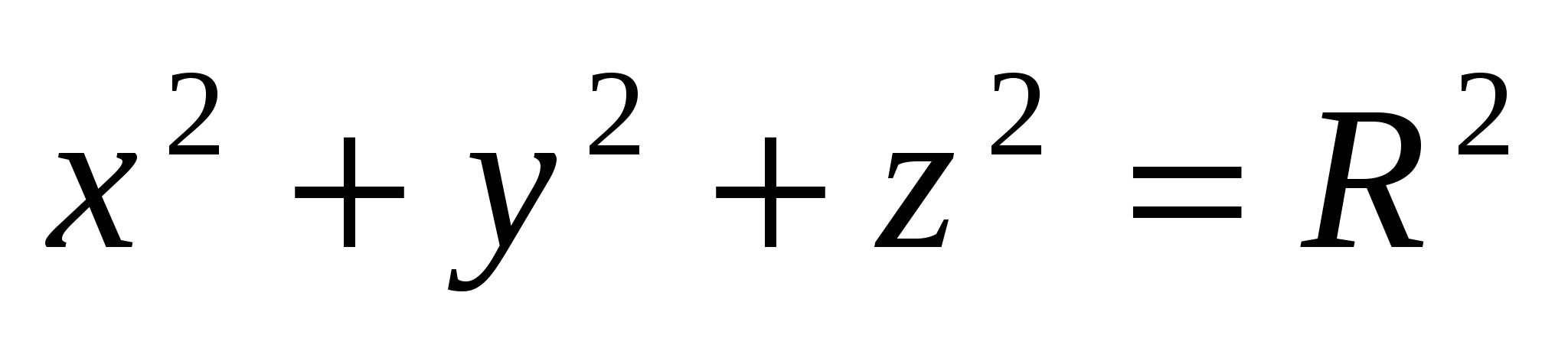
Задача 1. Найти периметр треугольника с вершинами А(1; 1; 0), В(1; 2; 2) и С(3; 2; 0).
Схема решения:
АВ =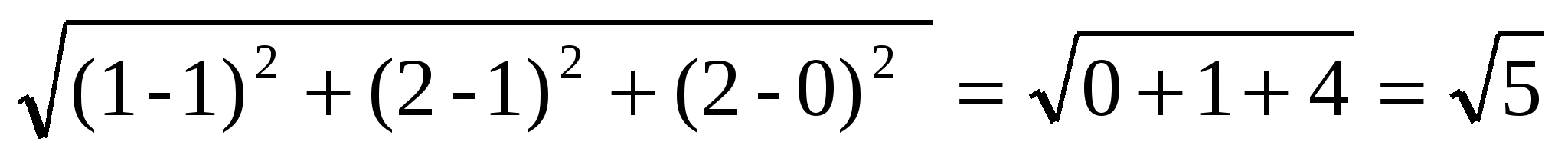 ,
,
ВС = 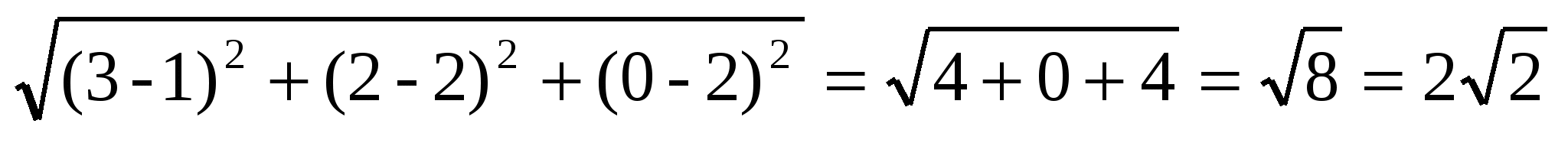 ,
,
АС = 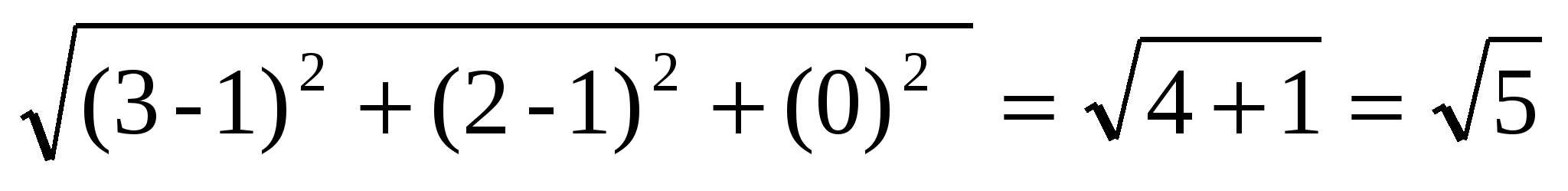 ,
,
Р = АВ + ВС + АС = 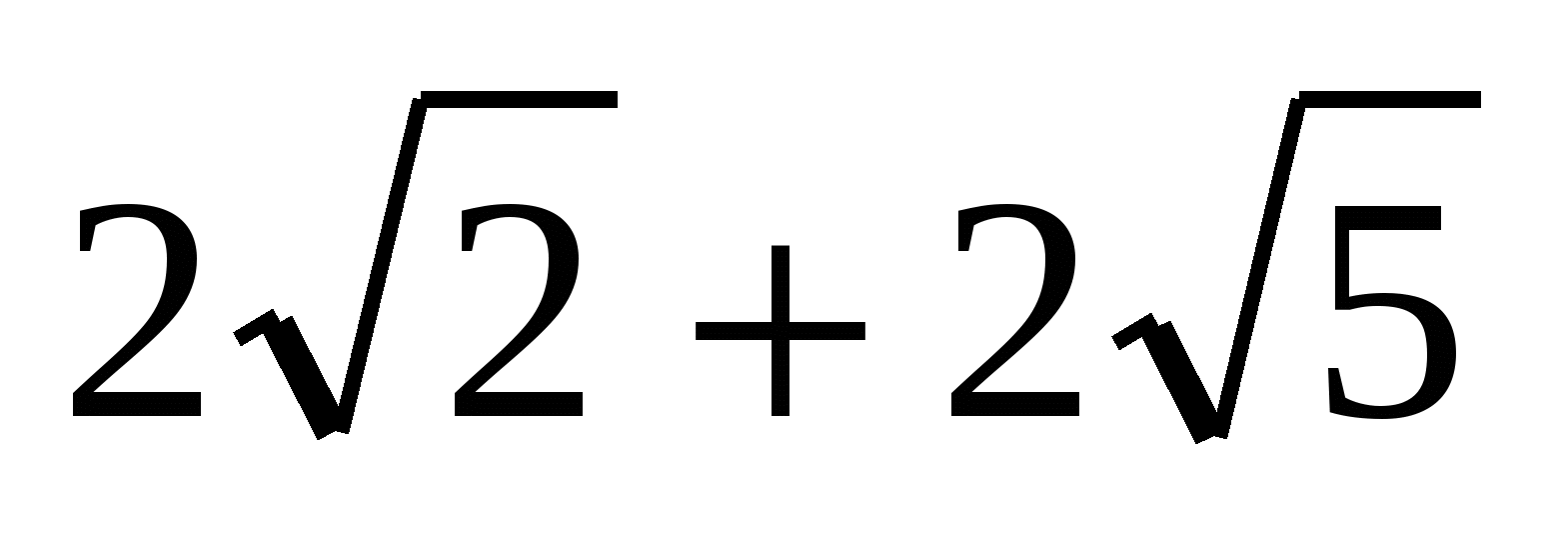 .
.
Ответ: 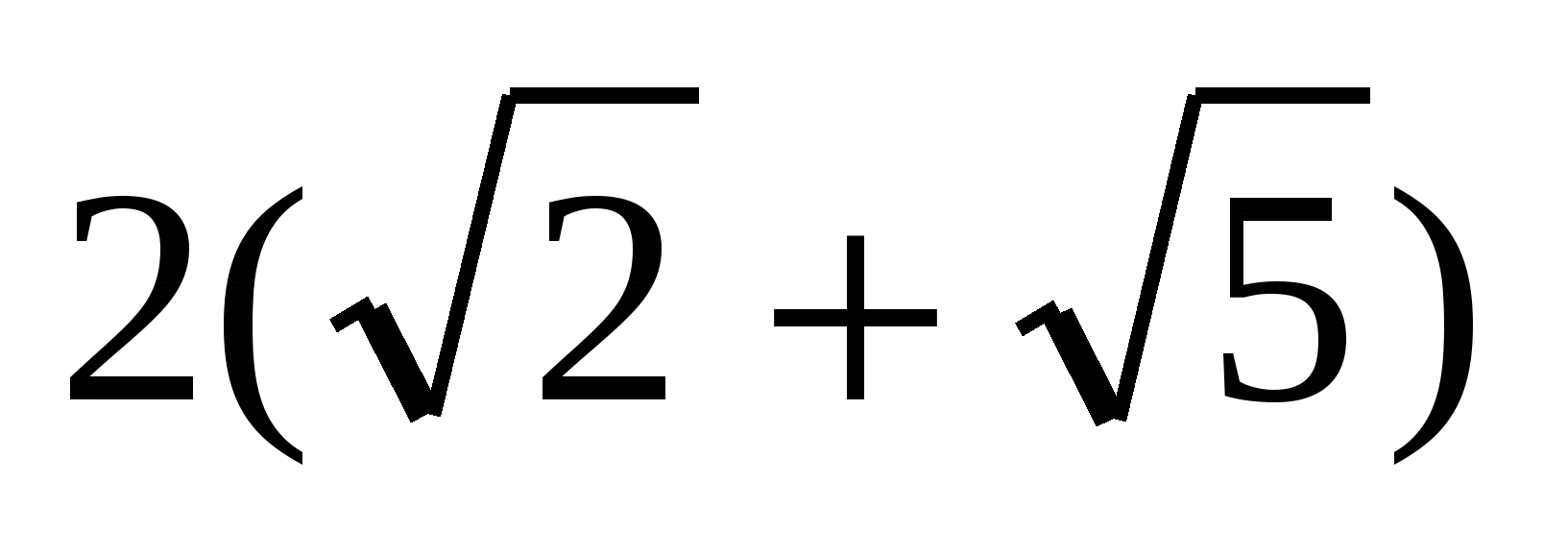 .
.
Задача 2. В равнобедренном треугольнике с вершинами в точках А(4; 3; -1), В(6; 4; 1) и С(2; 4; 1) найти длину высоты, опущенной на основание.
Схема решения:
1) Найдём длины сторон треугольника по формуле длины отрезка
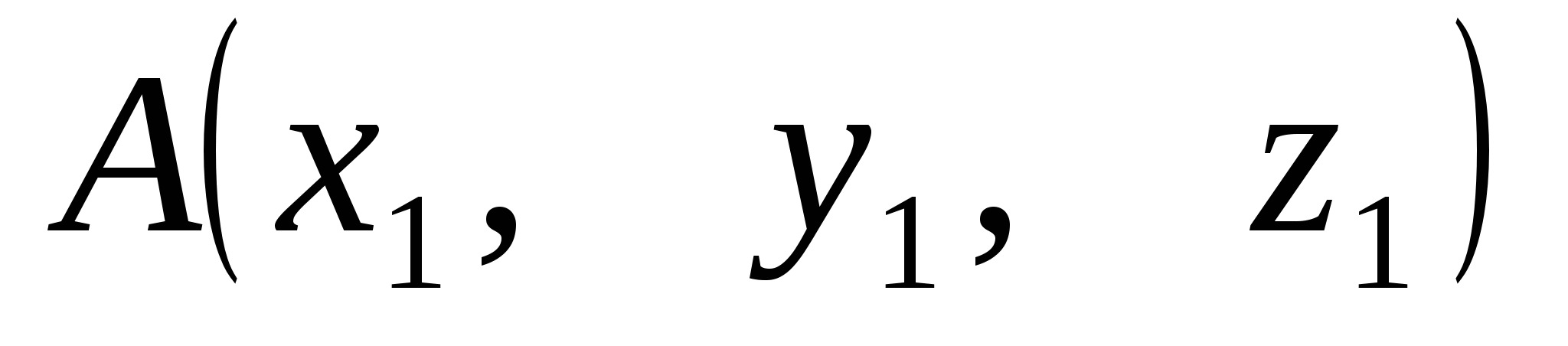 ,
, 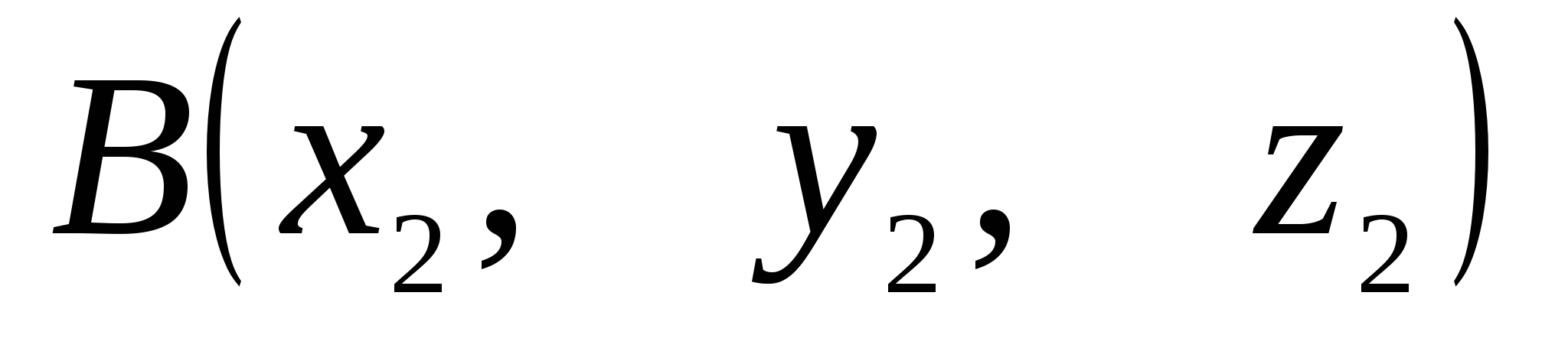 ,
,
АВ = 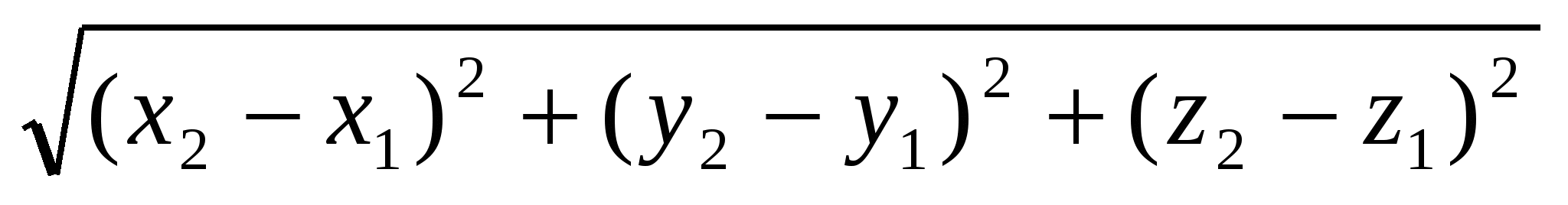 . Имеем:
. Имеем:
АВ =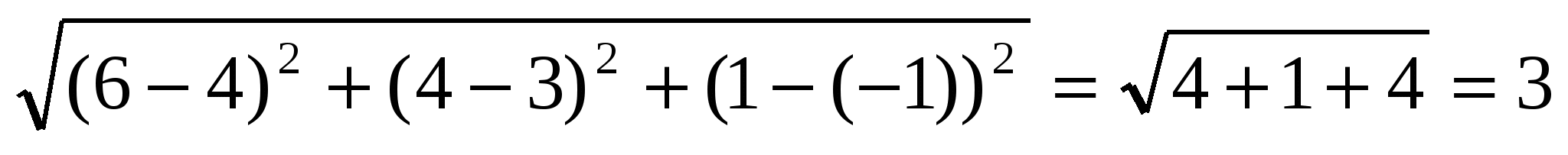 ;
;
ВС =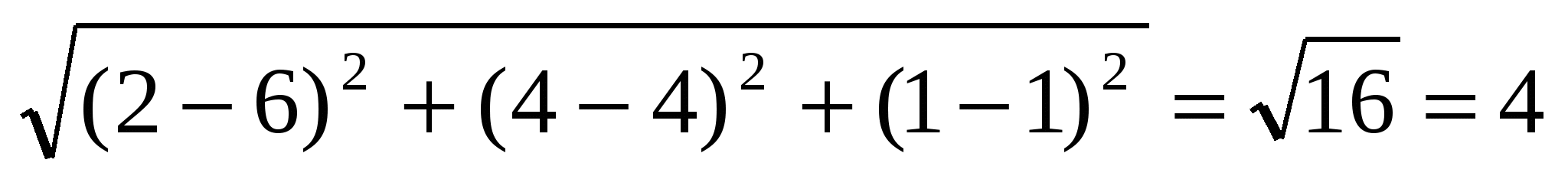 ;
;
АС = 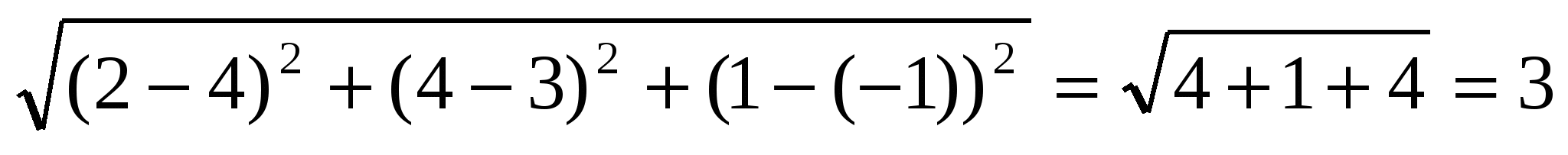 ;
;
АВ = АС, ВС - основание равнобедренного треугольника.
2) Найдём координаты точки М - середины ВС. М(4; 4; 1).
3) АМ - высота, опущенная на основание, т.е.
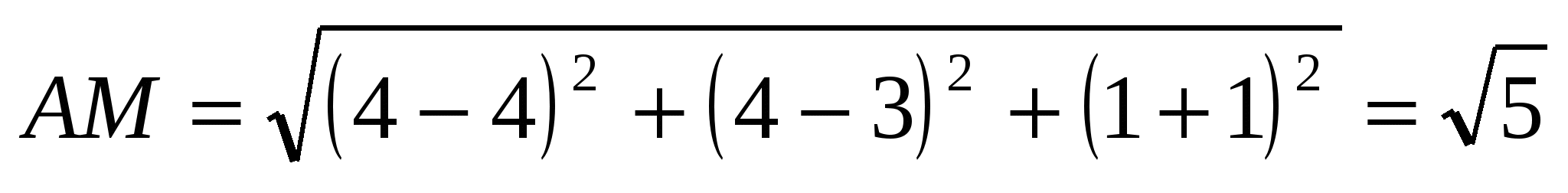 .
.
Ответ: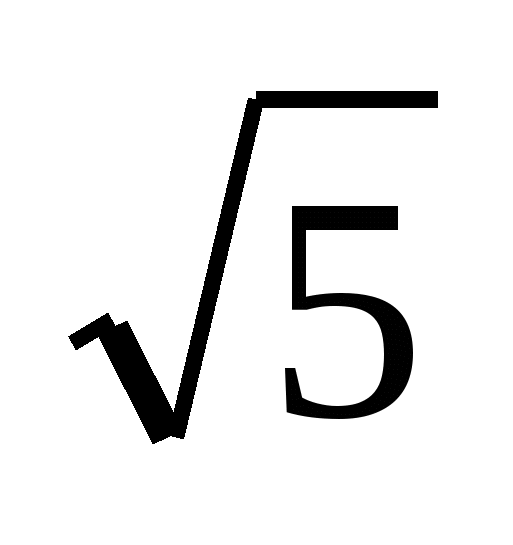 .
.
Задача 3. Внутри куба 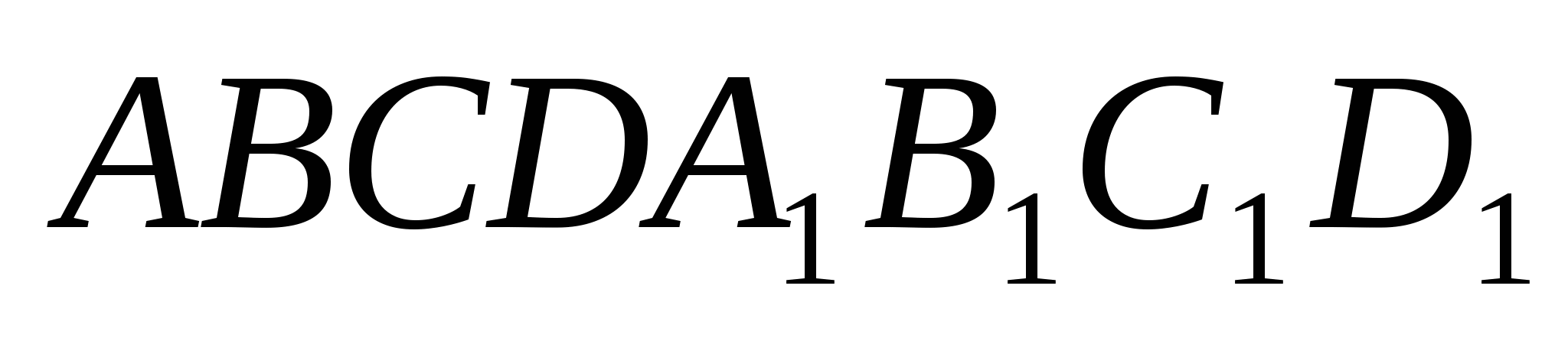 с ребром 4 взята точка М на одинаковым расстоянии, равном 1, от граней трёхгранного угла с вершиной
с ребром 4 взята точка М на одинаковым расстоянии, равном 1, от граней трёхгранного угла с вершиной ![]() . Найти расстояние от точки М до середины ребра DC.
. Найти расстояние от точки М до середины ребра DC.
Схема решения:
Пусть точка K - середина ребра DC. Введём в пространстве прямоугольную систему координат с началом в точке  . Найдём координаты точек М и K: - М(1; 1; 1), K(4; 2; 4). Применим формулу для вычисления расстояния между двумя точками:
. Найдём координаты точек М и K: - М(1; 1; 1), K(4; 2; 4). Применим формулу для вычисления расстояния между двумя точками:
МK = 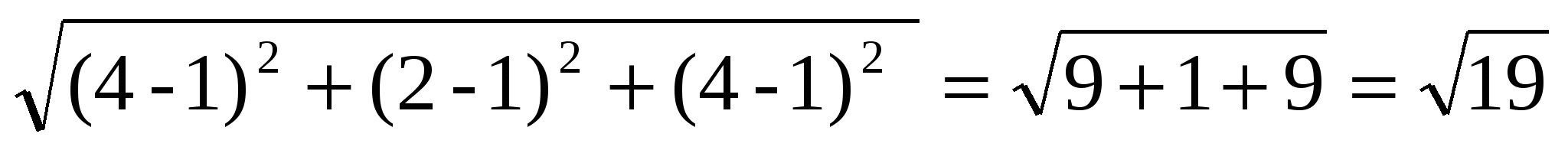 .
.
Ответ: МK =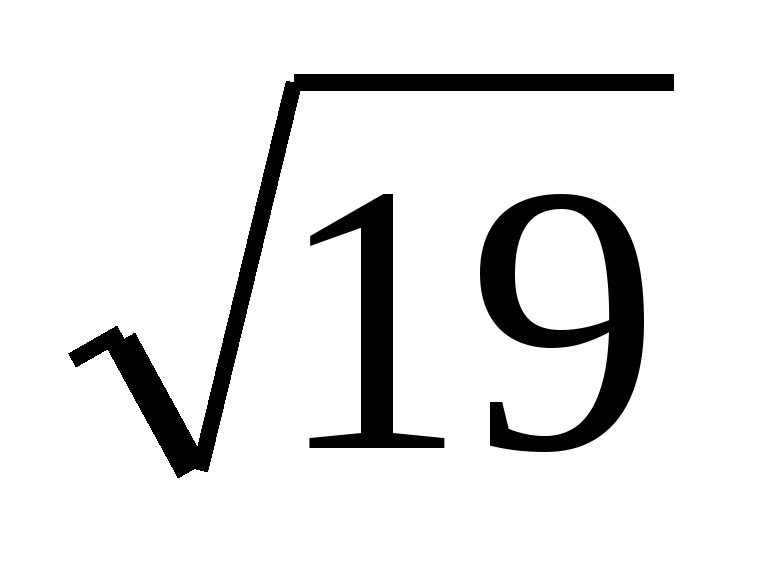 .
.
Задача 4. Сфера проходит через точки А, 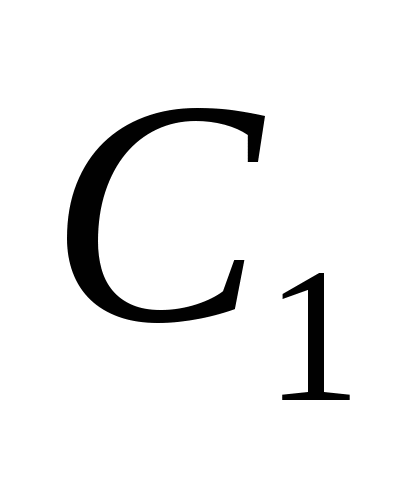 , М, N куба
, М, N куба 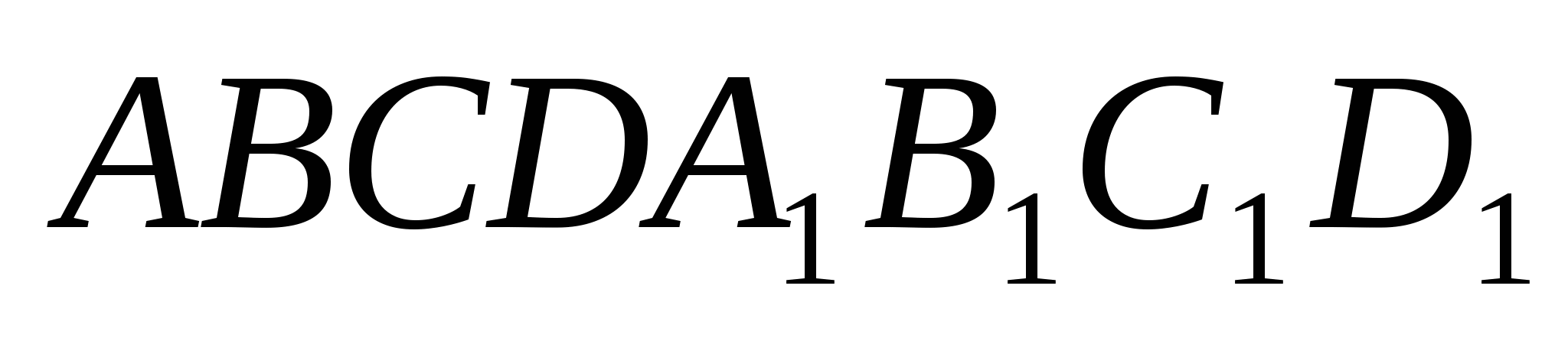 , где точка М - середина
, где точка М - середина  , N - середина
, N - середина 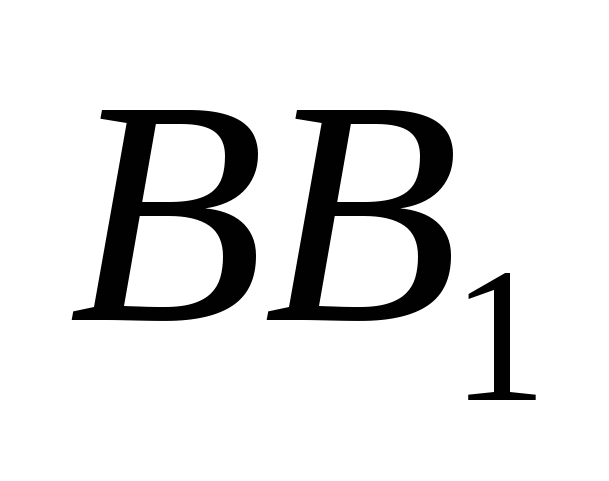 . Найти радиус сферы, если ребро куба равно а.
. Найти радиус сферы, если ребро куба равно а.
Схема решения:
Введём прямоугольную систему координат Axyz.
Найдём координаты точек:
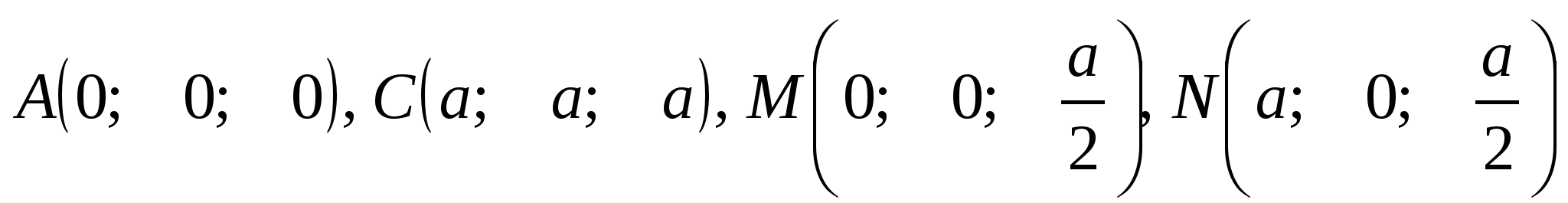 .
.
Пусть центром сферы является точка О(x; y; z).
Так как сфера проходит через точки А, 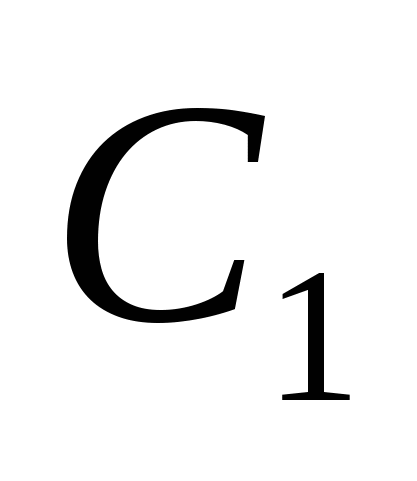 , М, N, следовательно, ОА, ОС1, ОМ, ОN являются радиусами сферы.
, М, N, следовательно, ОА, ОС1, ОМ, ОN являются радиусами сферы.
Найдём расстояние:
ОА = 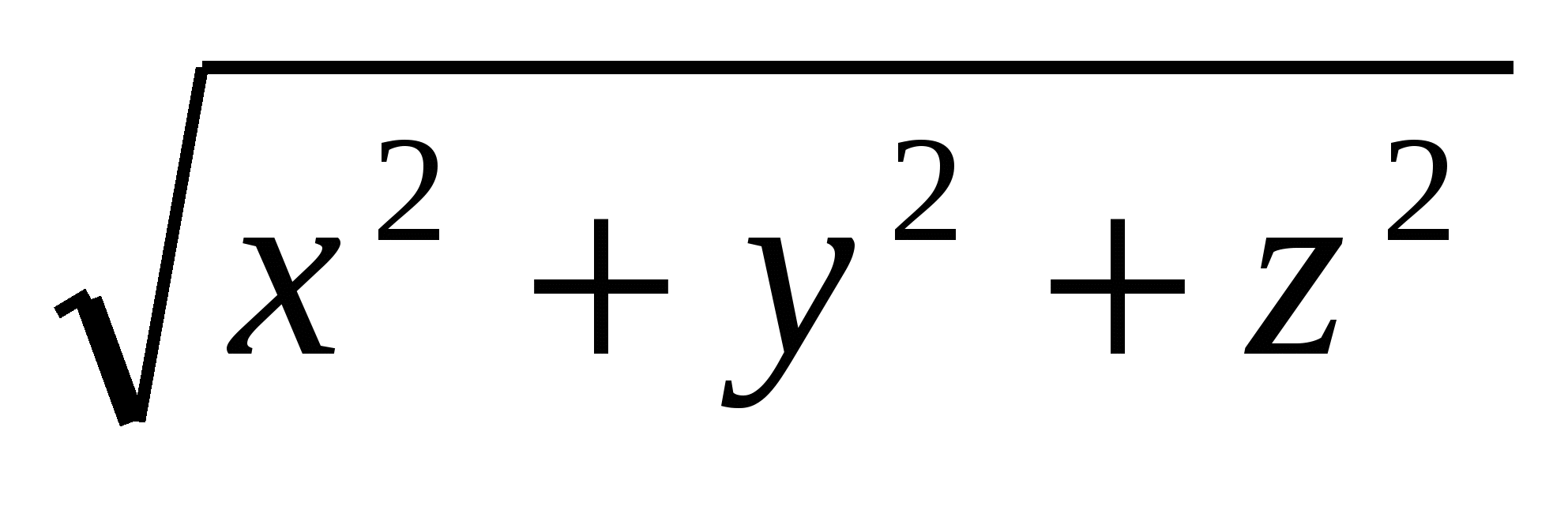 ,
,
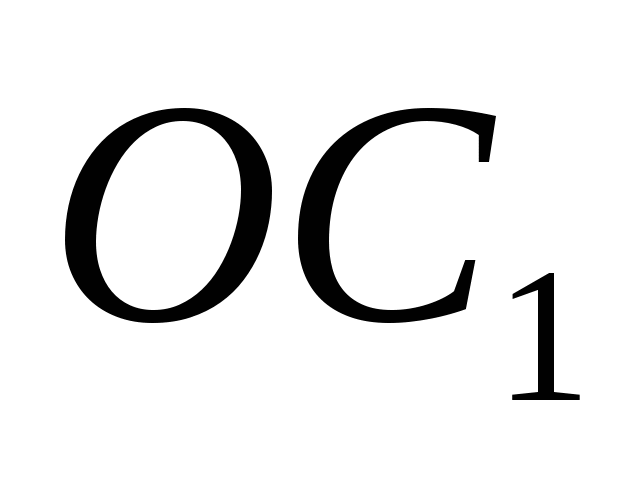 =
= 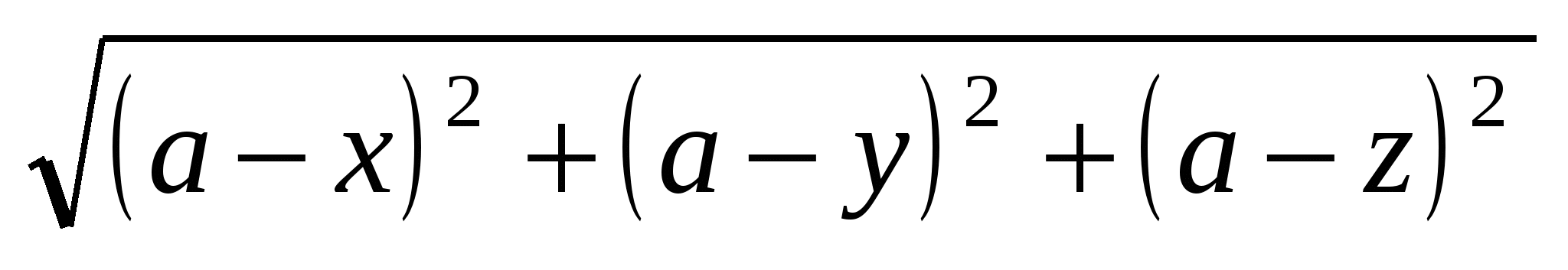 ,
,
OM = 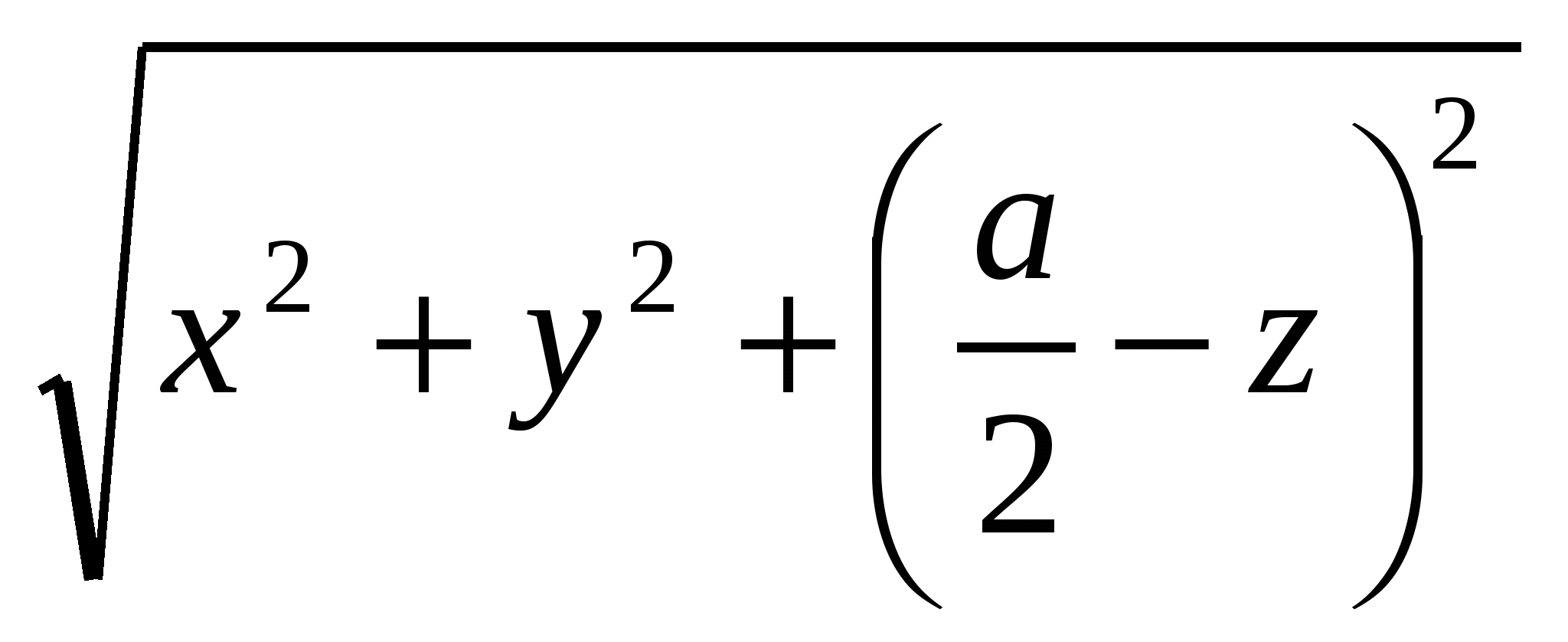 ,
,
ON = 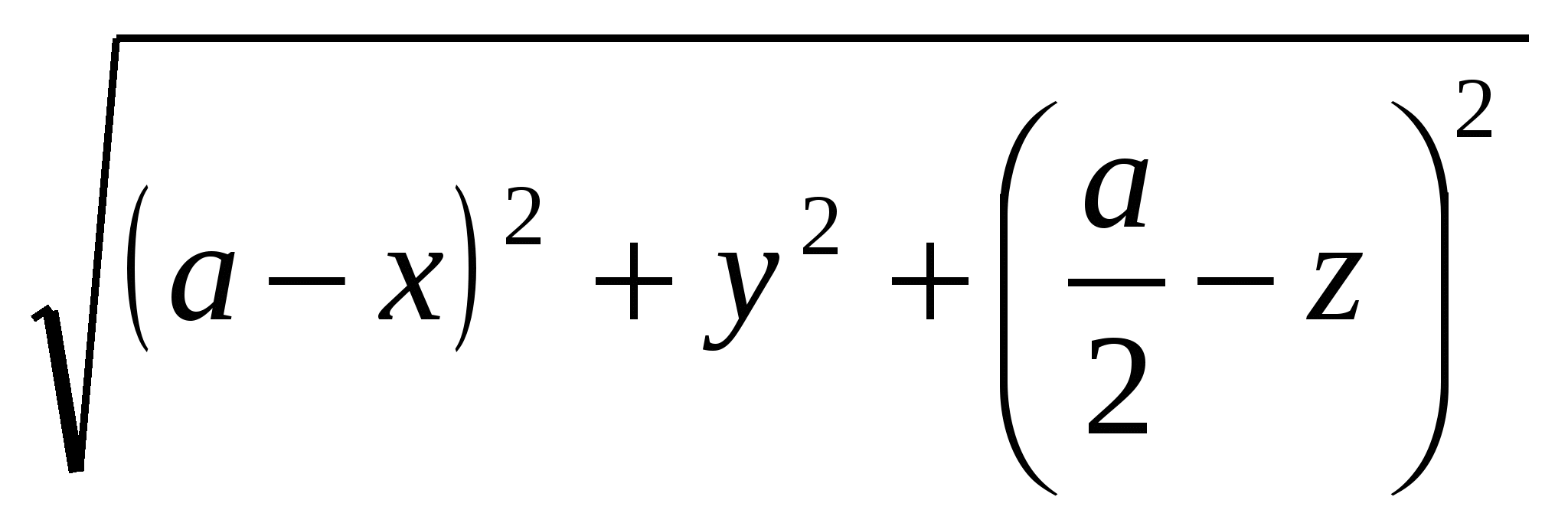 .
.
Из условия следует: 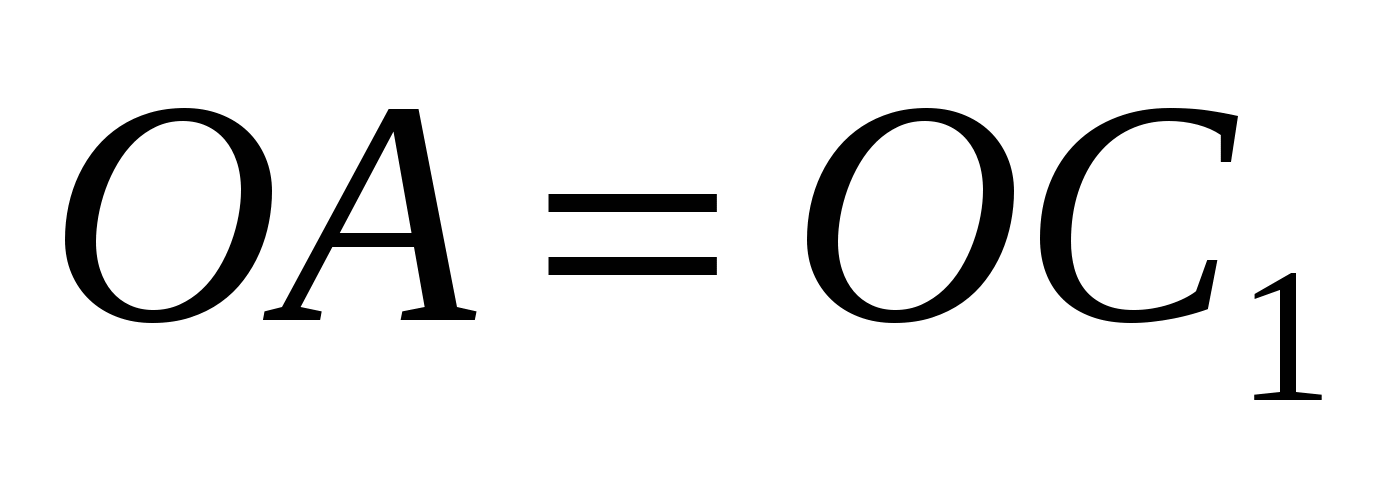 ,
,
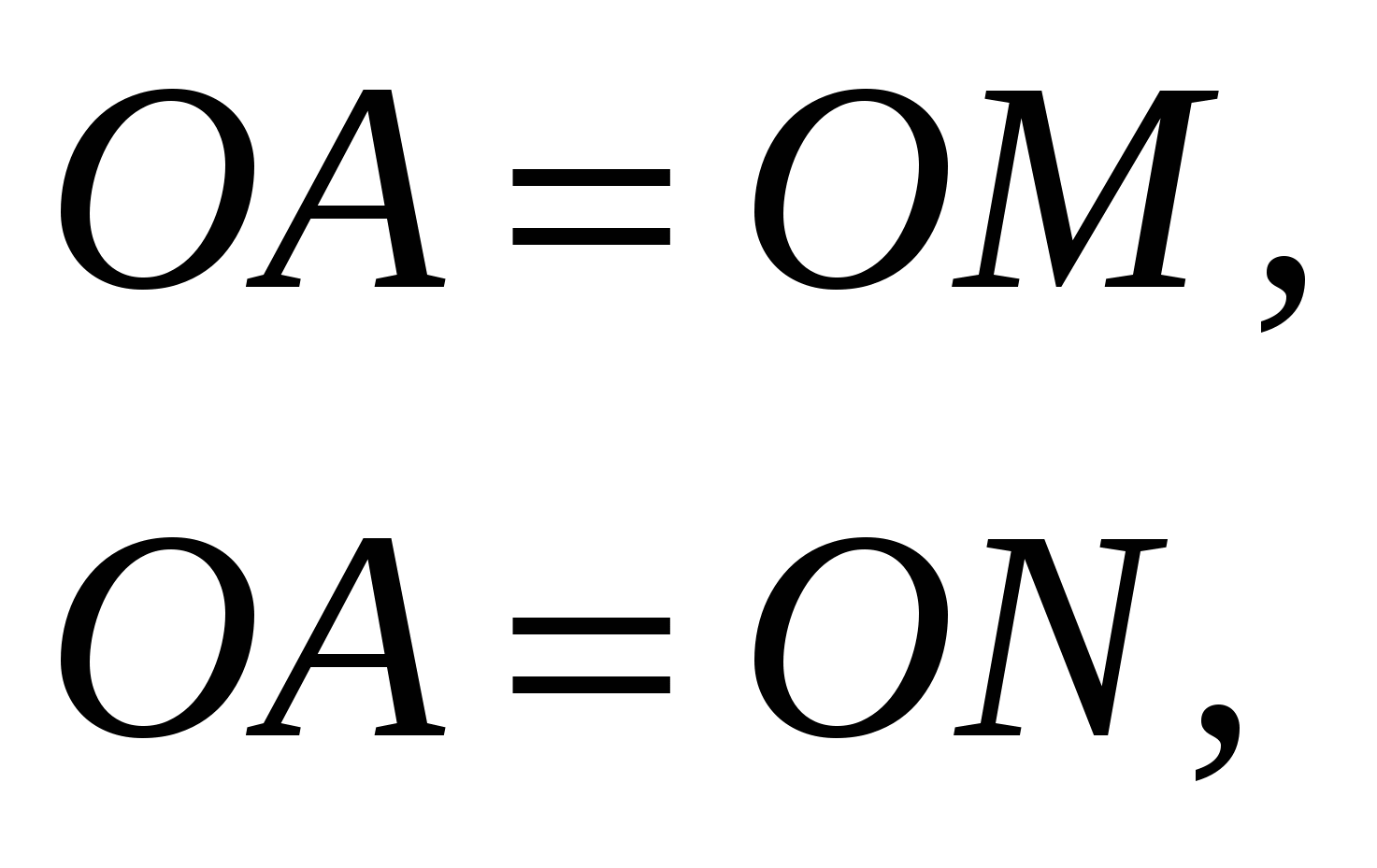
то есть имеем систему уравнений:
x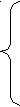 2 + y2 + z2 = (a - x)2 + (a - y)2 + (a - z)2,
2 + y2 + z2 = (a - x)2 + (a - y)2 + (a - z)2,
x2 + y2 + z2 = x2 + y2 + 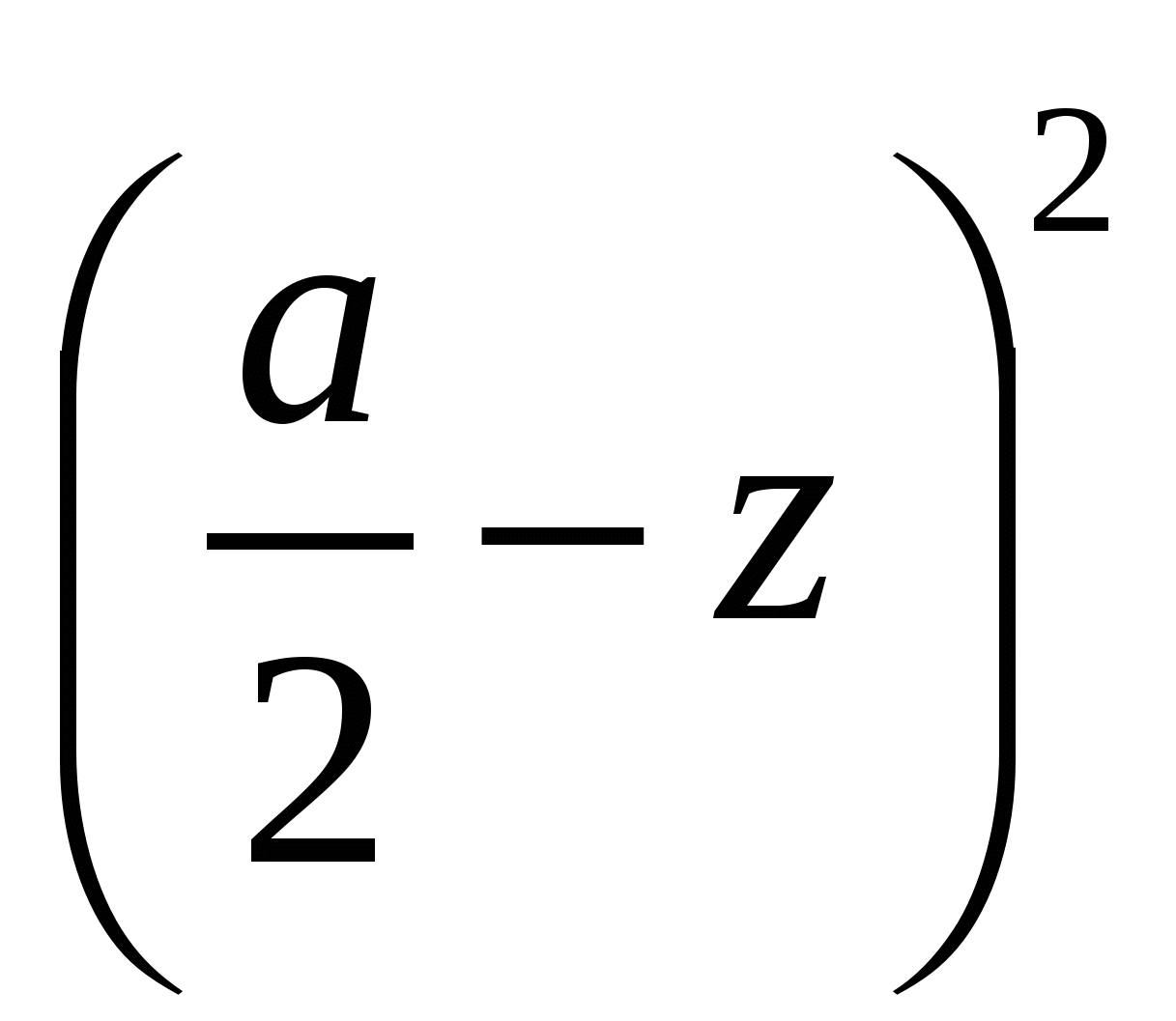 ,
,
x2 + y2 + z2 = (a - x)2 + y2 +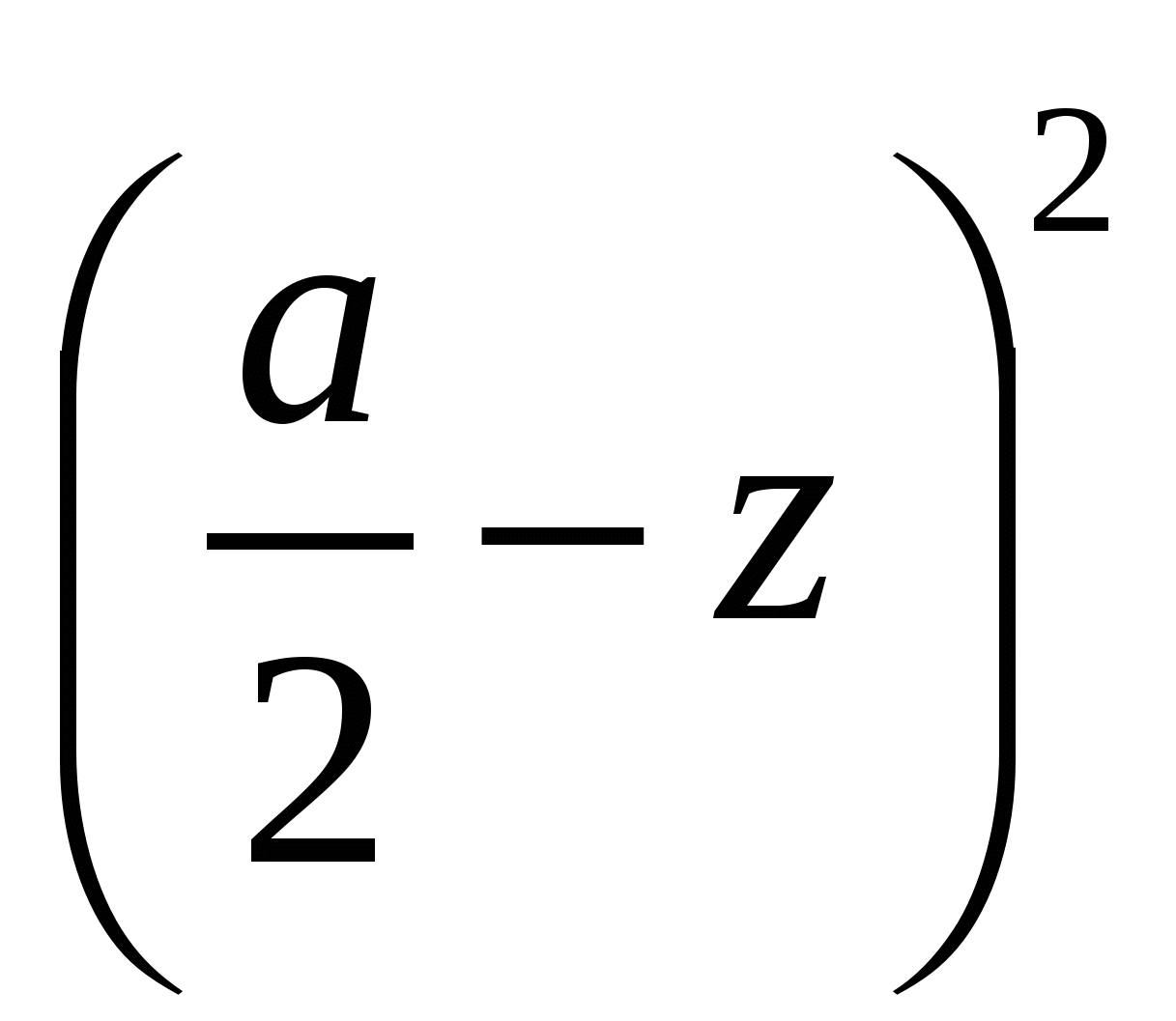 .
.
Решив её, получаем:
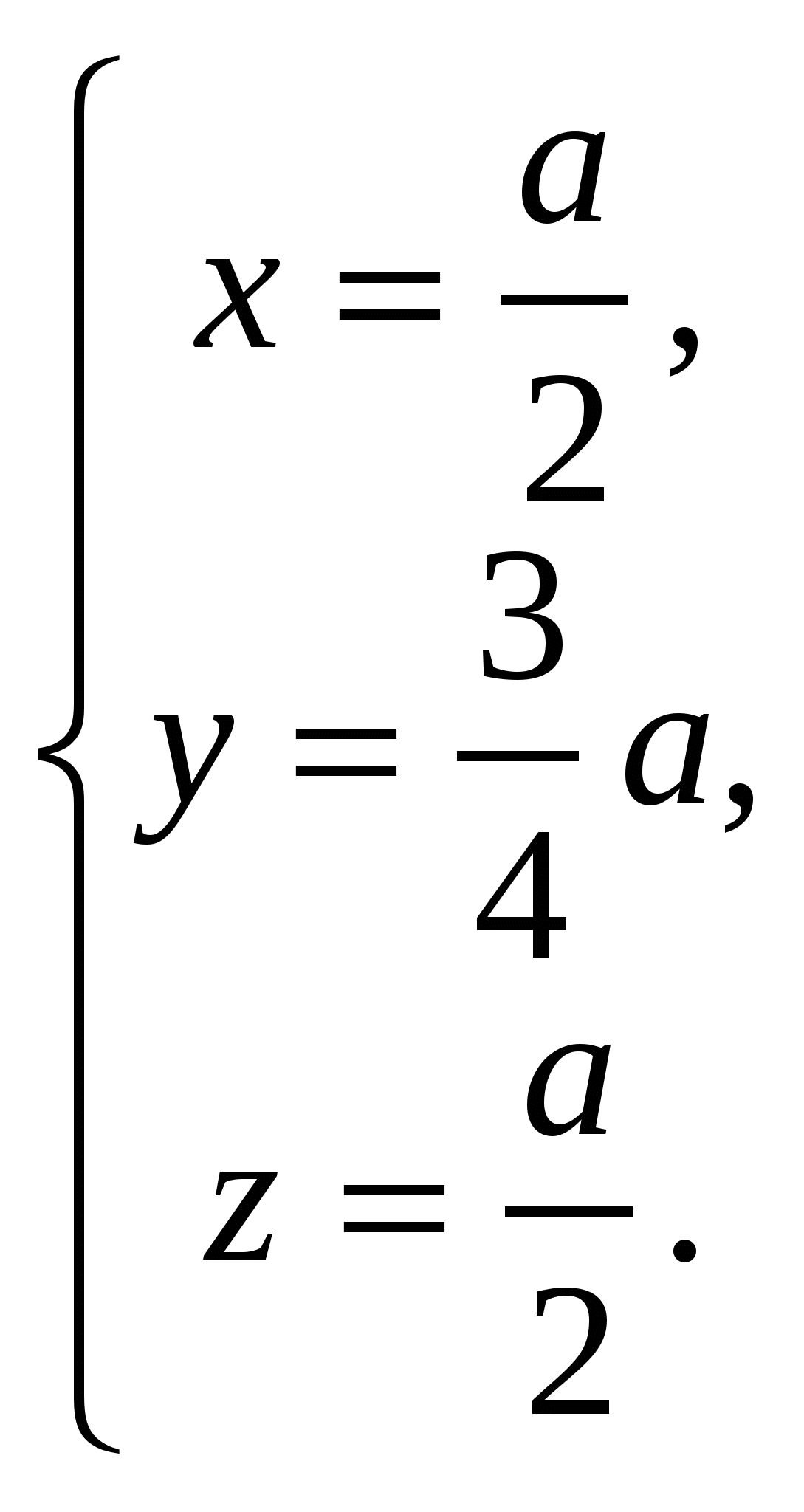
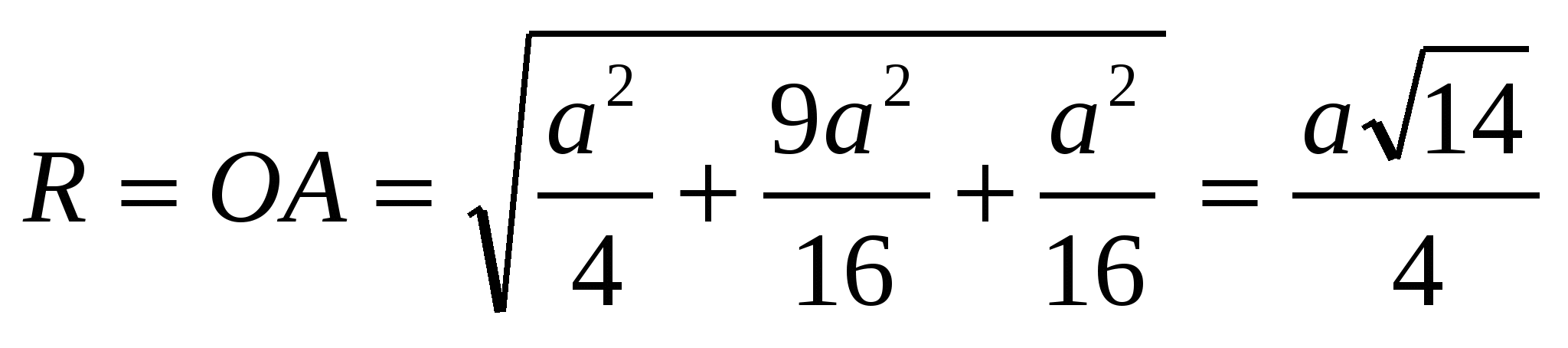 .
.
Ответ: R =![]() .
.
1.4. Векторно-координатный метод
Естественным продолжением векторного и координатного методов является векторно-координатный метод. Он основан на понятиях вектора и координат и сочетает основные подходы этих двух методов. Приведем основные сведения, используемые при решении задач этим методом.
Требуется
найти
На плоскости
В пространстве
1. Координаты
вектора
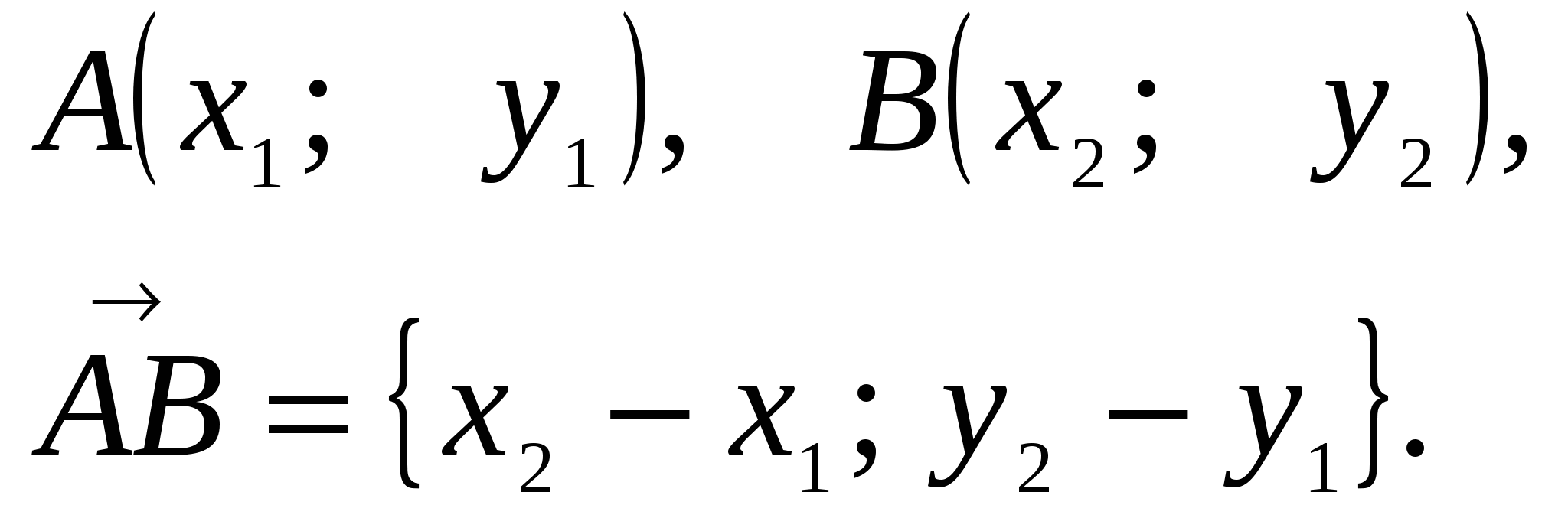
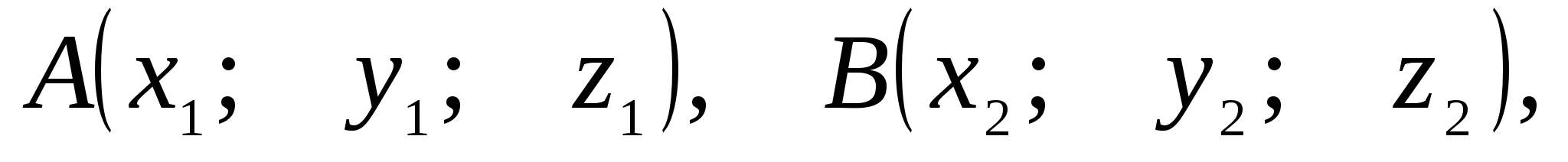
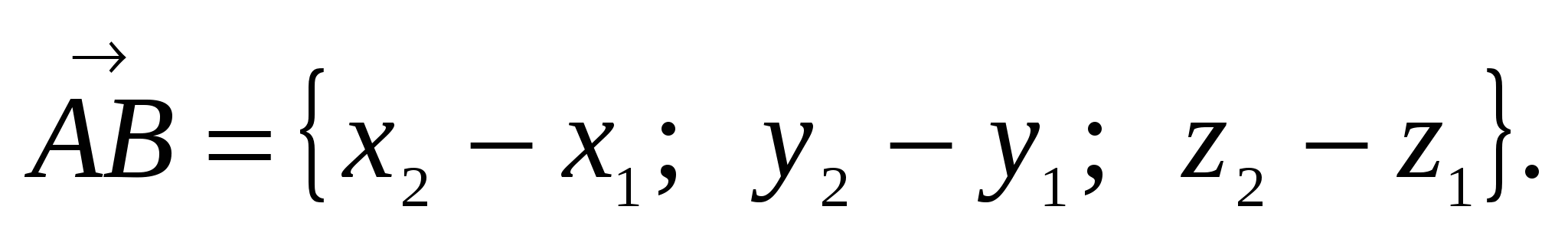
2. Сумму
и разность
векторов
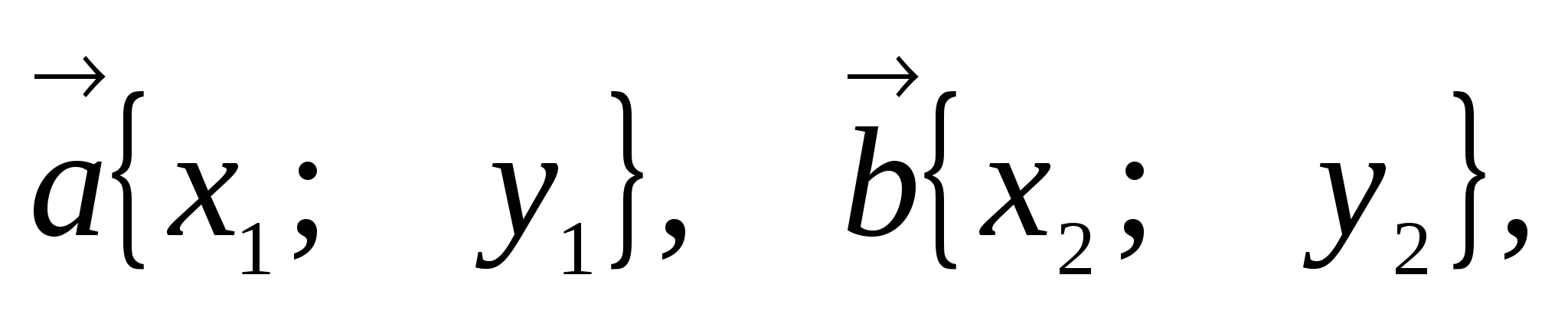
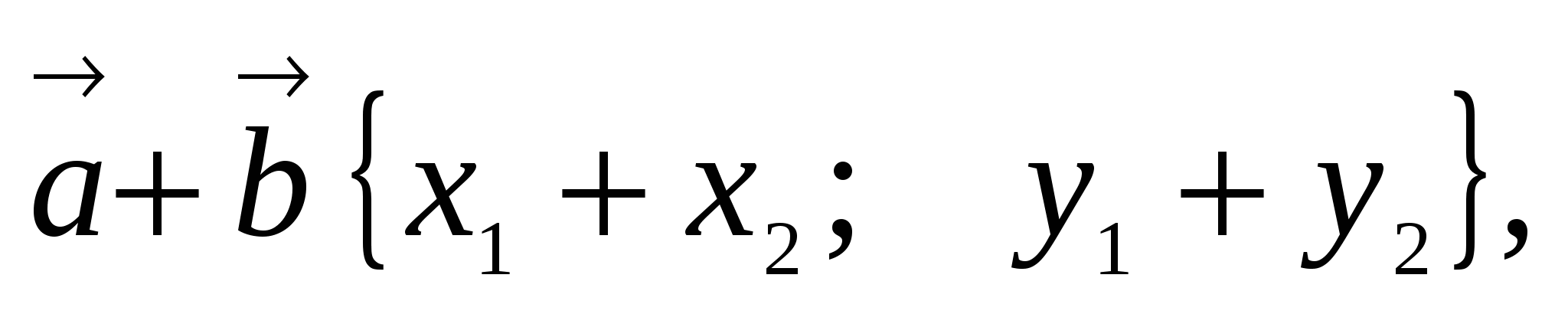
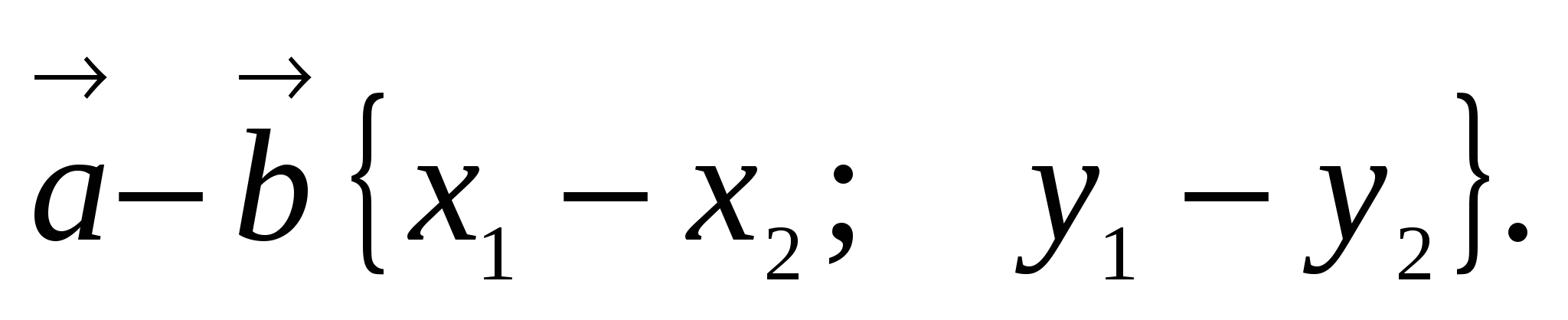
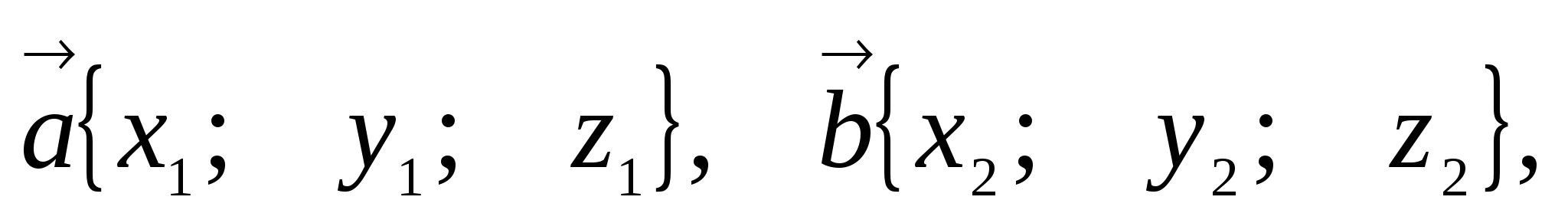
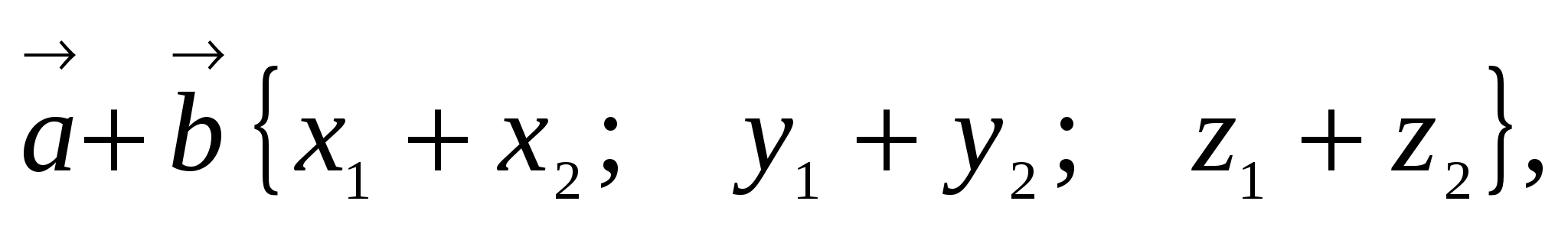
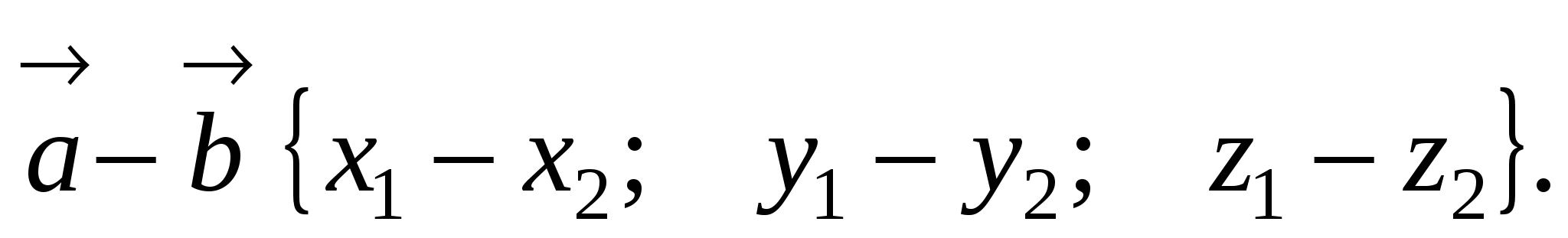
3. Произведение вектора на
число
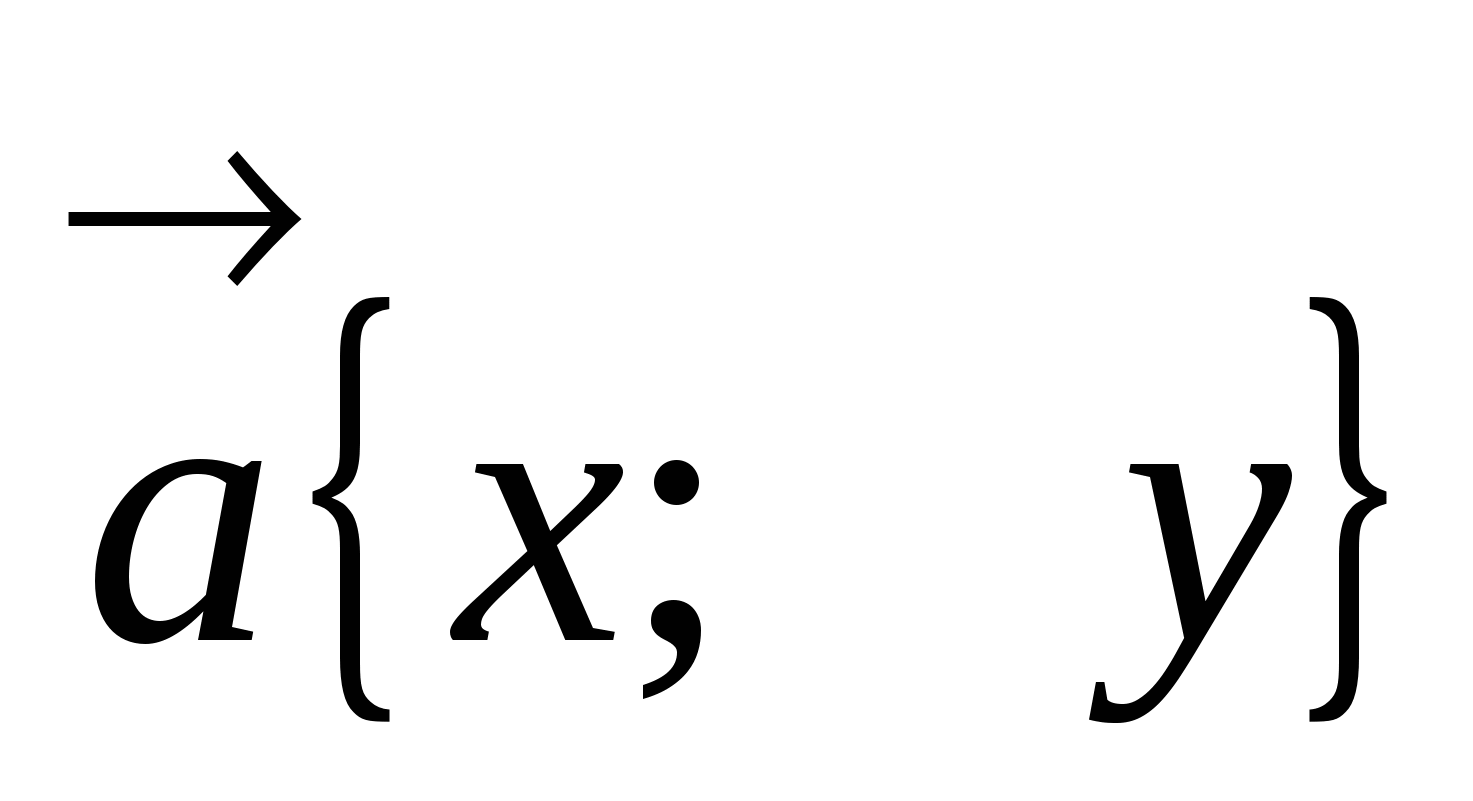 ,
,
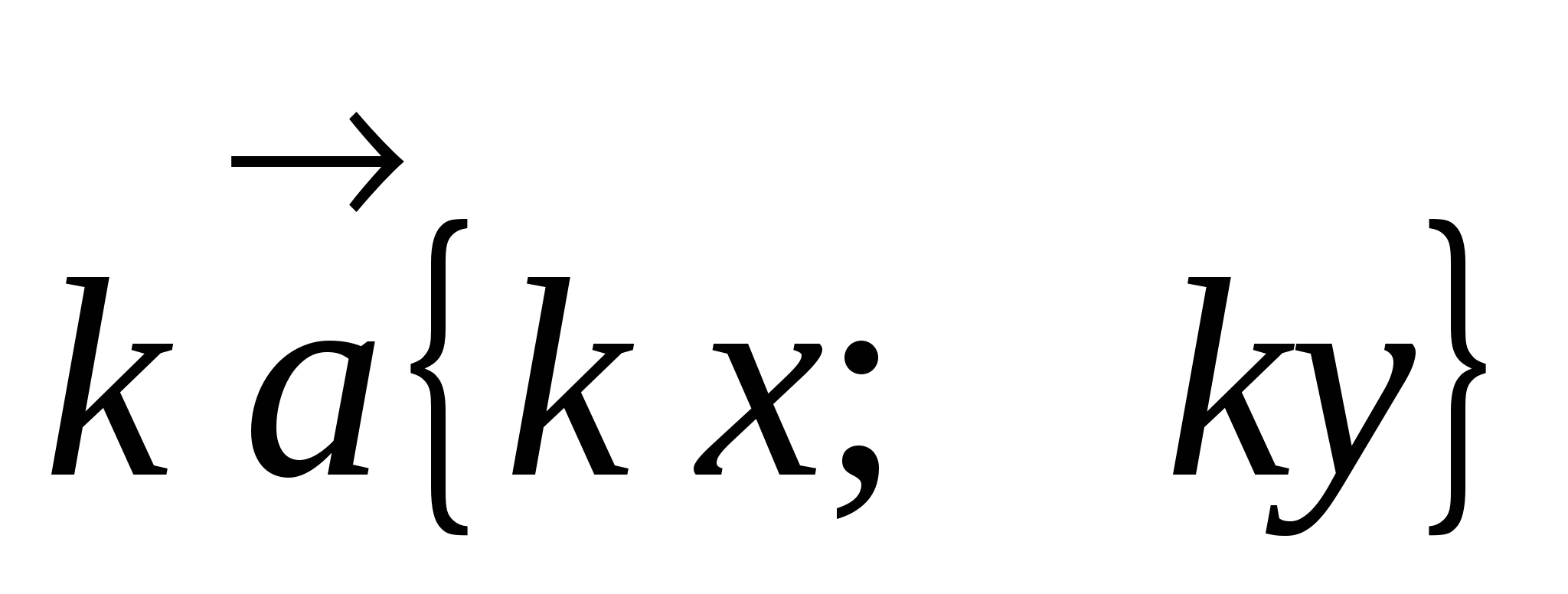 .
.
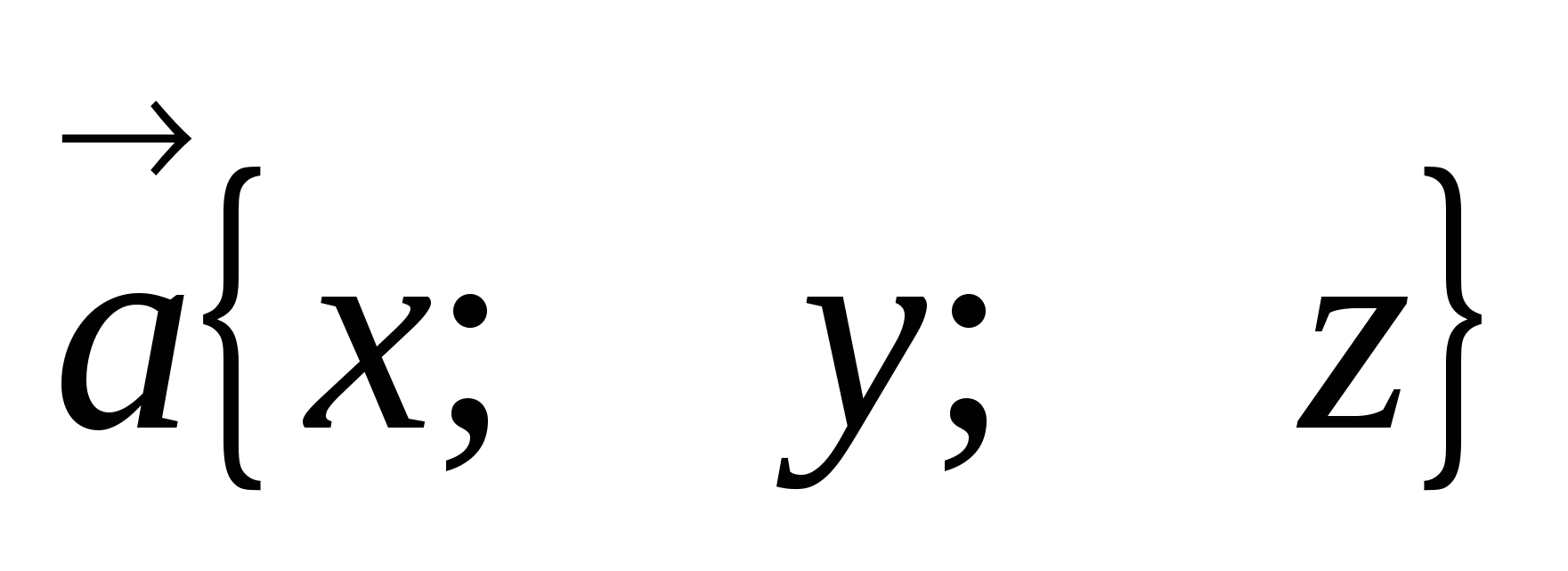 ,
,
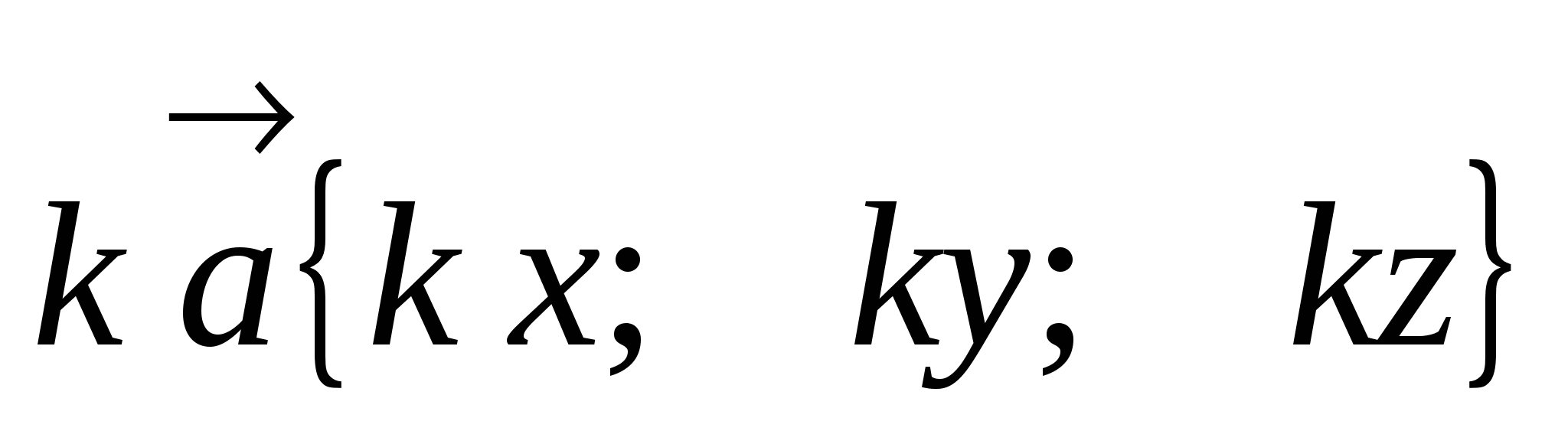 .
.
4. Скалярное
произведение векторов
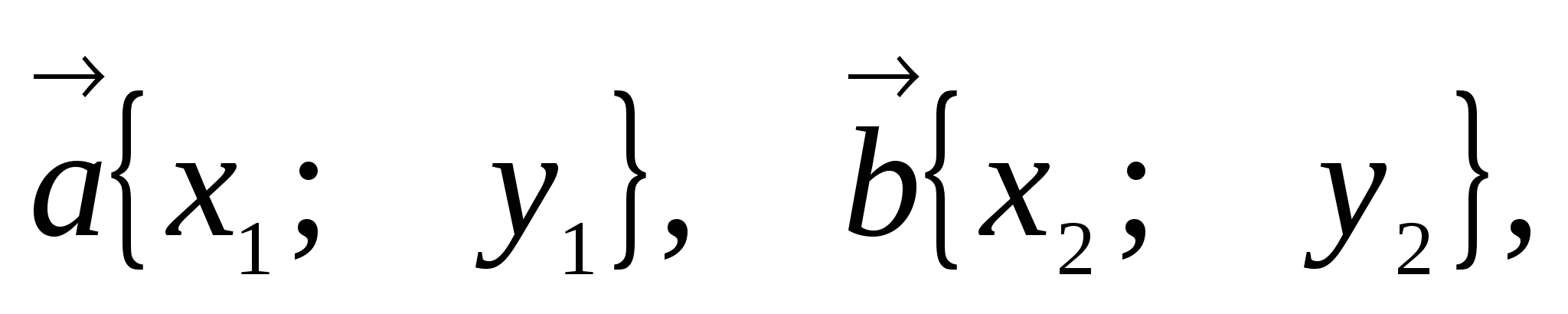
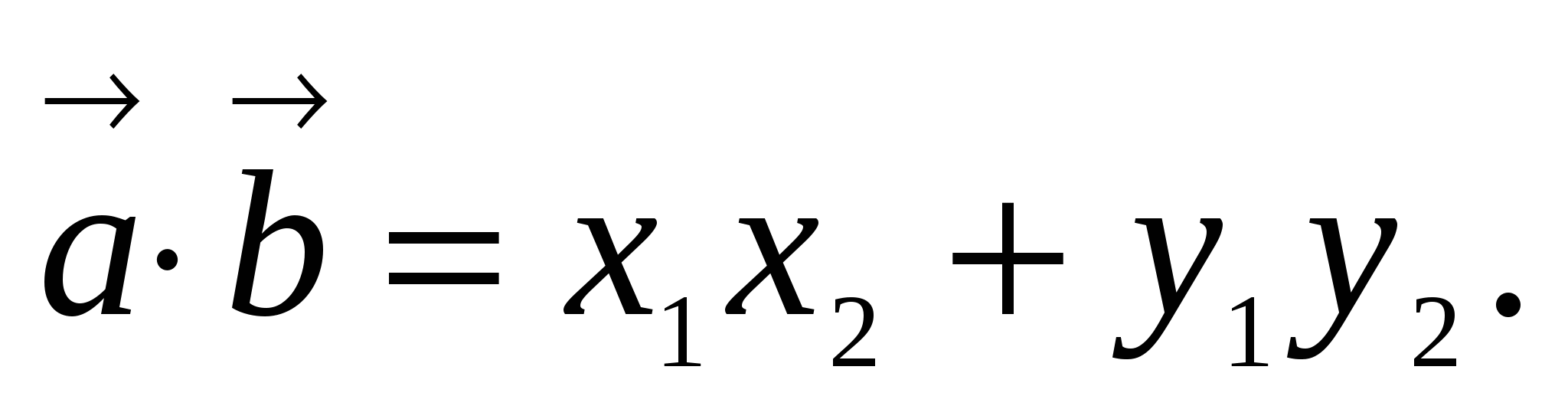
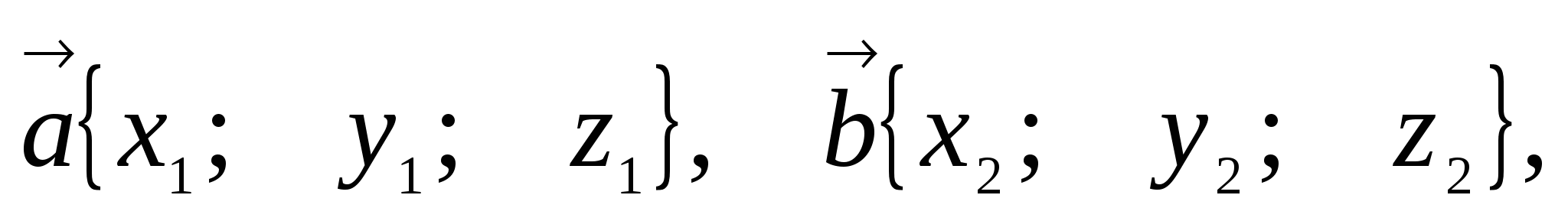
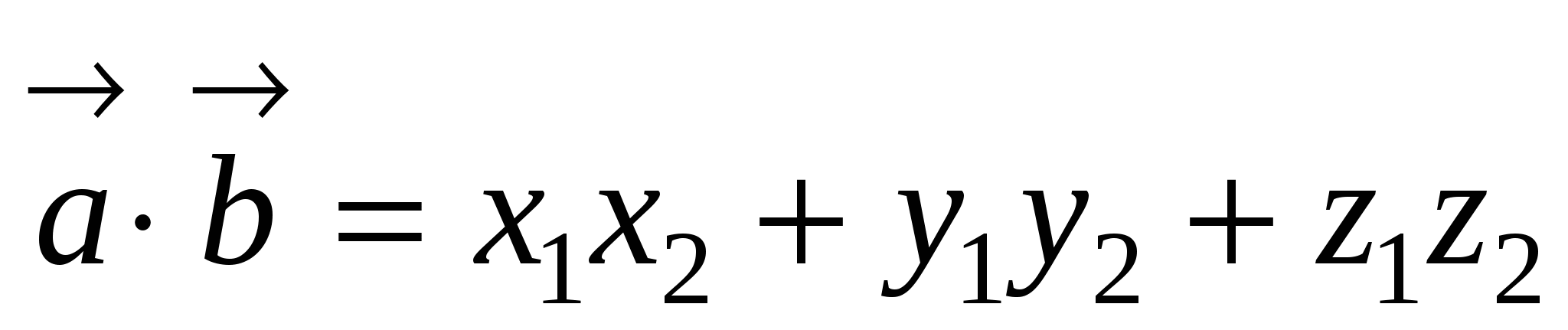 .
.
5. Длину
вектора
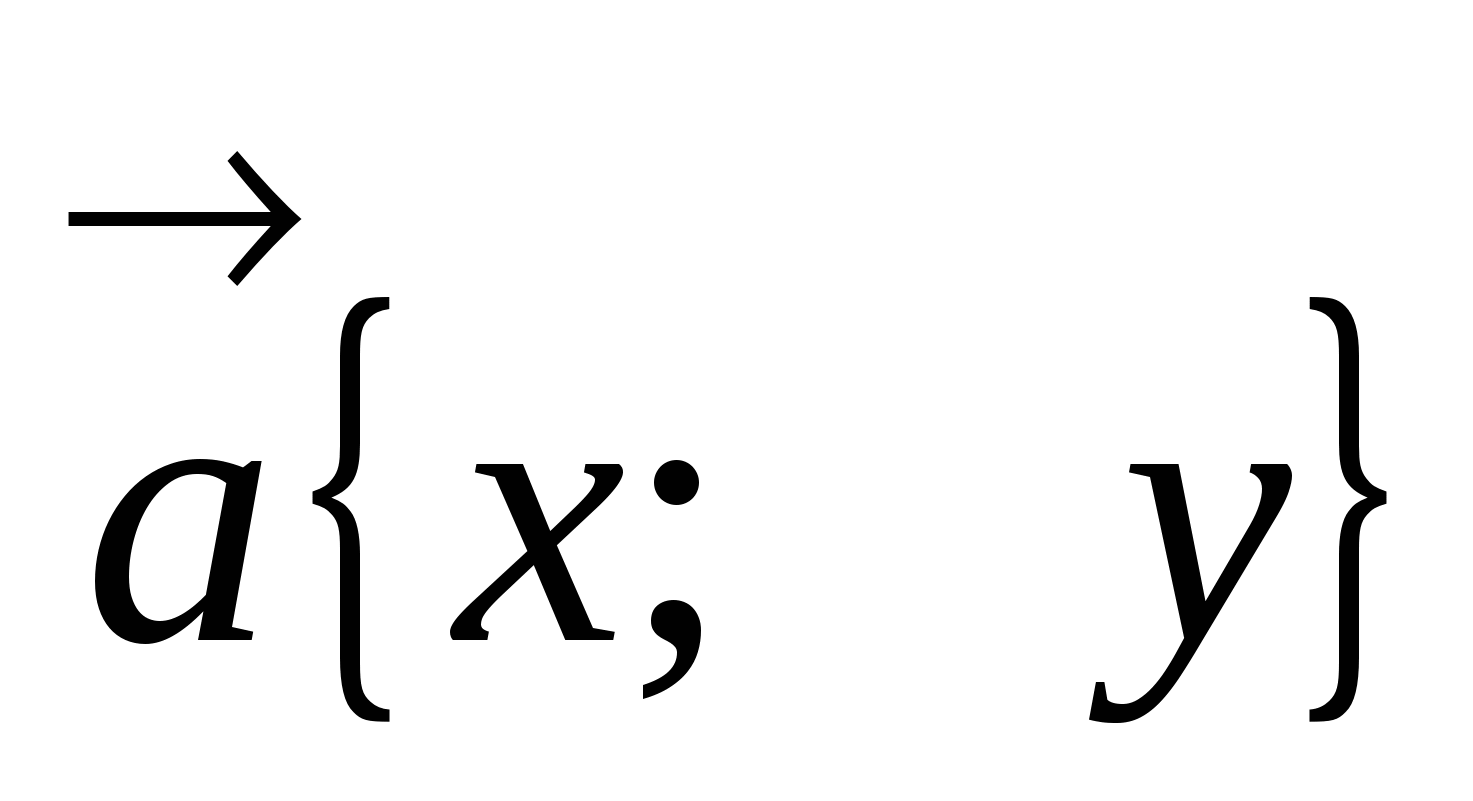 ,
,
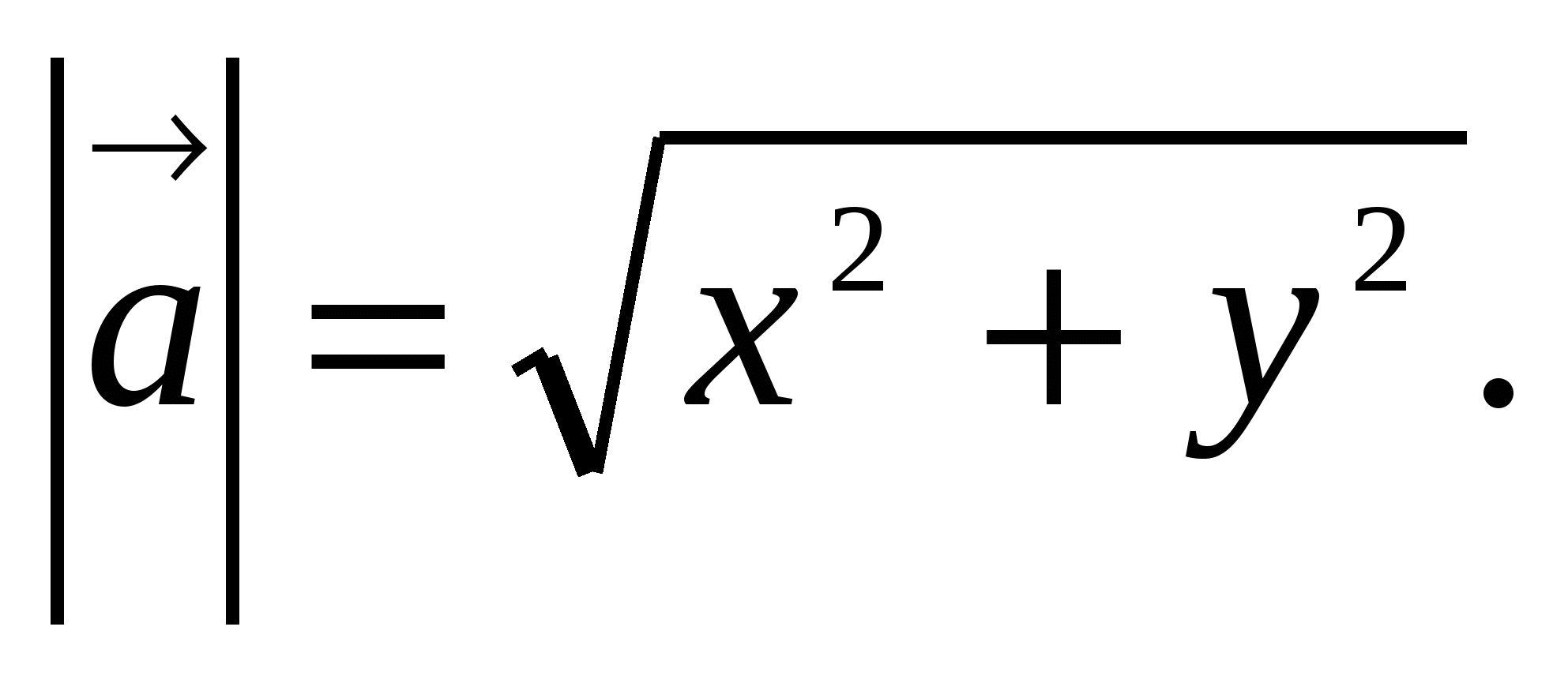
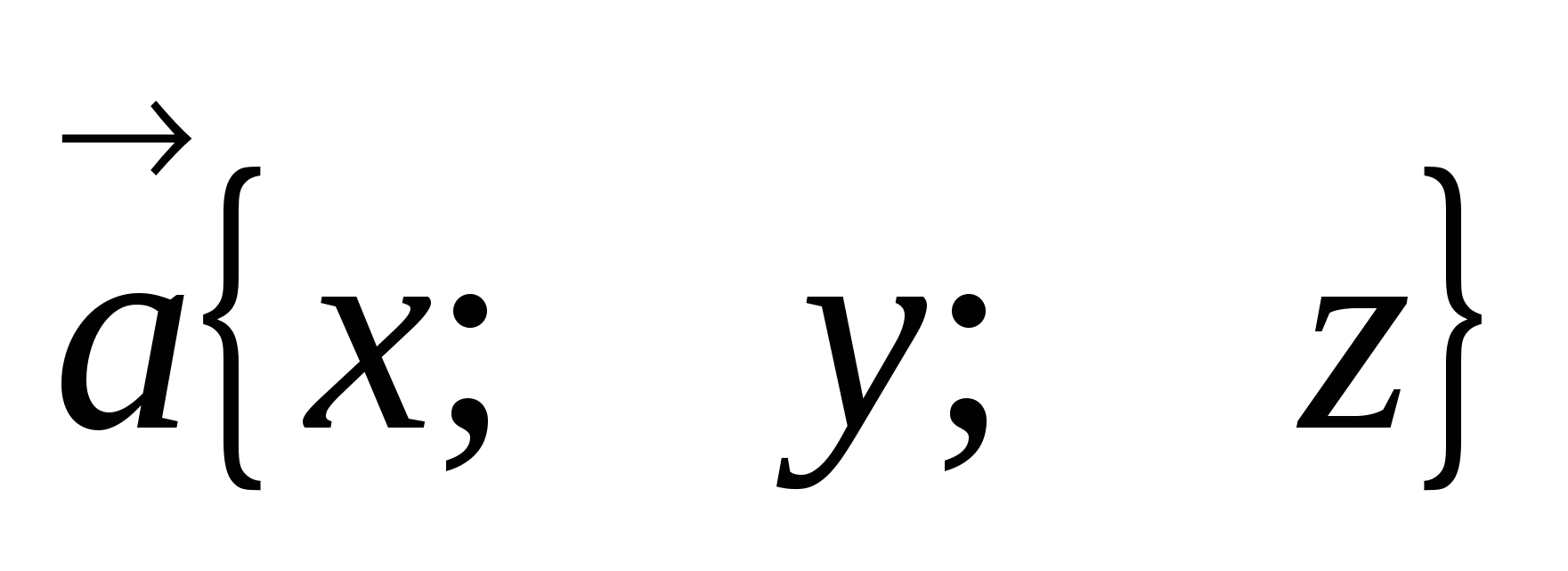 ,
,
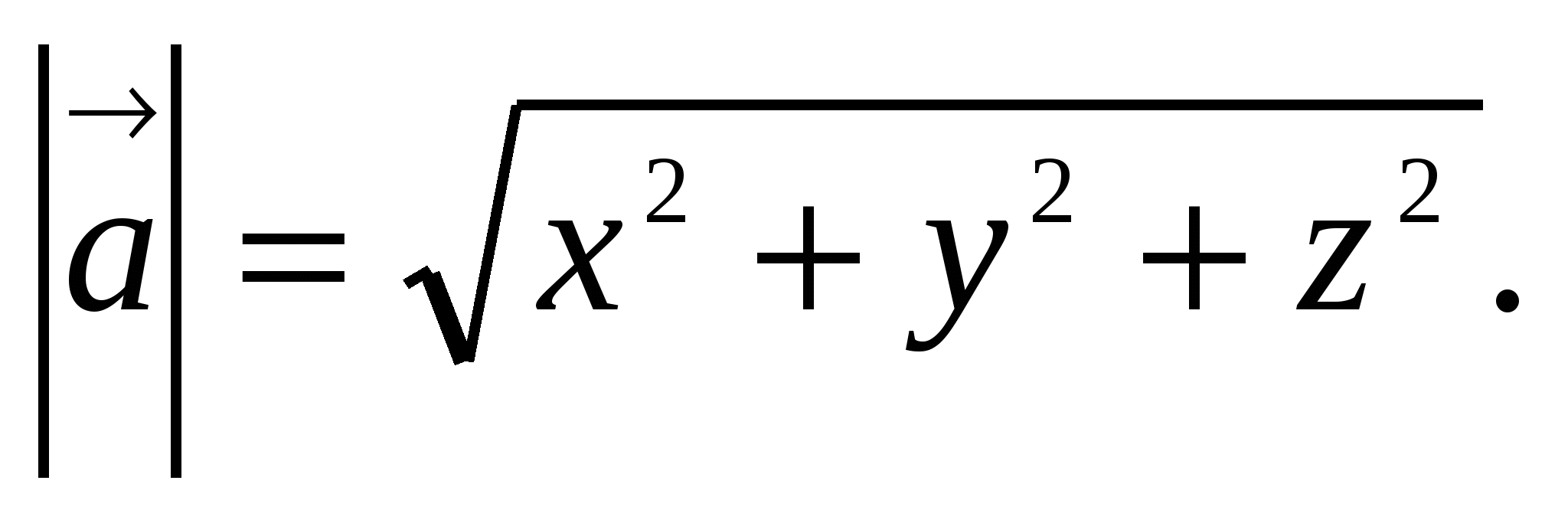
6. Угол между векторами
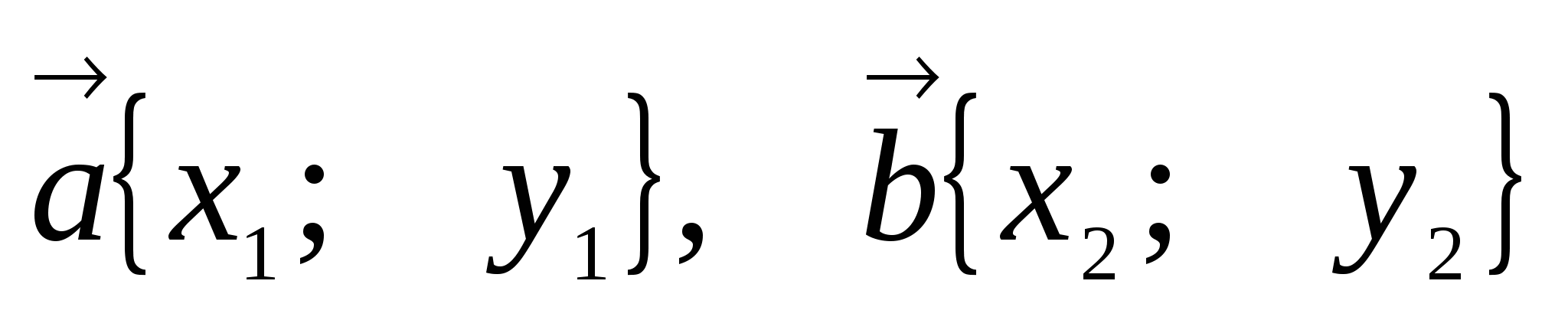 ,
,
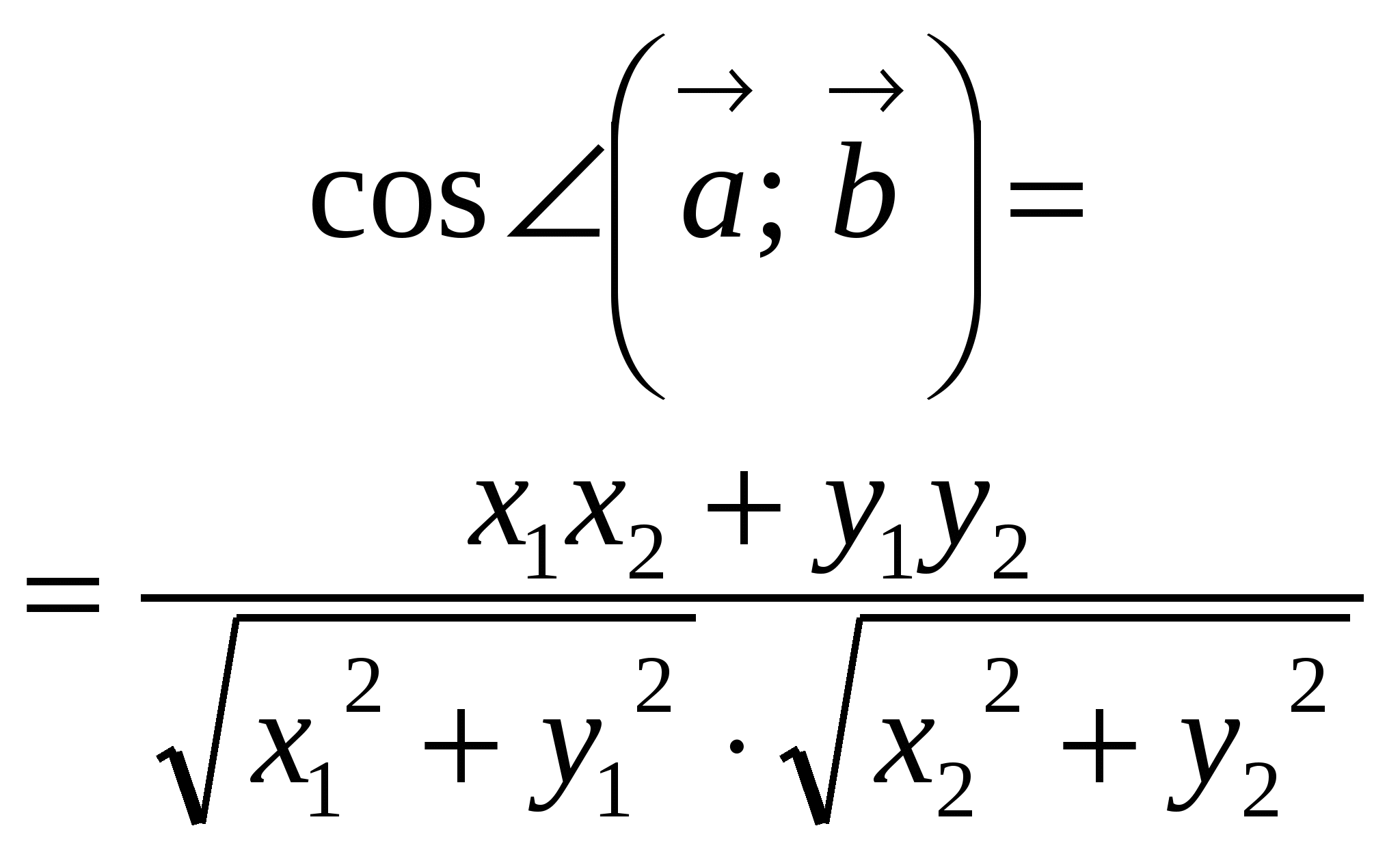
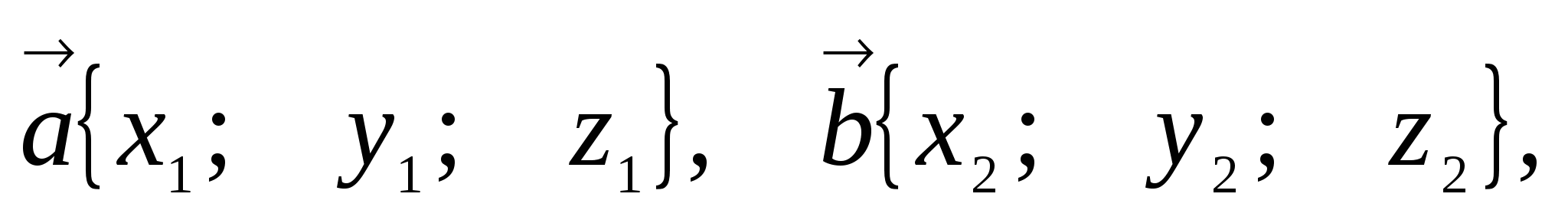
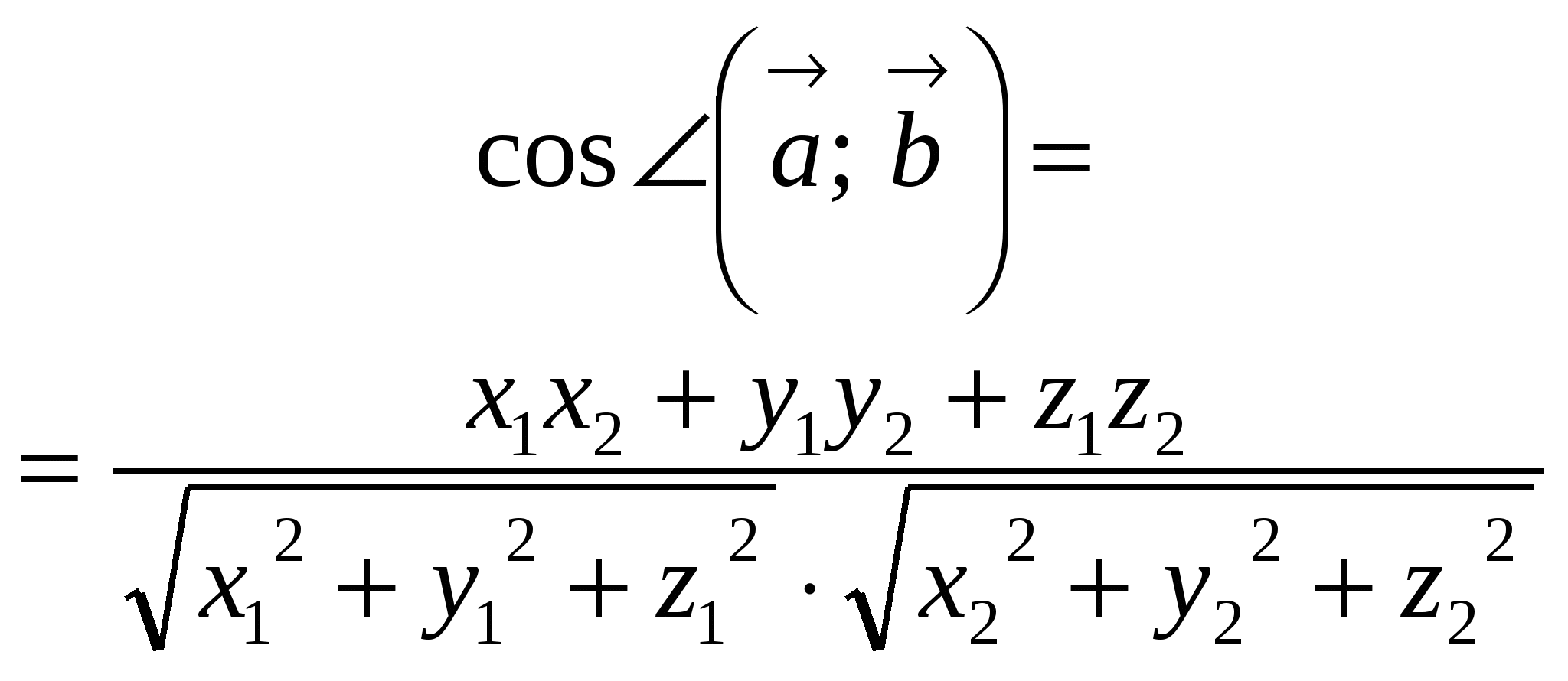
7. Угол
между
прямыми
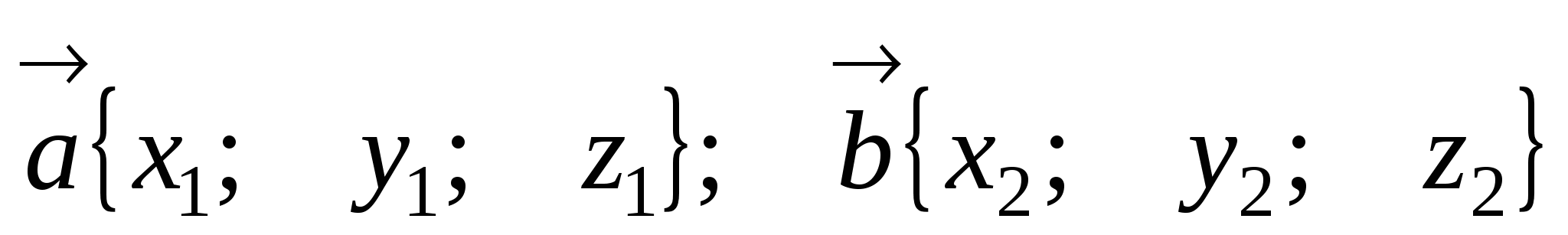 - направляющие векторы
- направляющие векторы
прямых;
![]() - угол между прямыми.
- угол между прямыми.
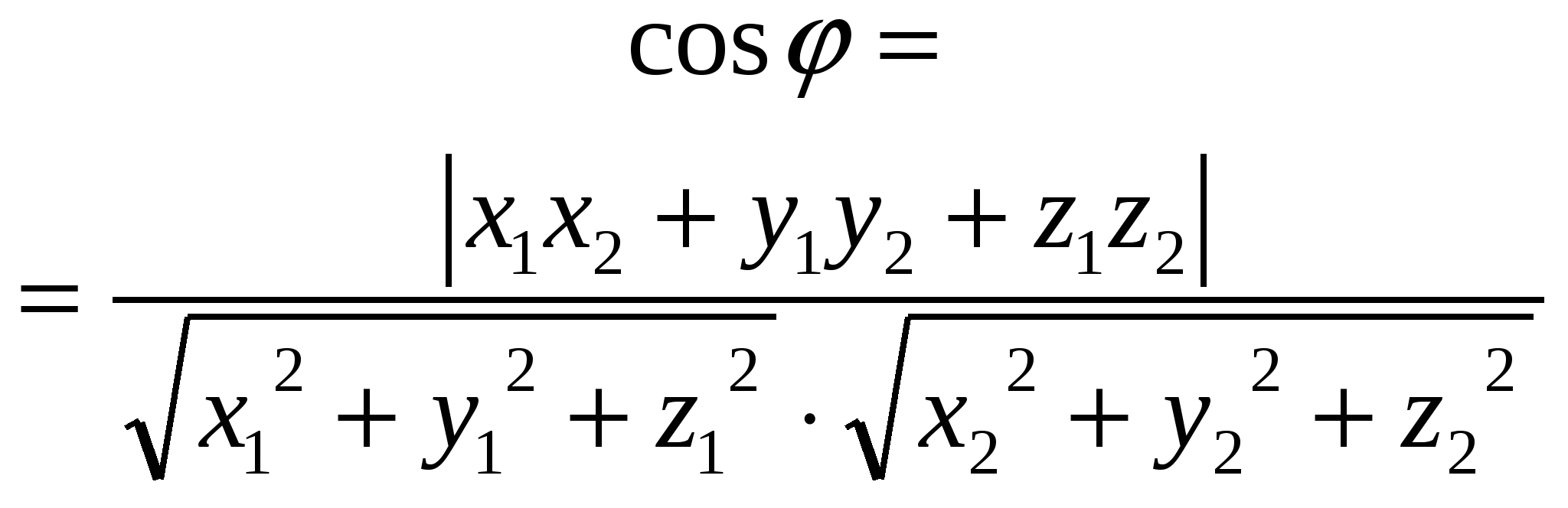
8. Угол
между
прямой и
плоскостью
![]() - направляющий вектор прямой,
- направляющий вектор прямой,
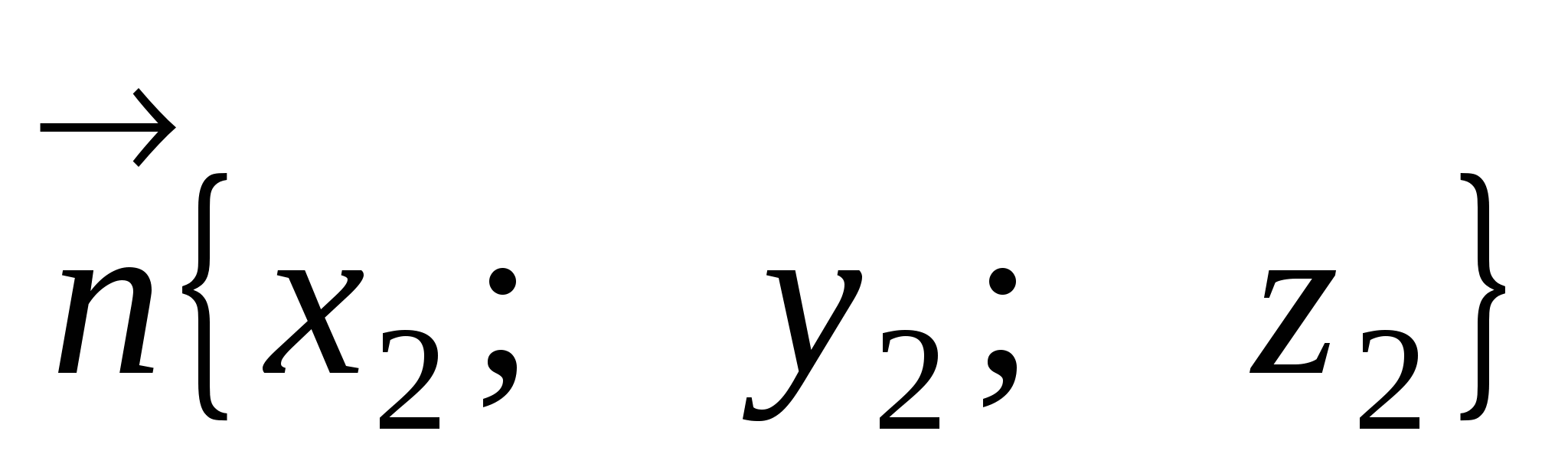 - вектор,
- вектор,
перпендикулярный к плоскости,
 - угол между прямой и
- угол между прямой и
плоскостью.
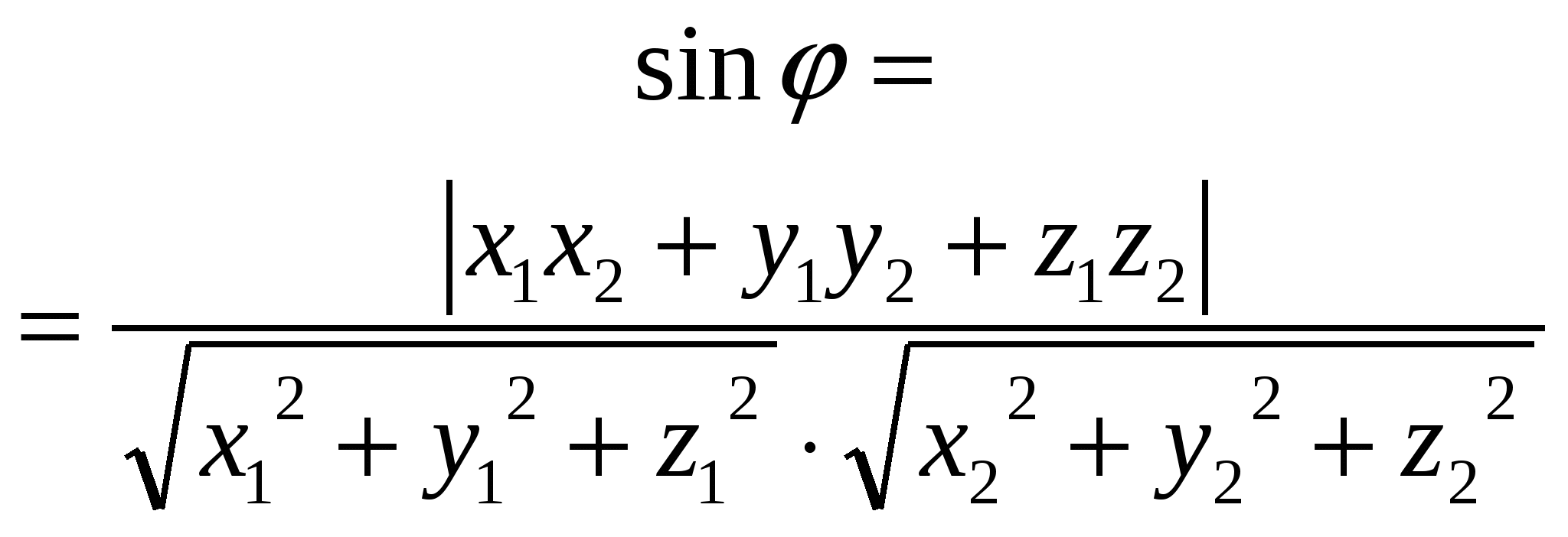
Задача 1. Дан куб АВСDА1В1С1D1с ребром 1. Найти градусную меру угла между прямыми АС1 и СВ1.

Схема решения:
АС1 и СВ1 -
- скрещивающиеся прямые.
Введём прямоугольную систему координат Axyz, так, как показано на рисунке.
Имеем:
-
А(0; 0; 0), С1(1; 1; 1), тогда
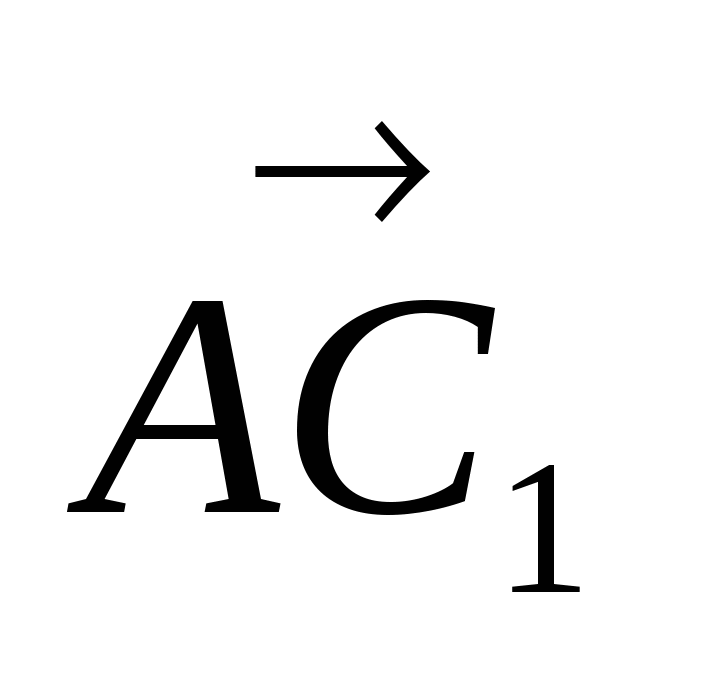 (1; 1; 1);
(1; 1; 1); -
С(1; 1; 0), В1(1; 0; 1), тогда
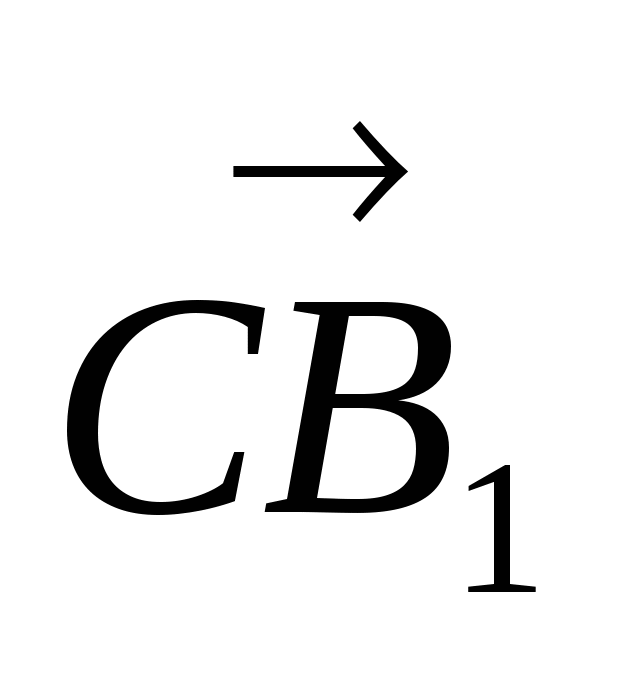 (0; -1; 1).
(0; -1; 1). -
Обозначим угол между скрещивающимися прямыми через
 и вычислим его, как угол между векторами
и вычислим его, как угол между векторами 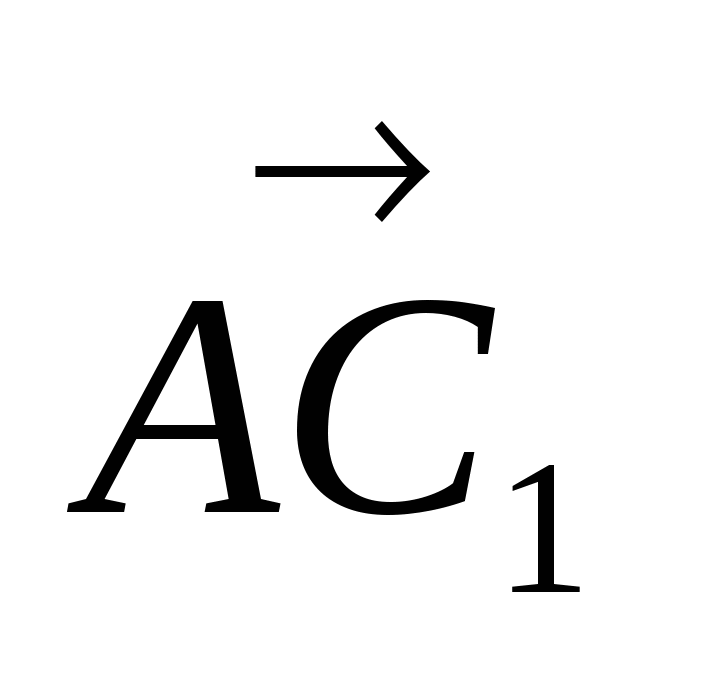 и
и 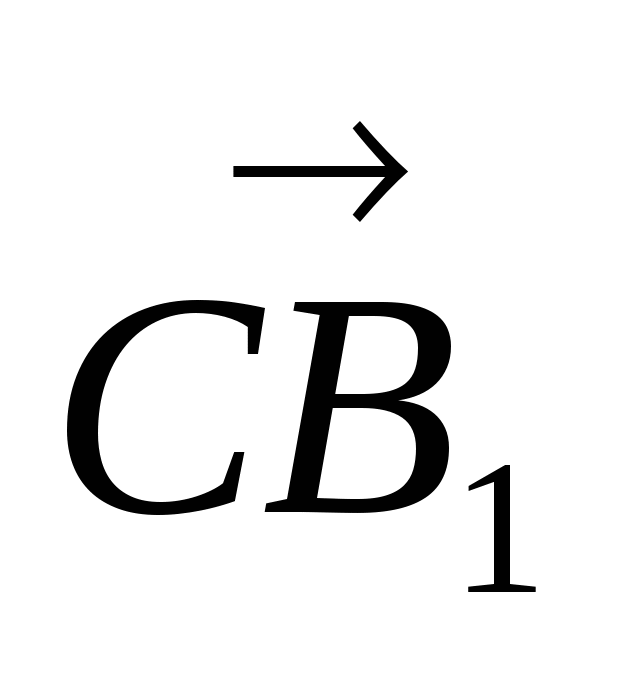 .:
.:
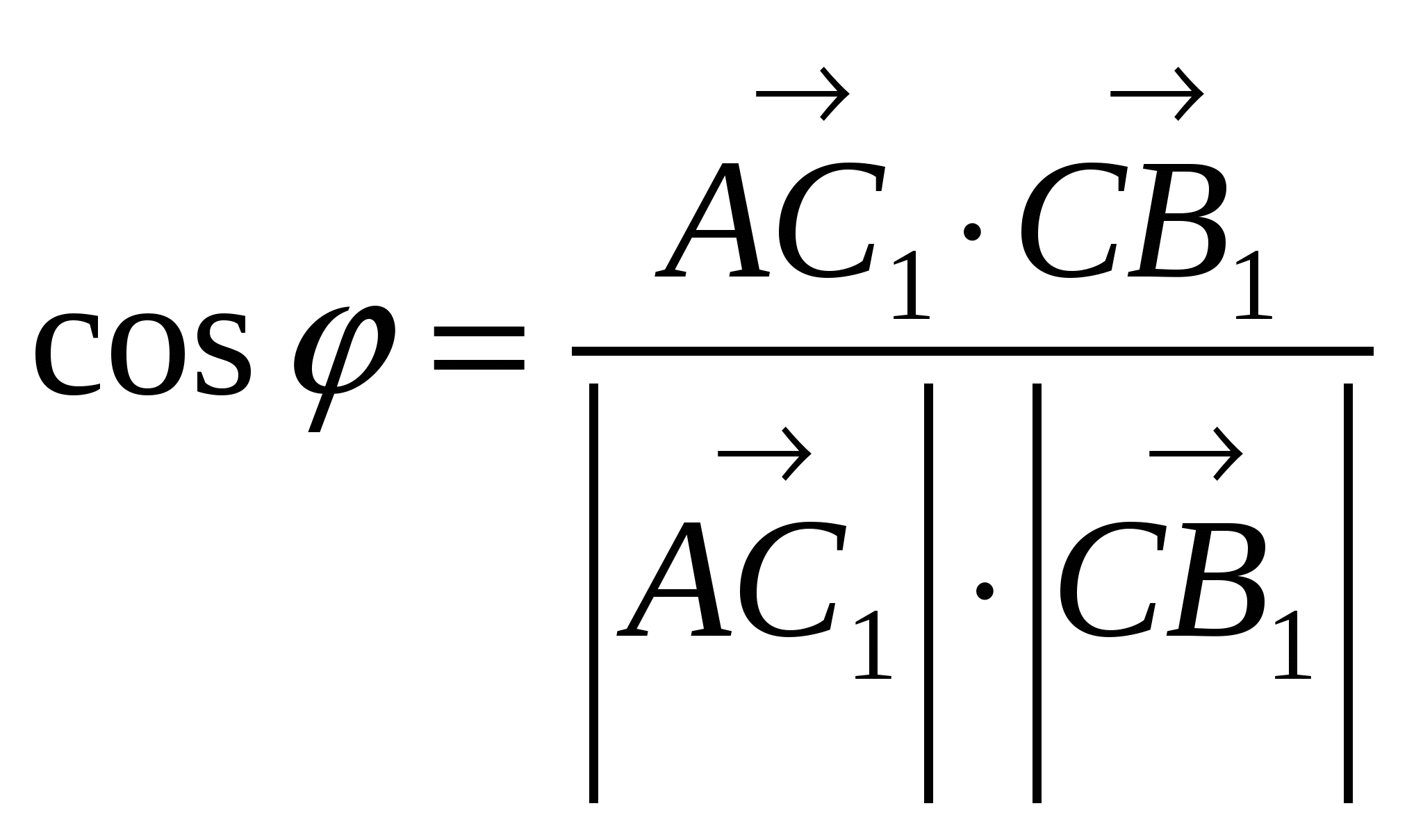 ,
,
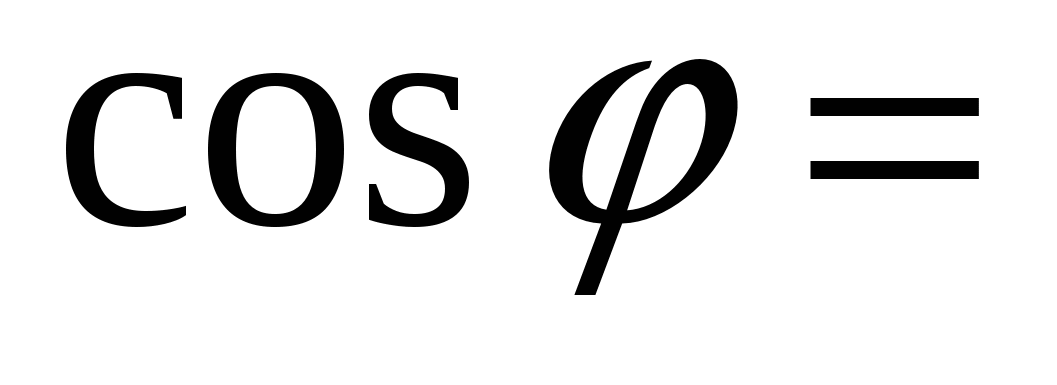
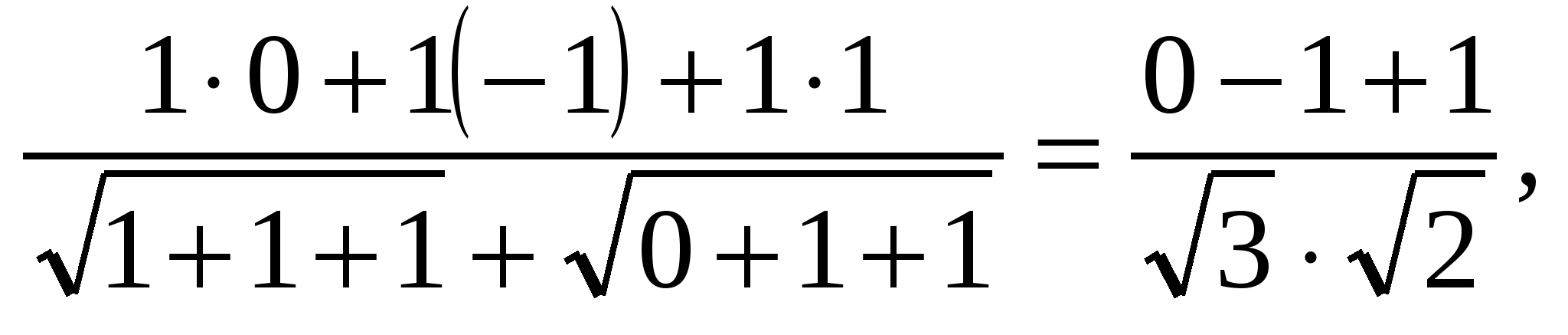
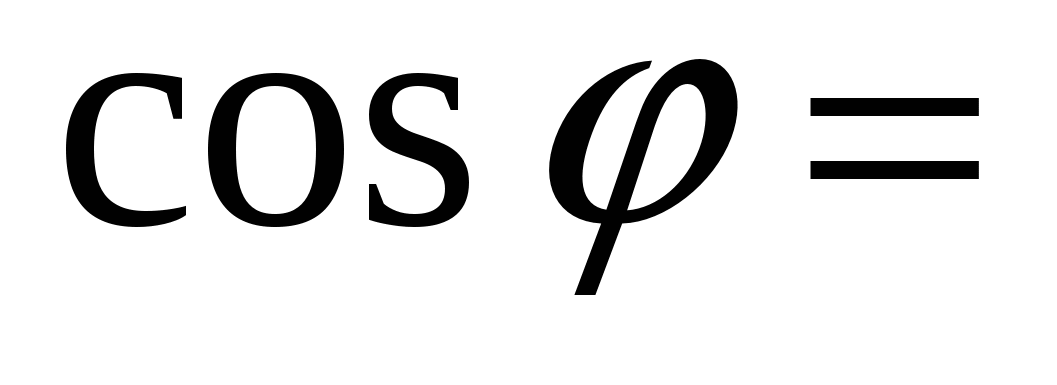 0, следовательно,
0, следовательно, ![]() .
.
Ответ: 90.
Задача 2. Основанием прямоугольного параллелепипеда
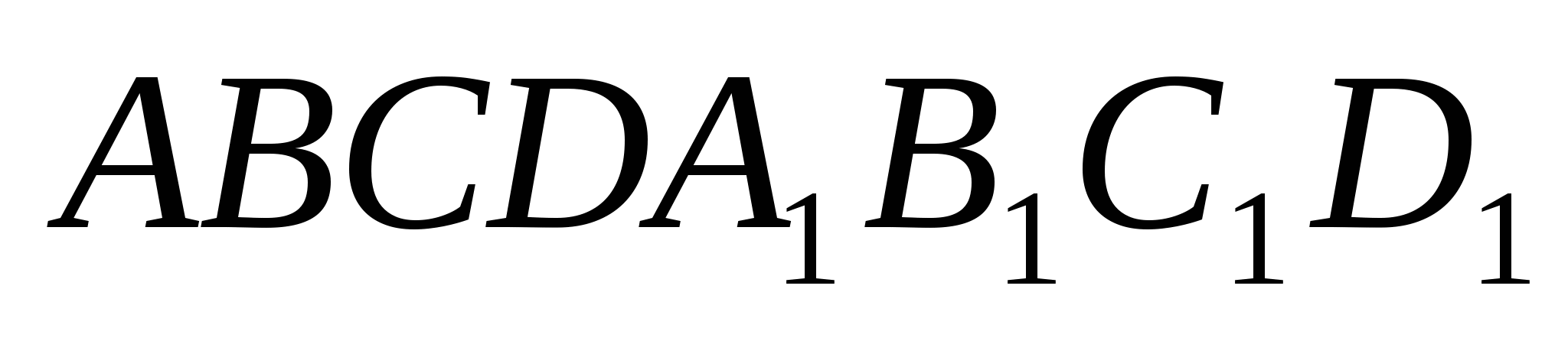 является прямоугольник АВСD со сторонами АВ = 6, ВС = 4. Боковые рёбра
является прямоугольник АВСD со сторонами АВ = 6, ВС = 4. Боковые рёбра ![]() имеют длину 3. На отрезке
имеют длину 3. На отрезке 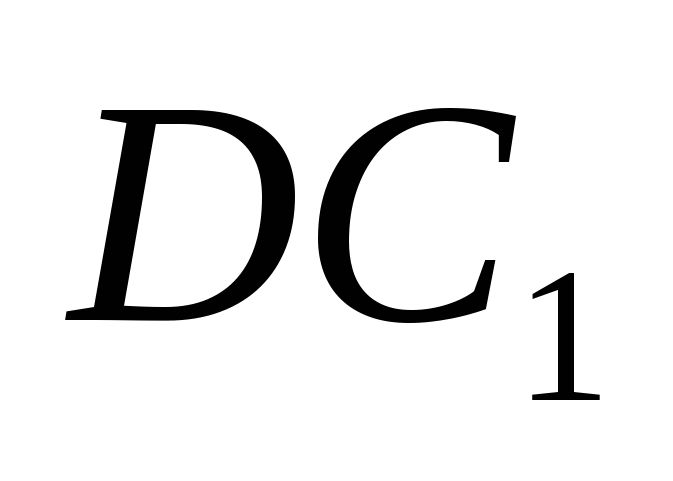 выбрана точка Р так, что угол между векторами
выбрана точка Р так, что угол между векторами 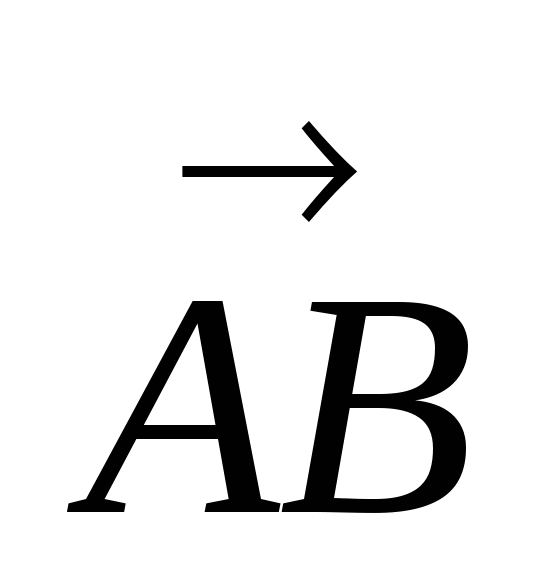 и
и  равен
равен 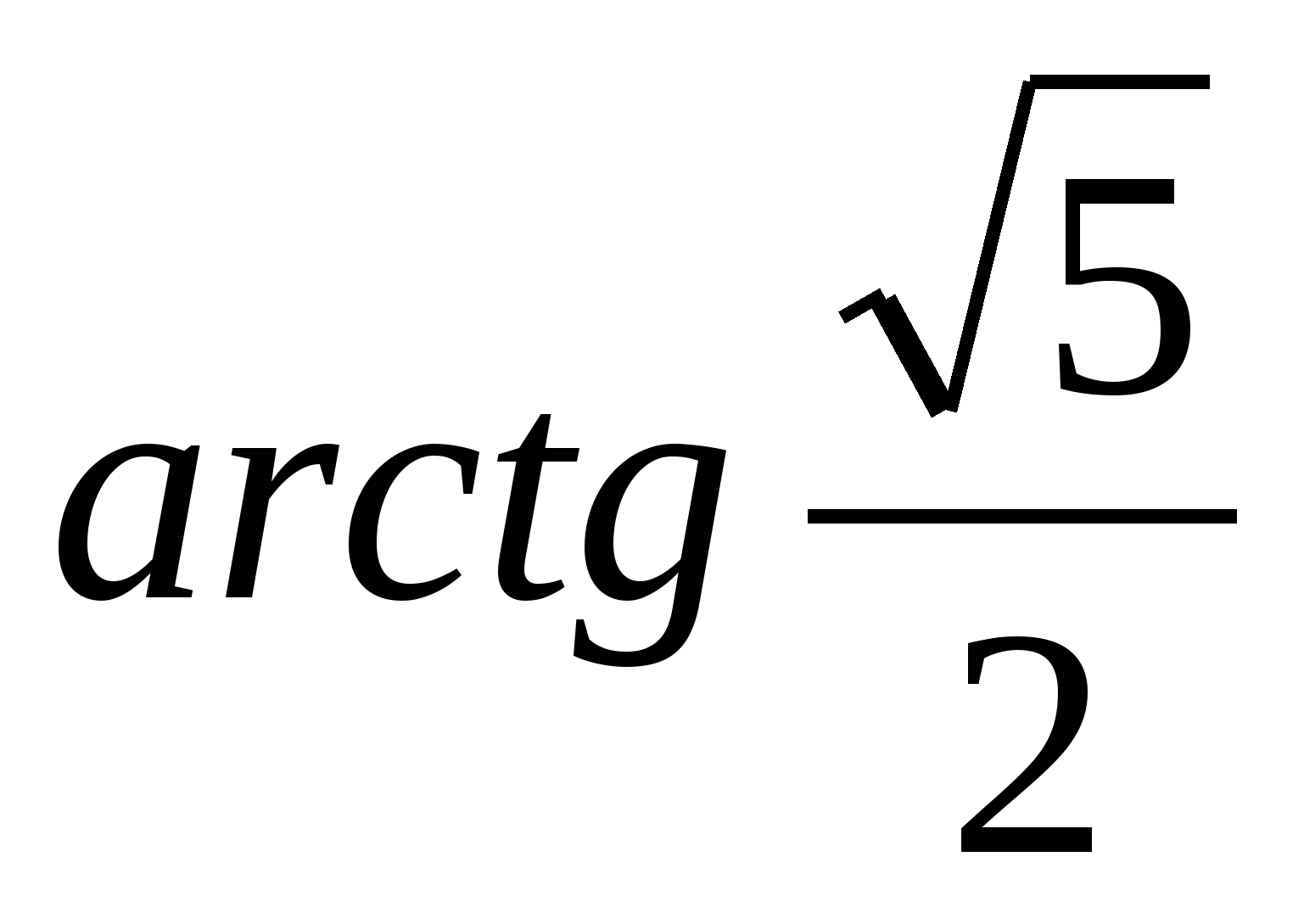 . Найти отношение DР :
. Найти отношение DР : 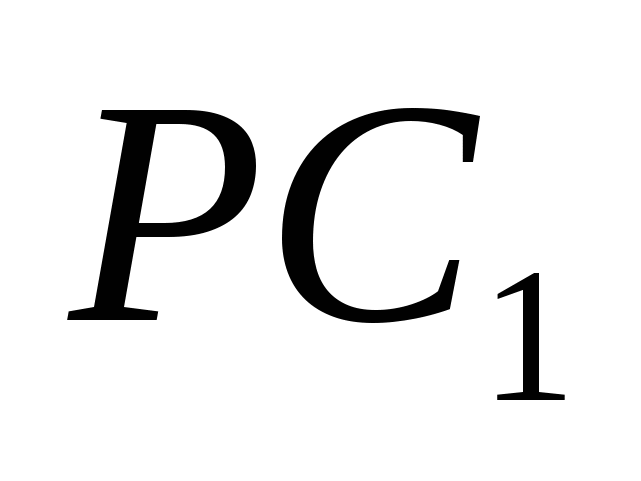 .
.
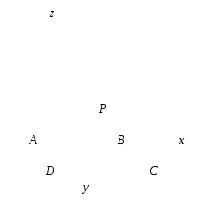
Схема решения:
Введём прямоугольную систему координат Axyz так, как показано на рисунке.
Найдём координаты векторов: 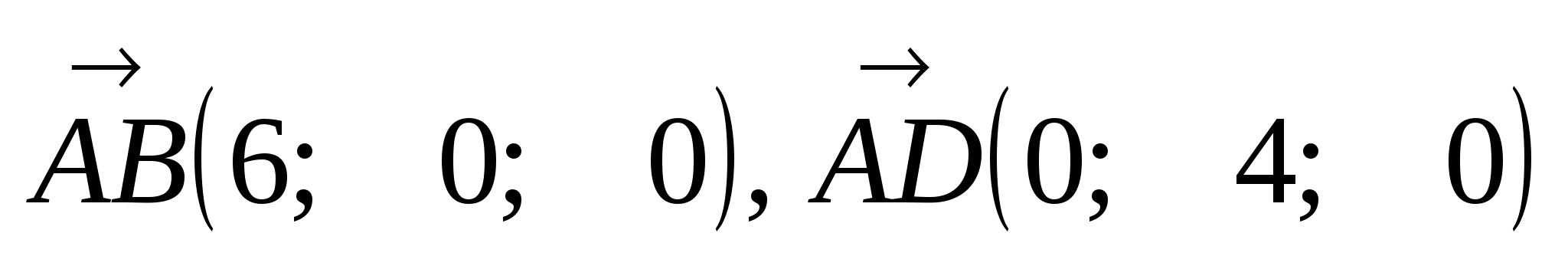 ,
, 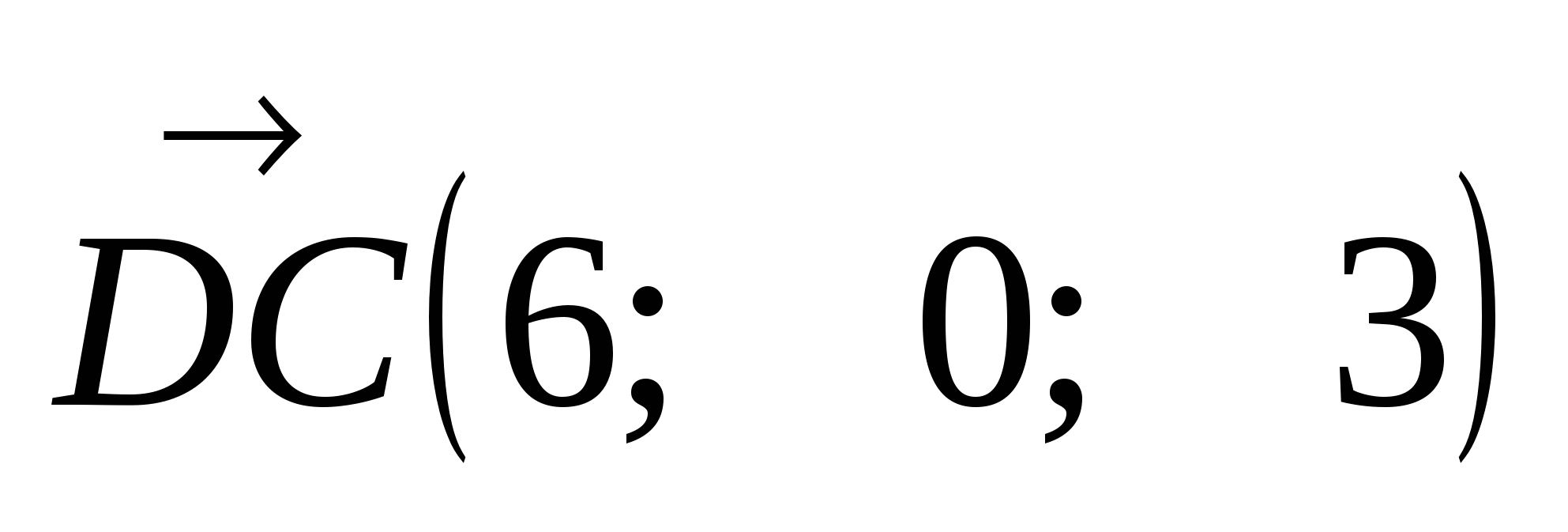 . Так как
. Так как 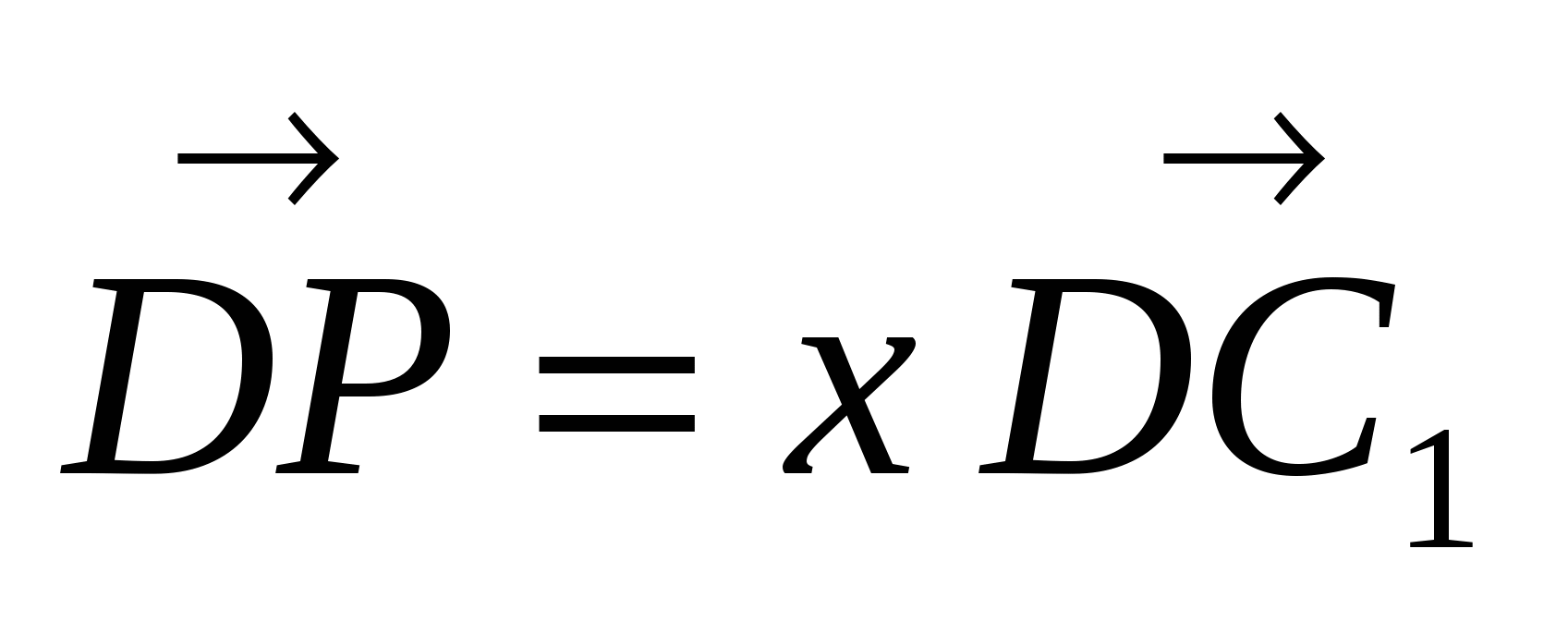 , то
, то 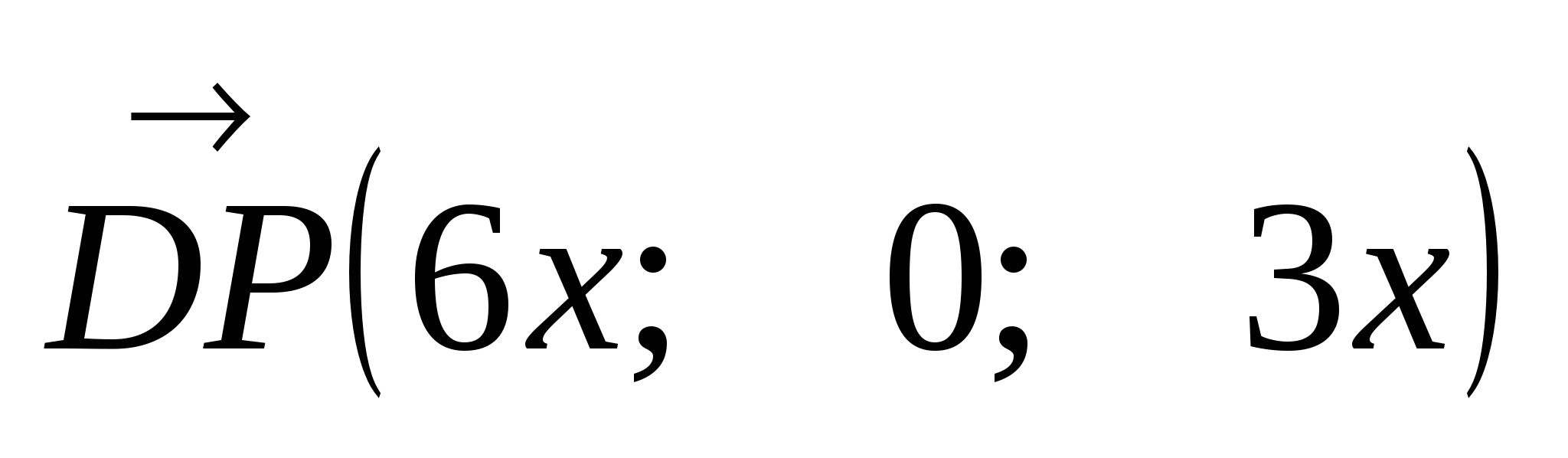 .
. 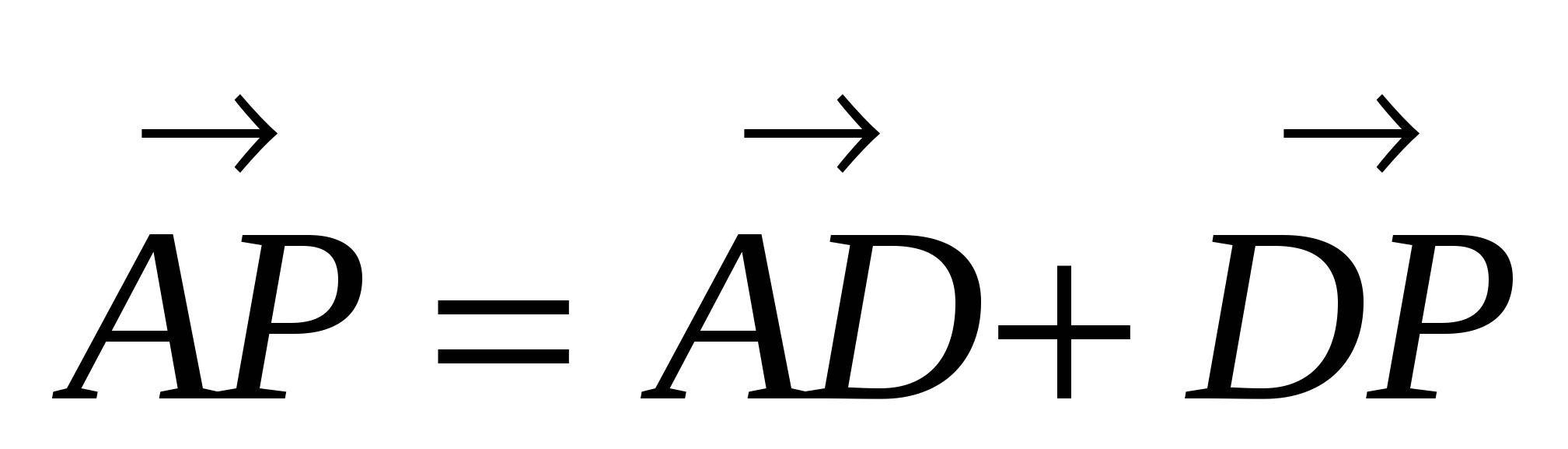 , следовательно,
, следовательно, 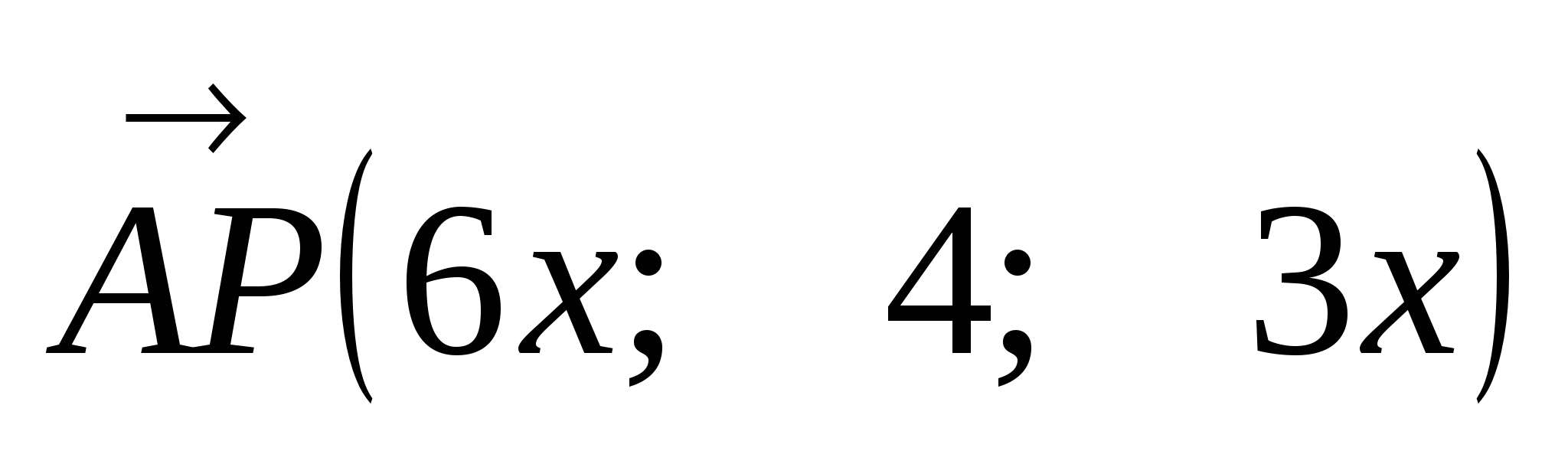 .
.
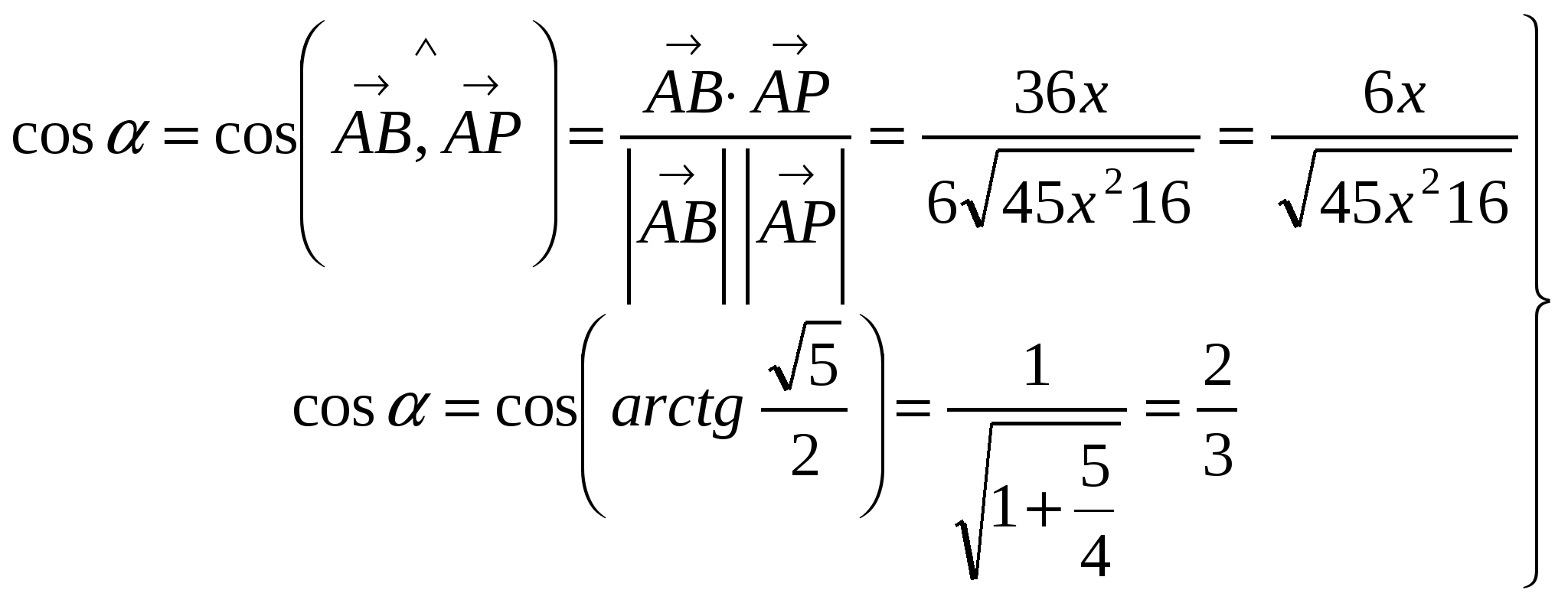
Отсюда получаем 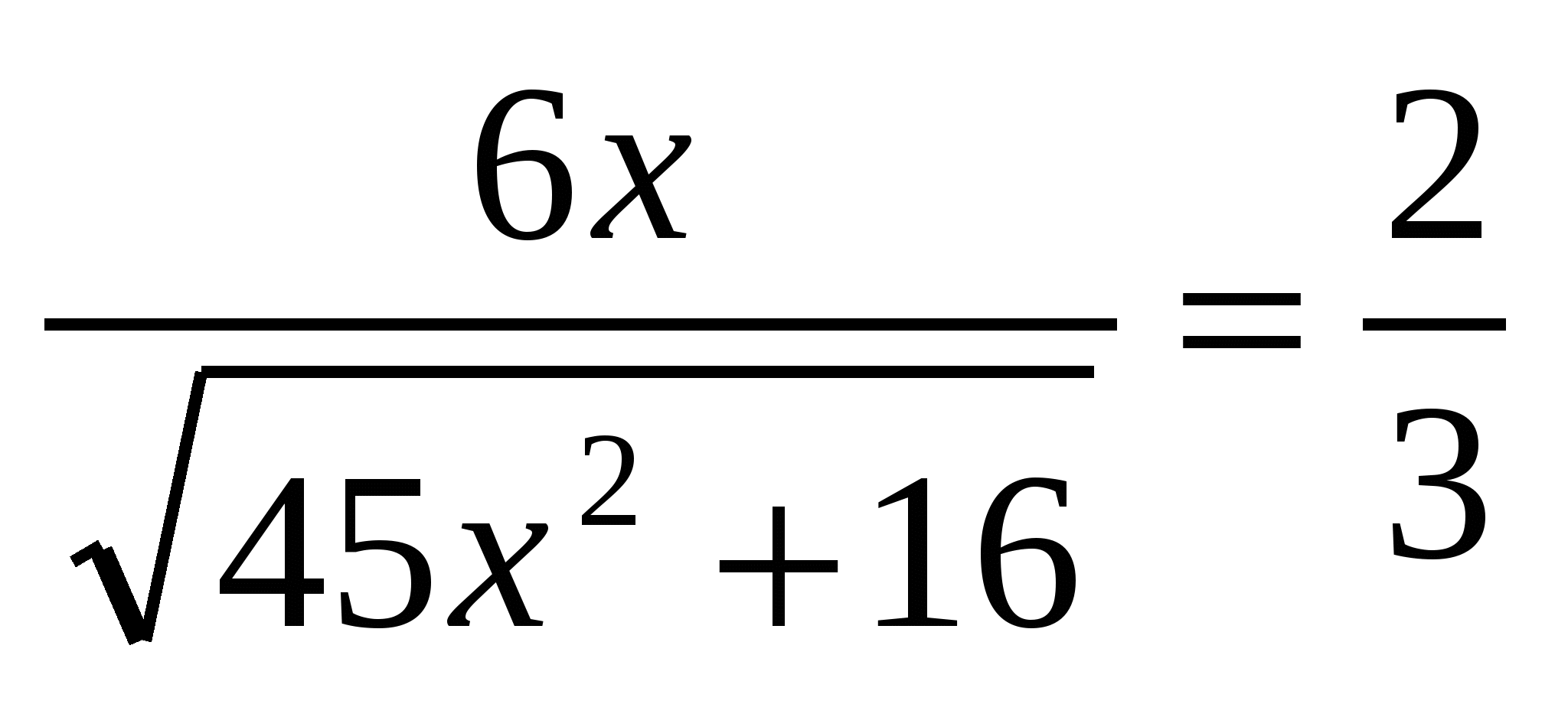 .
.
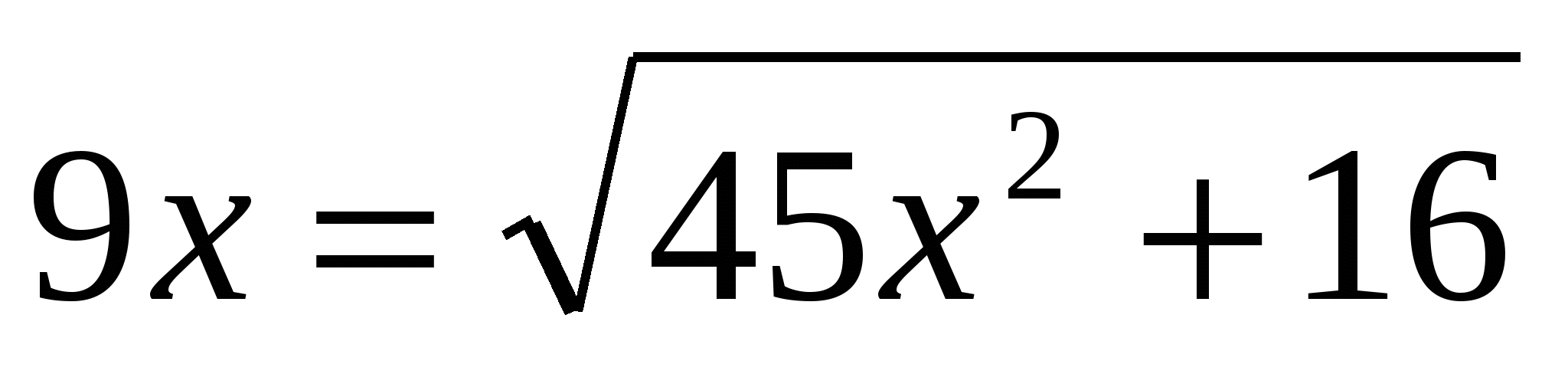 ,
, 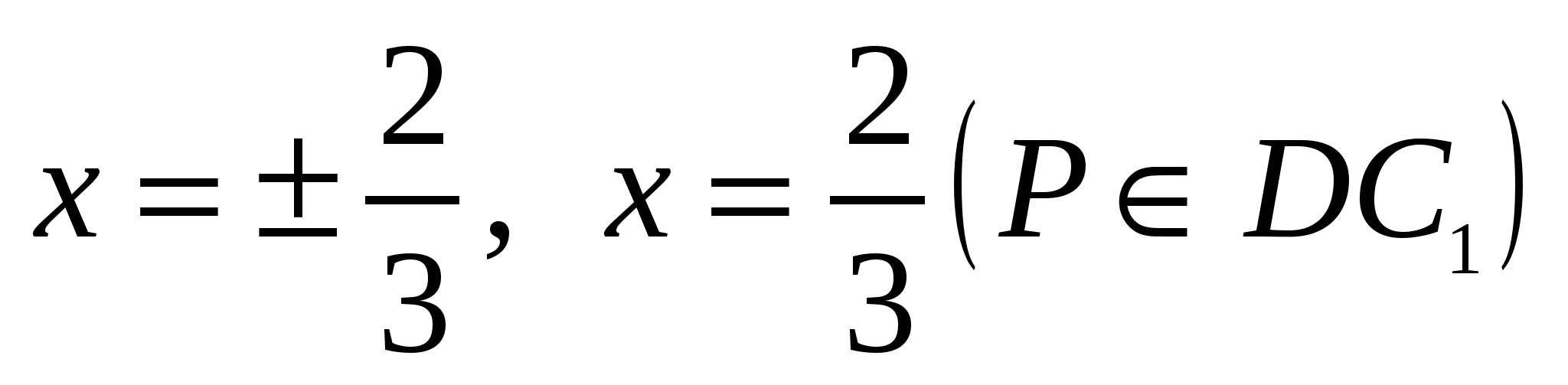 .
.
Следовательно, 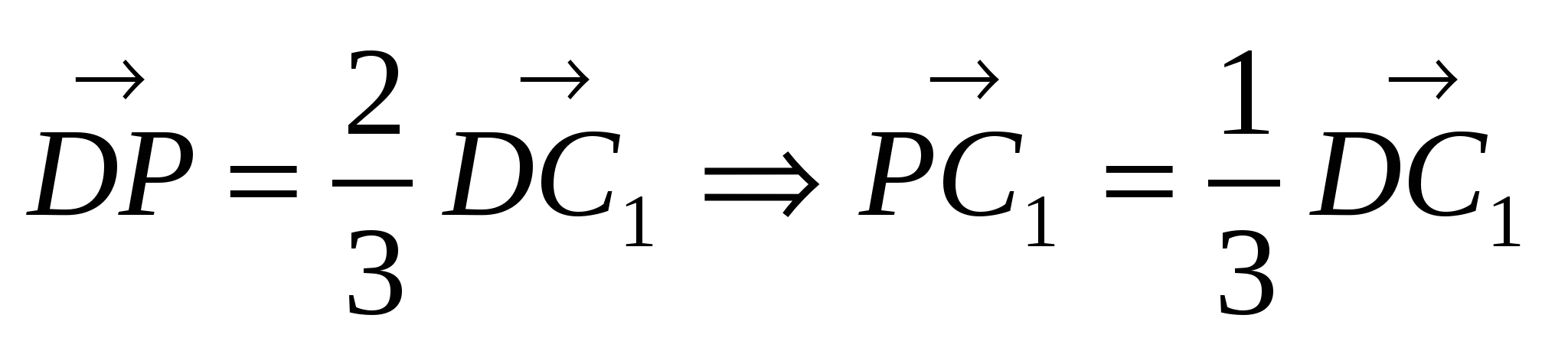 .
.
Ответ: DP : РС1 = 2 : 1.
Задача 3. В прямоугольном параллелепипеде 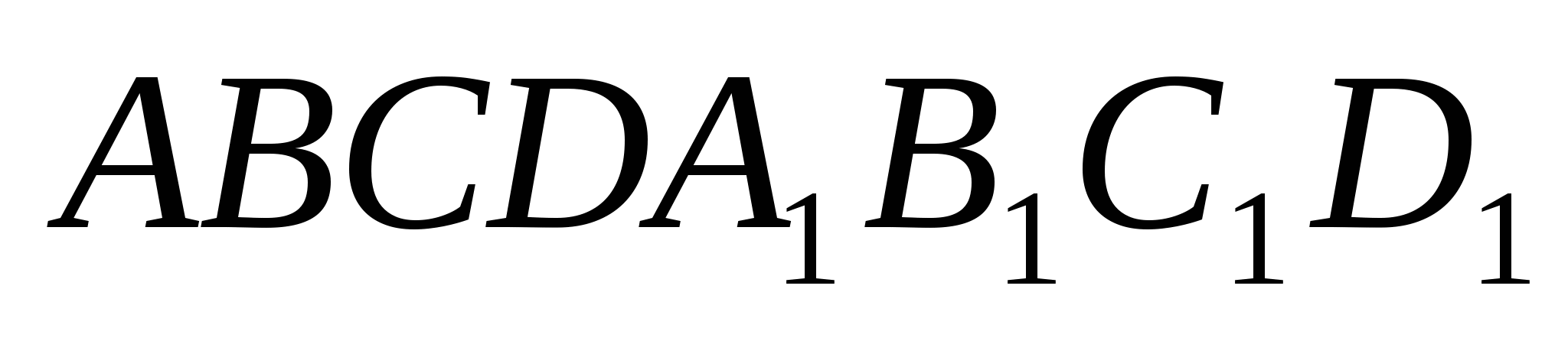 отношение рёбер АВ : АD = 1 : 2, а угол между прямыми В1D и СD1 равен 90. На ребре В1С1 взята точка М - такая, что В1М : МС1 = 1 : 3. Найти угол, который образуют прямые АС и ВМ.
отношение рёбер АВ : АD = 1 : 2, а угол между прямыми В1D и СD1 равен 90. На ребре В1С1 взята точка М - такая, что В1М : МС1 = 1 : 3. Найти угол, который образуют прямые АС и ВМ.
Схема решения:
Введём прямоугольную
систему координат Вxyz так, как показано на рисунке. Найдём координаты точек.
А(0; 1; 0), В(0; 0; 0), С(2; 0; 0), D(2; 1; 0),
А1(0; 1; z), В1(0; 0; z), С1(2; 0; z), D1(2; 1; z),
М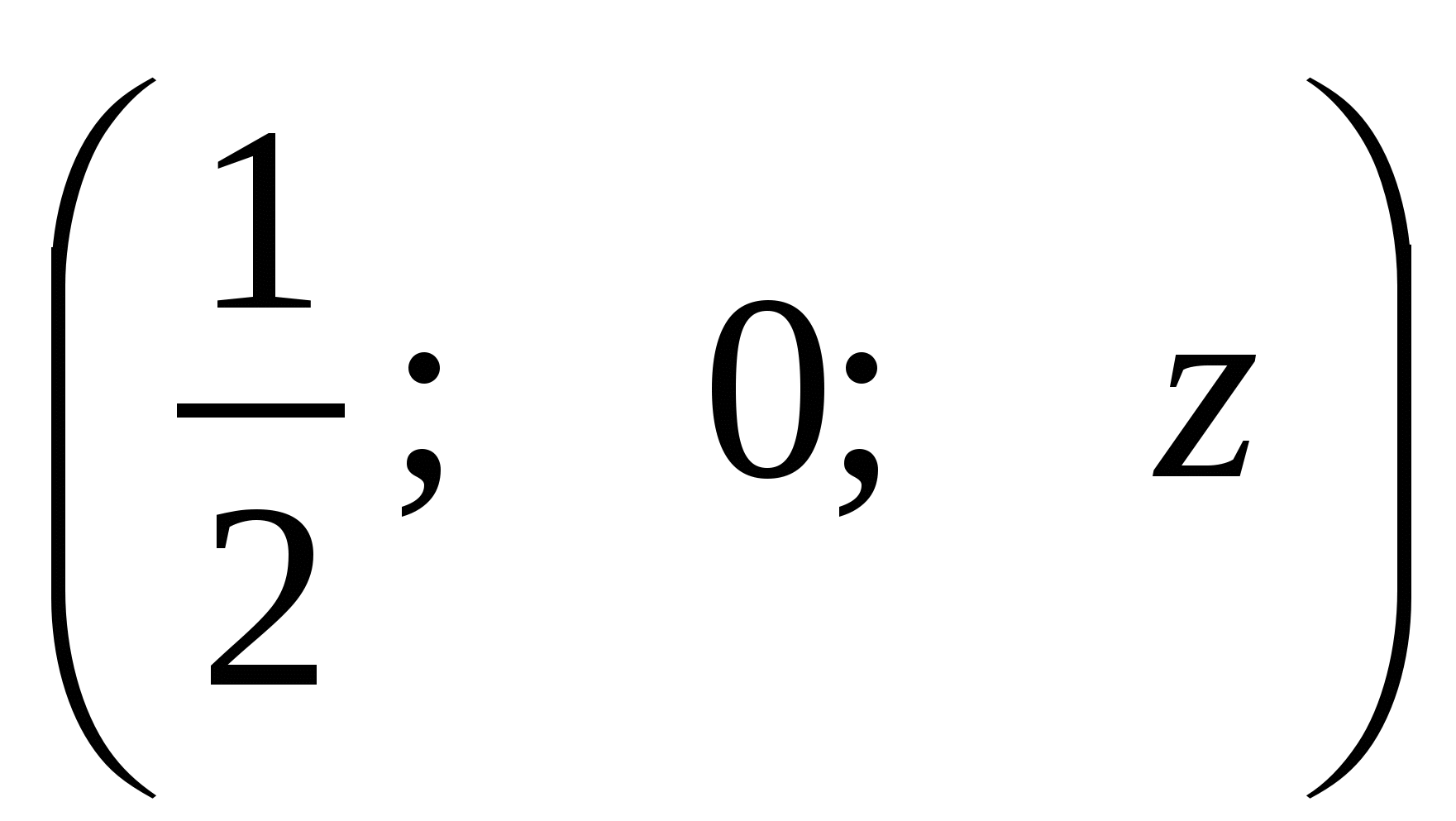 .
.
Так как В1D 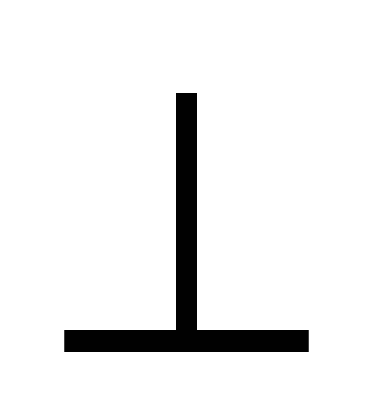 СD1, то
СD1, то 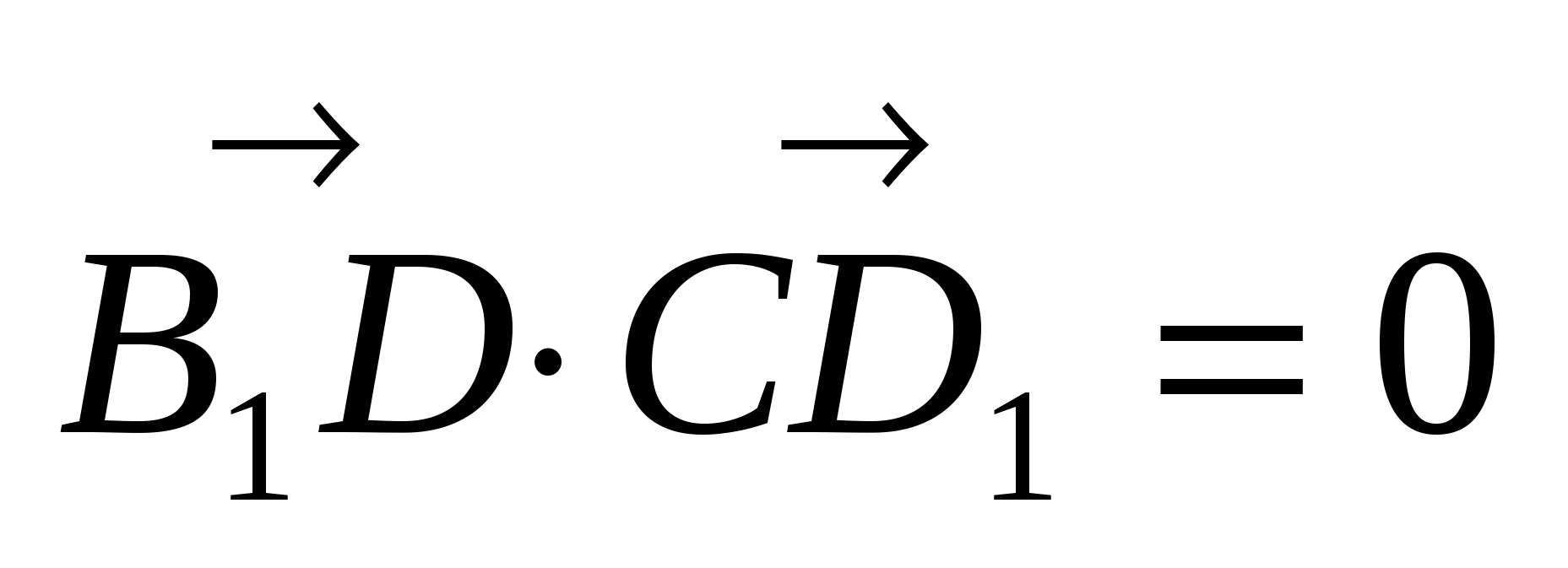 .
.
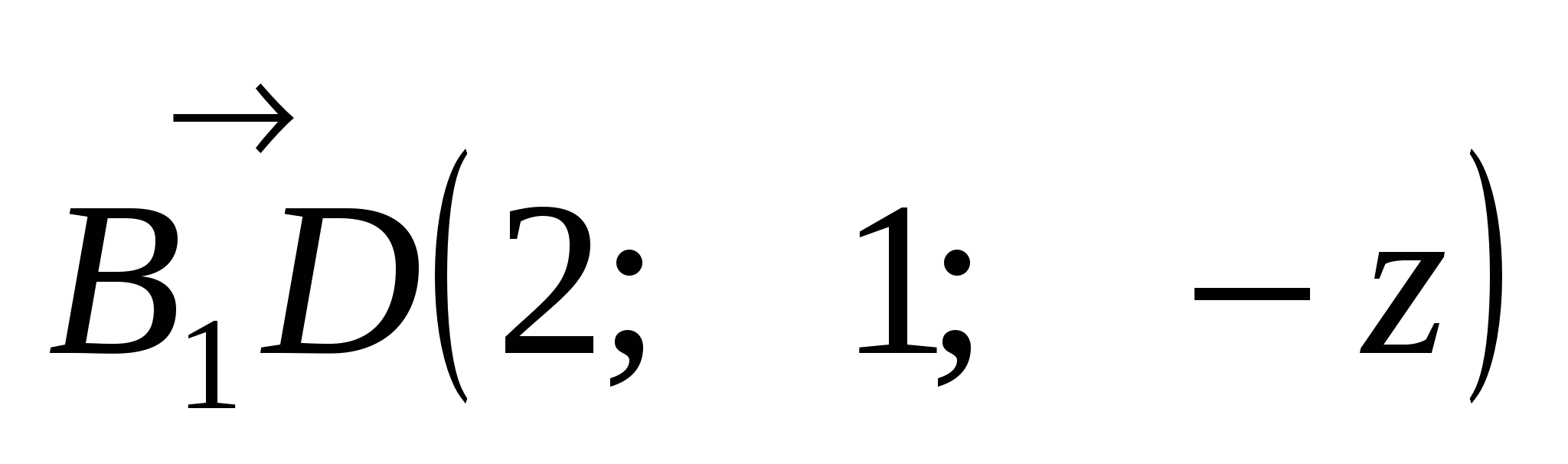 ,
, 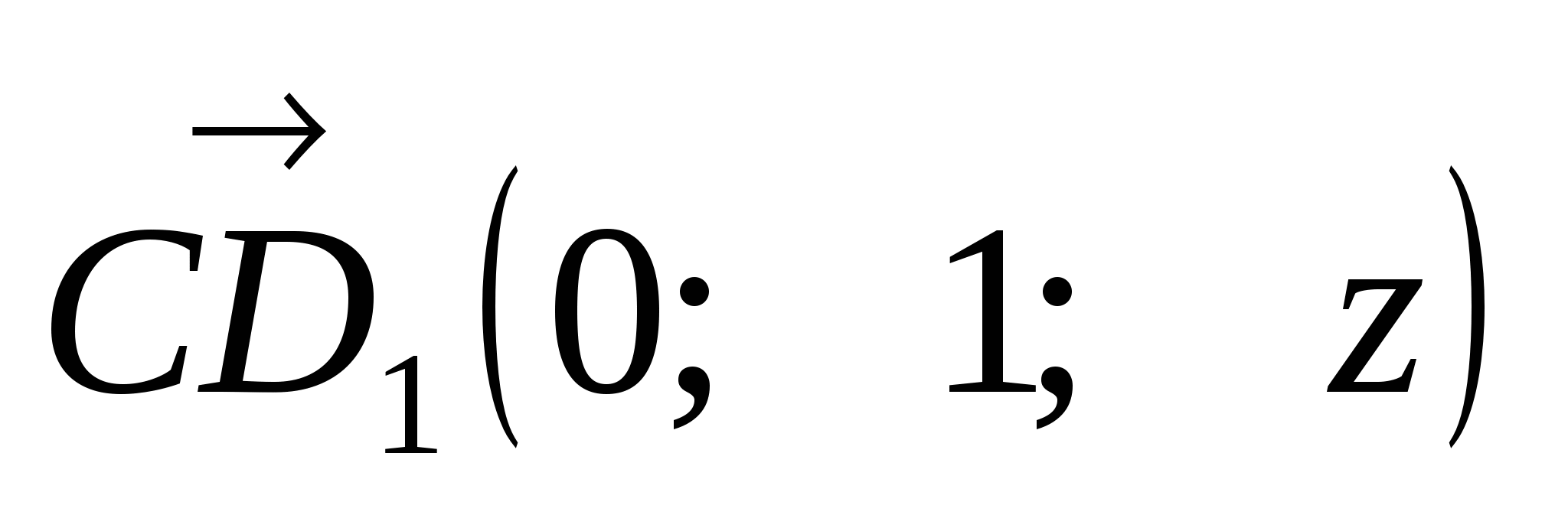 .
.
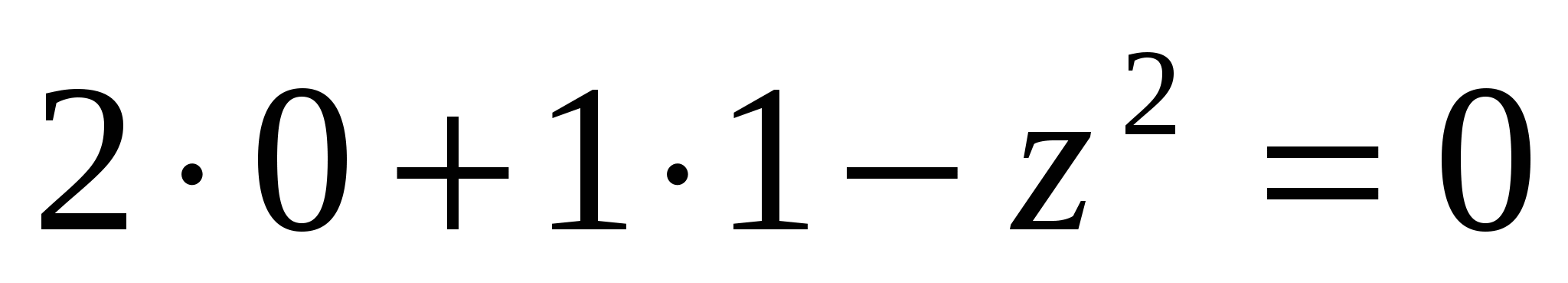 ; z = + 1; z = 1.
; z = + 1; z = 1.
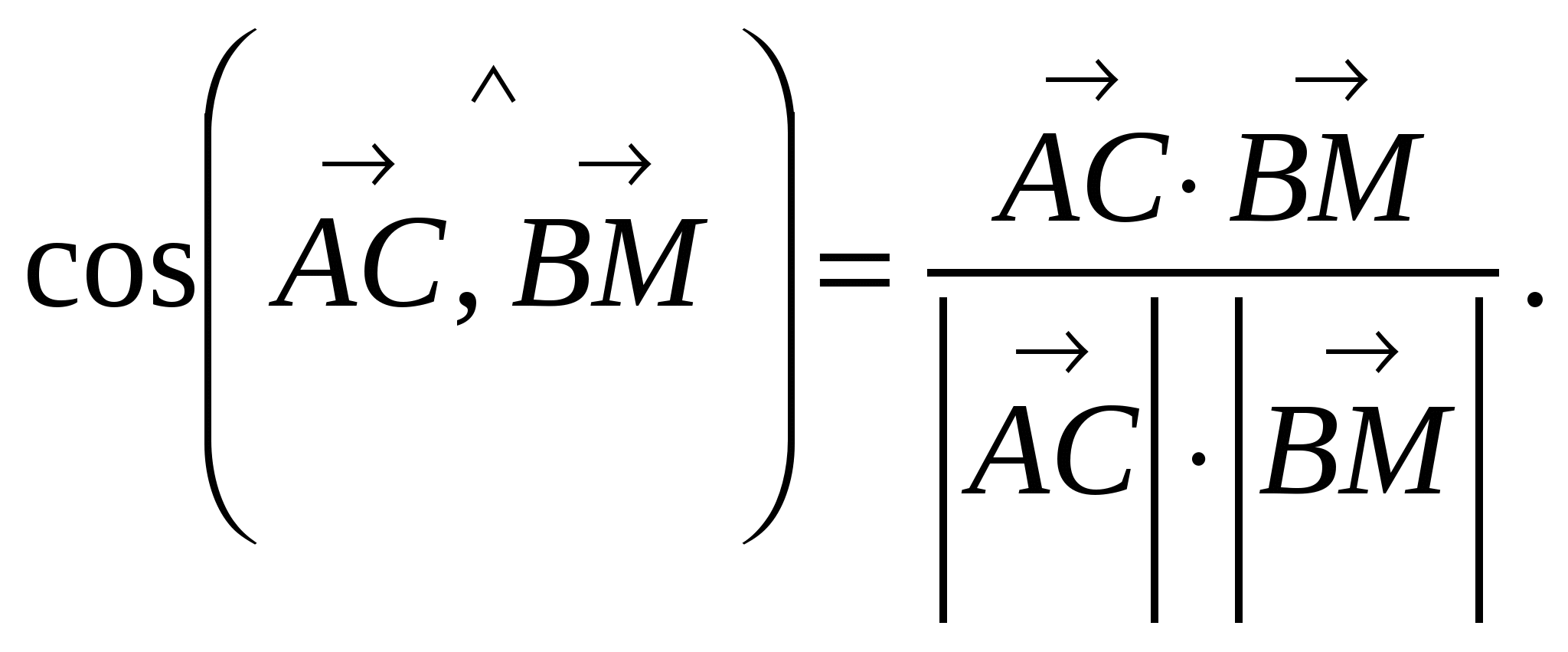
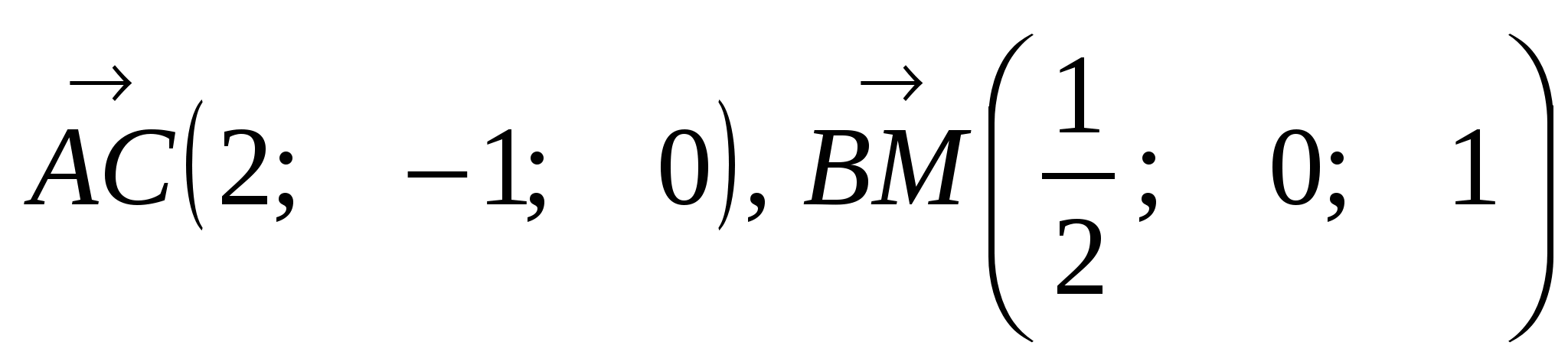 .
.
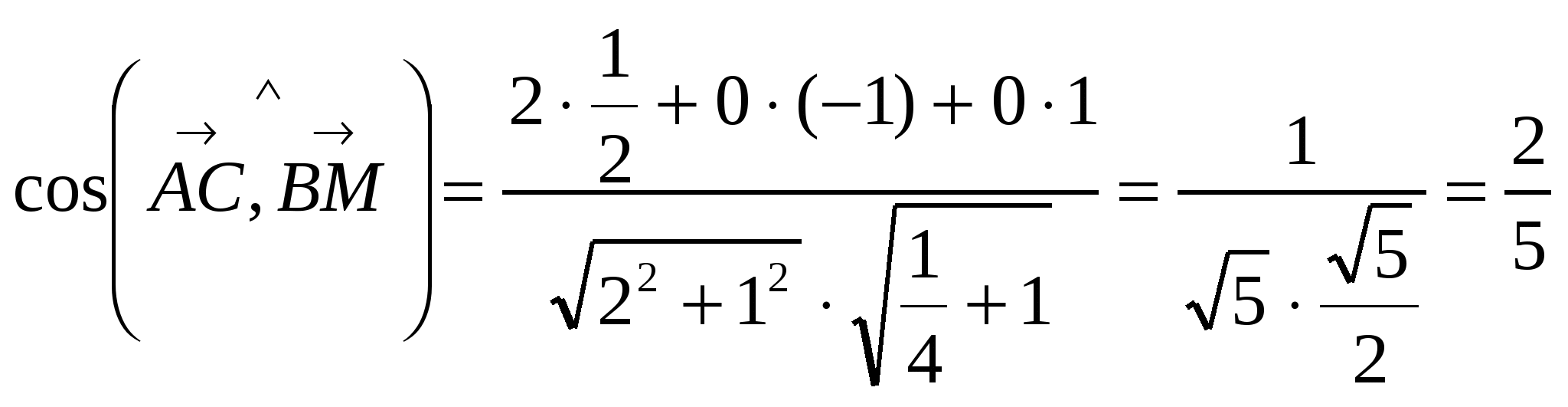 .
.
Ответ: 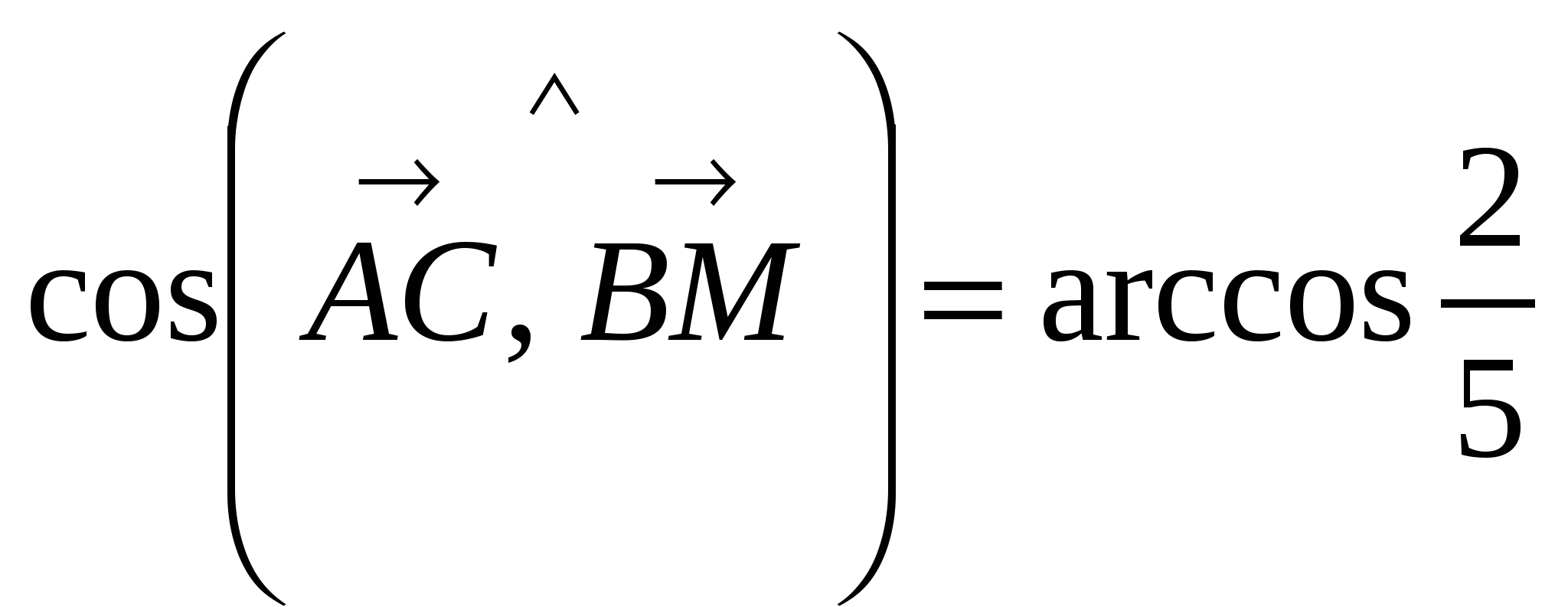 .
.
Задача 4. В трапеции АВСD с основаниями ВС и АD заданы 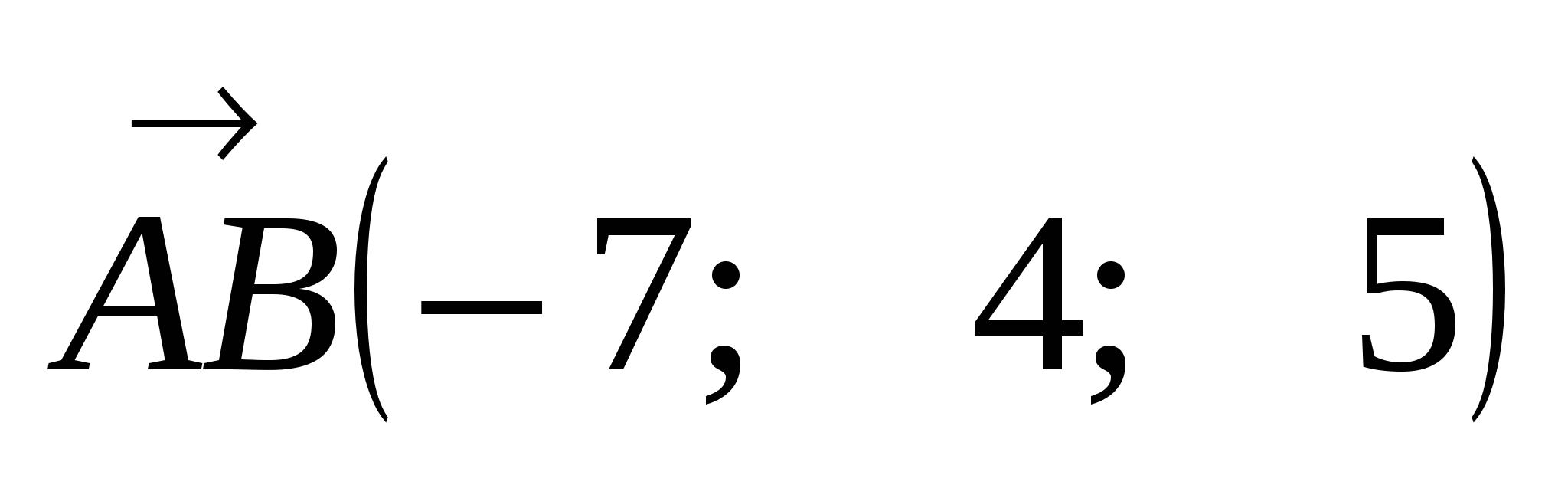 ,
, 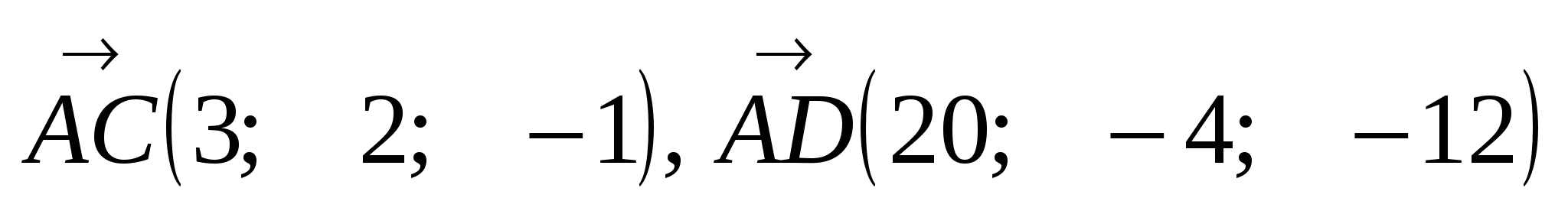 ,
,
М и N - середины отрезков АВ и СD соответственно.
Найти сумму координат вектора 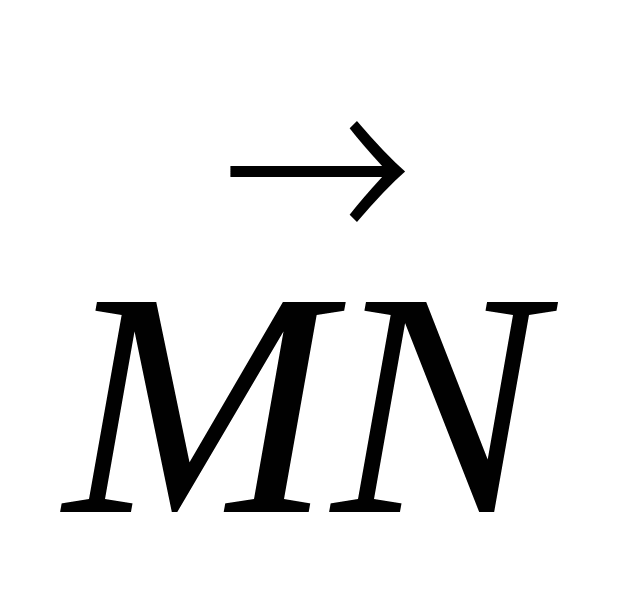 .
.
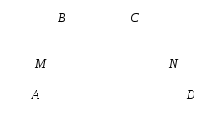
Схема решения:
1) Так как 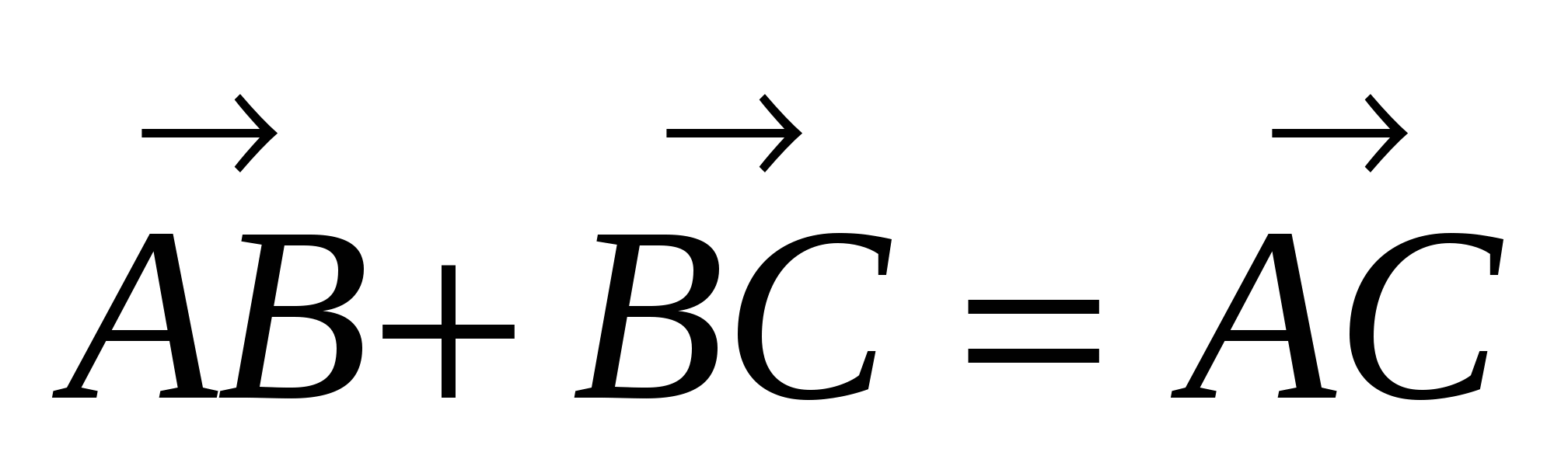 , то
, то 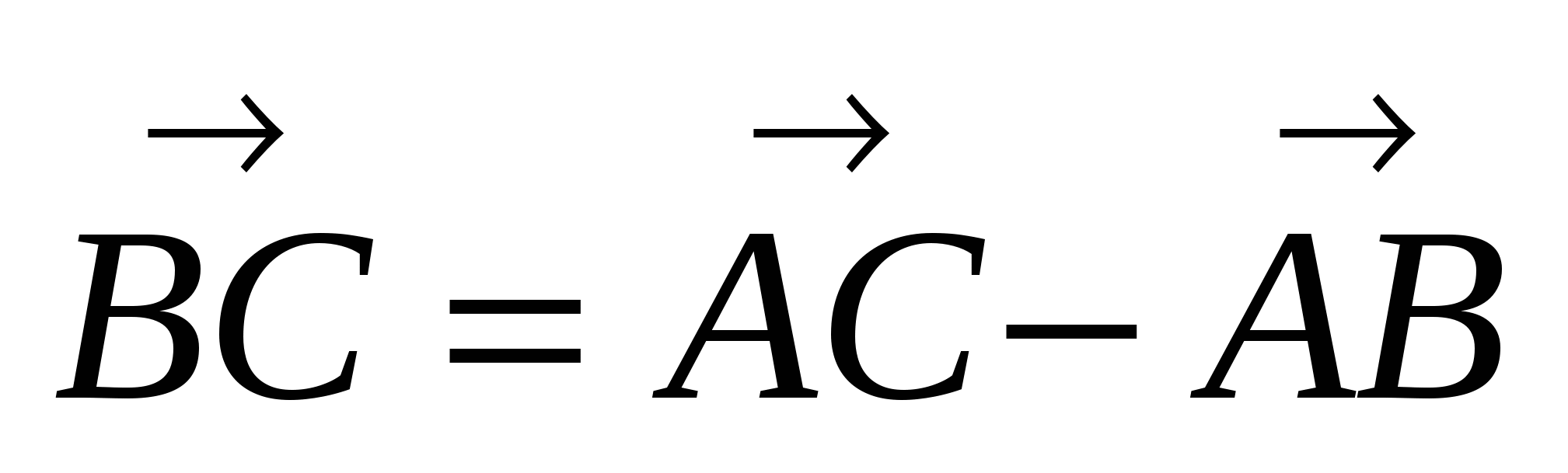 .
.
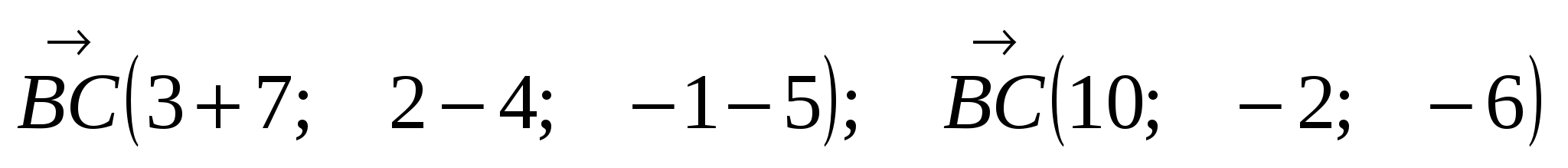 .
.
2) 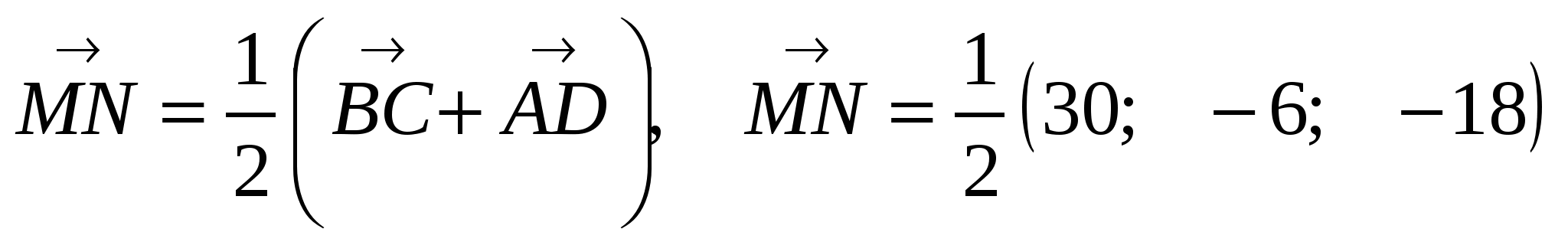 ,
,
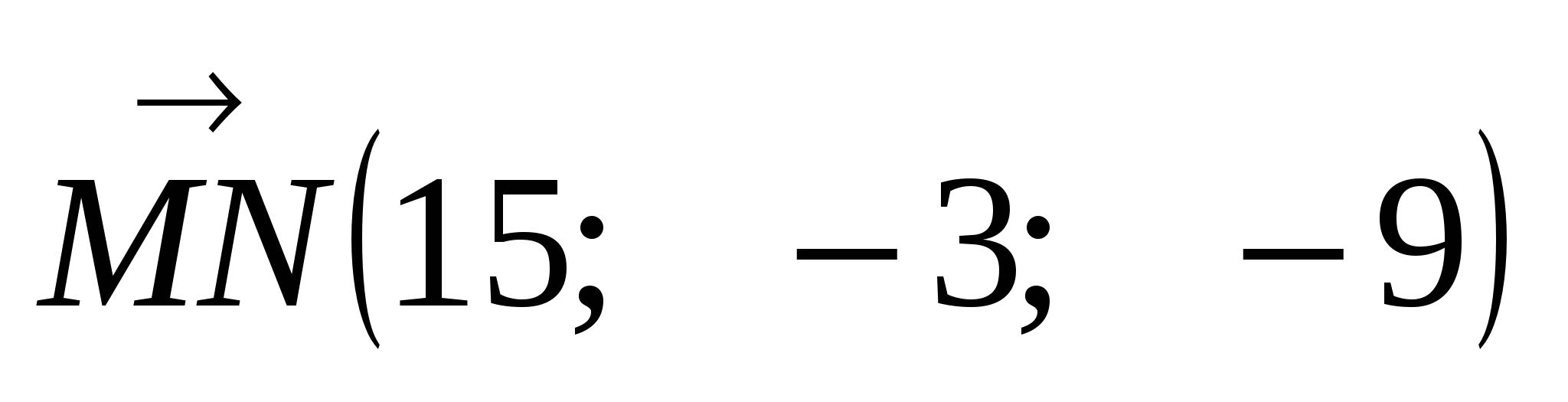 .
.
3) 15 + (-3) + (-9) = 15 - 12 = 3.
Ответ: 3.
1.5. Метод геометрических преобразований
Необходимость в использовании геометрических преобразований возникает, как правило, при решении достаточно сложных геометрических задач (здесь речь идет, во-первых, о задачах, в условии которых геометрические преобразования не фигурируют, и, во-вторых, о задачах, которые трудно решить без использования геометрических преобразований). Проиллюстрируем применение этих методов.
З адача 1 (поворот). Два равнобедренных прямоугольных треугольника АВМ и CDM с гипотенузами АВ и СD расположены так, что ABCD - четырёхугольник. Одна диагональ этого четырёхугольника равна d. Найти его площадь.
адача 1 (поворот). Два равнобедренных прямоугольных треугольника АВМ и CDM с гипотенузами АВ и СD расположены так, что ABCD - четырёхугольник. Одна диагональ этого четырёхугольника равна d. Найти его площадь.
Схема решения:
Повернём ∆АМС вокруг точки М на 90 в соответствующем направлении (по часовой стрелке). При этом точка А перейдёт в точку В, точка С в точку D, т.е. АС перейдёт в BD.
-
В четырёхугольнике ABCD диагонали АС и BD равны и перпендикулярны.
-
Используя формулу для вычисления площади четырёхугольника через диагонали, имеем
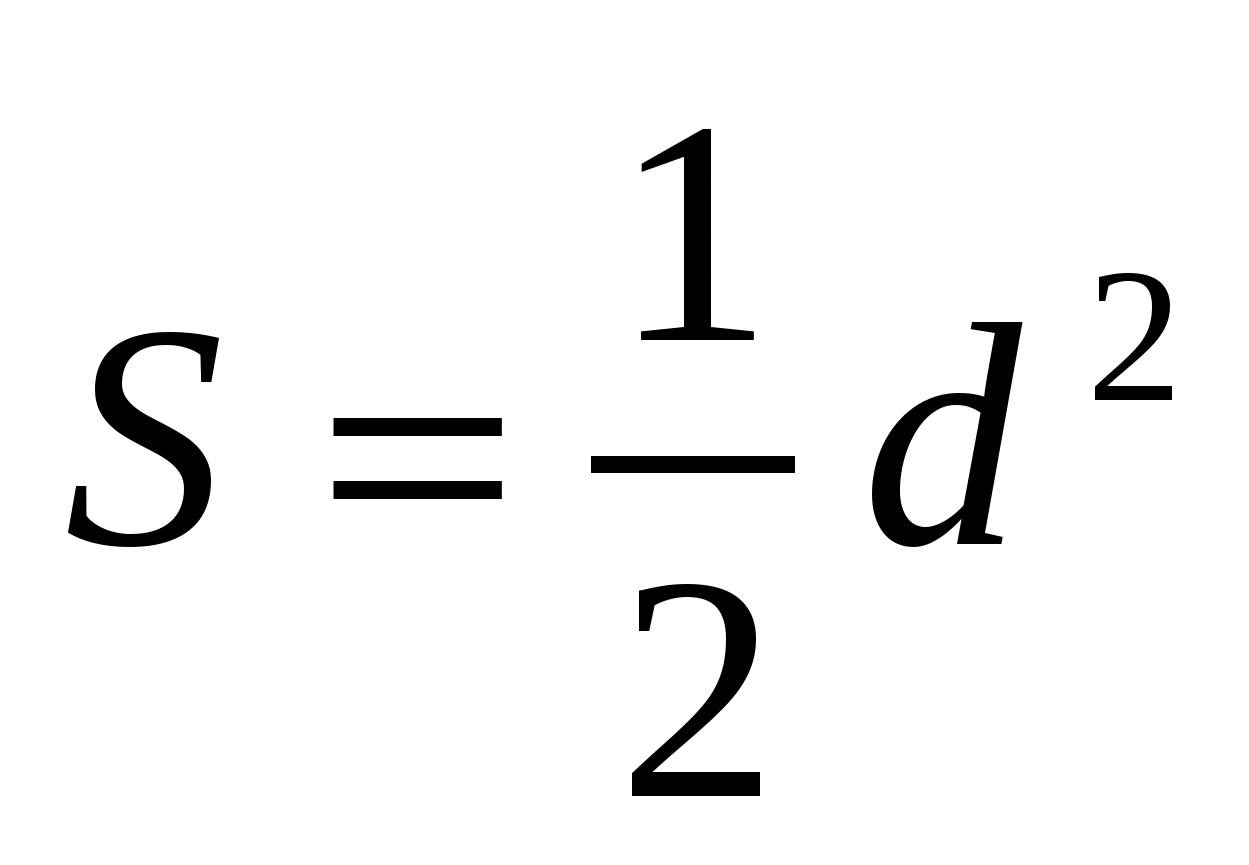 .
.
Задача 2 (осевая симметрия). В треугольнике АВС биссектриса ВЕ и медиана АD перпендикулярны и имеют одинаковую длину, равную 4. Найти стороны треугольника АВС.
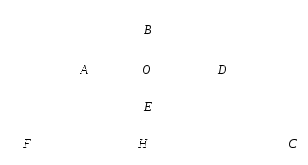
Схема решения:
1) Точки А и D симметричны относительно биссектрисы ВЕ. (так как ∆АВD - равнобедренный, то АО = ОD = 2, АВ = ВD).
-
Построим точку F, симметричную точке С относительно прямой ВЕ.
-
BF = BC, так как симметрия является движением.
-
Следовательно, ВН является медианой ∆FBC (точка Н является точкой пересечения FC и ВЕ).
-
Точка Е является точкой пересечения медиан ∆FBC. Следовательно
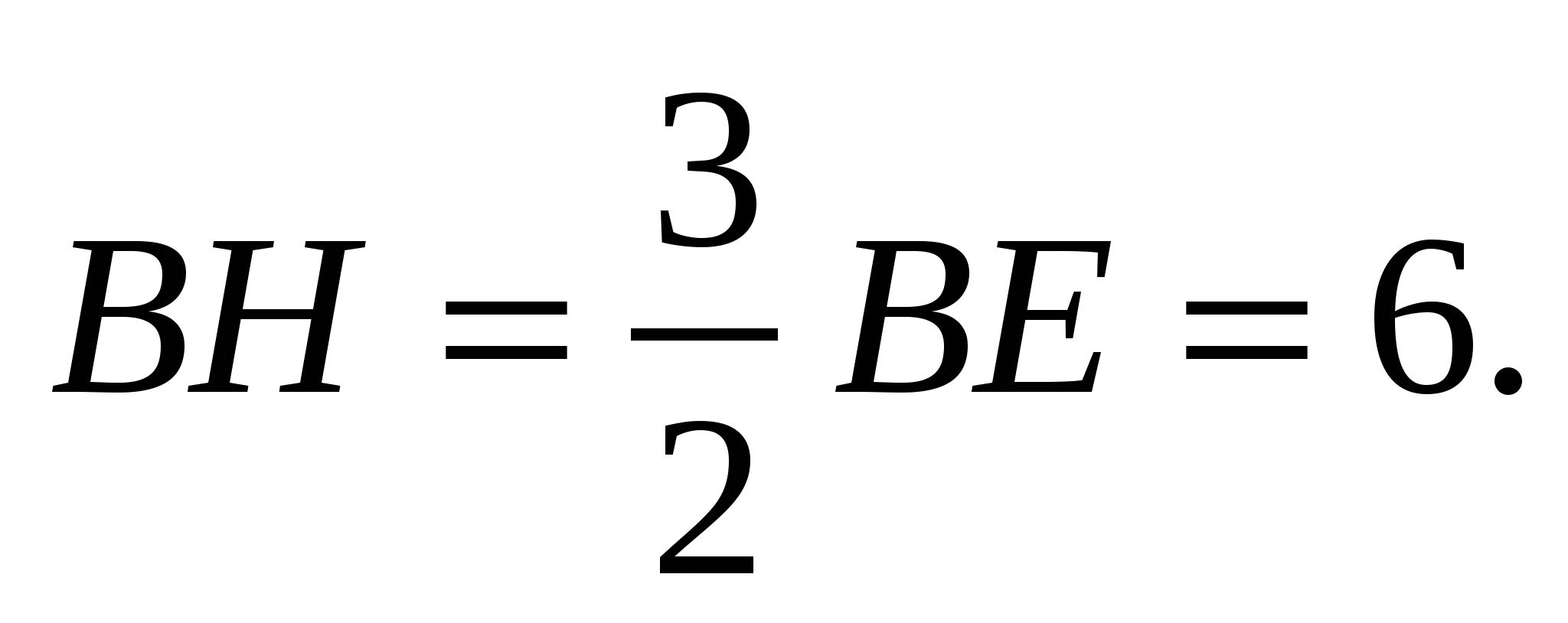
-
Так как AD - средняя линия ∆FBC, то
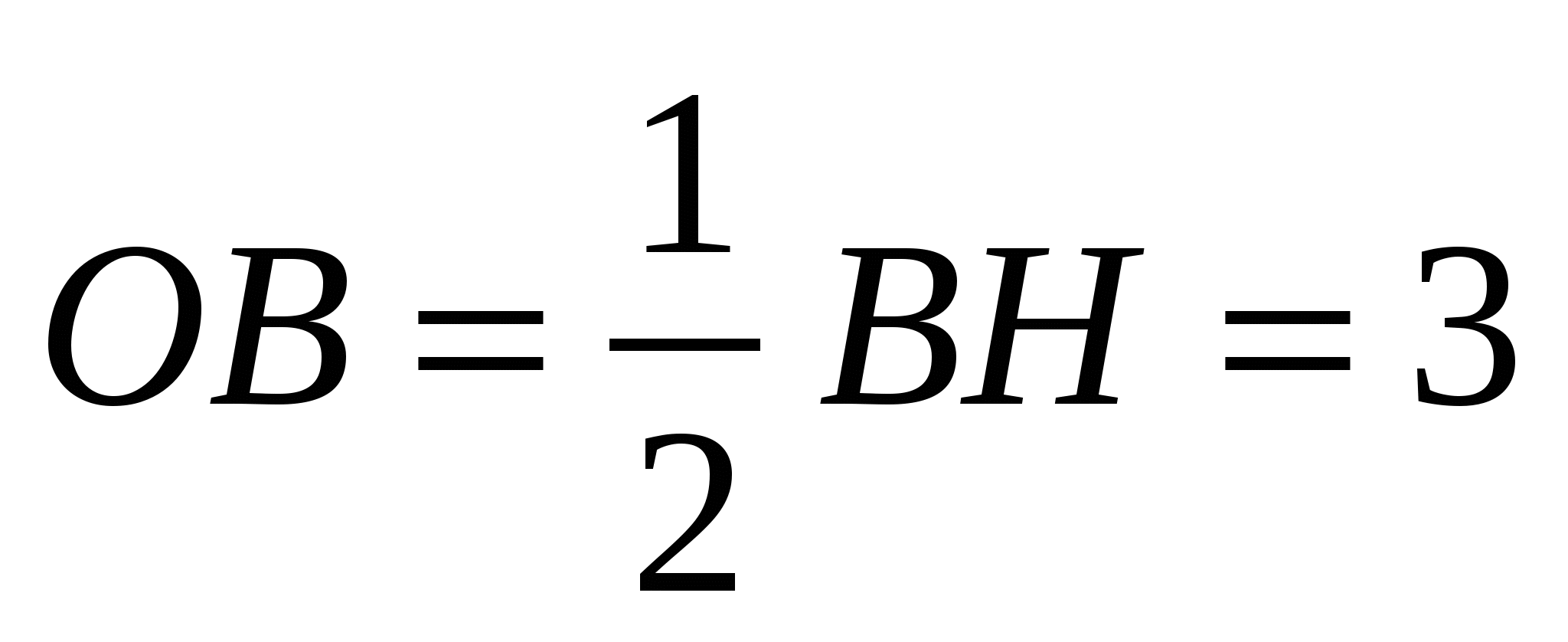 . Из ∆OBD находим
. Из ∆OBD находим 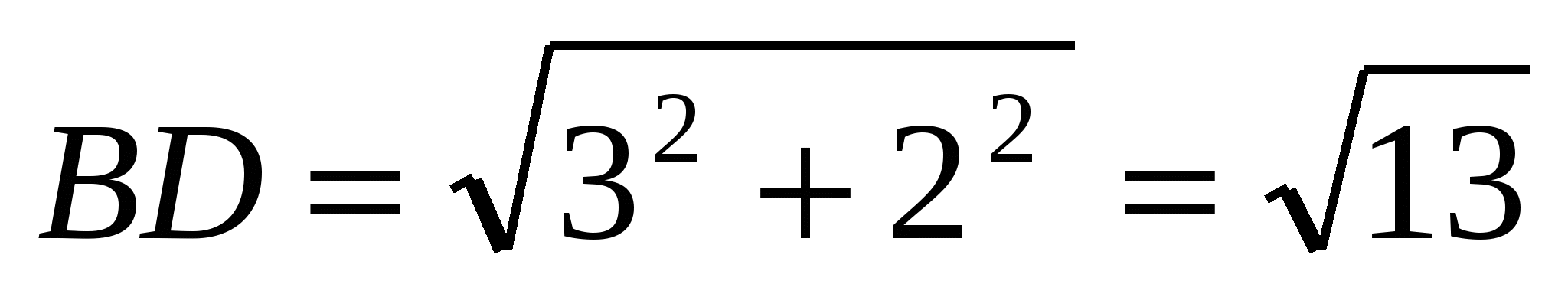 . Следовательно, АВ = BD =
. Следовательно, АВ = BD = 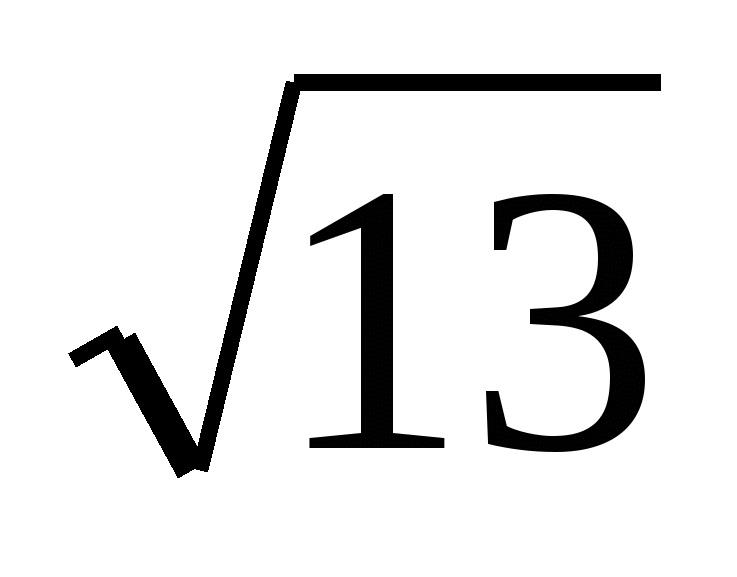 , ВС = 2ВD = 2
, ВС = 2ВD = 2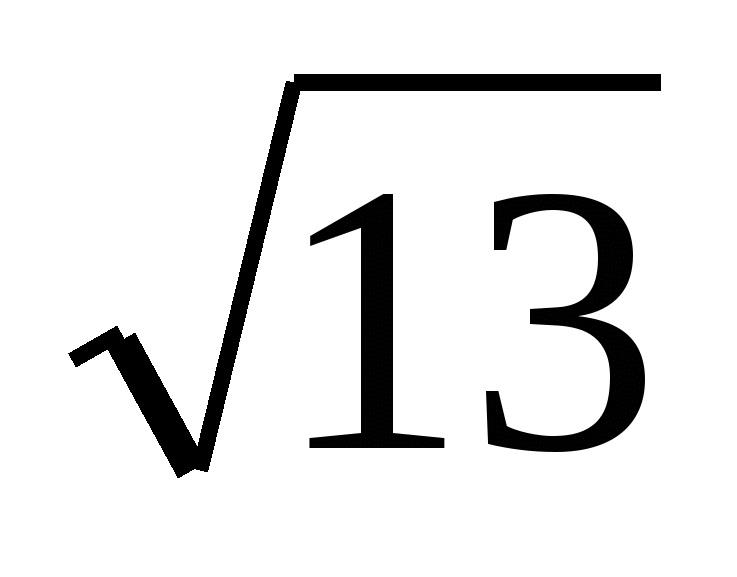 .
. -
Из ∆АОЕ находим АЕ =
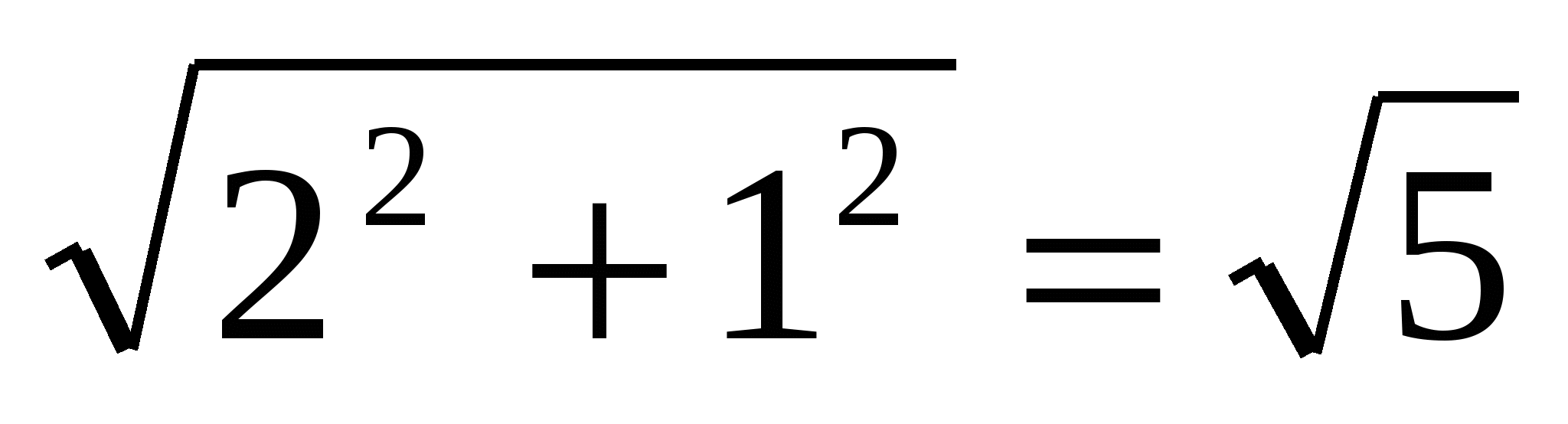 . По свойству медиан, имеем: АС = 3АЕ = 3
. По свойству медиан, имеем: АС = 3АЕ = 3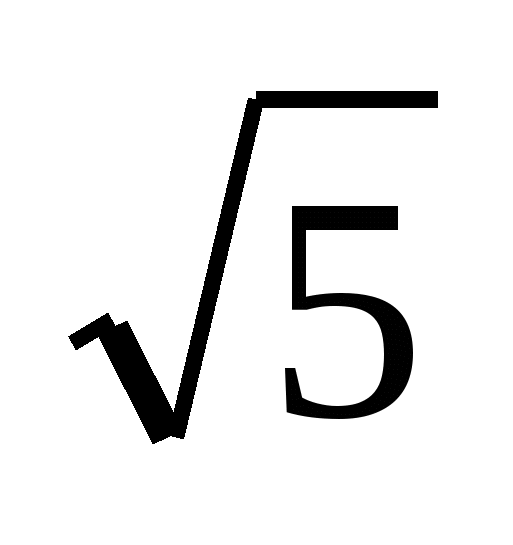 .
.
Ответ: АВ = 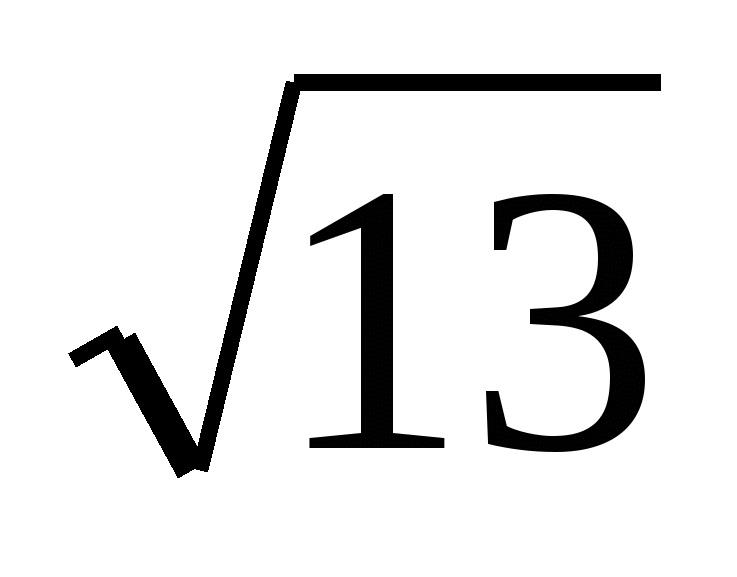 ; ВС = 2
; ВС = 2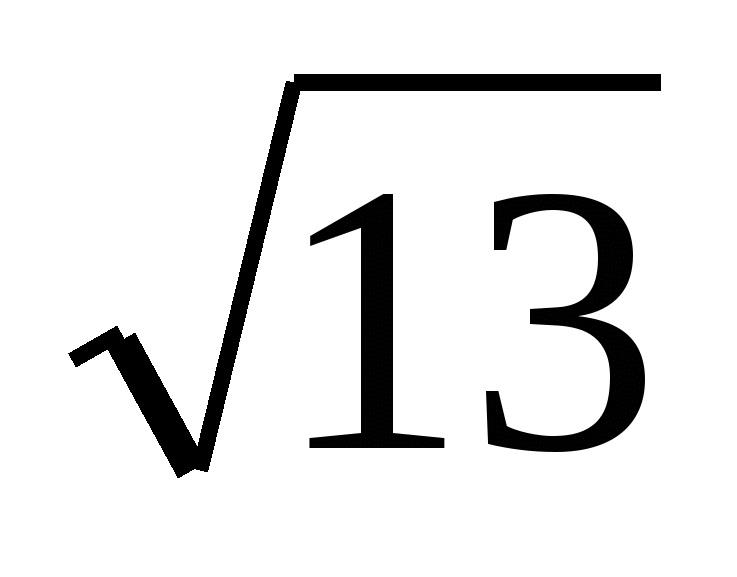 ; АС = 3
; АС = 3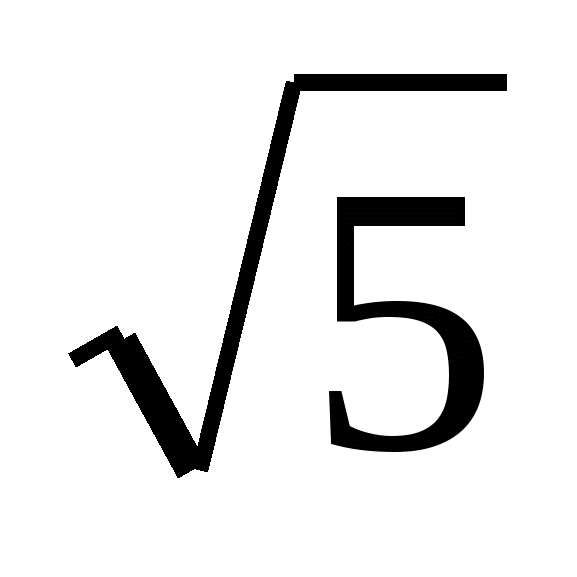 .
.
Задача 3 (подобие). Трапеция разделена на три трапеции прямыми, параллельными основаниям. Известно, что в каждую из трёх получивш ихся трапеций можно вписать окружность. Найти радиус окружности, вписанной в среднюю трапецию, если радиусы окружностей, вписанных в две оставшиеся, равны R и r.
ихся трапеций можно вписать окружность. Найти радиус окружности, вписанной в среднюю трапецию, если радиусы окружностей, вписанных в две оставшиеся, равны R и r.
Схема решения:
Пусть радиус средней окружности равен х.
1) ∆AKD ∆LKP. Паре окружностей с радиусами R и x в ∆AKD соответствует пара окружностей с радиусами х и r в ∆LKP.
2) 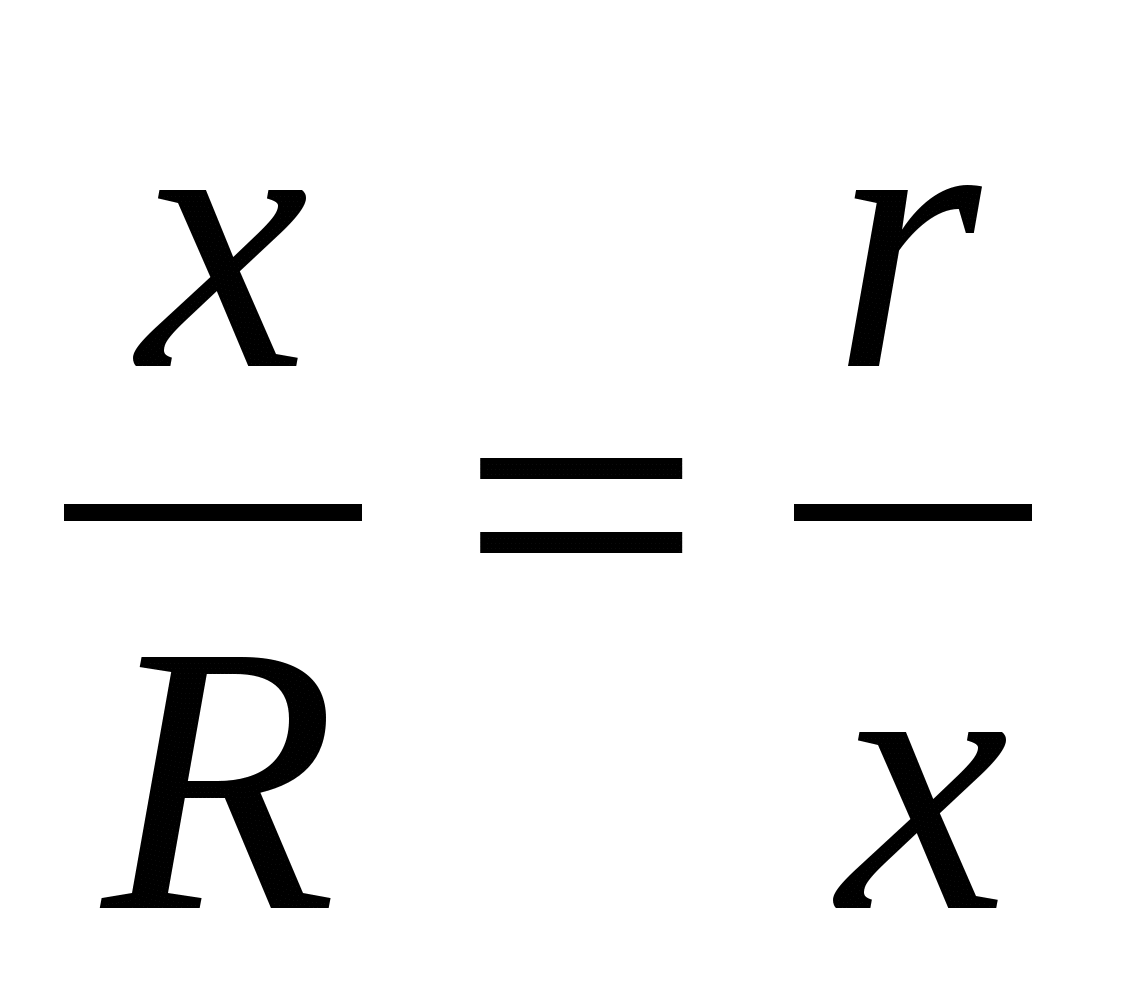 =>
=> 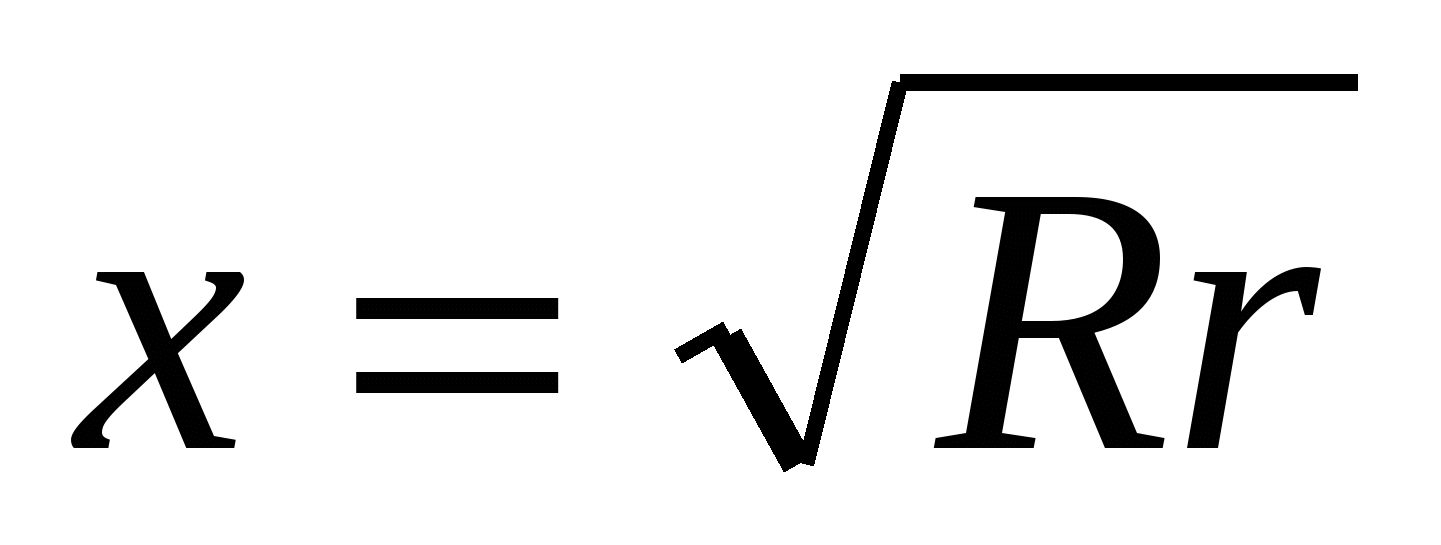 .
.
Задача 4 (параллельный перенос). Основания трапеции равны 4 см и 9 см, а диагонали равны 5 и 12 см. Найти площадь трапеции и угол между ее диагоналями.
Схема решения:
Перенесем диагональ ВD на вектор 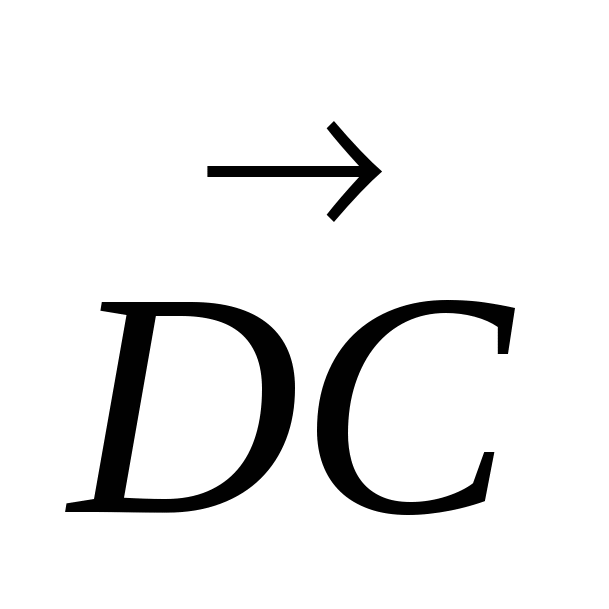 в положение
в положение 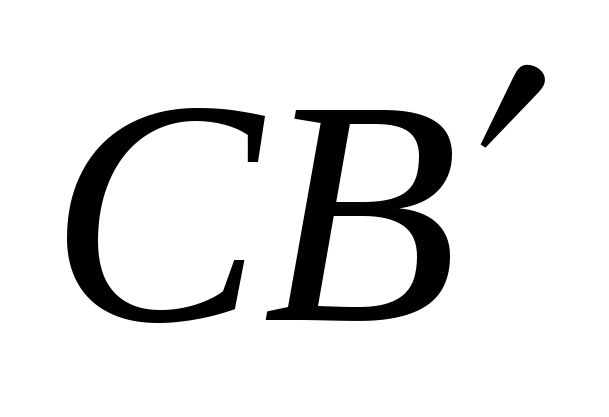 .
.
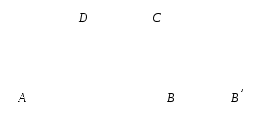
Рассмотрим треугольник 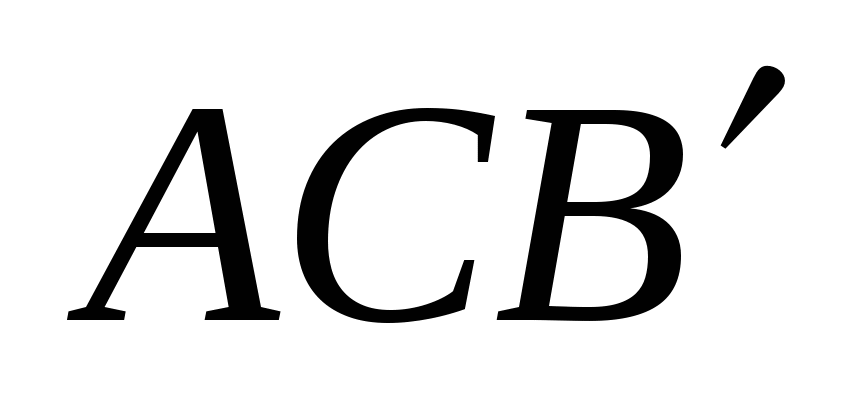 . Так как
. Так как 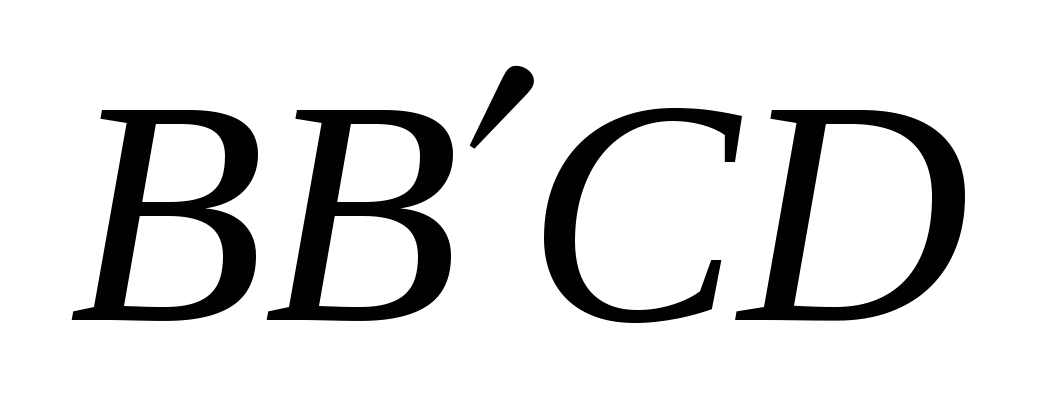 - параллелограмм, то
- параллелограмм, то
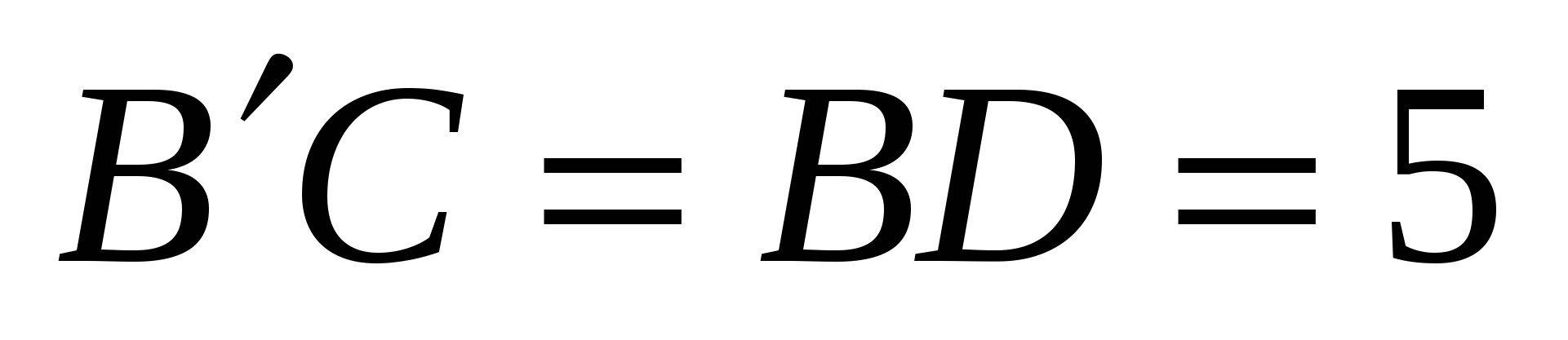 см,
см, 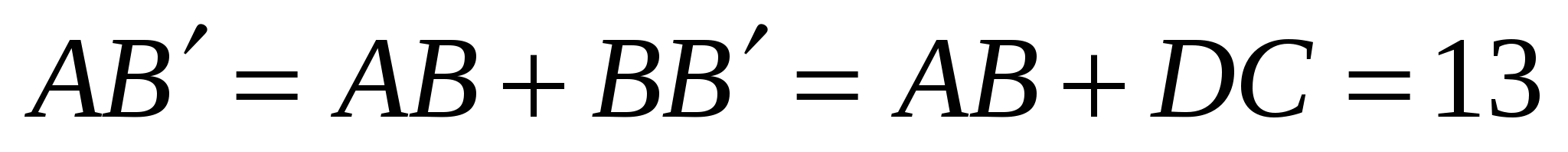 см.
см.
Известны три стороны треугольника 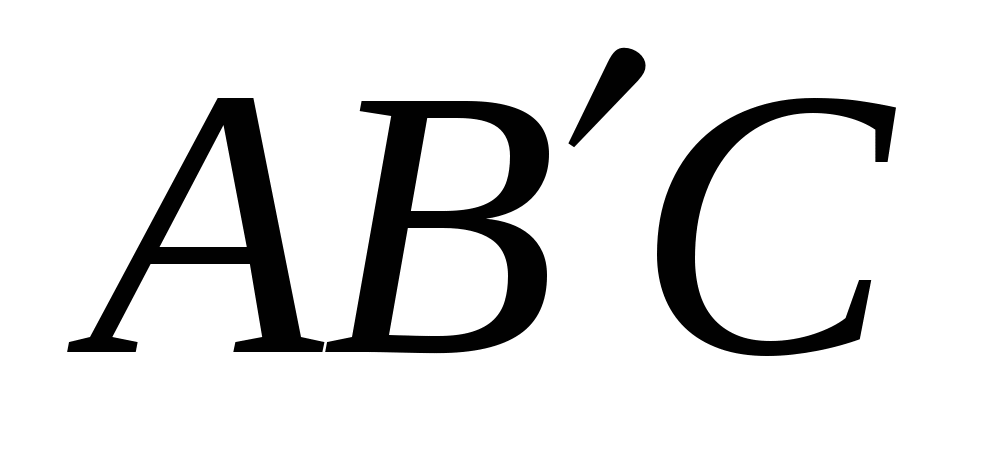 , значит, можно найти его высоту, а затем и площадь трапеции. Если не заметить, что площадь трапеции равна площади треугольника
, значит, можно найти его высоту, а затем и площадь трапеции. Если не заметить, что площадь трапеции равна площади треугольника 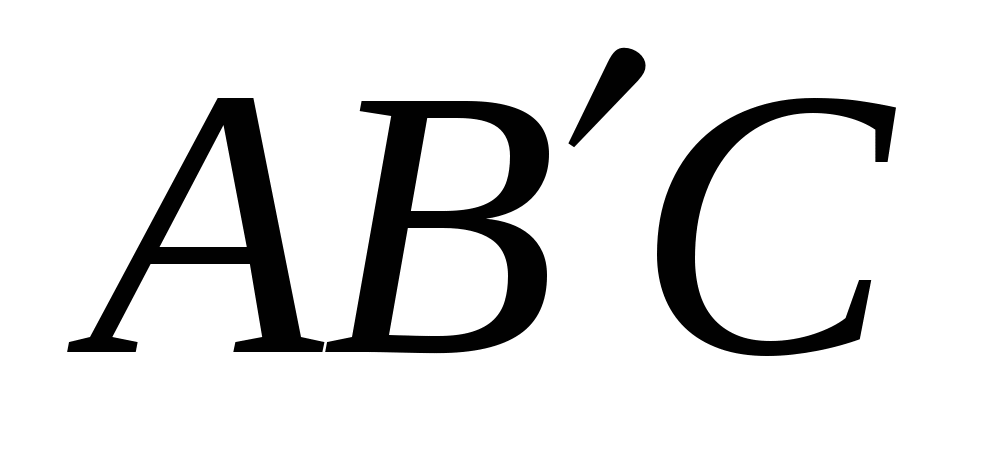 (доказать), то решение задачи можно еще упростить.
(доказать), то решение задачи можно еще упростить.
Так как 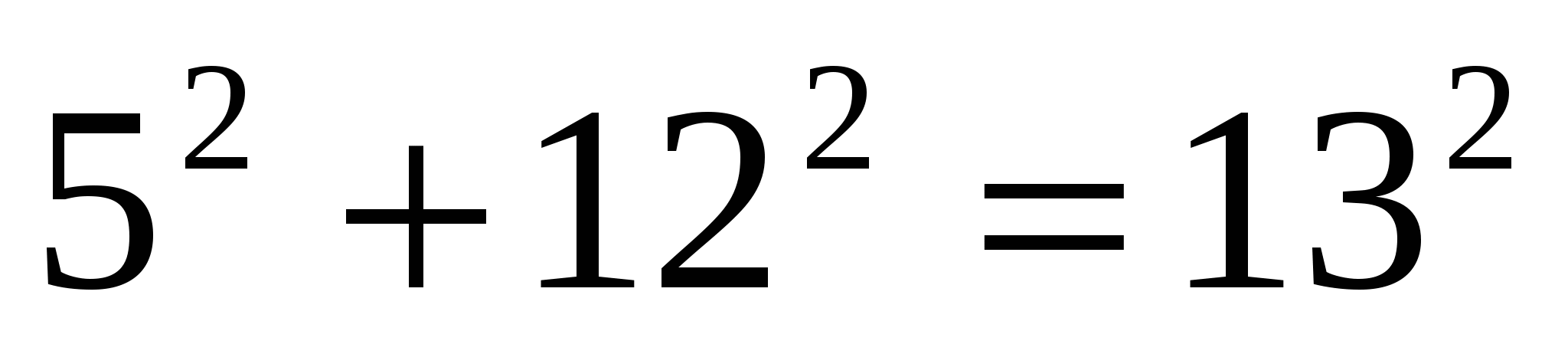 , то треугольник
, то треугольник 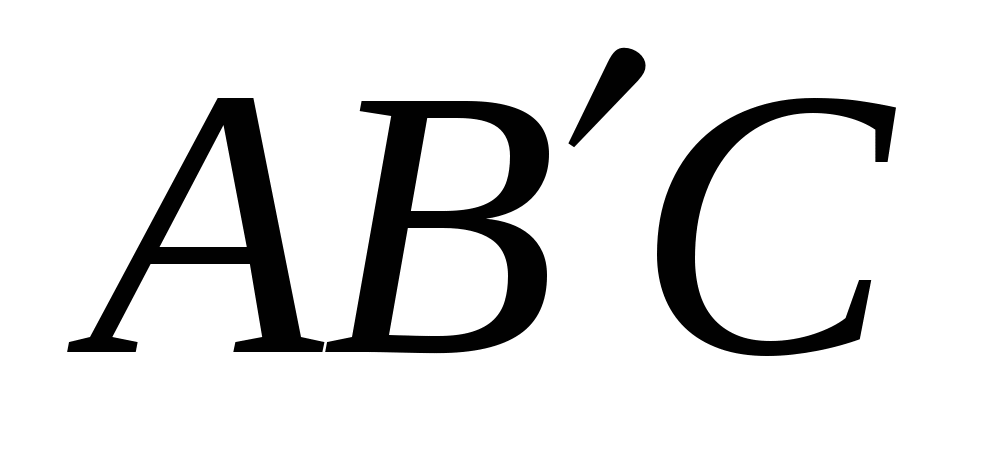 прямоугольный. Следовательно, площадь трапеции равна 30 см2. Угол между диагоналями трапеции равен углу
прямоугольный. Следовательно, площадь трапеции равна 30 см2. Угол между диагоналями трапеции равен углу 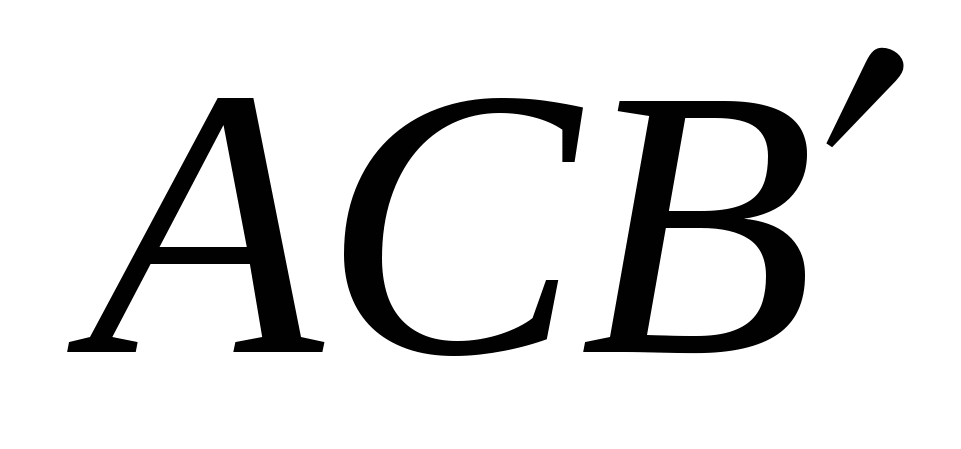 , значит, диагонали перпендикулярны.
, значит, диагонали перпендикулярны.
Задача 5 (гомотетия). В трапеции АВСD проведены диагонали
AC и BD, пересекающиеся в точке M (AB и CD - основания трапеции). Доказать, что площади треугольников ABM и CDM, равные соответственно S2 и S1,и площадь S трапеции связаны соотношением 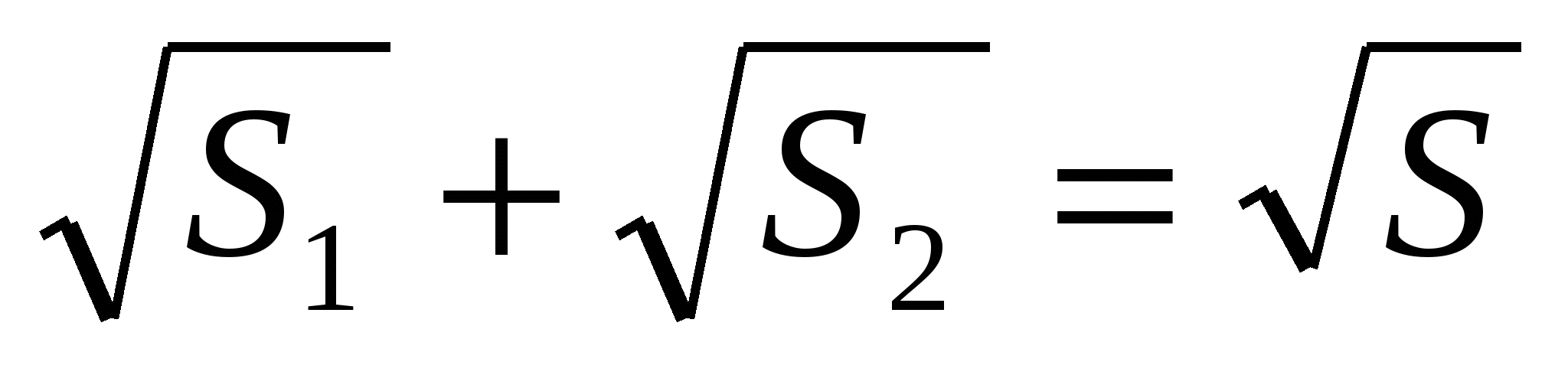 .
.
С хема решения:
хема решения:
Пусть точка N - точка пересечения прямой АВ и прямой, проходящей через точку C параллельно DB. Площадь треугольника ACN равна площади S данной трапеции. Проведем BF параллельно АС. Площадь треугольника BFN равна площади S1 треугольника DMC. Треугольники AMB и BFN гомотетичны треугольнику ACN с коэффициентами k1 и k2, причем k1 + k2 = 1. Но k1 = 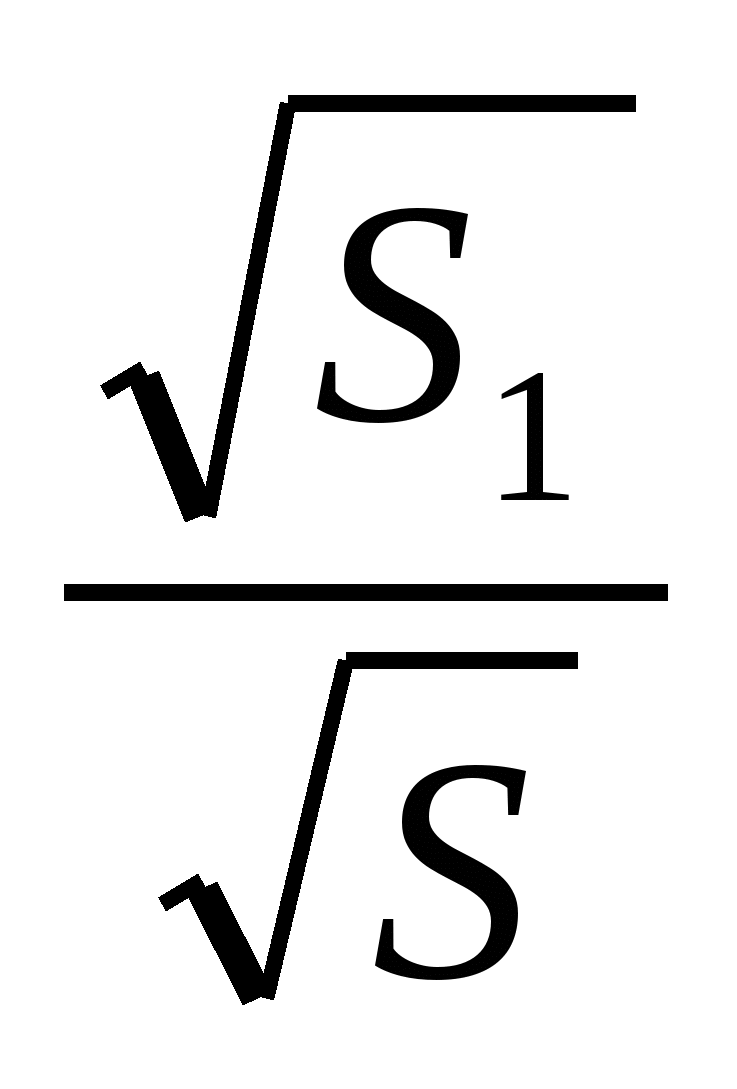 и k2 =
и k2 = 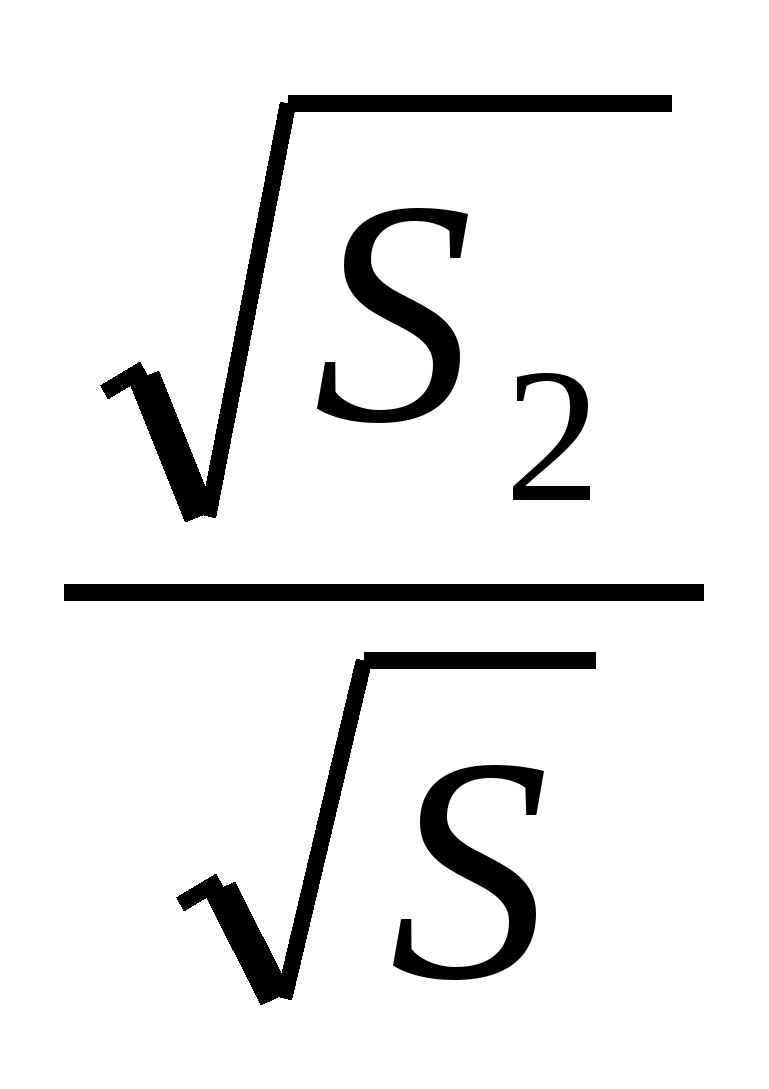 , следовательно,
, следовательно, 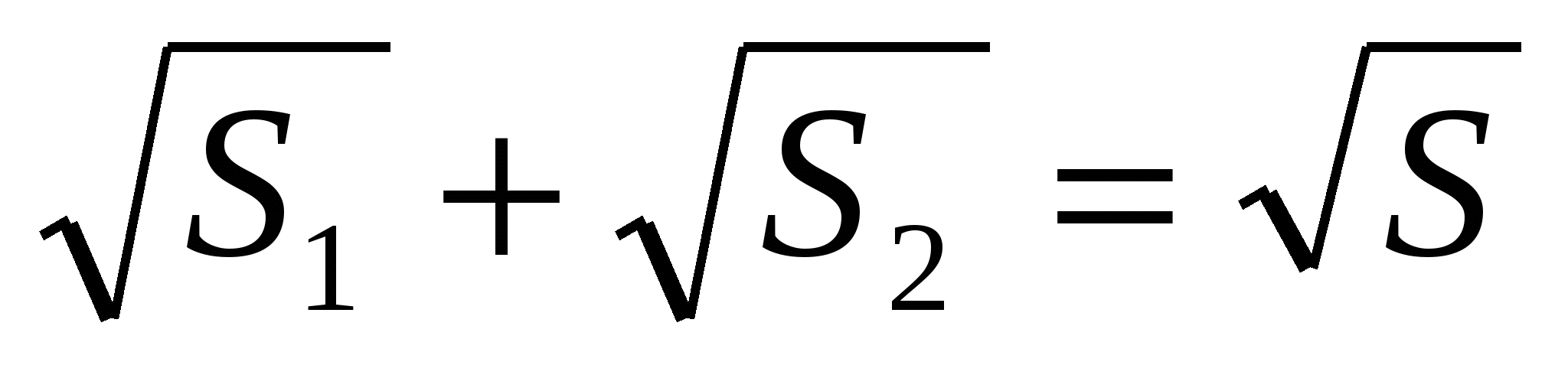 .
.
Задача 6 (гомотетия).
В треугольник АВС вписана окружность, касающаяся прямой АВ в точке М. Пусть точка М1 диаметрально противолежит точке М на вписанной окружности. Доказать, что прямая СМ1 пересекает прямую АВ в такой точке С1 ,что АС+ АС1=ВС+ ВС1.
Схема решения:
П остроим касательную к окружности в точке М1, пересекающую АС в точке А1 и ВС в В1. Тогда ясно, что СА1 + А1М1 = СВ1 + В1М1.
остроим касательную к окружности в точке М1, пересекающую АС в точке А1 и ВС в В1. Тогда ясно, что СА1 + А1М1 = СВ1 + В1М1.
Далее воспользуемся тем, что треугольники АВС и А1В1С1 гомотетичны, так как прямые АВ и А1В1 перпендикулярны диаметру ММ1 и поэтому АВ параллельна А1В1.
II. Решение задач различными методами
Каждая из рассмотренных нами задач, как правило, сопровождалась лишь одним решением, иллюстрирующим тот или иной прием, тот или иной метод решения. Бесспорно, изучение методов решения геометрических задач будет более эффективным, если рассматривать на примере одной задачи возможности использования различных геометрических и алгебраических методов.
Задача №1. В окружность радиуса 1 вписан равносторонний треугольник ABC, и на этой окружности взята произвольно точка D. Найти AD2+BD2+CD2.
Координатный метод

Схема решения:
Введем на плоскости прямоугольную систему координат с началом в точке О (центре правильного треугольника ABC).
Тогда А(0; 1); В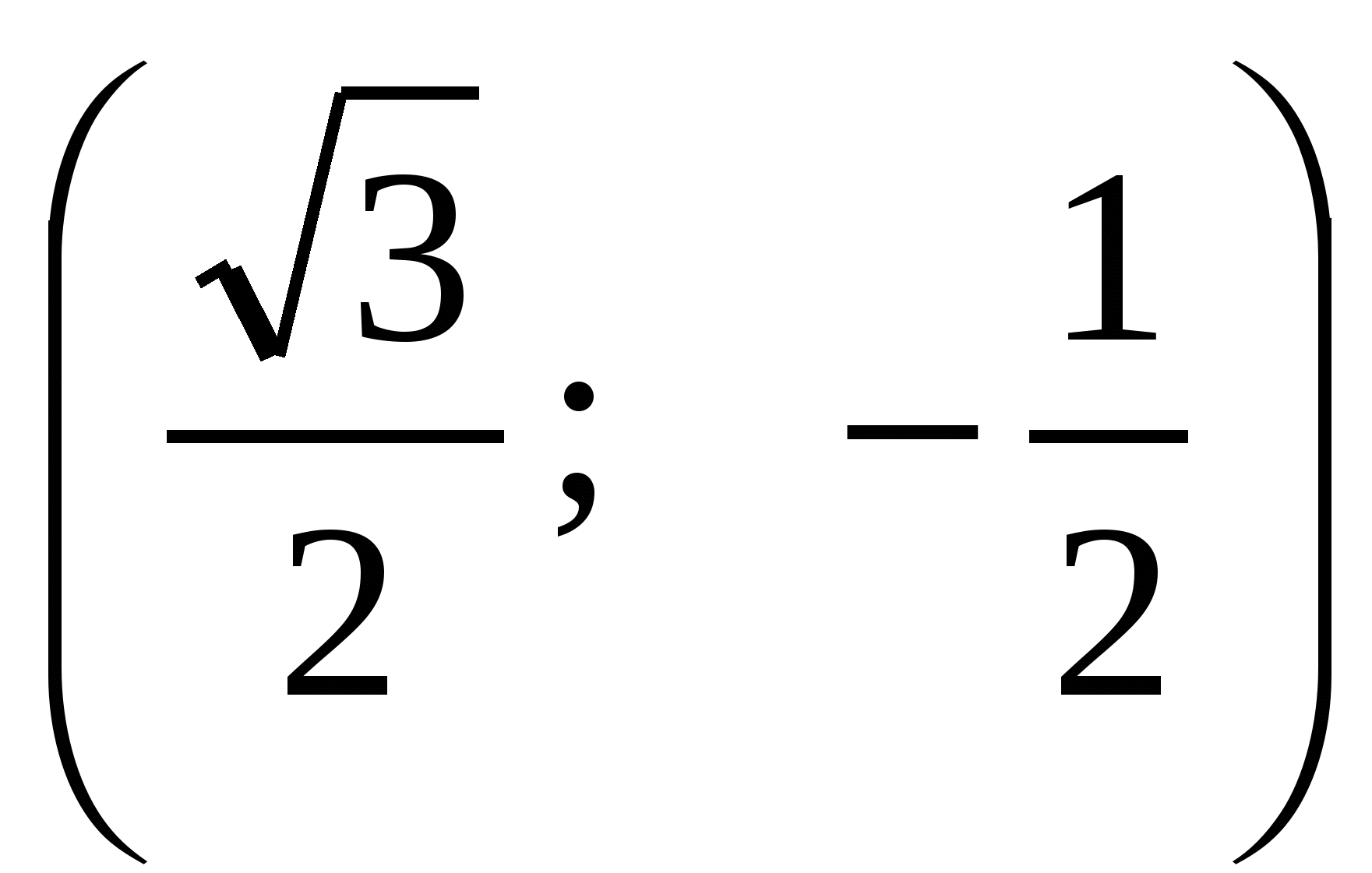 ; С
; С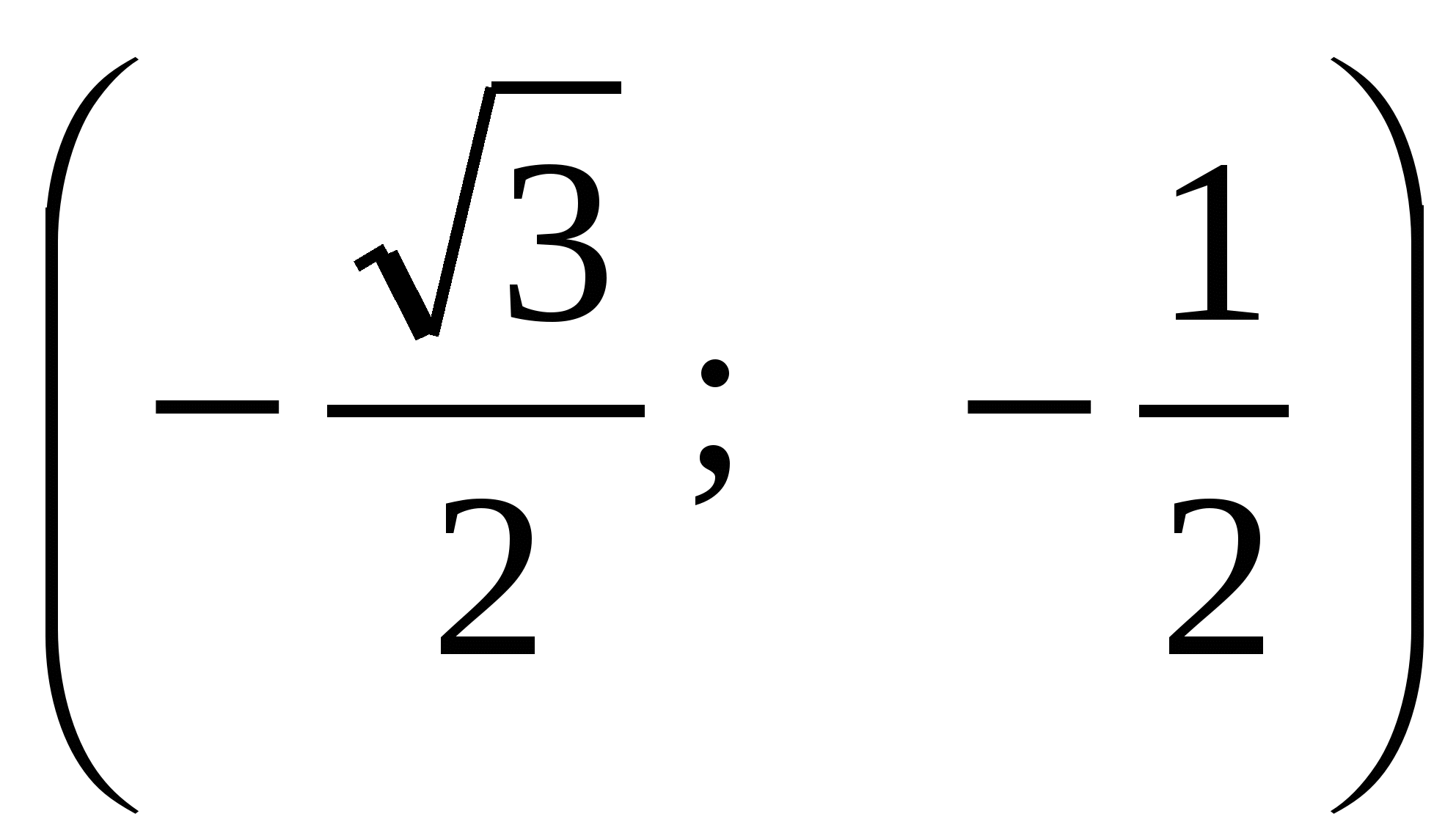 .
.
Пусть D(x; y), тогда AD2 + BD2 + CD2 =
![]()
Так как точка D(x; y) лежит на окружности, следовательно, её координаты удовлетворяют уравнению 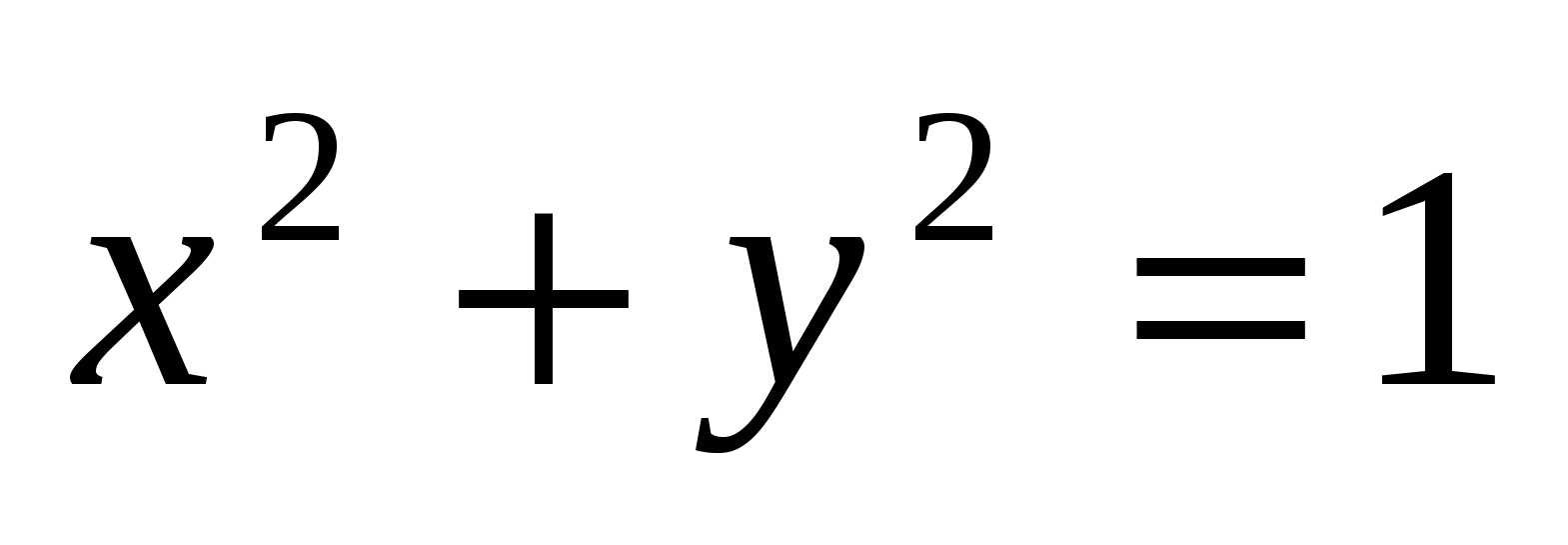 . Используя этот факт, имеем AD2+BD2+CD2 = 3(1+1) = 6.
. Используя этот факт, имеем AD2+BD2+CD2 = 3(1+1) = 6.
Векторный метод
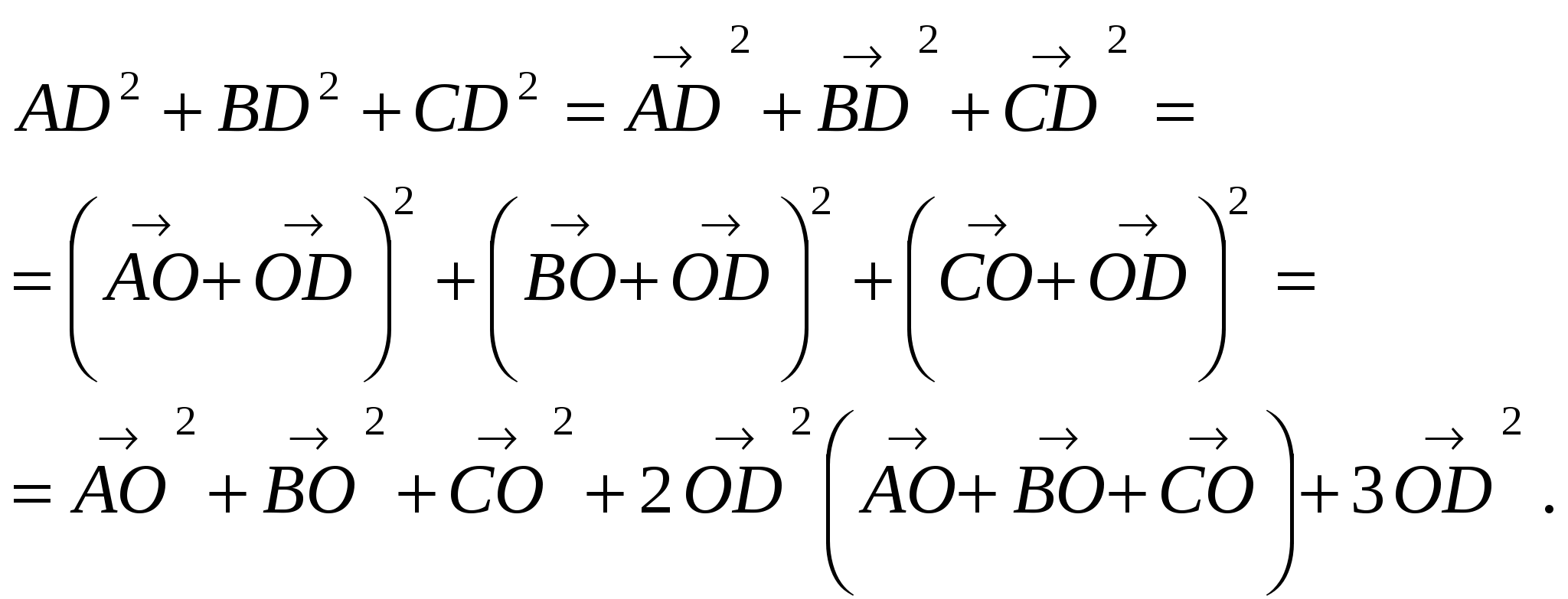
Используя, что 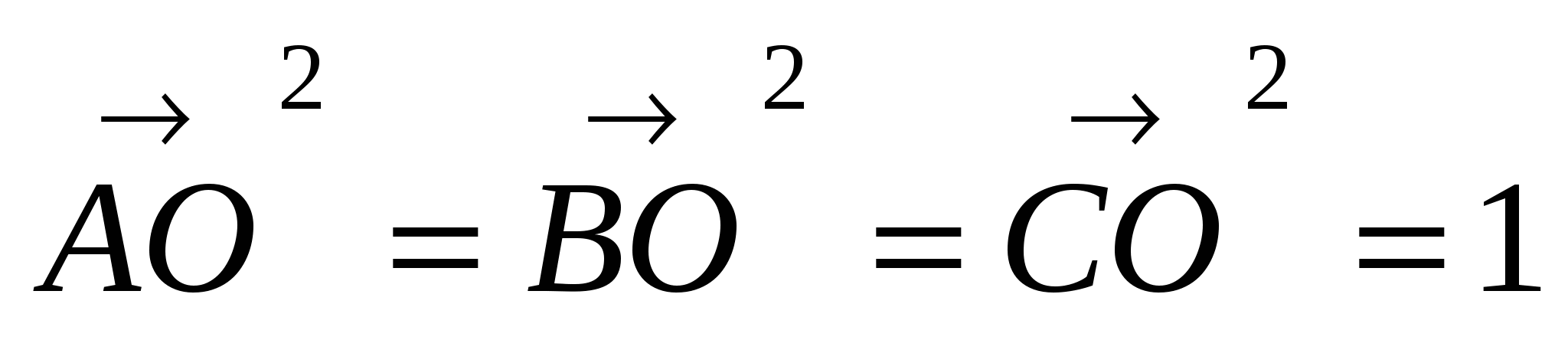 , а
, а 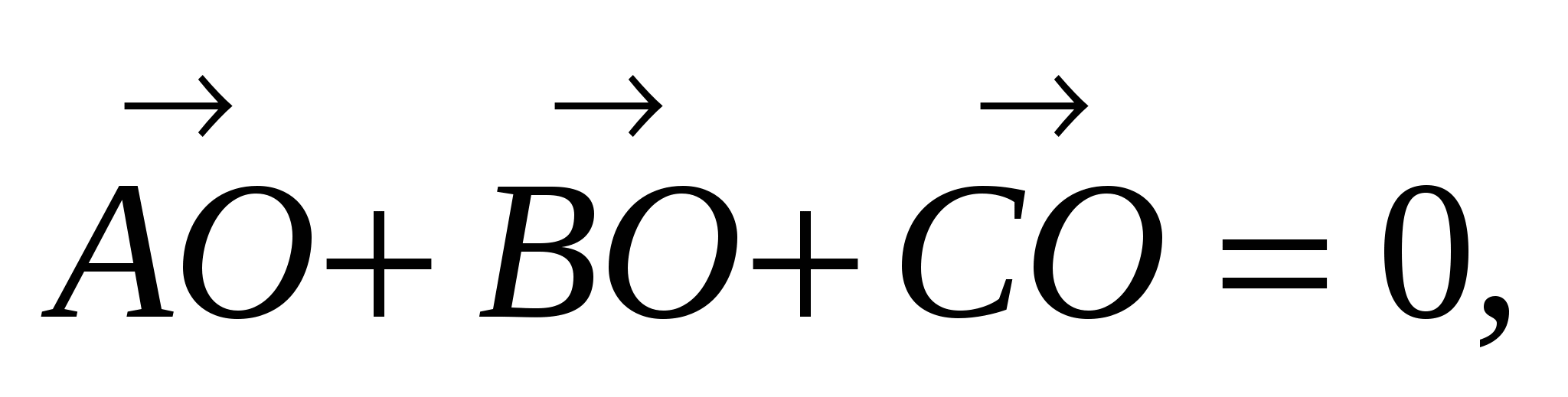
получим AD2 + BD2 + CD2 = 6.
Задача №2. В прямоугольном треугольнике с катетами 18 и 24 найти расстояние между центрами вписанной и описанной окружностей.
Координатный метод
Д ано: ∆ABC,
ано: ∆ABC, 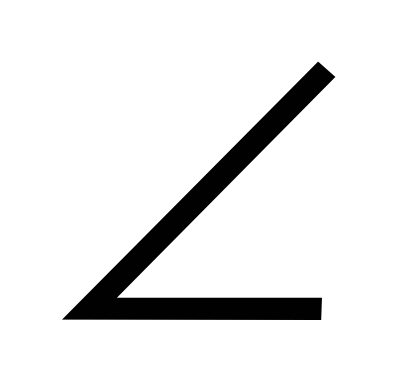 C = 90o,
C = 90o,
AC = 24,
CB = 18,
O1 - центр описанной окружности,
O2 - центр вписанной окружности.
Найти: O1O2.
Схема решения:
Введем прямоугольную систему координат с началом в точке C, тогда С (0; 0); A(0; 24);
B(18; 0).
Точка O1 - середина гипотенузы, следовательно, O1 (9; 12).
R - радиус вписанной окружности, следовательно, O2 (r; r).
Радиус вписанной окружности найдем по формуле:
![]() Имеем
Имеем 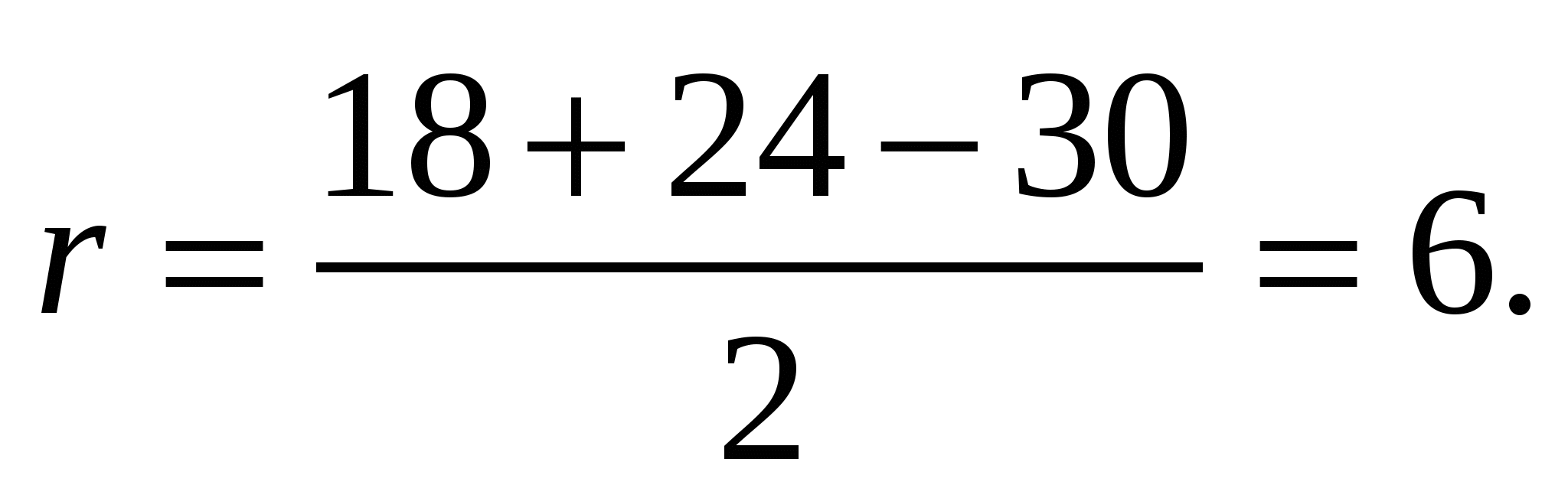
Таким образом, O2 (6; 6).
Вычислим расстояние 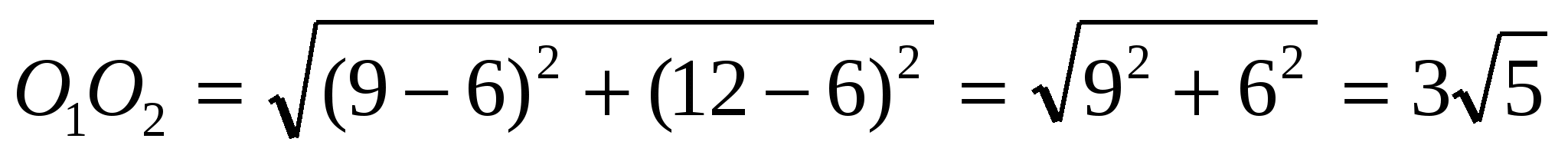 .
.
Поэтапный метод
Схема решения:
1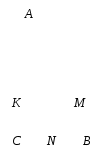 . AB = 30;
. AB = 30;
K, M, N - точки касания вписанной окружности.
2. KO2 = NO2 = MO2 = r; r = 6
(см. координатный метод).
3. NB = 18 - 6 = 12; NB = BM (отрезки касательных к окружности из одной точки).
4. O1M = O1B - BM = 15 - 12 = 3.
Так как O1 - середина AB, то O1B = 15.
5. Из ∆O1O2M O1O2=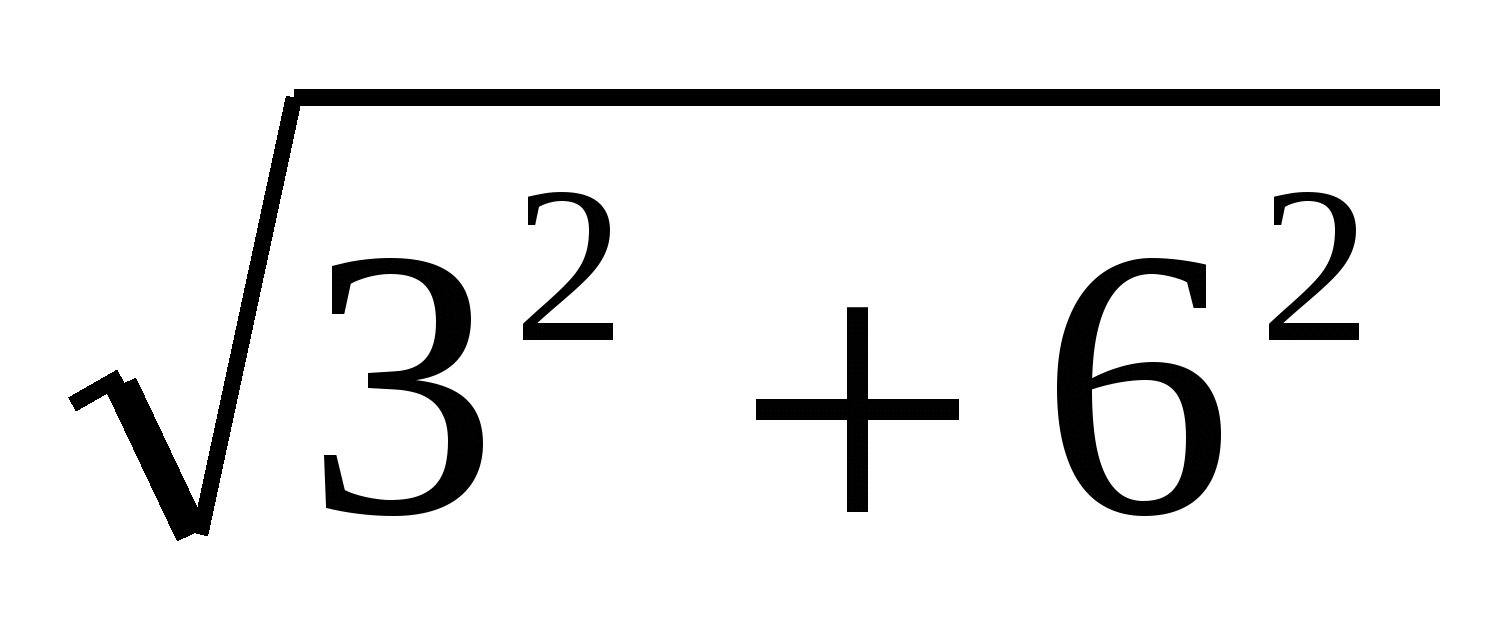 =
=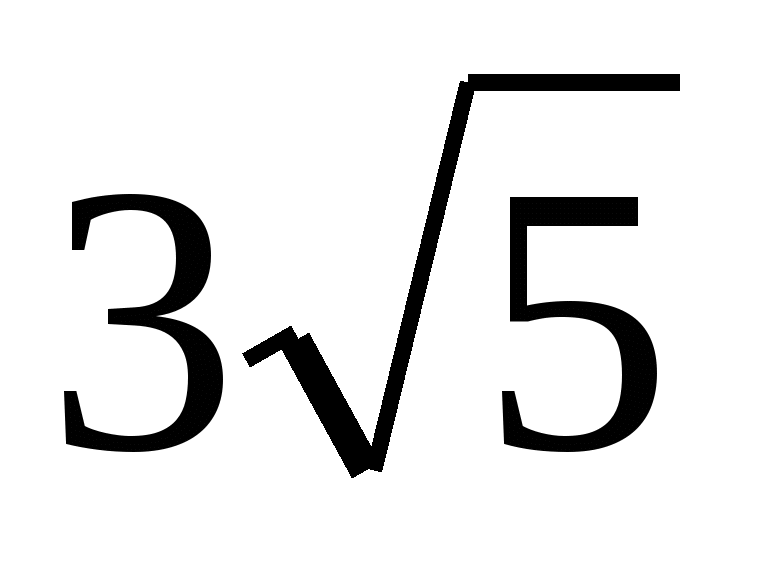 .
.
Задача №3. В параллелепипеде ABCDA1B1C1D1 все плоские углы при вершине A равны 60, AB = AA1 = AD = 1. Вычислить длины AC1 и BD1.
Векторный метод
Схема решения:
1. 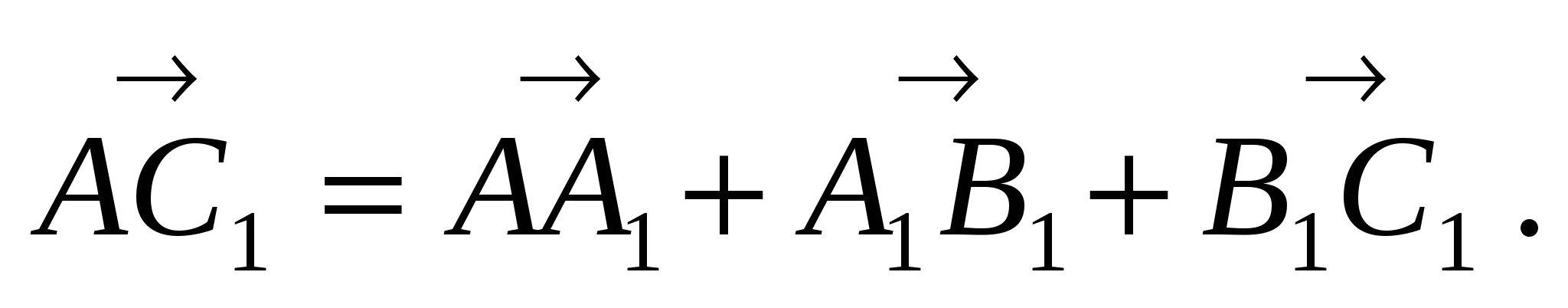
2. 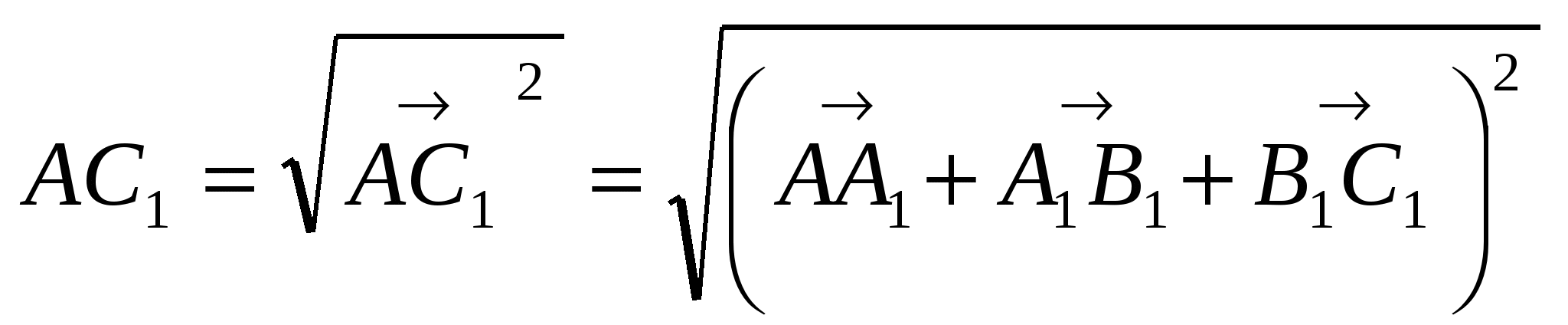 =
=
= 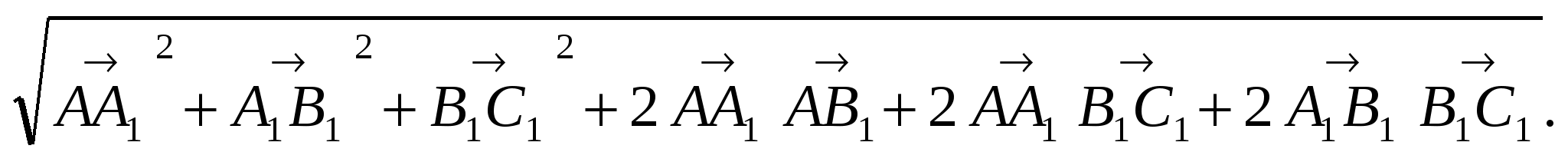
Учитывая, что 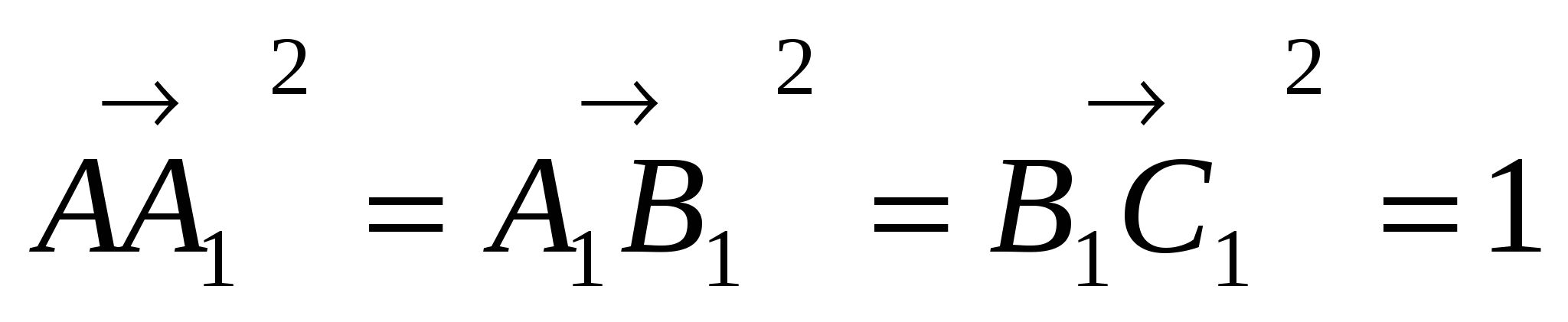 и
и
![]() = 1,
= 1,
имеем, что ![]() =
= 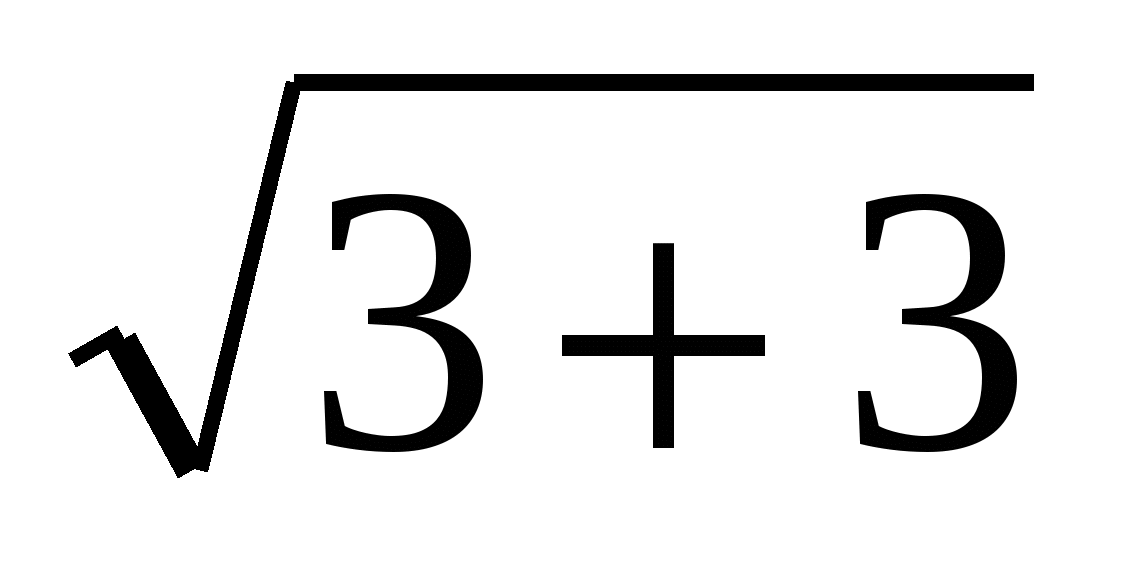 =
= 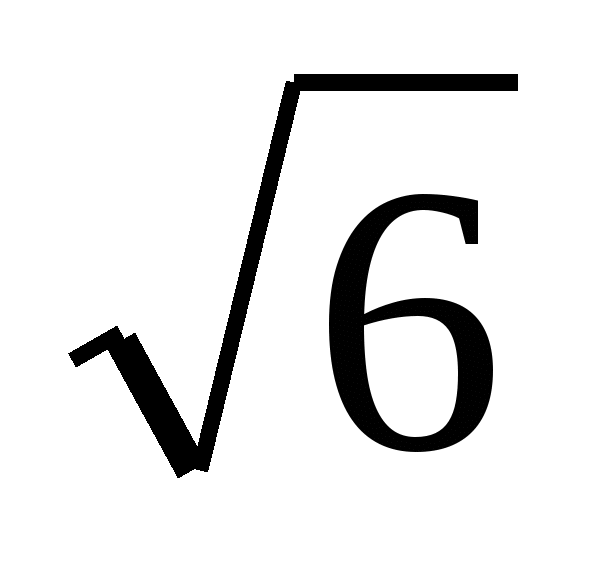 .
.
Аналогично рассуждая и используя, что
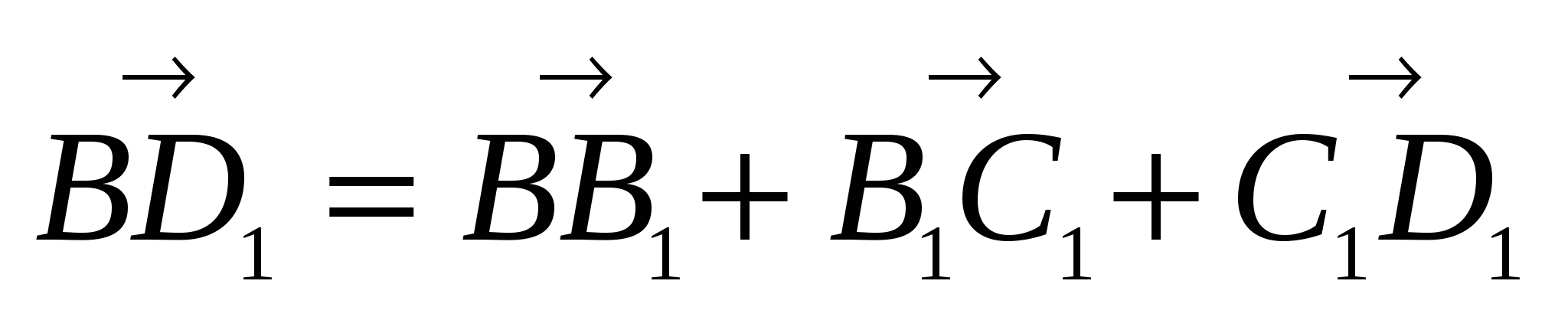 , имеем:
, имеем:
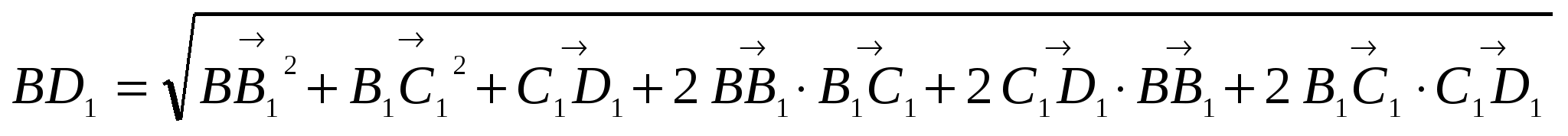 .
.
Так как углы между векторами BB1 и C1D1, B1C1 и C1D1 равны 120 , следовательно,
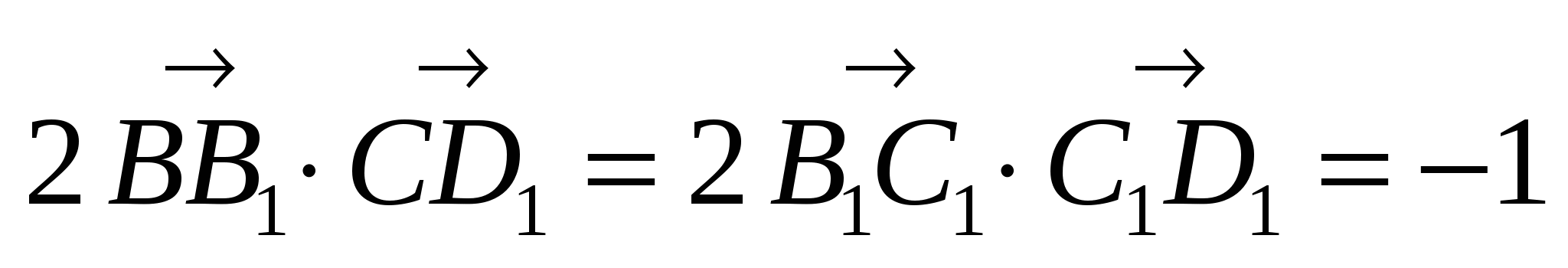 .
.
Тогда 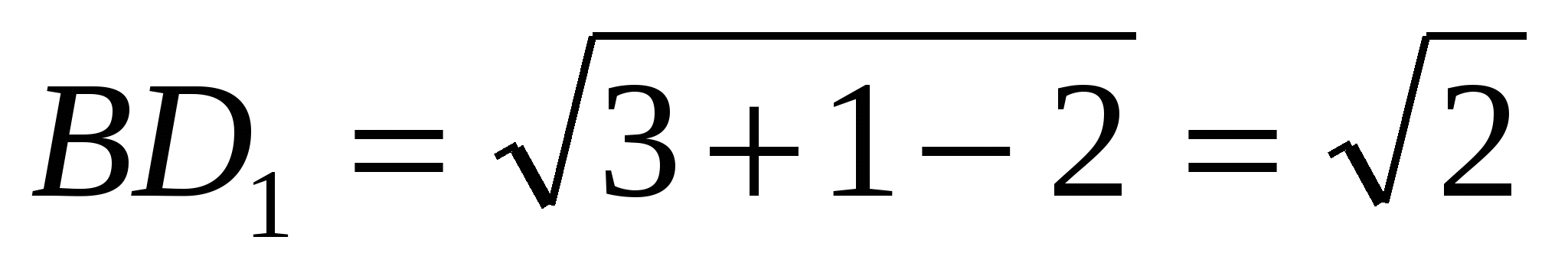 .
.
Геометрический метод
Р ассмотрим правильный тетраэдр A1ABD (доказать).
ассмотрим правильный тетраэдр A1ABD (доказать).
Проведем высоту A1H, H лежит на AC, H - центр правильного треугольника ABD, следовательно,
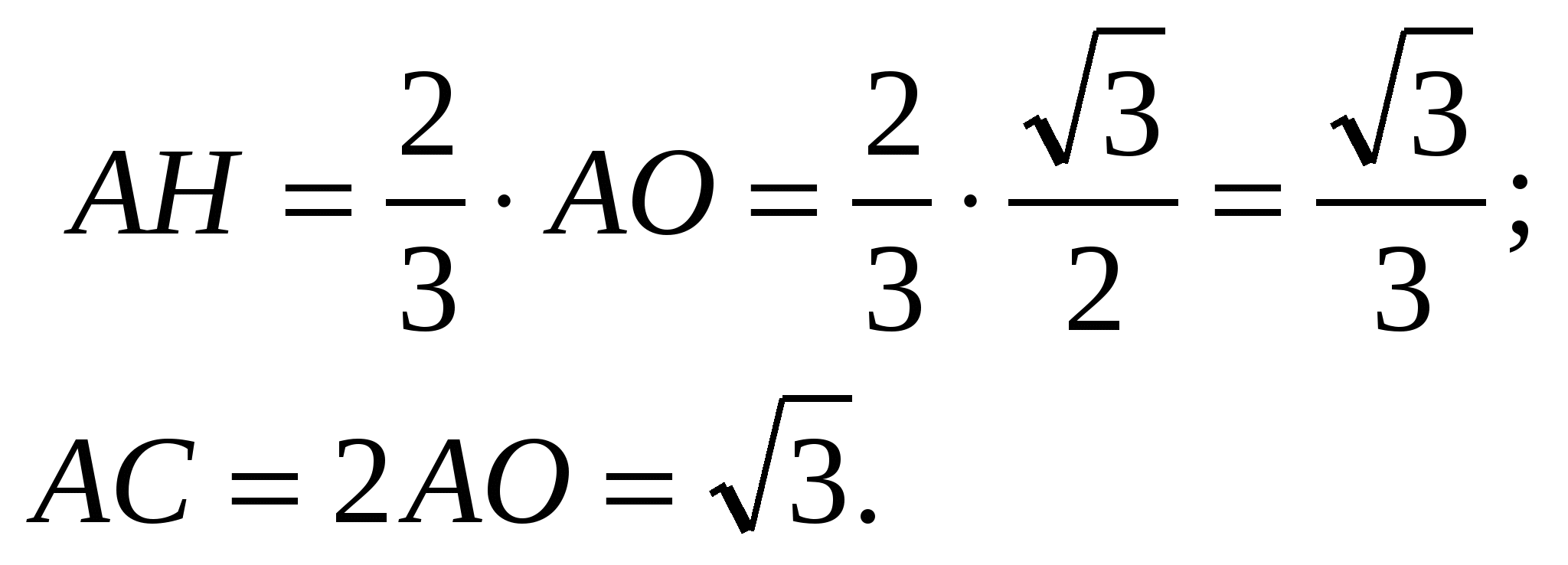
Из ∆AA1H найдем
сos A1AH = 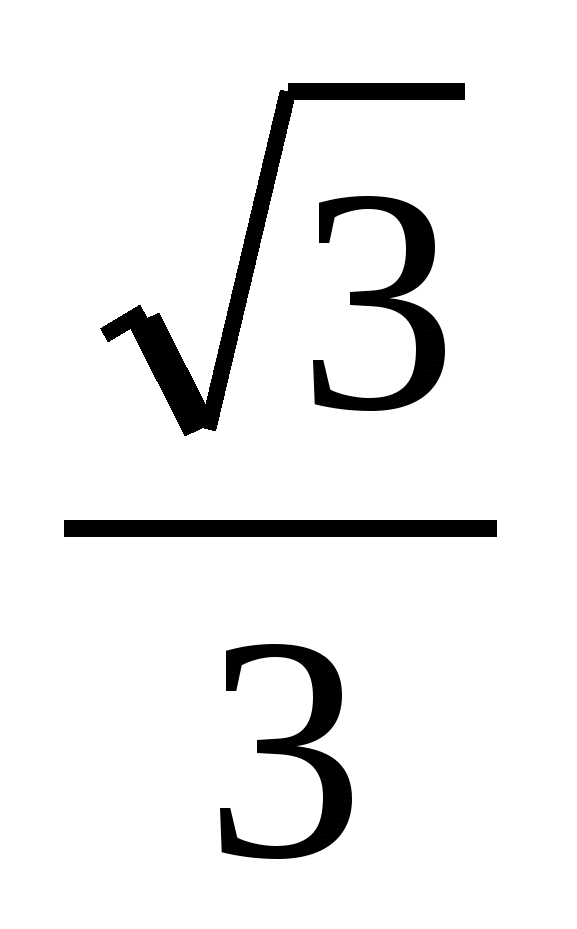 .
.
Из ∆ AC1C по теореме косинусов имеем:
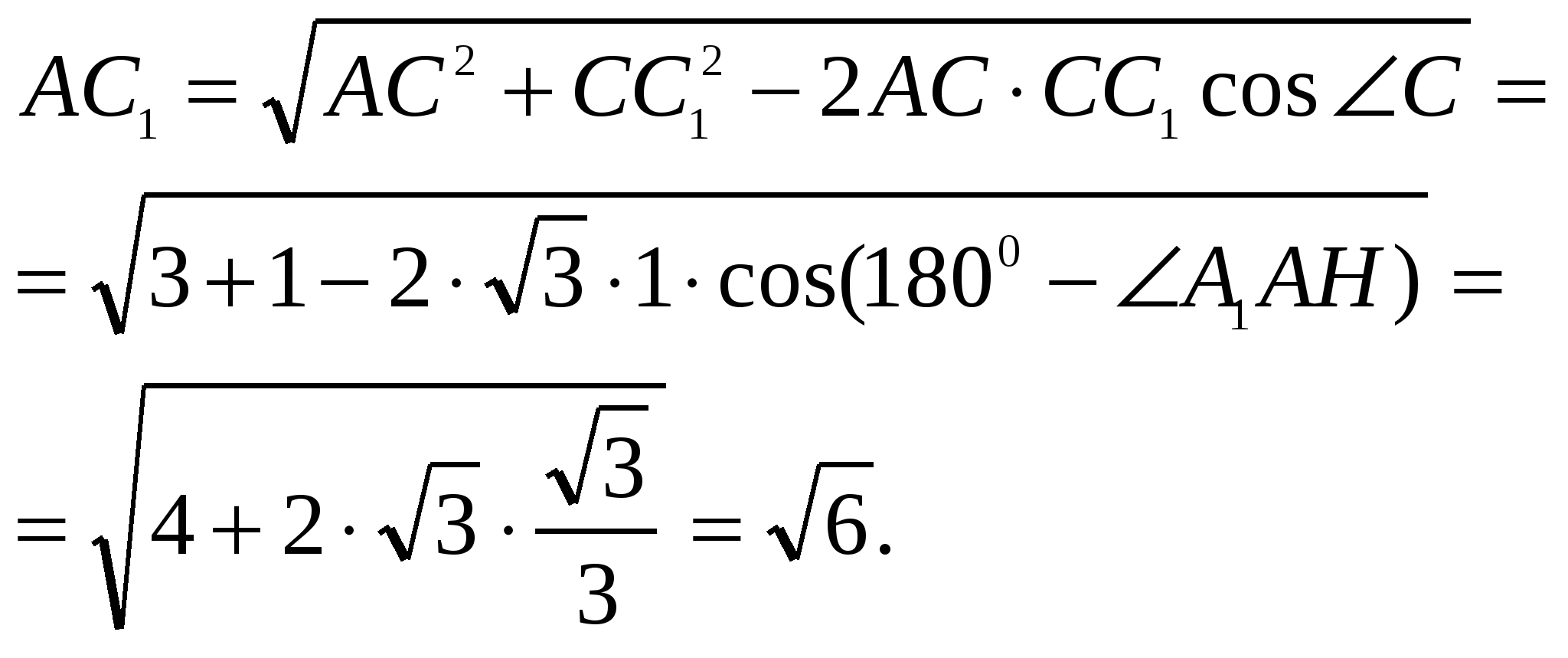
BD1 найдем как диагональ квадрата BB1D1D (доказать) со стороной BD = 1.
Следовательно, BD1 = 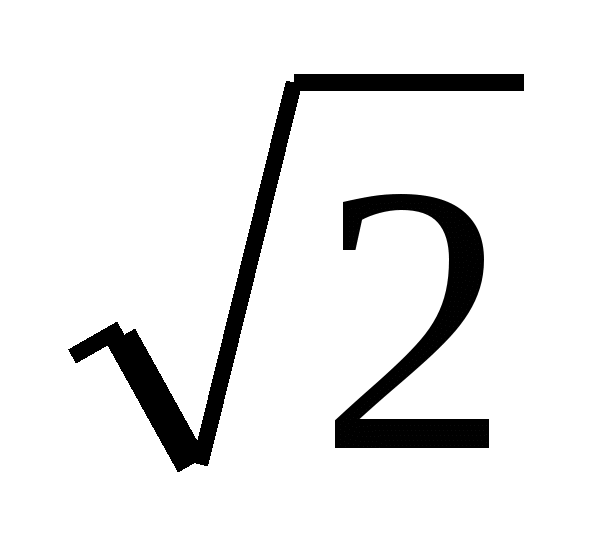 .
.
Задача №4. Дан равнобедренный прямоугольный треугольник ABC. Прямая, проведенная через вершину прямого угла C перпендикулярно медиане BD, пересекает гипотенузу в точке M. Найти отношение 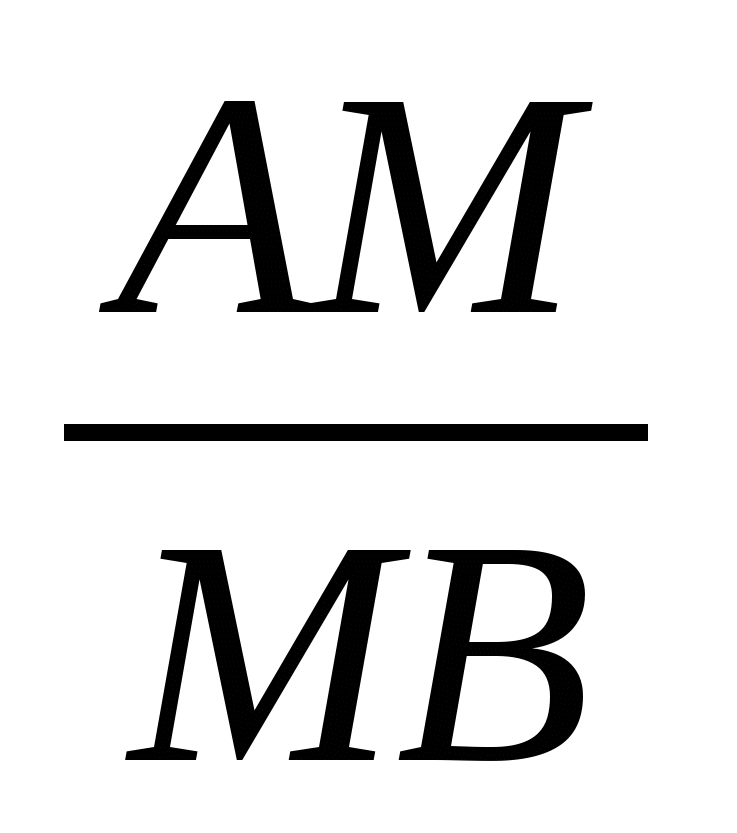 .
.
Координатный метод
В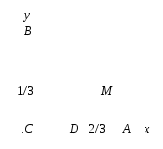 ведем прямоугольную систему координат с началом в точке C, то есть C(0; 0). Единичный отрезок равен катету AC. Тогда A(1; 0), B(0; 1), D
ведем прямоугольную систему координат с началом в точке C, то есть C(0; 0). Единичный отрезок равен катету AC. Тогда A(1; 0), B(0; 1), D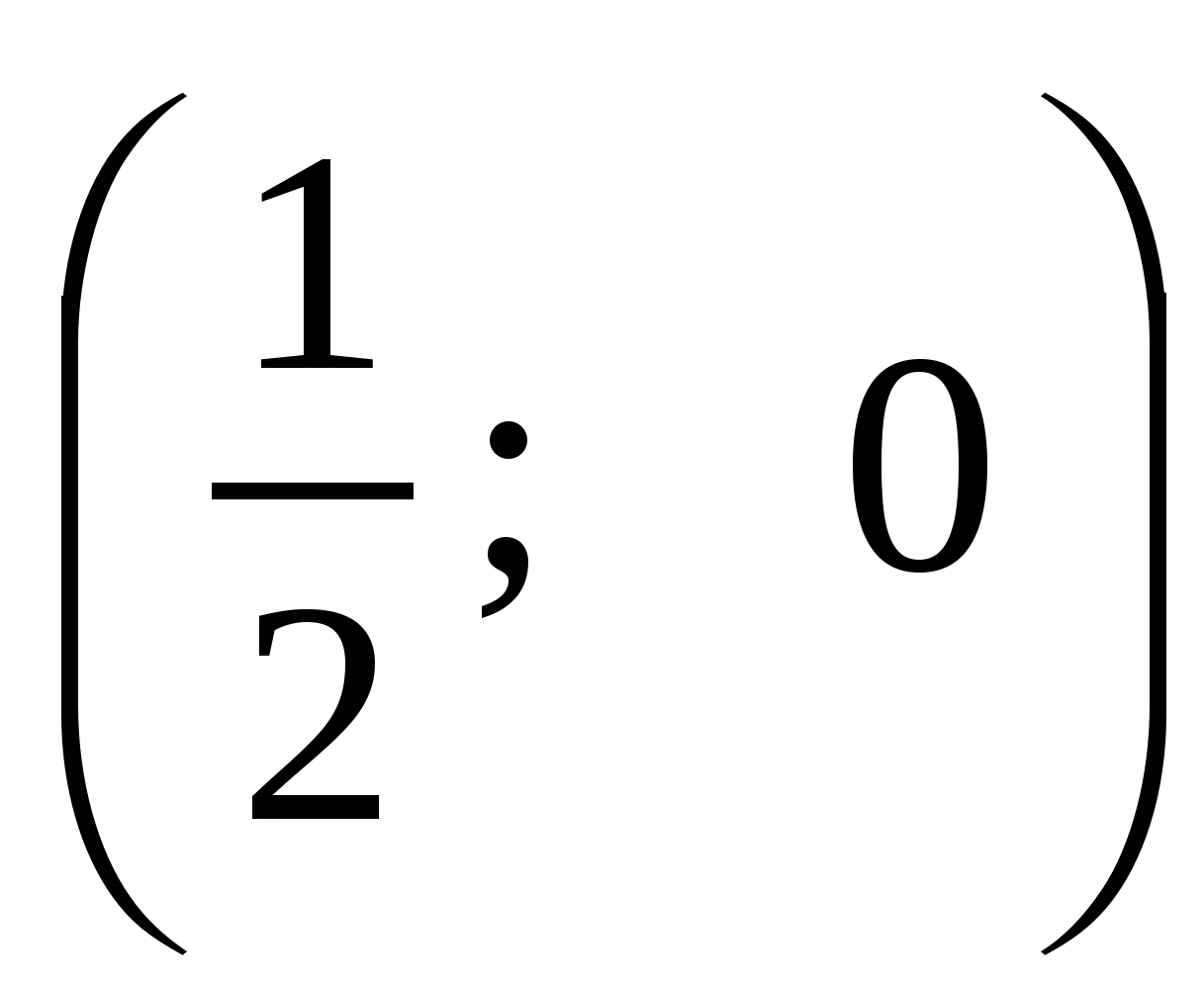 .
.
Угловой коэффициент прямой BD равен -2.
Угловой коэффициент прямой СМ, перпендикулярной прямой BD, равен 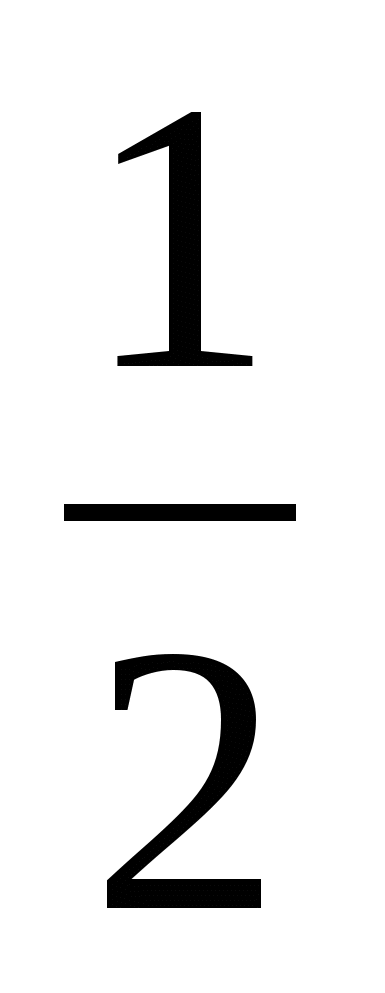 .
.
Запишем уравнения прямых CM и AB.
CM: y = 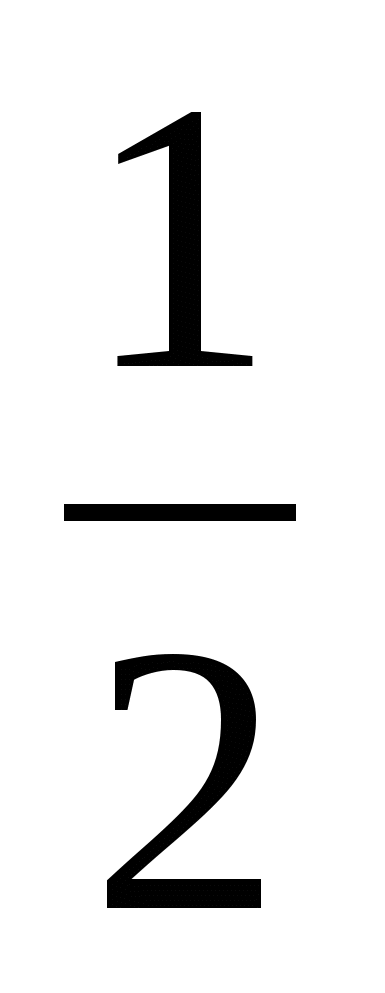 x; AB: y = -x + 1.
x; AB: y = -x + 1.
Найдем координаты точки M:
![]() x = -x + 1,
x = -x + 1, 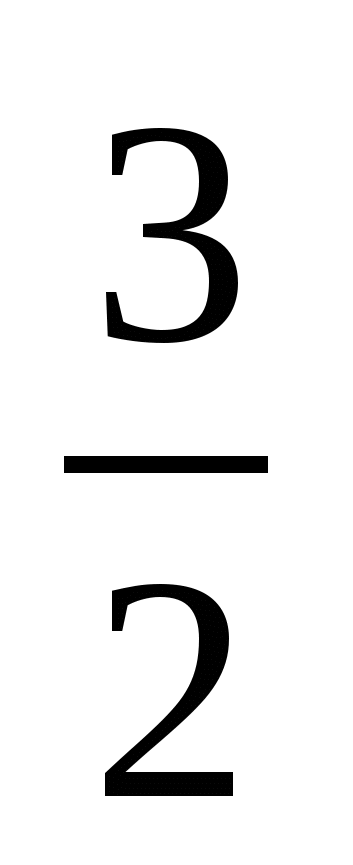 x = 1, x =
x = 1, x = 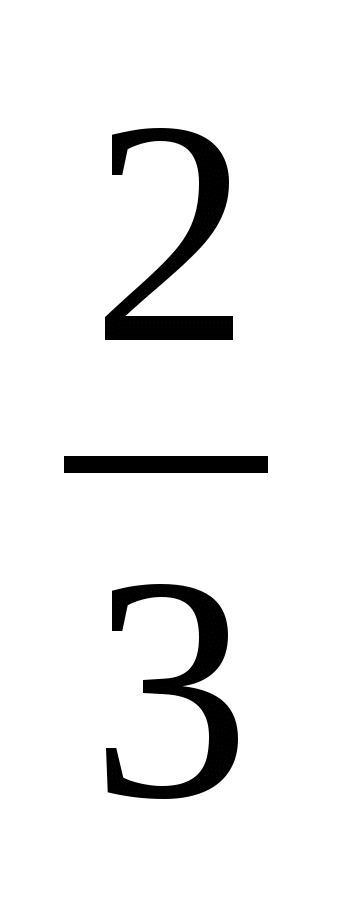 ; y =
; y = 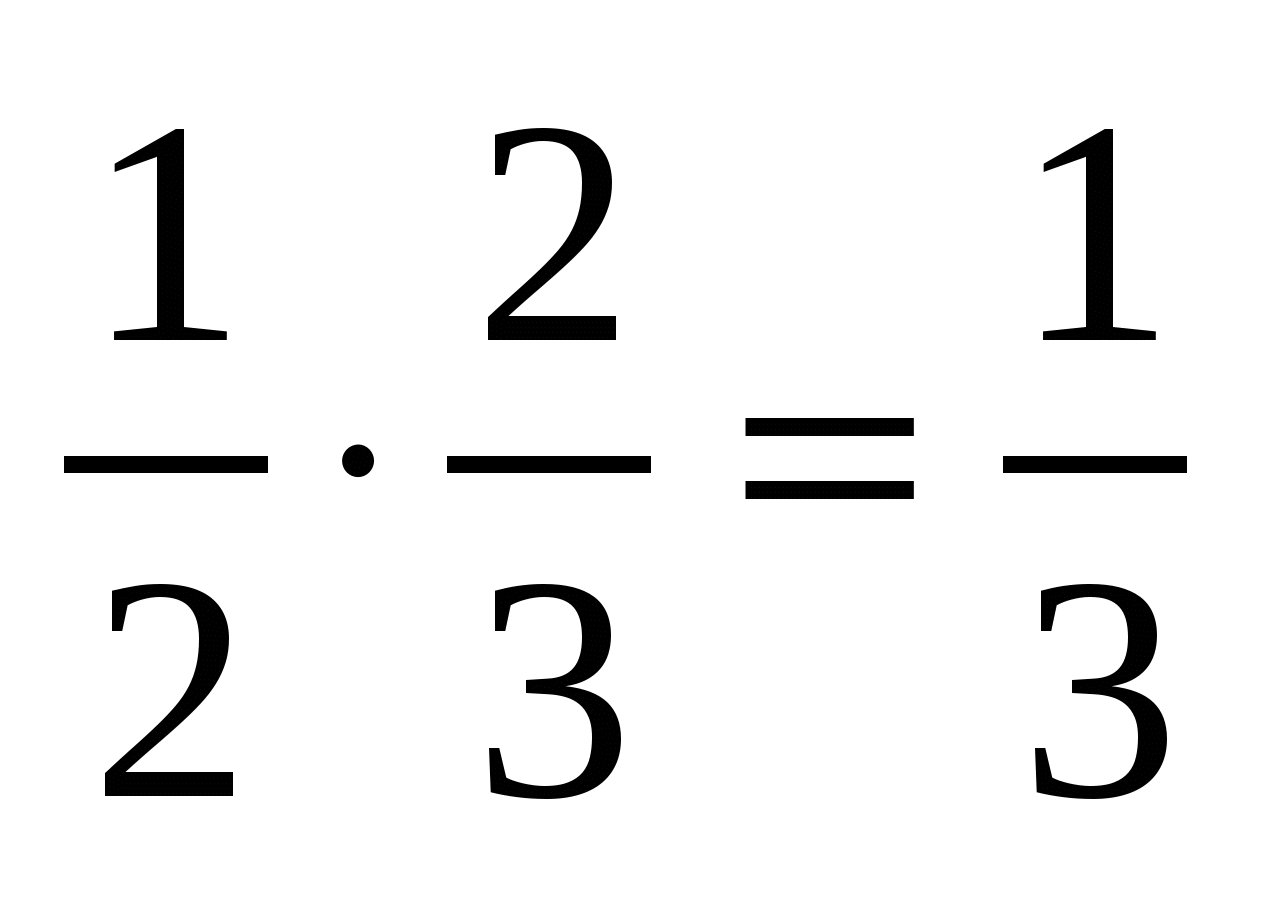 .
.
Следовательно, M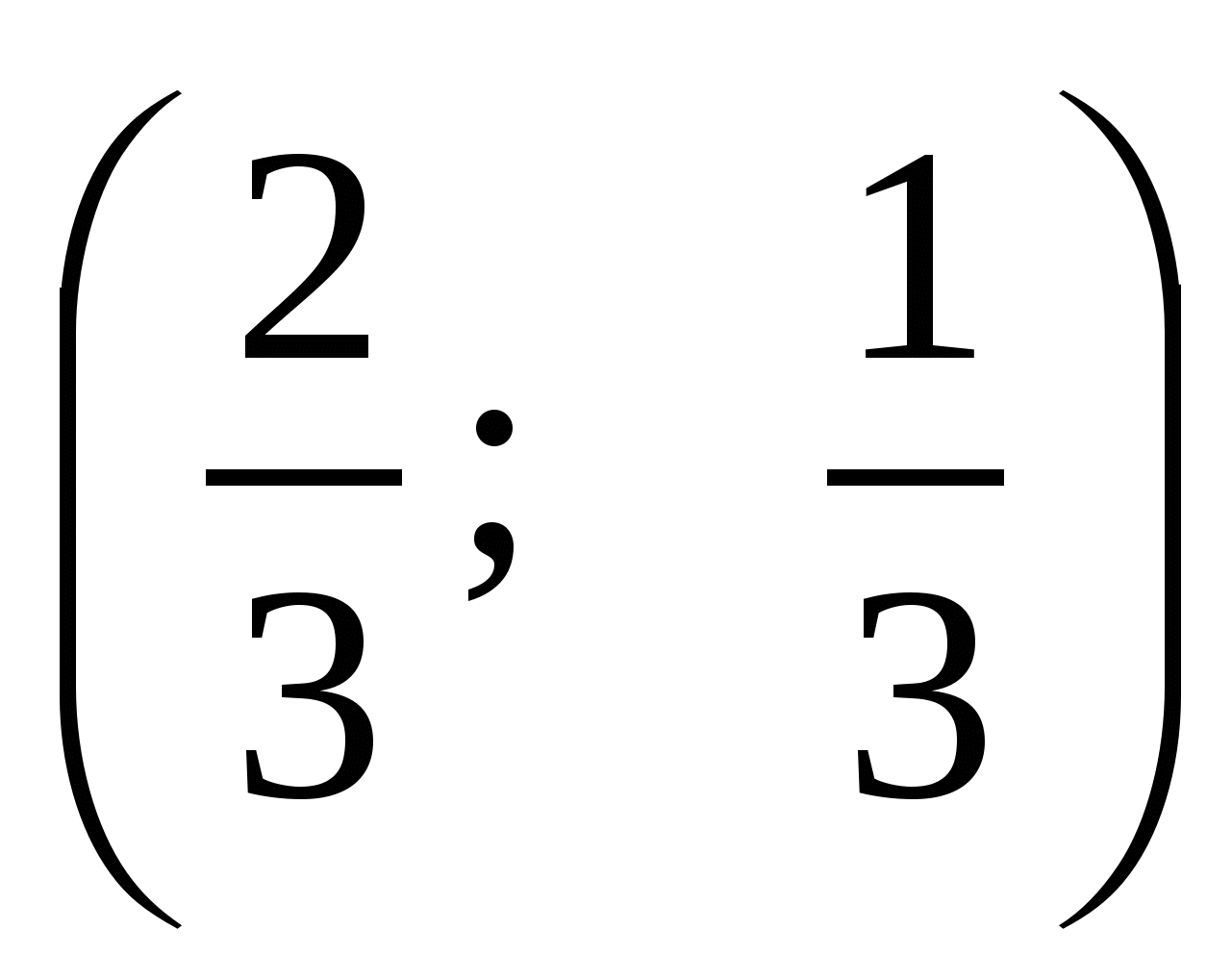 . Если N
. Если N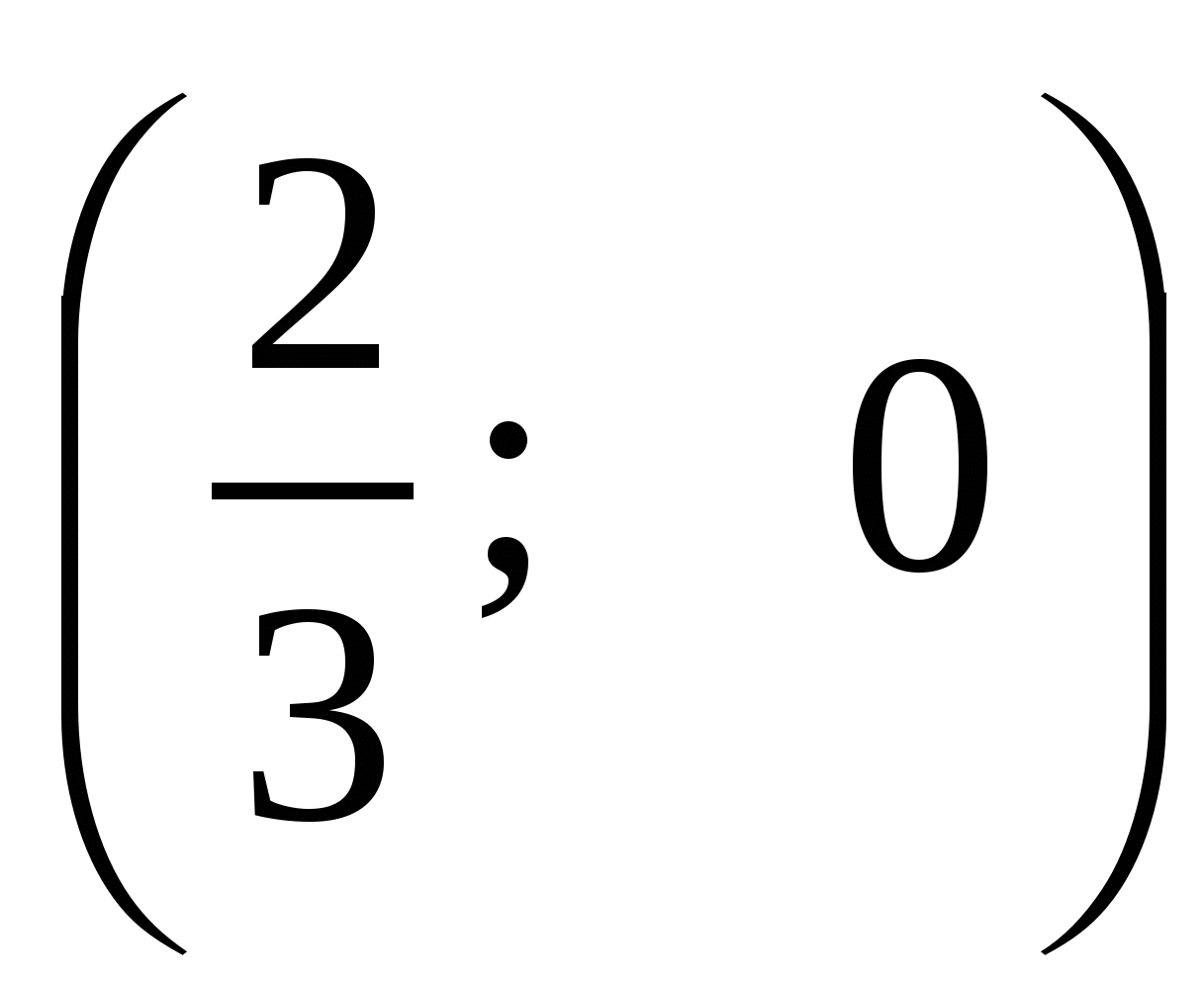 - проекция точки M на прямую AC; то
- проекция точки M на прямую AC; то 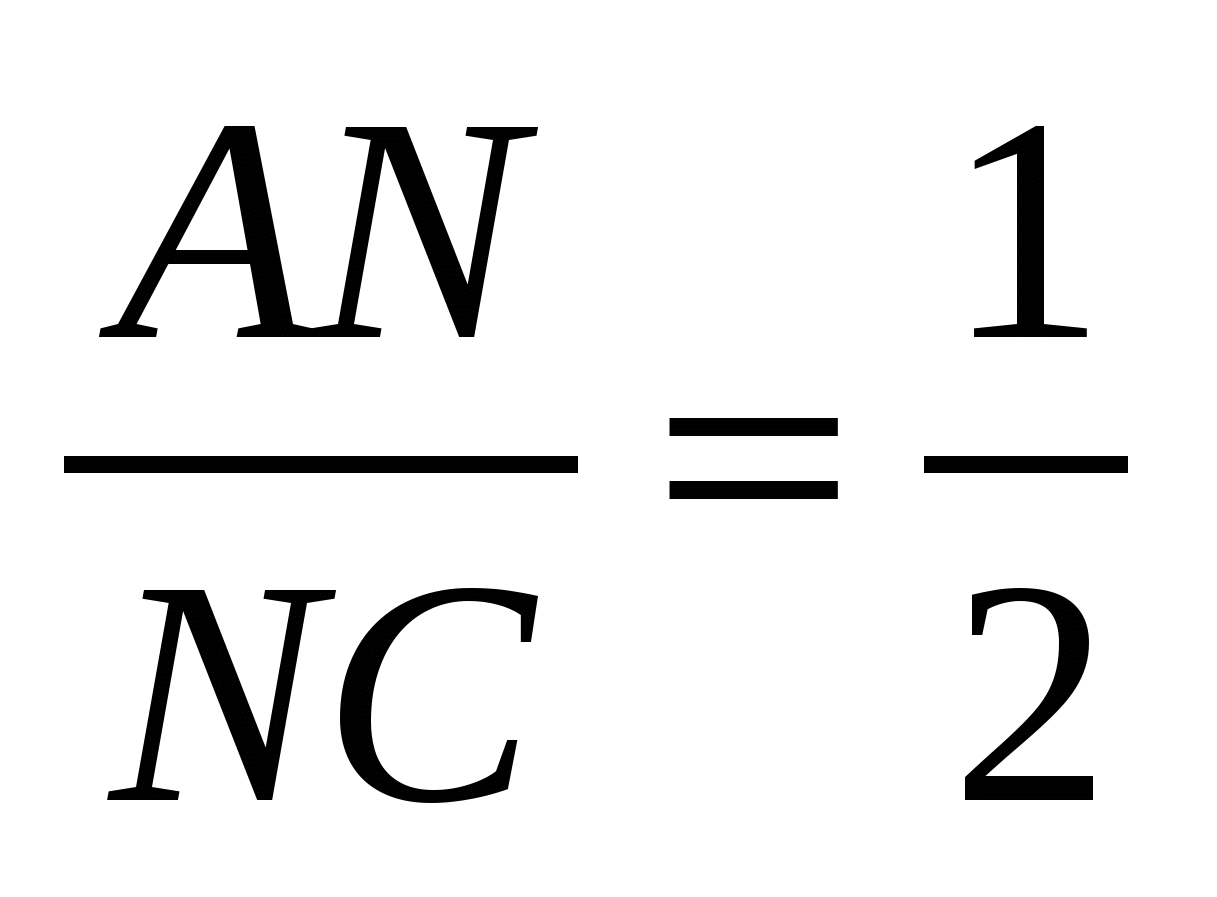 . Используя обобщенную теорему Фалеса, получаем:
. Используя обобщенную теорему Фалеса, получаем: 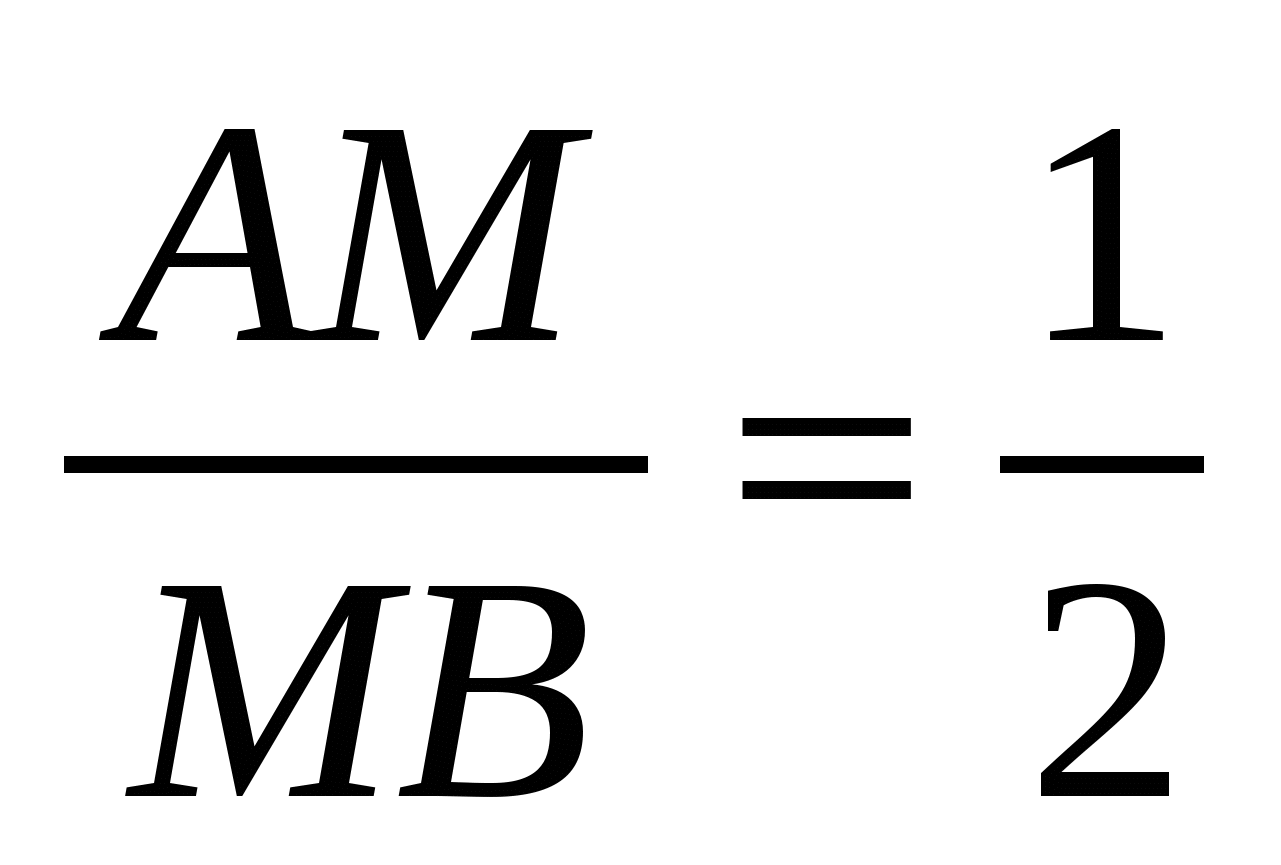 .
.
Векторный метод
Обозначим 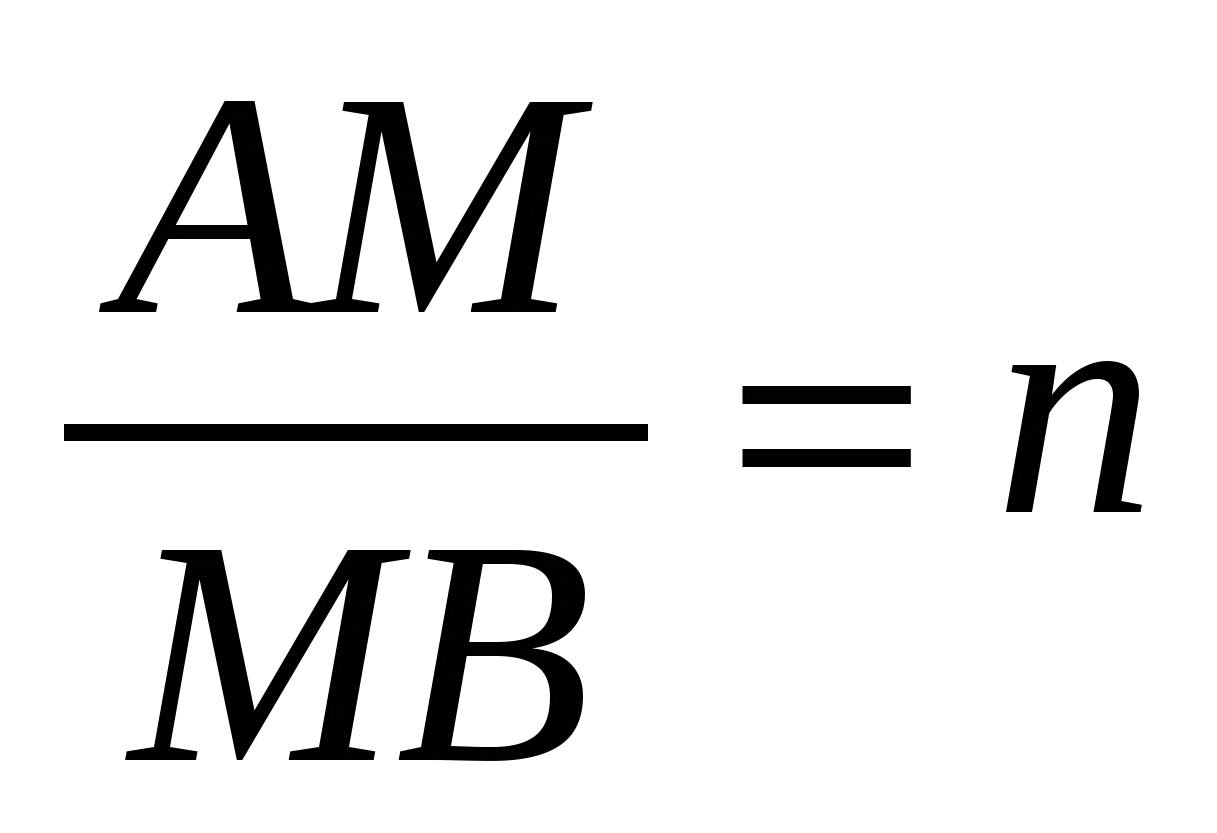 ,
, 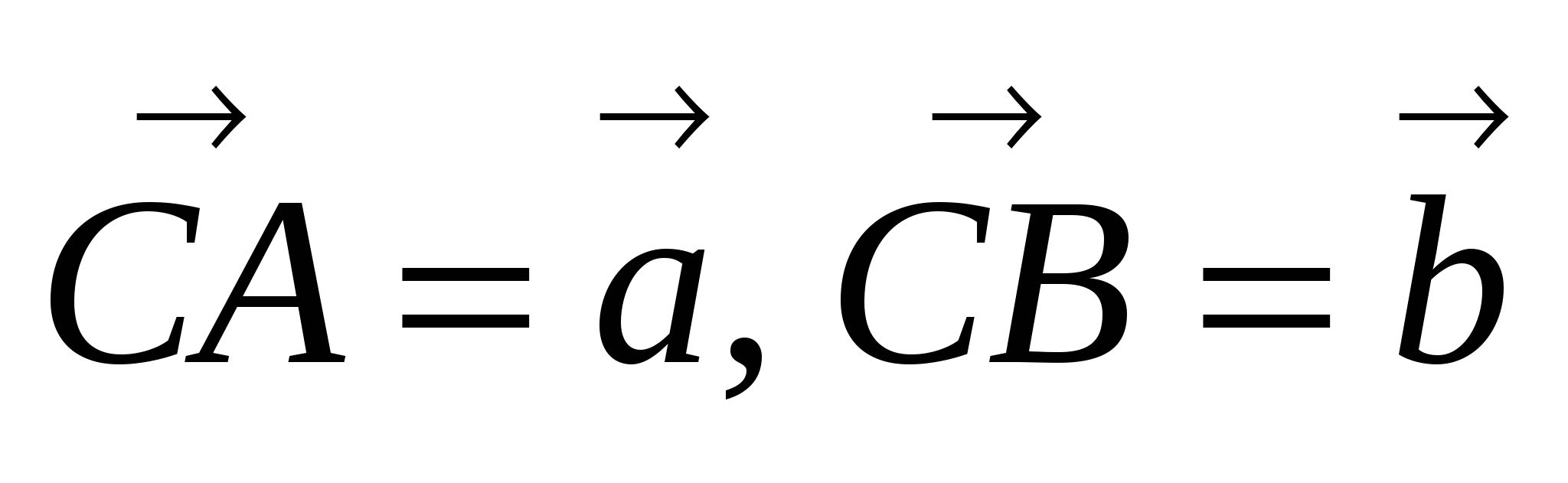 - единичные векторы.
- единичные векторы.
По формуле деления отрезка в данном отношении выразим вектор ![]() через
через 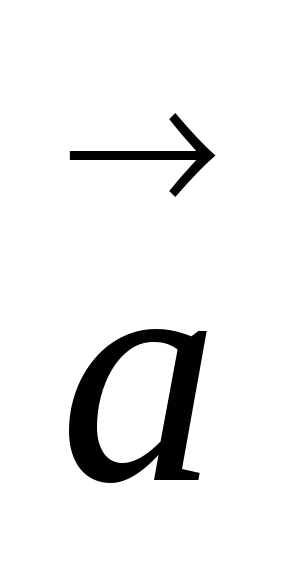 и
и 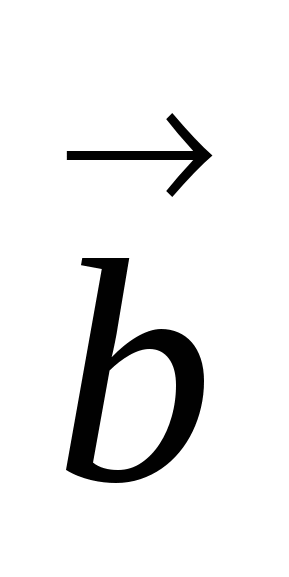 .Получим
.Получим 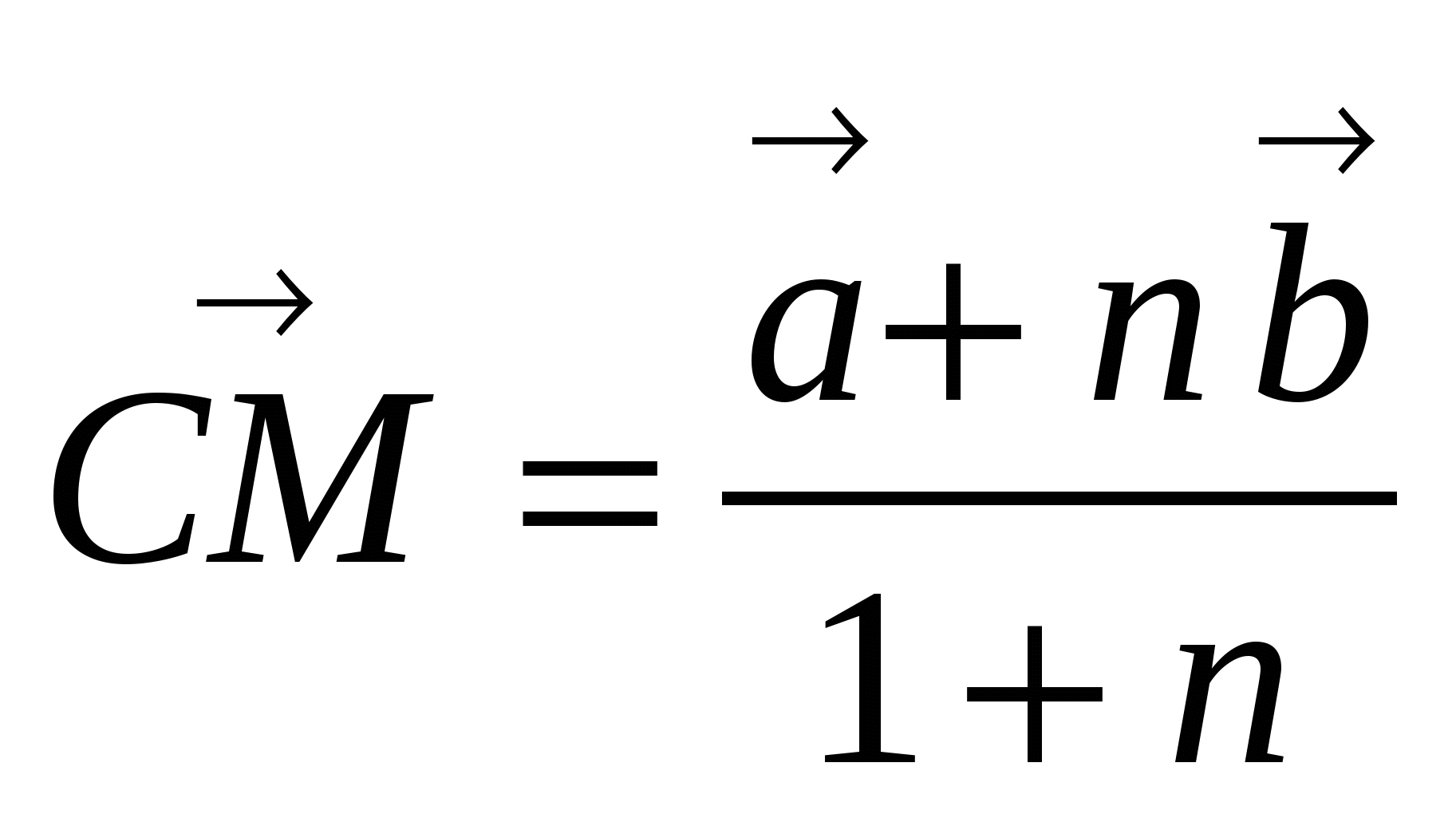 .
.
Согласно правилу вычитания векторов, имеем 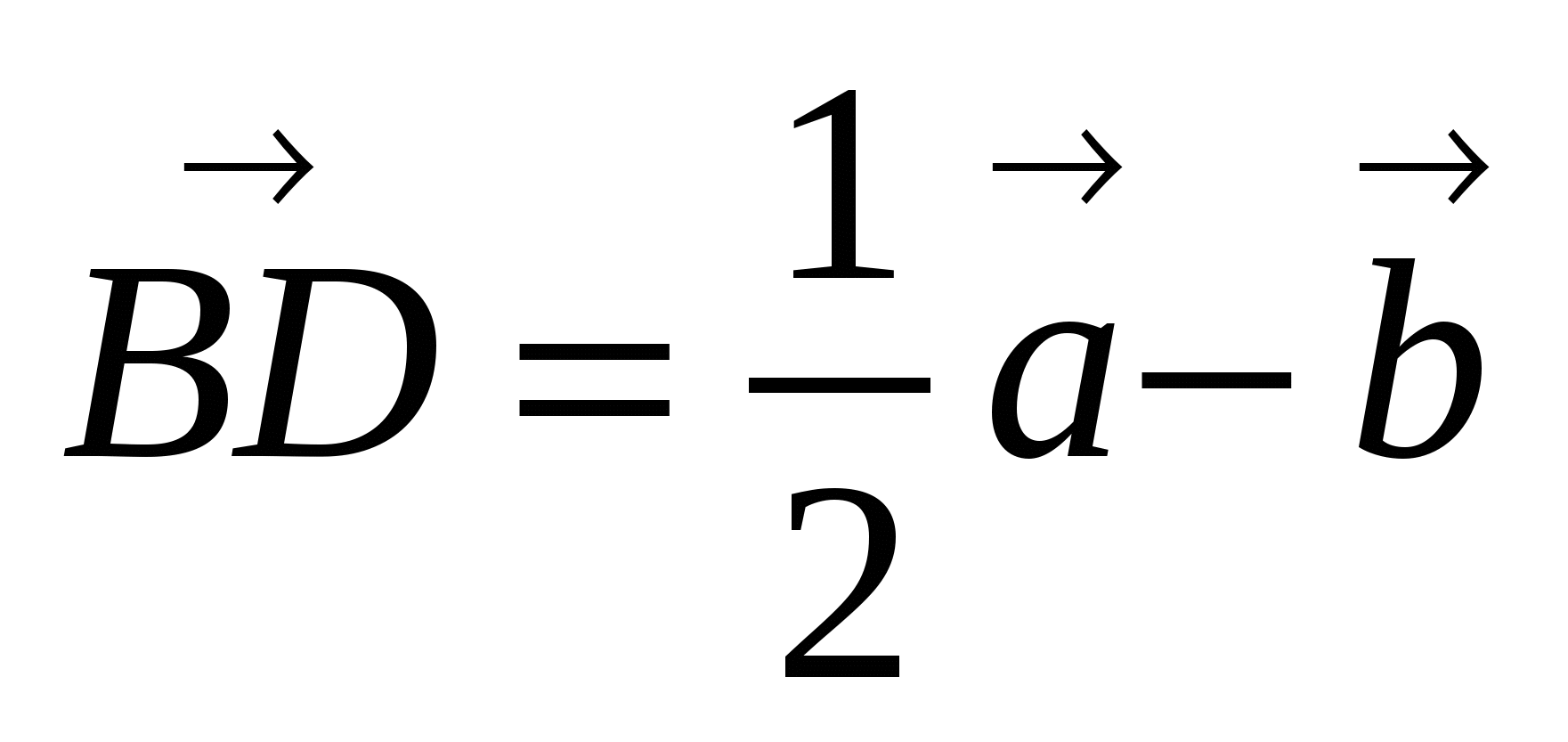 .
.
Так как 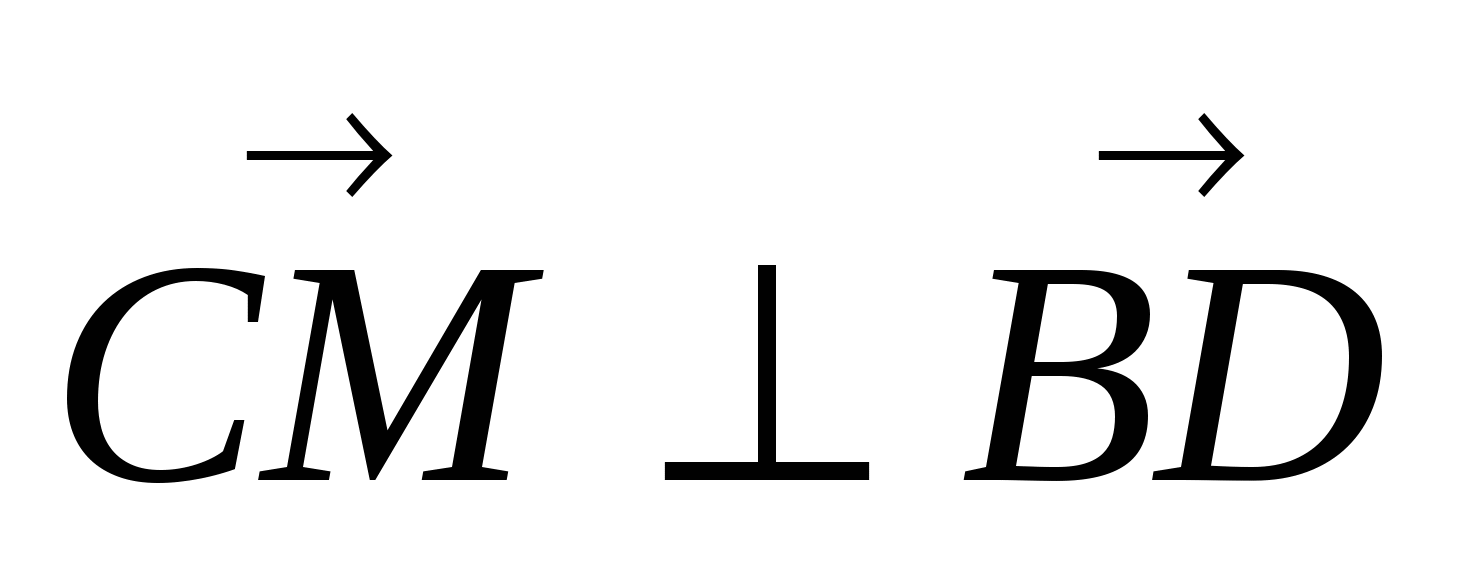 , следовательно,
, следовательно, ![]() или
или
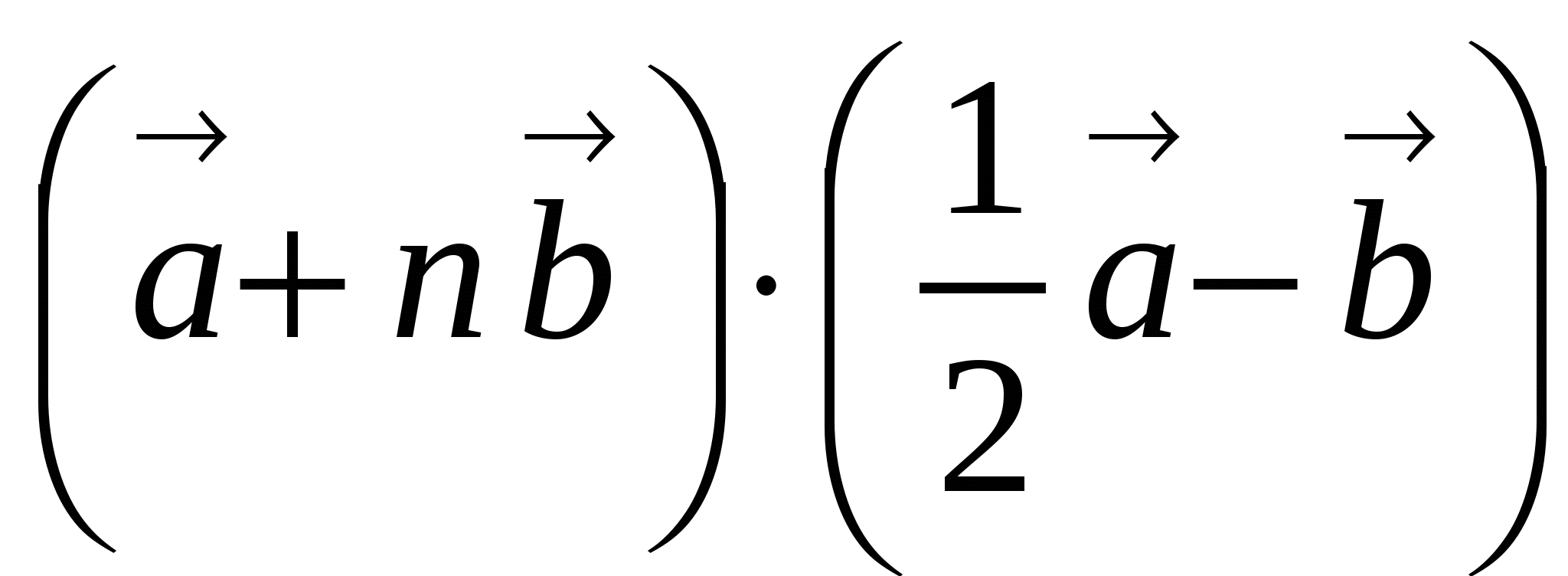 = 0.
= 0.
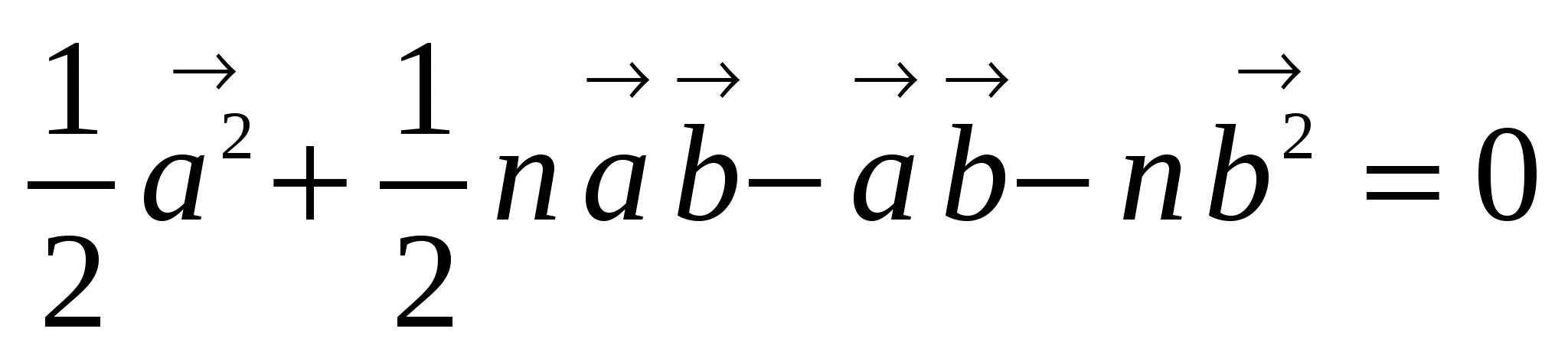 , учитывая, что
, учитывая, что 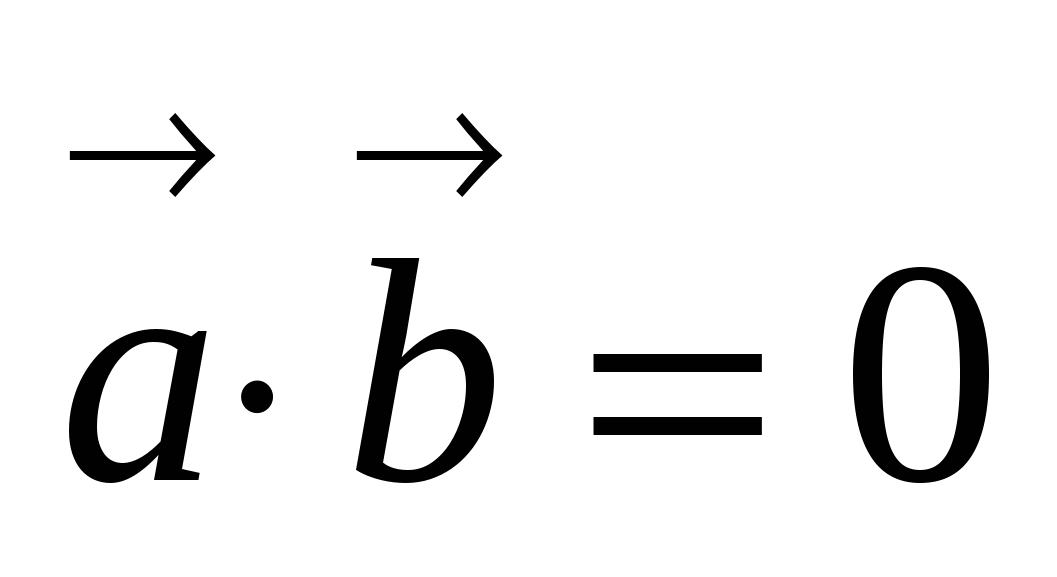 и
и 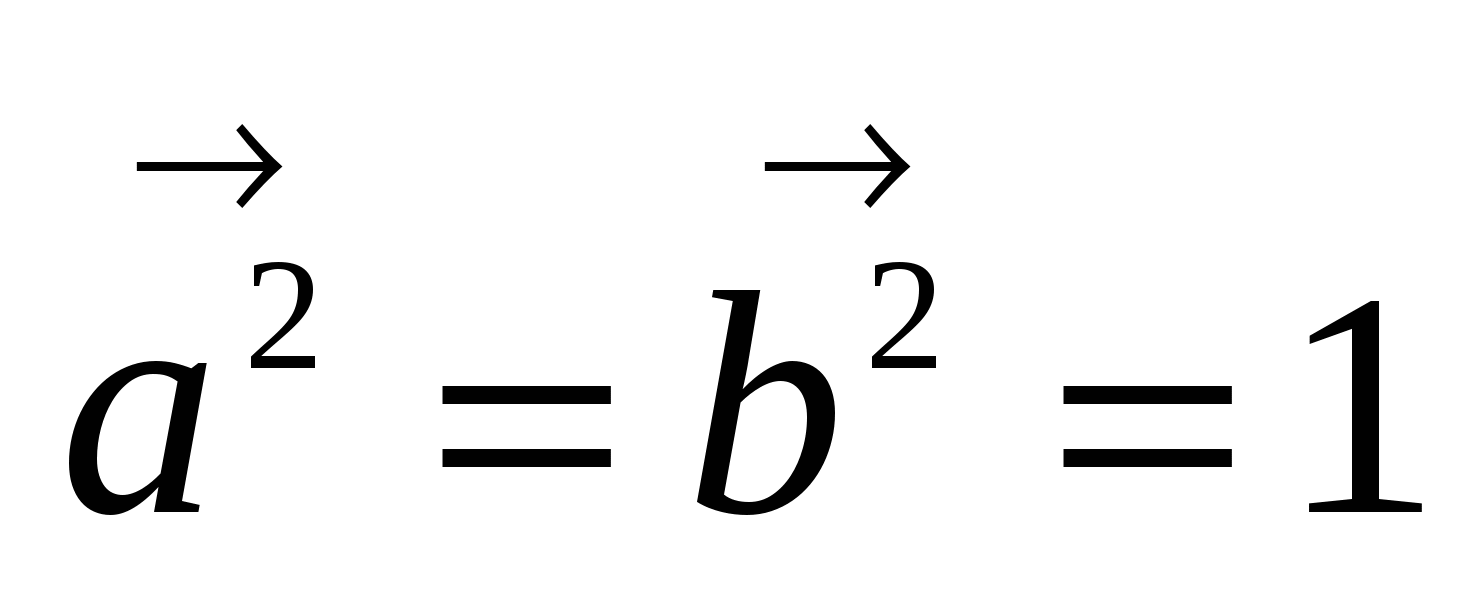 , получаем, что
, получаем, что
n = 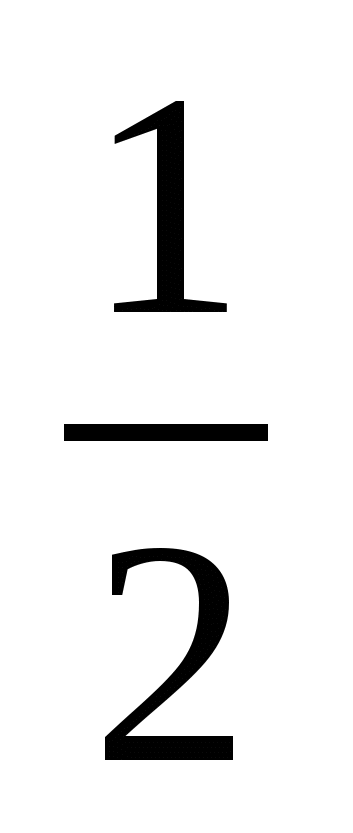 .
.
Метод геометрических
преобразований
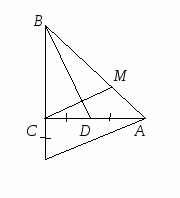 Рассмотрим поворот вокруг точки C на 90, при котором точка B переходит в точку A. Точка D перейдет в точку D1, лежащую на продолжении стороны BC, а треугольник BCD в треугольник ACD1. По свойству поворота
Рассмотрим поворот вокруг точки C на 90, при котором точка B переходит в точку A. Точка D перейдет в точку D1, лежащую на продолжении стороны BC, а треугольник BCD в треугольник ACD1. По свойству поворота 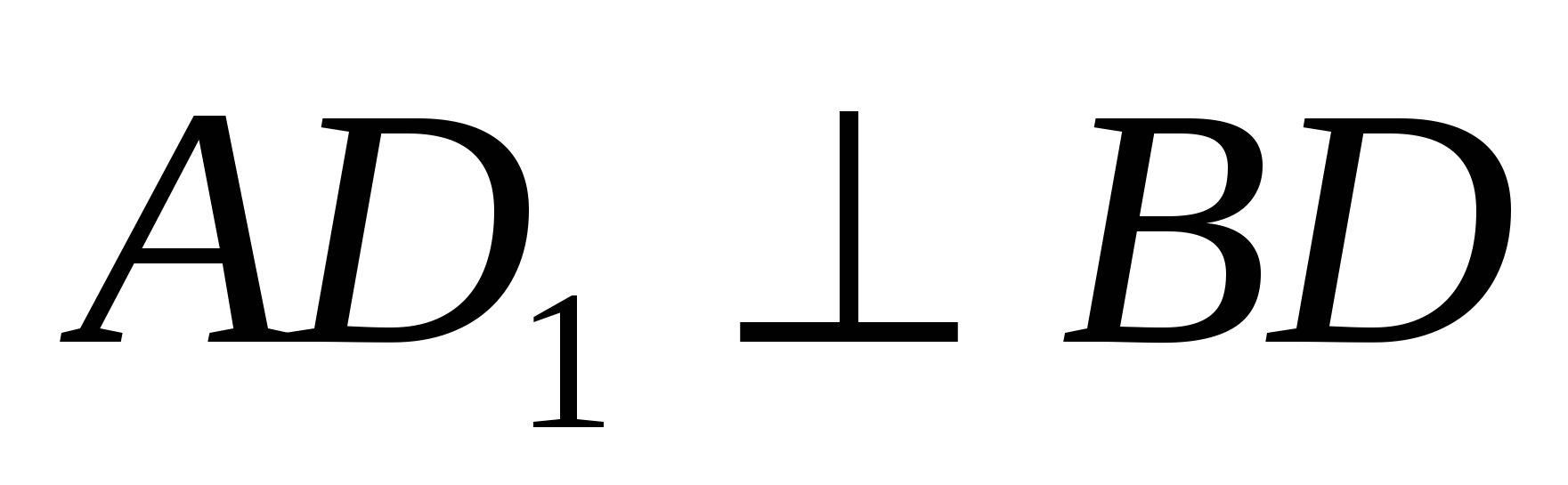 , а так как
, а так как 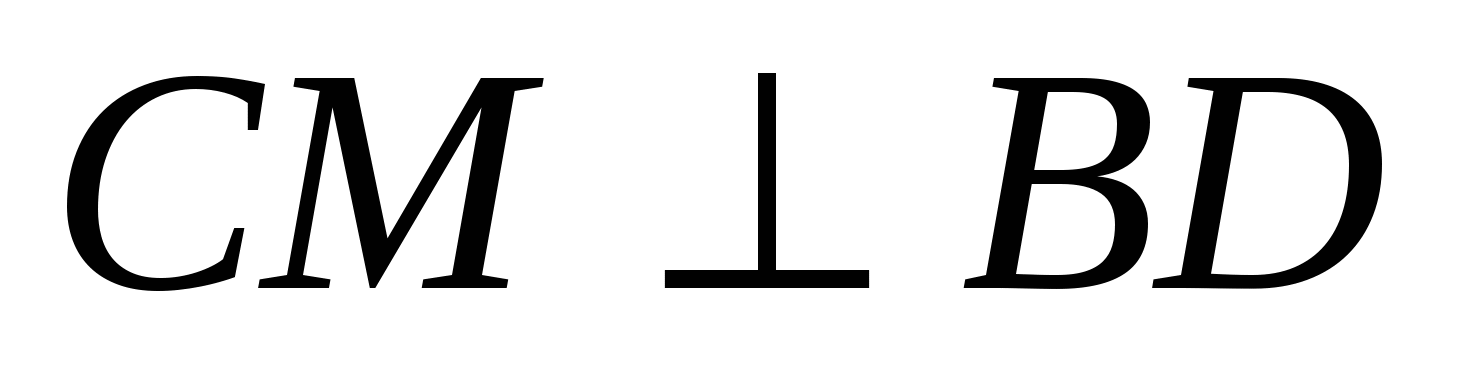 (по условию), следовательно, CM || AD1. Учитывая, что CD1 =
(по условию), следовательно, CM || AD1. Учитывая, что CD1 = 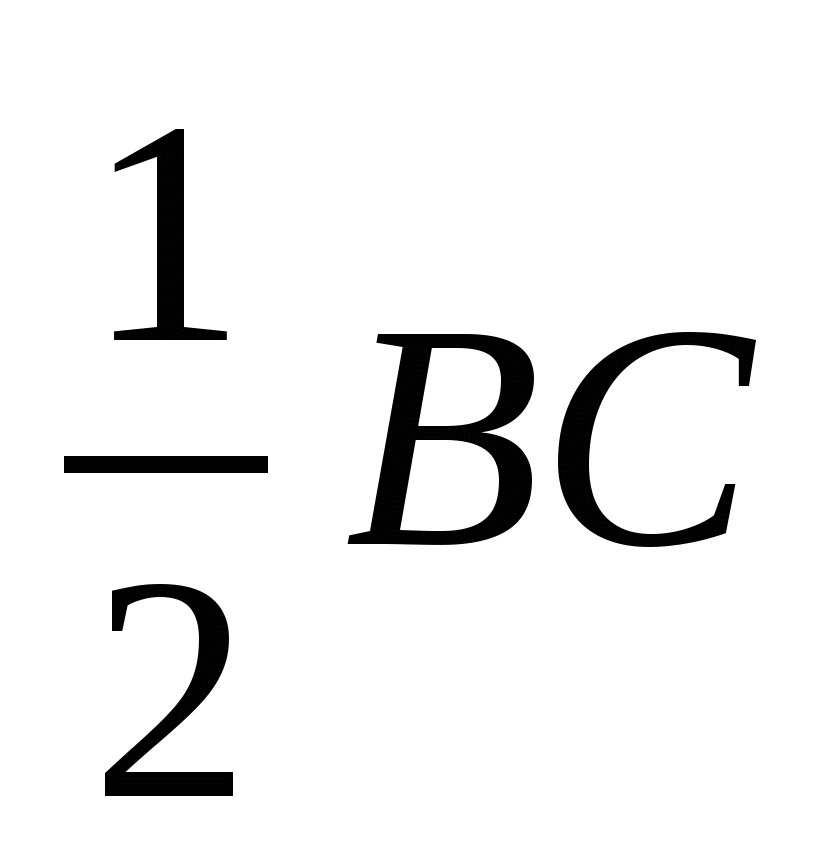 и используя обобщенную теорему Фалеса, делаем вывод, что
и используя обобщенную теорему Фалеса, делаем вывод, что 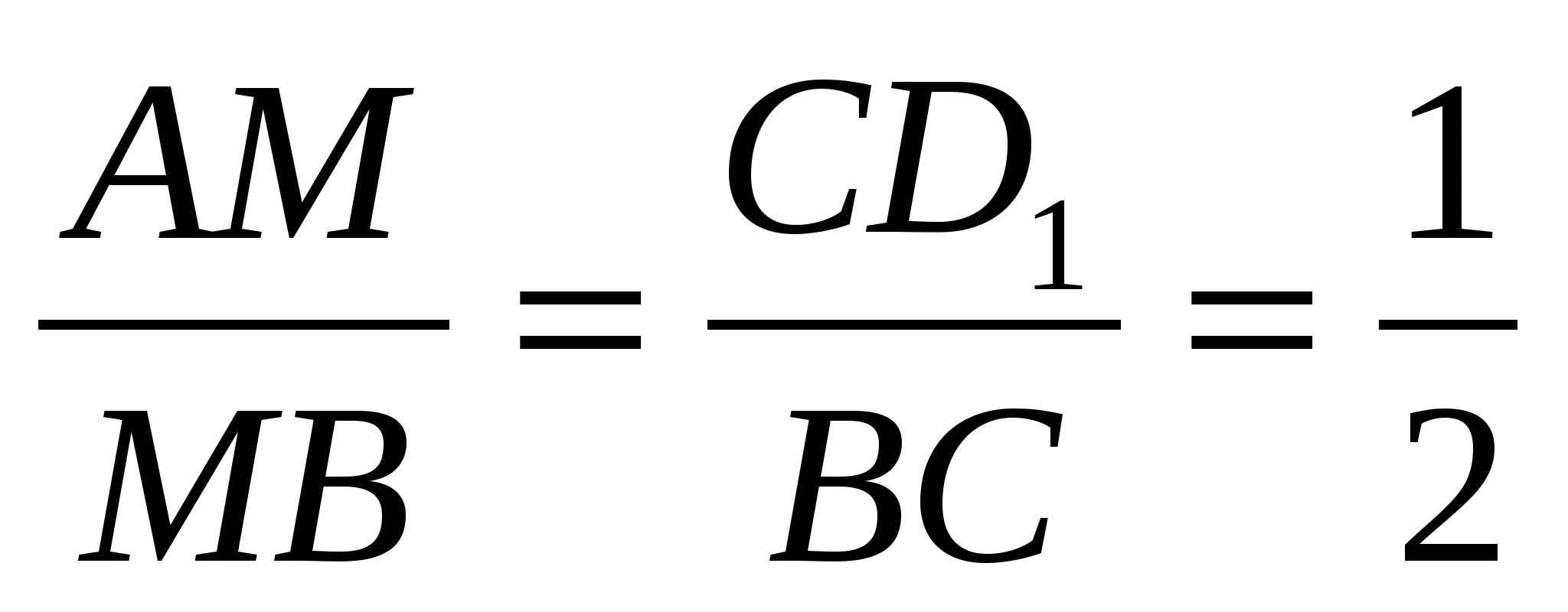 .
.
Метод тригонометрических соотношений
Обозначим 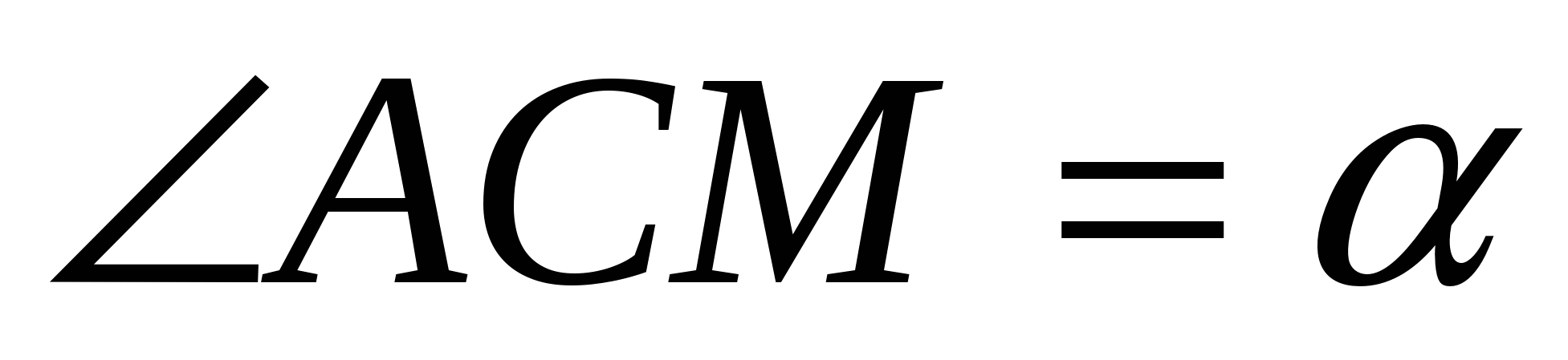 . Применим теорему синусов к треугольникам ACM и BCM. Получим:
. Применим теорему синусов к треугольникам ACM и BCM. Получим:
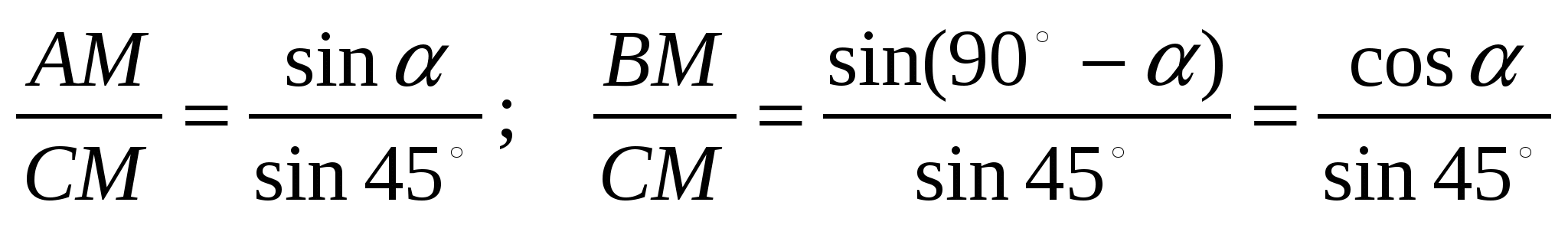 .
.
Отсюда 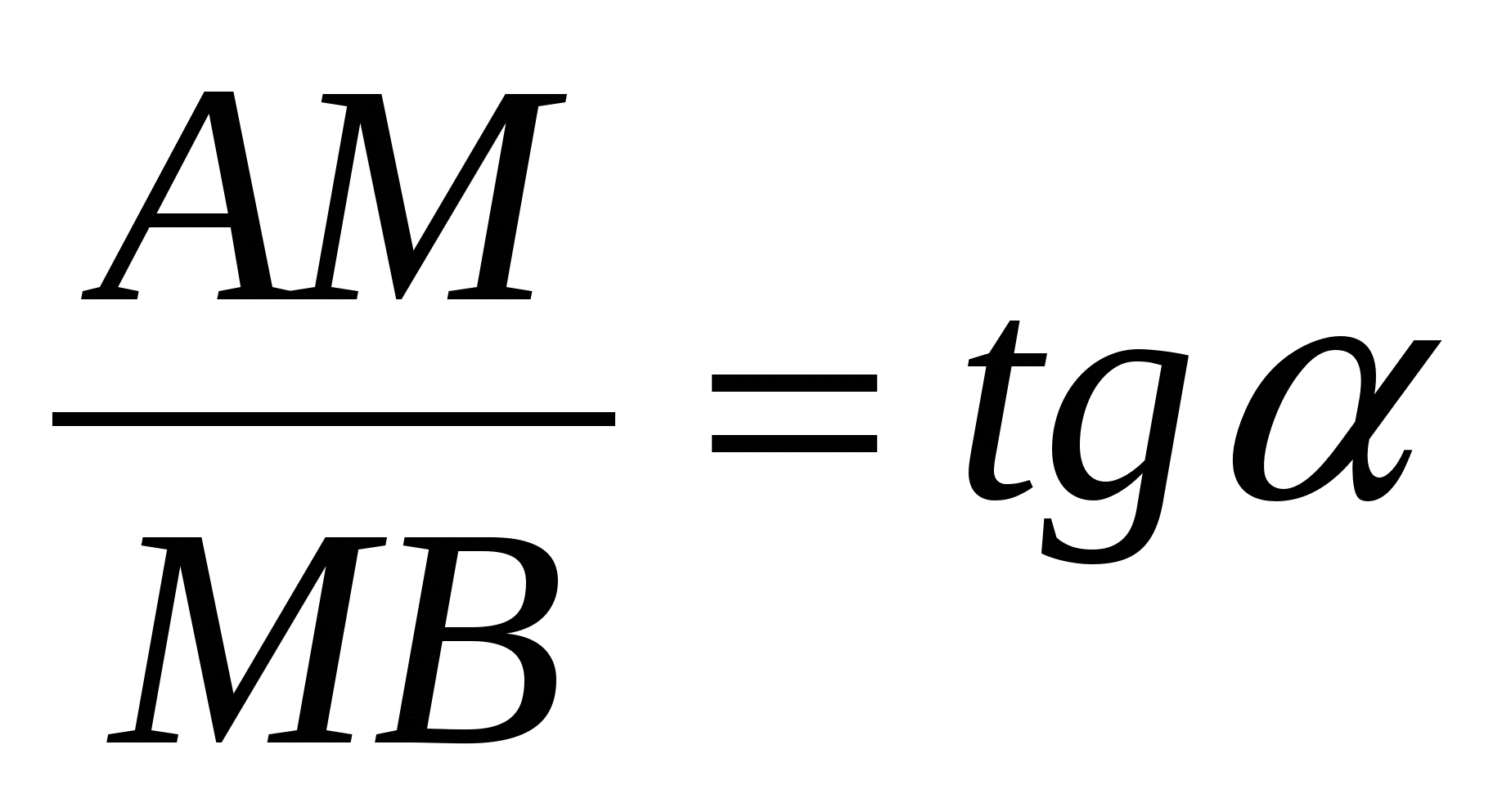 .
.
Из условия задачи следует, что углы ACM и CBD равны.
Тогда из ∆BCD имеем 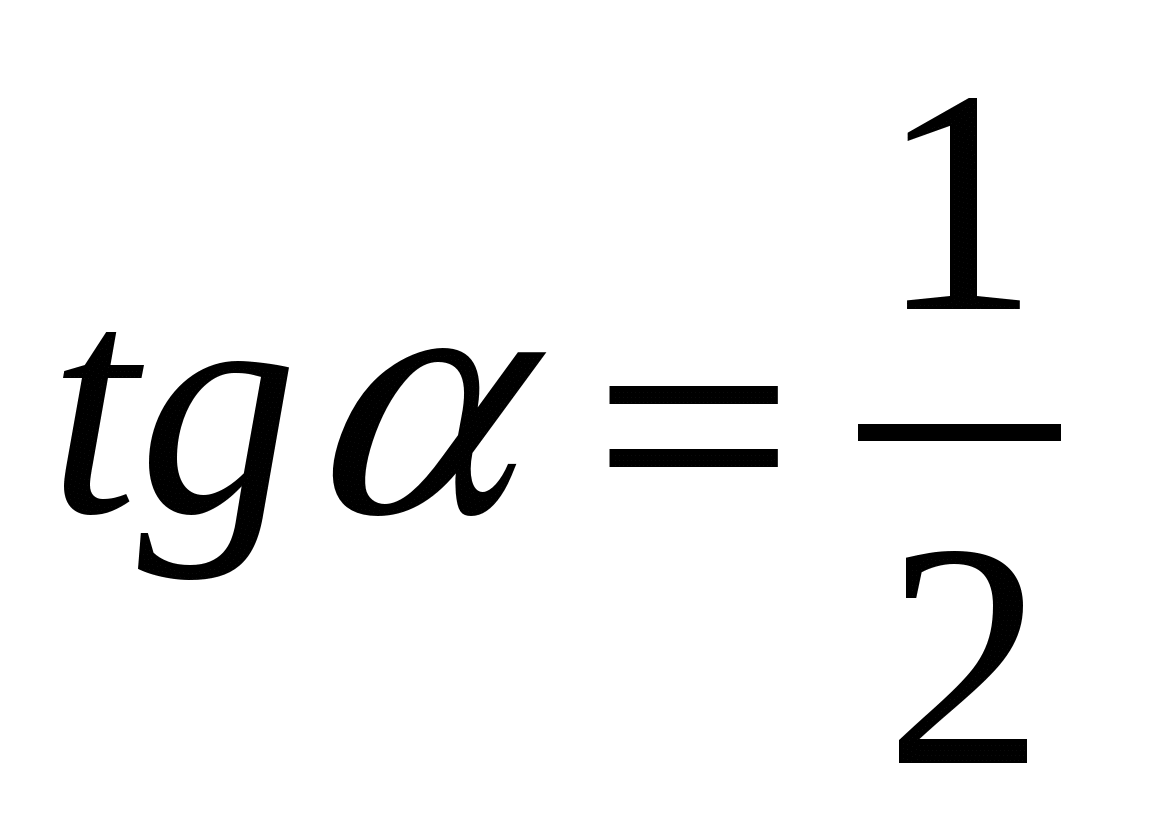 . Значит,
. Значит, 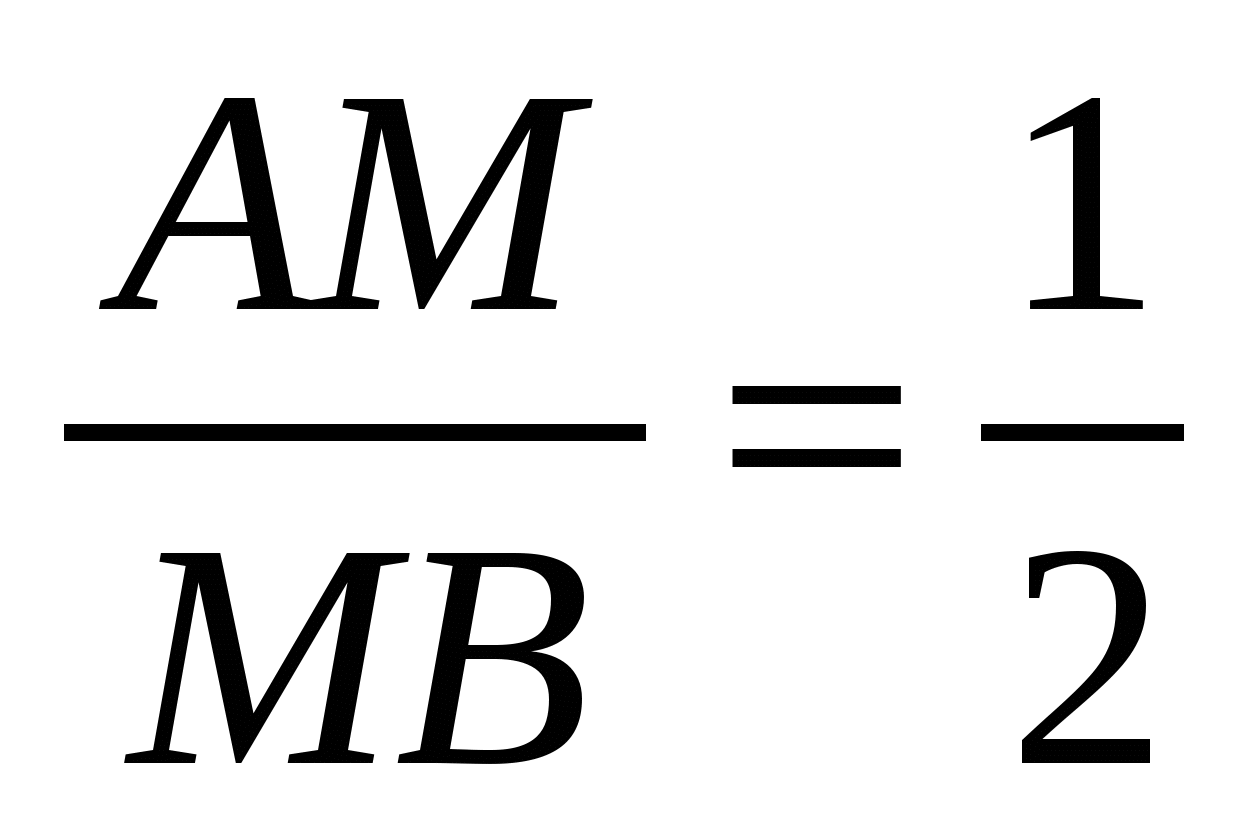 .
.
Геометрический метод
Проведем перпендикуляр MN к стороне AC.
Так как 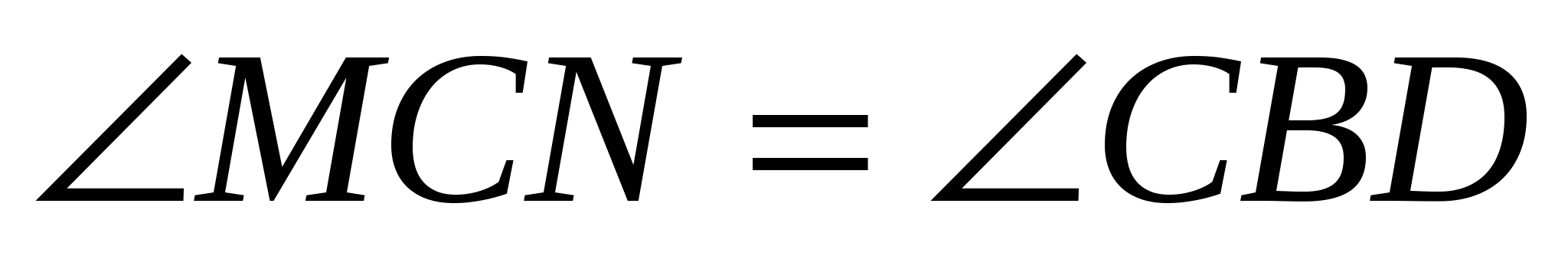 , то прямоугольные треугольники CMN и BCD подобны.
, то прямоугольные треугольники CMN и BCD подобны.
Следовательно, 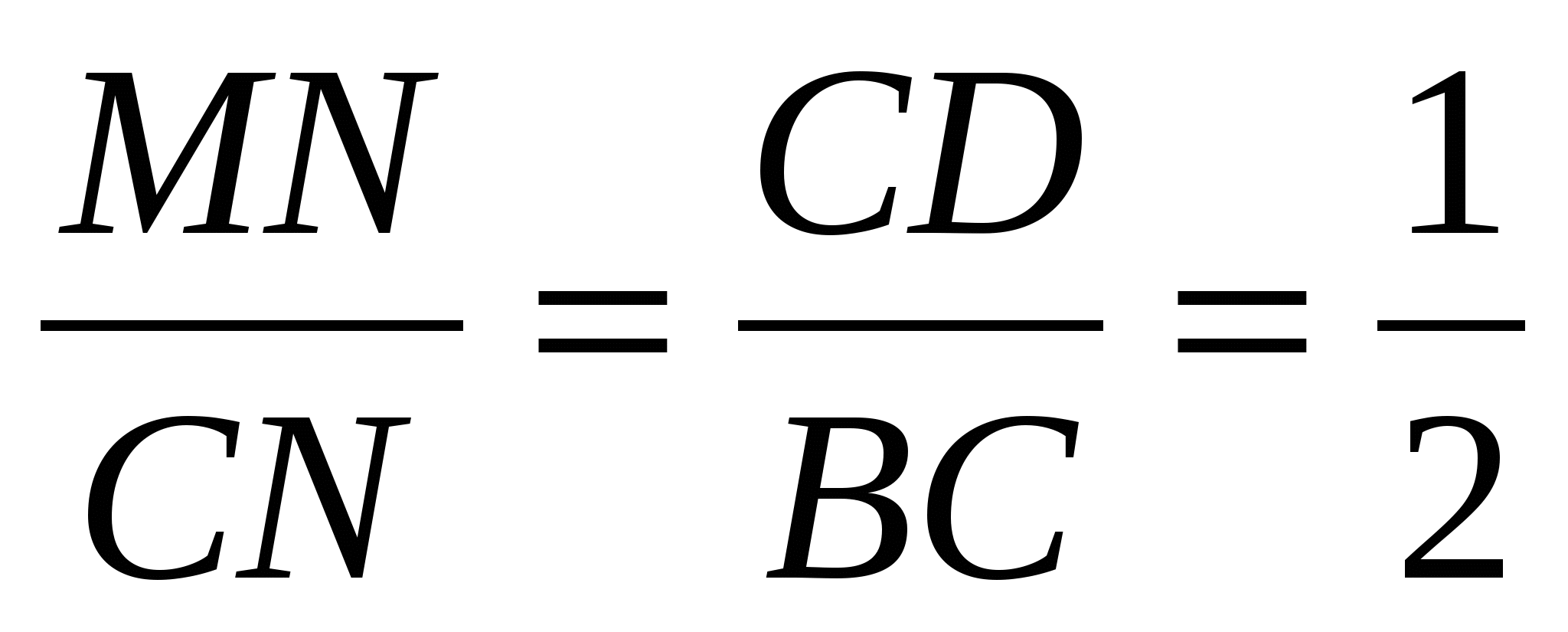 .
.
Но MN = AN, значит, 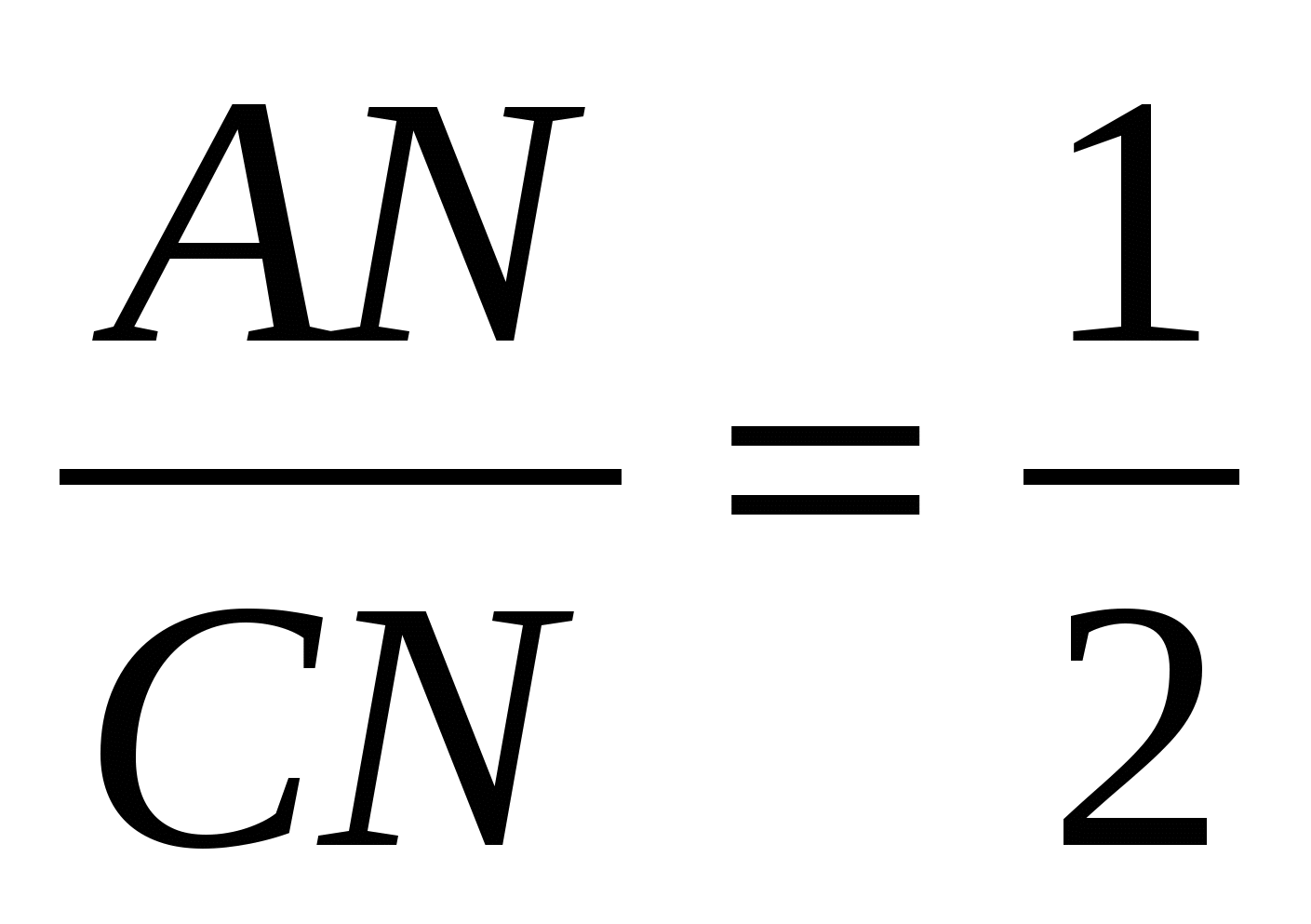 . Поскольку MN || BC, то
. Поскольку MN || BC, то 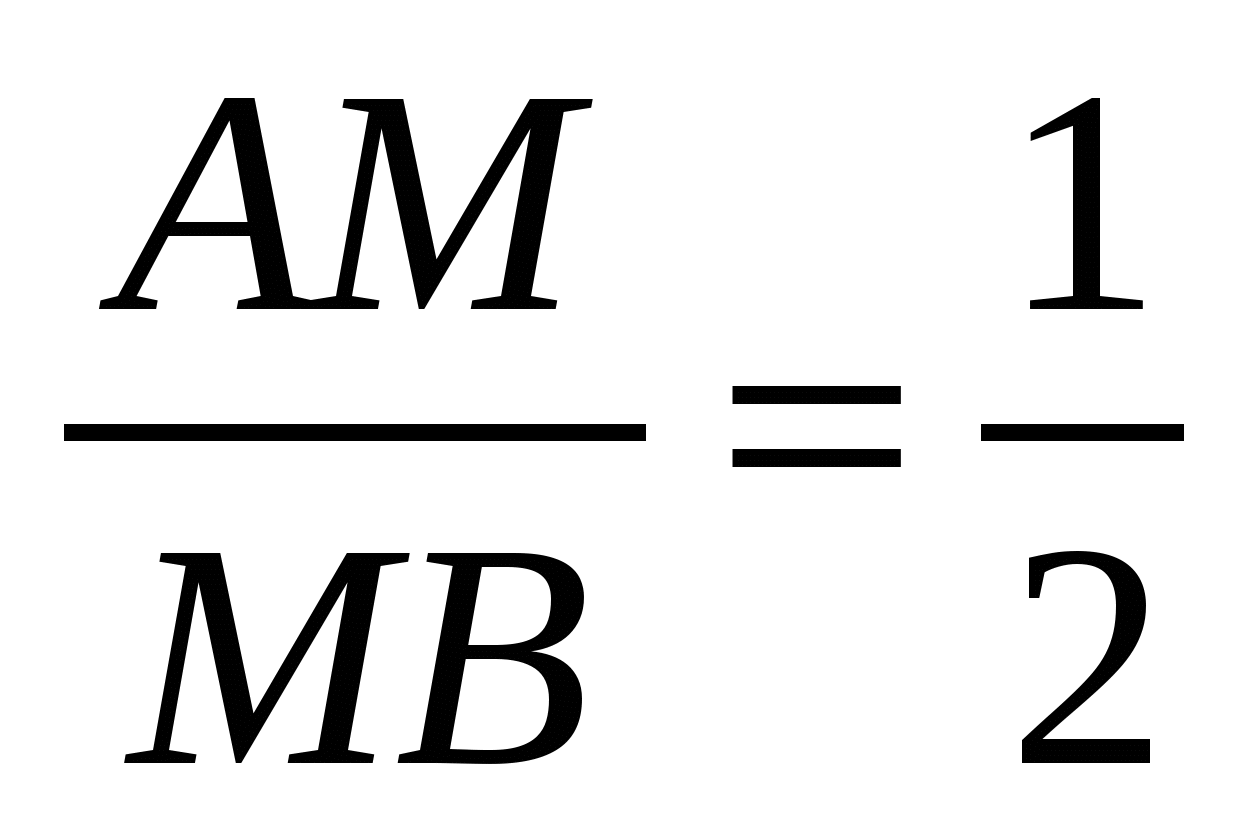 .
.
Задача 5. В треугольнике АВС биссектриса ВЕ и медиана АD перпендикулярны и имеют одинаковую длину, равную 4. Найти стороны треугольника АВС.
Приступая к решению задачи, замечаем, что прямоугольные треугольники АВО и DВО равны (точка О - точка пересечения биссектрисы ВЕ и медианы АD).
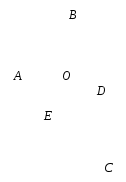
Следовательно, 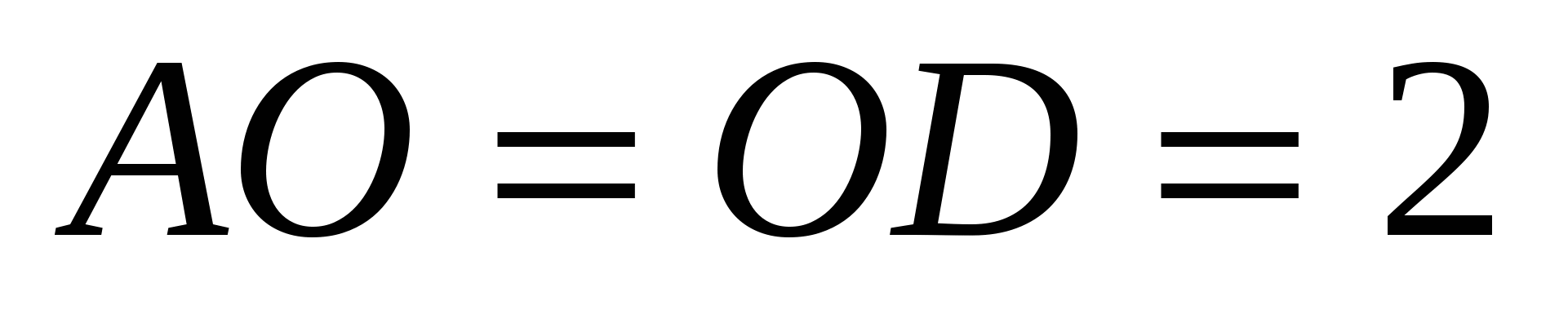 и
и 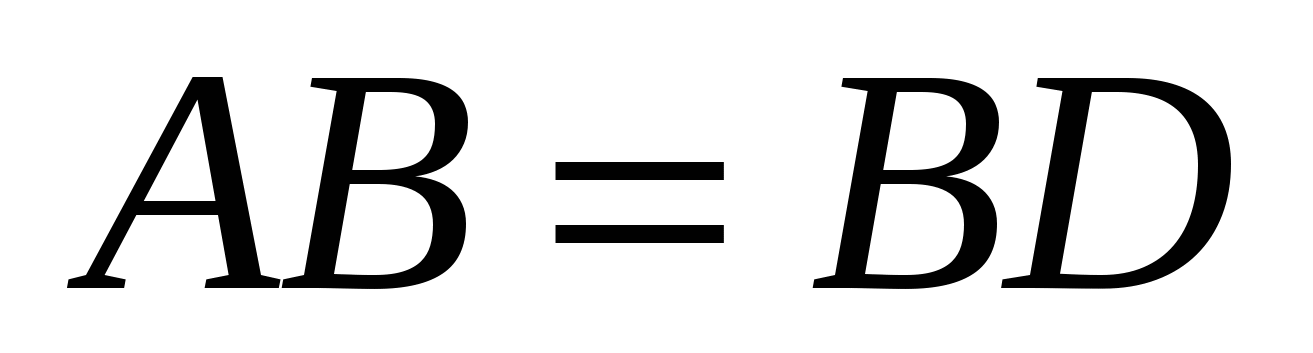 , то есть
, то есть 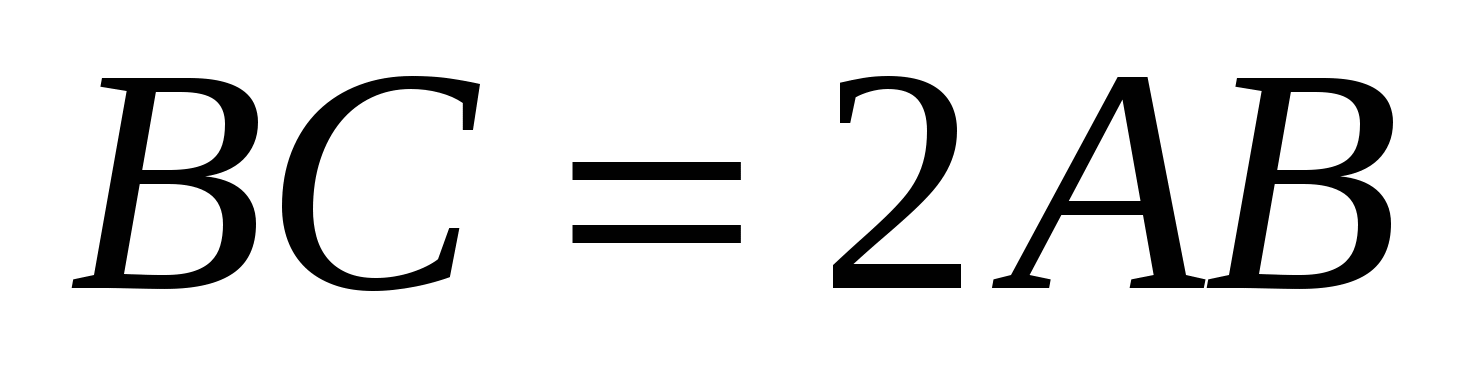 .
.
Применяя свойство биссектрисы, имеем:
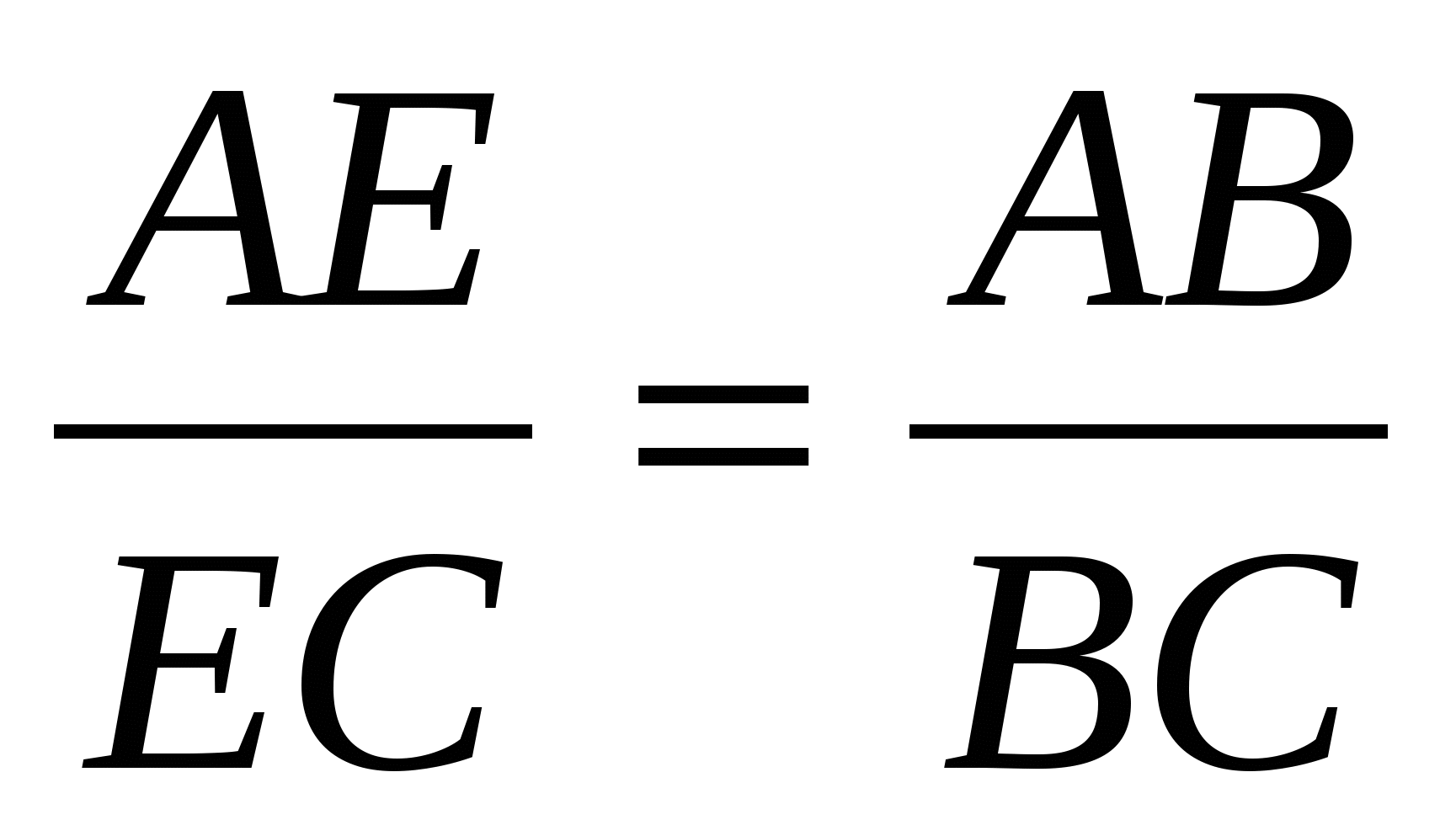 , то есть
, то есть 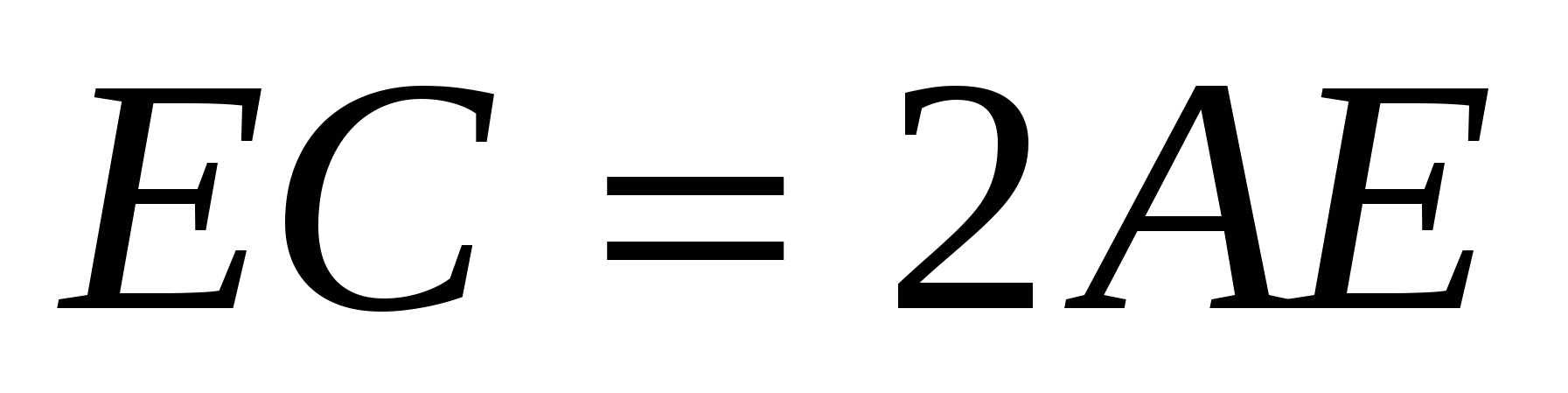 .
.
Координатный метод
Рассмотрим прямоугольную систему координат с началом в точке О и единичным отрезком равным 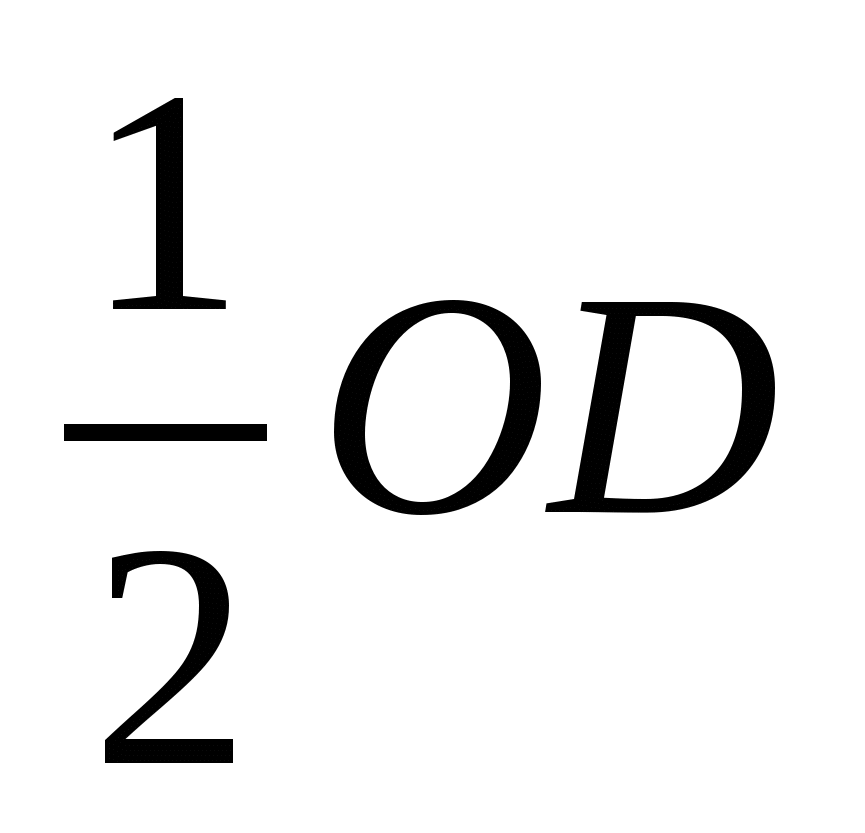 .
.
Тогда: А(-2; 0), D(2; 0), В(0; b).
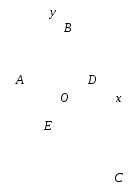
Используя формулу для нахождения координат середины отрезка ВС, найдем координаты точки С(х; у):
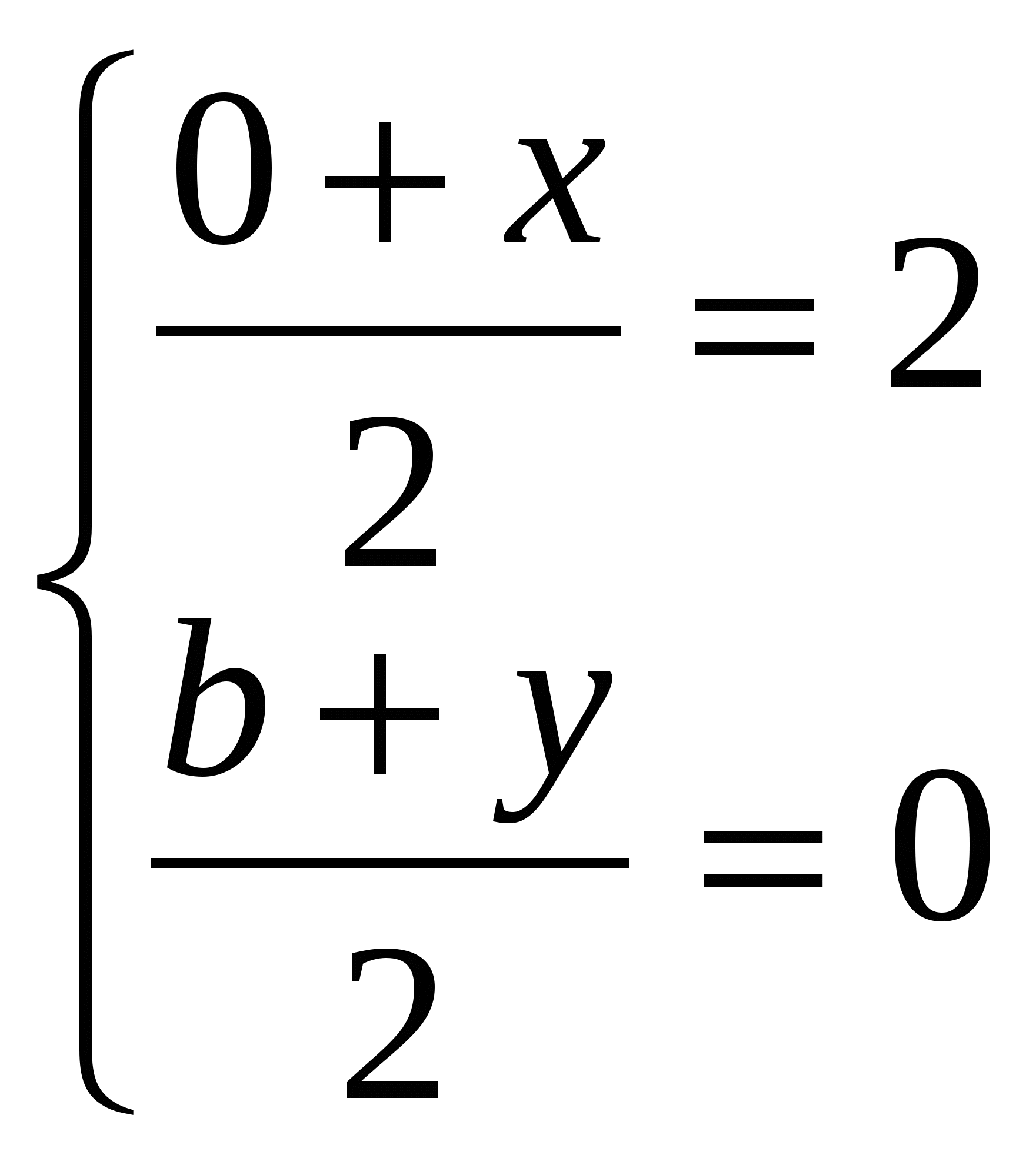 .
.
Следовательно, С(4; -b).
Запишем уравнение прямой АС по двум точкам:
![]() .
.
Координаты точки Е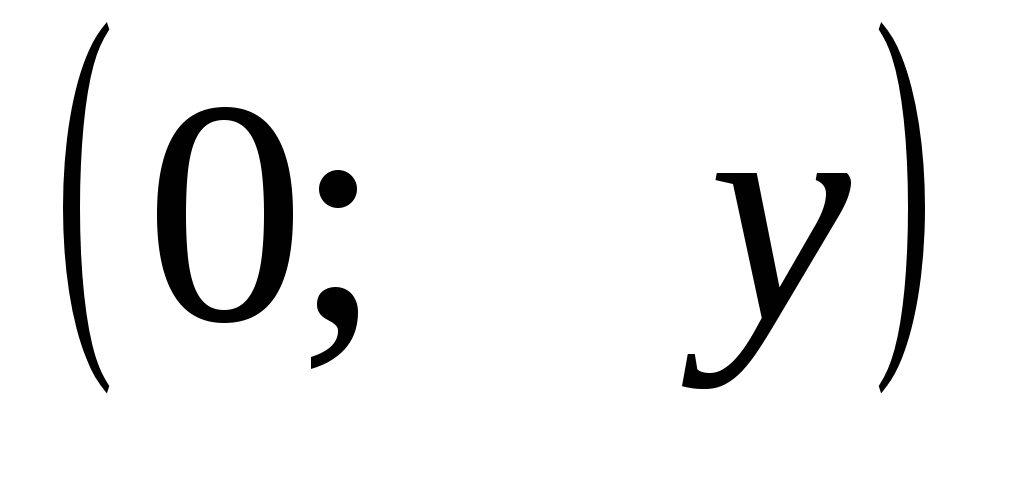 удовлетворяют этому уравнению, так как она принадлежит прямой АС. Имеем:
удовлетворяют этому уравнению, так как она принадлежит прямой АС. Имеем:
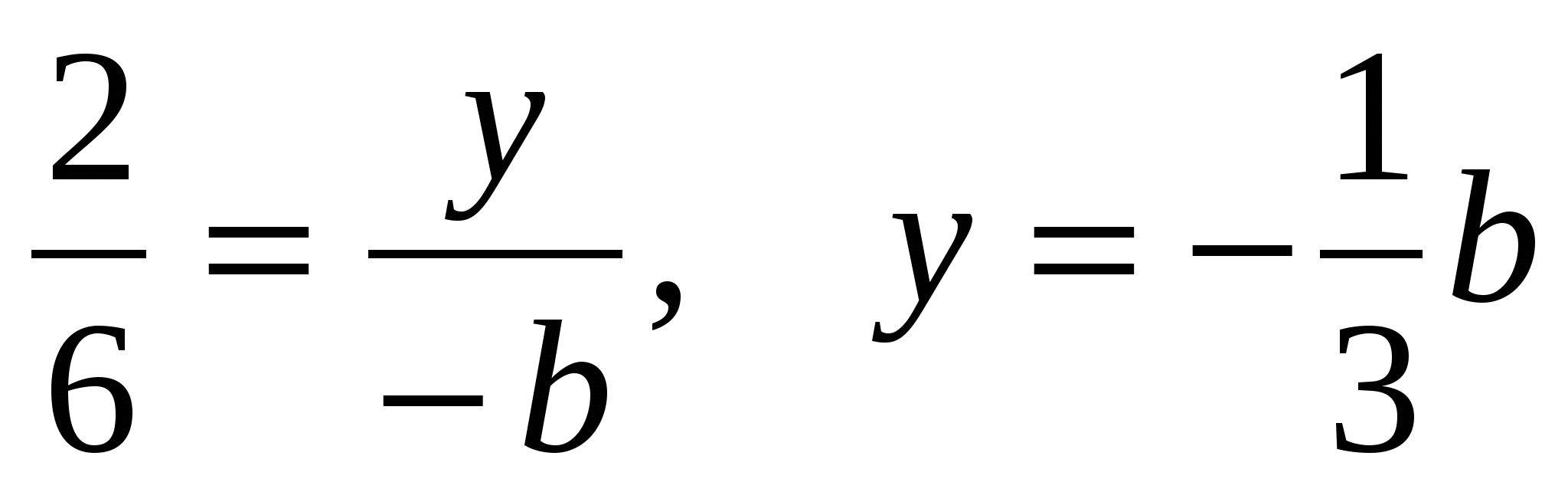 .
.
Следовательно, 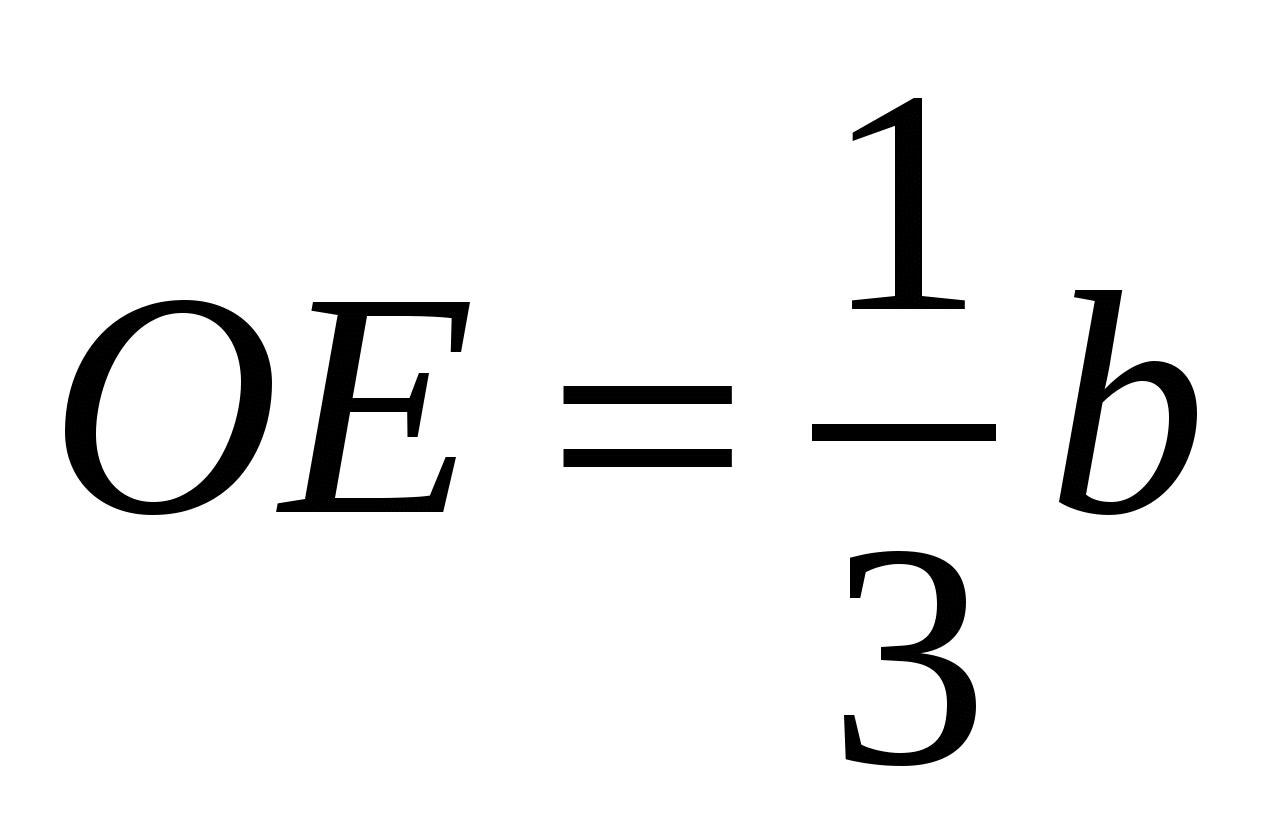 и
и 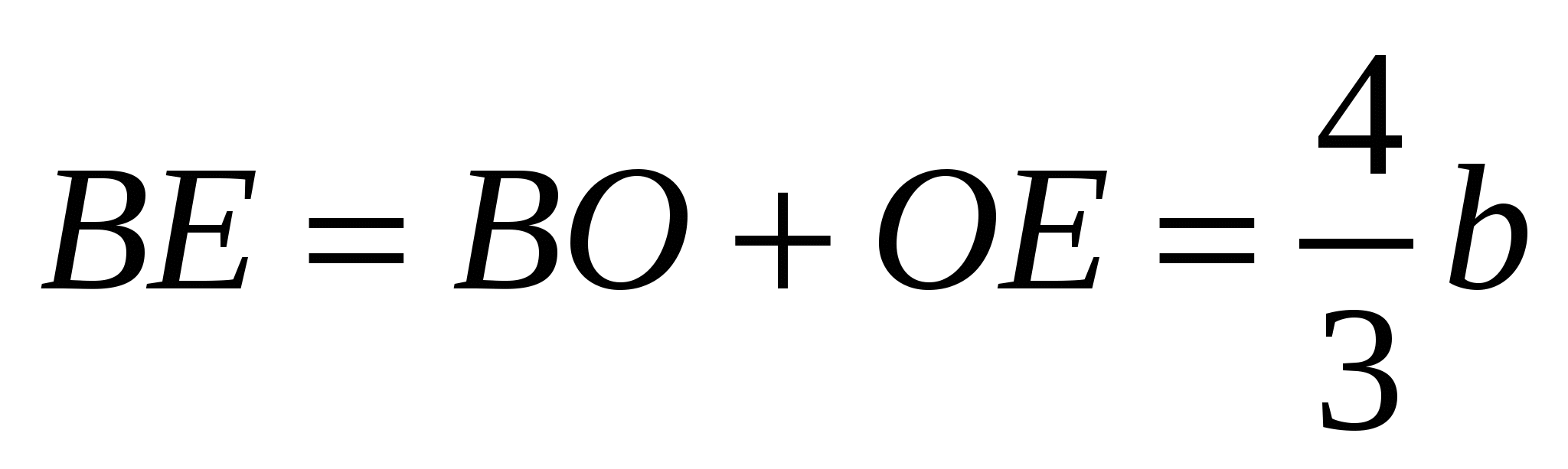 .
.
Применяя условие, получим: 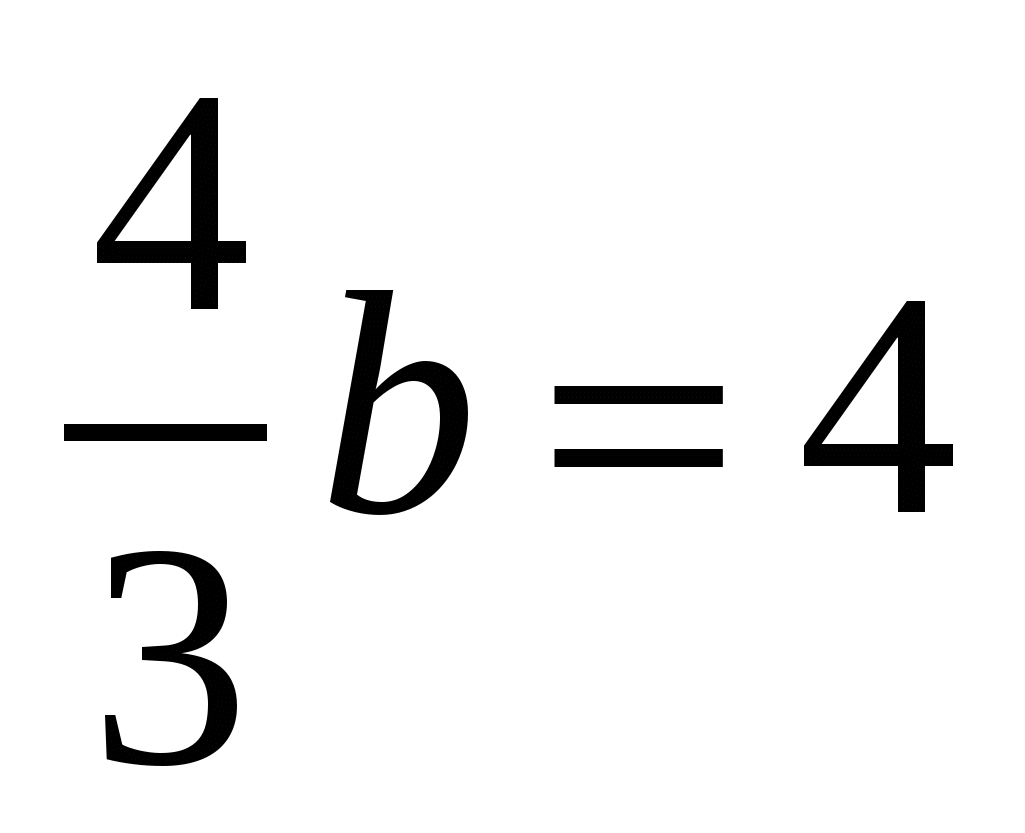 или
или 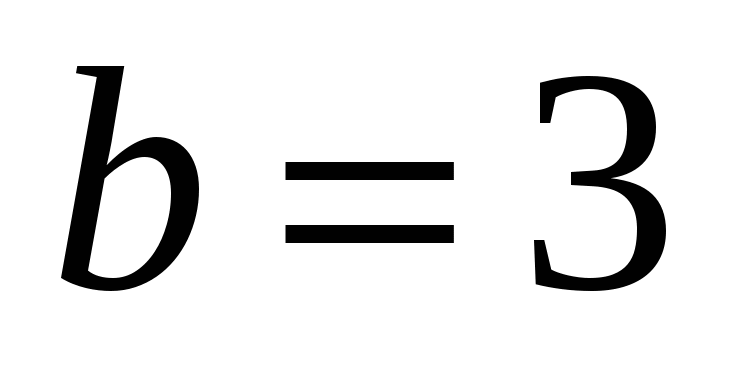 .
.
Итак, 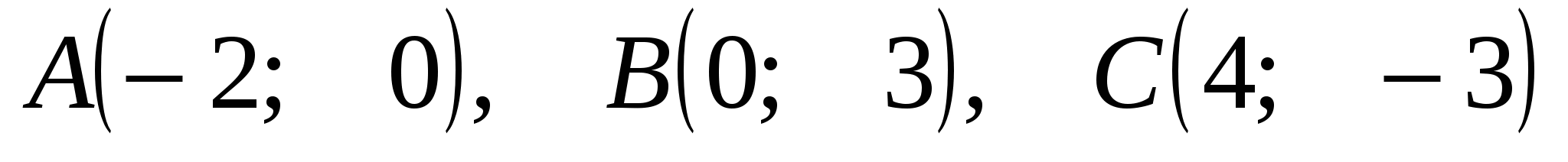 .
.
Найдем стороны треугольника АВС, используя формулу расстояния между двумя точками:
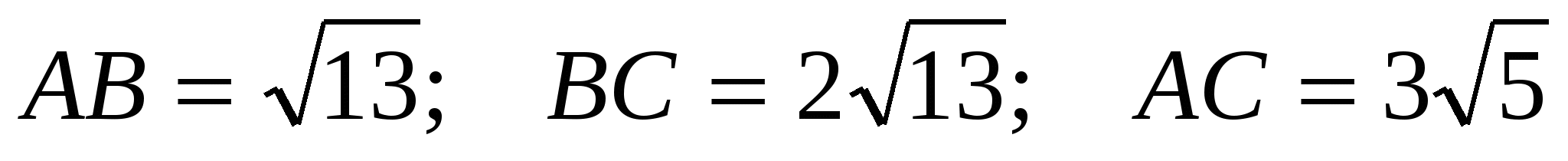 .
.
Векторный метод
Обозначим 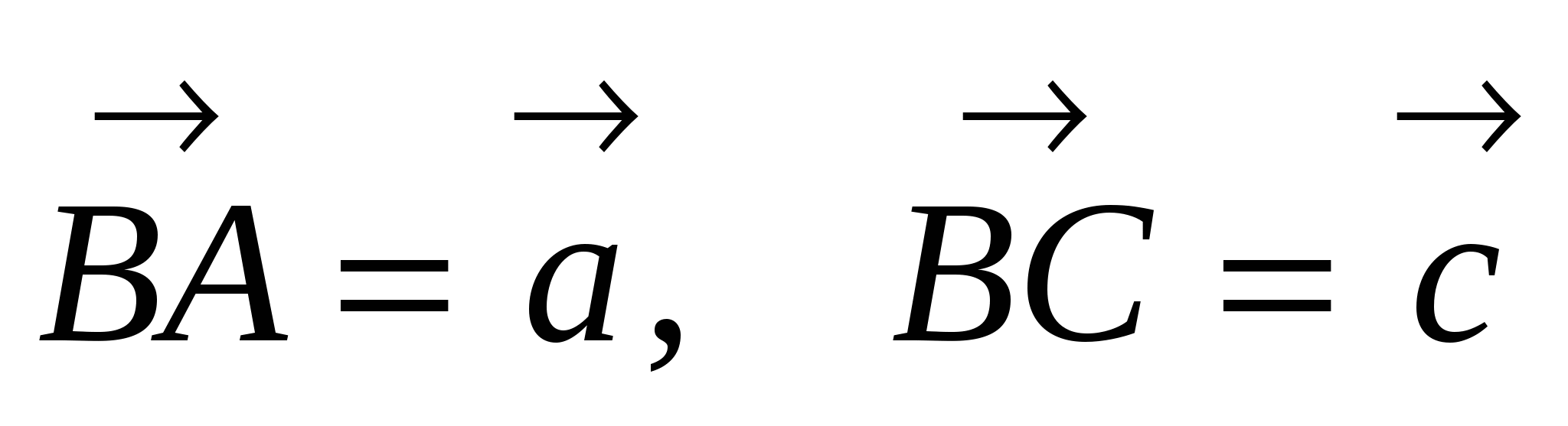 . Выразим
. Выразим 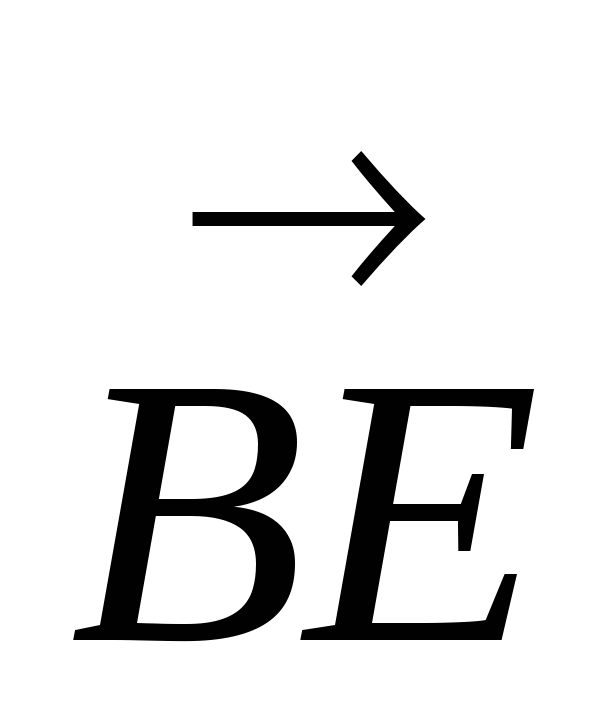 и
и  через
через 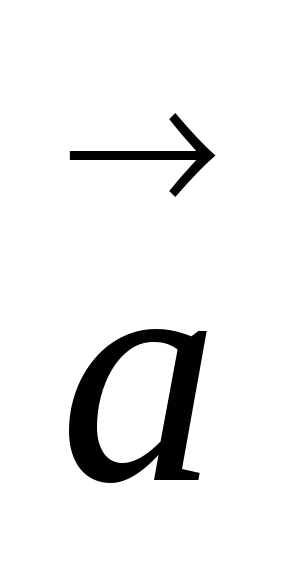 и
и 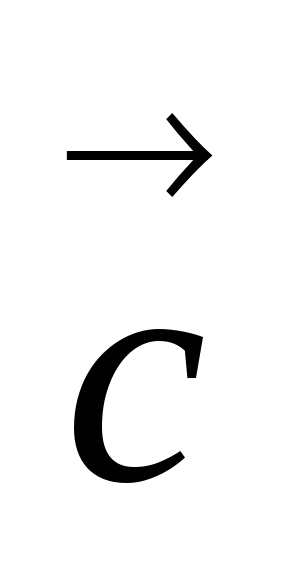 .
.
Используя, что 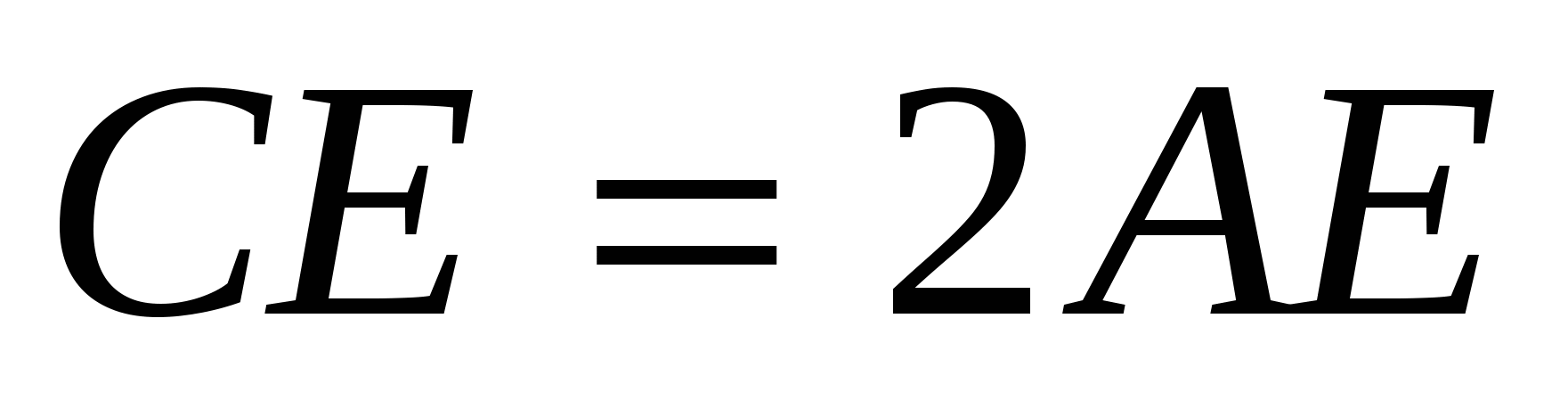 , применим формулу деления отрезка в данном отношении:
, применим формулу деления отрезка в данном отношении:
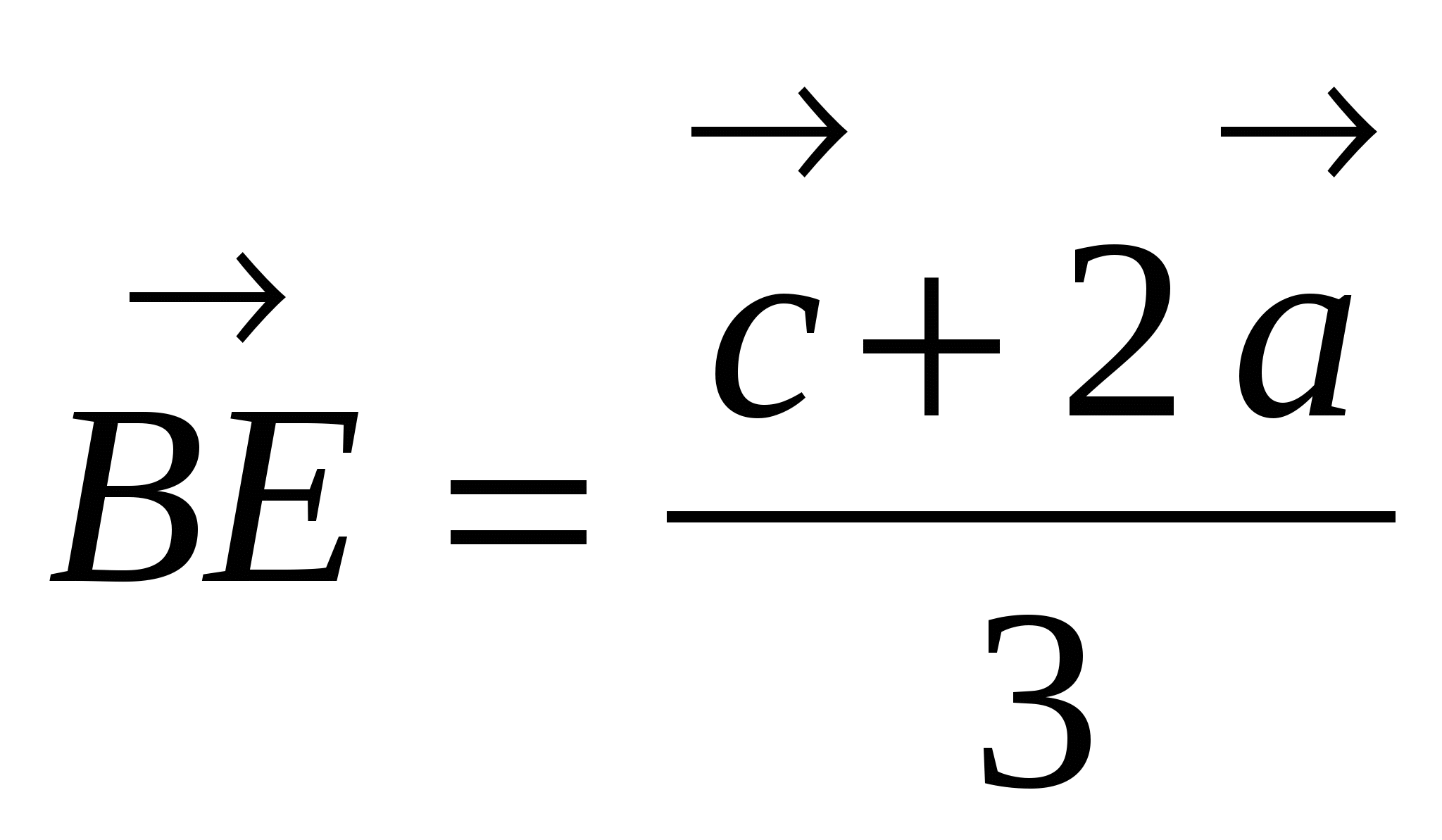 .
.
Согласно правилу вычитания векторов:
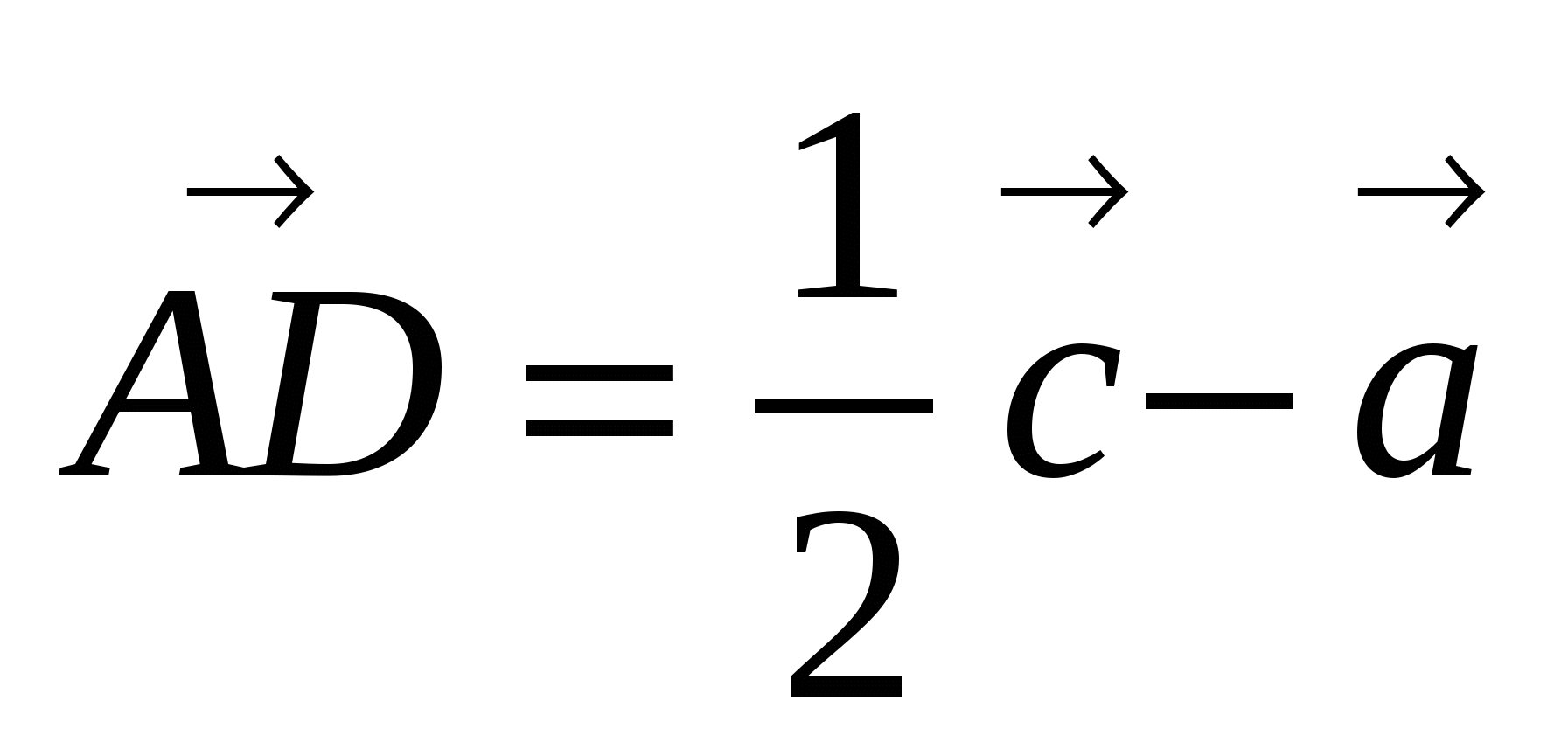 .
.
Пусть 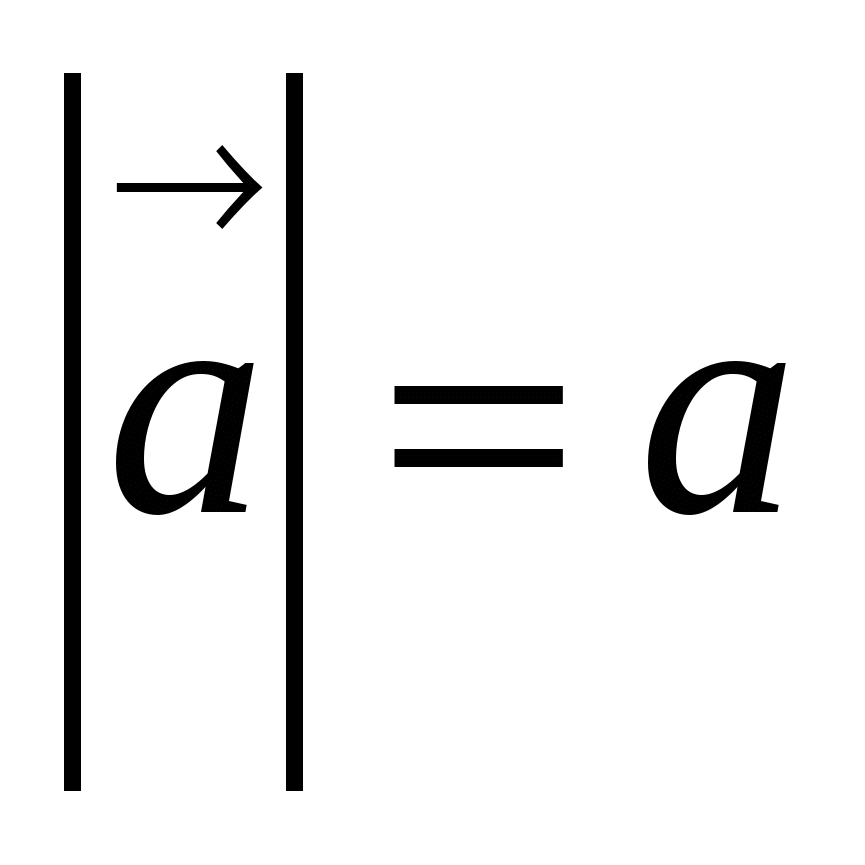 , тогда
, тогда 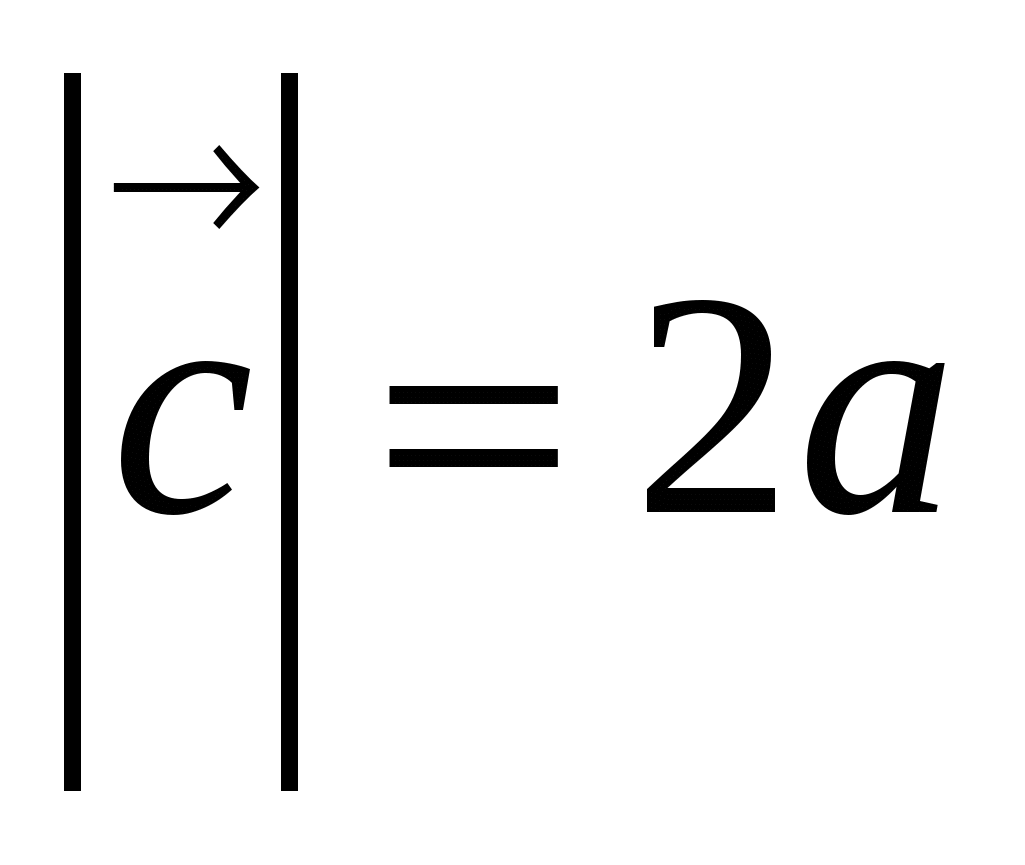 . Вычислив скалярные квадраты векторов
. Вычислив скалярные квадраты векторов 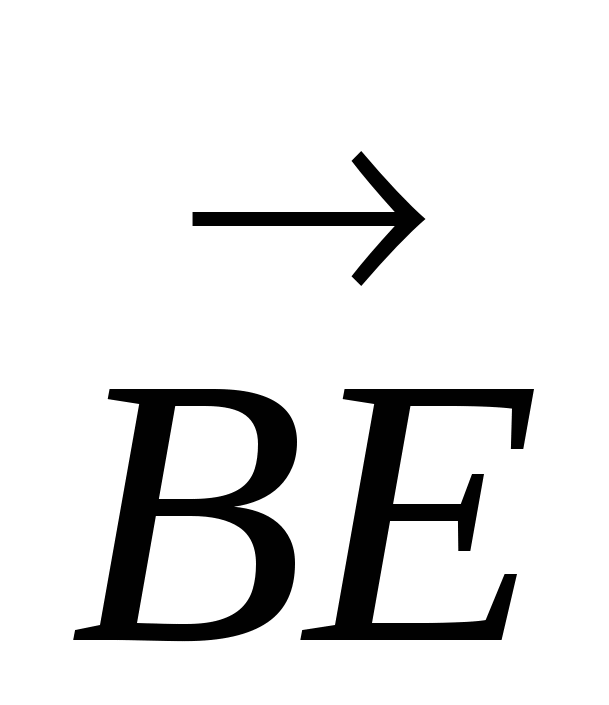 и
и  , получим уравнения:
, получим уравнения:
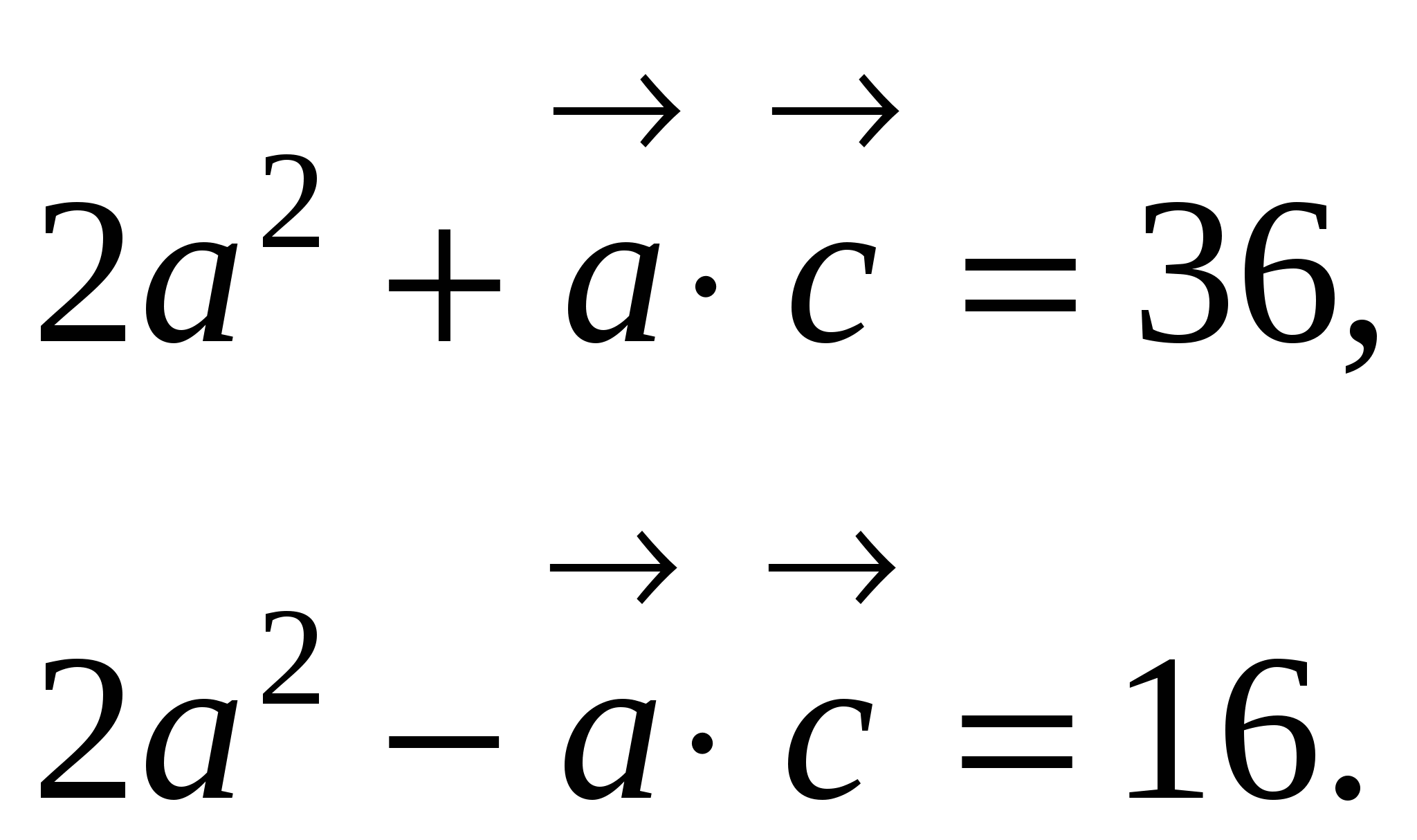
Отсюда, 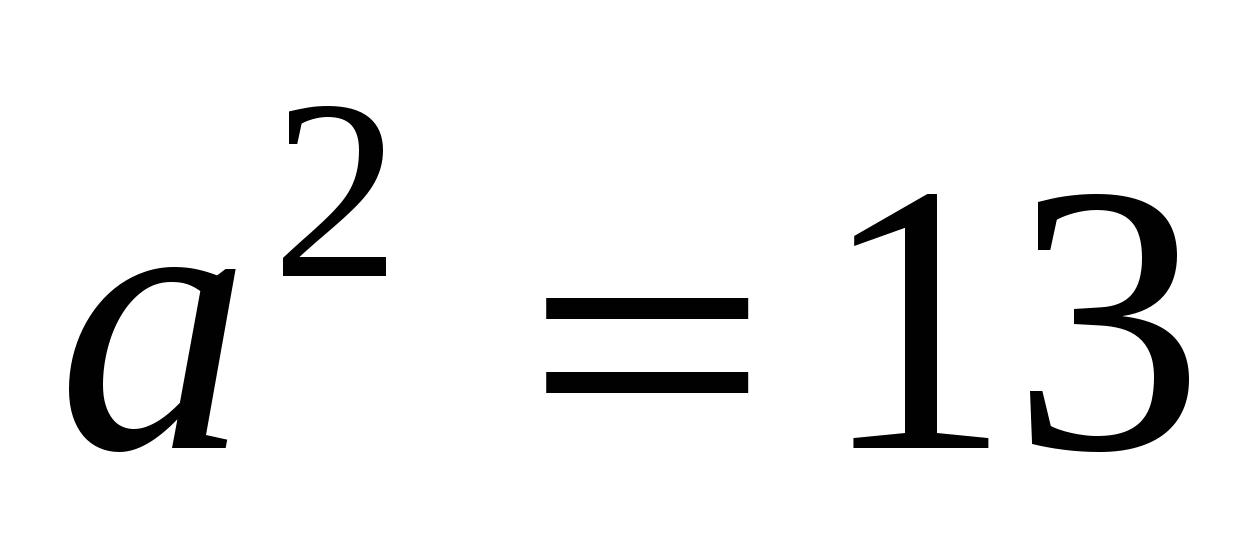 и
и 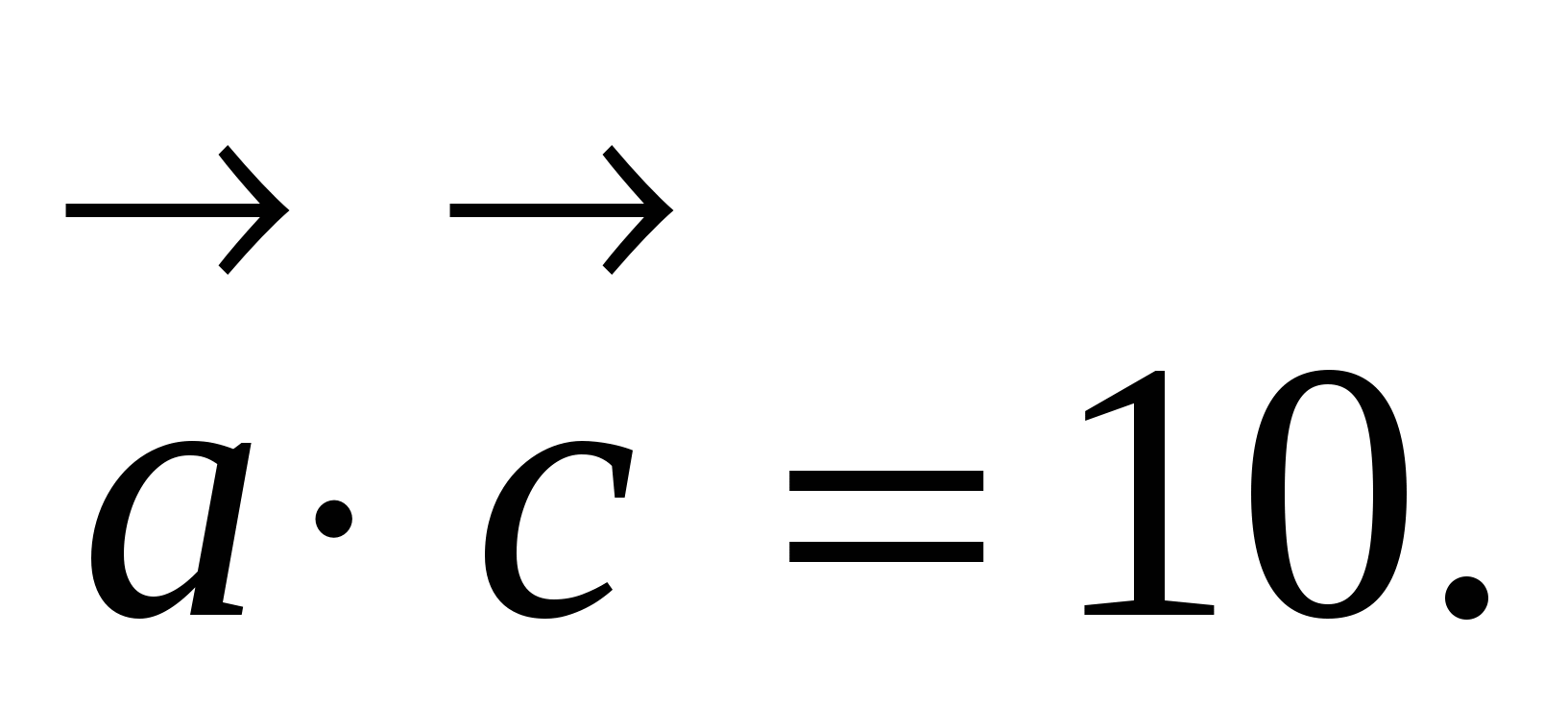 Значит,
Значит, 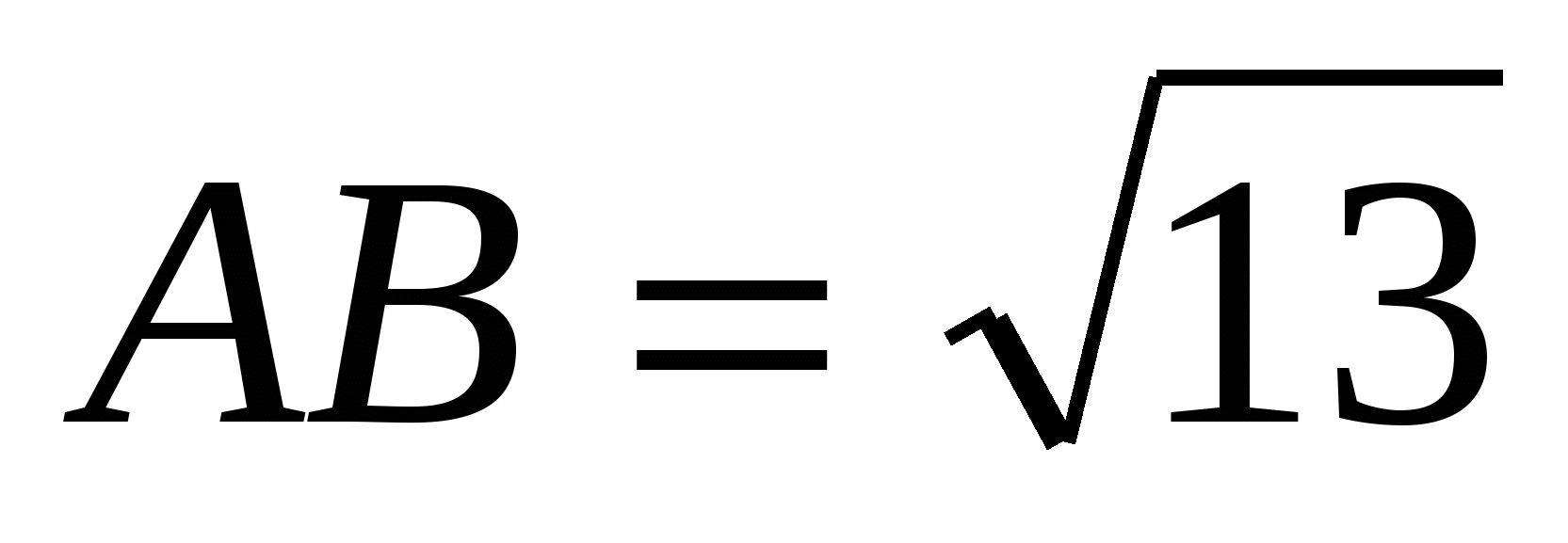 ,
, 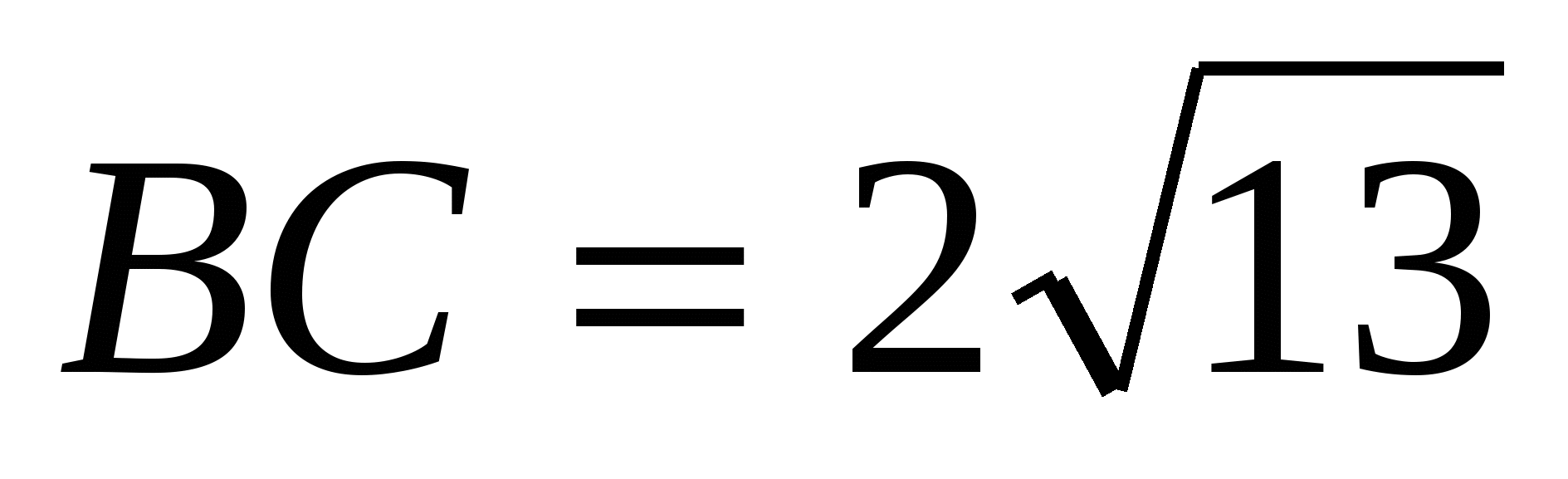 .
.
Так как 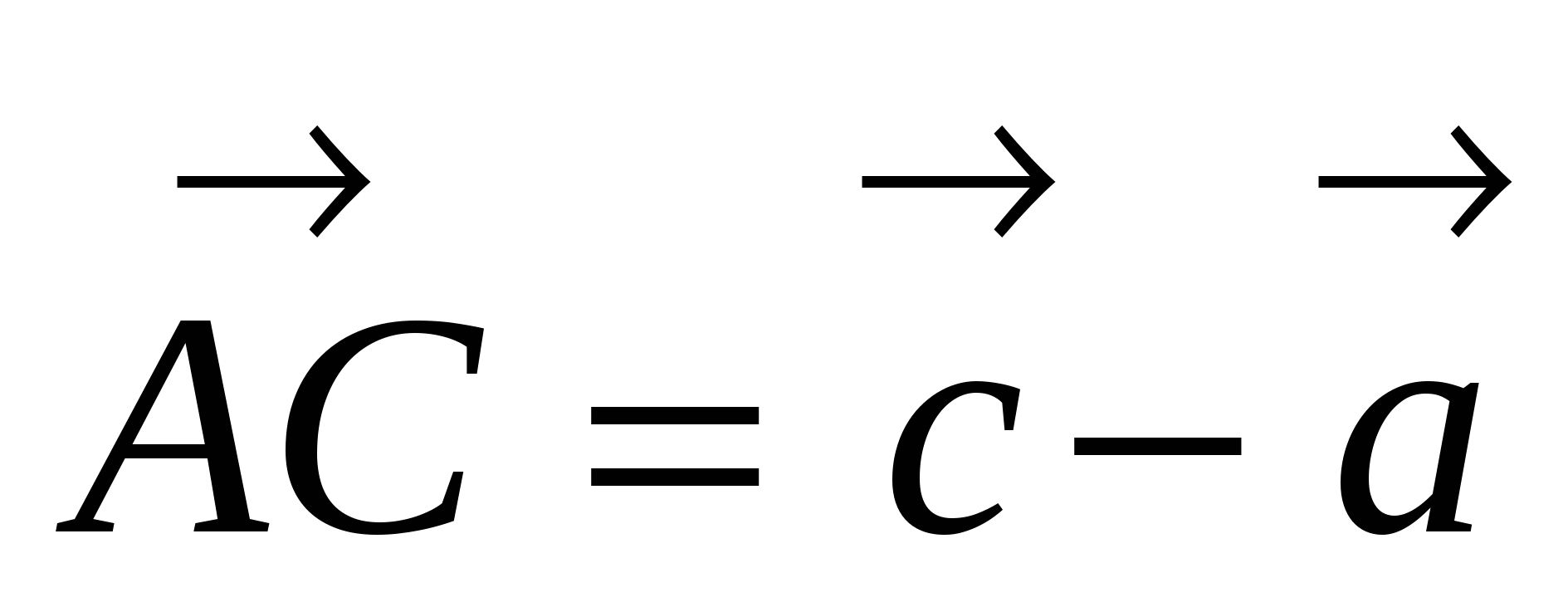 , найдем скалярный квадрат
, найдем скалярный квадрат ![]() :
:
![]() , то есть
, то есть 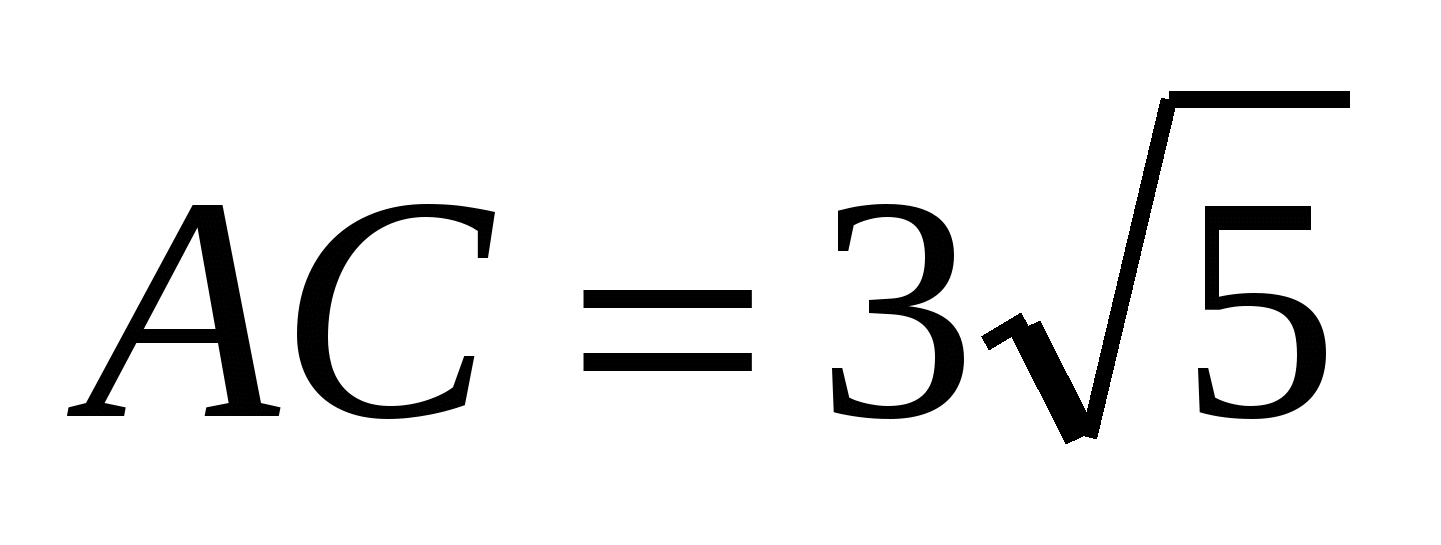 .
.
Алгебраический метод
Пусть 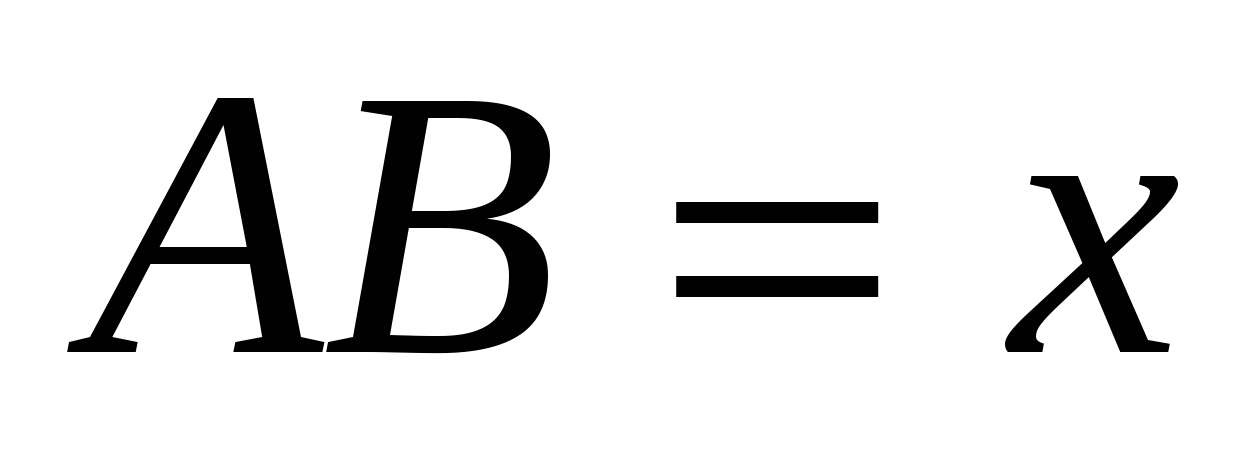 , АЕ = у, тогда
, АЕ = у, тогда 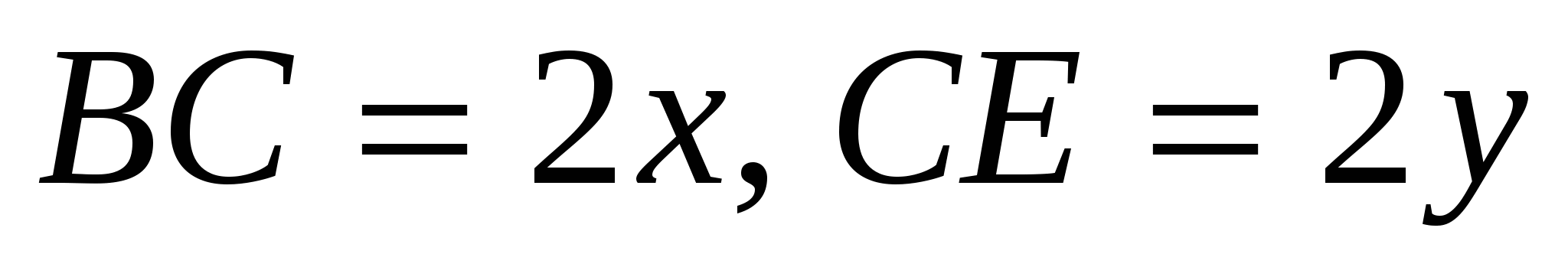 .
.
Выразим АD и ВЕ через длины сторон треугольника АВС по известным формулам для медианы и биссектрисы.
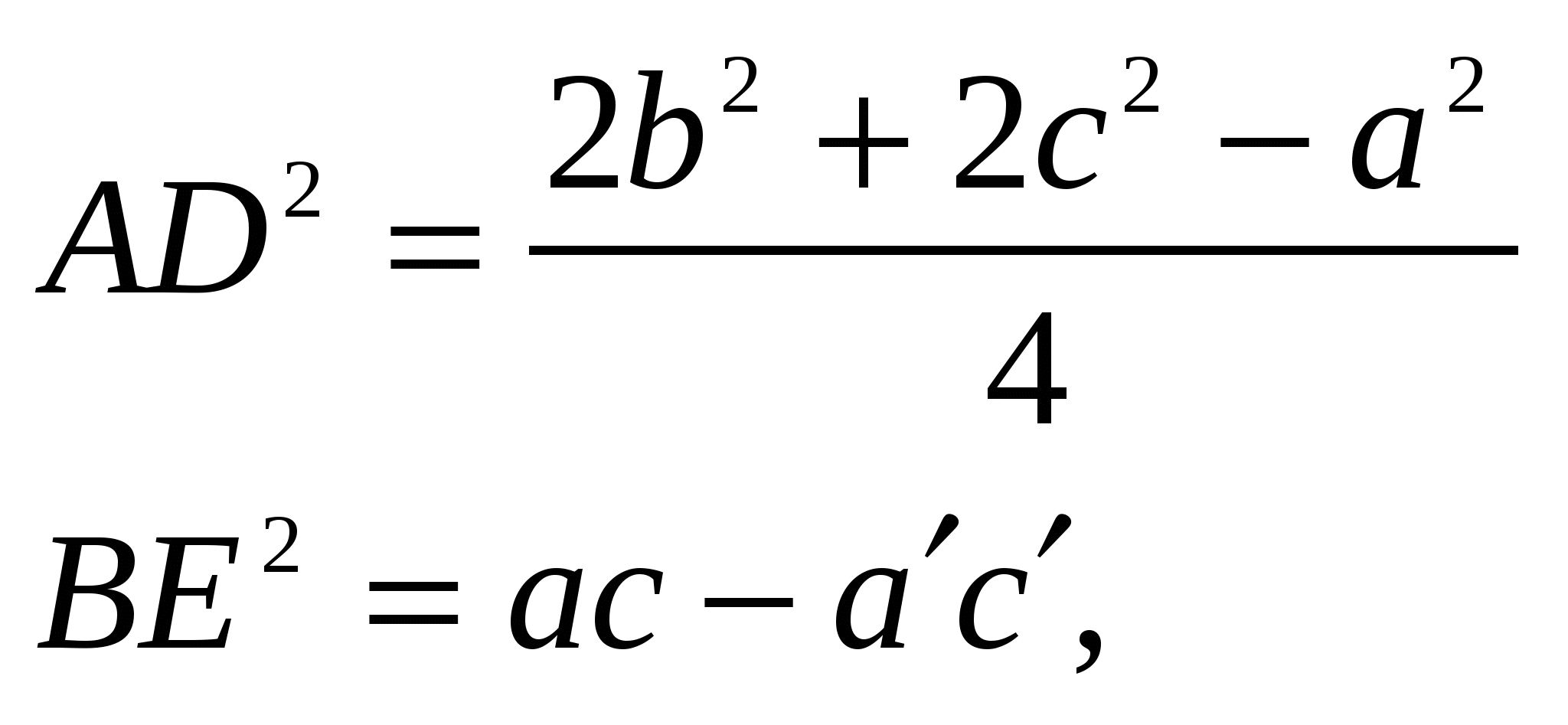
где 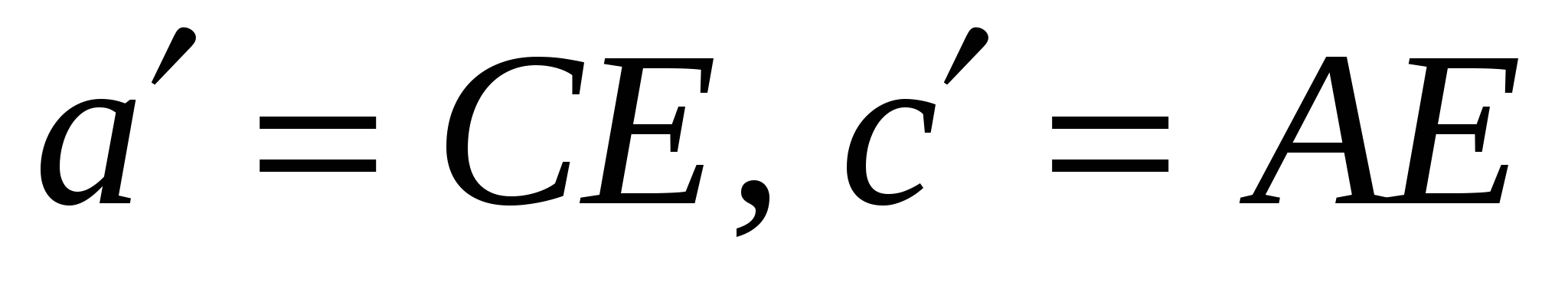 .
.
Получим систему уравнений:
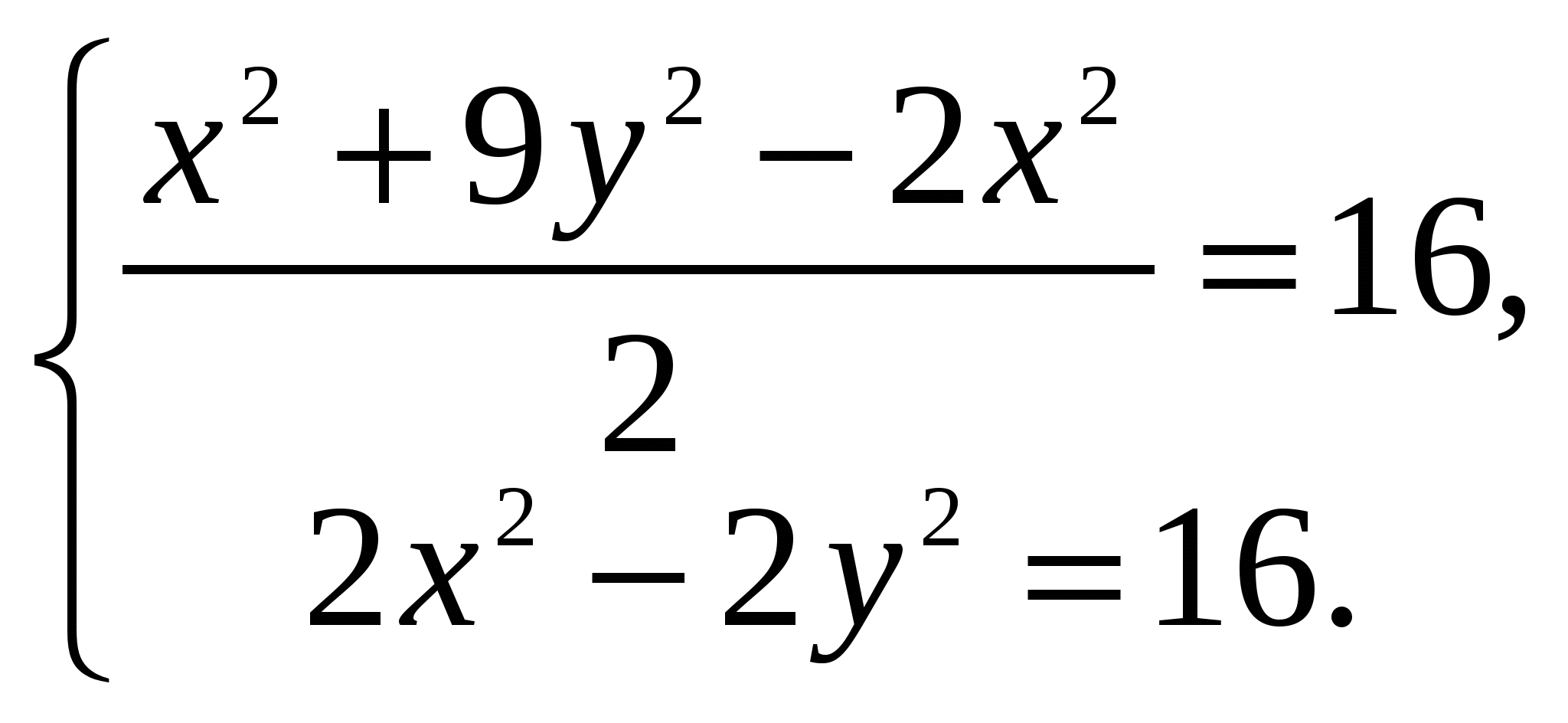
Отсюда 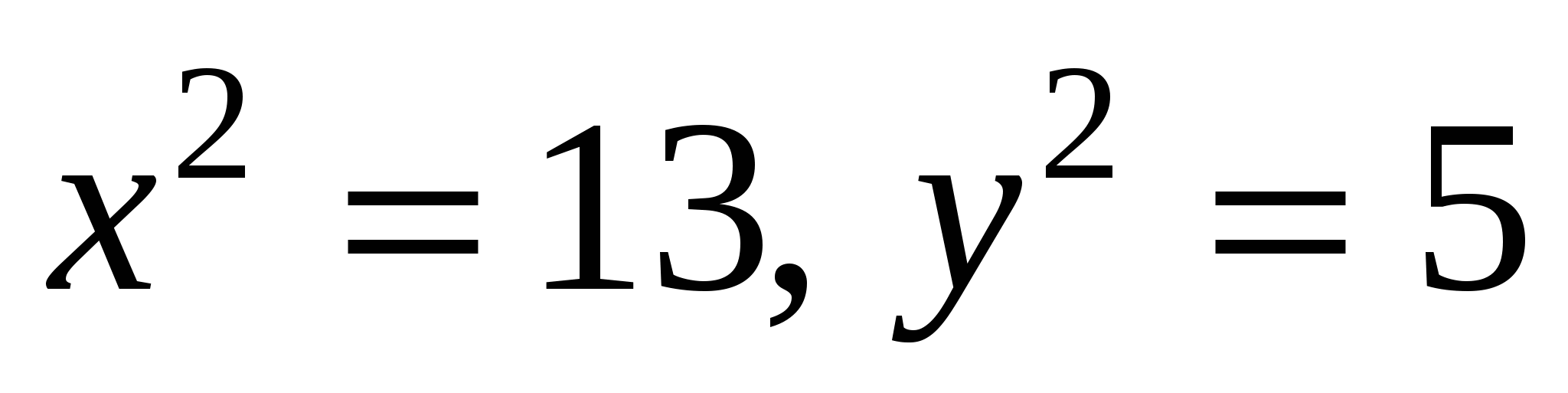 .
.
Значит, 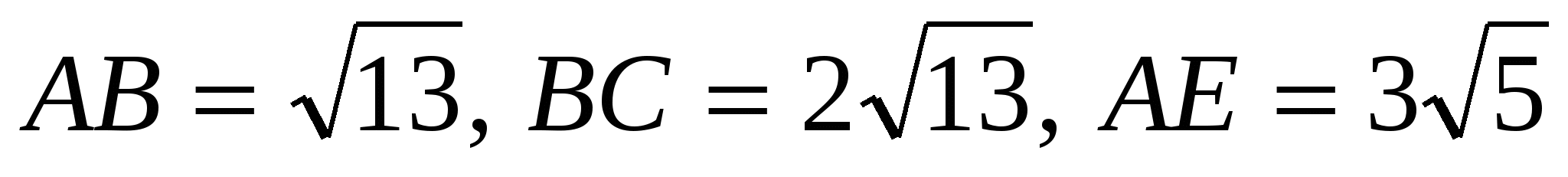 .
.
Метод тригонометрических соотношений
Обозначим 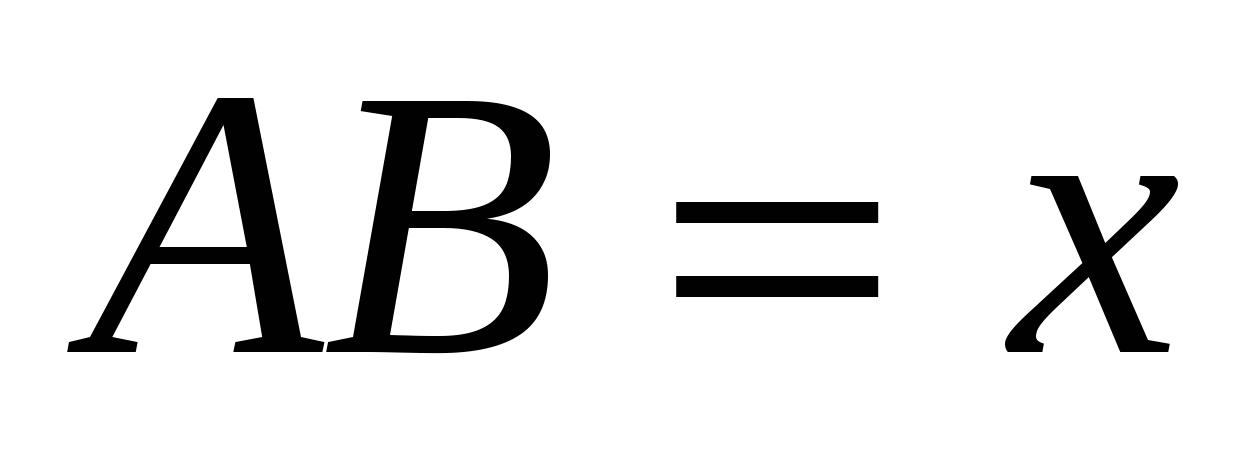 и
и 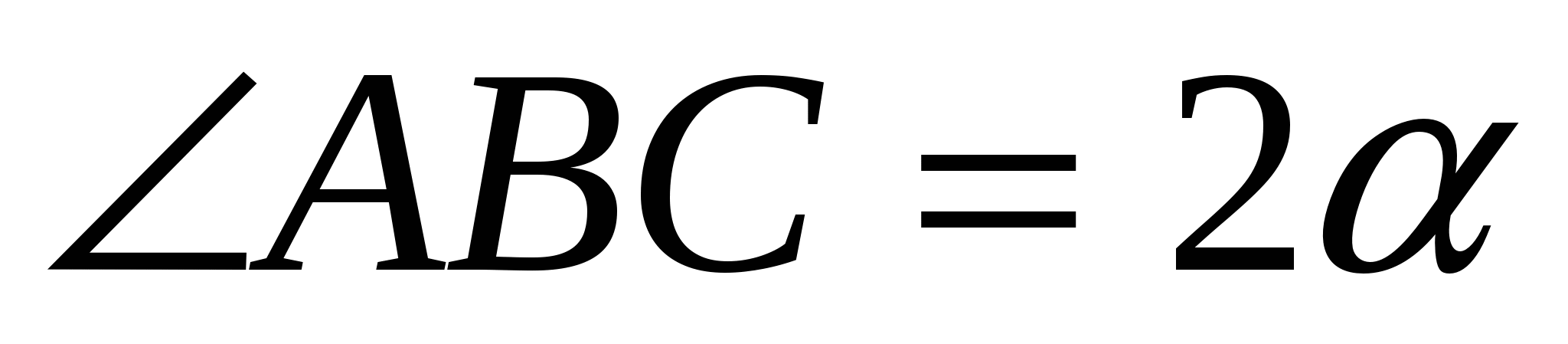 .
.
Применим теорему косинусов к треугольникам ABE и BCE, получим:
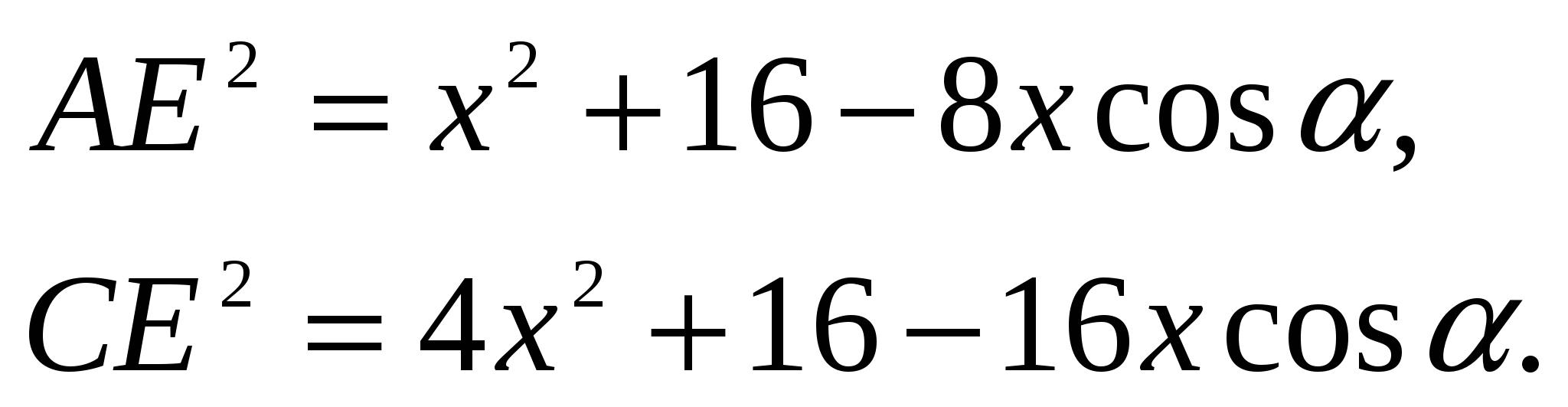
Учитывая, что 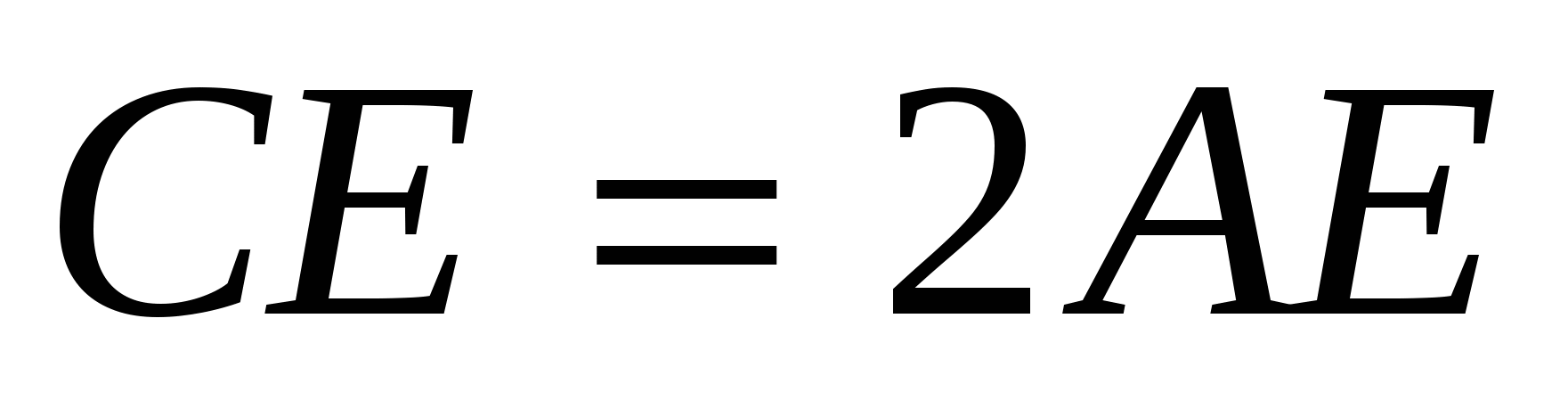 или
или 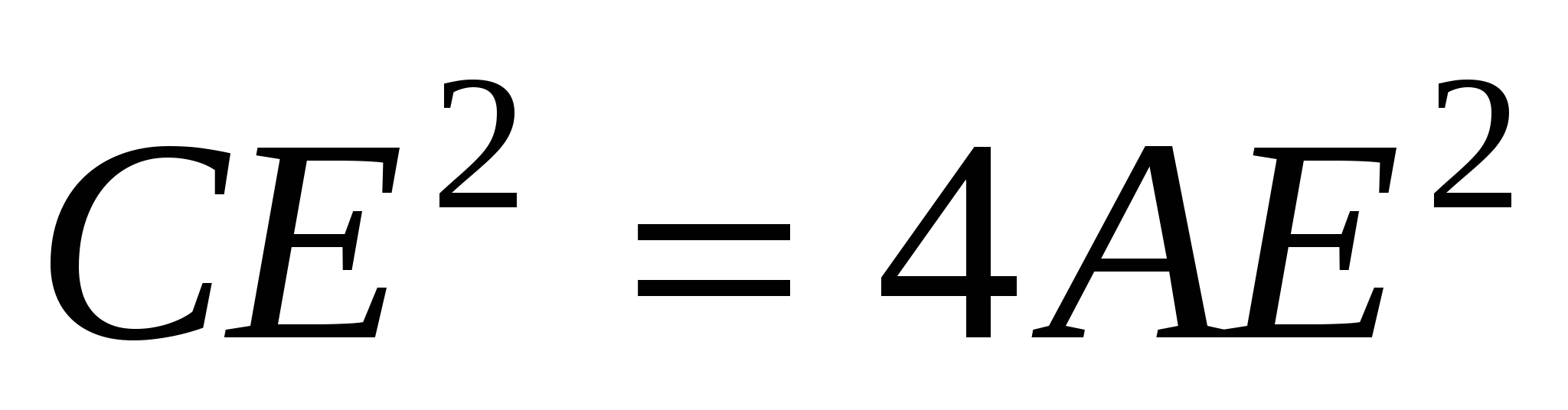 , получаем, что
, получаем, что 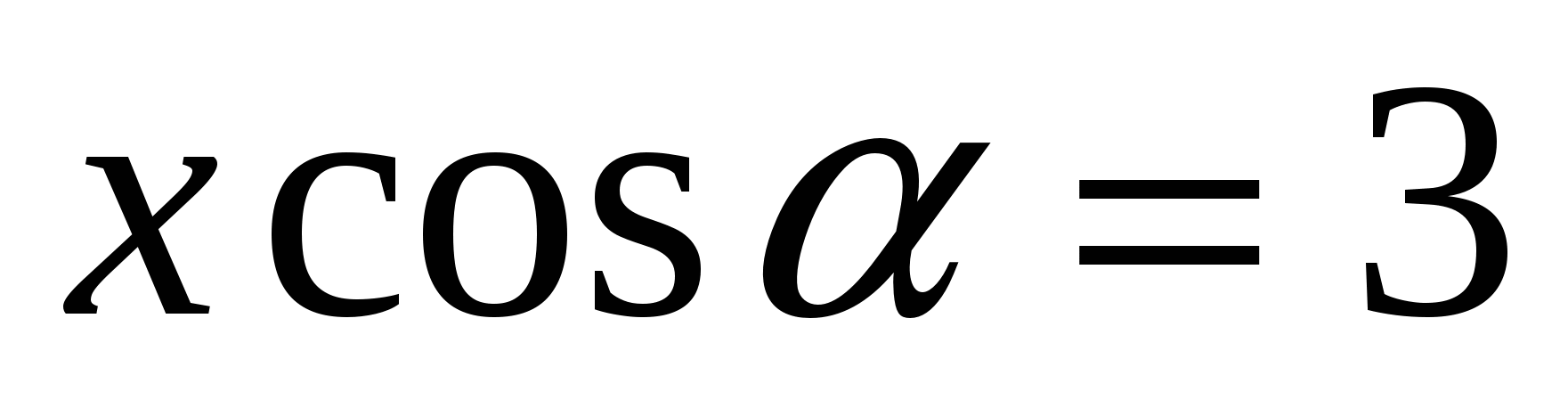 . Но
. Но 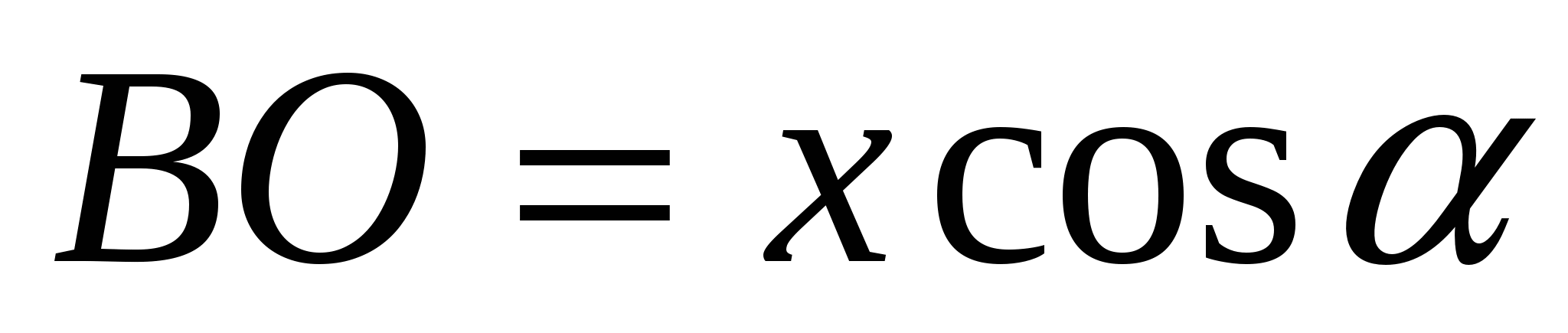 из треугольника АВО, то есть ВО = 3 и ОЕ= 1.
из треугольника АВО, то есть ВО = 3 и ОЕ= 1.
Далее, используя теорему Пифагора для треугольников АОВ и АОЕ, находим АВ и АЕ, а затем стороны 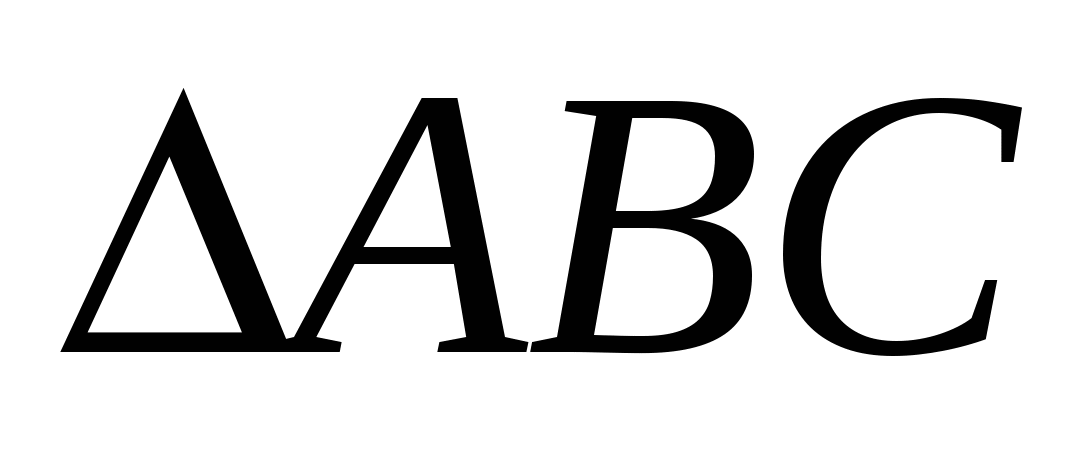 .
.
Геометрический метод
Проведем среднюю линию DK в треугольнике ВСЕ. Отсюда 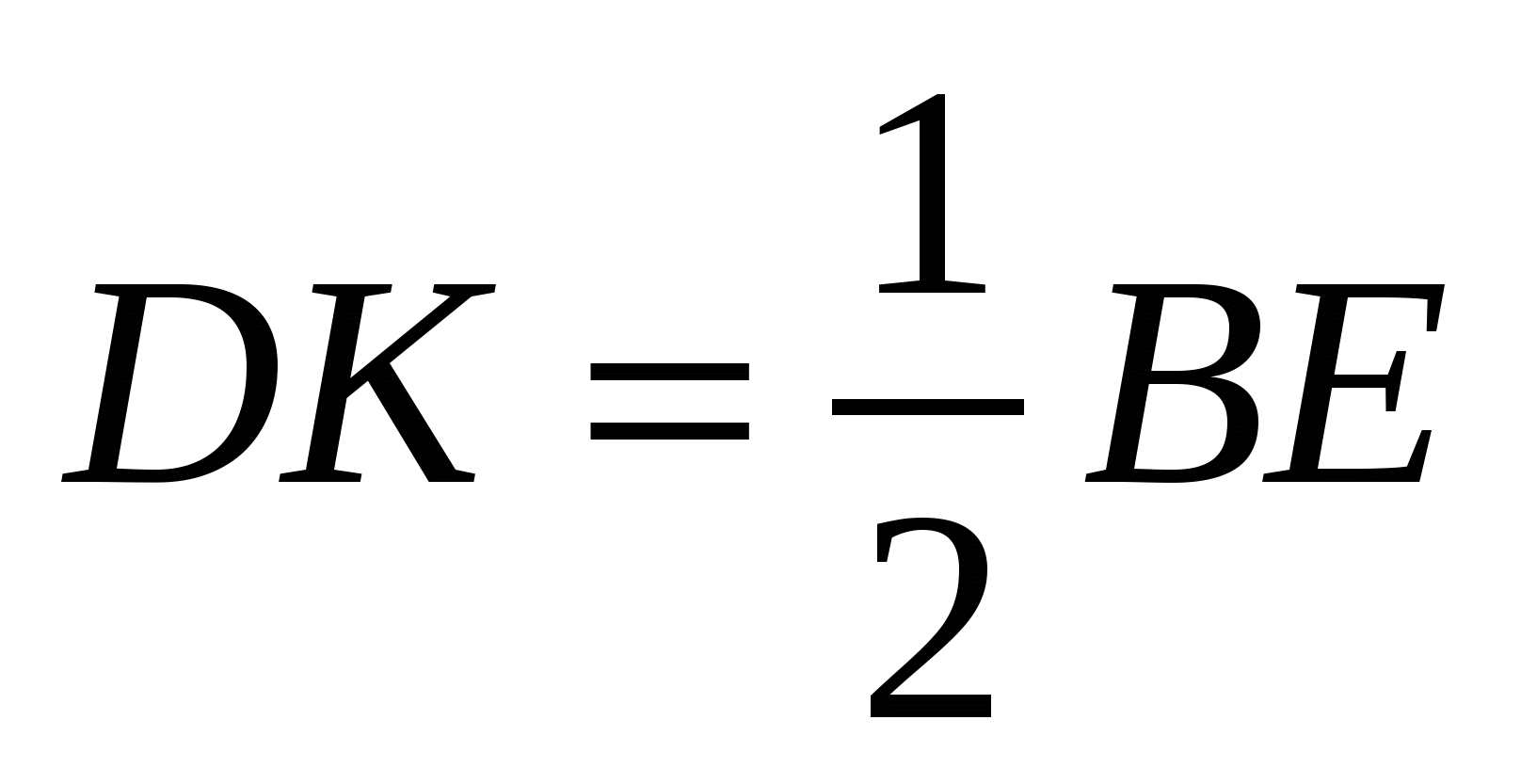 .
.
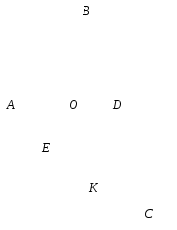
В треугольнике АDK ОЕ является средней линией, так как DK||ВЕ и АО = ОD.
Отсюда 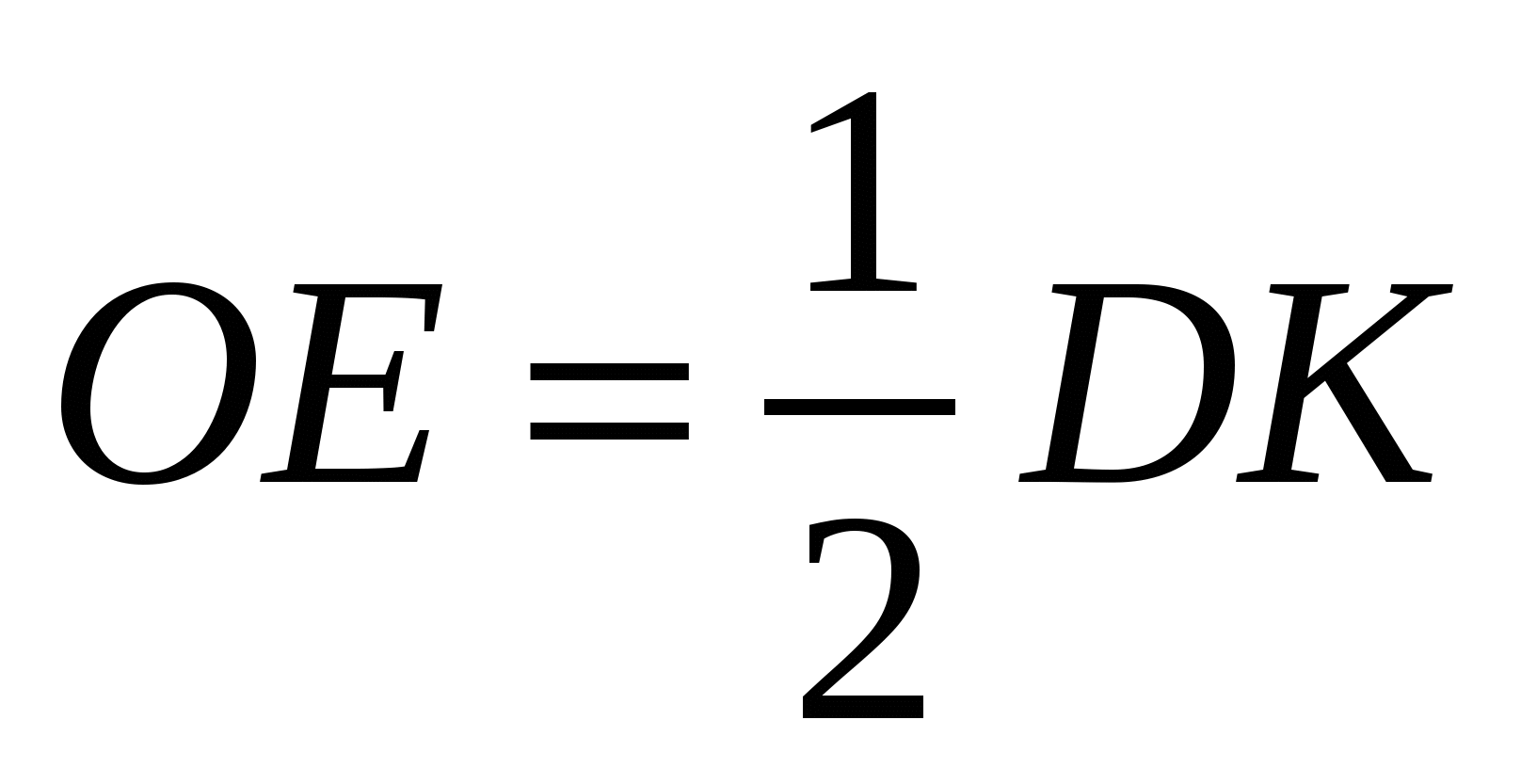 . Следовательно,
. Следовательно, ![]() . Значит,
. Значит, 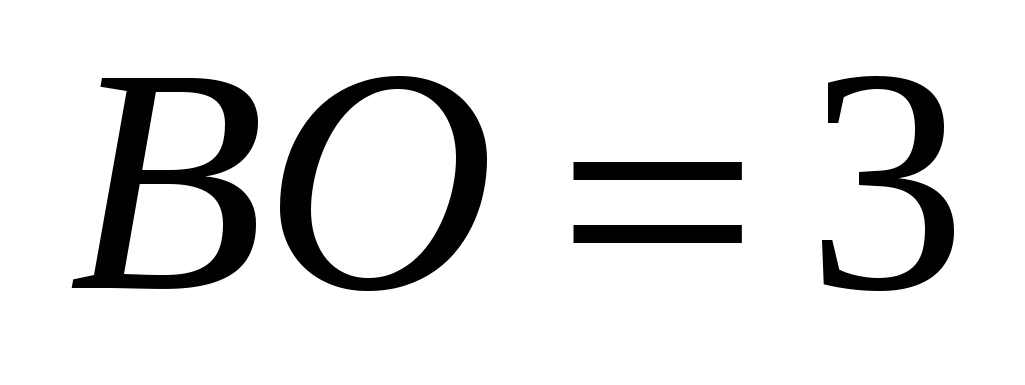 .
.
Далее, применяя теорему Пифагора, из треугольников АОВ и АОЕ находим АВ и АЕ, а затем и стороны треугольника АВС.
Решение этой задачи с использованием метода геометрических преобразований было рассмотрено в задаче 2(п. 1.5).
III. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
3.1. Векторный метод
1. Диагонали параллелограмма АВСD пересекаются в точке О. Найти площадь параллелограмма, если АВ = а, ВС b и 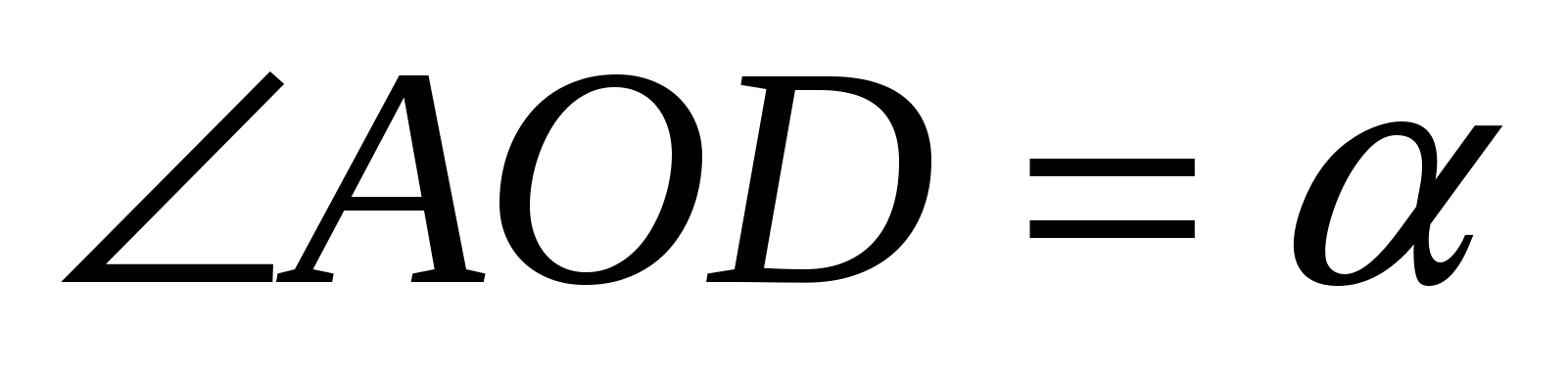 .
.
(Ответ: 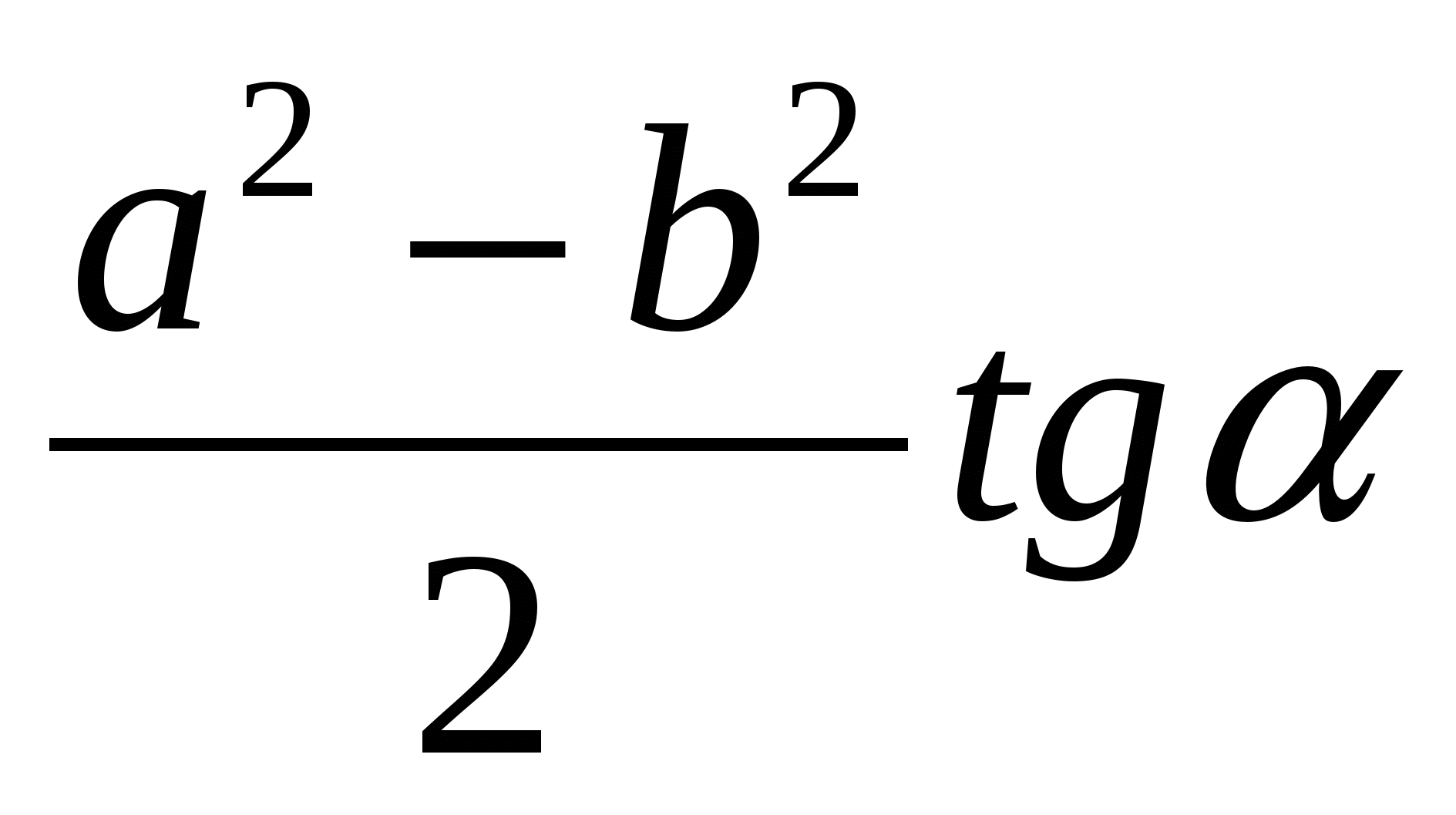 )
)
2. На стороне АВ треугольника АВС взята точка М, такая, что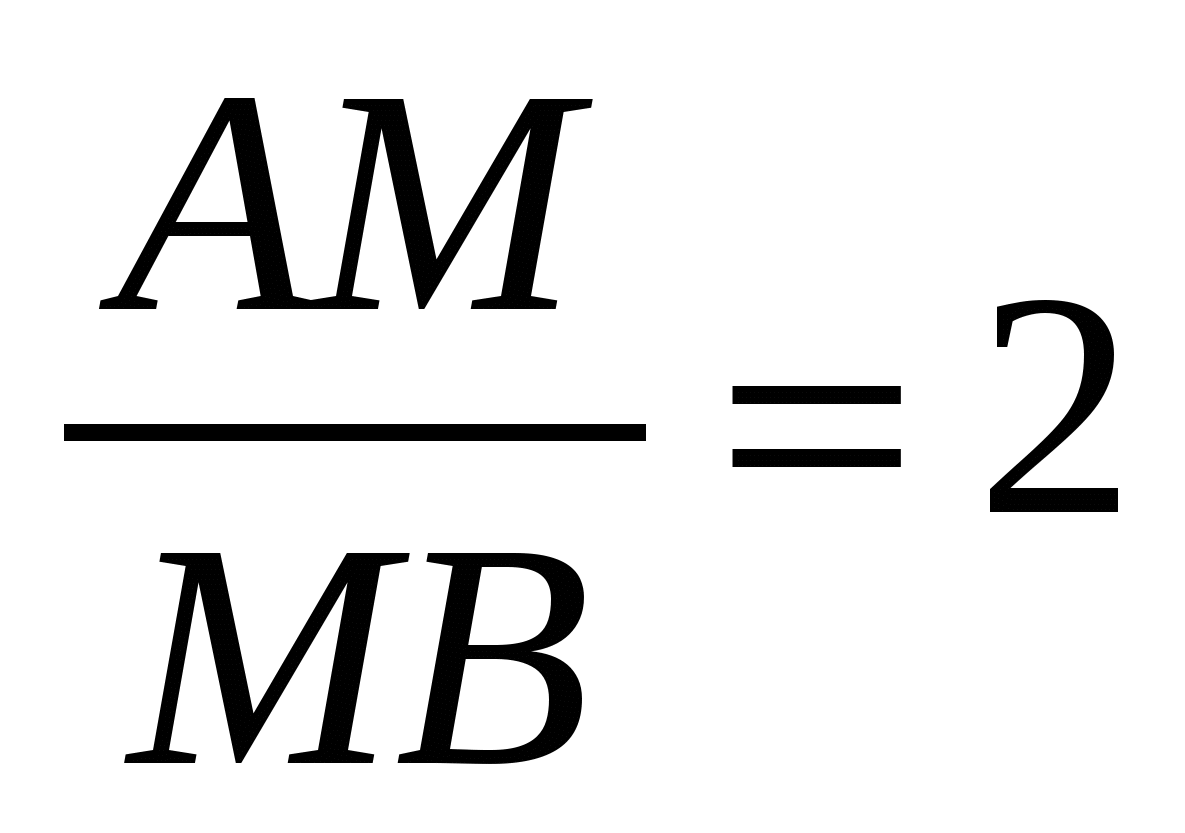 . Найти длину СМ, если
. Найти длину СМ, если 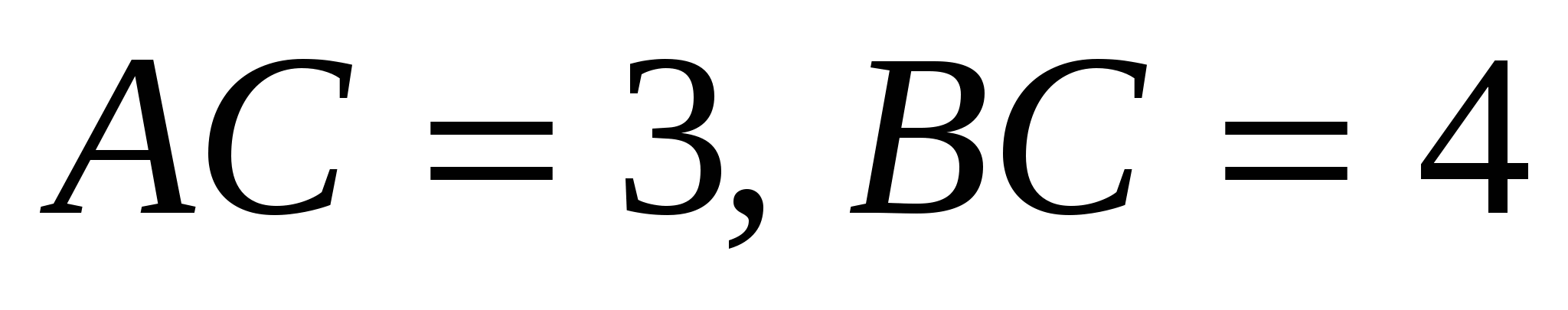 и АСВ=120.
и АСВ=120.
(Ответ: 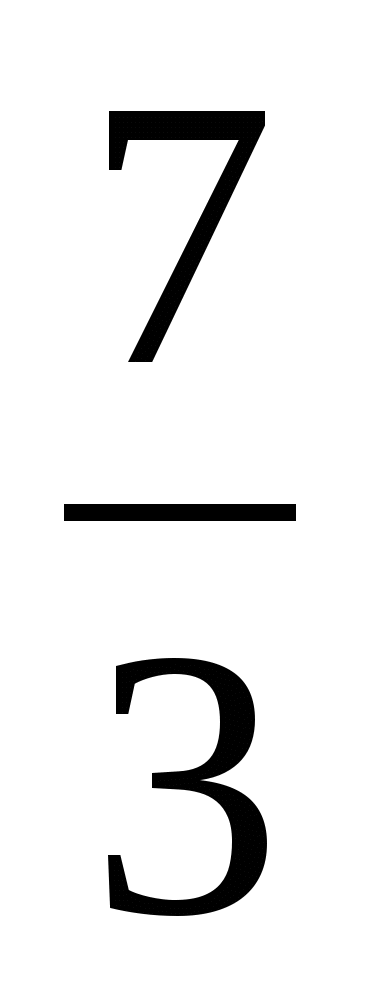 )
)
3. Ребро правильного тетраэдра АВСD равно 4. Найти скалярное произведение 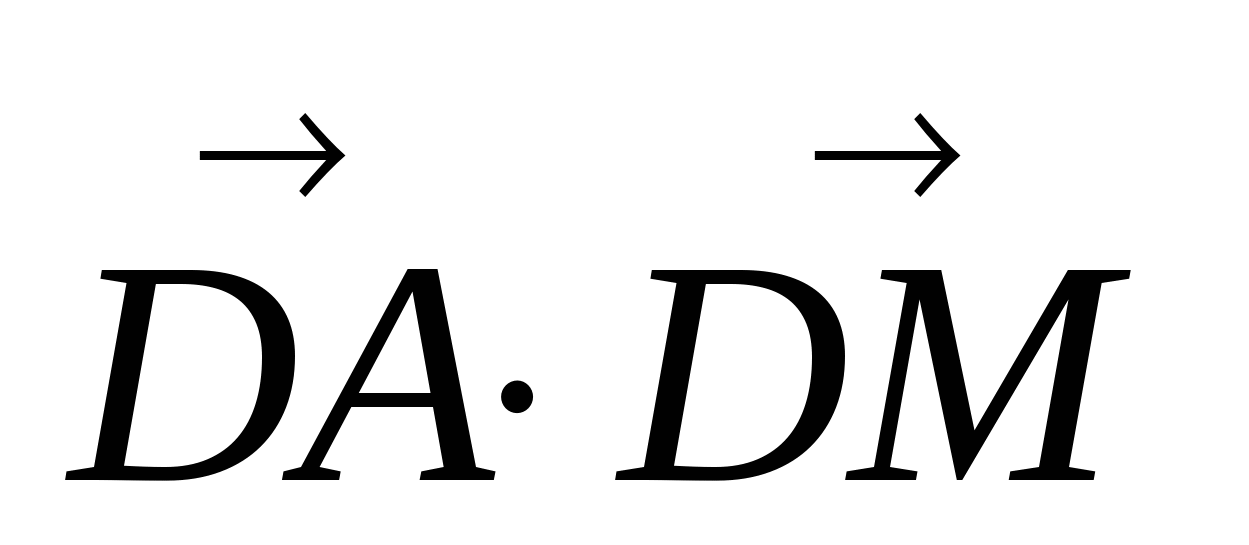 , где М - середина СD.
, где М - середина СD.
(Ответ: 4)
4. Площадь полной поверхности правильной треугольной призмы 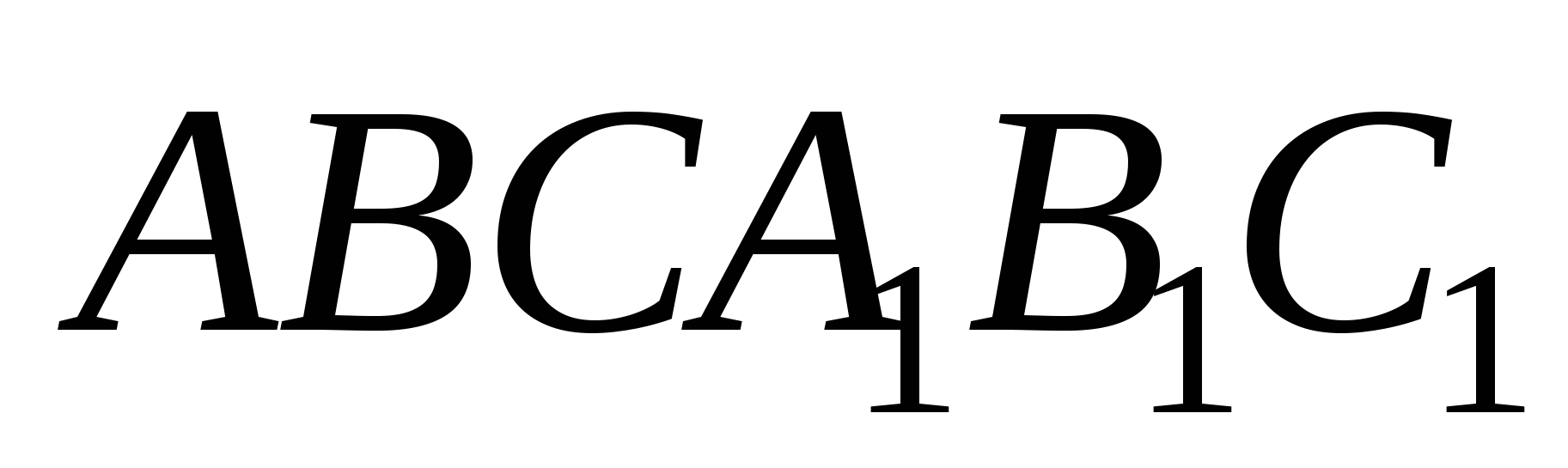 в 2 раза больше ее боковой поверхности. Найти угол между прямыми
в 2 раза больше ее боковой поверхности. Найти угол между прямыми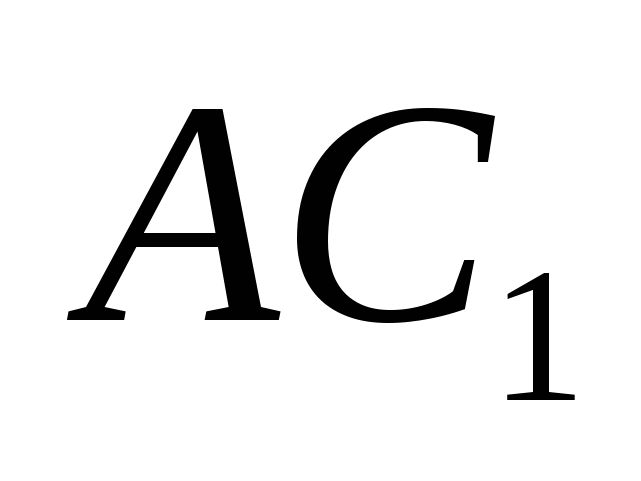 и
и  .
.
(Ответ: 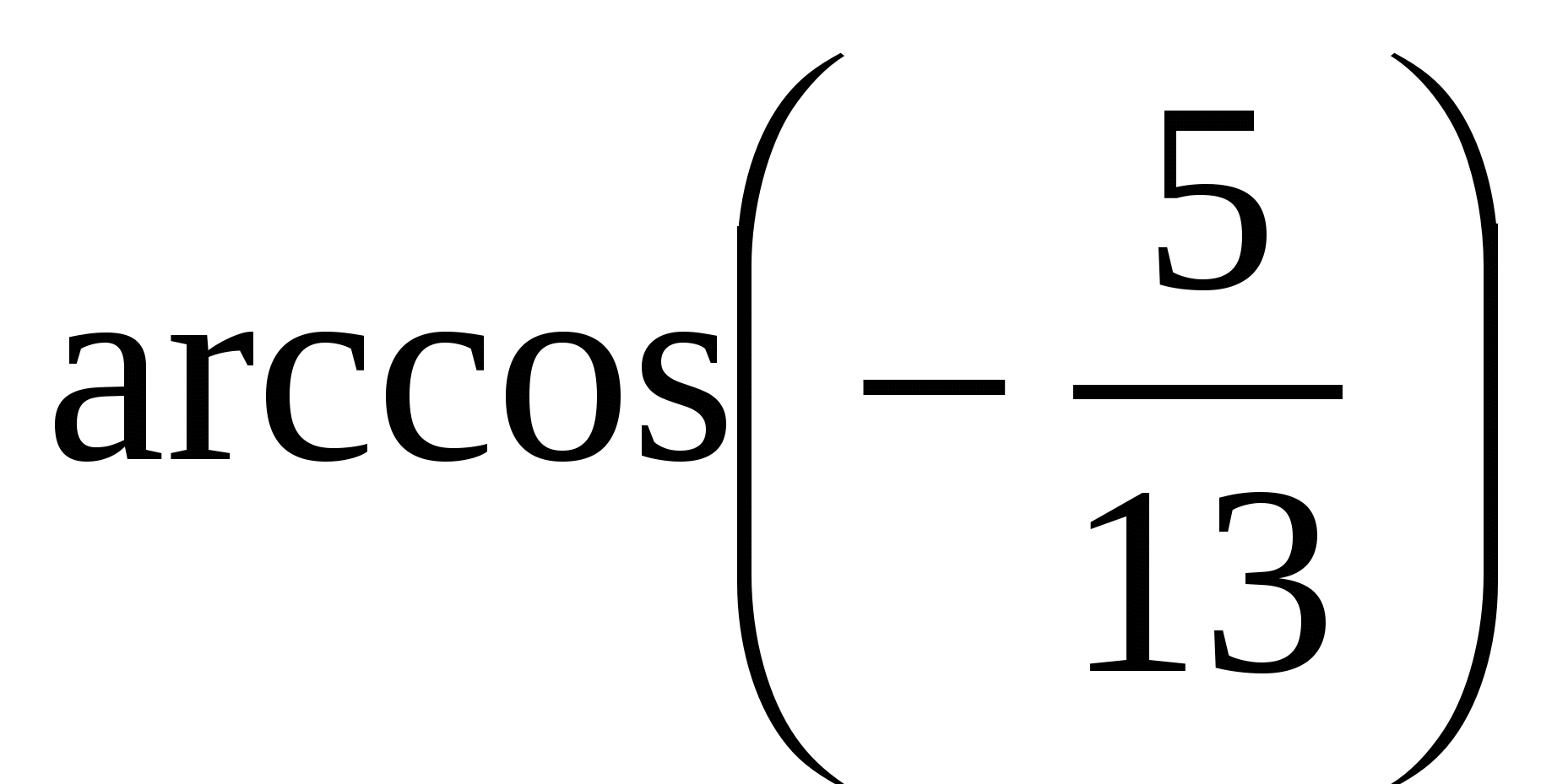 )
)
5. Найдите длину медианы СD треугольника АВС, зная, что 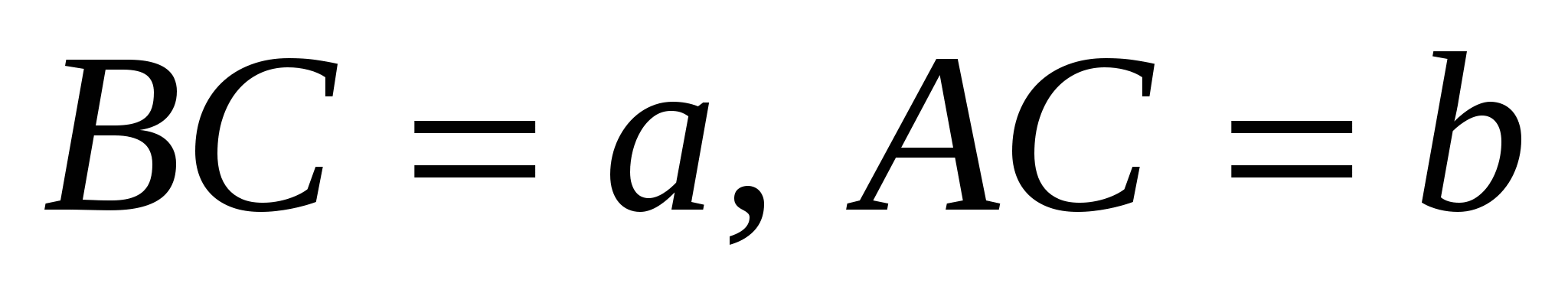 и
и 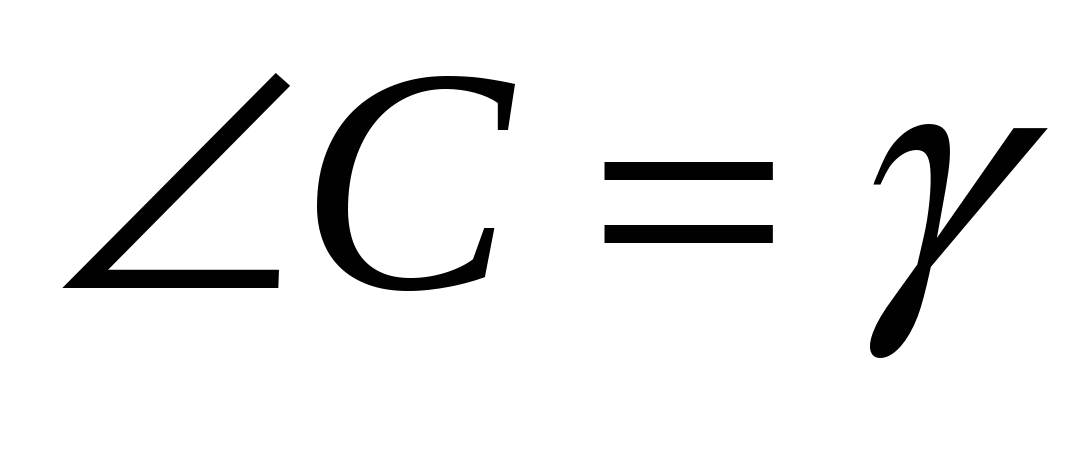 .
.
(Ответ: 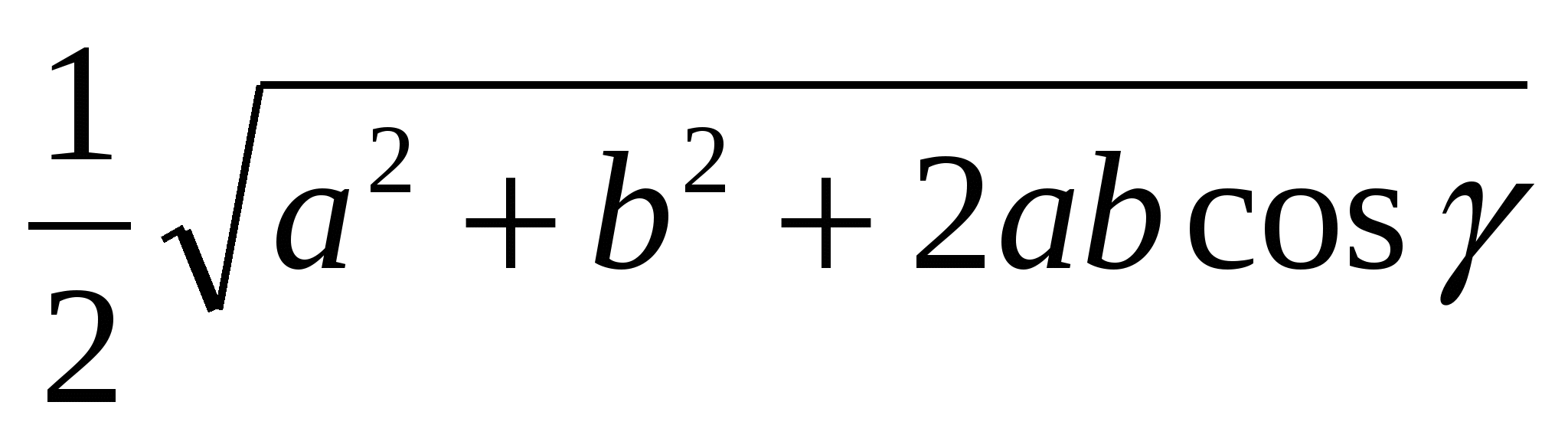 )
)
6. Определить, при каком значении х верно векторное равенство  =
= 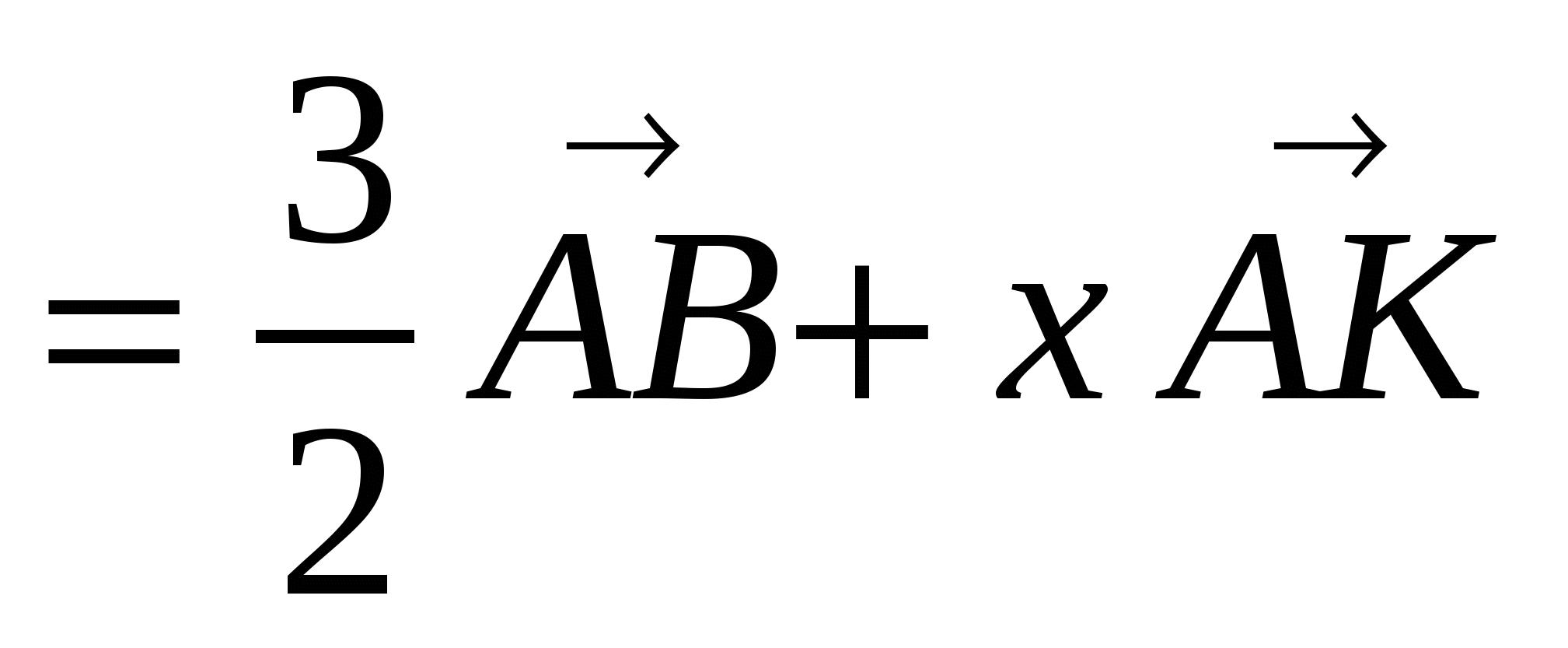 , если АK и СМ - медианы треугольника АВС.
, если АK и СМ - медианы треугольника АВС.
(Ответ: х = -2)
7. Определить 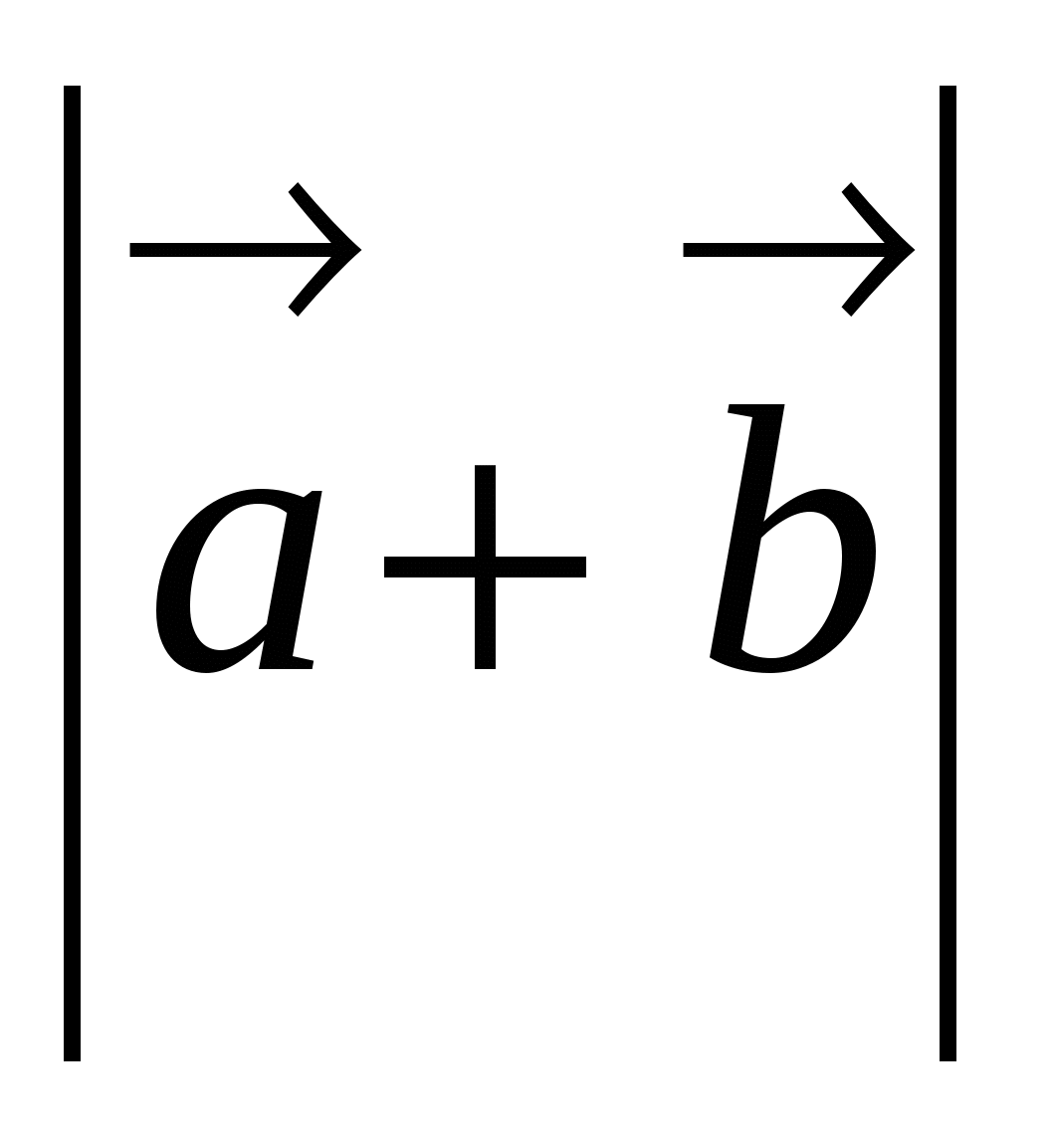 , если
, если 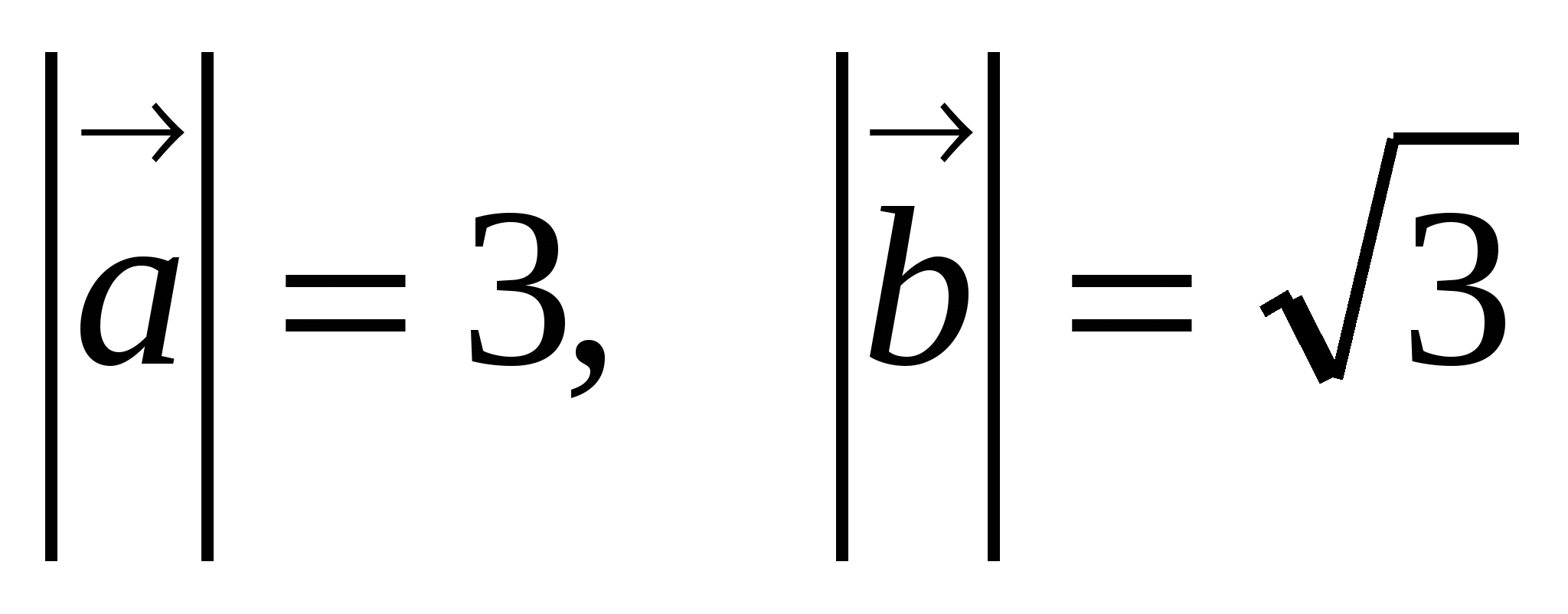 , а угол между векторами
, а угол между векторами 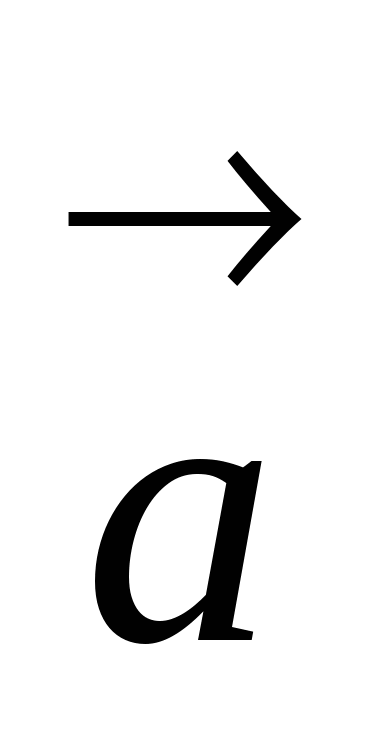 и
и 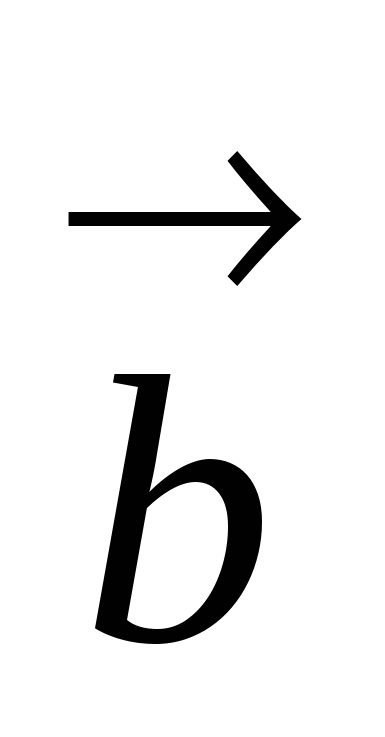 равен 210.
равен 210.
(Ответ:  )
)
8. Доказать, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей.
9. Найти х, при котором выполняется векторное равенство 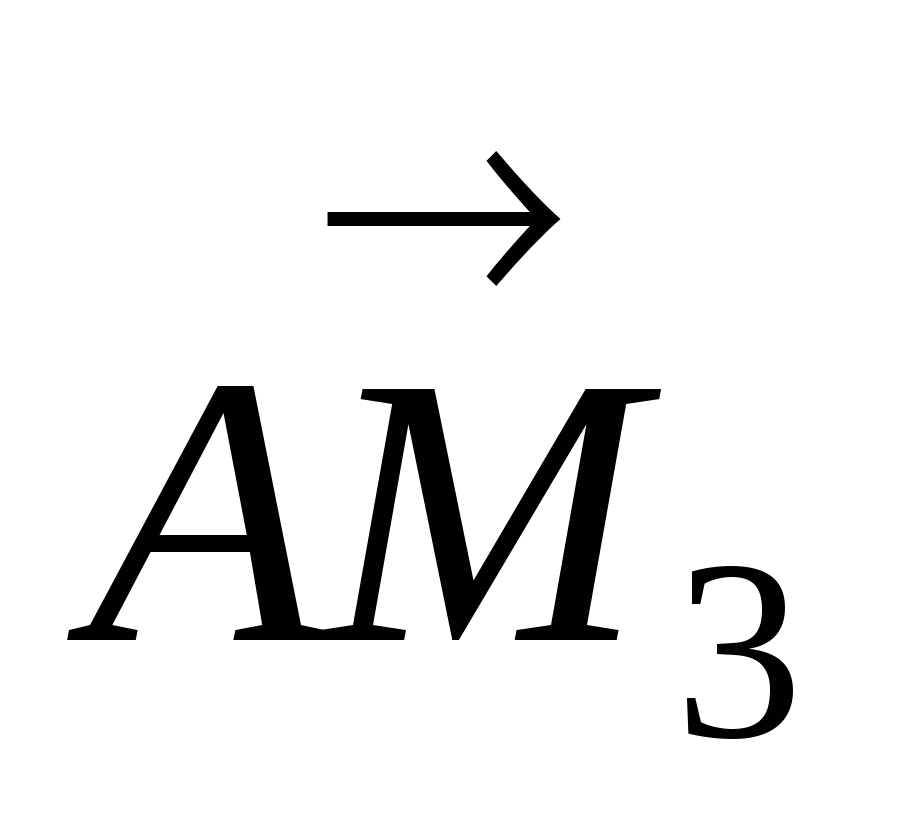 =
= 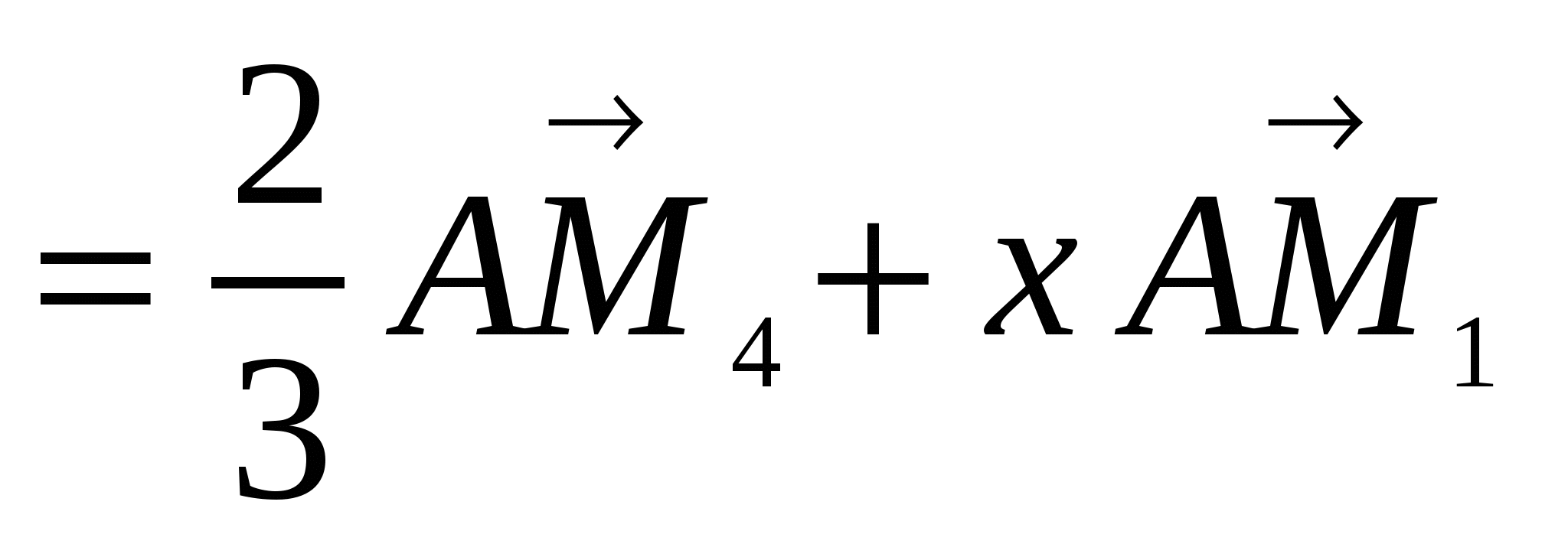 , где точки
, где точки 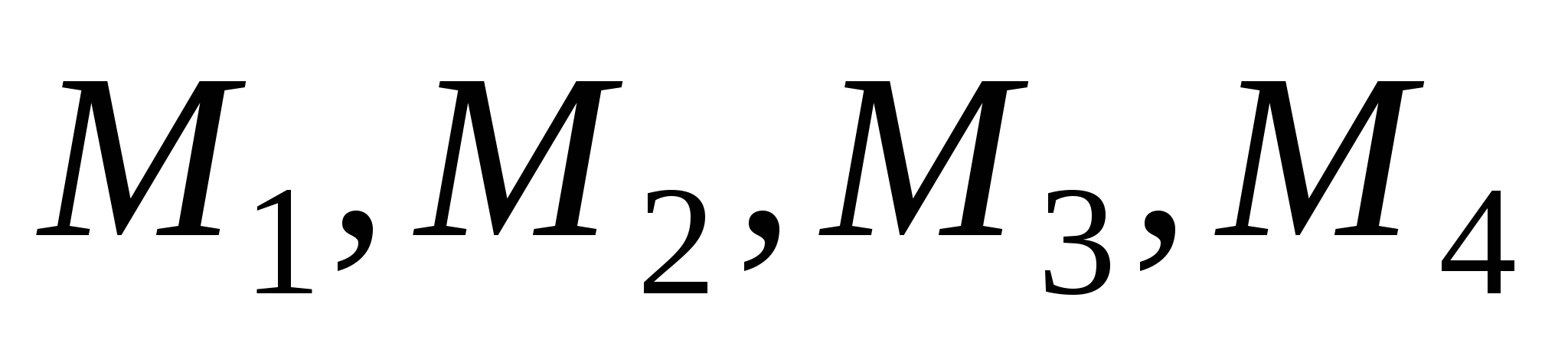 расположены на одной прямой так, что
расположены на одной прямой так, что 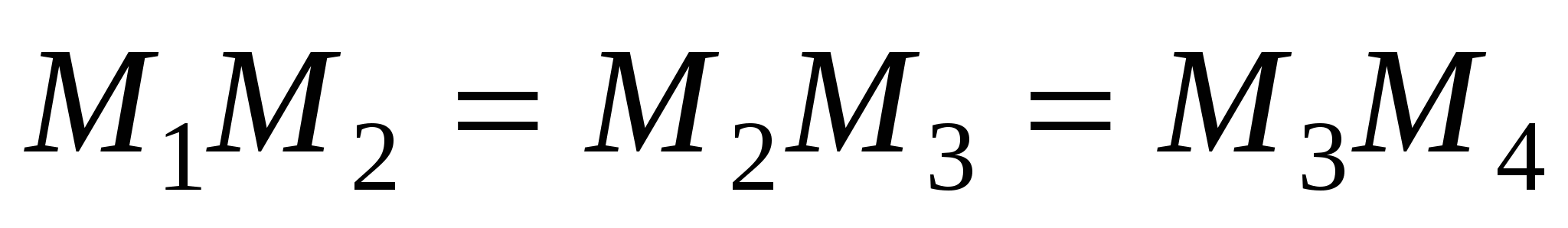 , а точка А не лежит на этой прямой.
, а точка А не лежит на этой прямой.
(Ответ: х = 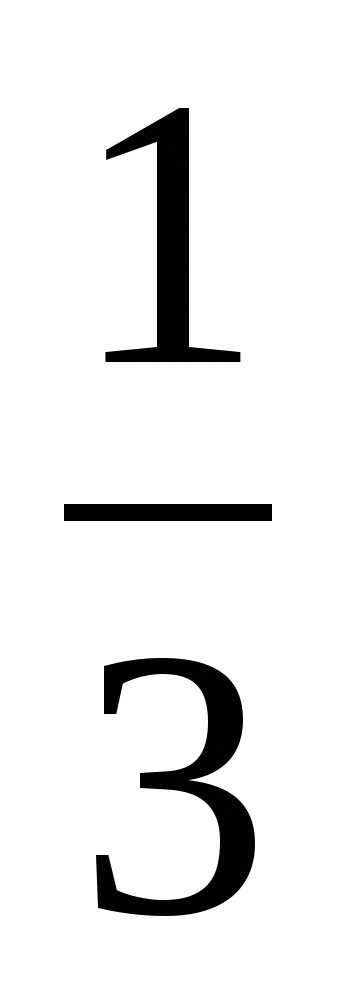 )
)
10. Найти угол между векторами 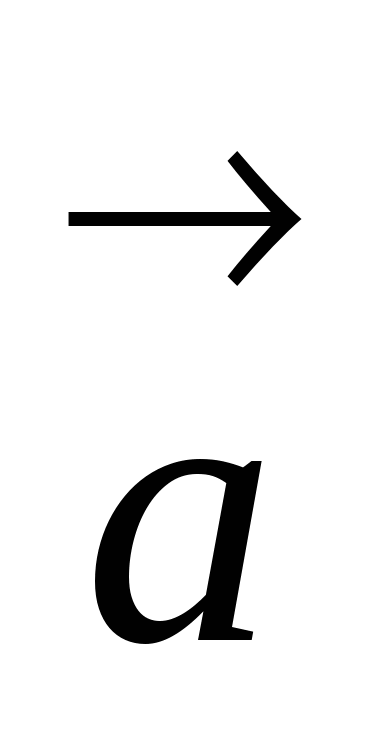 и
и 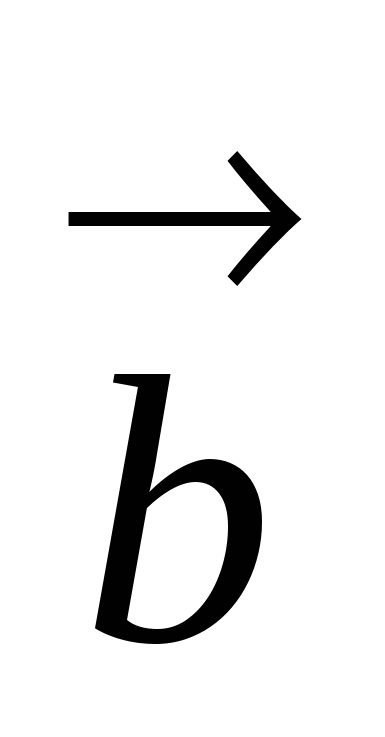 , если известно, что векторы
, если известно, что векторы 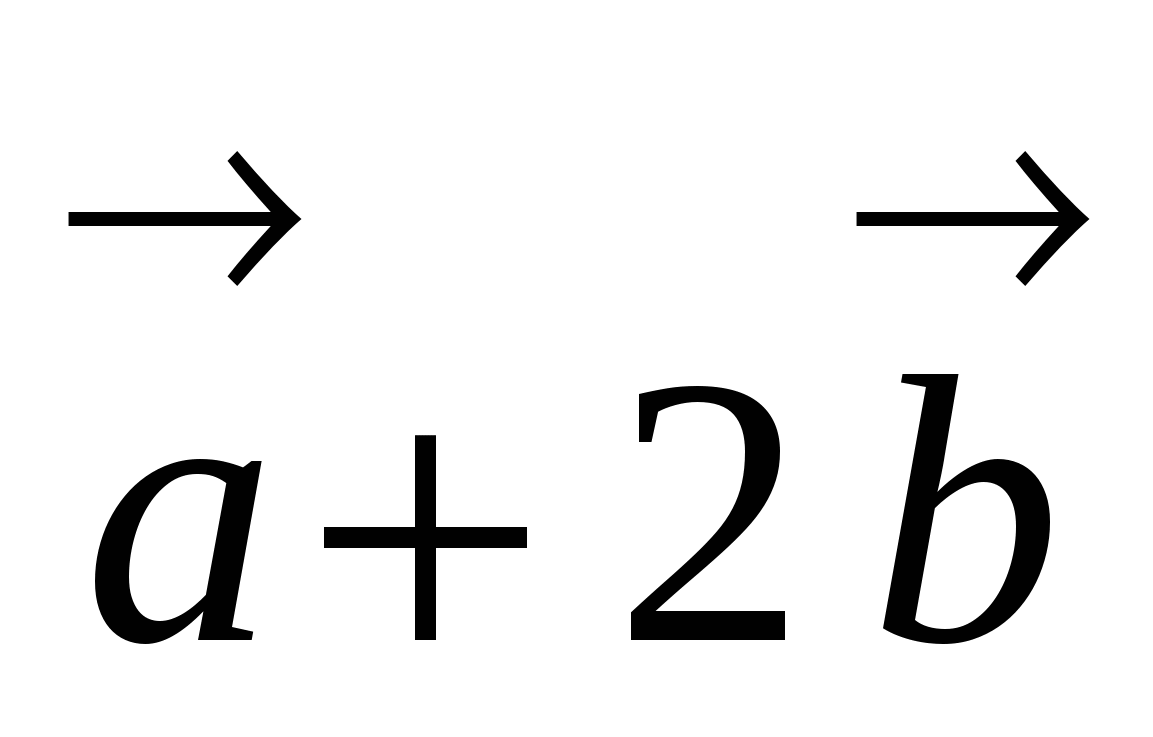 и
и 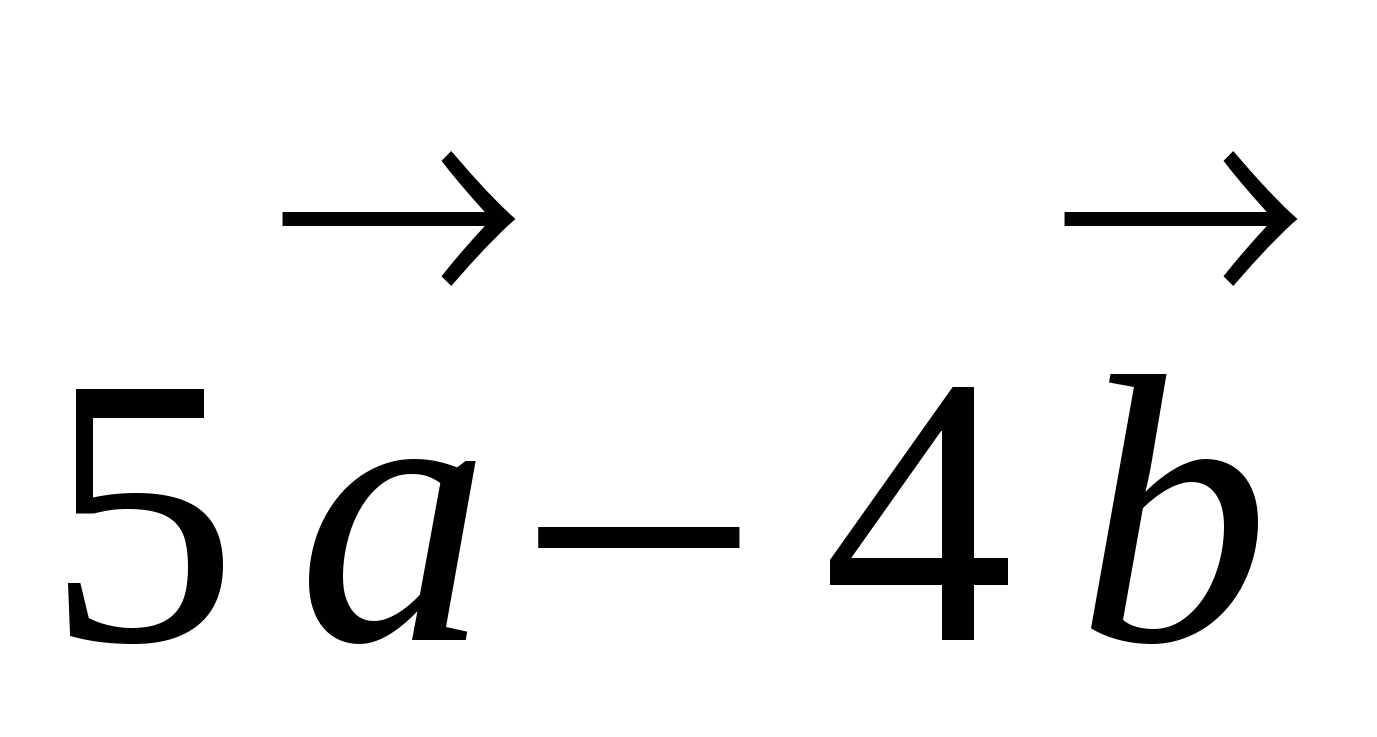 взаимно перпендикулярны.
взаимно перпендикулярны.
(Ответ: 60)
3.2. Координатный метод
1. В треугольнике с вершинами А(1;2;4), В(4;5;2) и С(2;3;4) найти длину медианы АD.
(Ответ: 3)
2. В ромб АВСD, сторона которого равна 2 и угол А равен 60, вписана окружность. Докажите, что для любой точки Р окружности 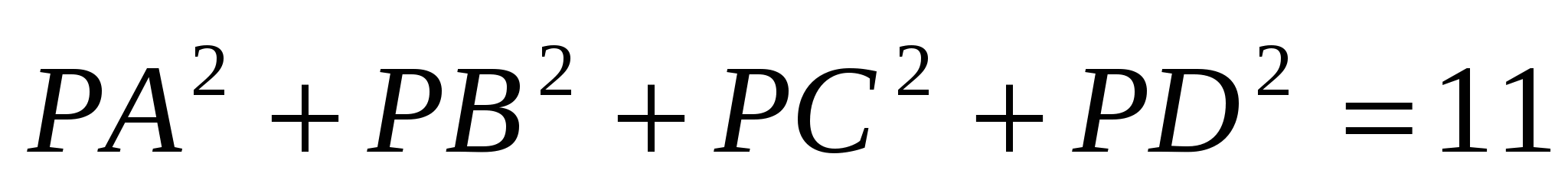 .
.
3. Найти стороны параллелограмма АВСD, если известны координаты двух его противоположных вершин А(-2; 1), С(6; -1) и точка
М(2; -2), являющаяся серединой стороны АВ.
(Ответ: 10; 4)
4. Доказать, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей.
5. Медиана, проведенная к основанию равнобедренного треугольника равна 160, а основание треугольника равно 80. Найти две другие медианы.
(Ответ: 100; 100)
6. Высота треугольника, равная 10, делит основание на два отрезка, равные 10 и 4. Найти медиану, проведенную к меньшей из двух других сторон.
(Ответ: 13)
7. Известны координаты вершин треугольника АВС:
а) А(1; 2), В(2; 3), С(2,5; 2,5);
б) А(1; 1), В(2; 4), С(8; 3);
в) А(2; 1), В(-1, 3), С(2; 5).
Является ли этот треугольник остроугольным, прямоугольным, тупоугольным?
(Ответ: а) прямоугольный, б) тупоугольный, с) остроугольный)
8. Шар проходит через вершины А и С куба ![]() , ребро которого равно а и через точки Р и Q - середины ребер
, ребро которого равно а и через точки Р и Q - середины ребер 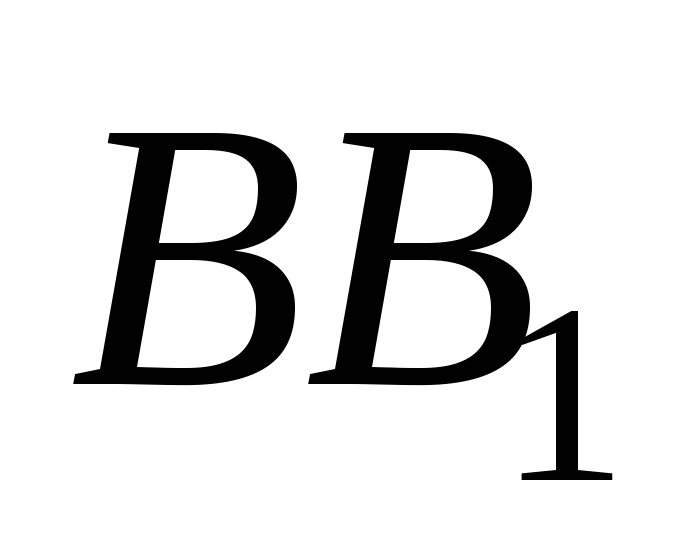 и
и 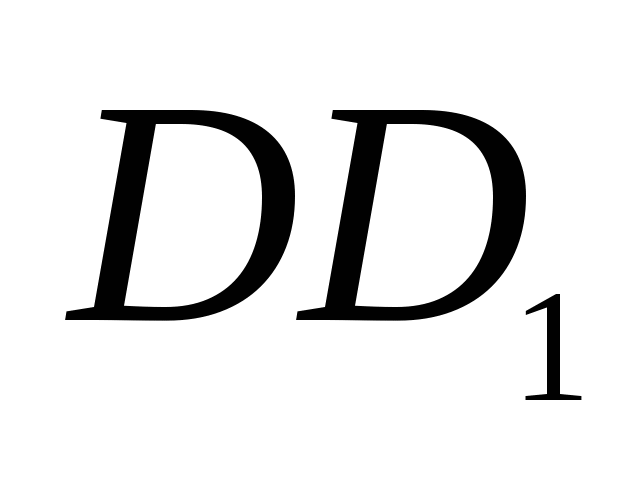 . Найти радиус шара.
. Найти радиус шара.
(Ответ: ![]() )
)
9. Дан куб 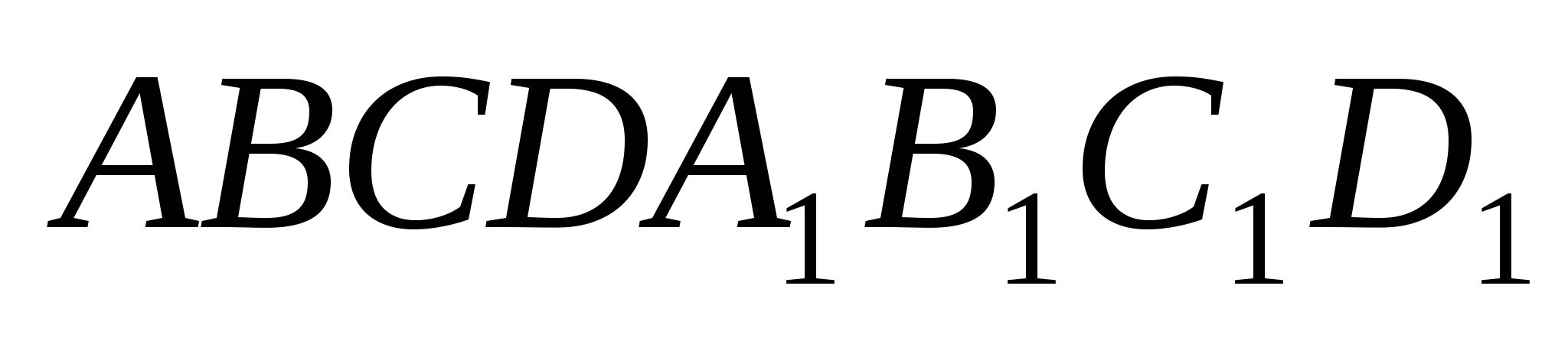 с ребром 1. Найти радиус сферы, проходящей через вершину А, середины ребер DС и
с ребром 1. Найти радиус сферы, проходящей через вершину А, середины ребер DС и ![]() и центр грани
и центр грани 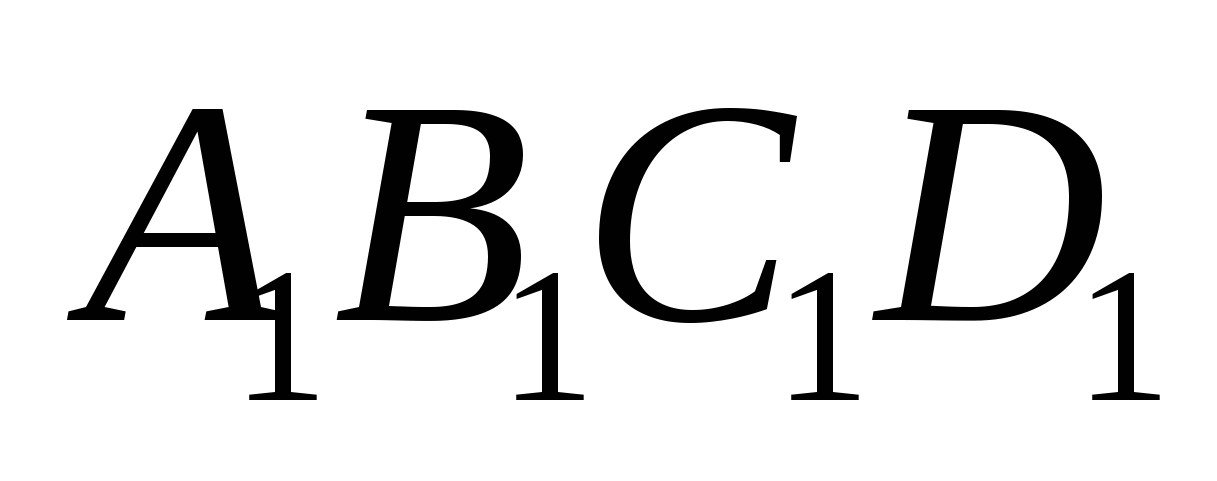 .
.
(Ответ: ![]() )
)
10. В основании правильной треугольной призмы 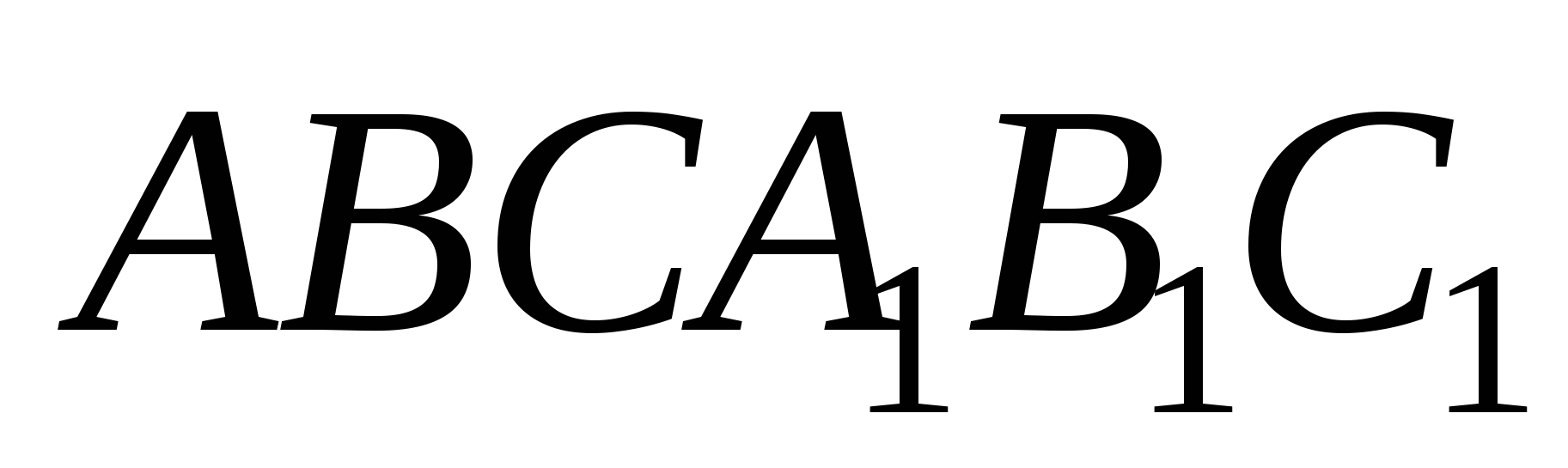 лежит треугольник АВС со стороной, равной а. Боковое ребро призмы равно 2а. На ребре
лежит треугольник АВС со стороной, равной а. Боковое ребро призмы равно 2а. На ребре 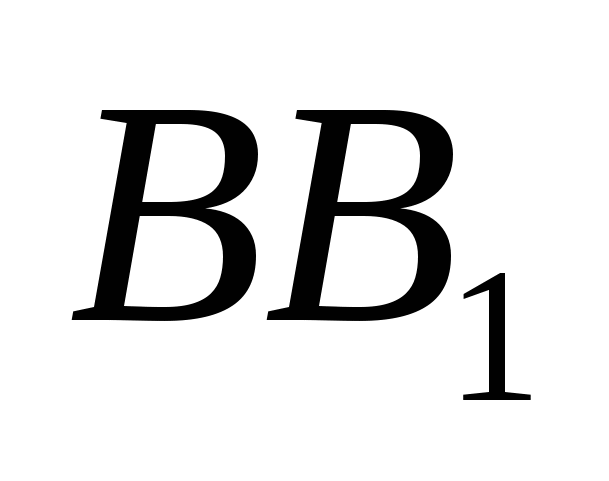 взята точка Р так, что
взята точка Р так, что 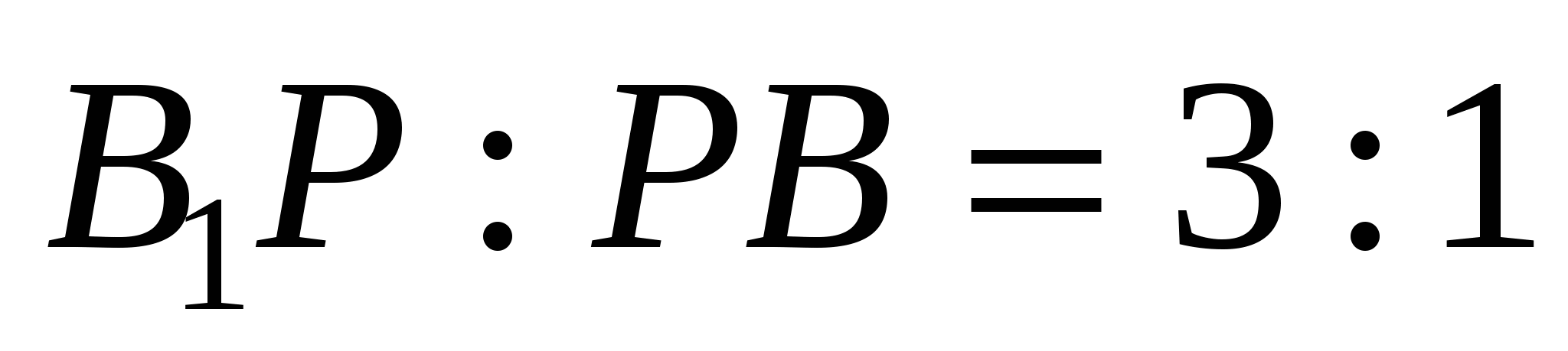 , а на стороне ВС взята точка Q так, что
, а на стороне ВС взята точка Q так, что 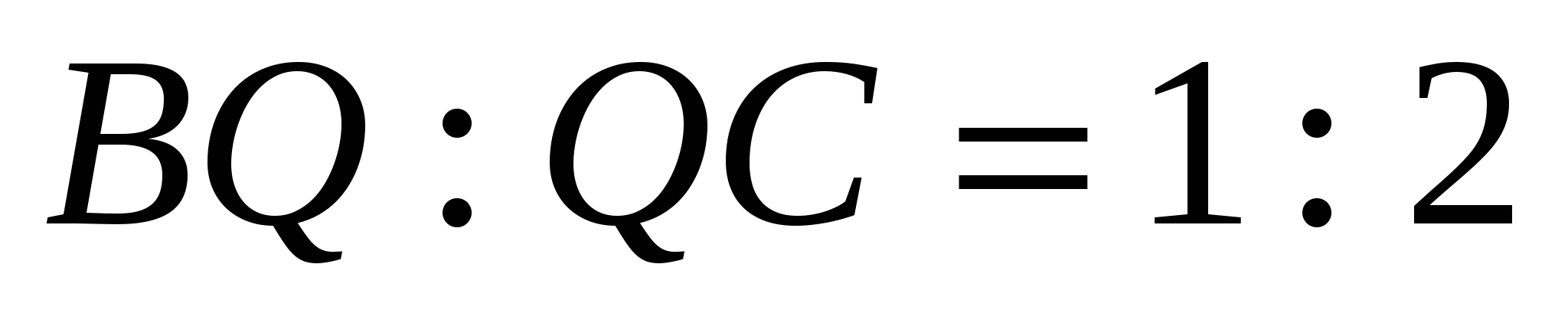 . Через точки
. Через точки 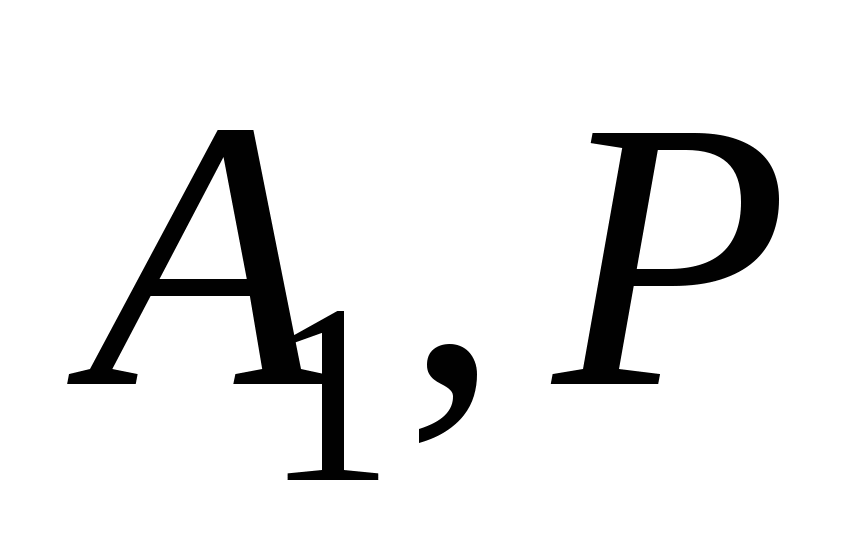 и Q проведена плоскость
и Q проведена плоскость  . Найти радиус шара с центром в точке В, касающегося плоскости
. Найти радиус шара с центром в точке В, касающегося плоскости  .
.
(Ответ: ![]() )
)
3.3. Векторно-координатный метод
1. В кубе 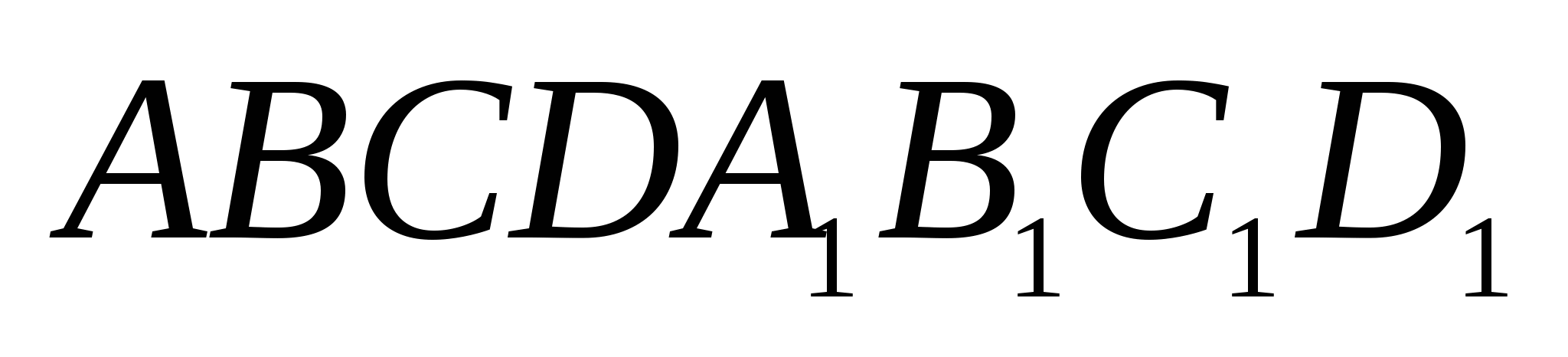 с длиной ребра, равной
с длиной ребра, равной 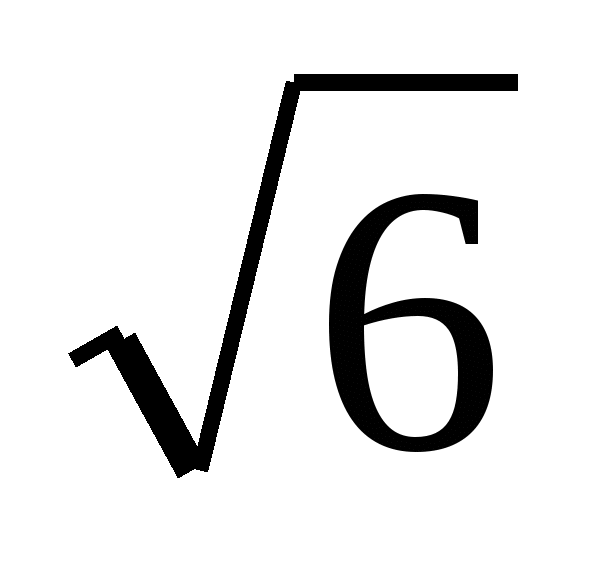 , через диагональ куба
, через диагональ куба ![]() параллельно диагонали основания BD проведена плоскость. Найти тангенс угла наклона ребра AD к этой плоскости и расстояние ребра
параллельно диагонали основания BD проведена плоскость. Найти тангенс угла наклона ребра AD к этой плоскости и расстояние ребра 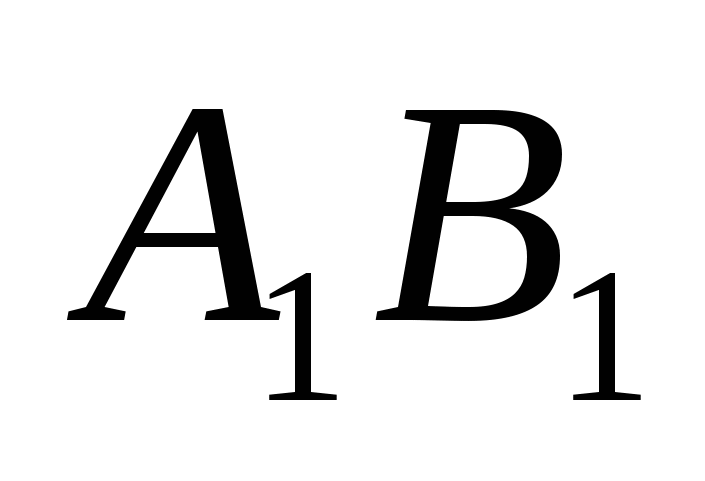 до этой плоскости.
до этой плоскости.
(Ответ: 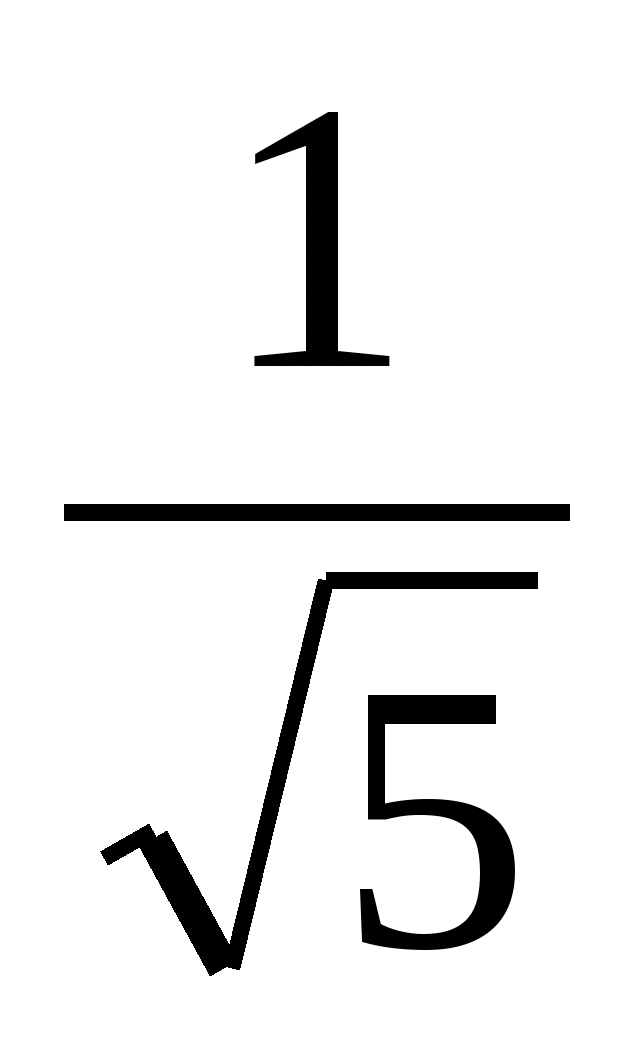 ; 1,5)
; 1,5)
2. Основанием прямоугольного параллелепипеда 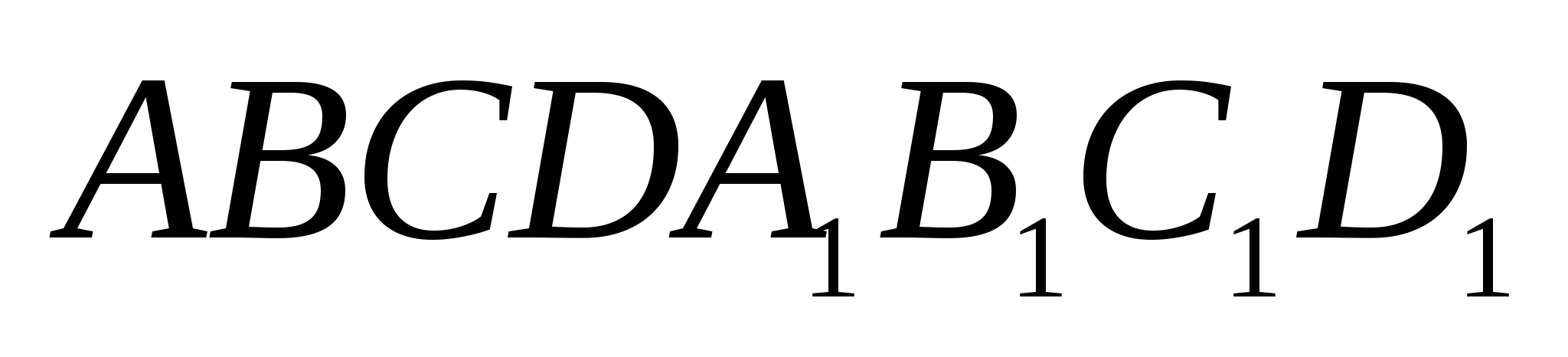 является прямоугольник АВСD со сторонами
является прямоугольник АВСD со сторонами 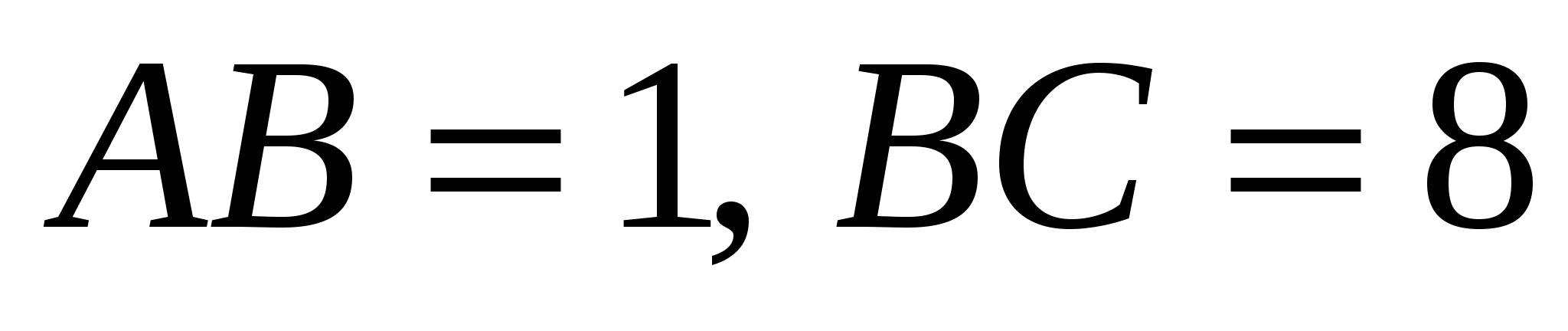 . Боковые ребра имеют длину 2. На отрезке
. Боковые ребра имеют длину 2. На отрезке 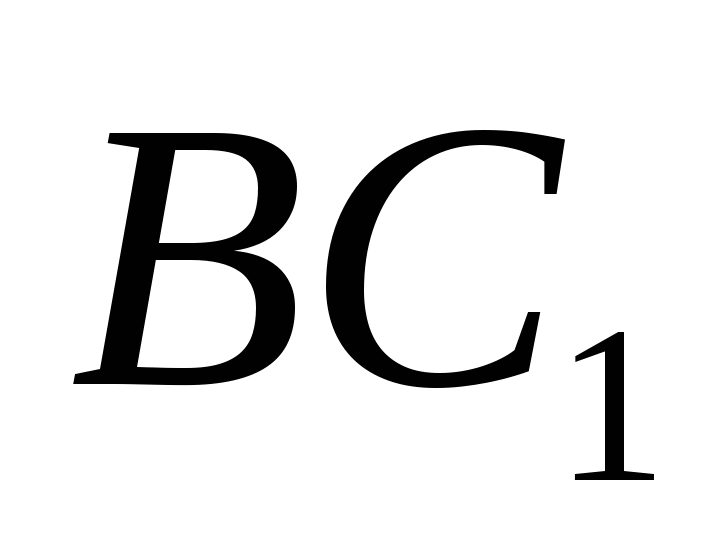 выбрана точка Р так, что угол между векторами
выбрана точка Р так, что угол между векторами 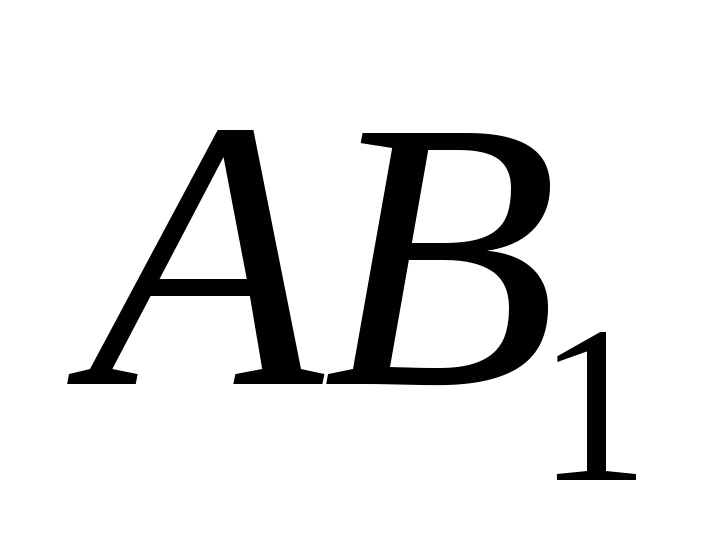 и АР равен
и АР равен 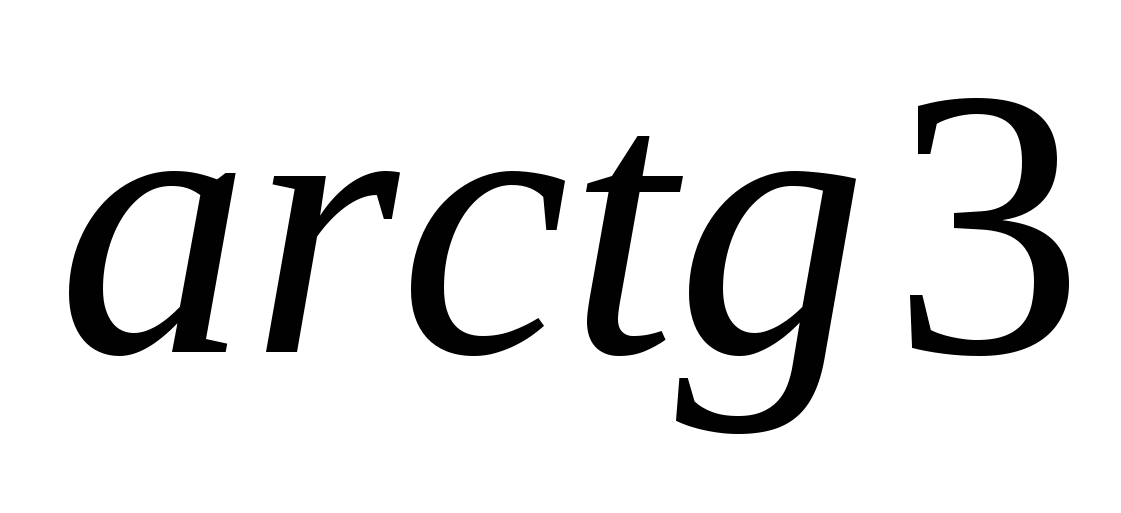 . Найти отношение
. Найти отношение 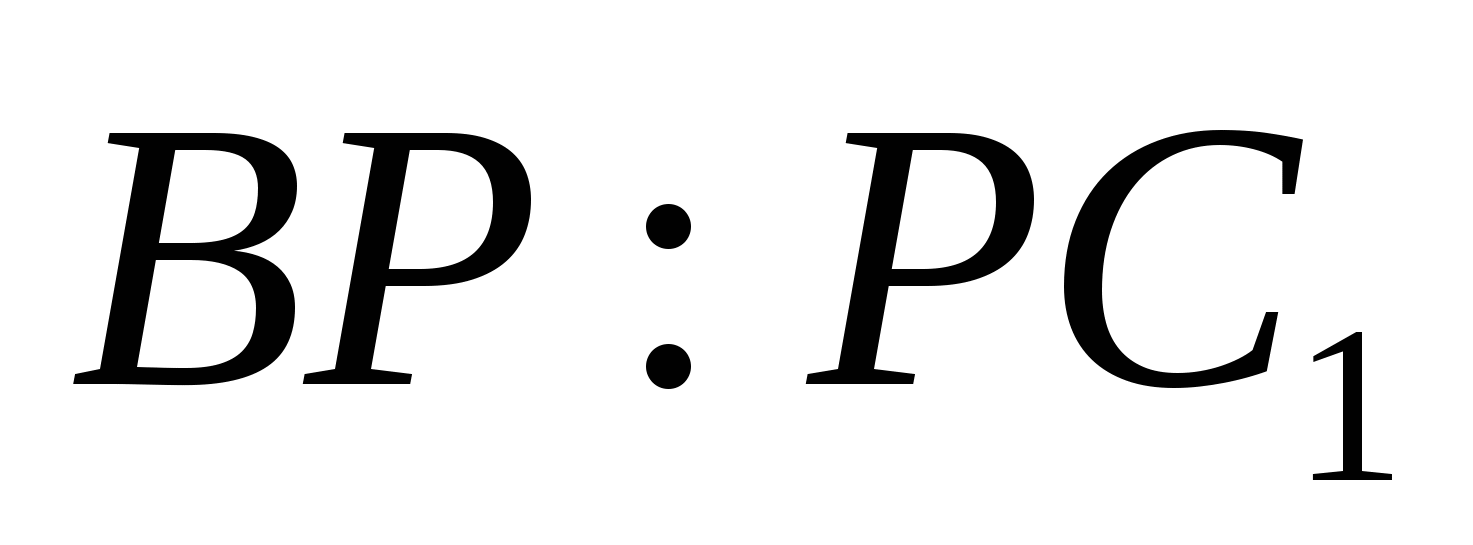 .
.
(Ответ: 1)
3. Основанием прямоугольного параллелепипеда 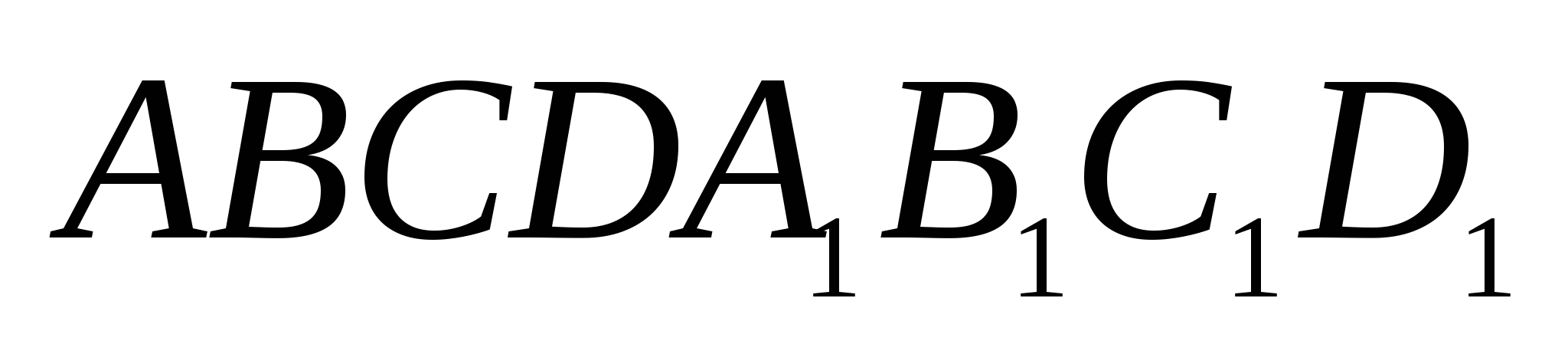 служит прямоугольник АВСD со сторонами
служит прямоугольник АВСD со сторонами 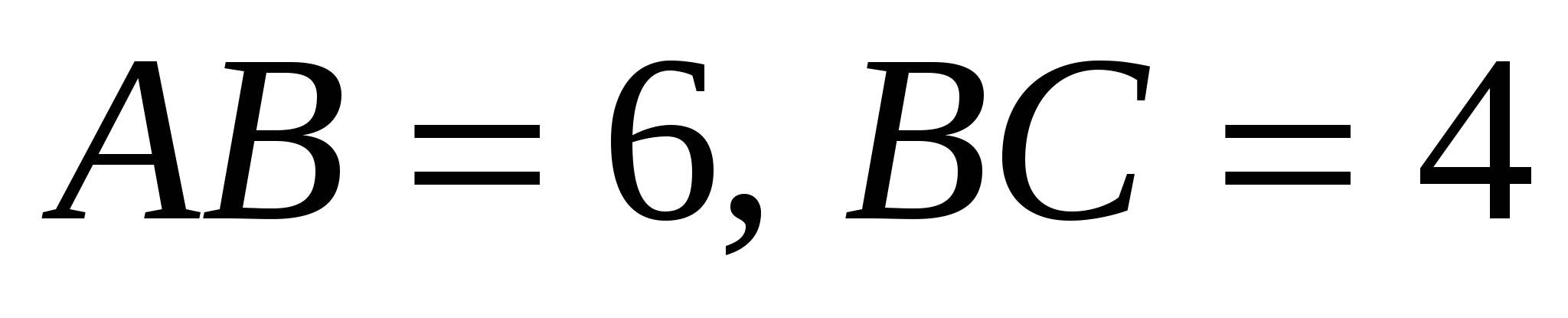 , боковые ребра имеют длину 3. На отрезке
, боковые ребра имеют длину 3. На отрезке 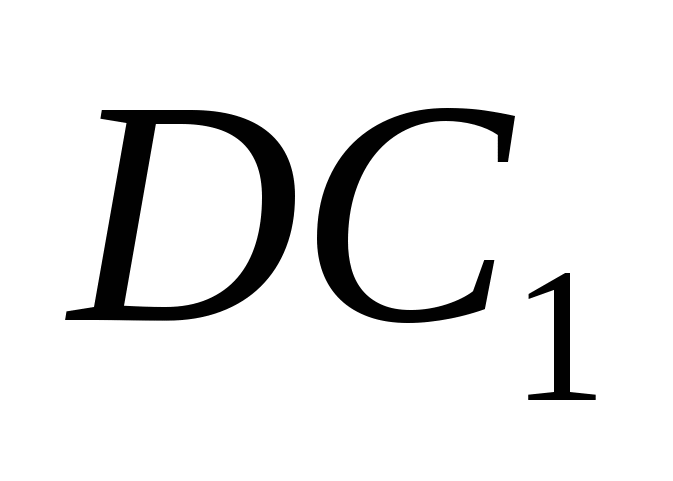 выбрана точка Р так, что угол между векторами
выбрана точка Р так, что угол между векторами 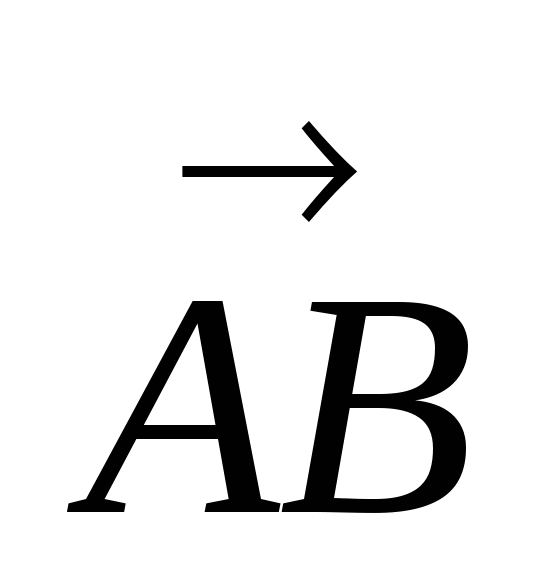 и
и  равен
равен 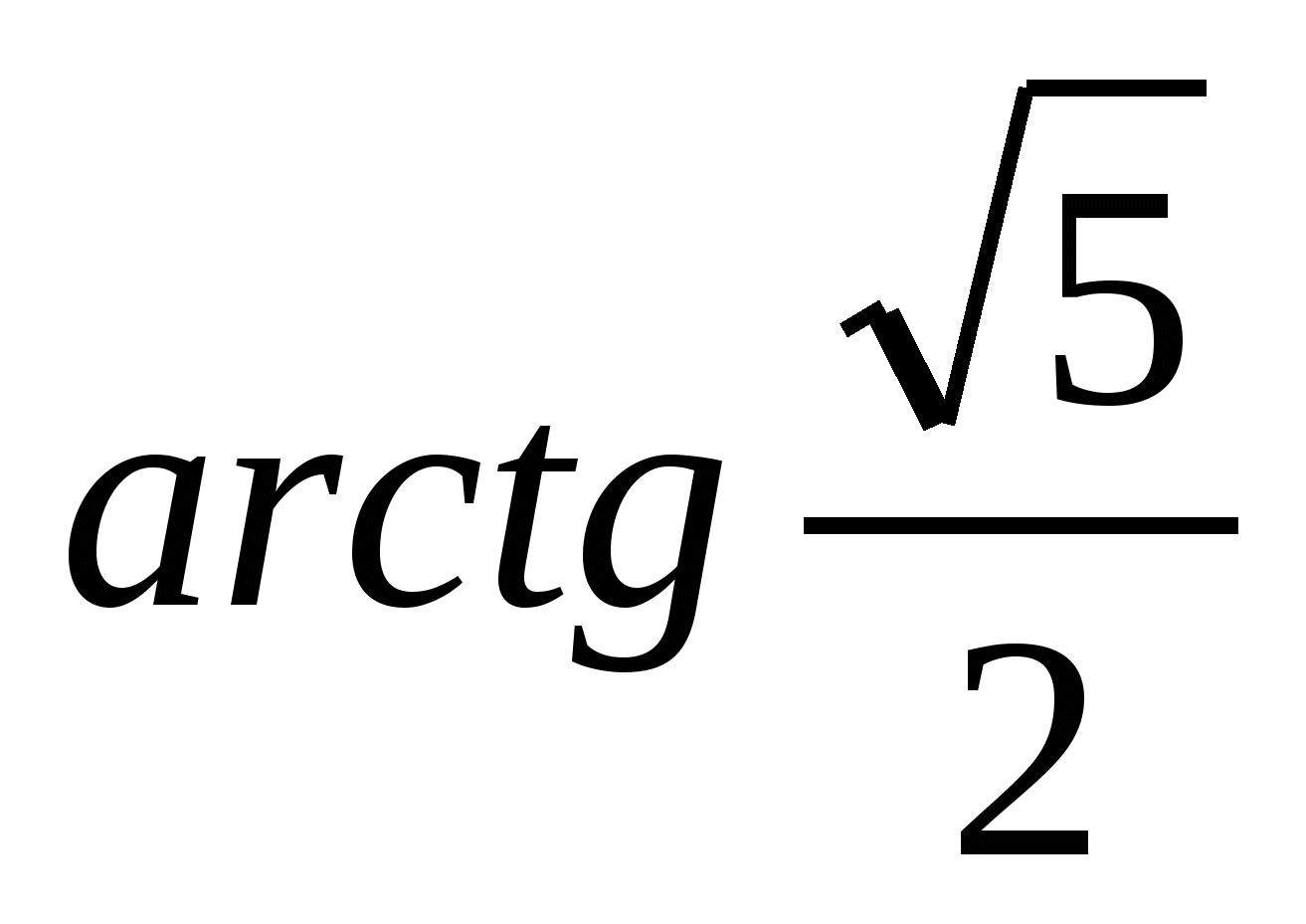 . Найти отношение
. Найти отношение 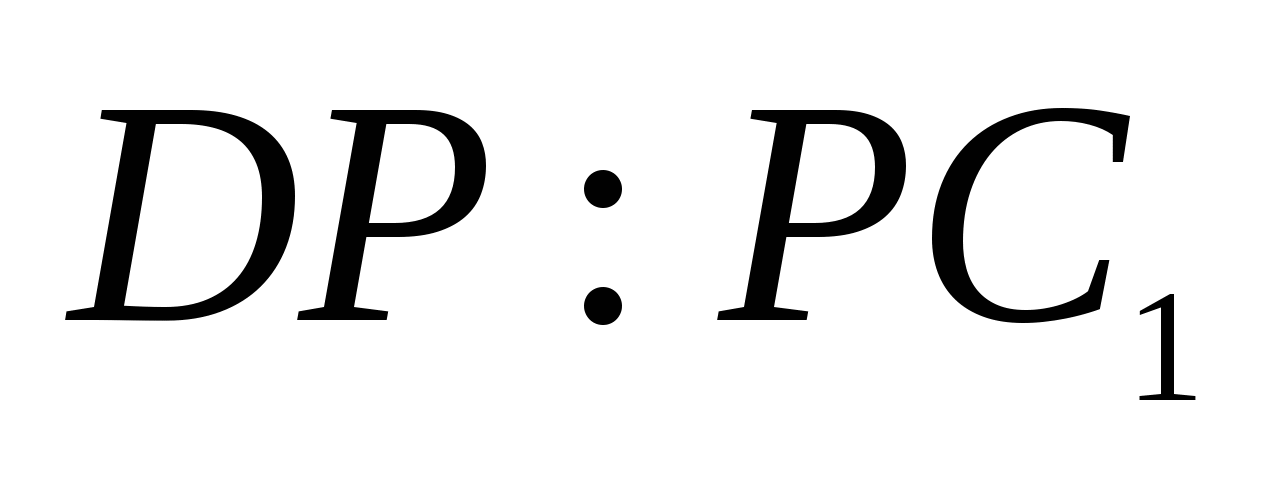 .
.
(Ответ: 2:1)
4. Высота прямой призмы 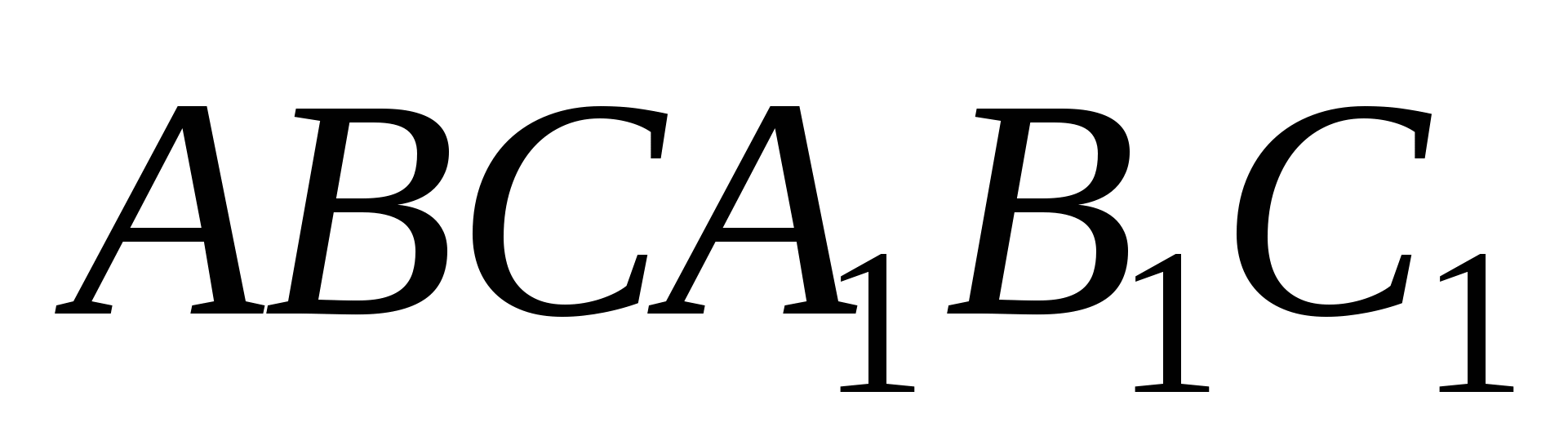 равна
равна 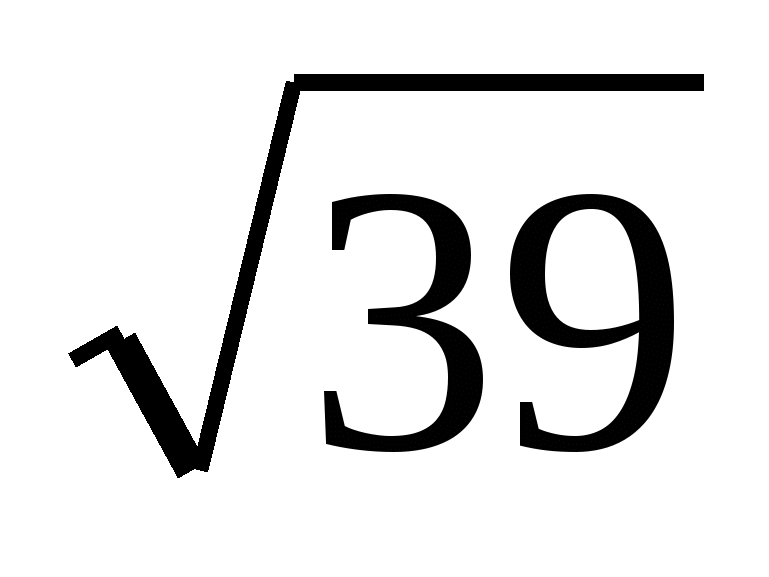 , угол С основания АВС равен 90, ВС = 4, АС = 3. Найти градусную меру угла между прямыми KМ и ВС, если точки K и М - середины ребер
, угол С основания АВС равен 90, ВС = 4, АС = 3. Найти градусную меру угла между прямыми KМ и ВС, если точки K и М - середины ребер 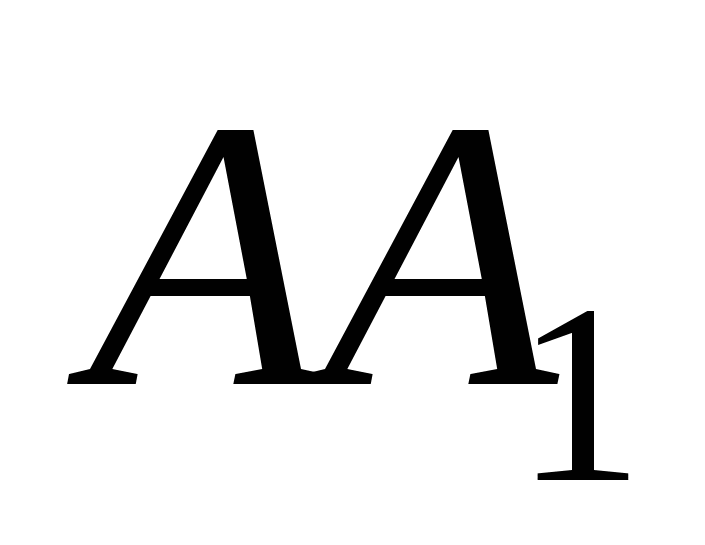 и АВ.
и АВ.
(Ответ: 60)
5. Дан куб 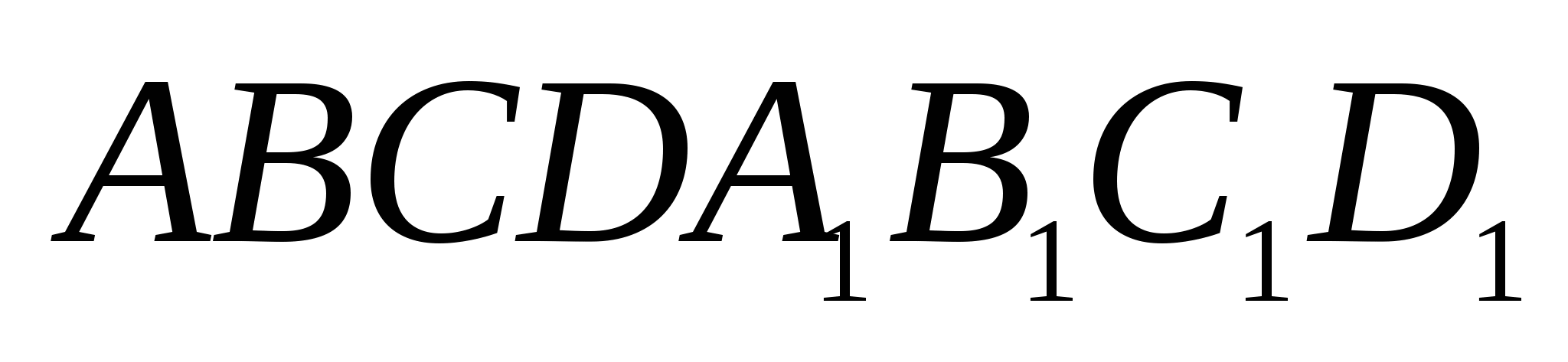 с ребром 1. Найти градусную меру угла между прямыми
с ребром 1. Найти градусную меру угла между прямыми 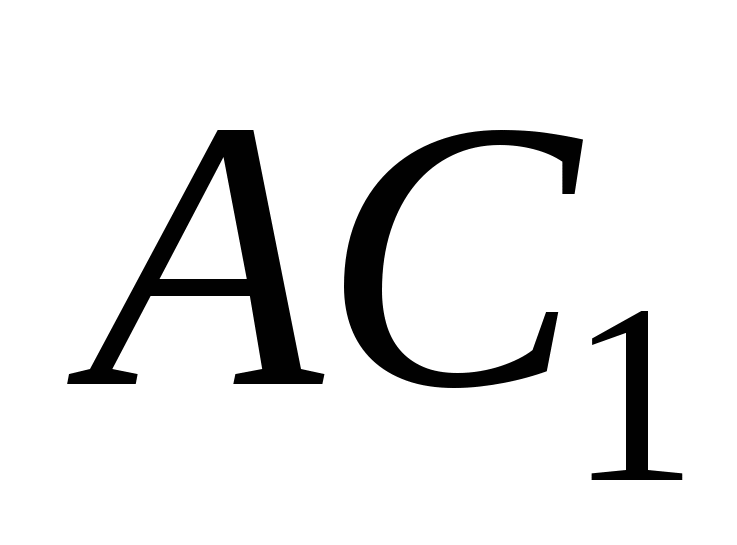 и
и 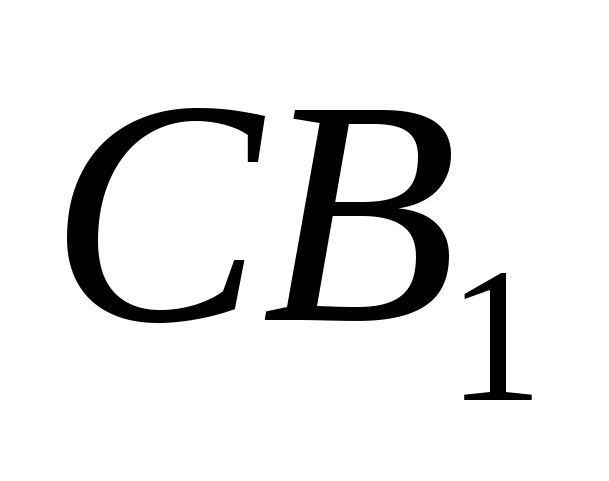 .
.
(Ответ: 90)
6. Площадь полной поверхности правильной треугольной призмы в два раза больше ее боковой поверхности. Найти угол между прямыми 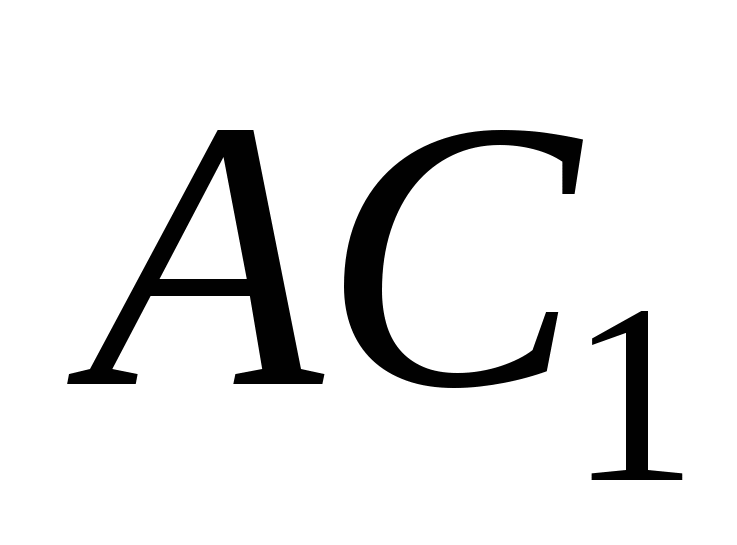 и
и  .
.
(Ответ: 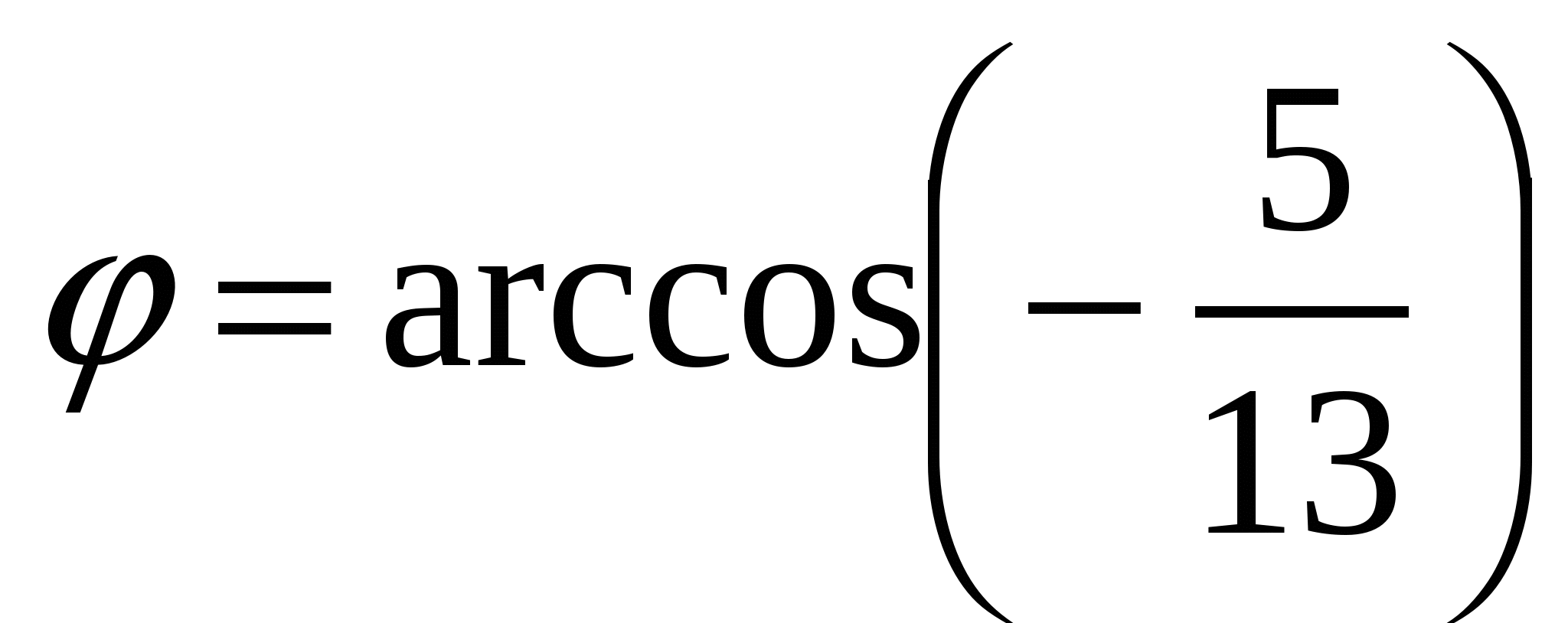 )
)
7. АВСD и EFKL - два взаимно перпендикулярных осевых сечения цилиндра, причем АD и EL - диаметры одного основания. М - середина образующей АВ. 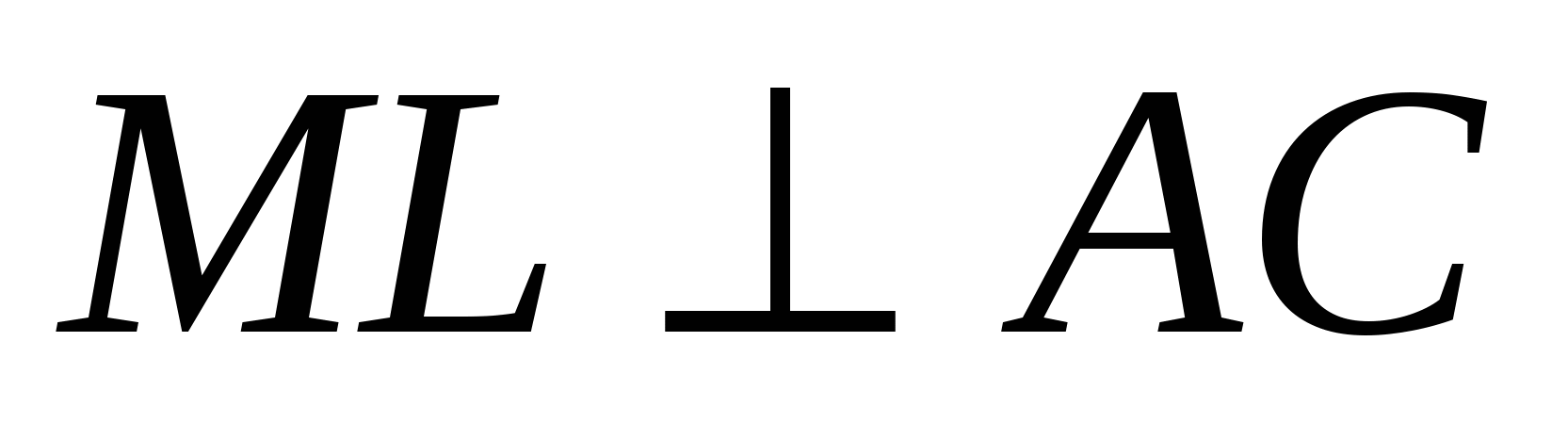 . Площадь осевого сечения равна 4. Найти площадь поверхности цилиндра.
. Площадь осевого сечения равна 4. Найти площадь поверхности цилиндра.
(Ответ: 6 )
)
8. В правильной четырехугольной пирамиде МАВСD сторона основания равна 2, а высота 1. Найти угол между АМ и плоскостью DМС.
(Ответ: 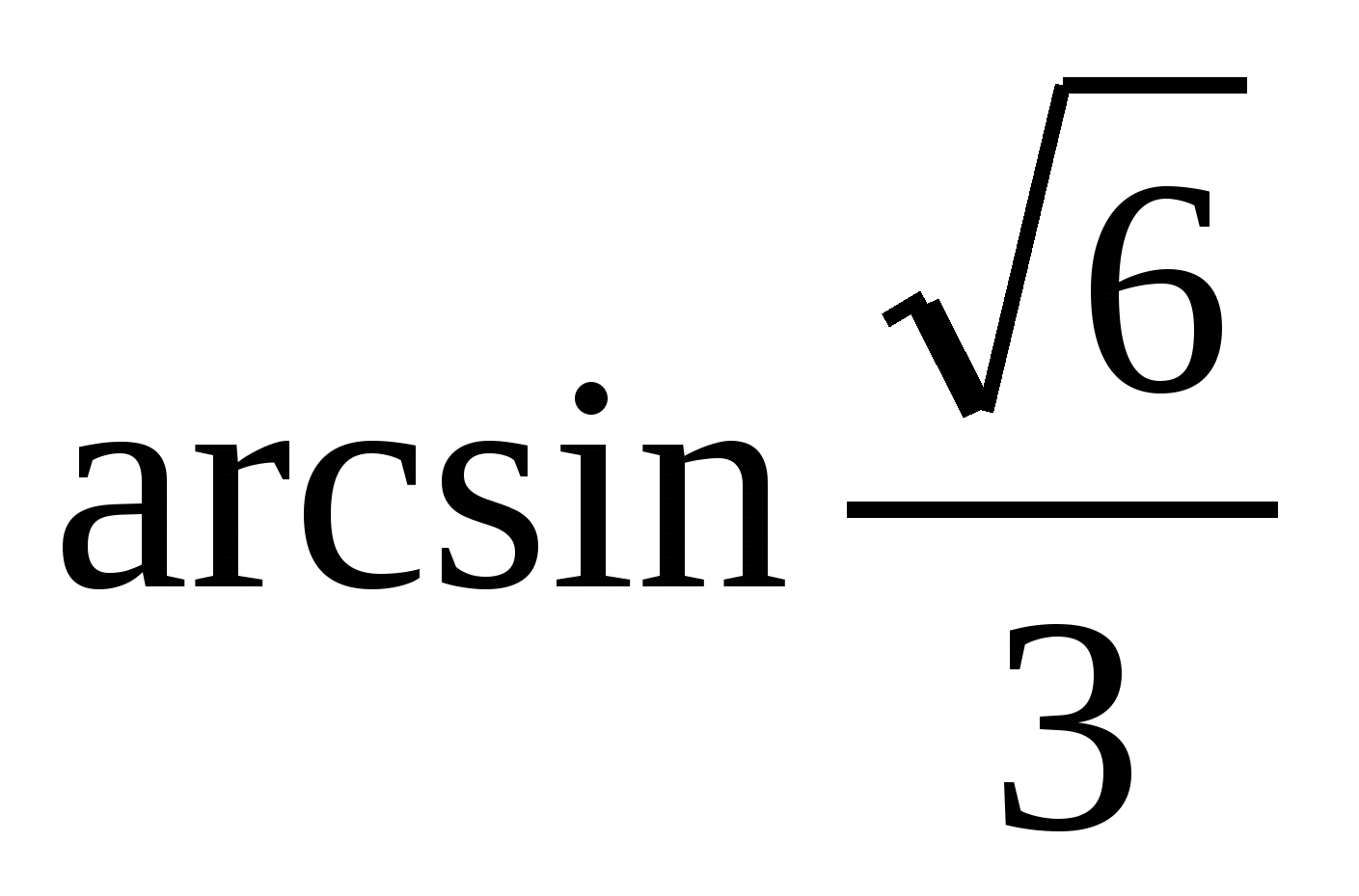 )
)
9. В кубе 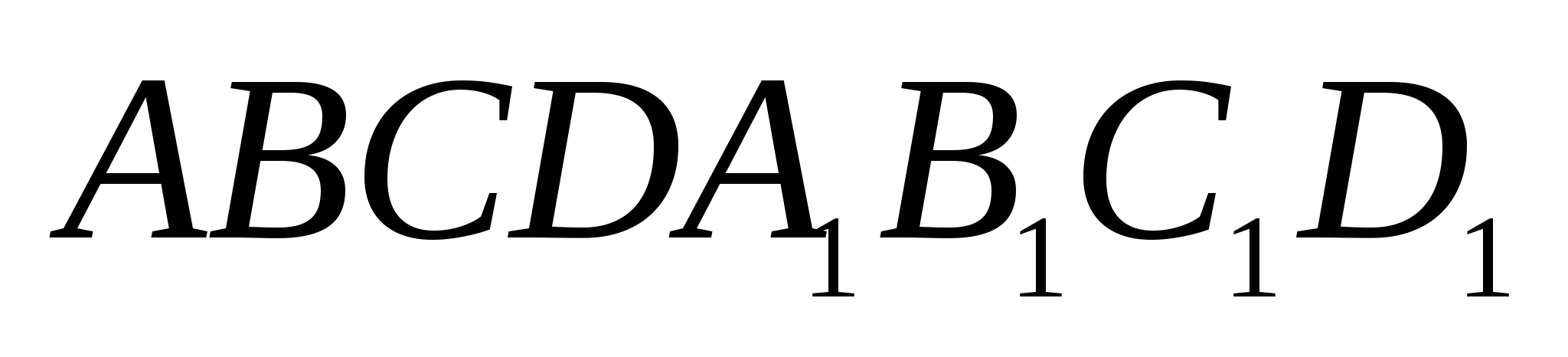 найти угол между
найти угол между 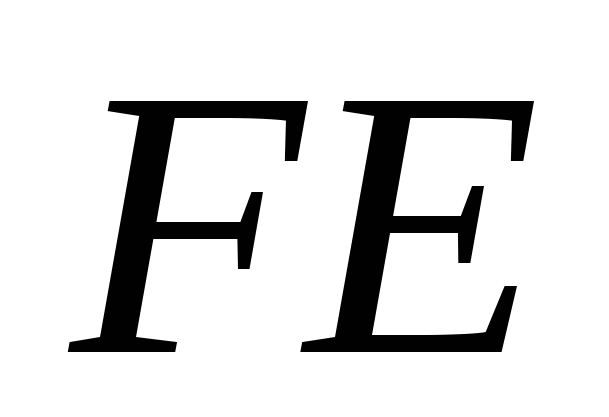 , где F - середина DС, а Е - середина
, где F - середина DС, а Е - середина 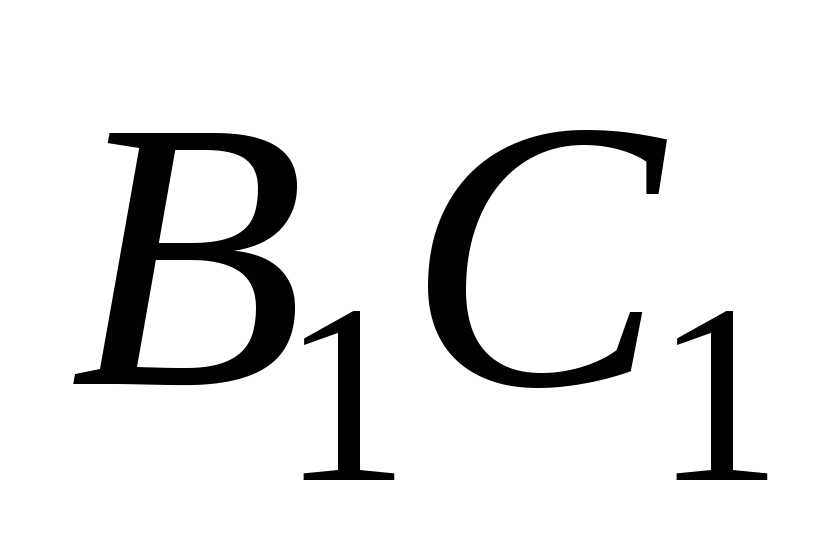 и плоскостью
и плоскостью 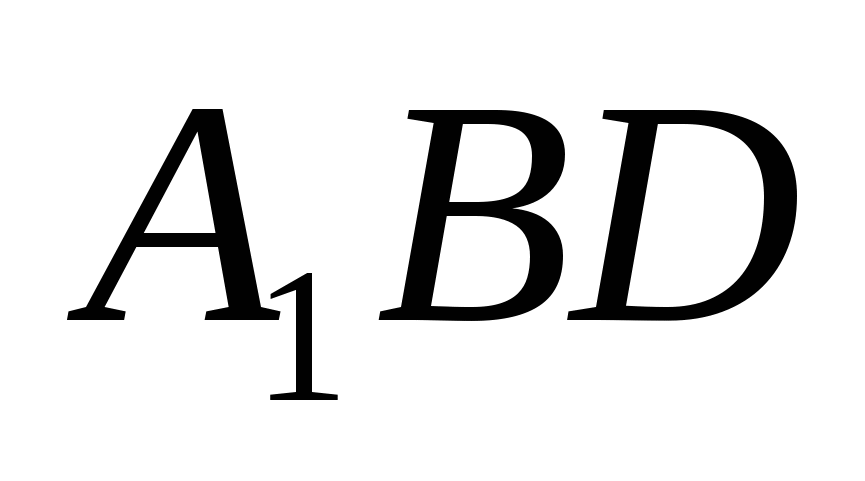 .
.
(Ответ: 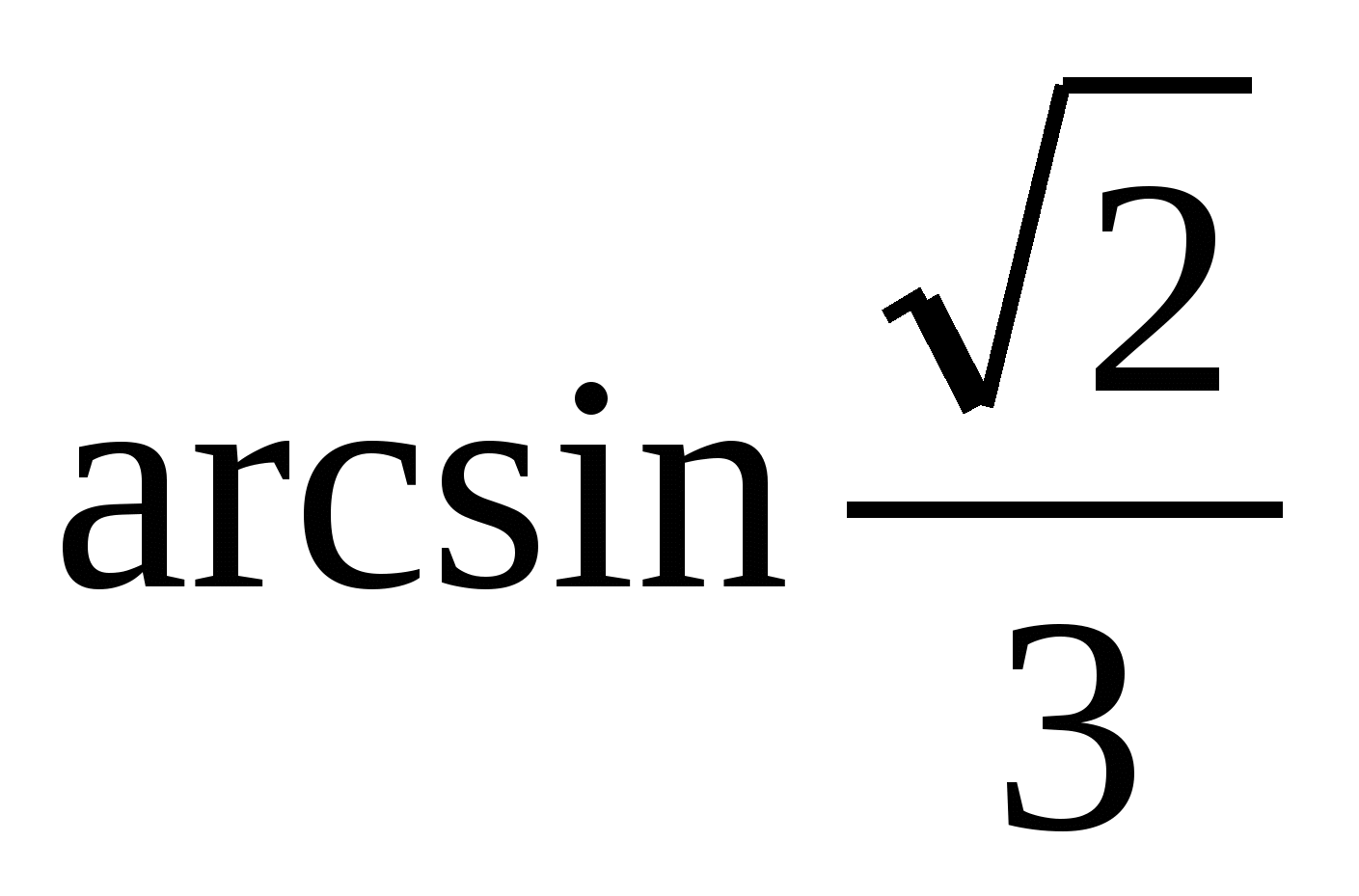 )
)
10. Основанием пирамиды МАВСD служит прямоугольник АВСD, где АВ = 2 и АD = 1. Грань АМВ - равнобедренный треугольник, плоскость которого перпендикулярна основанию пирамиды. Высота пирамиды равна 1. Найти угол между AF и DЕ, где F - середина МD, а Е - середина МС.
(Ответ: 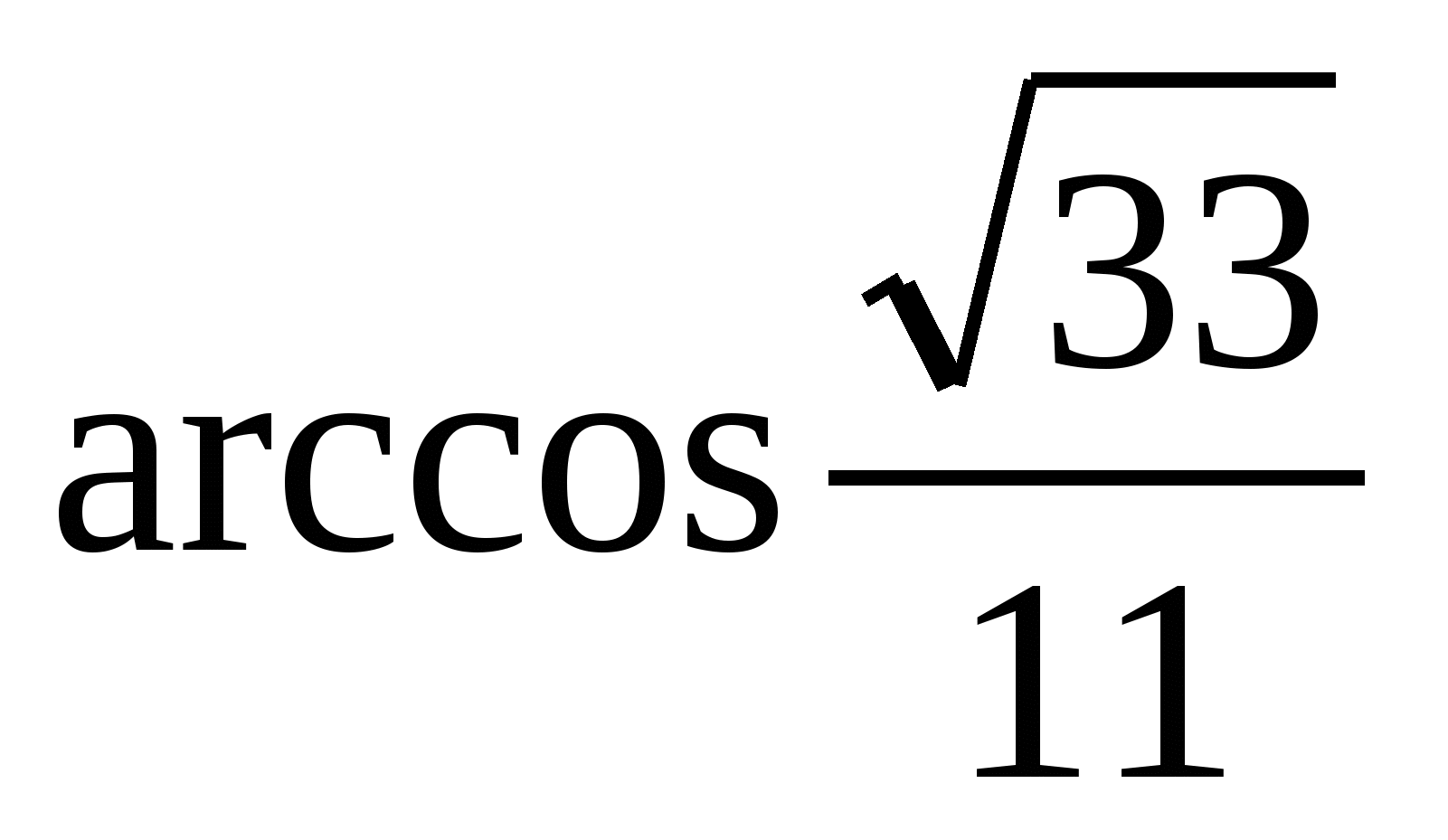 )
)
3.4. Метод геометрических преобразований
Осевая симметрия
1. В треугольнике АВС проведена биссектриса АK. Найдите сторону АС, углы В и С, если С - В = 45, СK = 1 и ВK = 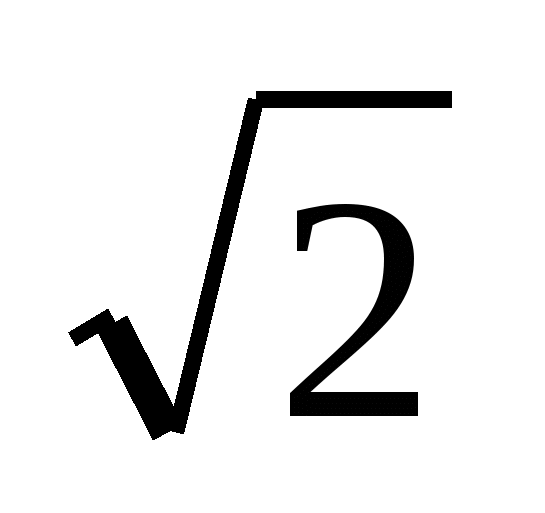 .
.
(Ответ: В = 45, С = 90, 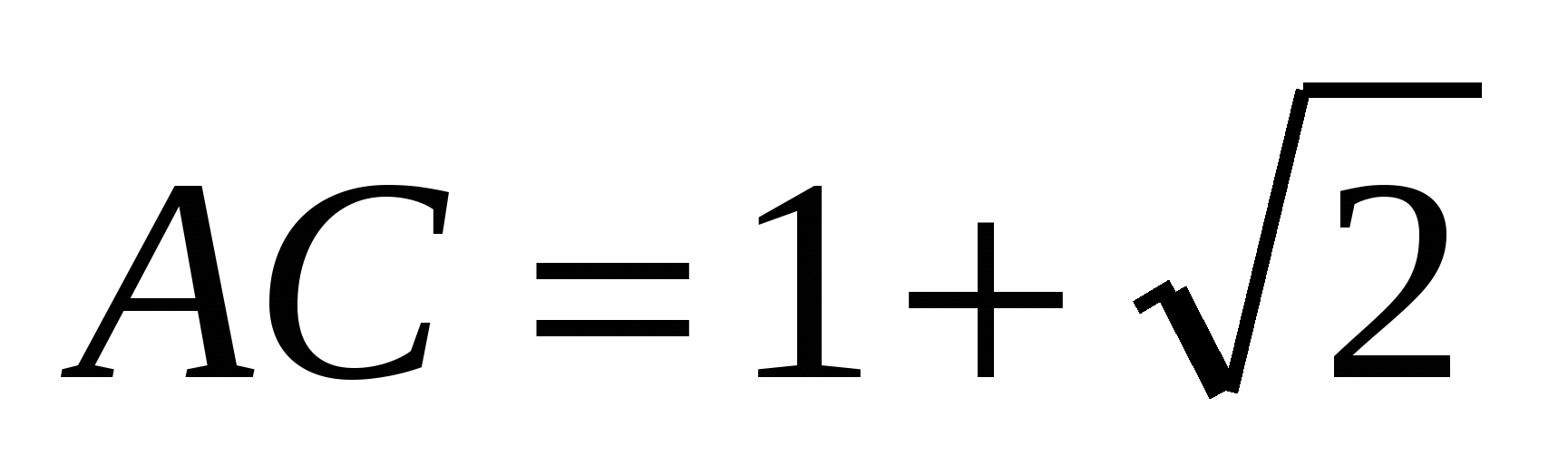 )
)
2. В треугольнике АВС проведена биссектриса СD. Найдите стороны АС и ВС, если 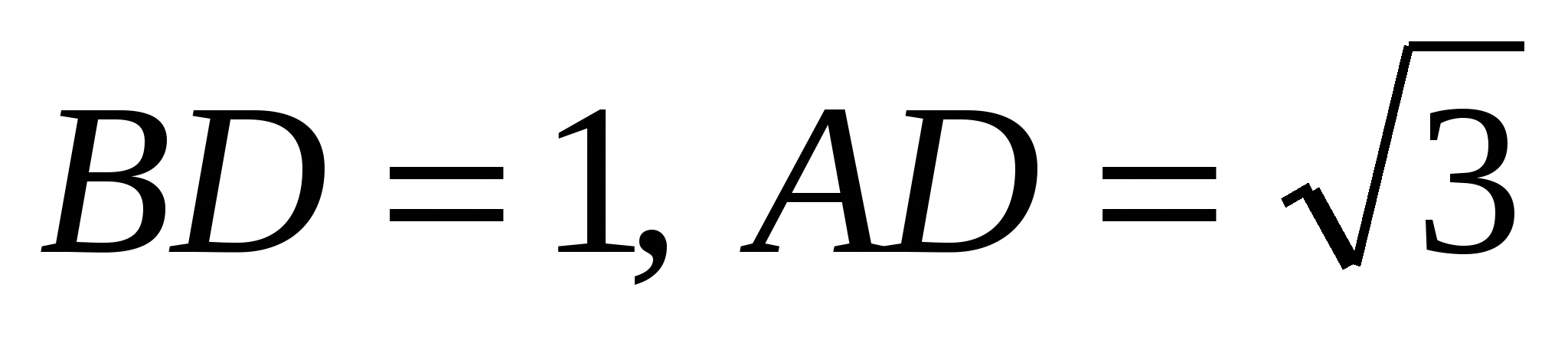 и
и 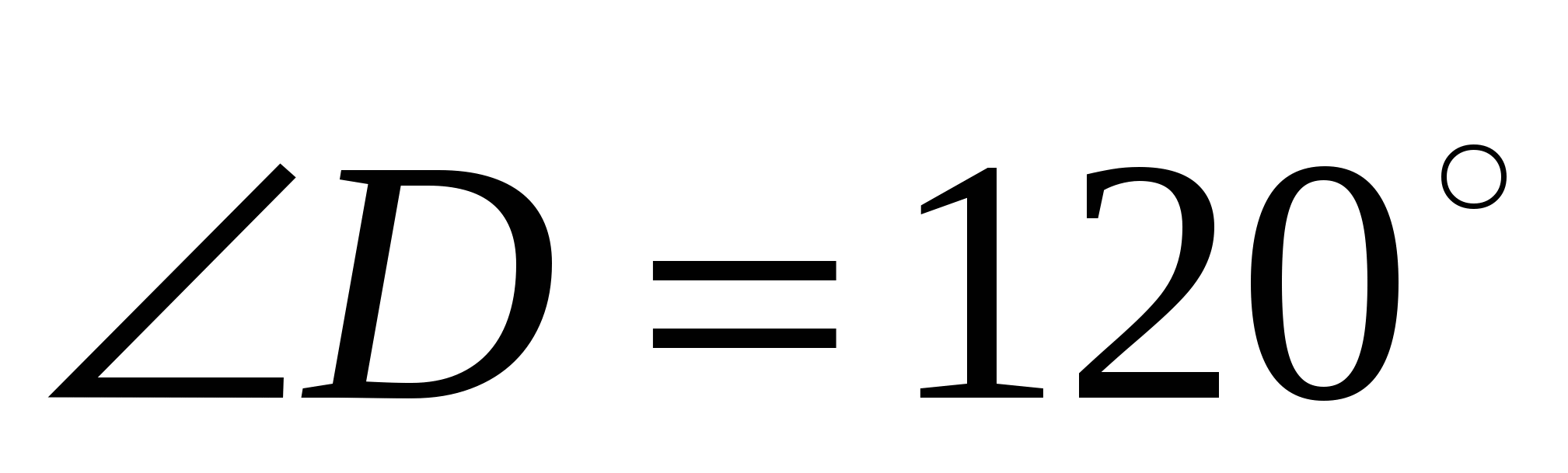 .
.
(Ответ: 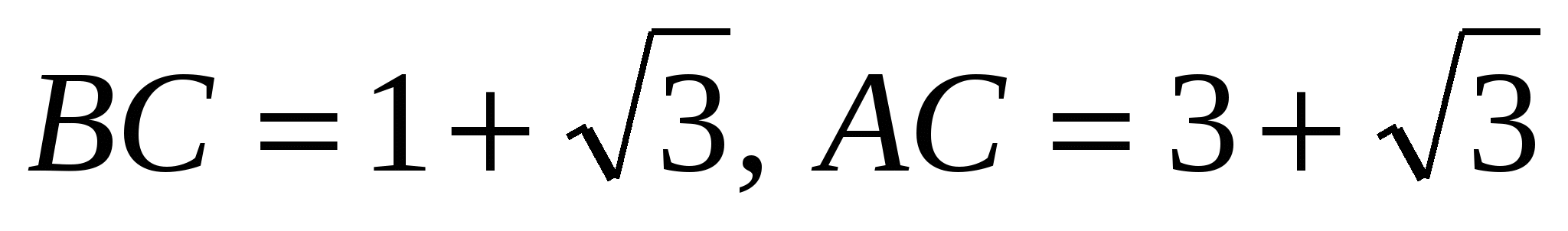 )
)
3. Дан четырехугольник ABCD, диагональ АС которого делит угол А пополам. Известно, что 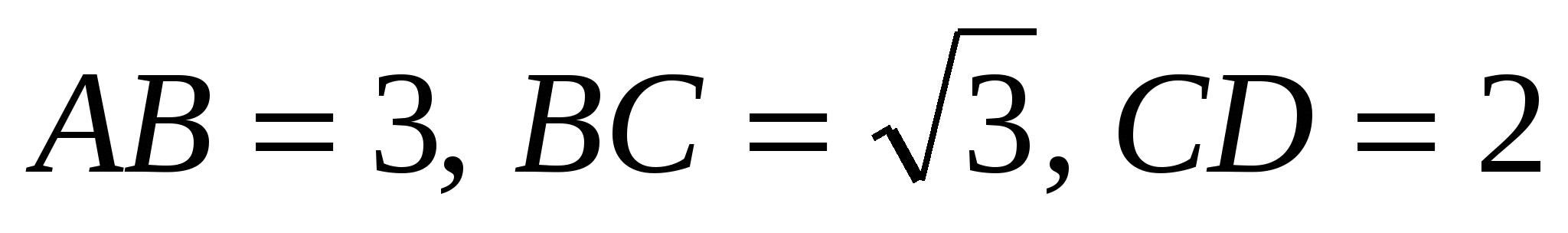 и AD = 4. Найдите угол А четырехугольника и диагональ АС.
и AD = 4. Найдите угол А четырехугольника и диагональ АС.
(Ответ: А=60;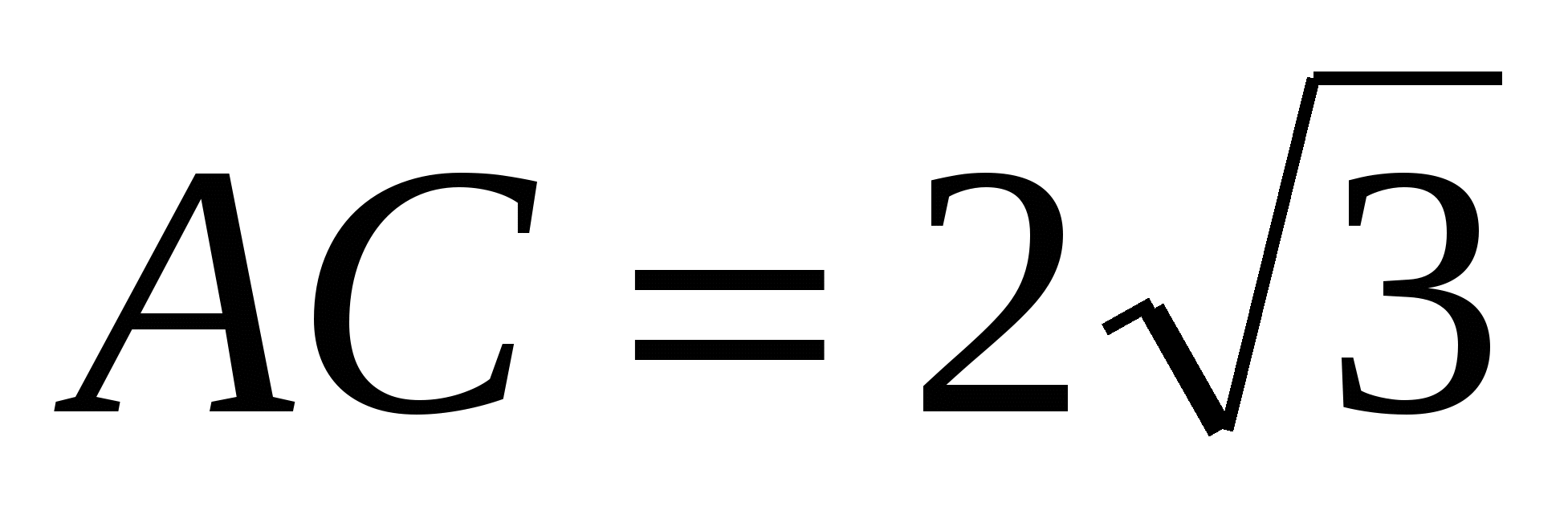 )
)
4. Найдите высоту СН треугольника АВС, если ВС = а, АС = b и разность углов А и В равна 90.
(Ответ: 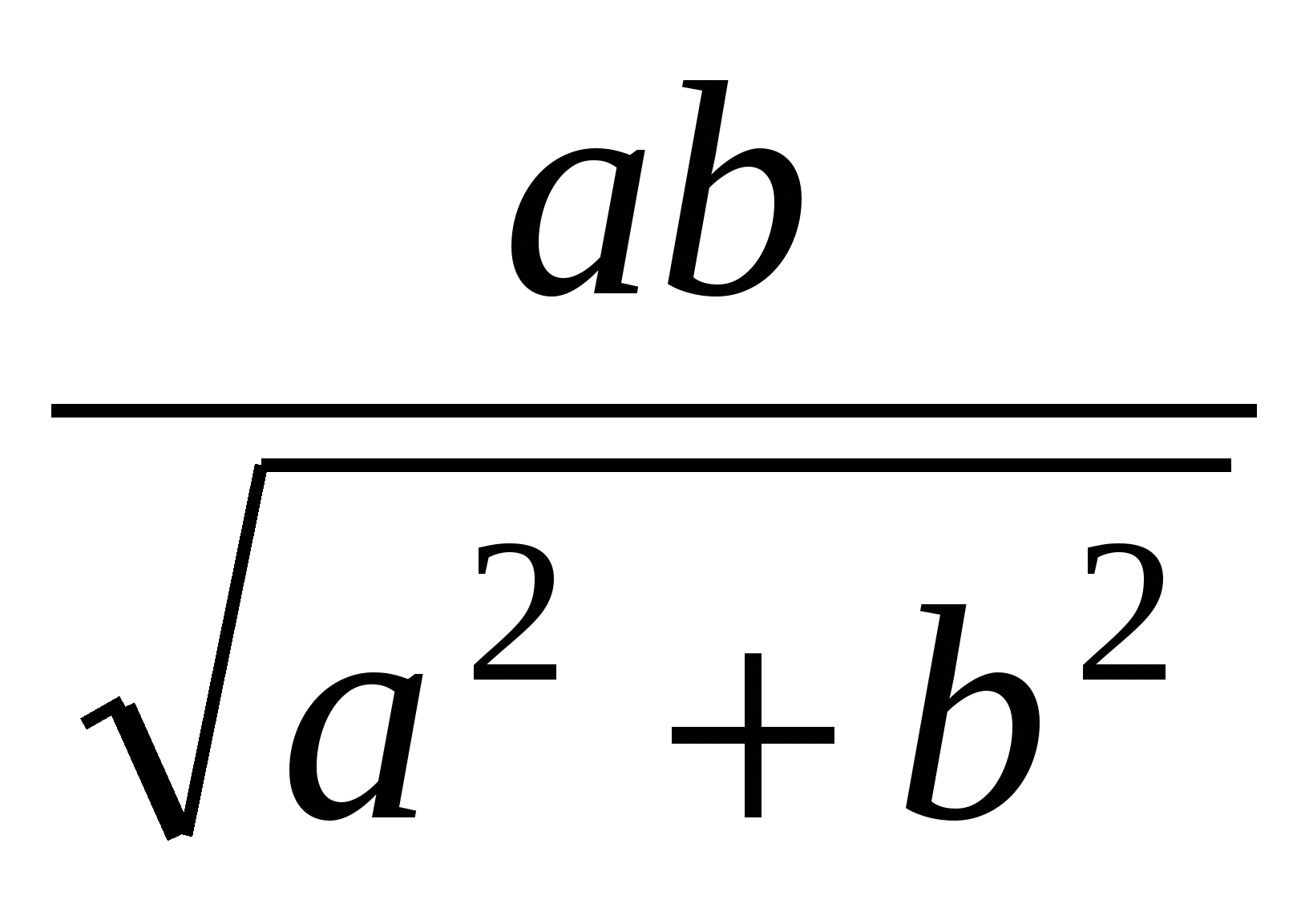 )
)
5. Дан прямоугольник АВСD. На его сторонах АВ, ВС, CD и DA взяты точки А1 В1 С1 и D1. Какое наименьшее значение может иметь периметр четырехугольника А1В1С1D1, если диагональ прямоугольника равна d?
(Ответ: 2d)
Параллельный перенос
1. Основания трапеции равны 1 и 3. Углы при большем основании равны 30 и 60. Найдите длины боковых сторон трапеции.
(Ответ: 1 и ![]() )
)
2. Основания трапеции равны 2 и 7, боковые стороны равны 3 и 4. Найдите длину отрезка, соединяющего середины оснований.
(Ответ: 2,5)
3. Диагонали трапеции равны 13 см и 20 см, а сумма длин оснований равна 21 см. Вычислите площадь трапеции.
(Ответ: 126 см2)
4. Диагонали трапеции равны 15 см и 20 см, высота равна 12 см. Вычислите площадь трапеции.
(Ответ: 150 см2)
5. Диагонали трапеции равны 13 см и 15 см, средняя линия равна 7 см. Найдите высоту трапеции.
(Ответ: 12 см)
Центральная симметрия
1. Вычислите площадь треугольника АВС, если стороны АС и ВС равны соответственно 11 см и 13 см, а медиана СD равна 10 см.
(Ответ: 66 см2)
2. Найдите высоту СН треугольника АВС, если АС = 6, ВС = 8 и
СD = 5, где СD - медиана треугольника АВС.
(Ответ: 4,8)
3. В треугольнике АВС проведена медиана СD. Найдите стороны АС и ВС треугольника, если АСD = 90, ВСD = 30и 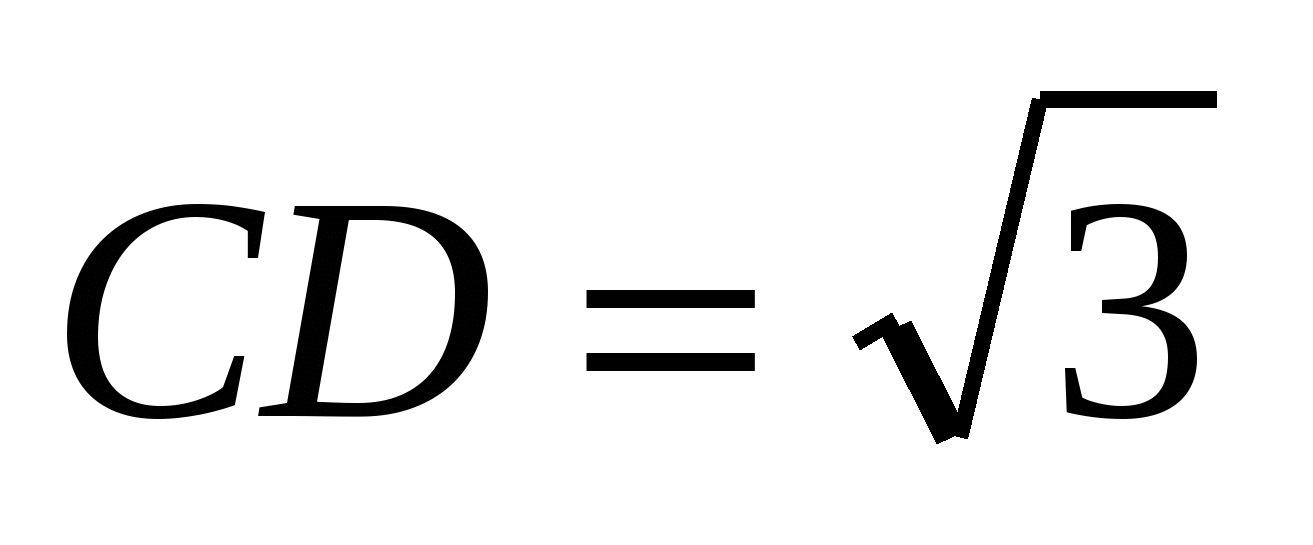 .
.
(Ответ: АС = 2; ВС = 4)
Поворот
1. На сторонах АС и ВС треугольника АВС вне его построены равносторонние треугольники 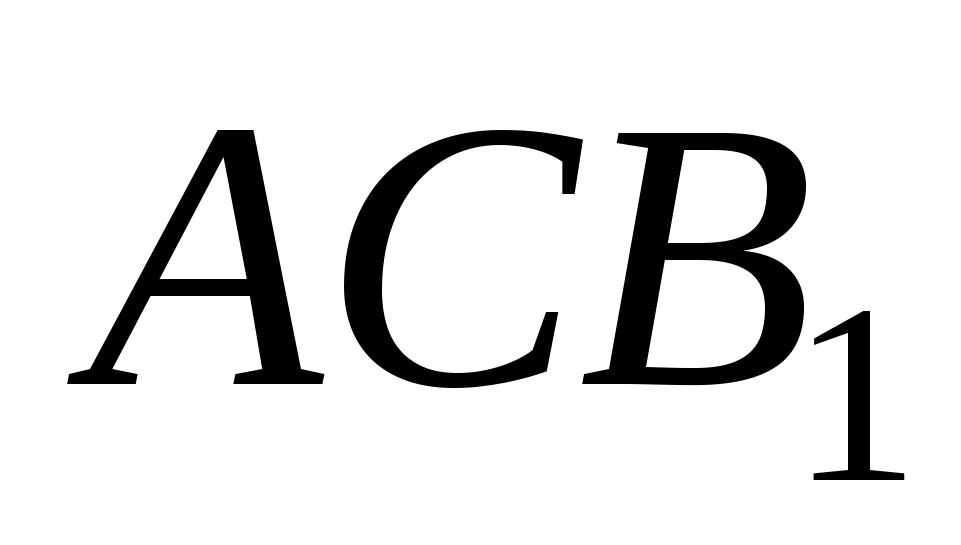 и
и 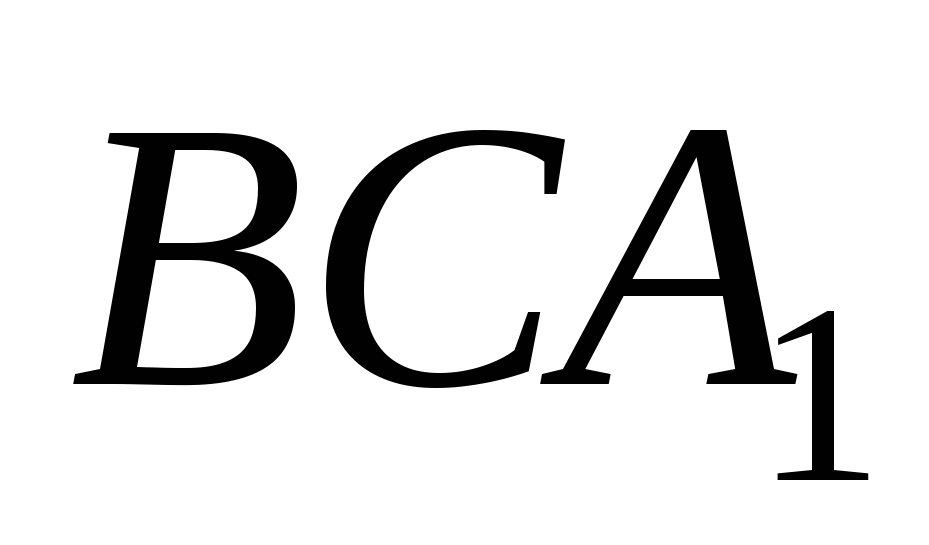 . Докажите, что отрезки
. Докажите, что отрезки 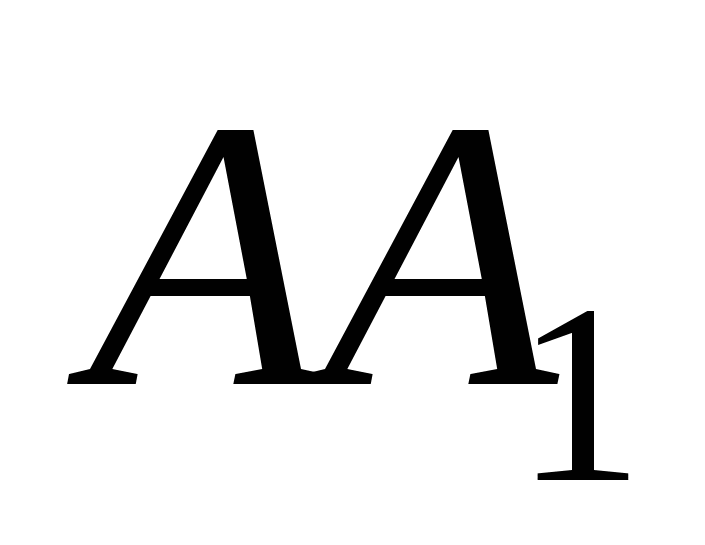 и
и 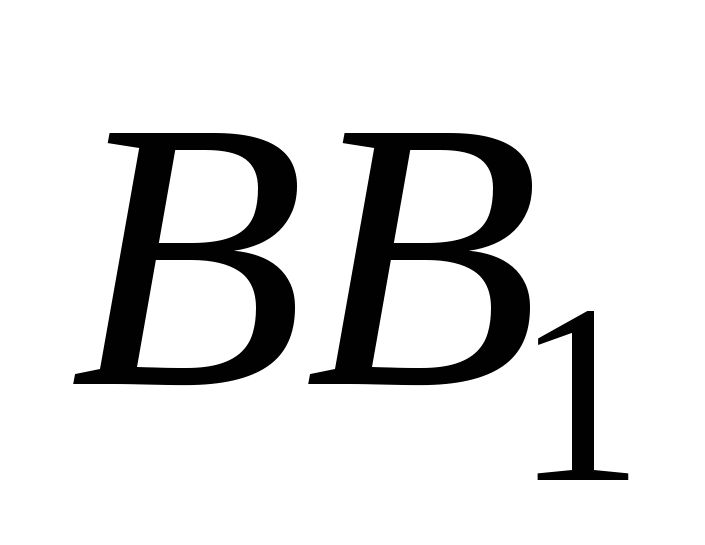 равны. Найдите величину угла между прямыми
равны. Найдите величину угла между прямыми 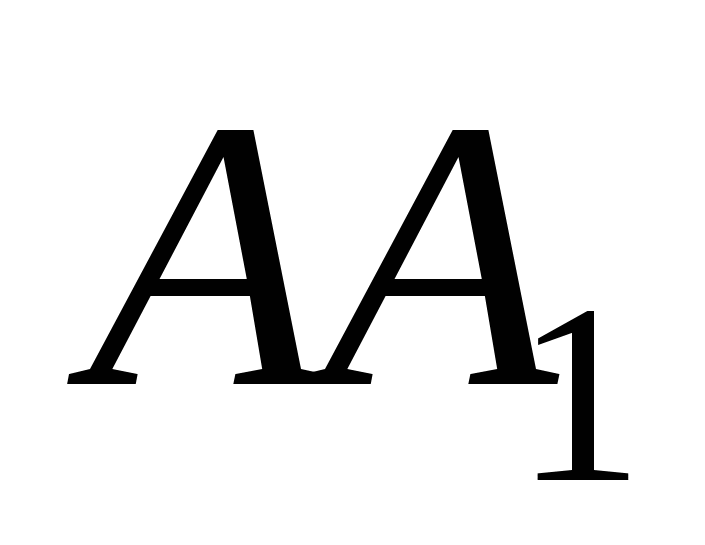 и
и 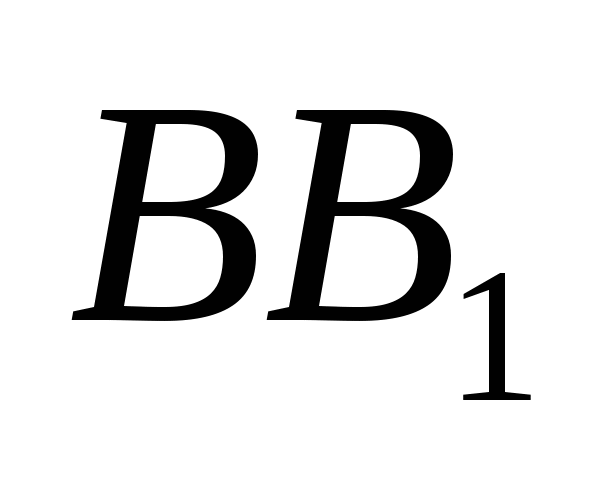 .
.
(Ответ: 60)
2. Внутри равностороннего треугольника АВС дана точка М. Известно, что АМ = 1, ВМ = 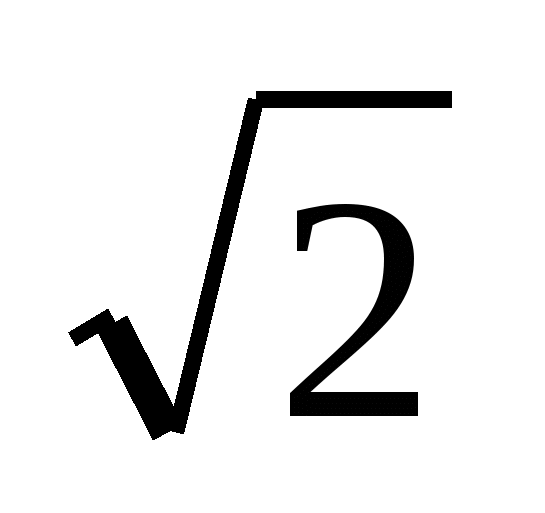 и АМВ = 105. Найдите СМ и ВМС.
и АМВ = 105. Найдите СМ и ВМС.
(Ответ: СМ =1, ВМС = 105)
3. Дан ромб АВСD, угол А которого равен 120. Внутри ромба взята точка М, такая, что АМ = 1, СМ = 2 и ВМ = 3. Найдите DМ и АВ.
(Ответ: DМ =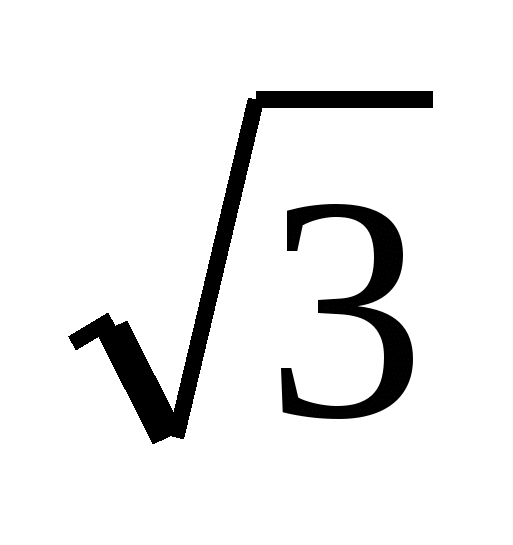 ,
, 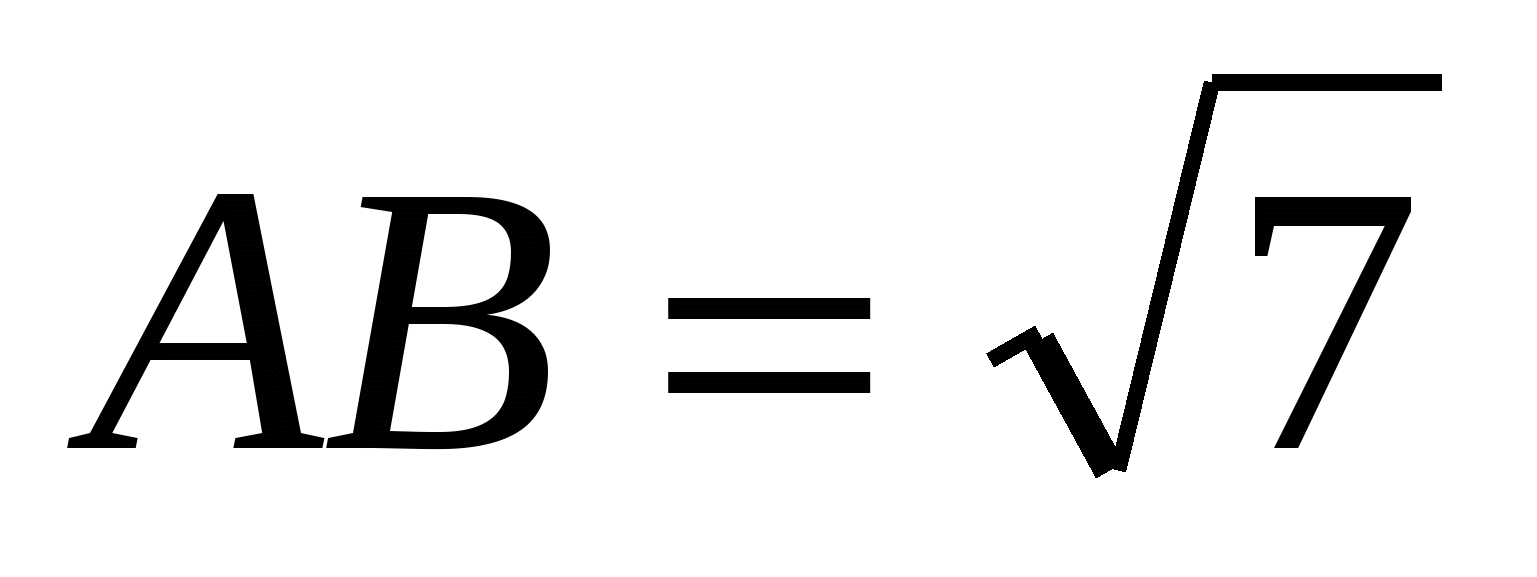 )
)
4. На сторонах ВС и СD квадрата АВСD взяты точки М и N. Найдите угол 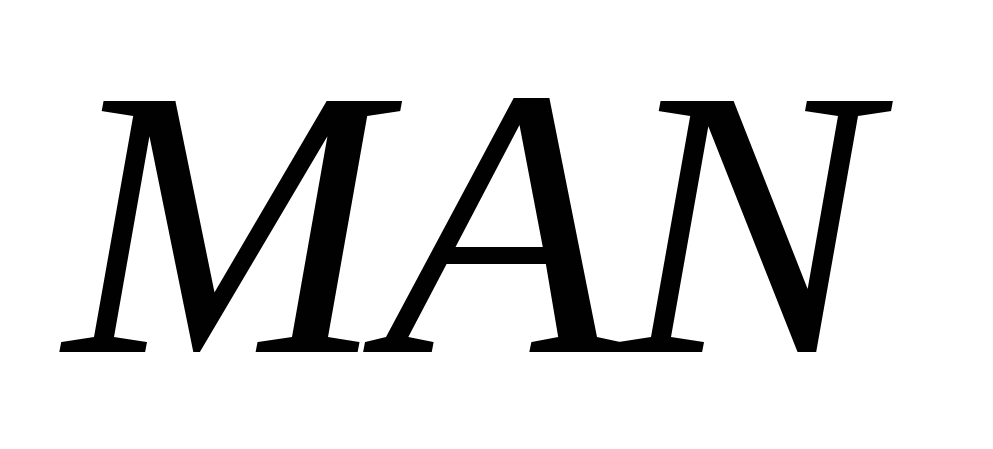 , если площадь
, если площадь 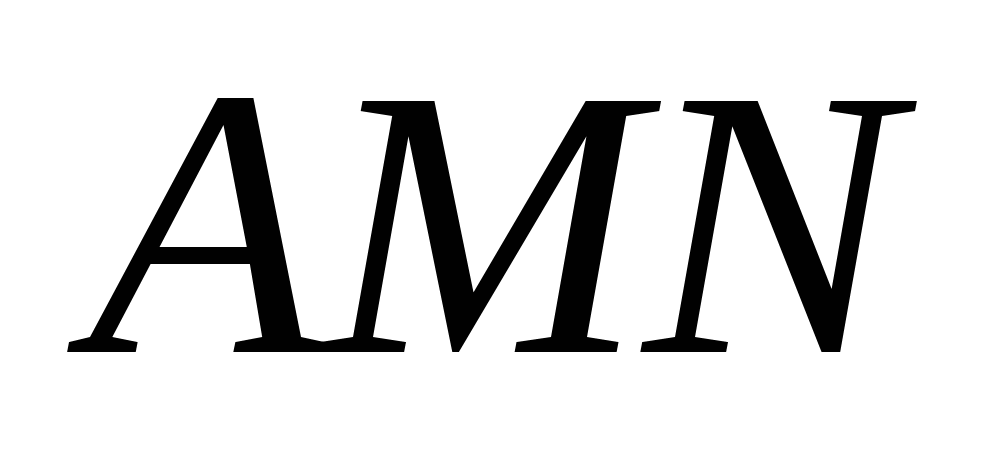 равна сумме площадей треугольников АВМ и АDN.
равна сумме площадей треугольников АВМ и АDN.
(Ответ: 45)
Подобие
1. В треугольнике АВС угол С равен 60, АВ = с. Найдите длину отрезка 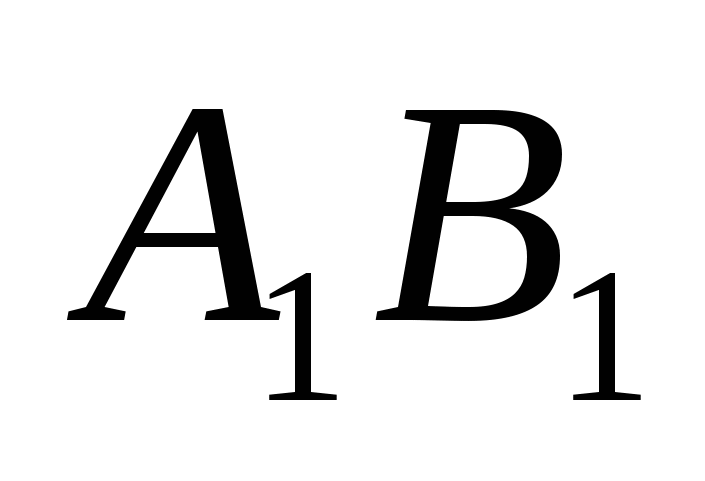 , соединяющего основания высот
, соединяющего основания высот  и
и 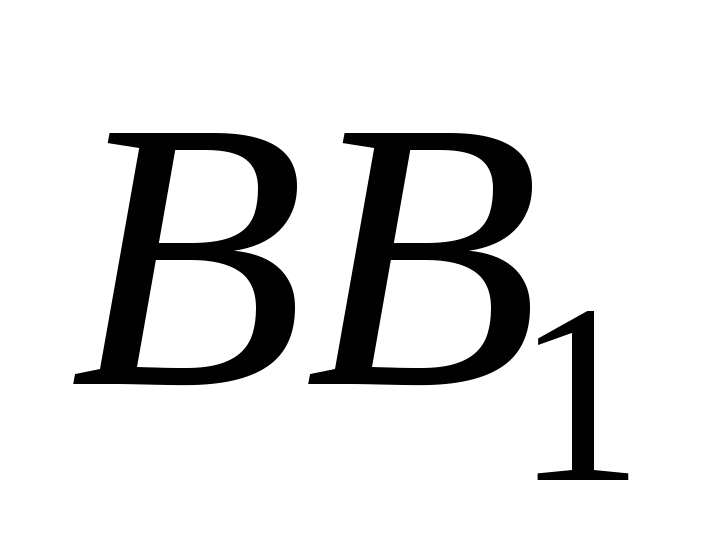 треугольника АВС.
треугольника АВС.
(Ответ: 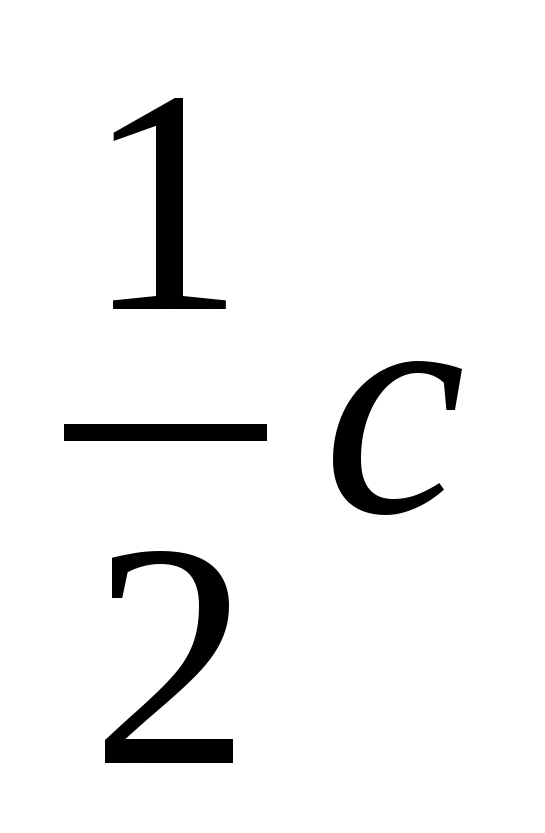 )
)
2. Дана трапеция АВСD с основанием АВ. Окружность, проходящая через вершины А, D и С, касается прямой ВС. Найдите АС, если 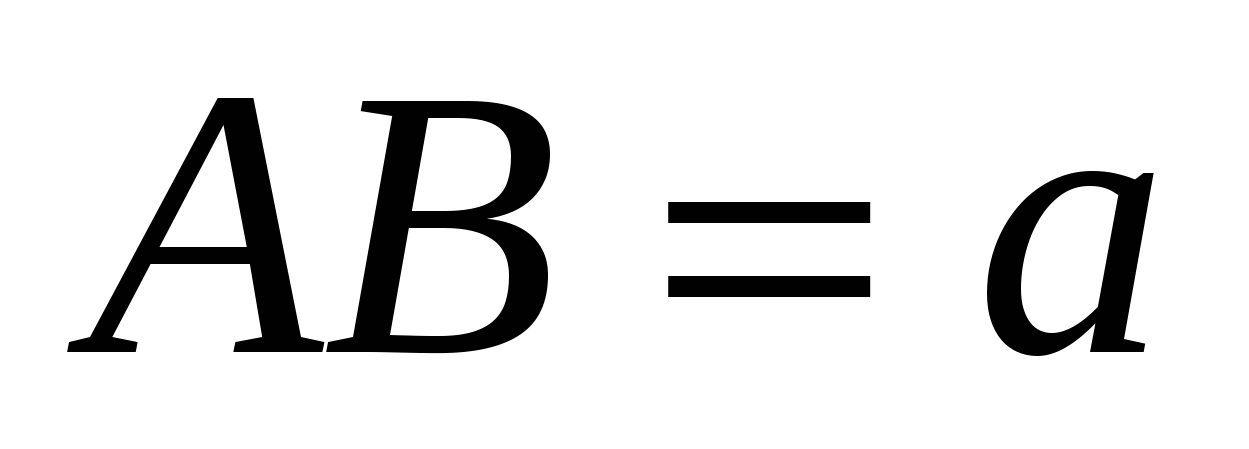 и
и 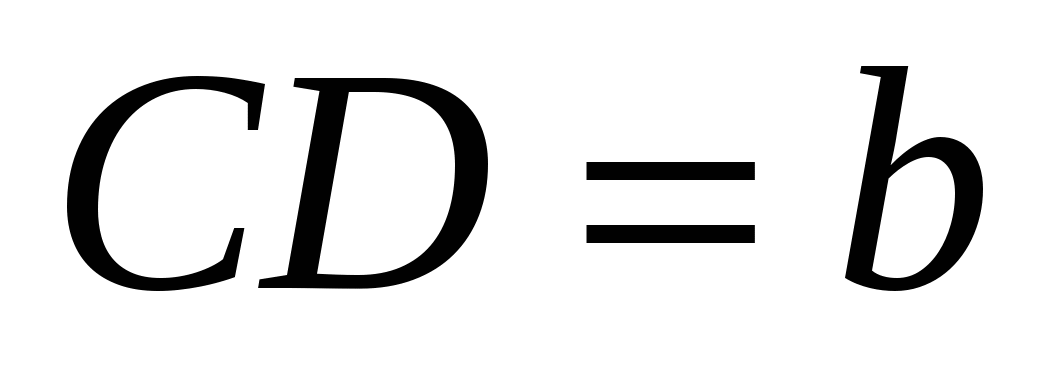 .
.
(Ответ: 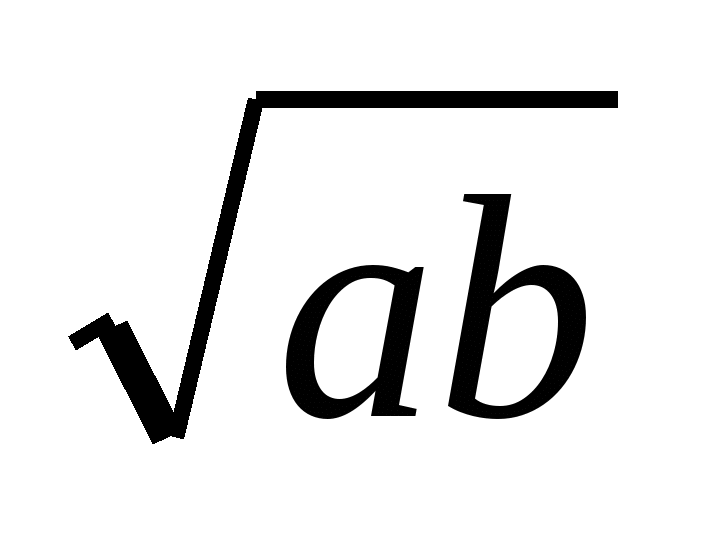 )
)
3. Дана трапеция АВСD (АВ и СD - основания), в которой 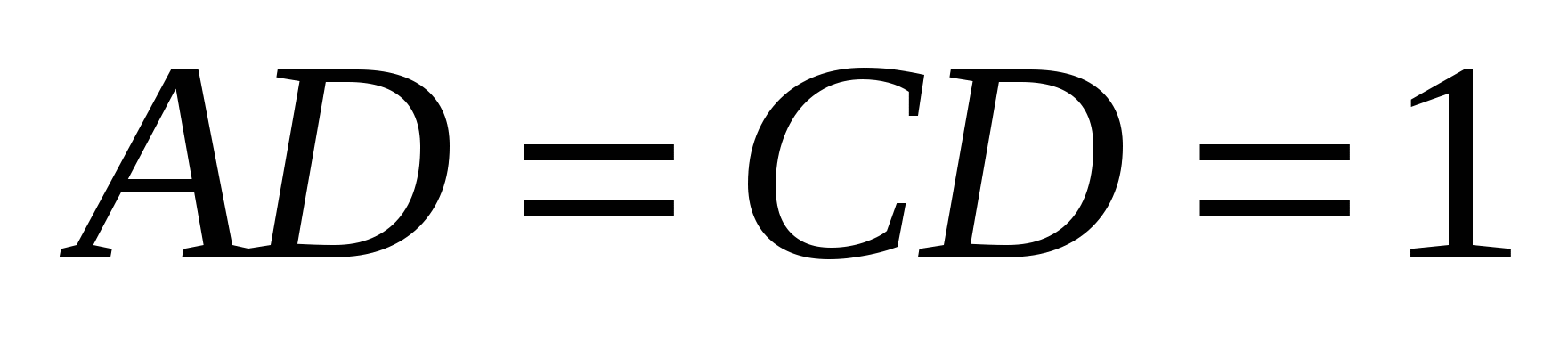 ,
, 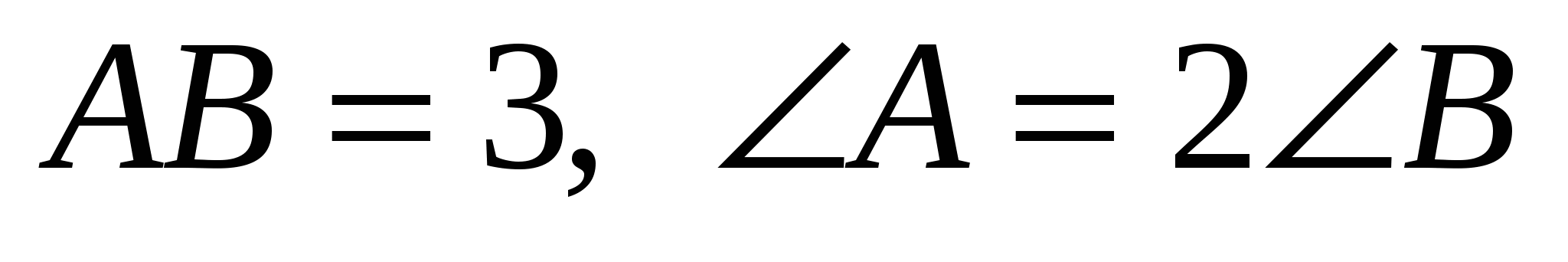 . Найдите ВС и
. Найдите ВС и 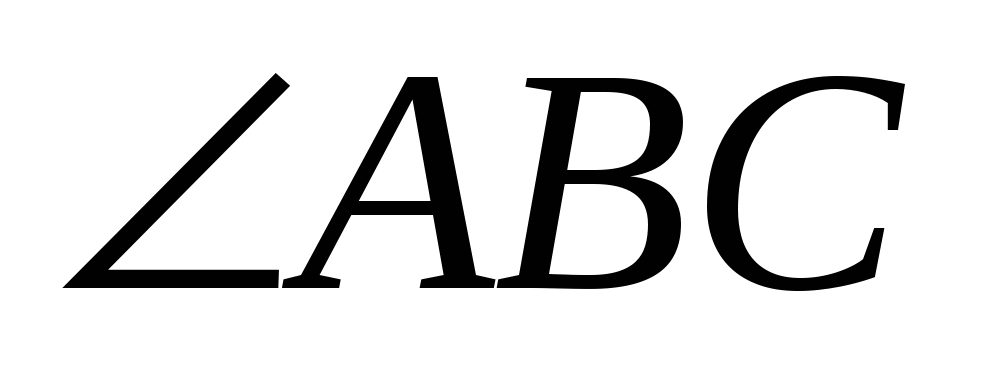 .
.
(Ответ: 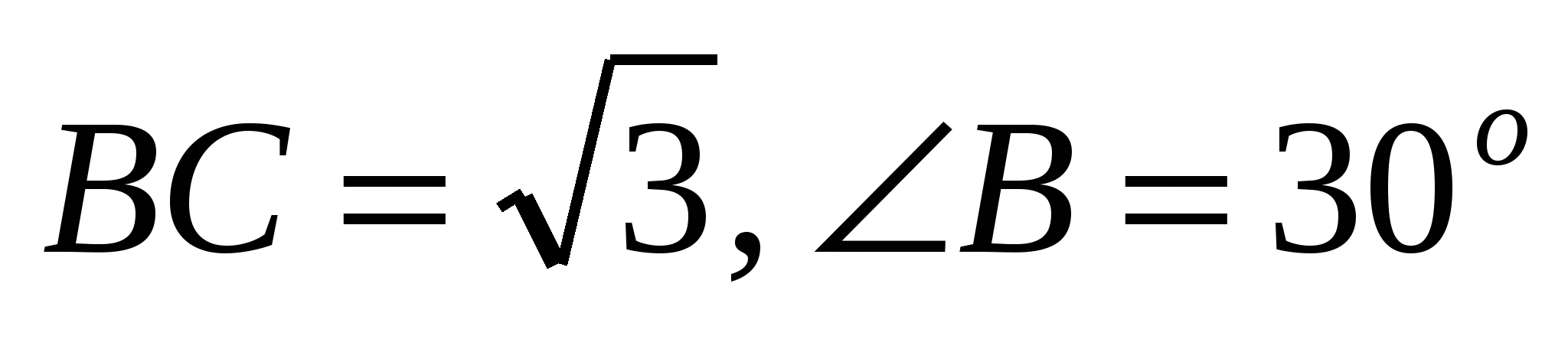 )
)
БИБЛИОГРАФИЯ
-
Александров А.Д. и др. Геометрия для 10-11 классов: Учеб. пособие для учащихся школ и классов с углубленным изучением математики - М.: Просвещение, 1992. - 464с.
-
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия: Учеб. для 10-11 кл. ср. шк. - М.: Просвещение, 1993 - 207с.
-
Болтянский В.Г., Яглом И.М. Преобразования. Векторы. - М.: Просвещение, 1964. - 303с.
-
Борзенко Е.К., Корнева И.Г. Решение стереометрических задач: Методические рекомендации. - Бийск: РИО БПГУ им. В.М. Шукшина, 2005. - 60с.
-
Готман Э.Г. Задачи по планиметрии и методы их решения: Пособие для учащихся. - М.: Просвещение, 1996. - 240с.
-
Гусев В.А., Литвиненко В.Н., Мордкович А.Г. Практикум по элементарной математике: Геометрия: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов и учителей - М.: Просвещение, 1992. - 352с.
-
Единый государственный экзамен: Математика: Cб. заданий. - М.: Просвещение, 2005. - 224с.
-
Зив Б.Г. Задачи к урокам геометрии, 7-11 классы. - СПб., 1998. - 624с.
-
Зив Б.Г. и др. Задачи по геометрии для 7-11 классов. - М.: Просвещение, 1991. - 171с.
-
Корнева И.Г., Пономарева Г.Д. Решение планиметрических задач. Методические рекомендации. - Бийск: НИЦ БПГУ им. В.М. Шукшина, 2004. - 42с.
-
Погорелов А.В. Геометрия: Учеб. для 7-11 кл. сред. шк., 4-е изд. - М.: Просвещение, 1993. - 383с.
-
Шарыгин И.Ф. Факультативный курс по математике. Решение задач: Учеб. пособие для 10 кл. ср. шк. - М.: Просвещение, 1989. - 252с.
-
Шарыгин И.Ф., Голубев В.И. Факультативный курс по математике: Решение задач: Учеб. пособие для 11 кл. сред. шк. - М.: Просвещение, 1991. - 384с.
Приложение

56