- Преподавателю
- Математика
- Учебное пособие по курсу Введение в геометрию, 6 класс
Учебное пособие по курсу Введение в геометрию, 6 класс
| Раздел | Математика |
| Класс | 6 класс |
| Тип | Другие методич. материалы |
| Автор | Антипина Г.В. |
| Дата | 19.07.2015 |
| Формат | docx |
| Изображения | Есть |
Учебно-Воспитательный комплекс «Лицей» Лениногорск стр. 38






















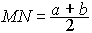
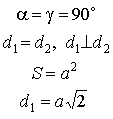

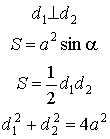
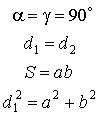



 Антипина Г. В.
Антипина Г. В.
6 класс
УВК «Лицей»
г. Риддер, 2011г.
Введение.
В пятом классе на уроках Введения в геометрию ты научился работать с инструментами, решать геометрические задачи, а главное, ты увидел, что геометрия - это не та скучная наука, которой тебя пугают старшеклассники. Геометрия - это жизнь, она присутствует в каждом предмете, растении, живом организме. Ты увидел, как причудливо переплетаются геометрические понятия и закономерности живых организмов. Наблюдая летом природу, ты увидел симметрию и спирали в растениях, убедился в связи чисел Фибоначчи с законами филлотаксиса.
В новом учебном году мы продолжим знакомство с замечательной наукой - Геометрией, научимся различать односторонние и двусторонние поверхности, познакомимся с графами и различными геометрическими фигурами.
Измерение величин.
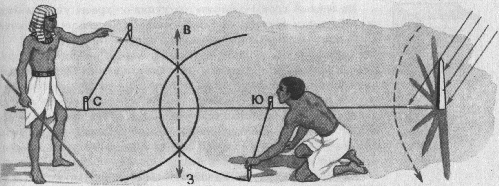
Давайте мысленно перенесемся на 4 тысячи лет назад и представим себе, что мы с вами египетские мастера, которые собираются строить пирамиду. С чего начать? Возьмем кусок папируса и нарисуем на нем чертеж постройки. Теперь выберем место для постройки пирамиды и наметим на нем основание, фундамент пирамиды. Поступим так, как это делали египетские строители. Воткнем в землю отвесный шест. В полдень, когда тень от шеста будет самой короткой, она покажет нам направление на север.
Наметим на земле линию север - юг. Теперь проведем линию восток - запад. Для этого возьмем веревку с двумя колышками и сделаем построения, как на рисунке. Линии север - юг и запад - восток пересекаются под прямым углом. С помощью веревочек построим прямой угол. Значит теперь можно из планок сделать себе угольник и использовать его, если понадобится.
Для измерения величин используют основные меры (метр, грамм, литр и др.), а также производные от них. Величины образуют другие, большие и меньшие меры одинаковым образом (за исключением, названий «микрон» «центнер», «тонна»). Для образования названий мер, больших основной единицы, к названию последней спереди прибавляются греческие слова: «дека» - «десять», «гекто» - «сто», «кило» - «тысяча», «мириа» - «десять тысяч»; для образования названий мер, меньших основной единицы, к названию основной единицы прибавляются, также спереди, частицы «деци» - «десять», «санти» - «сто», «милли» - «тысяча»
Таким образом, например:
1 мириаметр = 10 километрам = 100 гектометрам= 1000 декаметрам = 10 000 метрам;
1 метр==10 дециметрам = 100 сантиметрам = 1000 миллиметрам.
Аналогично:
1 мириаграмм =10 килограммам =100 гектограммам =
1000 декаграммам =10 000 граммам;
1 грамм = 10 дециграммам = 100 сантиграммам = 1000 миллиграммам;
1 мириалитр = 10 килолитрам = 100 гектолитрам = 1000 декалитрам =10 000 литрам;
1 литр =10 децилитрам =100 сантилитрам = 1000 миллилитрам.
Долгое время в качестве единицы длины применялся микрон, то есть 0,001 миллиметра. Высококвалифицированные слесари умеют изготовлять детали с микронной точностью,
Далеко не все из указанных выше названий употребляются на практике - вряд ли кто-нибудь слышал о сантиграммах или о децилитрах. Однако в некоторых зарубежных странах в магазинах говорят: «Отпустите, пожалуйста, тридцать декаграммов сыра».
Задачи на построение.
В пятом классе ты научился решать многие задачи на построение. Сегодня мы попробуем применить эти умения к решению не совсем стандартных задач. Использовать при решении задач на построение можно только циркуль и линейку. А для решения многих задач достаточно карандаша, так как главное в этих задачах - догадаться, что нужно делать. Тогда достаточно сделать эскиз решения, и мы будем считать, что задача решена.
Задание 1.
Ты видишь на рисунках изображения геометрических фигур. Распознай эти фигуры. Меняются ли свойства фигур в зависимости от способа их изображения.
Задание 2.
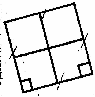
Я могу разделить квадрат на 4 равные части вот так:
Как разделить квадрат на 5 равных частей?
На 7 равных частей?
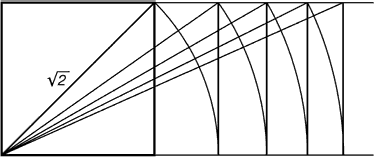
Как отрезок разделить на любое число равных частей?
Задание 3
Как разделить квадрат на 6 квадратов?
А на 8?
На сколько квадратов вообще можно разделить квадрат? Как это сделать?
Задание 4
Как разделить круглый торт на 8 равных частей, сделав при этом наименьшее число разрезов? Каково это наименьшее число?
Измерение отрезков на местности.
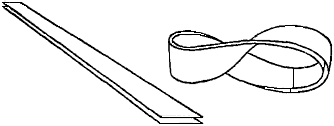
Из-за неровностей почвы на местности невозможно произвести измерение длины отрезка непосредственно. Если расстояние меньше длины мерной ленты, то можно просто натянуть её, встав в начале и в конце измеряемого отрезка. Но если расстояние значительно больше, то сначала измеряемый отрезок «провешивают», то есть намечают путь, по которому будет производиться измерение. Для проведения таких измерений необходимо иметь вехи - длинные шесты и рулетку.
Используя вехи, определите длину и ширину пришкольного участка, размеры здания.
Построение прямых углов на местности.
Для построения прямых углов на местности приготовим несколько простых приборов.
-
Эккер. Чтобы изготовить эккер, нужно сколотить две дощечки под прямым углом и вбить в каждый конец дощечек по гвоздику.
-
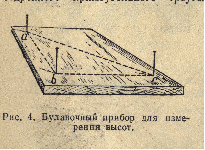
Булавочный прибор. На любой дощечке наметить вершины равнобедренного прямоугольного треугольника и вбить там по булавке или гвоздику.
-
Египетский прибор. Две веревки одинаковой длины привязать к колышкам с обеих сторон.
Задание 1.
Определите направление частей света. Провешайте линию по направлению север-юг. Постройте на местности участок прямоугольной формы. Измерьте его длину и ширину, найдите площадь.
Построение плана участка.
Используя результаты прошлых измерений, составьте план школьного участка, укажите на нем используемый масштаб и направление частей света.
Здание лицея
спортзал
Геометрические фигуры.
Треугольник.
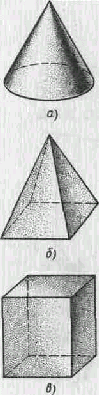
Последователи Фалеса, занявшиеся геометрией, оказались в том же затруднении, что и все первоначинатели. Так как до Фалеса никто в Греции геометрией не занимался, у геометрических фигур еще не было названий. Греки стали называть фигуры словами, обозначавшими окружающие их предметы похожей формы. Например, для прокатки белья женщины применяли скалку, которую по-гречески называли «каландер». Поэтому все вытянутые тела с округлым сечением получили название цилиндра. А тело, изображенное на рисунке а, похоже на еловую шишку. Эту шишку по-гречески называли «конос». Поэтому и тела такой формы получили название конуса. Ну, а тело, изображенное на рисунке б, напоминает нам египетские пирамиды. Поэтому такие тела и назвали пирамидами. При этом в Египте основания пирамид были четырехугольными, а греки изучали и четырехугольные, и треугольные, и даже шестиугольные пирамиды. Да, мы забыли сказать, откуда получила свое имя сфера. По-гречески так назывался мяч, с которым играли дети. Слово «параллельный» происходит от греческого «параллелос» - идти рядом. От него уже происходят слова «параллелепипед» (рис. в) и другие.
Дали названия и частям плоскости. У фигуры, изображенной внизу, две параллельные стороны. Такой вид сбоку имел столик для еды. Его сначала называли «тетрапецион» - четырехногий, а потом название сократилось до «трапезион» (и сейчас иногда говорят «трапеза» вместо еда). Поэтому фигуру такого вида назвали трапецией.
Таким образом, сами названия геометрических фигур показывали, что геометрия возникла для решения практических задач и с самого начала была тесно связана с практикой, с человеческим трудом.
Некоторые названия пришли к нам из латинского языка. Например, слово «биссектриса» означает луч, который выходит из вершины угла и делит этот угол пополам.
В пятом классе мы увидели, что треугольники бывают разных видов. Можно различать треугольники по их углам, а можно - по сторонам.
Если у треугольника все углы - острые, то это остроугольный треугольник. Если есть прямой угол - то это прямоугольный, а если есть тупой угол, то тупоугольный.
Задание 1.
Сколько тупых или прямых углов может иметь треугольник? Почему?
Задание 2.
Изобрази треугольники разных видов в зависимости от углов. Обозначь их вершины буквами, сделай записи.
Треугольники, у которых все стороны разной длины называются разносторонними. Если равны две стороны, то это равнобедренные. А если равны все три стороны, то равносторонние.
Задание 3.
Как с помощью циркуля и линейки построить равносторонний треугольник? Какова величина углов такого треугольника?
Пирамида.
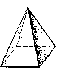 Как мы уже знаем, такая фигура называется пирамидой. Плоские многоугольники, которые её ограничивают, называются гранями. Причем одна из них, та, на которой стоит пирамида, называется основанием, а остальные - боковыми гранями. Все боковые грани у пирамиды - треугольники.
Как мы уже знаем, такая фигура называется пирамидой. Плоские многоугольники, которые её ограничивают, называются гранями. Причем одна из них, та, на которой стоит пирамида, называется основанием, а остальные - боковыми гранями. Все боковые грани у пирамиды - треугольники.
Задание 4: Нарисуйте развертку треугольной пирамиды, то есть такой пирамиды, у которой в основании лежит треугольник.
Для этого начертите окружность произвольным радиусом и отложите от любой точки три равных отрезка. Полученные точки соедините с центром окружности и последовательно друг с другом. Осталось пристроить правильный треугольник со стороной, равной отрезкам на окружности.
Задание 5: Сделайте развертку четырехугольной пирамиды, у которой в основании лежит квадрат.
Четырехугольники, их свойства
Если взять любые четыре точки и соединить их отрезками, то получится фигура, называемая четырехугольником. прямоугольник
квадрат
параллелограмм
трапеция
ромб
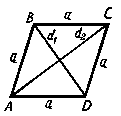
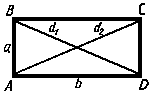
Параллелограмм
Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны. Ромб, прямоугольник и квадрат - это частные случаи прямоугольников, у которых равны или все углы, или все стороны.
А
ВЧтобы у тебя в тетради параллелограмм получился красивым, построй отрезок АВ и от обоих его концов отложи вправо (или влево) по одинаковому числу клеточек. А затем от полученных точек отложи вверх (или вниз) тоже по одинаковому количеству клеток. Так ты получишь еще две вершины параллелограмма.
|
|
a, b - стороны параллелограмма.
ha, hb - высоты параллелограмма, опущенные из вершин параллелограмма на прямые, содержащие стороны параллелограмма a, b.
d1, d2 - диагонали параллелограмма.
a, γ - углы параллелограмма, a + γ = 180°
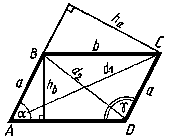
Прямоугольник
Ромб
Квадрат
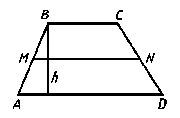
Трапеция
MN-средняя линия трапеции;
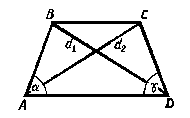
Равнобокая трапеция
AB=CD,
d1=d2
Многоугольники
Несколько точек, соединенных отрезками, образуют многоугольник. Называется многоугольник по числу его сторон - пятиугольники, шестиугольники и т. д.
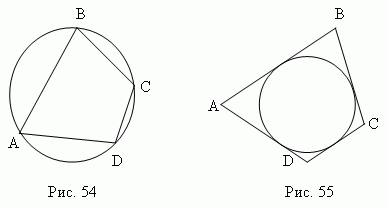
Вписанным в круг называется многоугольник, вершины которого расположены на окружности(рис.54). Описанным около круга называется многоугольник, стороны которого являются касательными к окружности
( рис.55).
Правильный многоугольник - это многоугольник с равными сторонами и углами.
Призмы, виды призм.
Призма - многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом.
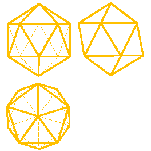
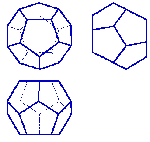
Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными. Углы при вершинах такого многогранника равны между собой.
Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.
Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.
Тетраэдр - правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (это - правильная треугольная пирамида).
Гексаэдр - правильный шестигранник. Это куб состоящий из шести равных квадратов.
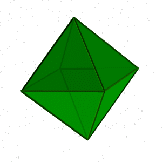
Октаэдр - правильный восьмигранник. Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.
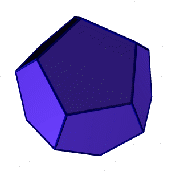
Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины.
Икосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины.
Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.
Звездчатый октаэдр - восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые "куски", внешние по отношению к октаэдру. Это малые тетраэдры, основания которых совпадают с гранями октаэдра. Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stella octangula - восьмиугольная звезда.
|
|
|
Малый звездчатый додекаэдр - звездчатый додекаэдр первого продолжения. Он образован продолжением граней выпуклого додекаэдра до их первого пересечения. Каждая грань выпуклого додекаэдра при продолжении образует правильный звездчатый пятиугольник. Пересекающиеся плоскости граней додекаэдра отделяют от пространства новые "куски", внешние по отношению к додекаэдру. Это двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра. При дальнейшем продолжении граней до нового пересечения образуется средний звездчатый додекаэдр - звездчатый додекаэдр второго продолжения. Последней же звездчатой формой правильного додекаэдра является звездчатый додекаэдр третьего продолжения - большой звездчатый додекаэдр. Он образован продолжением граней звездчатого додекаэдра второго продолжения до их нового пересечения.
Понятие объема.
Величина части пространства, занимаемого геометрическим телом называется объемом этого тела.
В повседневной жизни нам часто приходится определять объемы различных тел. Например, коробки, банки. В житейской практике единицами объема служили меры емкости, используемые для хранения сыпучих и жидких тел.
Среди них английские меры:
-
Бушель - 36,4 кубических дм
-
Галлон - 4,5 кубических дм
-
Баррель (сухой) - 115,628 кубических дм
-
Баррель (нефтяной) - 158,988 кубических дм
-
Английский баррель для сыпучих веществ 163,65 кубических дм.
Меры когда-то, применявшиеся в России:
-
Ведро - 12 кубических дм
-
Бочка - 490 кубических дм
-
Штоф - 1,23 кубических дм = 10 чарок
-
Чарка - 0,123 кубических дм=0,1 штофа = 2 шкалика
-
Шкалик - 0,06 кубических дм = 0,5 чарки.
Поиск формул, позволяющих вычислять объемы различных тел, был долог.
В древнеегипетских папирусах, в вавилонских клинописных табличках встречаются правила для нахождения объема усеченной пирамиды, но не сообщаются правила для вычисления объема полной пирамиды.
Определять объемы призмы, пирамиды, цилиндра и конуса умели древние греки еще задолго до Архимеда. Но только он имел общий метод, позволяющий определить любую площадь или объем. Идеи Архимеда легли в основу интегрального исчисления. Сам ученый определил с помощью своего метода площади объемы почти всех тел, которые рассматривались в античной математике.
На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда - о том, что объемы этих тел относятся как 3 : 2.
Когда Римский оратор и общественный деятель Цицерон, живший в 1 в. до н.э., был в Сицилии, он еще видел этот заросший кустами и терновником памятник с шаром и цилиндром.
Для вычисления объемов воспользуемся исходными положениями:
-
Равнее тела имеют равные объемы.
-
Объем тела, состоящего из некоторых частей, равен сумме объемов этих частей.
Процедура измерения объемов аналогична процедуре измерения площадей. Число измерения (единичных кубов) и частей единицы, содержащихся в данном теле, принимается за числовое значение объема.
Задание1: Приготовьте полые модели призмы и пирамиды с одинаковыми основаниями и одинаковой высотой. Налейте воду в модель пирамиды и перелейте её в модель призмы. Сколько раз можно повторить эту операцию? Если объем прямой призмы, равен произведению площади основания на высоту, то как найти объем пирамиды?
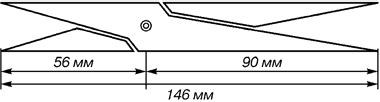
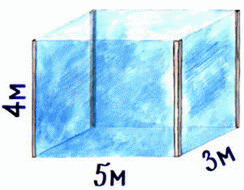
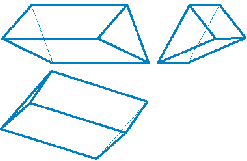
Задание 2: Найдите объём аквариума, изображённого на рисунке.
Окружность, круг.
В жизни мы часто встречаемся с такими фигурами, как окружность и круг. Кругами расходятся волны на воде при бросании камня, форму круга имеет блин, а форму окружности - обруч.
Математики говорят, что окружность - это множество точек, расположенных на одном расстоянии от данной точки, называемой центром окружности. Само это расстояние называют радиусом окружности. А часть плоскости, ограниченная окружностью, называется кругом. Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, называется диаметром.
Задание 1: Начертите с помощью циркуля окружность с радиусом 3 см. Укажите центр окружности, проведите радиус, диаметр, хорду.
Задание 2: Начертите из одной точки три окружности с радиусами 2 см, 3 см, 4 см. Такие окружности называются концентрическими. Проведите ось симметрии полученной фигуры. Сколько таких осей можно провести?
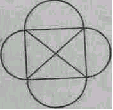
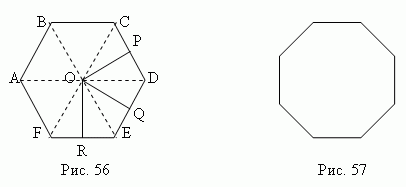
Задание 3: Начертите окружность с радиусом 2см, разделите её при помощи циркуля на 6 равных частей. Из каждой точки деления проведите окружность такого же радиуса. На что похожа полученная фигура? Имеет ли она оси симметрии? Сколько? А центр симметрии?
Цилиндр. Конус.
Вы уже знаете, что слово "цилиндр" произошло от греческого слова "каландер", означающего "валик", "каток". На рубеже XVIII - XIX веков мужчины многих стран носили твёрдые шляпы с небольшими полями, которые так и назывались цилиндрами из-за большого сходства с геометрической фигурой цилиндром.
Какие ещё предметы имеют цилиндрическую форму?
Варианты ответов: стакан, карандаш, многие баночки, кастрюли, бидоны, часть скалки и т.д.
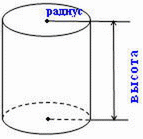
Высота цилиндра - это расстояние между основаниями, радиус цилиндра - радиус круга, являющегося основанием цилиндра.
Цилиндр
Задание 1:Представьте, что у каждого из вас в руках деревянный цилиндр и топорик, с помощью которого вы легко можете рассечь или расколоть цилиндр. "Аккуратно" топориком ударяем по верхнему основанию и раскалываем его. Он распадётся на две половинки. Форму какой геометрической фигуры имеет срез или по научному говорят сечение цилиндра? Нарисуйте сечение цилиндра.
А если рубить не вдоль, а поперек цилиндра, то что получится в сечении? Сделайте рисунок.
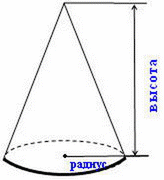
Конус, в отличие от цилиндра, имеет вершину, высоту и радиус основания.
Конус
Если вершину и верхнюю часть конуса отсечь, то мы получим так называемый усечённый конус.
Задание 1: Какие предметы имеют форму конуса или усечённого конуса?
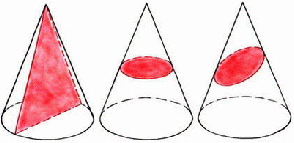
Задание2: А сейчас снова представим, что мы рассекаем деревянный конус. Формы каких геометрических фигур могут иметь сечения конуса?
Понятие односторонней
и двусторонней поверхности.
Возьмем полоску бумаги и склеим из неё кольцо. Раскрасим одну сторону кольца в один цвет, вторую - в другой. Очевидно, что кольцо имеет две стороны, то есть это двусторонняя поверхность.
Лента Мёбиуса получается из обыкновенной бумажной полоски, склеенной концами, но не в обычное кольцо, а в кольцо, перекрученное на пол-оборота. То есть, склеивая кольцо из полосы бумаги, мы просто совмещаем верх одного ее конца с низом другого. Для того чтобы сделать ленту Мёбиуса, нужно перевернуть один конец, и тогда получится, что низ склеится с низом, или, что то же самое, верх с верхом. Иначе говоря, мы должны совместить одноименные стороны обоих концов. Что мы знаем о такой поверхности?
Мы знаем, что у нее только одна сторона, в то время как у кольца, естественно, две. То есть ставим ручку и проводим, не отрывая ее от бумаги, линию вдоль бумажной полосы, пока эта линия не замкнется. Что будет у кольца? Одна сторона - с линией, другая - пустая. Что будет у ленты Мёбиуса? Линия будет везде! Пустого места не останется. Это и означает, что лента является односторонней поверхностью. Второй стороны просто нет!
Но и это еще не все! Если разрезать обычное кольцо вдоль, получатся всего лишь два таких же кольца потоньше.
А если разрезать ленту Мёбиуса - получим ОДНУ новую ленту, но уже с двукратным перегибом.
Но ленту Мёбиуса нельзя разрезать сколько хочешь! При разрезании в первый раз она становится перекрученной дважды. А любое четное скручивание дает две стороны!
Изучением таких фигур занимается раздел математики, который носит название топологии. У людей, интересующихся математикой не всерьез, а от случая к случаю, может сложиться впечатление, что тополог - это праздный любитель забав, проводящий все свое время за конструированием листов Мёбиуса и других занимательных математических моделей. Если бы такие люди раскрыли любой современный учебник топологии, то они были бы весьма поражены, увидев страницы, сплошь испещренные математическими символами, среди которых изредка встречаются картинки или чертежи. Топология и в самом деле возникла из рассмотрения геометрических головоломок, но сейчас она давно уже разрослась в непроходимые дебри абстрактной теории. В наши дни топологи с подозрением относятся к теоремам, при доказательстве которых приходится использовать наглядные представления.
Рис. 28. Двойной лист Мёбиуса можно сделать из двух полосок бумаги (слева), перекрутив их на полоборота и склеив так, как показано на рисунке справа.
Тем не менее серьезные топологические исследования служат неисчерпаемым источником занимательных моделей самого необычайного свойства. Рассмотрим, например, двойной лист Мёбиуса. Он получится, если наложить друг на друга две полоски бумаги, перекрутить их, повернув как единое целое на пол-оборота, и соединить концы так, как показано на рис. 28.
На первый взгляд кажется, что в результате мы получаем два вложенных друг в друга листа Мёбиуса. В самом деле, просунув палец между полосками бумаги и обводя им вокруг них до тех пор, пока не возвратитесь в исходную точку, вы «докажете», что фигура состоит из двух отдельных лент. Насекомое, заползшее в щель между бумажными лентами, могло бы совершать такое «кругосветное путешествие» до бесконечности. При этом оно всегда ползало бы по одной полоске бумаги, спинка его касалась бы другой полоски, и ему нигде не удалось бы найти точку, в которой «пол» сходится с «потолком». Отсюда наделенное разумом насекомое заключило бы, что оно путешествует между поверхностями двух отдельных полосок.
Но представим себе, что наше насекомое оставило на полу метку и совершает обход вокруг полосок до тех пор, пока не встретит ее снова. Тогда оно обнаружит, что метка находится не на полу, а на потолке и что необходимо обойти еще раз вокруг полосок, чтобы метка снова очутилась на полу!
Насекомое вряд ли должно обладать недюжинным воображением, чтобы понять, что и пол и потолок образуют одну сторону одной-единственной полоски То, что на первый взгляд казалось двумя вложенными друг в друга лентами, на самом деле представляет собой одну большую ленту.
Двусторонние поверхности можно получить, разрезая односторонние.
Бутылка Клейна.
Что такое бутылка Клейна?
«Бутылка Клейна» - это односторонняя поверхность. В трехмерном пространстве она имеет линию самопересечения. Без самопересечения может быть построена только в четырехмерном пространстве.
Представьте себе обыкновенную бутылку, которая сделана из «пластичного» стекла, которое можно гнуть и скручивать. И вот мы проделываем в ее боку дырку, берем за горлышко, сгибаем, и вставляем горлышко в эту дырку. Пропускаем его внутри до самого дна. В дне проделываем еще одну дырку. Края горлышка и дырки аккуратно склеиваем. Готово!!!
Получилась тоже ОДНОСТОРОННЯЯ поверхность! Но так как ручкой по ней не повозишь - неудобно, - пустим по ней ползать муху. И вот эта муха будет ползать везде, ни разу не перейдя изнутри наружу (или снаружи вовнутрь). В отличие от любой обычной бутылки, у которой есть внутренняя и внешняя стороны, и граница между ними проходит по горлышку, у этой бутылки нет ничего внешнего и внутреннего. Она как бы ввернута сама в себя.
На картинке это выглядит вот так:
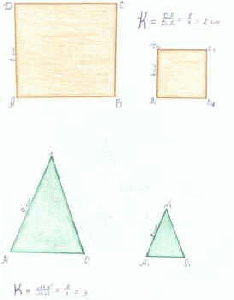
Понятие подобия.
Две фигуры, имеющие одинаковую форму, но разные размеры, называются подобными. Карты одной и той же местности, имеющие разные масштабы
являются подобными. Любые две окружности подобны. Можно привести много примеров подобных фигур, в жизни мы с ними сталкиваемся на каждом шагу.
Задание1: Нарисуй две фигуры одинаковой формы, но разных размеров, например, большую и маленькую бабочки, большой и маленький треугольник, большой и маленький квадрат. Измерь длину стороны большой и маленькой фигуры, найди их отношение.
Отношение расстояний между любыми двумя соответственными точками на этих фигурах равно одному и тому же числу, называемому коэффициентом подобия. У всех изображенных здесь фигур коэффициент подобия равен 2.
Например, при увеличении фотографии все размеры увеличиваются в одном и том же отношении, т. е. происходит подобное преобразование с фотопленки на фотобумагу. Подобное преобразование совершается и тогда, когда делают уменьшенную копию чертежа, рисунка и т. д. так, например, вы поступаете, когда срисовываете чертеж с доски в свою тетрадь. Подобные фигуры имеют одинаковую форму, но различные размеры.
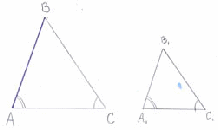
У подобных многоугольников соответственные углы равны, а стороны пропорциональны, т. е.  А=
А= А1,
А1,  В=
В= В1,
В1,  С=
С= С1 и
С1 и 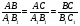
Понятие гомотетии.
Отрезки АС и А1С1 называются гомотетичными, потому что лучи А1А и С1С пресекаются в точке О так, что ОА1= к ОА и ОС1= к ОС.
То есть, чтобы построить точку, гомотетичную данной точке А, нужно через точку А и точку О провести луч и от точки О отложить отрезок ОА столько раз, каков коэффициент гомотетии. При этом получится фигура, подобная данной и коэффициент подобия будет равен коэффициенту гомотетии.
Так на рисунке большой четырехугольник подобен маленькому, потому что они гомотетичны.
Применение подобия для решения задач.
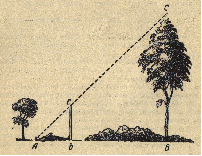
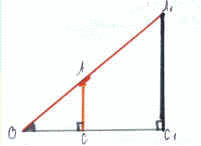
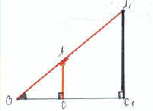
Понятие подобия широко применяется в практической деятельности человека. Часто приходится находить расстояния, измерить которые непосредственно невозможно, например высоту большого дерева, огромного небоскреба или ширину реки. Пусть А1С1 - высота трубы, которую нужно измерить, а АС - палка в руках человека. Так как ΔОАС подобен ΔОА1С1, то длина трубы А1С1 во столько раз больше, чем длина палки, во сколько раз отрезок ОС1 больше отрезка ОС, которые легко измерить.
Измерения на местности.
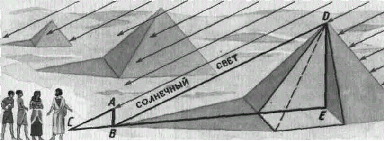
Искусны были египетские писцы и гарпедонапты! Но однажды им пришлось устыдиться, потому что пришелец из далекой Греции оказался намного искуснее их. Это случилось в VI веке до новой эры, а пришельцем был Фалес из Милета. В те времена греки не занимались геометрией, и Фалес решил на месте познакомиться с египетской наукой. Египтяне задали ему трудную задачу: как найти высоту одной из громадных пирамид? Фалес нашел для этой задачи простое и красивое решение (а в математике очень часто простота - признак красоты). Он воткнул длинную палку вертикально в землю и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды».
Чтобы сообразить это, Фалес должен был уже много знать про геометрические фигуры, а особенно про ту, которая получается, если разбить квадрат на два треугольника. Ясно, что эти треугольники равны друг другу. Кроме того, у них по прямому углу, а катеты в этих треугольниках равны друг другу. В геометрии такие треугольники называют прямоугольными и равнобедренными. А дальше, вероятно, Фалес рассуждал так. Солнце от Земли очень далеко, поэтому идущие от него лучи параллельны. Значит, и на палку, и на пирамиду лучи идут параллельно и тени от них тоже параллельны. А значит, высота пирамиды во столько раз больше высоты палки во сколько раз её тень больше тени, отбрасываемой палкой.
Измерение высоты.
На природе для определения высоты дерева можно воспользоваться шестом, длина которого равна вашему росту. Место для шеста нужно выбрать так, чтобы лежа вы видели верхушку дерева на одной прямой линии с верхней точкой шеста. Так как полученные треугольники прямоугольные и равнобедренные и они подобны, то расстояние от дерева до вашей головы будет равно высоте дерева, то есть АВ=ВС.
В качества прибора для приблизительной оценки недоступной высоты вы можете использовать свою записную книжку. Книжку нужно держать возле глаз в отвесной плоскости, а приложенный к ней карандаш bc выдвигается над верхним обрезом книжки настолько, чтобы, глядя из точки а, видеть вершину дерева В покрытой кончиком b карандаша. Тогда вследствие подобия треугольников abc и aBC высота ВС определится из пропорции BC:bc=aC:ac. Достаточно теперь прибавить к найденному размеру свой рост и вы узнаете высоту дерева.
|
A K C E
| Можно измерить высоту объекта при помощи зеркала. На некотором расстоянии от измеряемого объекта АВ на ровной земле в точке С кладут горизонтально зеркало и отходят от него назад в такую точку Е, стоя в которой наблюдатель видит в зеркале верхнюю точку А объекта. Тогда высота объекта во столько раз выше роста наблюдателя, во сколько раз расстояние ВС от зеркала до объекта больше расстояния СЕ от зеркала до наблюдателя: АВ: КЕ = ВС: СЕ. |
Измерение расстояния до недоступной точки.
D
А
В
С
Е
Не переплывая реки, измерить её ширину - так же просто для знающего геометрию, как определить высоту дерева, не взбираясь на вершину. Недоступное расстояние измеряют теми же приемами, как и недоступную высоту.
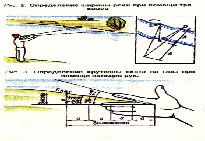
Для первого способа нам понадобится прибор с тремя булавками а, b, с на вершинах равнобедренного треугольника. Пусть требуется определить ширину реки АВ, стоя на том берегу, где точка В. Став где-нибудь у точки С держите булавочный прибор так, чтобы, смотря одним глазом вдоль двух булавок, мы видели, как обе они покрывают точки А и В. Теперь, не двигая дощечки прибора, смотрите вдоль двух других булавок (перпендикулярно прежнему направлению) и заметьте какую-нибудь точку D, покрываемую этими булавками, т.е. лежащую на прямой, перпендикулярной к АС. После этого воткните в точку С веху и идите с вашим прибором вдоль прямой СD, пока не найдете на ней такую точку E, откуда можно одновременно покрыть для глаза булавкой b шест точки С, а булавкой а - точку А. Это будет означать, что вы нашли на берегу третью вершину треугольника АСЕ, в котором угол С - прямой, а угол Е равен 45, тогда АС = СЕ. Если измерить расстояние СЕ хотя бы шагами, вы узнаете расстояние АС. Отняв ВС найдем ширину реки.
Можно определить ширину реки, используя травинку, если вы видите на противоположном берегу два объекта, расстояние между которыми приблизительно можно определить шагами по своему берегу. Приложите травинку к глазам так, чтобы направление взгляда через один конец травинки попадало на один объект, а через другой конец - на второй объект. Тогда ширина реки во столько раз больше расстояния от глаз до травинки, во сколько раз расстояние между объектами больше длины травинки.
Понятие о графах.
Пусть несколько точек обозначают какие-то объекты, а отрезки, их соединяющие, - отношения между объектами. Такой рисунок называется графом. Существует целая теория графов и большое количество задач, решаемых с помощью графов. При взгляде на географическую карту сразу бросается в глаза сеть железных дорог. Это типичный граф: кружочки обозначают станции - вершины графа, а соединяющие их пути - ребра графа. В строительстве графы используют при планировании проведения работ, так называемые «сетевые графики строительства». Вершины графа обозначают виды работ, указаны числа - сроки исполнения работ.
Впервые основы теории графов появились в работе Л. Эйлера, где он описывал решения головоломок и математических развлекательных задач. Широкое развитие теория графов получила с 50-тых годов 20 века в связи с развитием кибернетики и вычислительной техники.
Известен анекдот: некто давал миллион рублей каждому, кто начертит следующую фигуру. Но при вычерчивании ставилось одно условие. Требовалась, чтобы фигура эта была вычерчена одним непрерывным росчерком, т. е. не отнимая пера или карандаша от бумаги и не удваивая ни одной линии, другими словами, по раз проведенной линии нельзя уже было пройти второй раз.
Надежда стать «миллионером», решив такую легкую задачу, может заставить испортить много бумаги и потратить много времени на попытки вычертить эту фигуру, как требовалось, одним росчерком. Задача, однако, не решается, и это тем досаднее, что она не решается только «чуть-чуть»... Никак не удается провести только одной «последней» какой-либо линии. Удается даже открыть секрет, что вся трудность в том, чтобы вычертить сначала одним росчерком, не повторяя линии, еще более простую фигуру - четырехугольник с двумя диагоналями. Это, казалось бы, уже совсем просто, а все-таки... не удается.
Сомнения в невозможности решения этой задачи все-таки остаются, тем более что фигуры, гораздо более сложные и трудные с виду, легко вычерчиваются, одним росчерком. Так, например, выпуклый пятиугольник со всеми его диагоналями легко вычерчивается одним непрерывным движением без повторения, причем получается фигура, представленная на рисунке. То же самое легко удается со всяким многоугольником с нечетным числом сторон и никак не удается с квадратом, шестиугольником и т. д. - словом, с многоугольником с четным числом сторон.
Легко нарисовать окружность, не отрывая карандаша от бумаги и не проводя никакую линию дважды. Это можно сделать и когда надо нарисовать окружность вместе с ее диаметром: выйдем из конца диаметра, пройдем его, а потом по окружности вернемся обратно. Но как провести и второй диаметр? Как бы мы ни старались, нарисовать такую фигуру одним росчерком пера (или одним движением карандаша) не удастся,
Какие же фигуры можно нарисовать таким образом? Впервые этим вопросом занялся упоминавшийся ранее знаменитый математик Леонард Эйлер. Он поставил задачу, можно ли совершить прогулку через мосты на рисунке, пройдя через каждый мост по одному разу и вернувшись назад. Все его попытки нарисовать такой маршрут успеха не имели.
Ответ Эйлера был очень прост: обойти всю фигуру, не отрывая карандаша от бумаги, не проходя ни одной линии дважды и вернувшись в исходную точку, можно лишь в случае, когда все вершины имеют четное число «дорог» или как говорил Эйлер «четные веса».
Эйлер выяснил и то, в каком случае можно пройти по одному разу каждую линию, если начало и конец пути не обязаны совпадать. Это оказалось возможным, если лишь две вершины имеют нечетные веса. В этом случае надо обязательно начинать с точки с нечетным весом
Если взять шахматную доску с 64 клетками, то в ней - 28 точек нечетного порядка, и, чтобы вычертить ее, надо чертить 14-кратную линию. С другой стороны, если взять треугольник, поделить каждую из его сторон на 12 (или сколько угодно) равных частей и провести из точек деления линии, параллельные другим сторонам, то полученная сетчатая фигура может быть вычерчена одним непрерывным движением без повторений. Таких примеров можно подобрать сколько угодно.
Теперь нам нетрудно будет разобраться и показать, какую из любых данных фигур можно вычертить одним росчерком, без повторения линий, а какую нет. Каждую из задач подобного рода можно свести к разобранной уже нами Эйлеровой задаче о мостах.
Простейшие задачи.
Графы часто используют для решения логических проблем, связанных с перебором вариантов. Для примера используем такую задачу: В ведре 8л воды, требуется отлить в 5-литровую кастрюлю 4л воды и оставить в ведре 4л. Имеются еще две кастрюли емкостью 5л и 3 л.
Есть 2решения этой задачи - в 7 ходов и в 8 ходов:
8 5 3 8 5 3
8 0 0 8 0 0
5 0 3 3 5 0
5 3 0 3 2 3
2 3 3 6 2 0
2 5 1 6 0 2
7 0 1 1 5 2
7 1 0 1 4 3
4 1 3 4 4 0
4 4 0
Подобным образом можно составить граф любой позиционной игры, где позиции станут вершинами, а направленные отрезки между вершинами будут означать, что одним ходом можно перейти от одной позиции к другой по направлению стрелки.
Свойства графов не зависят от того, соединены вершины отрезками или кривыми линиями. Это дает возможность изучения их свойств с помощью одной из молодых наук - топологии.
ПУТЕШЕСТВИЕ КОНТРАБАНДИСТА
Задачу о переходе через мосты можно предлагать в различных видоизменениях. Можно представить ее, например, как путешествие контрабандиста, который решил побывать во всех странах Европы, но так, чтобы через границу каждого государства ему пришлось переходить только один раз.
В данном случае очевидно, что различные страны и их границы будут соответствовать разным местностям и рукавам реки, через которые переброшено по одному мосту (для каждой границы, общей двум странам).
Исследуя разрешимость задачи, сразу видим, что Финляндия, Испания и Дания имеют нечетное число границ с соседними государствами, т. е. число нечетных местностей более двух, а, следовательно, путешествие, которое предполагает совершить контрабандист, невозможно.
Дополнительные материалы.
Золотой треугольник
Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.
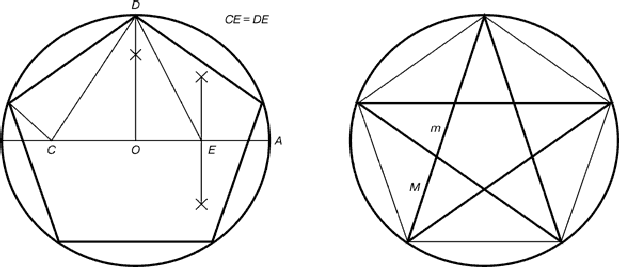
Рис. 5. Построение правильного пятиугольника и пентаграммы
Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471...1528). Пусть O - центр окружности, A - точка на окружности и Е - середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника.
Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
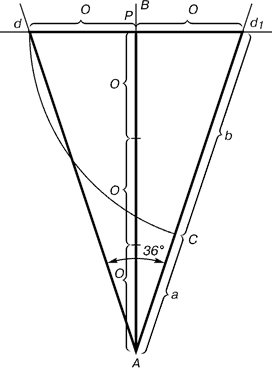
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Рис. 6. Построение золотого
треугольника
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.
История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления
| . Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
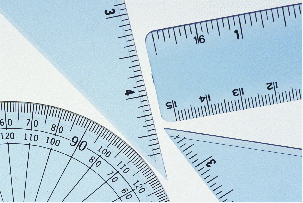
Рис. 7. Динамические прямоугольники Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
Рис. 8. Античный циркуль золотого сечения В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным. В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии. Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок - бога отца, а весь отрезок - бога духа святого). Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное. В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать». Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д. Известен пропорциональный циркуль Дюрера. Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, - писал он, - что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд). Золотое сечение в музыке
|
Музыка - посредник между духовной и чувственной жизнью"
Арним
Один из видных деятелей русской и советской музыкальной культуры Э.К.Розенов впервые применил закон «золотого сечения» в музыке. Анализируя «Хроматическую фантазию и фугу» И.С.Баха, ученый пришел к выводу, что «она, оказывается, сотворена по естественным законам природного формообразования, подобно человеческому организму, в котором совершенно также господствуют оба закона - закон золотого сечения и закон симметрии, с такими же мелкими художественными неточностями в индивидуальном строении живого тела, которыми оно отличается от мертвых форм отвлеченного или фабричного происхождения». Определяя зону золотого сечения, можно убедиться, что она не в начале, не в середине пьесы, а ближе к концу (кульминация произведения), то есть в третьей четверти целого. В мире, живом и неживом, все связано и все взаимообусловлено, все подчинено одним законам. Человек в своей разносторонней деятельности - в науке, технике, художественном творчестве - не может не подчиняться тем же законам.
Заключение
Датский физик Нильс Бор говорил, что математика является значительно большим, чем наука, поскольку она является языком науки. И действительно, математика стала для многих отраслей знания не только орудием количественного расчета, но также методом точного исследования.
Математический стиль мышления, умение рассуждать строго, без логических скачков нужны и будущим юристам и историкам, биологам и лингвистам, инженерам и врачам.
Многим из вас самим придется принять участие в решении научных проблем. И чем больше и глубже вам удастся усвоить дух математики и научиться использовать её методы хотя бы в простейших ситуациях, тем дальше и быстрее вы сможете продвинуться в своих исследованиях.
В добрый путь, друзья!
Автор Антипина Г.В.
1998 год


