- Преподавателю
- Математика
- Великие математики и задачи тысячилетия
Великие математики и задачи тысячилетия
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Савченко С.Г. |
| Дата | 29.11.2015 |
| Формат | docx |
| Изображения | Есть |
Великие математики и задачи тысячелетия
Жюль Анри́ Пуанкаре́ - французский математик, физик, астроном и философ. Глава Парижской академии наук (1906), член Французской академии (1908) и ещё более 30 академий мира, в том числе иностранный член-корреспондент Петербургской академии наук (1895).
Историки причисляют Анри Пуанкаре к величайшим математикам всех времён. Он считается, наряду с Гильбертом, последним математиком-универсалом, учёным, способным охватить все математические результаты своего времени. Его перу принадлежат более 500 статей и книг. «Не будет преувеличением сказать, что не было такой области современной ему математики, "чистой" или "прикладной", которую бы он не обогатил замечательными методами и результатами».
Среди его самых крупных достижений:
-
Создание топологии.
-
Качественная теория дифференциальных уравнений.
-
Теория автоморфных функций.
-
Разработка новых, чрезвычайно эффективных методов небесной механики.
-
Создание математических основ теории относительности.
-
Наглядная модель геометрии Лобачевского.

Анри Пуанкаре родился 29 апреля1854 года в Нанси (Лотарингия, Франция). Его отец, Леон Пуанкаре (1828-1892), был профессором медицины в Университете Нанси. Мать Анри, Эжени Лануа (EugénieLaunois), всё свободное время посвящала воспитанию детей - сына Анри и младшей дочери Алины.
Политехническая школа, старое здание на ул. Декарта (ныне Министерство высшего образования)
Пуанкаре-студент (1873)
С самого детства за Анри закрепилась репутация рассеянного человека, которую он сохранил на всю жизнь. В детстве он перенёс дифтерию, которая осложнилась временным параличом ног и мягкого нёба. Болезнь затянулась на несколько месяцев, в течение которых он не мог ни ходить, ни говорить. За это время у него очень сильно развилось слуховое восприятие и, в частности, появилась необычная способность - цветовое восприятие звуков, которое осталось у него до конца жизни. Хорошая домашняя подготовка позволила Анри в восемь с половиной лет поступить сразу на второй год обучения в лицее. Там его отметили как прилежного и любознательного ученика с широкой эрудицией. В последующие годы математические таланты Пуанкаре проявлялись всё более и более явно. В октябре 1873 года он стал студентом престижной парижской Политехнической школы, где на вступительных экзаменах занял первое место. Его наставником по математике был Шарль Эрмит. В следующем году Пуанкаре опубликовал в «Анналах математики» свою первую научную работу по дифференциальной геометрии.
В 1879 г.
По результатам двухлетнего обучения (1875) Пуанкаре приняли в Горную школу, наиболее авторитетное в то время специальное высшее учебное заведение. Там он через несколько лет (1879), под руководством Эрмита, защитил докторскую диссертацию, о которой Гастон Дарбу, входивший в состав комиссии, сказал: «С первого же взгляда мне стало ясно, что работа выходит за рамки обычного и с избытком заслуживает того, чтобы её приняли. Она содержала вполне достаточно результатов, чтобы обеспечить материалом много хороших диссертаций». Получив учёную степень, Пуанкаре начал преподавательскую деятельность в университете города Кан в Нормандии (декабрь 1879 года). Тогда же он опубликовал свои первые серьёзные статьи - они посвящены введённому им классу автоморфных функций.Там же, в Кане, он познакомился со своей будущей женой Луизой Пуленд'Андеси. 20 апреля 1881 года состоялась их свадьба. У них родились сын и три дочери. Оригинальность, широта и высокий научный уровень работ Пуанкаре сразу поставили его в ряд крупнейших математиков Европы и привлекли внимание других видных математиков. В 1881 году Пуанкаре был приглашён занять должность преподавателя на Факультете наук в Парижском университете и принял это приглашение. Параллельно, с 1883 по 1897, он преподавал математический анализ в Высшей Политехнической школе. В 1881-1882 годах Пуанкаре создал новый раздел математики - качественную теорию дифференциальных уравнений. Он показал, каким образом можно, не решая уравнения (поскольку это не всегда возможно), получить практически важную информацию о поведении семейства решений. Этот подход он с большим успехом применил к решению задач небесной механики и математической физики. Десятилетие после завершения исследования автоморфных функций (1885-1895) Пуанкаре посвятил решению нескольких сложнейших задач астрономии и математической физики. Он исследовал устойчивость фигур планет, сформированных в жидкой (расплавленной) фазе, и обнаружил, кроме эллипсоидальных, несколько других возможных фигур равновесия. 

Математическая деятельность Пуанкаре носила междисциплинарный характер, благодаря чему за тридцать с небольшим лет своей напряжённой творческой деятельности он оставил фундаментальные труды практически во всех областях математики. Работы Пуанкаре, опубликованные Парижской Академией наук в 1916-1956, составляют 11 томов. Это труды по созданной им топологии, автоморфным функциям, теории дифференциальных уравнений, интегральным уравнениям, неевклидовой геометрии, теории вероятностей, теории чисел, небесной механике, физике, философии математики и философии науки.
Одна из последних фотографий. Пуанкаре и Мария Склодовская-Кюри на Сольвеевском конгрессе 1911Во всех разнообразных областях своего творчества Пуанкаре получил важные и глубокие результаты. Хотя в его научном наследии немало крупных работ по «чистой математике» (абстрактная алгебра, алгебраическая геометрия, теория чисел и др.), всё же существенно преобладают труды, результаты которых имеют непосредственное прикладное применение. Особенно это заметно в его работах последних 15-20 лет. Тем не менее открытия Пуанкаре, как правило, имели общий характер и позднее с успехом применялись в других областях науки.
Творческий метод Пуанкаре опирался на создание интуитивной модели поставленной проблемы: он всегда сначала полностью решал задачи в голове, а затем записывал решение. Пуанкаре обладал феноменальной памятью и мог слово в слово цитировать прочитанные книги и проведённые беседы (память, интуиция и воображение Анри Пуанкаре даже стали предметом настоящего психологического исследования). Кроме того, он никогда не работал над одной задачей долгое время, считая, что подсознание уже получило задачу и продолжает работу, даже когда он размышляет о других вещах. Свой творческий метод Пуанкаре подробно описал в докладе «Математическое творчество» (парижское Психологическое общество, 1908).
Особые точки интегральных кривых
После защиты докторской диссертации, посвящённой изучению особых точек системы дифференциальных уравнений, Пуанкаре написал ряд мемуаров под общим названием «О кривых, определяемых дифференциальными уравнениями» . В этих статьях он построил новый раздел математики, который получил название «качественная теория дифференциальных уравнений». Пуанкаре показал, что даже если дифференциальное уравнение не решается через известные функции, тем не менее из самого вида уравнения можно получить обширную информацию о свойствах и особенностях поведении семейства его решений. В частности, Пуанкаре исследовал характер хода интегральных кривых на плоскости, дал классификацию особых точек (седло, фокус, центр, узел), ввёл понятия предельного цикла и индекса цикла, доказал, что число предельных циклов всегда конечно, за исключением нескольких специальных случаев.
Узел
Центр
Фокус
седло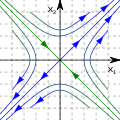



Отзывы о Пуанкаре как о человеке чаще всего восторженные. В любой ситуации он неизменно выбирал благородную позицию. В научных спорах был твёрд, но неукоснительно корректен. Никогда не был замешан в скандалах, приоритетных спорах, оскорблениях. Равнодушен к славе: он неоднократно добровольно уступал научный приоритет, даже если имел серьёзные права на него; например, он ввёл термины «фуксовы функции», «группа Клейна», «устойчивость по Пуассону», «числа Бетти» - хотя имел все основания назвать эти объекты своим именем. Друзья Пуанкаре отмечают его скромность, остроумие, терпимость, чистосердечность и доброжелательность. Внешне он мог производить впечатление человека замкнутого и малообщительного, но в действительности такое поведение было следствием его застенчивости и постоянной сосредоточенности.
В 1906 году Пуанкаре избран президентом Парижской академии наук. В 1908 году он тяжело заболел и не смог сам прочитать свой доклад «Будущее математики» на Четвёртом математическом конгрессе. Первая операция закончилась успешно, но спустя 4 года состояние Пуанкаре вновь ухудшилось. Скончался в Париже после операции от эмболии17 июля1912 года в возрасте 58 лет. Похоронен в семейном склепе на кладбище Монпарнас.
Вероятно, Пуанкаре предчувствовал свою неожиданную смерть, так как в последней статье описал нерешённую им задачу («последнюю теорему Пуанкаре»), чего никогда раньше не делал. Спустя несколько месяцев эта теорема была доказана Джорджем Биркгофом. Позже при содействии Биркгофа во Франции был создан Институт теоретической физики имени Пуанкаре.
Гипотеза Пуанкаре́ является одной из наиболее известных задач топологии. Она даёт достаточное условие того, что пространство является трёхмерной сферой с точностью до деформации.
Всякое односвязное компактное трёхмерное
многообразие без края гомеоморфно трёхмерной сфере.
В исходной форме гипотеза
Пуанкаре утверждает:
Обобщённая гипотеза Пуанкаре утверждает:
Для любого натурального числа n всякое многообразие размерности nгомотопически эквивалентно сфере размерности n тогда и только тогда, когда оно гомеоморфно ей.
Исходная гипотеза Пуанкаре является частным случаем обобщённой гипотезы при n = 3.
В 1900 году Пуанкаре сделал предположение, что трёхмерное многообразие со всеми группами гомологий как у сферы гомеоморфно сфере. В 1904 году он же нашёл контр-пример, называемый теперь сферой Пуанкаре, и сформулировал окончательный вариант своей гипотезы. Попытки доказать гипотезу Пуанкаре привели к многочисленным продвижениям в топологии многообразий.
Соль премии
Мораль в том, что если смотреть сильно вблизи, поверхность шарика (сфера) неотличима от плоскости. Двинемся дальше. Возьмем обычный круг на плоскости. У него есть граница - окружность. Ясно, что если вырезать этот круг ножницами, а потом стянуть границу в одну точку и надуть что получится воздухом, то круг расправится в двумерную сферу (тут надо думать о воздушных шарах и все такое).
Мораль - двумерная сфера получается из круга склеиванием всех точек границы в одну. И наоборот, если вырезать в двумерной сфере маленькую дырку и растянуть ее, то двумерная сфера расправится в плоский круг.
Аналогично, если взять обычный шарик и склеить все точки его границы в одну, то получится трехмерная сфера.
Аналогично, наше трехмерное пространство - это просто трехмерная сфера с вырезанной дыркой. Если смотреть на трехмерную сферу вблизи, то ее нельзя отличить от трехмерного пространства - дырка сильно далеко, и мы ее не замечаем.
Так вот. Трехмерная сфера - пример трехмерного многообразия (это значит, что, глядя вблизи, она неотличима от трехмерного пространства). На самом деле, разных трехмерных многообразий столько же, сколько натуральных чисел. Взглянуть на них издалека мы не можем - воображения не хватает. А вблизи они все устроены одинаково. Как быть?
Французский математик Пуанкаре высказал гипотезу, что если трехмерное многообразие удовлетворяет некоторым свойствам, то ничем иным, кроме трехмерной сферы, оно быть не может. Потом институт Клея решил, что если кто это докажет - то тот сильно умный и заслуживает миллиона денег.
Лет тридцать назад Терстон придумал, что хоть трехмерных многообразий и сильно много, но они все должны быть устроены вроде конструктора Лего. То есть, достаточно задаться восемью типами деталек и по-разному клеить их друг к другу, чтобы можно было получить вообще все возможные трехмерные многообразия. Идея была шибко красивая, но опять же, доказать ее Терстон не мог. Позже она получила название «гипотеза геометризации». Среди деталек Терстона только одна удовлетворяла условиям Пуанкаре - трехмерная сфера. То есть, доказательство гипотезы геометризации влекло бы за собой доказательство гипотезы Пуанкаре.
Заслуга Григория Перельмана - доказательство гипотезы геометризации. За это ему сразу, как только поняли, что доказательство правильное, дали Филдса и 15k, от коих он отказался. И немедленно стали говорить о том, что ему дадут миллион. Но по правилам института Клея для того, чтобы претендовать на миллион, нужно, чтобы доказательство было опубликовано в уважаемом журнале.
Доказательство исходной гипотезы Пуанкаре было найдено только в 2002 году Григорием Перельманом. Впоследствии доказательство Перельмана было проверено и представлено в развёрнутом виде как минимум тремя группами учёных.
Григо́рий Я́ковлевич Перельма́н (р. 13 июня1966, Ленинград, СССР) - выдающийся российский математик, первым доказавший гипотезу Пуанкаре.
Григорий Перельман родился 13 июня1966 года в Ленинграде в еврейской семье. Его отец Яков был инженером-электриком, в 1993 году эмигрировал в Израиль. Мать, Любовь Лейбовна, осталась в Санкт-Петербурге, работала учителем математики в ПТУ. Именно мать, игравшая на скрипке, привила будущему математику любовь к классической музыке.
До 9 класса Перельман учился в средней школе на окраине города, однако, в 5 классе начал заниматься в математическом центре при Дворце пионеров под руководством доцента РГПУ Сергея Рукшина, чьи ученики завоевали множество наград на математических олимпиадах. В 1982 году в составе команды советских школьников завоевал золотую медаль на Международной математической олимпиаде в Будапеште, получив полный балл за безукоризненное решение всех задач. Перельман окончил 239-ю физико-математическую школу города Ленинграда. Хорошо играл в настольный теннис, посещал музыкальную школу. Золотую медаль не получил только из-за физкультуры, не сдав нормы ГТО.
Был без экзаменов зачислен на математико-механический факультет Ленинградского государственного университета. Побеждал на факультетских, городских и всесоюзных студенческих математических олимпиадах. Все годы учился только на «отлично». За успехи в учёбе получал Ленинскую стипендию. Окончив с отличием университет, поступил в аспирантуру (руководитель - академик А. Д. Александров) при Ленинградском отделении Математического института им. В. А. Стеклова (ЛОМИ - до 1992 г.; затем - ПОМИ). Защитив в 1990 году кандидатскую диссертацию, остался работать в институте старшим научным сотрудником.
В начале 1990-х годов Перельман приехал в США, где работал научным сотрудником в разных университетах. Удивлял коллег аскетичностью быта, любимой едой были молоко, хлеб и сыр. В 1996 году вернулся в Санкт-Петербург, где продолжил работу в ПОМИ. В декабре 2005 года он ушёл с поста ведущего научного сотрудника лаборатории математической физики, уволился из ПОМИ и практически полностью прервал контакты с коллегами. К дальнейшей научной карьере интереса не проявлял. В настоящее время живёт в Купчино в одной квартире с матерью, ведёт замкнутый образ жизни, игнорирует прессу. Будучи представителем ленинградской геометрической школы, развил и применил сугубо ленинградскую теорию пространств Александрова для анализа потоков Риччи. В 2002 году Перельман впервые опубликовал свою новаторскую работу, посвящённую решению одного из частных случаев гипотезы геометризации Уильяма Тёрстона, из которой следует справедливость знаменитой гипотезы Пуанкаре, сформулированной французским математиком, физиком и философом Анри Пуанкаре в 1904 году. Описанный учёным метод изучения потока Риччи получил название теории Гамильтона - Перельмана. В 1996 году был удостоен премии Европейского математического общества для молодых математиков, но отказался её получать.
В 2006 году Григорию Перельману за решение гипотезы Пуанкаре присуждена международная премия «Медаль Филдса», однако он отказался и от неё.
В 2006 году журнал Science назвал доказательство теоремы Пуанкаре научным «прорывом года» («BreakthroughoftheYear»). Это первая работа по математике, заслужившая такое звание. В 2006 году Сильвия Назар и Дэвид Грубер опубликовали статью «ManifoldDestiny», которая рассказывает о Григории Перельмане и математическом сообществе и содержит редкое интервью с ним самим. В 2007 году британская газета TheDailyTelegraph опубликовала список «Сто ныне живущих гениев», в котором Григорий Перельман занимает 9-е место. Кроме Перельмана в этот список попали всего лишь 2 россиянина - Гарри Каспаров (25-е место) и Михаил Калашников (83-е место). В марте 2010 года Математический институт Клэя присудил Григорию Перельману премию в размере одного миллиона долларов США за доказательство гипотезы Пуанкаре, что стало первым в истории присуждением премии за решение одной из Проблем тысячелетия. В июне 2010 года Перельман проигнорировал математическую конференцию в Париже, на которой предполагалось вручение «Премии тысячелетия», а 1 июля2010 года публично заявил о своём отказе от премии:
Я отказался. Вы знаете, у меня было очень много причин и в ту, и в другую сторону. Поэтому я так долго решал. Если говорить совсем коротко, то главная причина - это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми. Я считаю, что вклад в решение этой задачи американского математика Гамильтона ничуть не меньше, чем мой.
Г. Я. Перельман
Задачи математики, которые ещё не решены учёными их называют «Задачи тысячелетия»
-
Задачи тысячелетия
Равенство классов P и NP
Гипотеза Ходжа
Гипотеза Пуанкаре
Гипотеза Римана
Квантовая теория
Янга - МиллсаСуществование и гладкость
решений уравнений
Навье - СтоксаГипотеза
Бёрча - Свиннертон-Дайера
Ресурсы:
ru.wikipedia.org/w/index.php?title=Гипотеза_Пуанкаре&oldid=48363787
ru.wikipedia.org/wiki
6


