- Преподавателю
- Математика
- Метод ключевой задачи
Метод ключевой задачи
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Савченко И.В. |
| Дата | 16.04.2014 |
| Формат | docx |
| Изображения | Есть |
Итоговое повторение курса планиметрии с привлечением метода ключевой задачи
Метод составления системы задач, построенной по принципу - каждая задача системы использует результат решения одной какой-либо (ключевой) задачи, будем называть методом ключевой задачи.
Существует две точки зрения на понятие ключевой задачи. Первая из них состоит в рассмотрении ключевой задачи как задачи-факта. Зачастую такая ключевая задача оказывается дополнительной теоремой школьного курса. Вторая точка зрения состоит в рассмотрении ключевой задачи как задачи-метода. При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме.
«Ключевая» задача является средством решения других задач, поэтому ее знание учащимися обязательно. Разворачивающаяся система задач, с одной стороны, способствует усвоению факта или метода решения, изложенных в «ключевой» задаче, с другой, позволяет увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная данным методом система задач является эффективным средством повторения, обобщения и систематизации учебного материала.
Свойство биссектрисы
Ключевая задача. Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные прилежащим сторонам.
F
C
D
А
Д о к а з а т е л ь с т в о. Проведем CF, параллельно биссектрисе BD. Тогда по теореме о пропорциональных отрезках 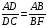 .
.
Треугольник BCF - равнобедренный.
Так как углы 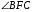 и
и 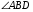 равны как соответственные при параллельных прямых BD и CF и секущей AF, углы
равны как соответственные при параллельных прямых BD и CF и секущей AF, углы 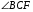 и
и 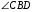 равны как накрест лежащие при параллельных прямых BD и CF и секущей ВС,
равны как накрест лежащие при параллельных прямых BD и CF и секущей ВС, 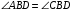 по свойству биссектрисы.
по свойству биссектрисы.
Следовательно, BF=BC. Тогда 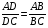 .
.
Следствие:
F
В
D
С
А
Если BD - биссектриса внешнего угла треугольника АВС, то 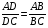 .
.
Доказательство аналогичное.
Задачи системы:
Задача 1. В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу на отрезки 3 и 4. Найдите площадь треугольника.
a
4
3
С
A
D
Р е ш е н и е. Пусть 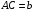 ,
, 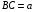 . Тогда по свойству биссектрисы
. Тогда по свойству биссектрисы 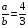 , а по теореме Пифагора
, а по теореме Пифагора 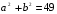 . Решая систему получим:
. Решая систему получим: 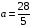 ,
, 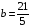 . Вычисляя площадь треугольника по формуле
. Вычисляя площадь треугольника по формуле 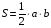 , получим
, получим 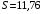 .
.
О т в е т: 11,76.
Задача 2. В прямоугольном треугольнике проведена биссектриса острого угла. Отрезок, соединяющий ее с основание с точкой пересечения медиан, перпендикулярен катету. Найдите острые углы треугольника.
O
D
С
M
A
Р е ш е н и е. Пусть AD - биссектриса прямоугольного треугольника АВС.
Точка О - точка пересечения медиан. Тогда по условию задачи 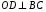 .
.
По свойству медиан 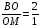 .
.
По теореме Фалеса 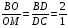 .
.
Так как AD - биссектриса, то 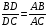 . Следовательно,
. Следовательно, 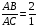 .
.
Так как гипотенуза АВ в два раза больше катета АС, то 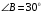 . Следовательно,
. Следовательно, 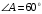 .
.
О т в е т: 300; 600.
Задача 3. В равнобедренный треугольник АВС с основанием АС вписана окружность с центром О. Луч АО пересекает сторону ВС в точке К, причем 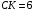 ,
, 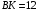 . Найдите периметр треугольника АВС.
. Найдите периметр треугольника АВС.
18
12
6
К
В
С
А
О
Р е ш е н и е. Так как О - центр вписанной окружности, то АК - биссектриса треугольника АВС. Тогда 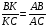 . Имеем
. Имеем 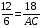 ,
, 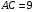 .
.
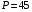 .
.
О т в е т: 45.
Задача 4. В окружность радиуса 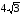 см вписан треугольник АВС, в котором
см вписан треугольник АВС, в котором 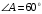 , а сторона АВ в два раза больше стороны АС. В треугольнике проведена биссектриса АМ. Найдите длину отрезка С.
, а сторона АВ в два раза больше стороны АС. В треугольнике проведена биссектриса АМ. Найдите длину отрезка С.
12-х
х
М
С
А
В
Р е ш е н и е. АМ - биссектриса треугольника АВС. Тогда 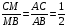 .
.
Чтобы воспользоваться свойством биссектрисы, необходимо найти длину стороны ВС. По теореме синусов 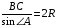 . Отсюда
. Отсюда 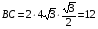 .
.
Пусть 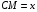 , тогда
, тогда 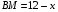 . Имеем
. Имеем 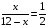 , откуда
, откуда 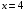 .
.
О т в е т: 4.
Задача 5. В треугольнике АВС проведена биссектриса ВЕ, которую центр О вписанной окружности делит в отношении 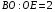 . Найдите АВ, если
. Найдите АВ, если 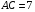 ,
, 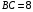 .
.
3
D
M
О
4
8
k
2k
A
В
C
Е
Р е ш е н и е. Так как О - центр вписанной окружности, то АМ и CD - биссектрисы.
По свойству биссектрисы треугольника ВСЕ 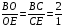 ,
, 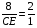 ,
, 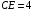 .
.
Следовательно, 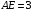 .
.
По свойству биссектрисы треугольника АВЕ 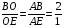 ,
, 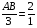 ,
, 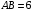 .
.
О т в е т: 6.
Задача 6. Найдите стороны треугольника, если медиана и высота, проведенные из одного угла, делят его на три равные части, а длина медианы равна 10.
x
x
2x
A
K
N
С
Р е ш е н и е. Пусть СN - медиана, а СК - высота.
Так как СК - высота и биссектриса, то треугольник CNB равнобедренный, следовательно, 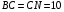 и
и 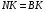 .
.
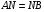 , следовательно,
, следовательно, 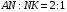 .
.
CN - биссектриса в треугольнике АСК, следовательно, 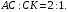
Треугольник 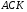 - прямоугольный, поэтому
- прямоугольный, поэтому 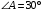 ,
, 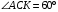 ,
, 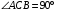 ,
, 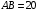 ,
, 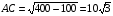 .
.
О т в е т: 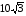 .
.
Задача 7. Биссектриса BD внутреннего угла треугольника АВС равна 6, а биссектриса ВF смежного с ним угла равна 8. Найдите площадь треугольника АВС, если 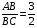 .
.
10
6
8
F
M
C
A
D
В
Р е ш е н и е. Биссектрисы смежных углов перпендикулярны, поэтому 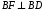 .
.
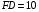 по теореме Пифагора.
по теореме Пифагора.
По свойству биссектрисы 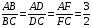 .
.
Пусть 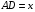 , тогда
, тогда 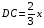 ,
, 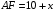 ,
, 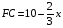 .
.
Имеем 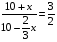 ,
, 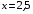 .
.
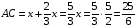 .
.
Чтобы найти площадь треугольника АВС необходимо знать длину высоты ВМ, проведенной к стороне АС. Из треугольника BDF найдем 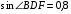 . Тогда
. Тогда 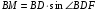 ,
, 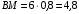 .
.
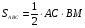 ,
, 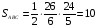 .
.
О т в е т: 10.
Задачи для самостоятельного решения
1. В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5. Найдите площадь треугольника.
О т в е т: 54.
2. В треугольнике ВСЕ 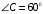 ,
, 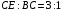 . Отрезок СК - биссектриса треугольника. Найдите КЕ, если радиус описанной около треугольника окружности равен
. Отрезок СК - биссектриса треугольника. Найдите КЕ, если радиус описанной около треугольника окружности равен 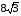 .
.
О т в е т: 18.
3. Дан треугольник АВС. Его высота BD равна 30. Из основания Е биссектрисы АЕ опущен перпендикуляр EF на сторону АС. Найдите длину этого перпендикуляра, если 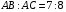 .
.
О т в е т:16.
4. В треугольнике АВС из вершины В проведена высота BD и биссектриса BL. Найдите площадь треугольника BLD, если известны длины сторон треугольника АВС: 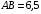 см;
см; 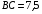 см;
см; 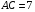 см.
см.
О т в е т: 2,25.
5. В треугольнике АВС биссектриса угла С пересекает сторону АВ в точке D. Найдите площадь треугольника ADC, если 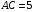 ,
, 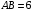 ,
, 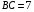 .
.
О т в е т: 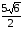 .
.
6. В треугольнике АВС 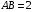 ,
, 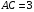 ,
, 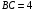 . Найдите отношение, в котором точка пересечения биссектрис делит биссектрису угла В.
. Найдите отношение, в котором точка пересечения биссектрис делит биссектрису угла В.
О т в е т: 1:2.
7. Основание равнобедренного треугольника равно 8, а боковая сторона 12. Найдите длину отрезка, соединяющего точки пересечения биссектрис углов при основании с боковыми сторонами треугольника.
О т в е т: 4,8.


