- Преподавателю
- Математика
- Подготовка к олимпиаде. Пути решения задач
Подготовка к олимпиаде. Пути решения задач
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Юсупова Р.Ш. |
| Дата | 06.01.2016 |
| Формат | docx |
| Изображения | Есть |
Подготовка к олимпиаде. Пути решения логических задач.
Выявление и воспитание одарённых, талантливых детей - одно из приоритетных направлений в современной системе образования. Важно уже в начальной школе выявлять таких учеников, развивать их способности и таланты, поддерживать интерес детей к знаниям.
Одна из форм выявления одарённых детей - олимпиада.
Олимпиады способствуют повышению интереса школьников к знаниям, развитию их способностей и творческой инициативы. Кроме того, олимпиады позволяют ученику познать себя, дают возможность утвердиться в собственных глазах.
Залог успеха при подготовке к олимпиадам - это правильное выявление одарённого и заинтересованного в данной предметной области ребёнка, индивидуальные занятия с ним, направленные не только на изучение материала, намного опережающего школьную программу, но и на умение применять свои знания в нестандартной ситуации, умение мыслить при выполнении заданий олимпиадного характера.
Хочу поделиться своим опытом работы с учащимися младшего звена в этом направлении. Подготовка к олимпиаде - дело ответственное. Здесь важна постепенность. Начинаю подготовку к участию в олимпиадах с работы на уроке. Уже в начальном курсе математики, выявляются способности у детей разгадывать ребусы, решать задачи на смекалку, справляться с логическими заданиями. Поэтому, практически на каждом уроке стараюсь найти время для выполнения нестандартных решений, заданий на «смекалку». На самостоятельных и контрольных работах также предлагаю детям нестандартные задания в качестве дополнительного, необязательного задания.
Работу на уроках математики дополняю занятиями по математики во внеурочное время. Такие занятия дети посещают по собственному желанию. На дополнительных занятиях с детьми рассматриваем различные типы олимпиадных задач, выполняем самостоятельные задания. Предлагаю ученику упражнения, которые соответствуют его возрасту и уровню знаний. При работе с маленькими детьми начинать лучше с простеньких логических и геометрических задач. Упражнения подбираю таким образом, чтобы ребенок мог с некоторым усилием справиться с большей их частью.
Чтобы повысить интерес к изучению предмета, занятия по внеурочной деятельности стараюсь проводить в игровой форме (викторины, командные игры, составление кроссвордов и др.)
Обязательным компонентом подготовки к решению олимпиадных задач является решение логических задач. Логическая задача - задача, для которой в курсе математики не имеется общих правил и положений, определяющих точную программу их решения, основным способом решения которых являются логические рассуждения.
Подготовить детей к предметной олимпиаде по математике можно только путём усвоения детьми принципов и методов работы с логическими задачами. В то же время не только учащиеся, но и учителя иногда испытывают трудности при решении задач, отличных от шаблонных. Отчасти это объясняется недостаточным опытом обращения с задачами данной категории в процессе изучения математики в деятельности учителя, дефицит учебного времени.
Поэтому, сегодня я предлагаю познакомиться с основными способами решения логических задач.
Эффективность обучения младшего школьника решению логических задач зависит от нескольких условий:
-
Задачи следует вводить в процессе обучения в определенной последовательности, с постепенным нарастанием сложности.
-
Необходимо предоставить ученикам максимальную самостоятельность в поиске решения задач, дать возможность дойти до конца даже по ложному пути и убедиться в ошибке.
-
Помочь осознать некоторые способы, приёмы, общие подходы к решению логических задач.
Разнообразие логических задач велико. Известно несколько различных способов решения логических задач. Это:
- метод рассуждений;
- метод графов;
- метод блок-схем;
- метод таблиц;
- метод кругов Эйлера.
Предлагаю рассмотреть следующие методы: метод таблиц и метод кругов Эйлера.
Решение логических задач табличным способом прост и нагляден. Главным в предлагаемых задачах является способ решения - построение таблицы, строки которой соответствуют элементам одного из рассматриваемых в условии задачи множеств, столбцы - элементам другого, пересечение строки и столбца - комбинации двух элементов разных множеств. С помощью такой таблицы анализируются условия задачи, делаются выводы, проверяется избыточность, полнота и правильность выводов.
Приведём пример решения такой задачи.
Задача: Витя, Коля, Павлик и Серёжа учатся в разных классах. Они отправились в лес за грибами. Шестикласснику не повезло, он не нашёл ни одного гриба, а Павлик с пятиклассником нашли по 10 грибов. Витя и семиклассник нашли ежа и позвали Колю показать находку. Восьмиклассник, шестиклассник и Коля объяснили Серёже, как ориентироваться на местности. В каких классах учатся мальчики?
Начертим таблицу
Витя
Коля
Павлик
Серёжа
5
6
7
8
Анализируем каждое предложение и отмечаем в таблице.
-
Шестикласснику не повезло, он не нашёл ни одного гриба, а Павлик с пятиклассником нашли по 10 грибов.
Значит Павлик не пятиклассник и не шестиклассник.
Витя
Коля
Павлик
Серёжа
5
-
6
-
7
8
-
Витя и семиклассник нашли ежа и позвали Колю показать находку.
Витя не семиклассник и Коля не семиклассник, и Павлик не семиклассник (он нашёл грибы, а не ежа).
Витя
Коля
Павлик
Серёжа
5
-
6
-
7
-
-
-
8
+
По закону составления таблиц: если в строке (или столбце) все «места», кроме одного, заняты знаком «-», то на свободное место нужно поставить знак «+»; если в строке (или столбце) уже есть знак «+», то остальные места должны быть заняты знаком «-».
Павлик - восьмиклассник. Значит Серёжа, Коля и Витя не могут быть восьмиклассниками.
Витя
Коля
Павлик
Серёжа
5
-
6
-
7
-
-
-
8
-
-
+
-
-
8-классник, 6-классник и Коля объяснили Серёже, как ориентироваться на местности.
Значит Коля не 8-классник и не 6-классник, Серёжа тоже не 6-классник и не 8-классник. Коля - 5-классник.
Витя
Коля
Павлик
Серёжа
5
+
-
6
-
-
-
7
-
-
-
8
-
-
+
-
Серёжа и Витя - не пятиклассники.
Витя
Коля
Павлик
Серёжа
5
-
+
-
-
6
+
-
-
-
7
-
-
-
8
-
-
+
-
Витя - шестиклассник. Значит, Серёжа шестиклассником быть не может. Он - семиклассник.
Витя
Коля
Павлик
Серёжа
5
-
+
-
-
6
+
-
-
-
7
-
-
-
+
8
-
-
+
-
Ответ: пятиклассник - Коля, шестиклассник - Витя, семиклассник - Серёжа, восьмиклассник - Павлик.
Способ решения данного вида задач закрепляется на занятиях по внеурочной деятельности, через включение в задания для самостоятельного решения.
Как решать логические задачи с помощью кругов Эйлера?
Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к их решению. Задачи, решаемые с помощью кругов Эйлера, предлагаются на математических олимпиадах, но в школьной программе не отводятся часы на изучение данной темы. Ценность использования кругов Эйлера состоит в том, что решения задач с громоздкими условиями и со многими данными становятся проще. Подобные задачи часто имеют практический характер, что немаловажно в современной жизни. Они заставляют задумываться, подходить к решению какой-либо проблемы с разных сторон, уметь выбирать из множества способов решения наиболее простой, легкий путь.
Приведём пример решения такой задачи. Рассмотрим ситуацию с двумя множествами.
Задача1. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят лилии, а пятеро - фиалки. И только у двоих есть и лилии, и фиалки. Угадайте, сколько у меня подруг?
Решение:
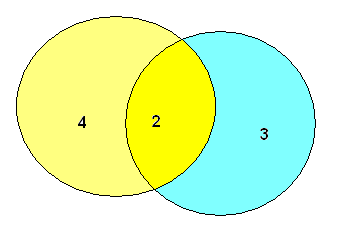
Изобразим два множества. Первое множество Л - те, которые разводят лилии, второе множество Ф - те, кто разводят фиалки. Поскольку, некоторые из них разводят и лилии, и фиалки, то круги нарисую так, чтобы у них была общая часть (пересечение). В этой общей части ставим цифру 2.
В оставшейся части множества Л ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
Аналогичным образом при помощи кругов Эйлера можно решать и другие схожие по смыслу логические задачи. Рассмотрим ситуацию с тремя множествами.
Задача 2.В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?
Решение.
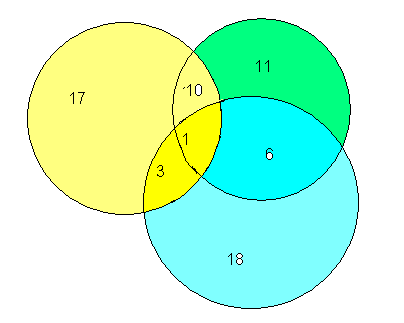
18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит, вратарей будет 30-28=2. Ответ: 2 вратаря.
Рассмотрев два способа решения логических задач, приходим к выводу: таблицы помогают делать правильные логические выводы в ходе решения задачи и позволяют наглядно представить условие задачи и ответ. Ценность использования кругов Эйлера состоит в том, что решения задач с громоздкими условиями и со многими данными становятся проще. Решение этих задач развивают логическое мышление и помогают при подготовке к олимпиадам.
Итог занятия: Подготовка к олимпиаде проходит по-разному. Это зависит от учителя и от ученика. Чтобы подготовка к олимпиаде принесла хорошие плоды, педагогам следует, прежде всего, быть увлечёнными процессом вовлечения учеников в познавательный процесс. Учитель должен находить такие задания, которые развивали бы творческое начало в ученике, провоцировали бы ученика на поиск выхода из ситуации, вызвали бы потребность в поиске нестандартных методов решения. Тогда ученики будут и интересом вовлекаться в различные дополнительные занятия и смогут полностью погрузиться в изучение интересующего предмета.


