- Преподавателю
- Математика
- Тригонометрические уравнения и неравенства
Тригонометрические уравнения и неравенства
| Раздел | Математика |
| Класс | 10 класс |
| Тип | Конспекты |
| Автор | Поворова Т.А. |
| Дата | 28.03.2015 |
| Формат | doc |
| Изображения | Есть |
Контрольные работы к учебнику «Алгебра и начала
математического анализа,10» С.М. Никольского и др.
Контрольная работа №1
Тригонометрические уравнения и неравенства
Вариант №1
1.Решите уравнение
а) cos x=-1; б) sinx=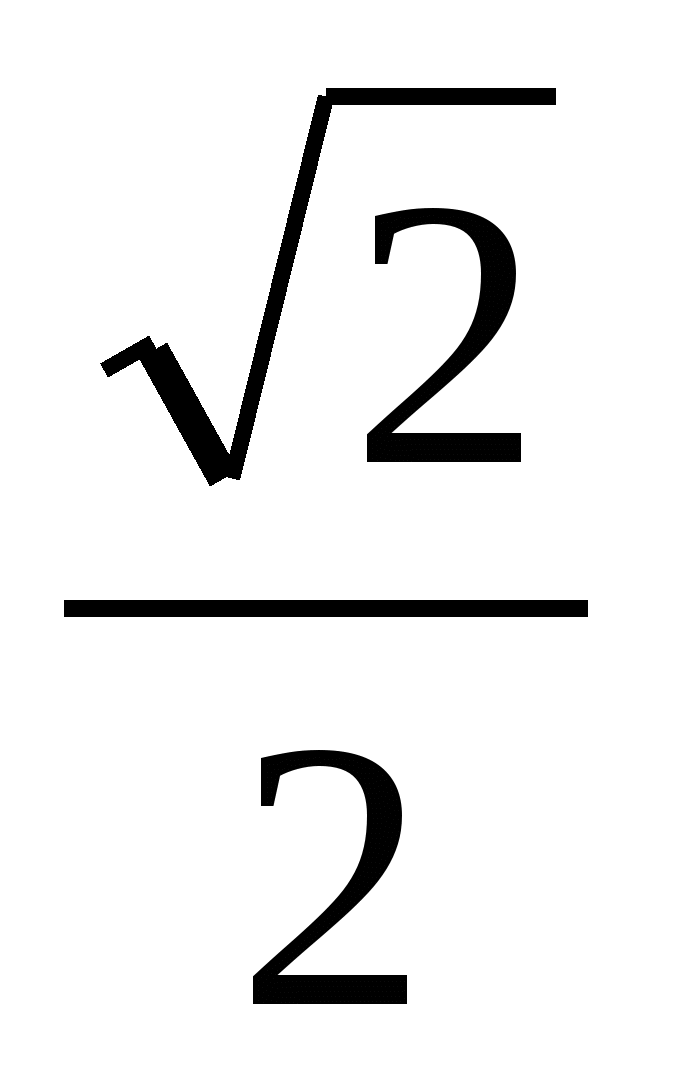 ; в) ctgx=-
; в) ctgx=-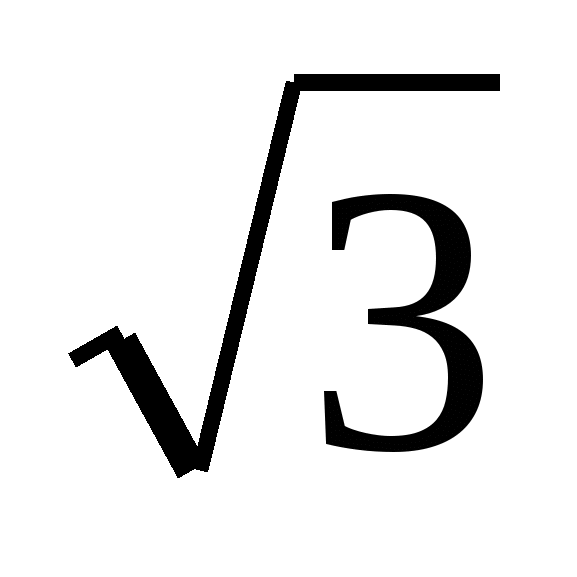 .
.
2. а) sin2x+sinx-2=0; б) 3sin2x-cosx+1=0.
3. a) sinx- cosx=0; б) 3sin2x+2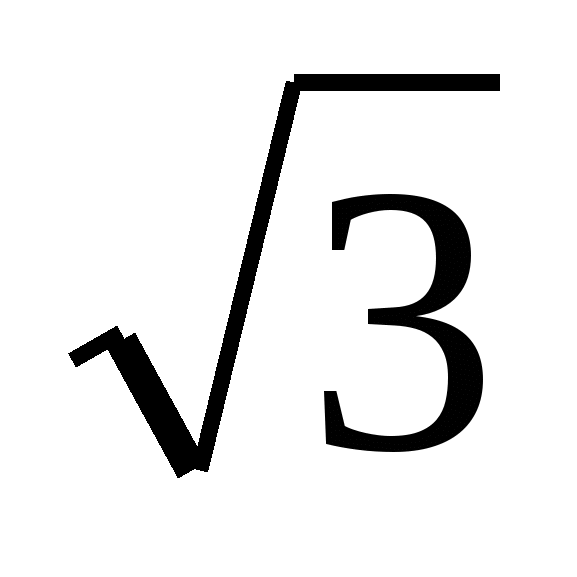 sinx cosx+cos 2x=0.
sinx cosx+cos 2x=0.
4. а) sin x =- 0,5; б) cos x=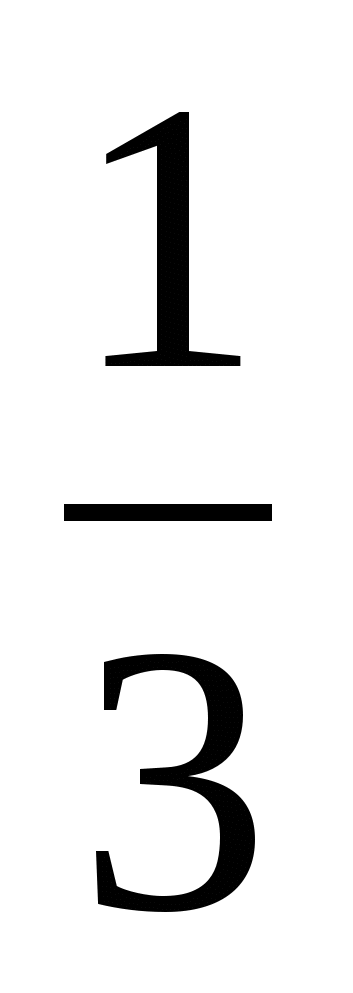 ; в) tgx=-3.
; в) tgx=-3.
5 a) sinx+ cosx=1; б) 2cos2x+sin4x=1.
6 Решите неравенство :
а) Sin x<0,5; б)cos x>0,5; в) tgx ≤-3.
г) 2cos2 x+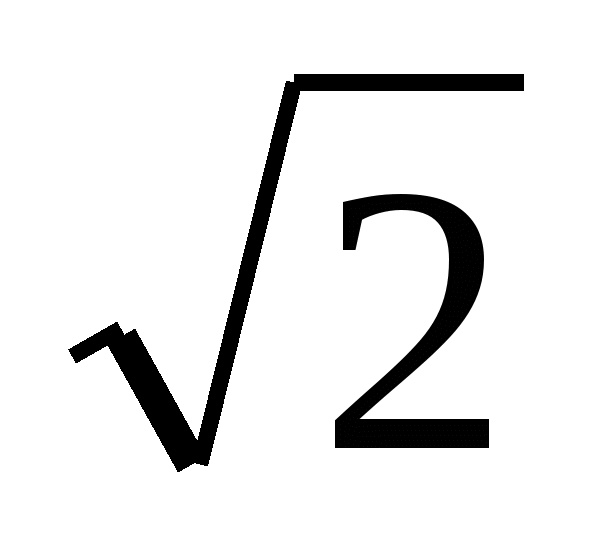 sin x >2
sin x >2
7) sin 2x=cos 4![]() -sin4
-sin4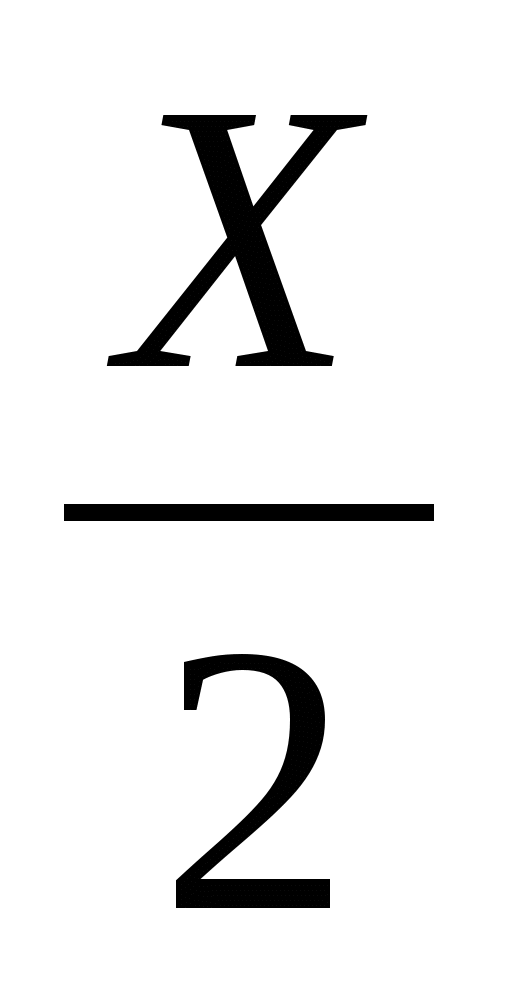
8) 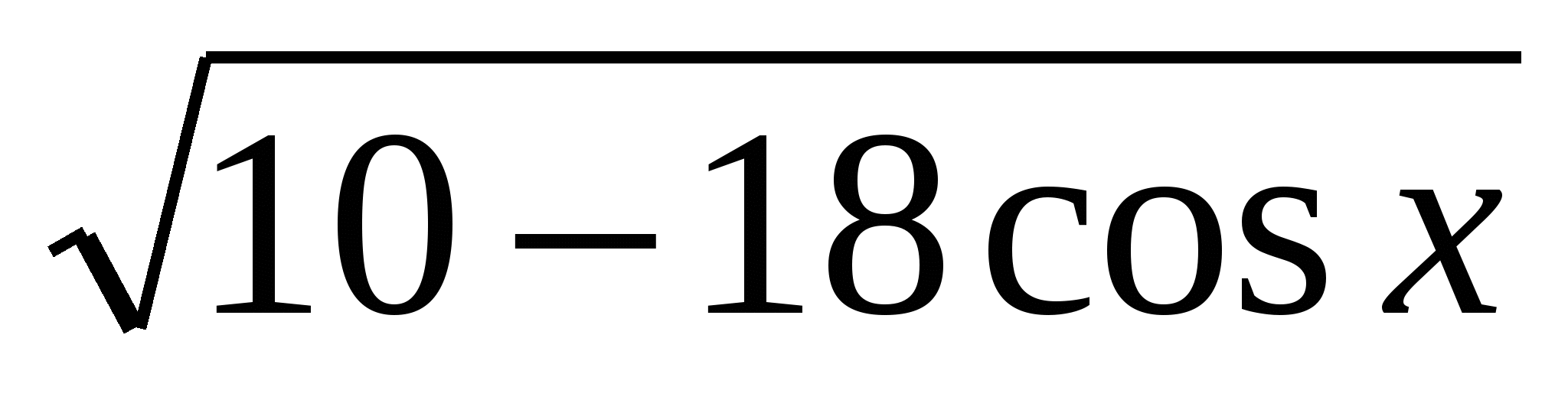 =6cos x-2
=6cos x-2
9) 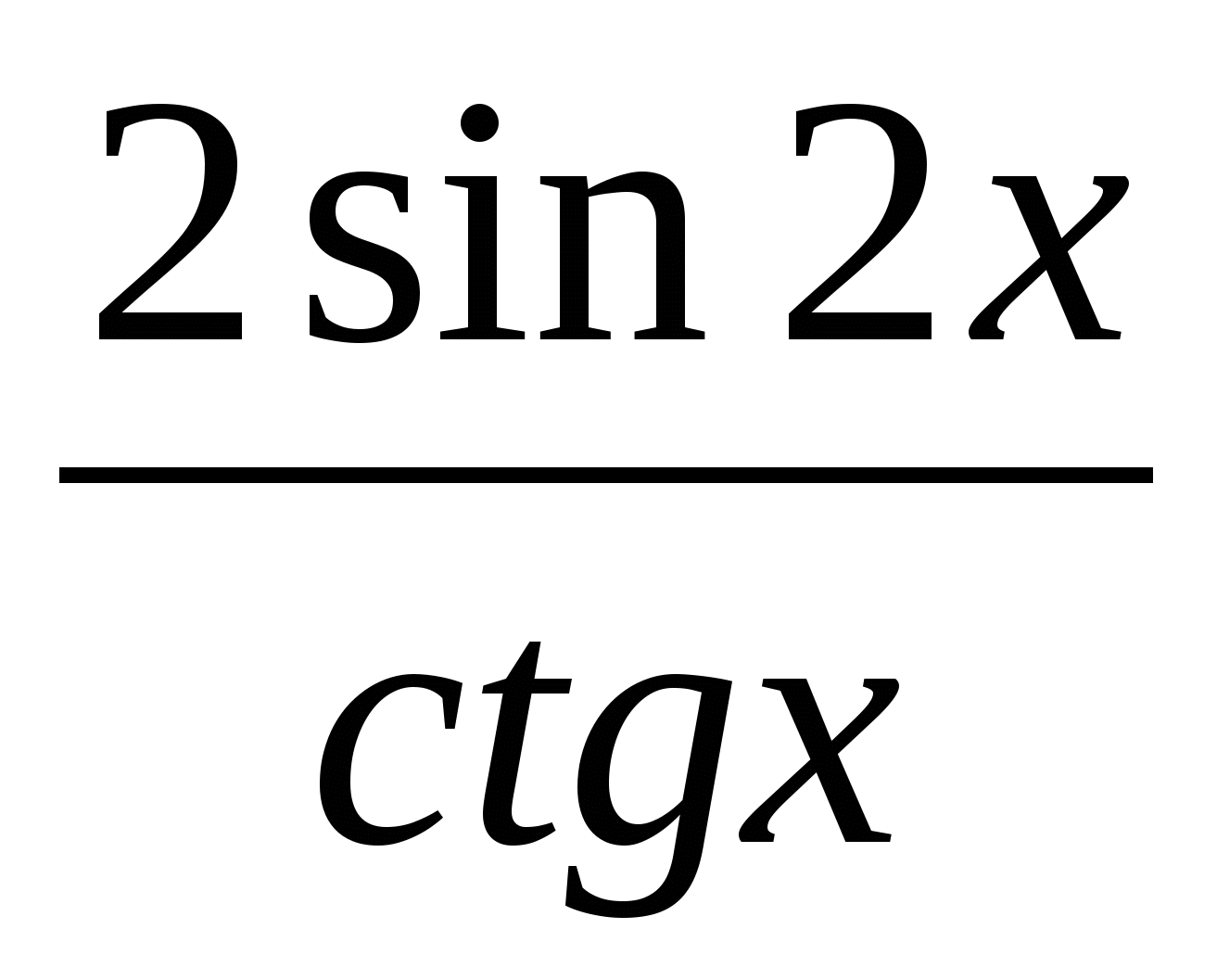 +3cos2 x=1-2cos x
+3cos2 x=1-2cos x
Вариант №2
1.Решите уравнение
а) sinx=-1; б) cosx=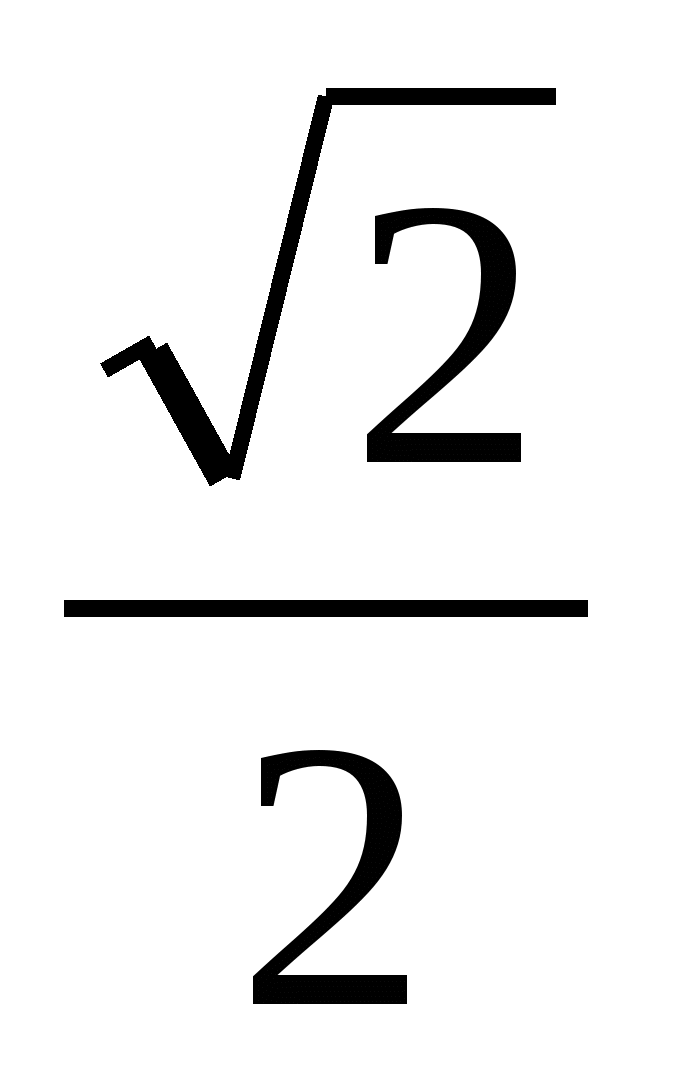 ; в) tgx=-
; в) tgx=-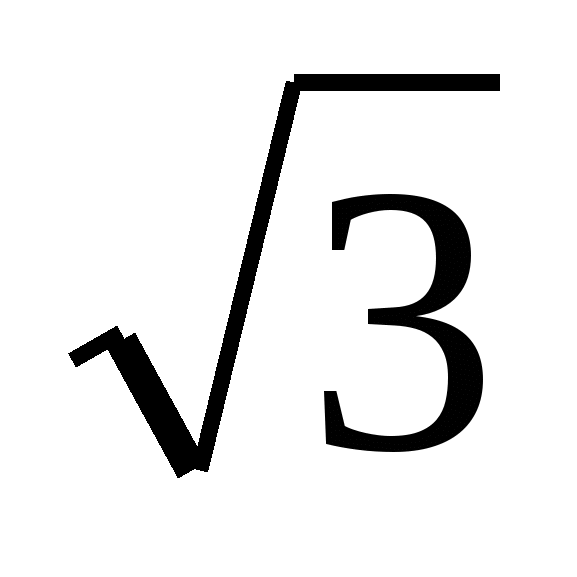 .
.
2. а) cos2x-cos x-2=0; б) 3cos2x-2sinx+2=0.
3. a) sinx+ cosx=0; б) 3sin2x-2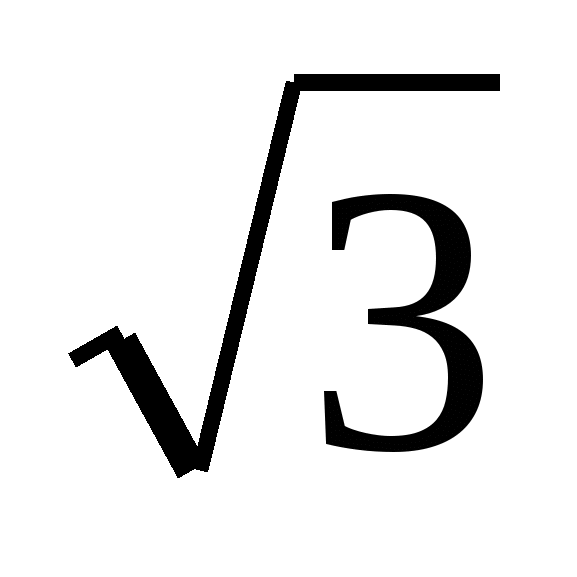 sinx cosx +cos 2x=0.
sinx cosx +cos 2x=0.
4. а) cos x =- 0,5; б) sin x=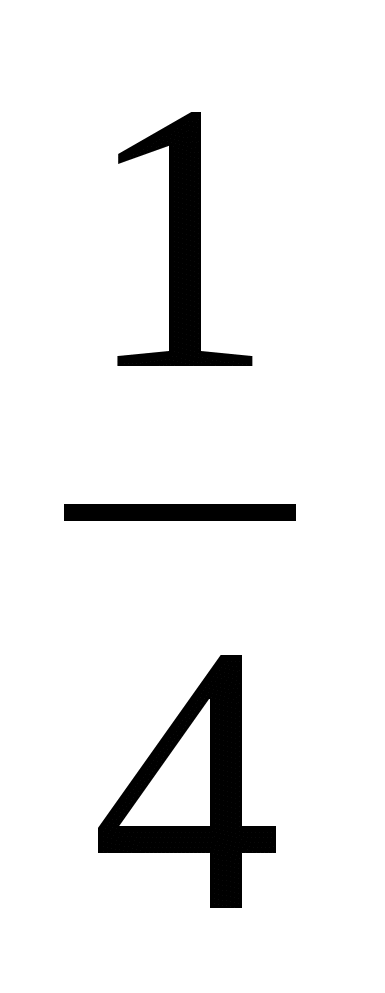 ; в) tg x=2
; в) tg x=2
5 a) sinx- cosx=1; б) 2cos2x-sin4x=1.
6 Решите неравенство
а) Sin x>0,5; б)cos x<0,5; tg x ≥-3.
г) 2sin2 x- cos x >2
7) ctg x-sinx=2sin2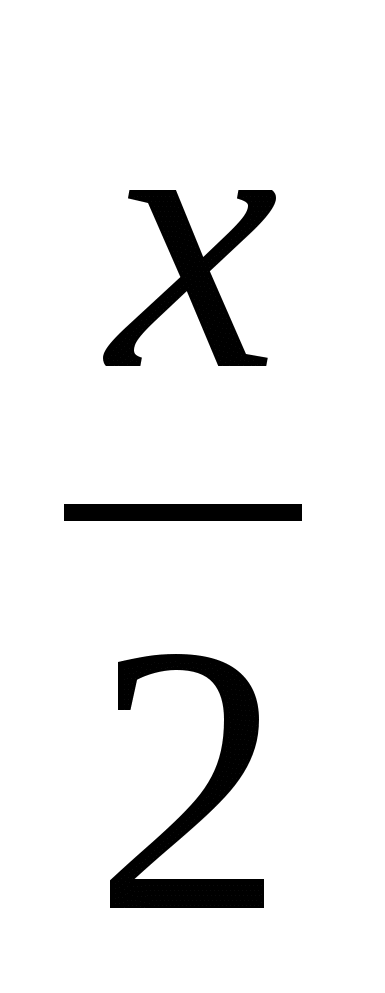
8) 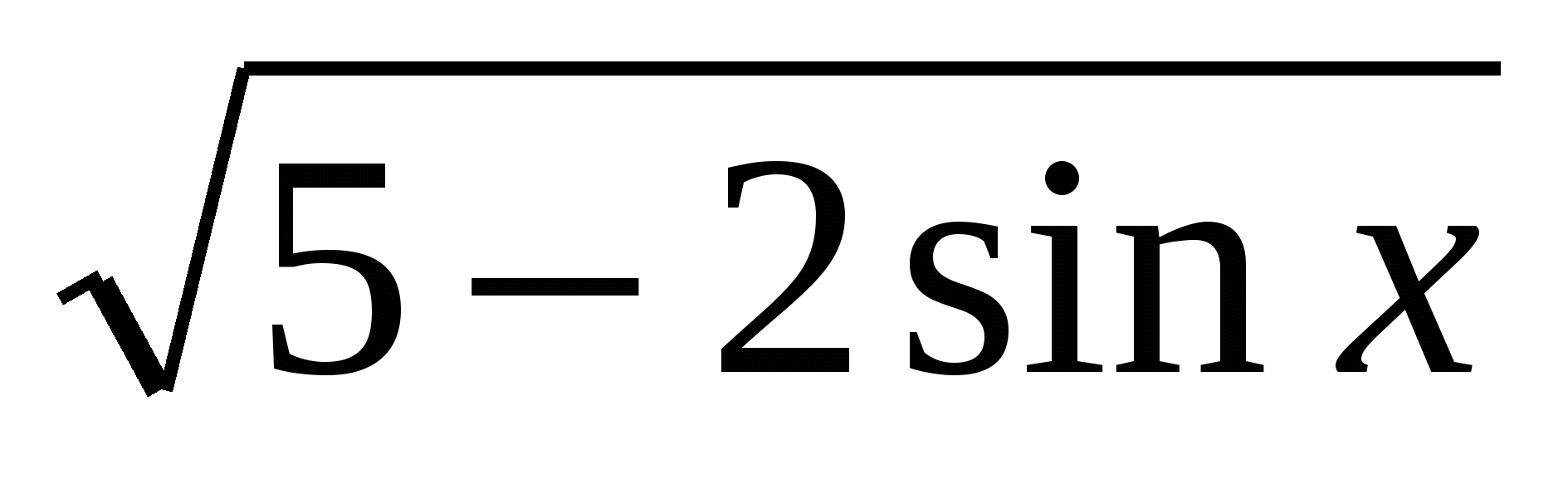 =6sinx-1
=6sinx-1
9) 8-4sin2x=sin2x ctgx - 9cosx
Вариант №7
1.Решите уравнение
а) cos x=1; б) sinx=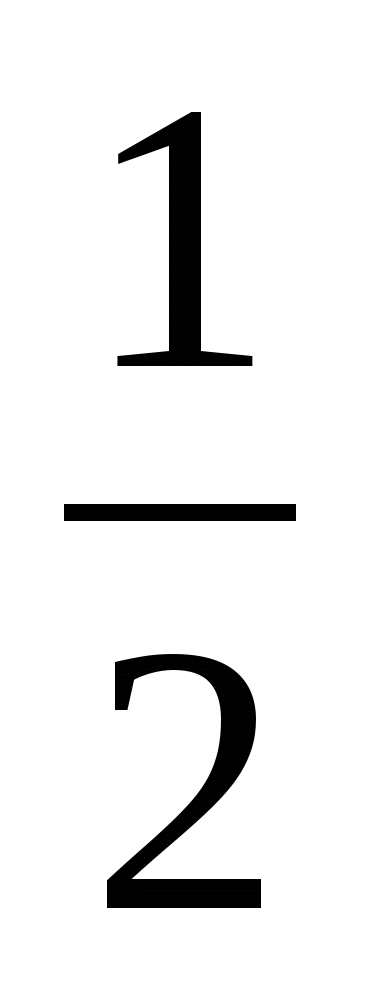 ; в) ctgx=-
; в) ctgx=-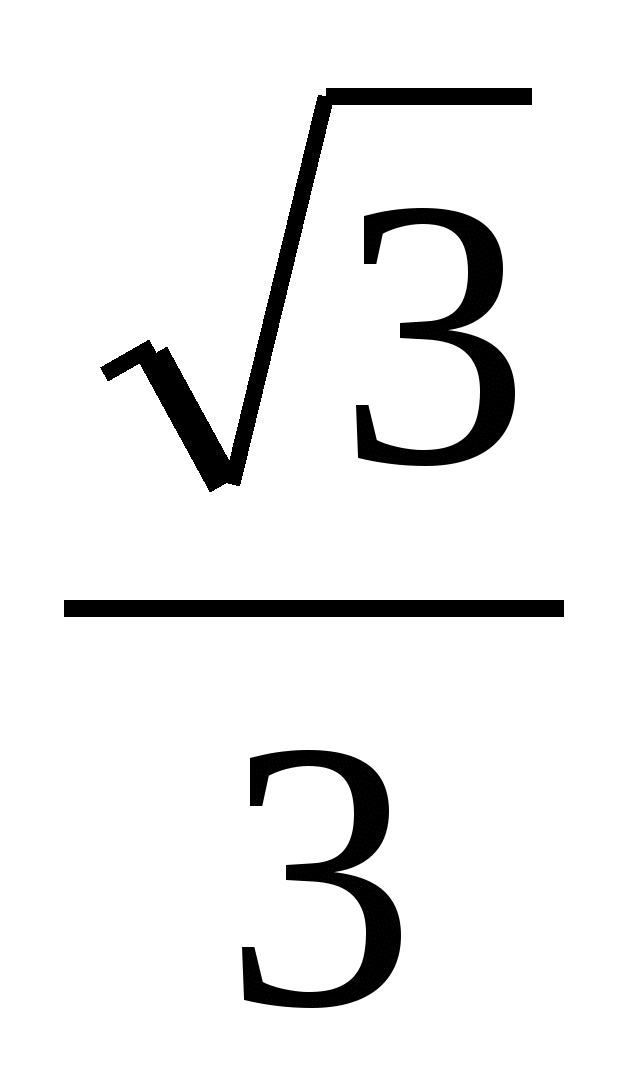 .
.
2. а) 2 sin2x+sinx-1=0; б) 3cos2x-sinx+1=0.
3. a) 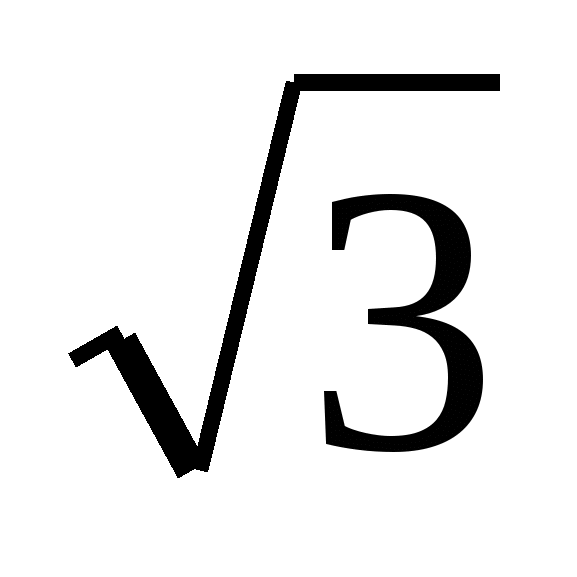 sinx- cosx=0; б) sin2x+2
sinx- cosx=0; б) sin2x+2![]() sinx cosx+3cos 2x=0.
sinx cosx+3cos 2x=0.
4. а) sin x = -0,6; б) cos x=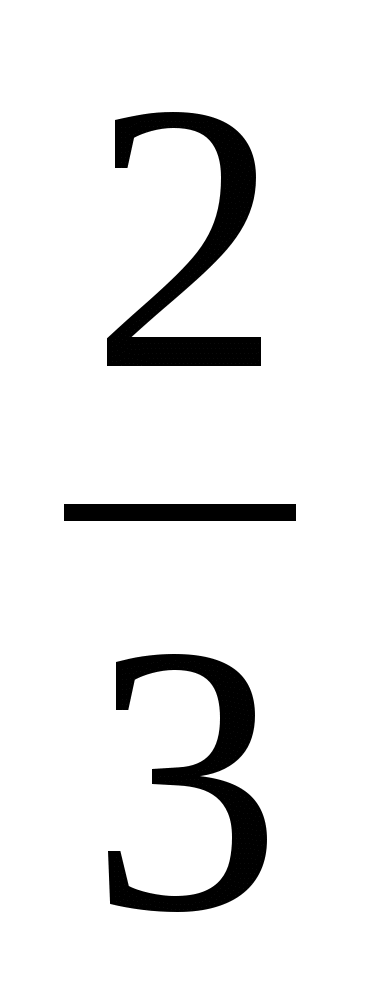 ; в) tgx=-4
; в) tgx=-4
5 a) sinx+ cosx=-1; б) 2cos 4x+cos2 x=1.
6 Решите неравенство:
а) Sin x>-0,5; б)cos x<-0,5; tgx ≥ 2
г) 4cos2 x- (2![]() -2)sin x > 4-
-2)sin x > 4-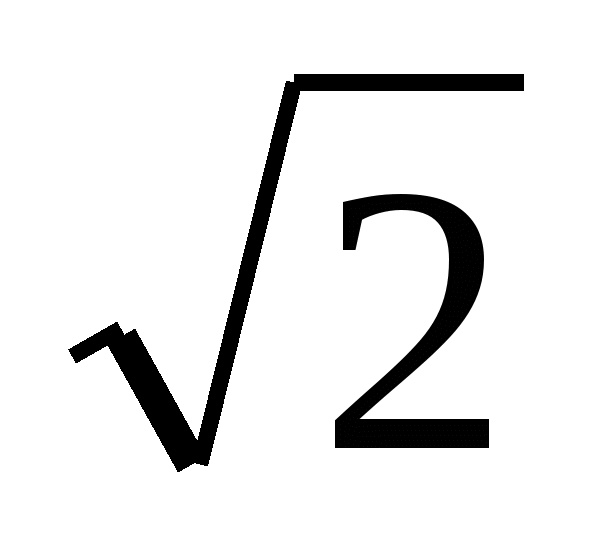
7) sin 2x=cos 4![]() -sin4
-sin4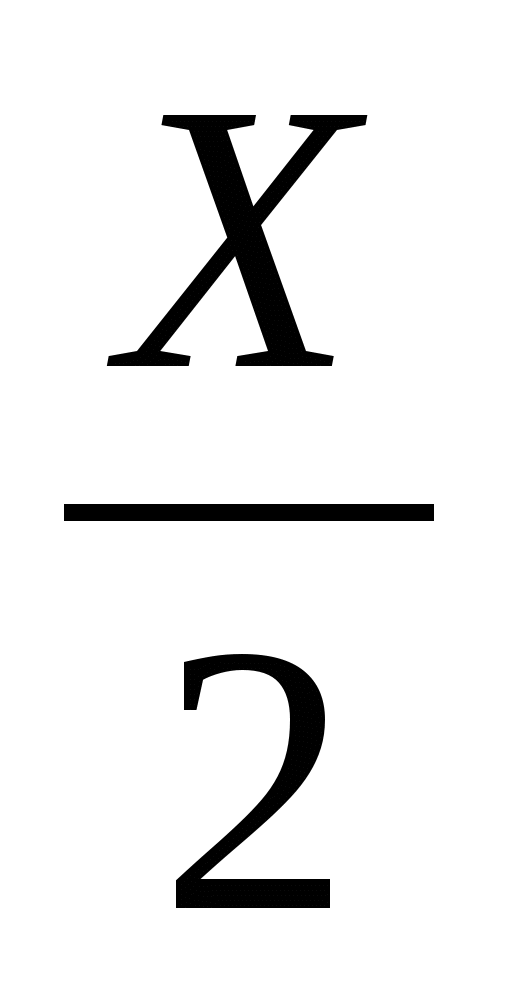
8) 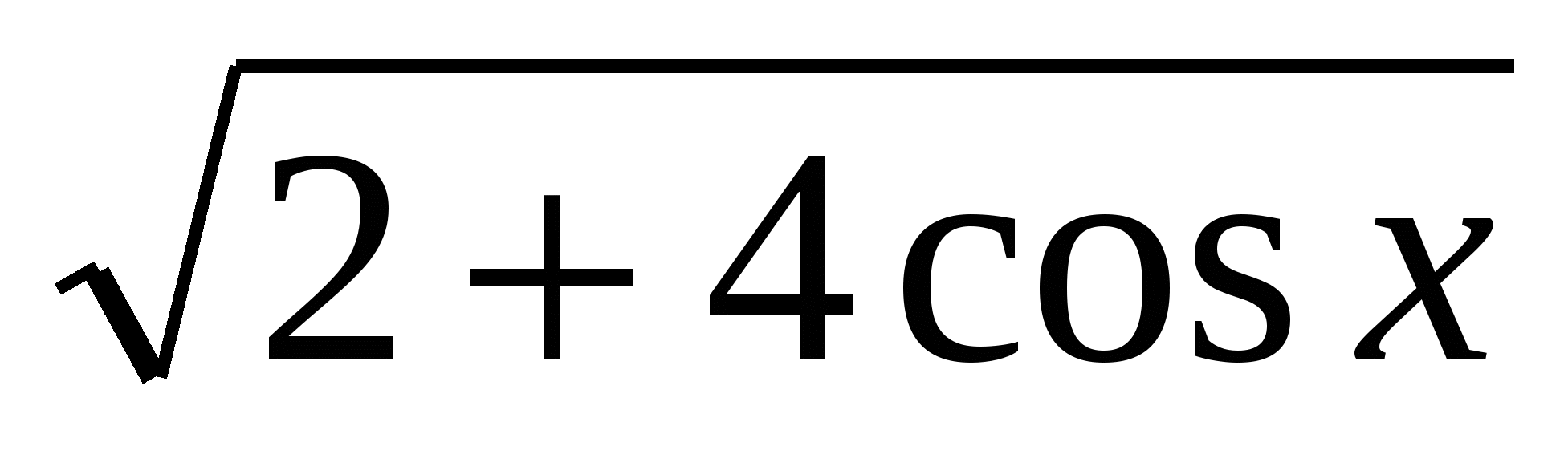 =
=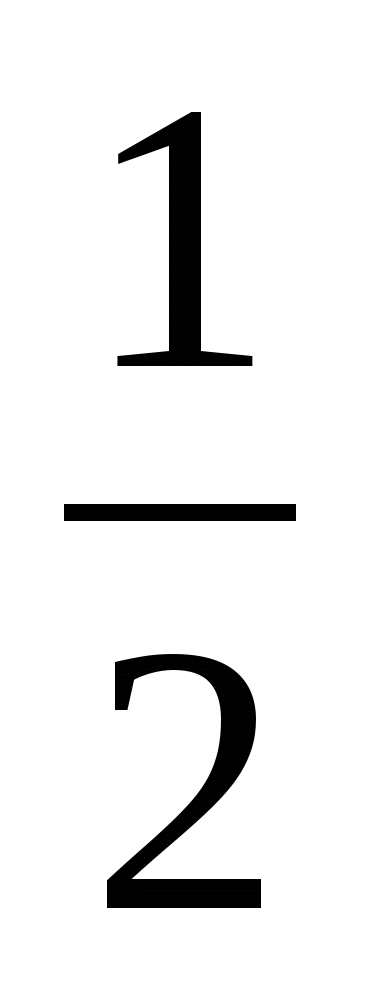 +cos x
+cos x
9) 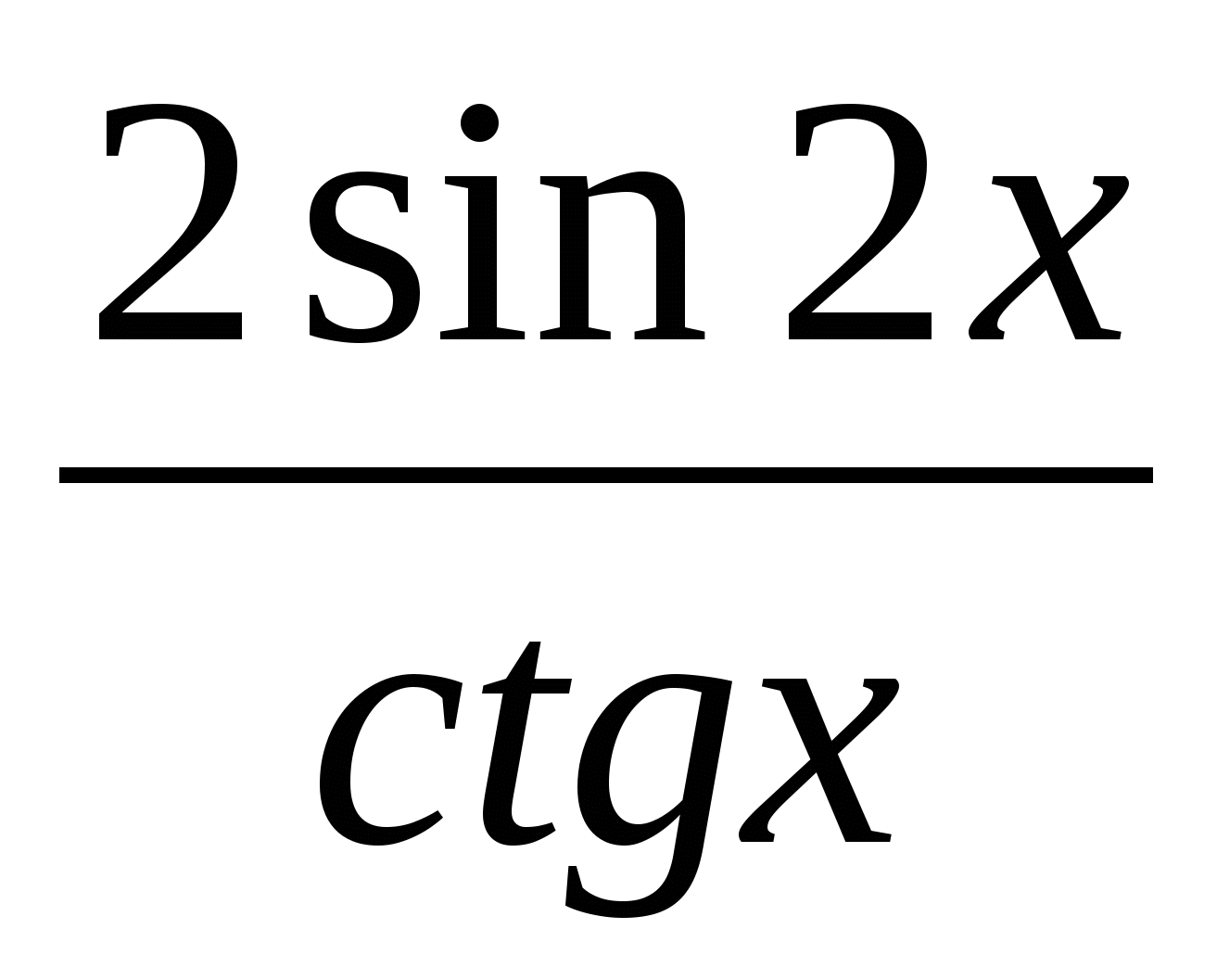 +3cos2 x=1-2cos x
+3cos2 x=1-2cos x
Вариант №4
1.Решите уравнение
а) sin x=1; б) cosx=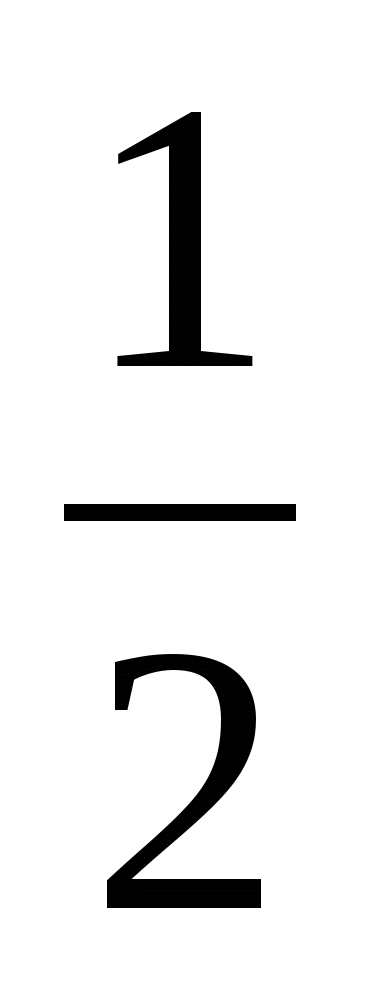 ; в) tgx=-
; в) tgx=-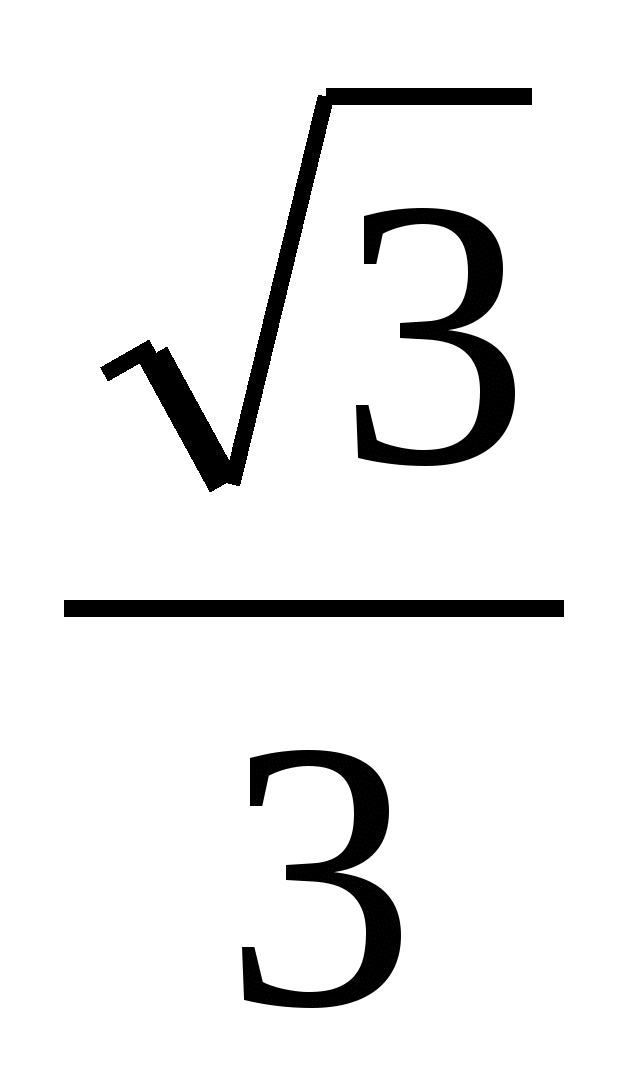 .
.
2. а) 2 cos2x-cosx-1=0; б) 3sin2x-2cosx+2=0.
3. a) 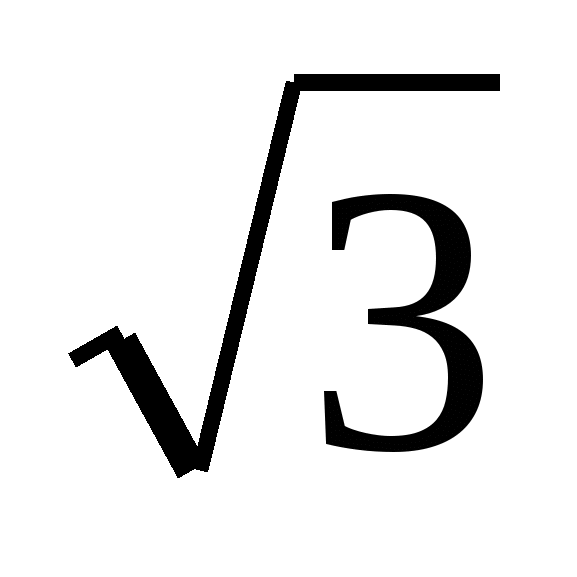 sinx+ cosx=0; б) sin2x-2
sinx+ cosx=0; б) sin2x-2![]() sinx cosx+3cos 2x=0.
sinx cosx+3cos 2x=0.
4. а) cos x = -0,7 б) cos x=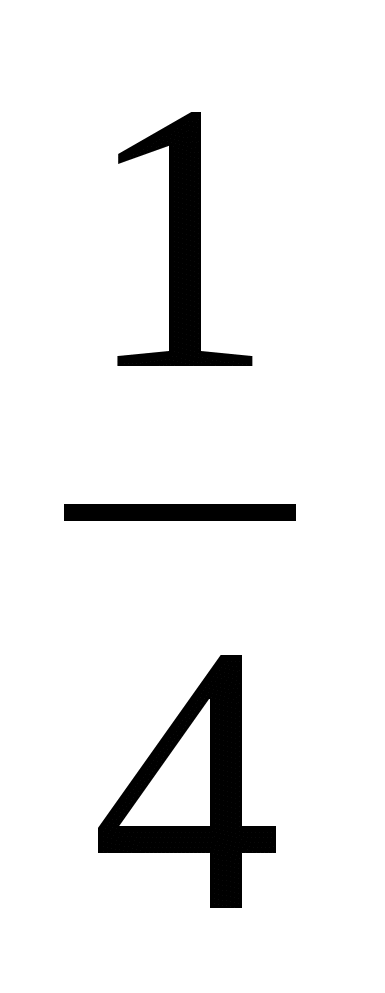 ; в) tg x =5
; в) tg x =5
5 a) sinx- cosx=-1; б) cos 4x-sin2 x=1.
6 Решите неравенство:
а) Sin x<-0,5; б)cos x>-0,5; tgx ≤ 2
г) 4 sin2 x+ (2![]() -2)cos x > 4-
-2)cos x > 4-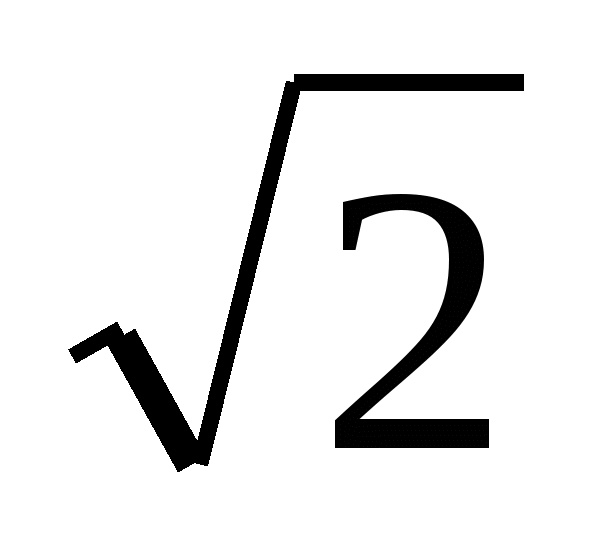
7) ctg x-sinx=2sin2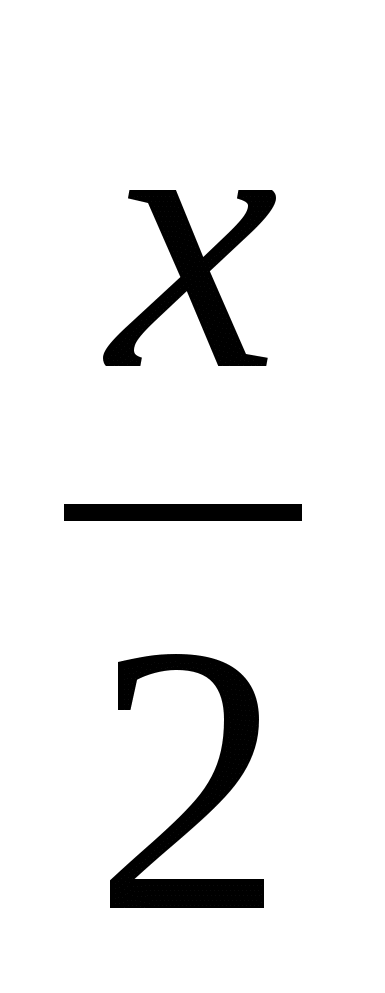
8) 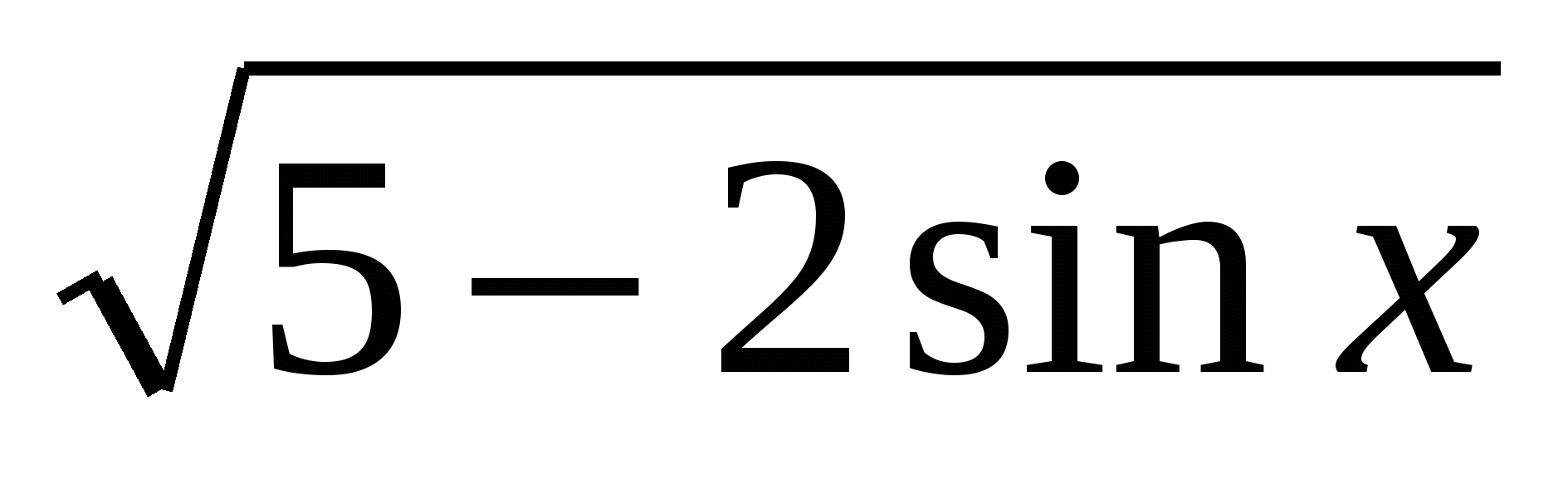 =6sinx-1
=6sinx-1
9) sin x sin3x+sin4x sin8x=0
Контрольная работа №2
Вариант № 1
1. Найдите ƒ'(х), ƒ'(х0), если
а) ƒ(х)=6х4 +5х3+3х2+3, х0 =1; б) ƒ(х)=х соs x , х0=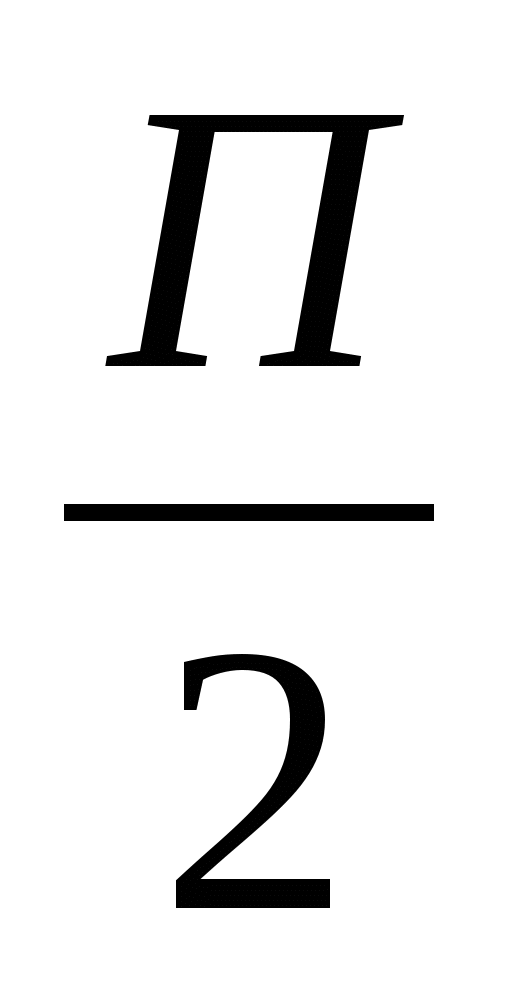
2. Найдите ƒ'(х), если:
а) ƒ(х)=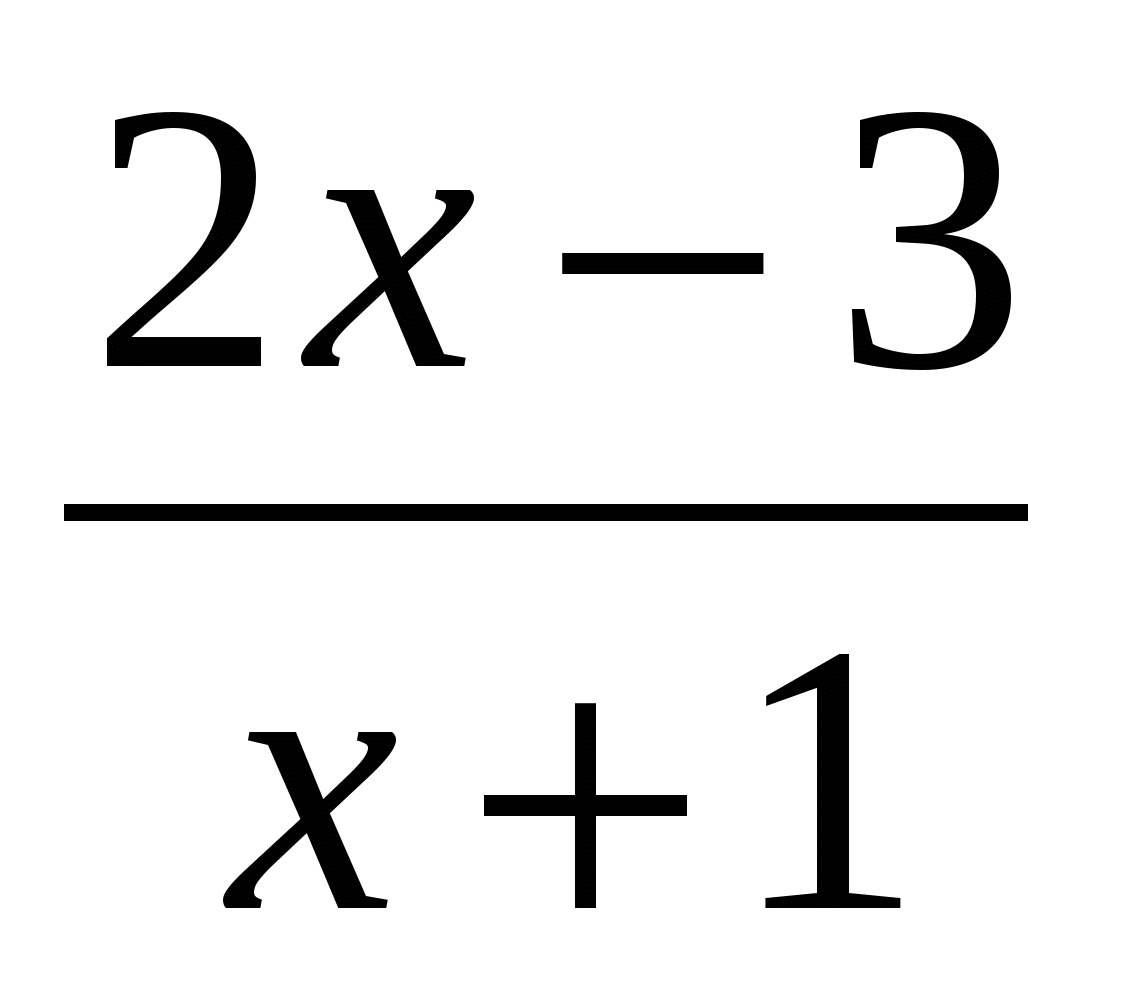 ; б) ƒ(х)=7 7
; б) ƒ(х)=7 7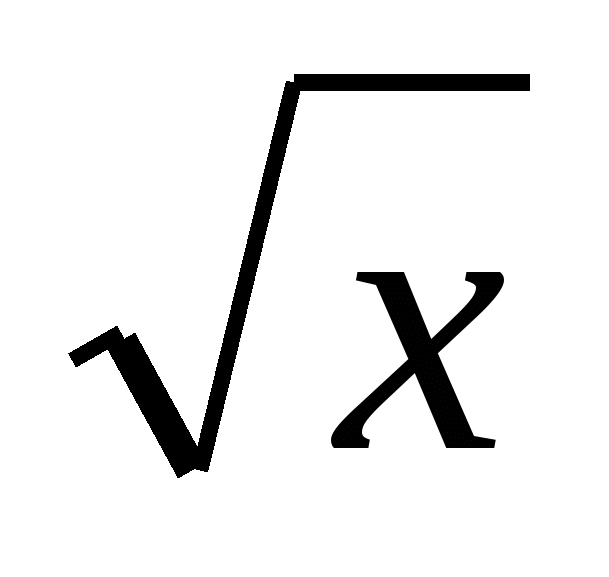 3 ; в) ƒ(х)=log5 x; г) ƒ(х) =
3 ; в) ƒ(х)=log5 x; г) ƒ(х) = 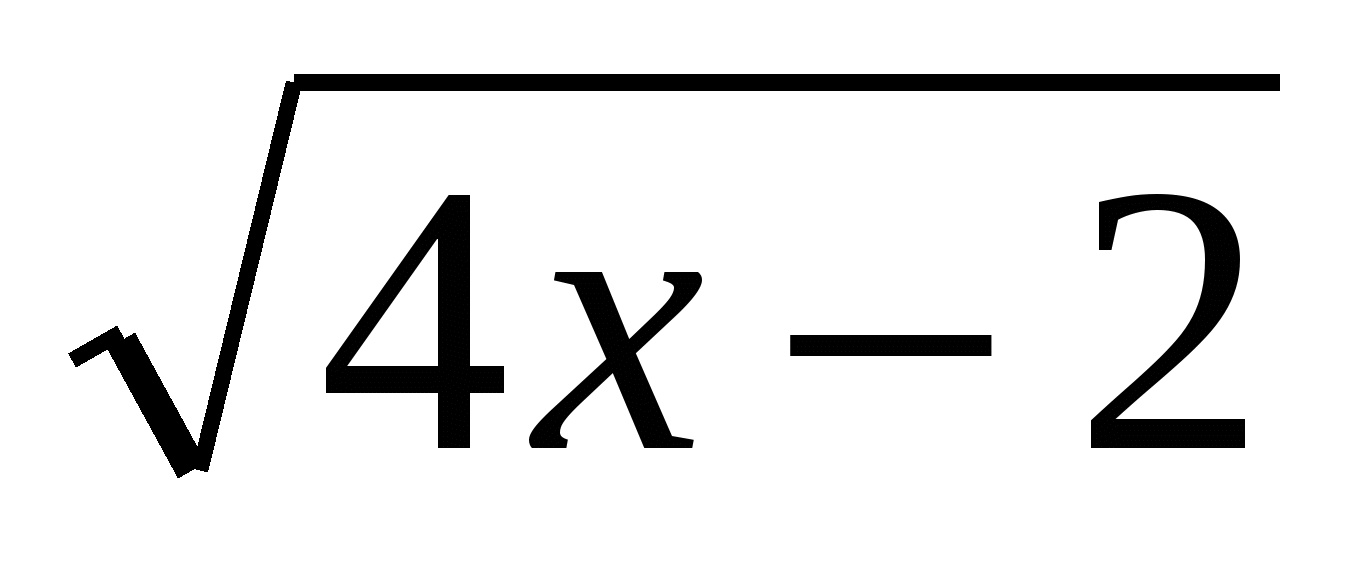
3.Вычислите значение производной функции у=сtg 3x в точке х0=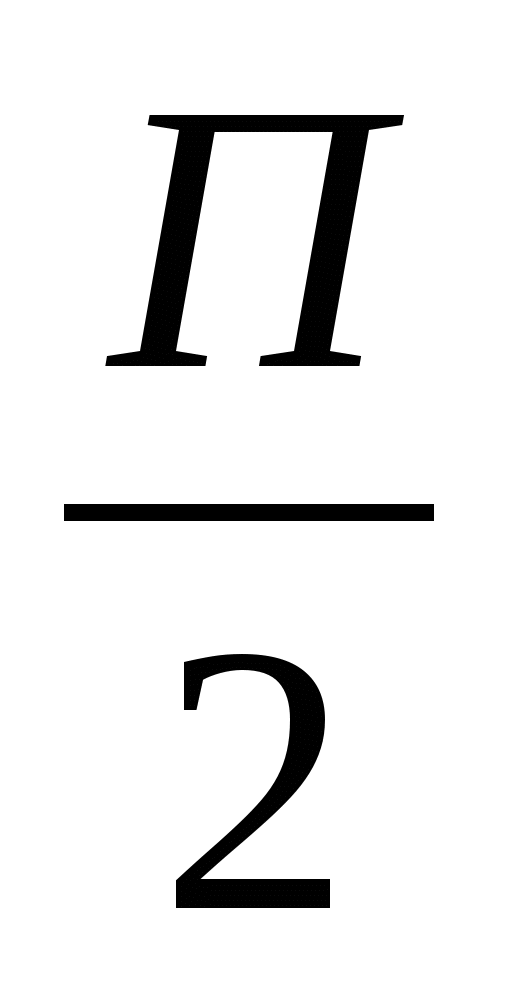
4. Найдите все значения х, при каждом из которых производная функции
а) ƒ(х)=х3+3х2-9х-13 равна нулю.
5. Найдите ƒ'(х), если:
а) ƒ(х)=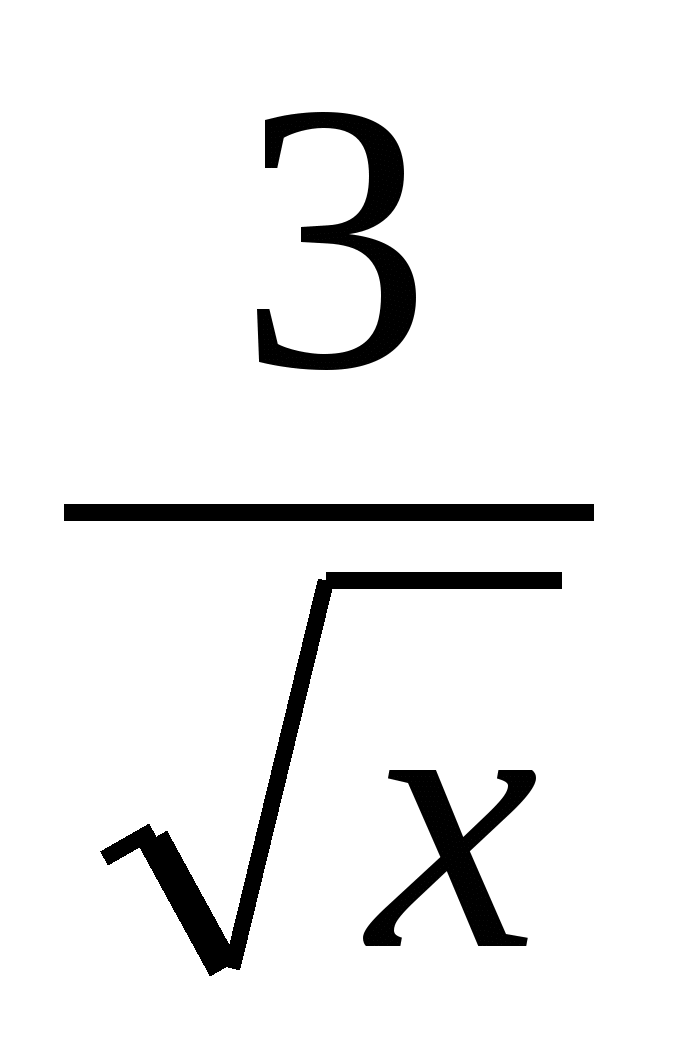 - 6 3
- 6 3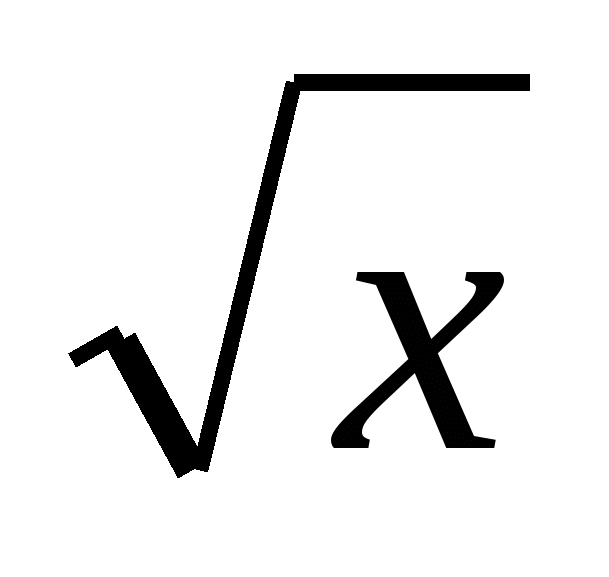 4; б) ƒ(х)=e3х+2; в) ƒ(х)=х√х2-3х+4
4; б) ƒ(х)=e3х+2; в) ƒ(х)=х√х2-3х+4
6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=17+24х-4t2.Найдите момент времени t, когда точка остановится.
7. Найдите производную функции 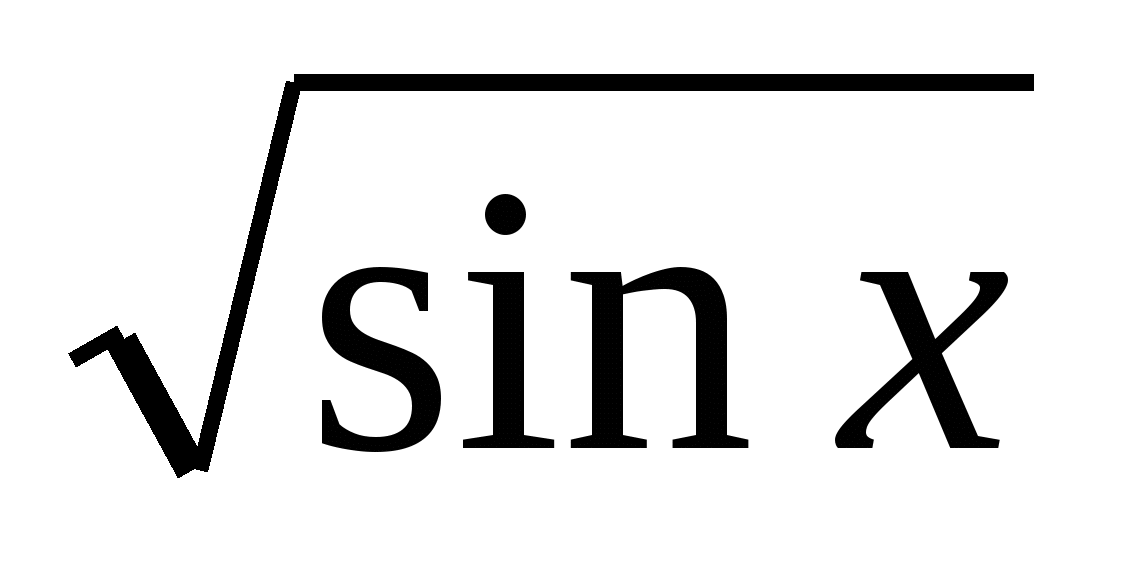
ƒ(х)=e
8. Найдите производную функции
а) у=х3 соs 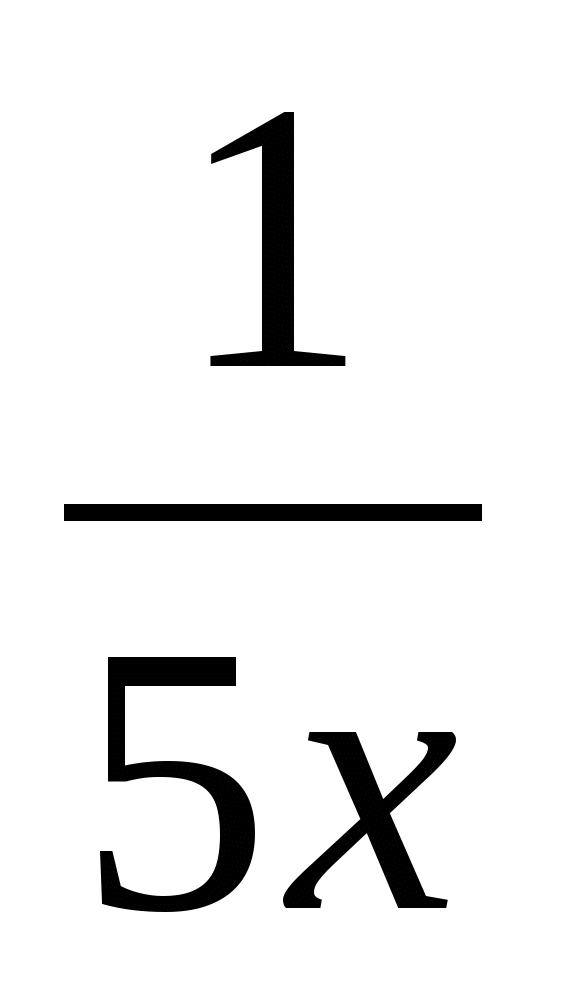 б) y=
б) y=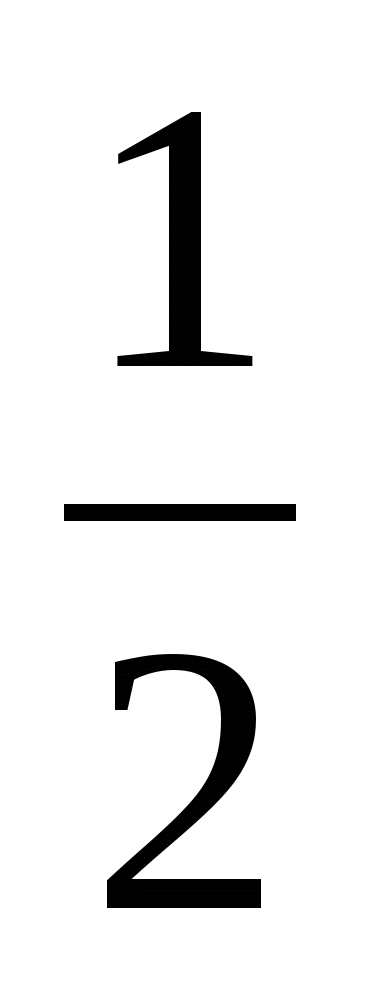 log8(9x+7)· arctg2 3x4
log8(9x+7)· arctg2 3x4
в) y=cos 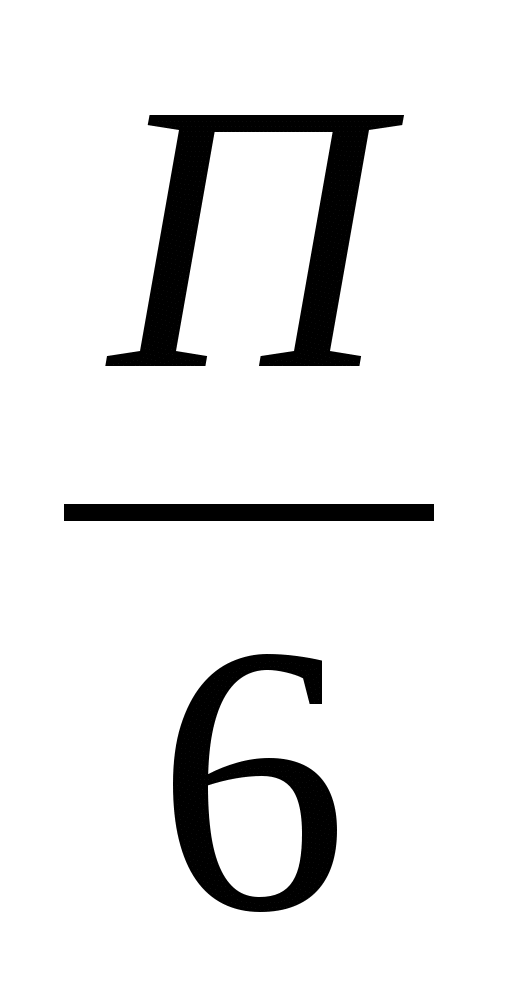 -
-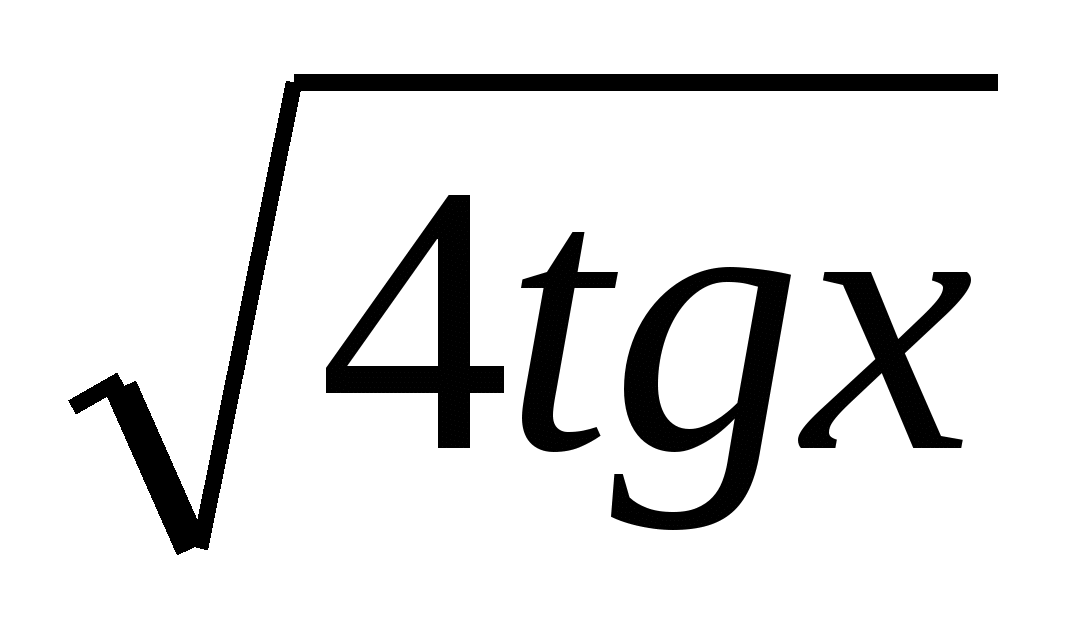
Вариант № 2
1. Найдите ƒ'(х), ƒ'(х0), если
а) ƒ(х)=3х5 -12х2+6х+3, х0 =1; б) ƒ(х)=х sinx х0=![]()
2. Найдите ƒ'(х), если:
а) ƒ(х)=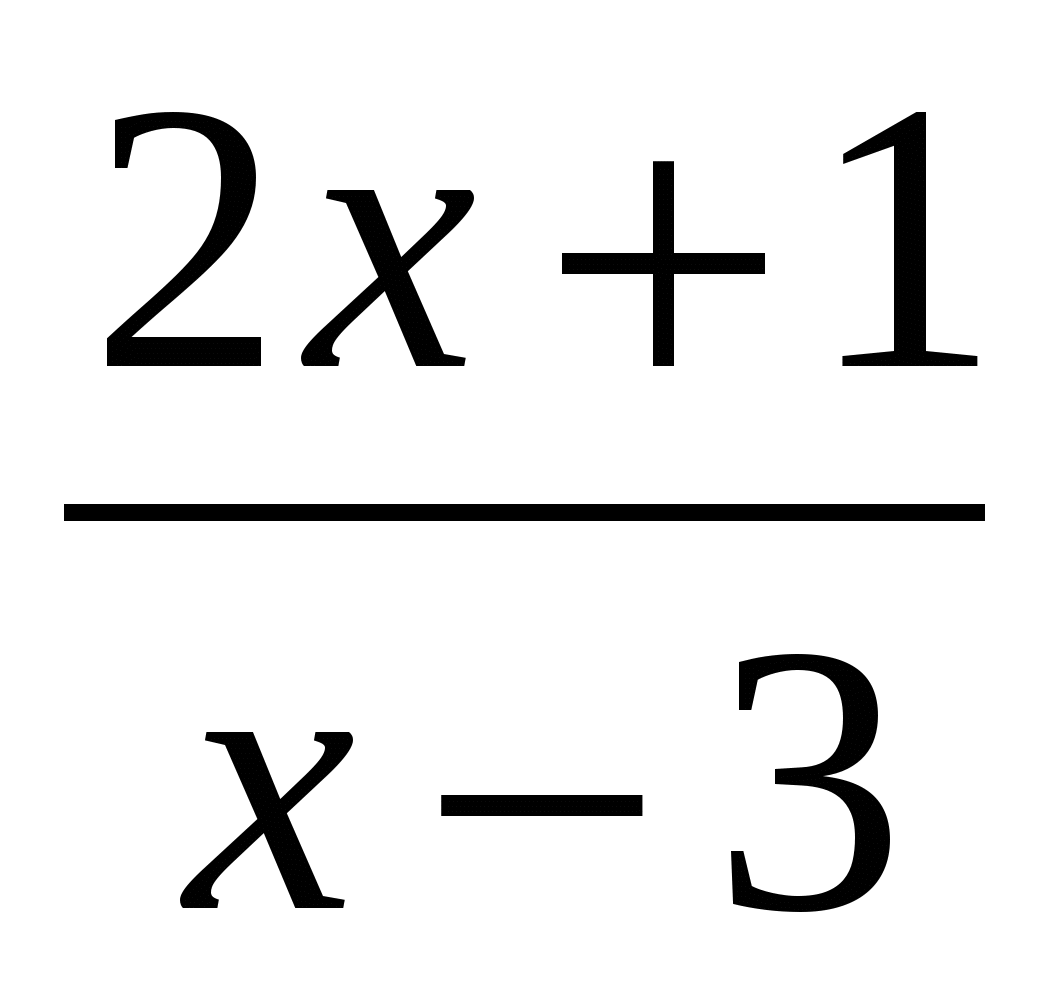 ; б) ƒ(х)=5 5
; б) ƒ(х)=5 5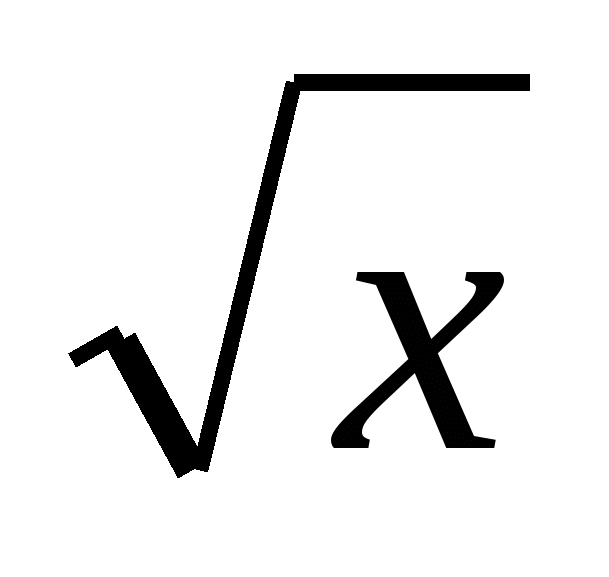 3 ; в) ƒ(х)=5x; г) ƒ(х) =
3 ; в) ƒ(х)=5x; г) ƒ(х) = 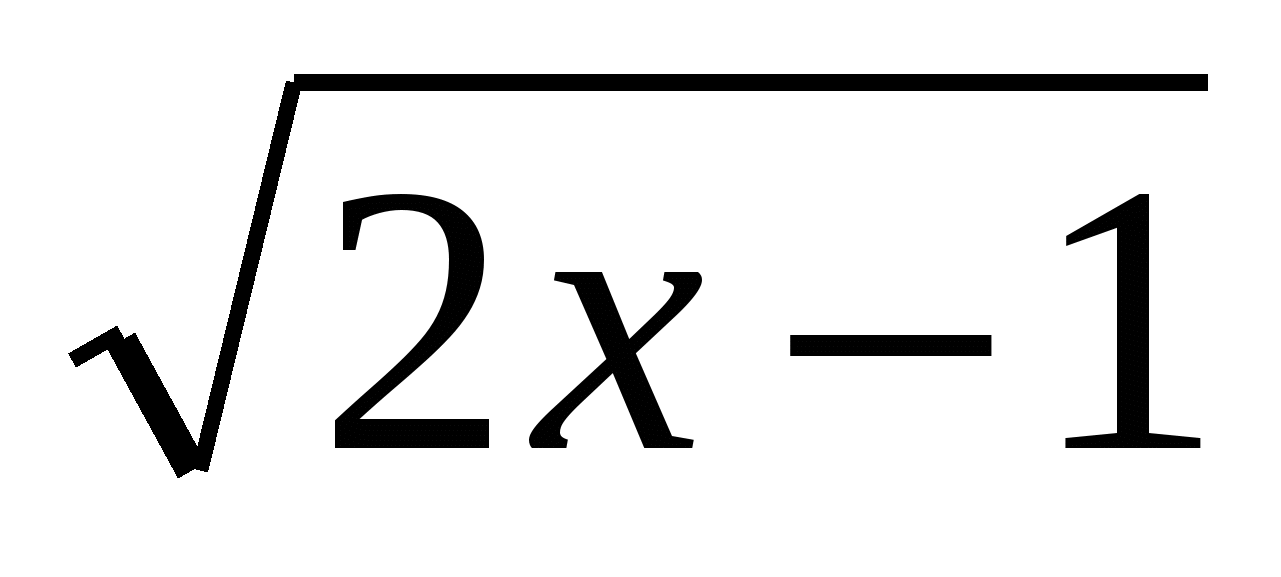
3.Вычислите значение производной функции у=tg 4x в точке х0=-![]()
4. Найдите все значения х, при каждом из которых производная функции
а) ƒ(х)=х3-6х2+9х-11 равна нулю.
5. Найдите ƒ'(х), если:
а) ƒ(х)=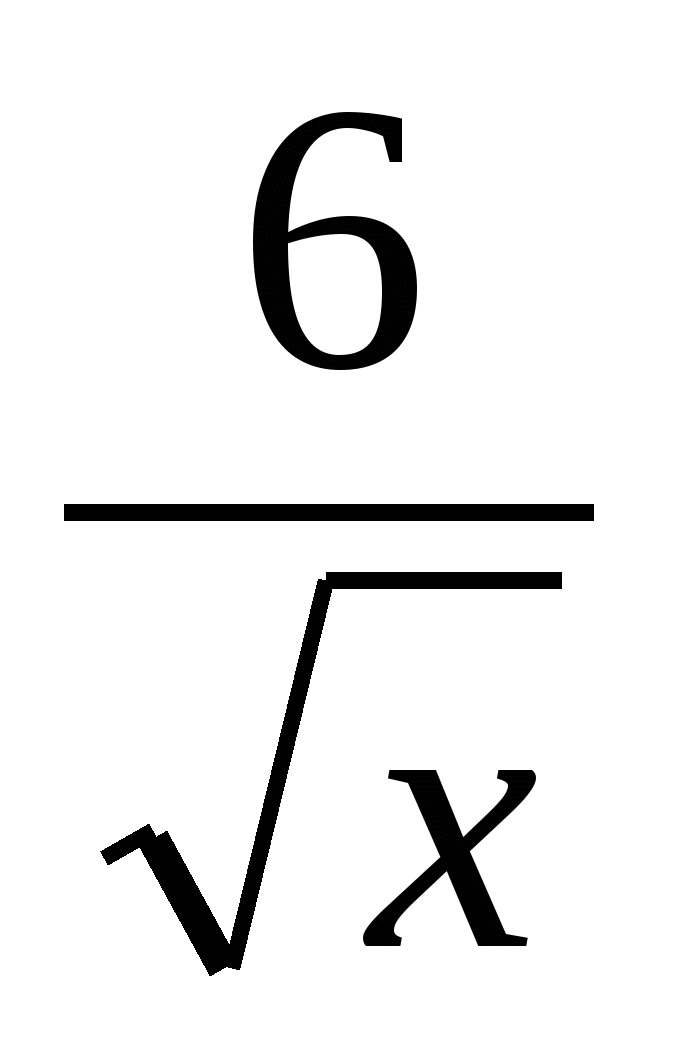 - 3 3
- 3 3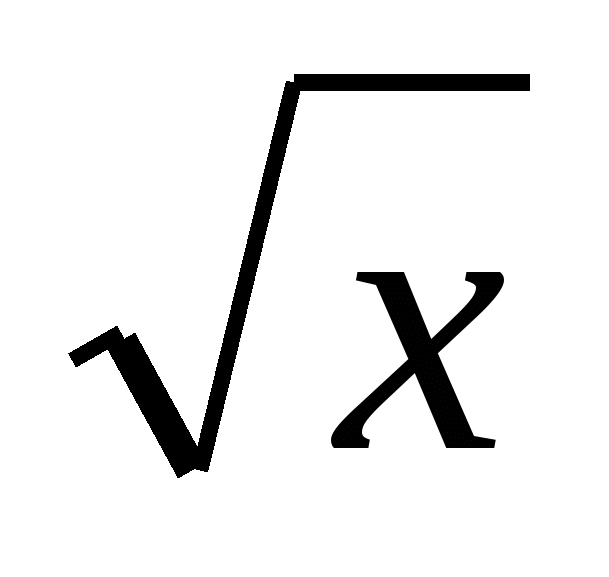 4; б) ƒ(х)=ln(3+2x); в) ƒ(х)=х√х2+2х+3
4; б) ƒ(х)=ln(3+2x); в) ƒ(х)=х√х2+2х+3
6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=13+10t-5t2.Найдите момент времени t, когда точка остановится.
7. Найдите производную функции
ƒ(х)=ln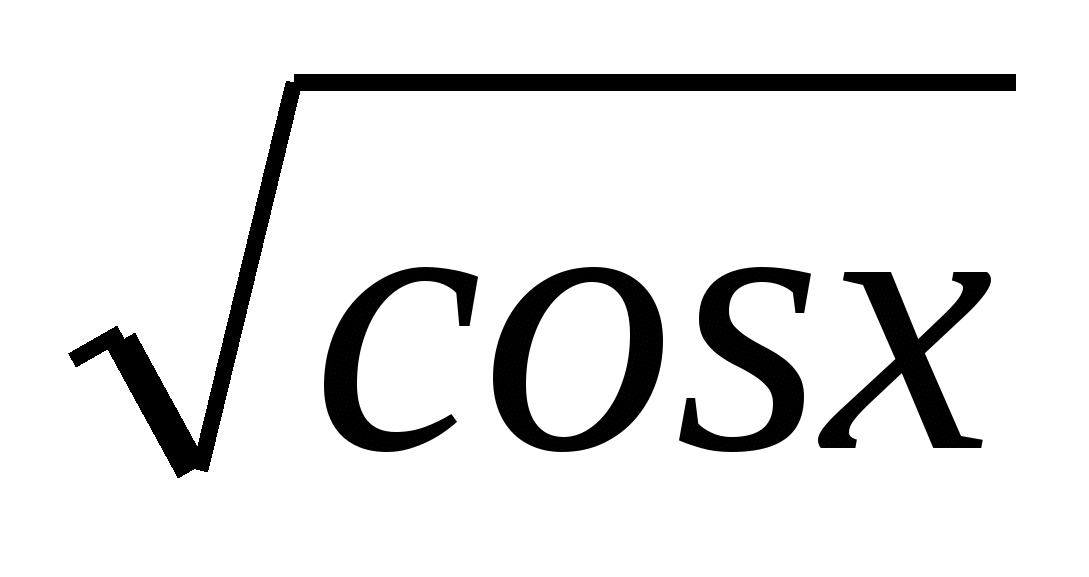
8. Найдите производную функции
а) у=х2 соs 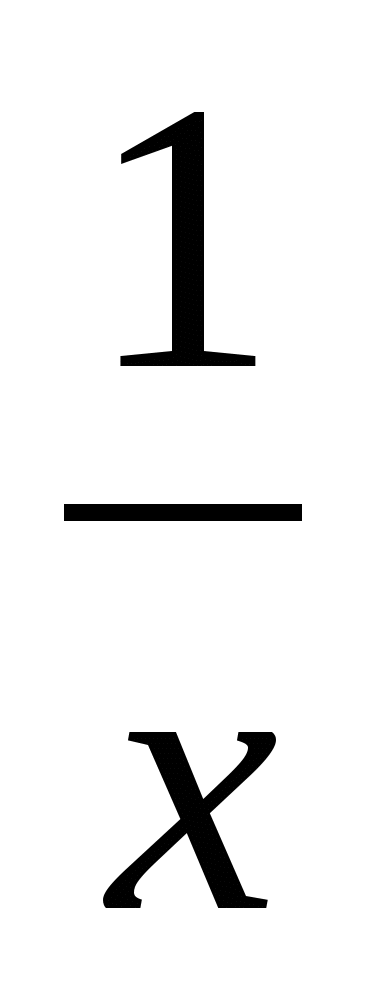 б) y=
б) y=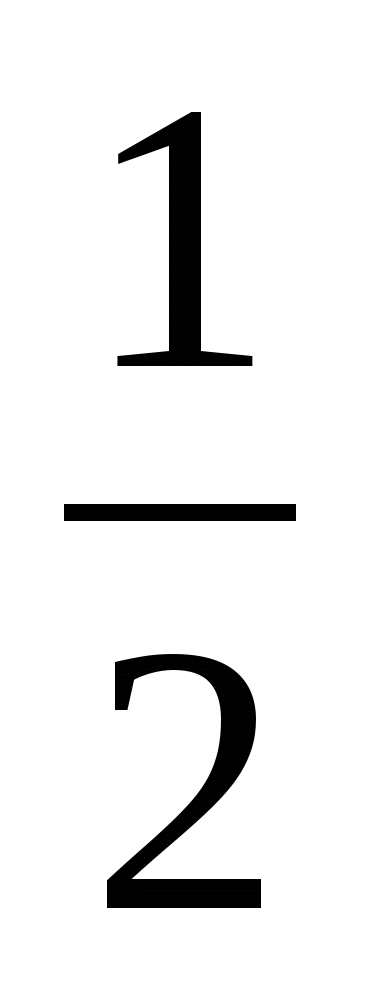 log3(9x+7)· arcctg2 x3
log3(9x+7)· arcctg2 x3
в) y=sin 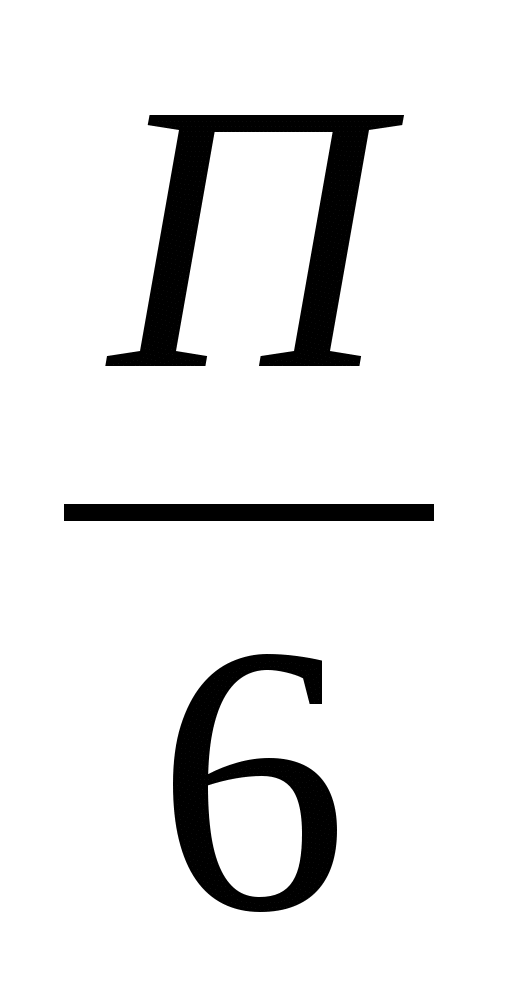 -
-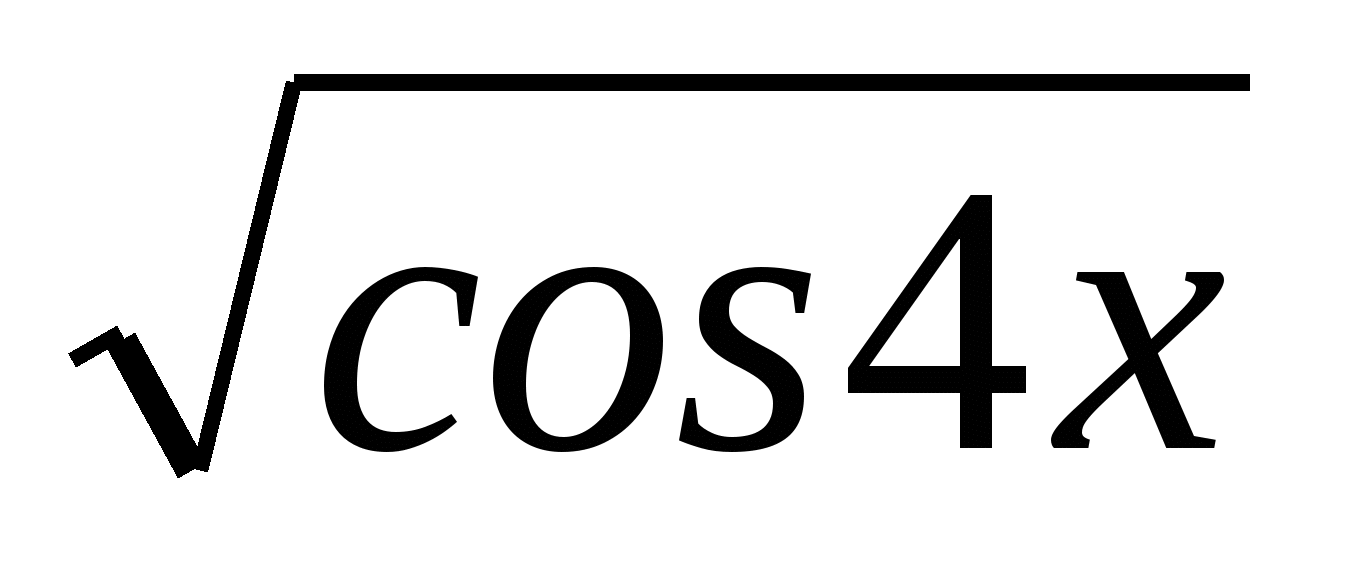
Вариант № 3
1. Найдите ƒ'(х), ƒ'(х0), если
а) ƒ(х)=-5х4 +4х3+6х2-2x+3, х0 =1; б) ƒ(х)=х tgx х0=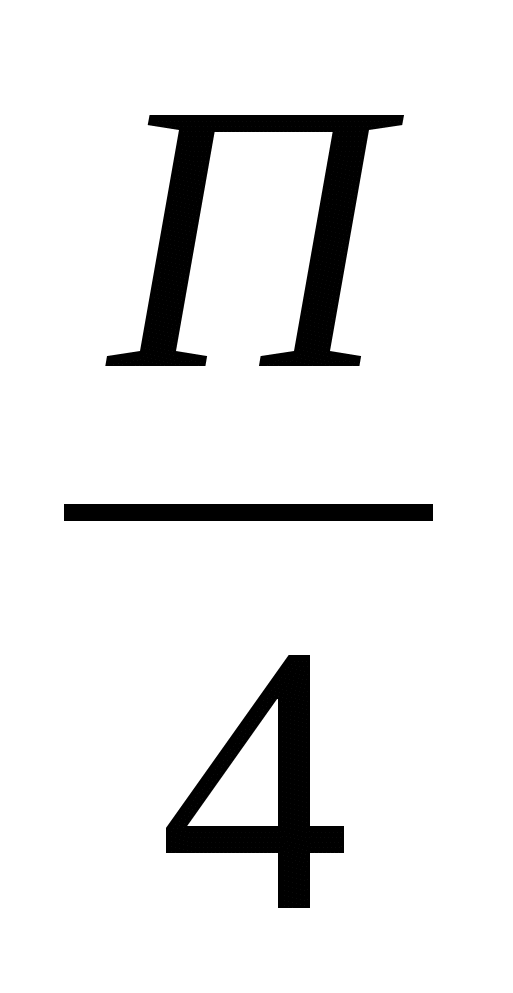
2. Найдите ƒ'(х), если:
а) ƒ(х)=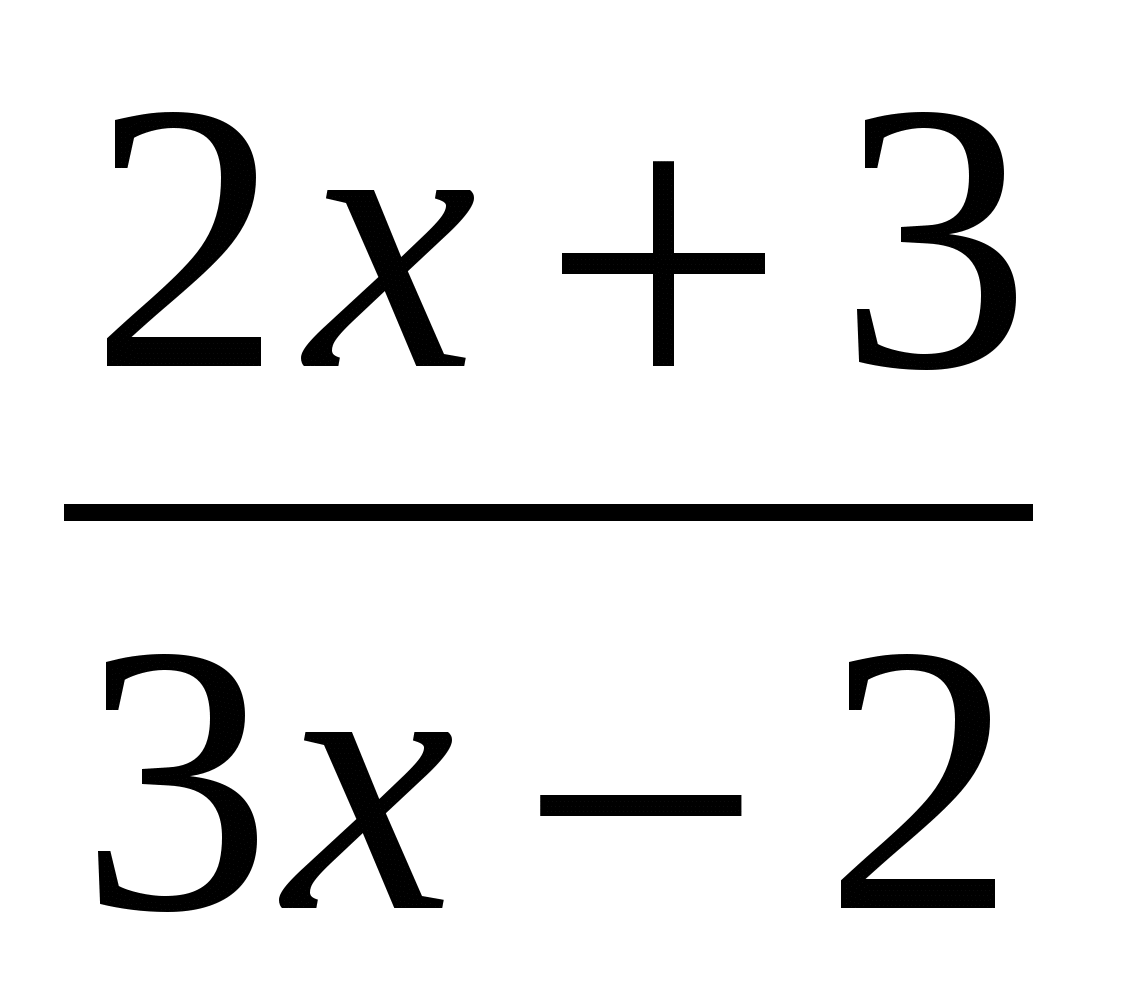 ; б) ƒ(х)=5 5
; б) ƒ(х)=5 5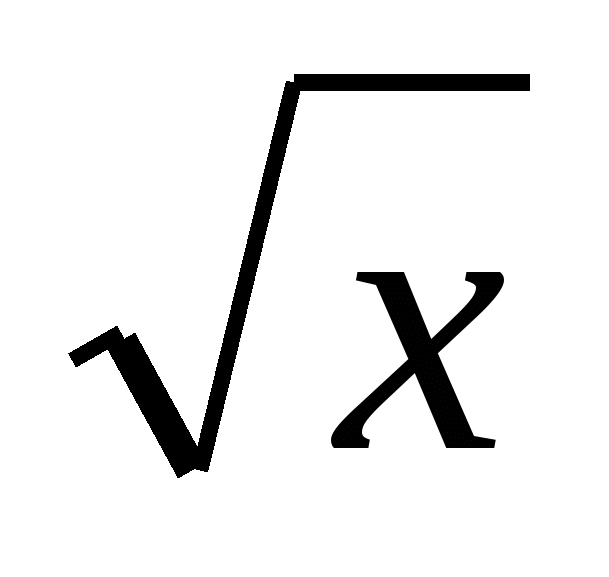 4 ; в) ƒ(х)=10x; г) ƒ(х) =
4 ; в) ƒ(х)=10x; г) ƒ(х) = 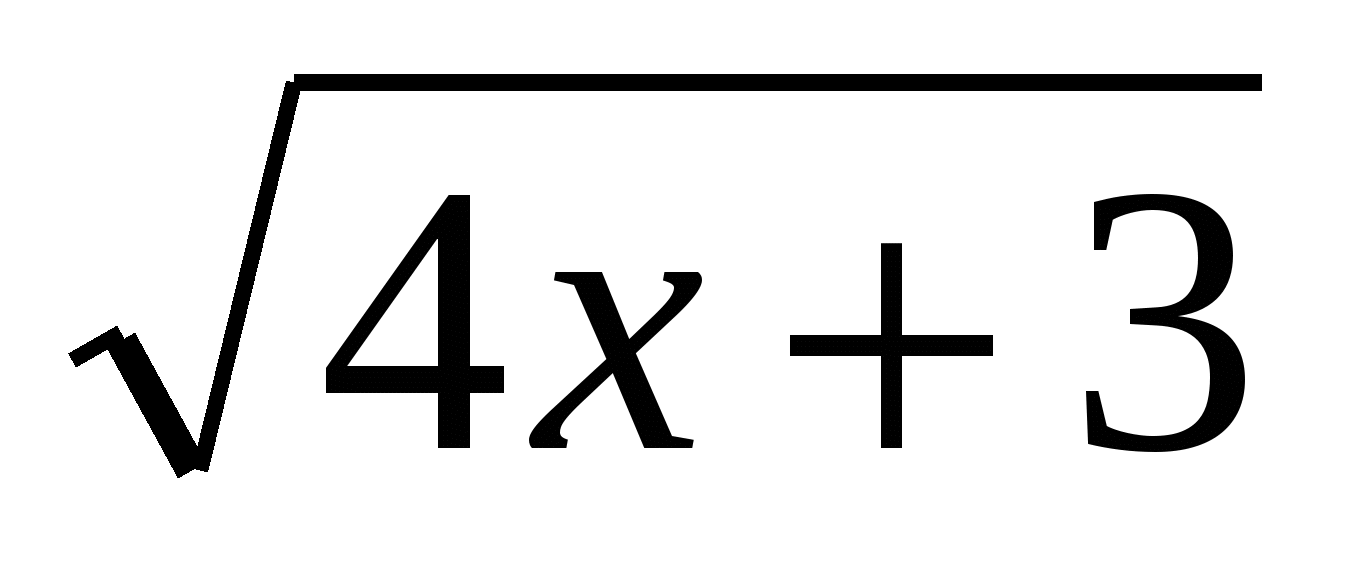
3.Вычислите значение производной функции у=cos 3x в точке х0=-![]()
4. Найдите все значения х, при каждом из которых производная функции
а) ƒ(х)=х3-4х2+5х-17 равна нулю.
5. Найдите ƒ'(х), если:
а) ƒ(х)=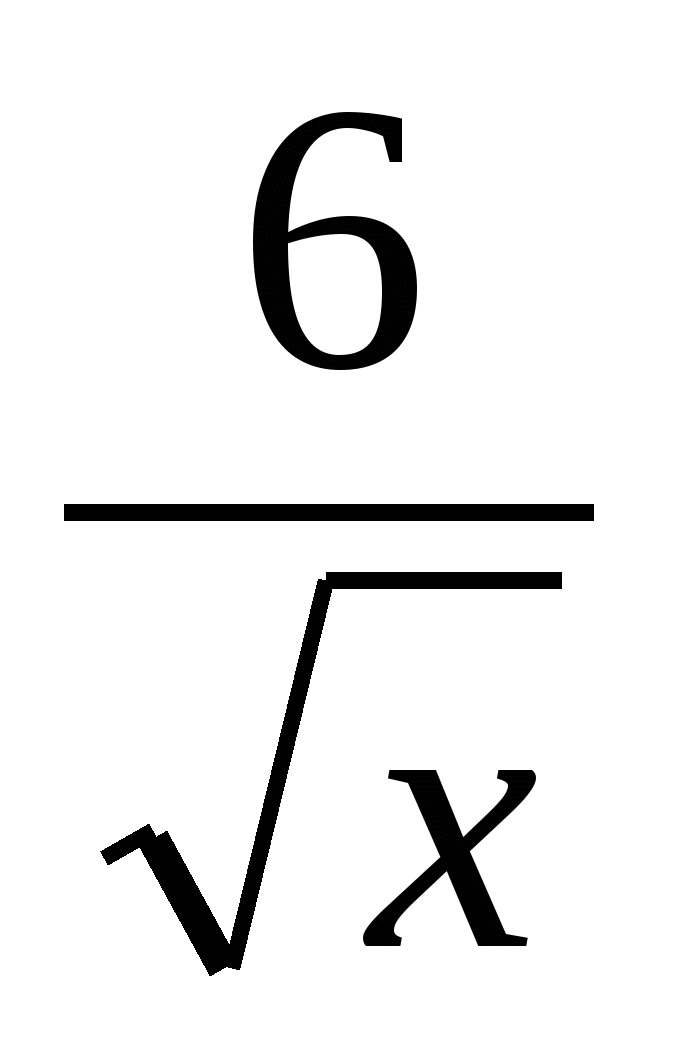 - 12 3
- 12 3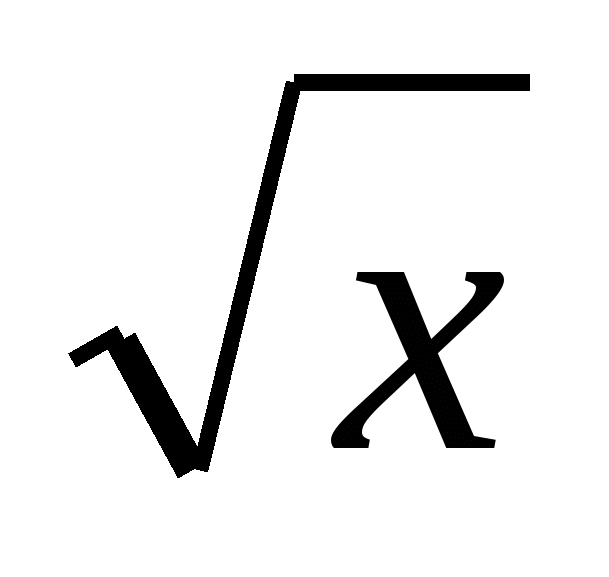 5; б) ƒ(х)=lg(4-3x); в) ƒ(х)=4х√3х2-2х+1
5; б) ƒ(х)=lg(4-3x); в) ƒ(х)=4х√3х2-2х+1
6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=23+20t-5t2.Найдите момент времени t, когда точка остановится.
7. Найдите производную функции
ƒ(х)=ln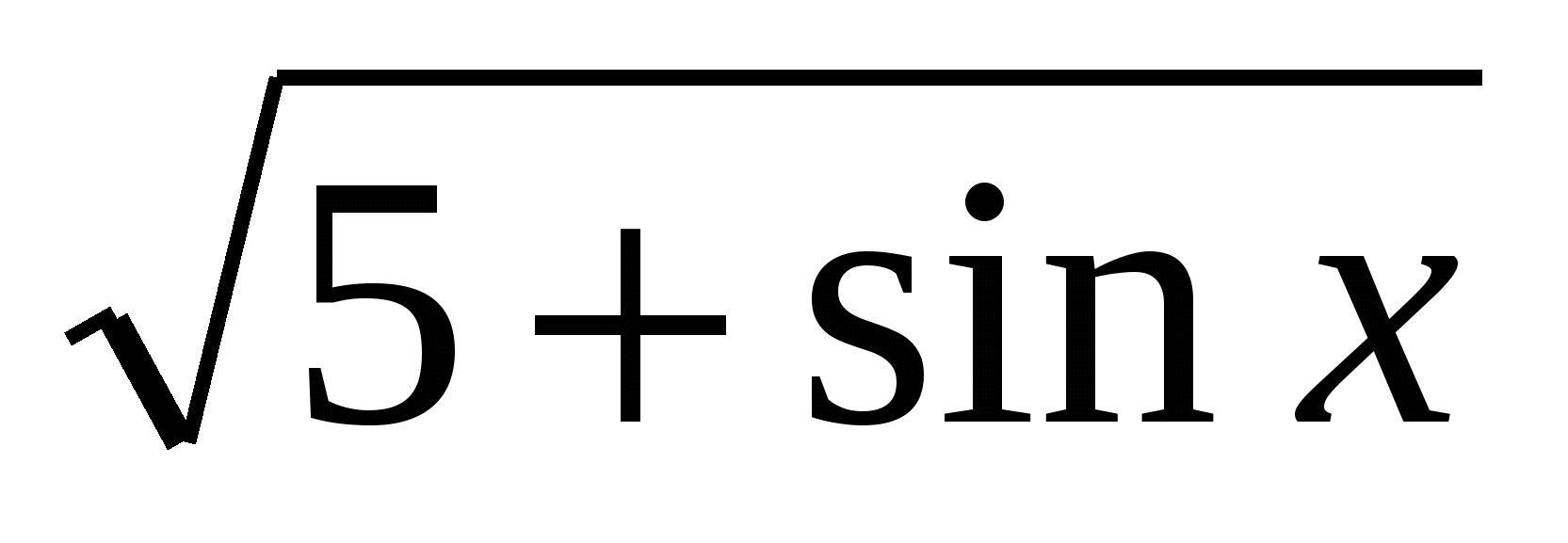
8. Найдите производную функции
а) у=х3 соs 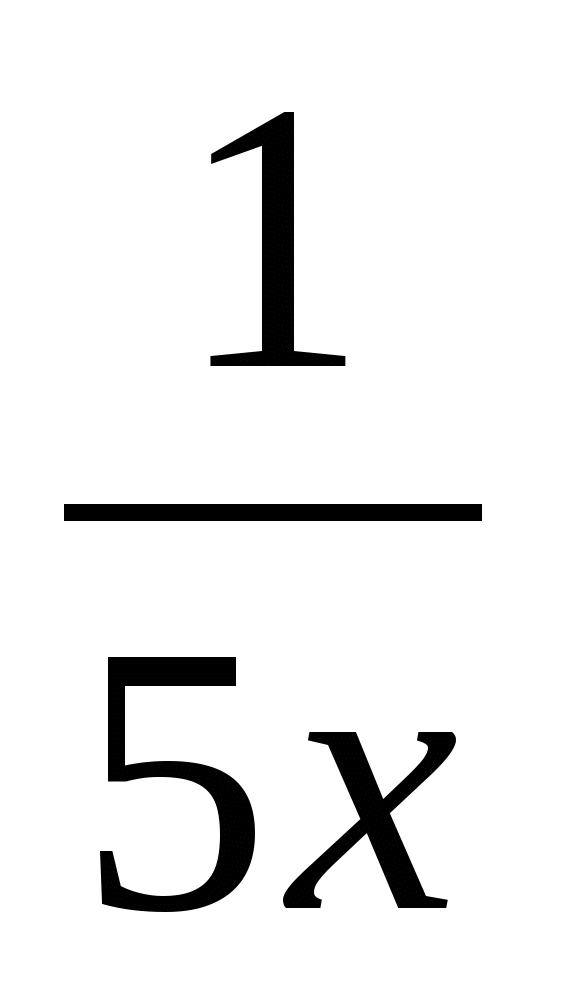 б) y=
б) y=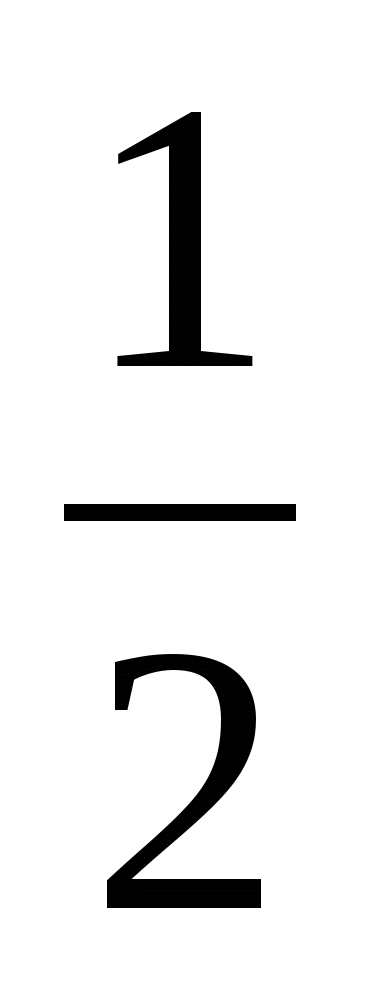 log8(9x+7)· arctg2 3x4
log8(9x+7)· arctg2 3x4
в) y=cos 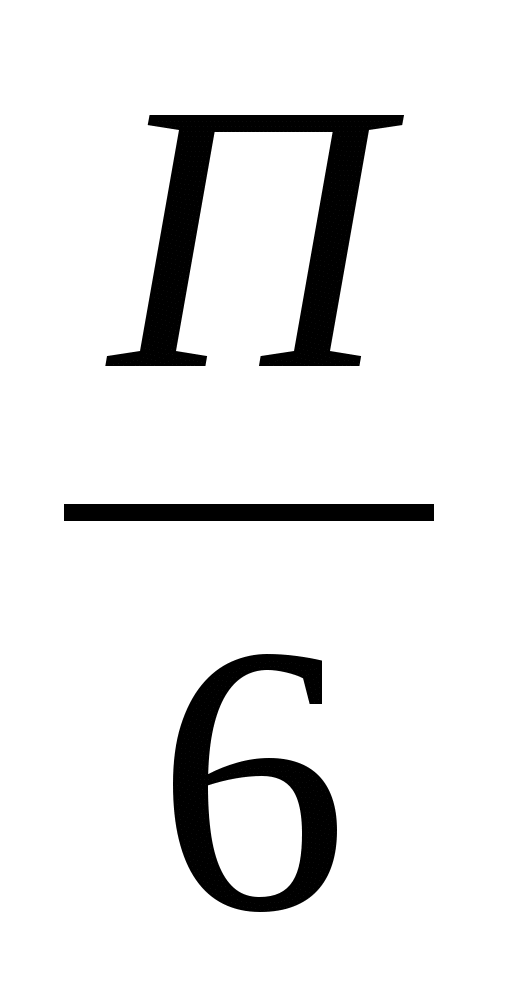 -
-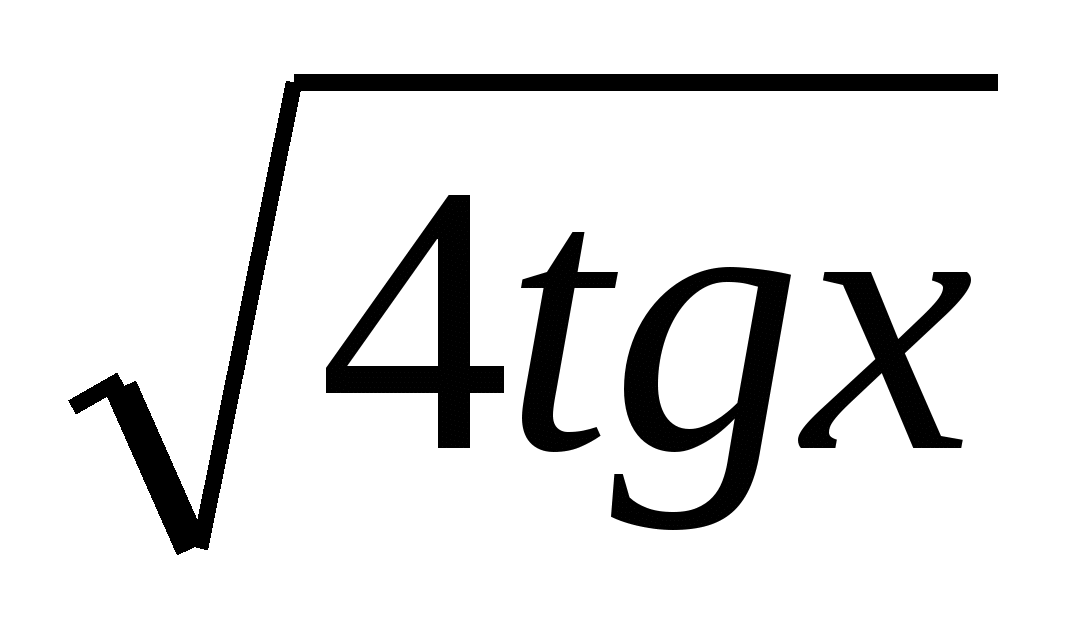
Вариант № 4
1. Найдите ƒ'(х), ƒ'(х0), если
а) ƒ(х)=5х3-4х4+2х2-2x+5, х0 =1; б) ƒ(х)=х ctgx х0=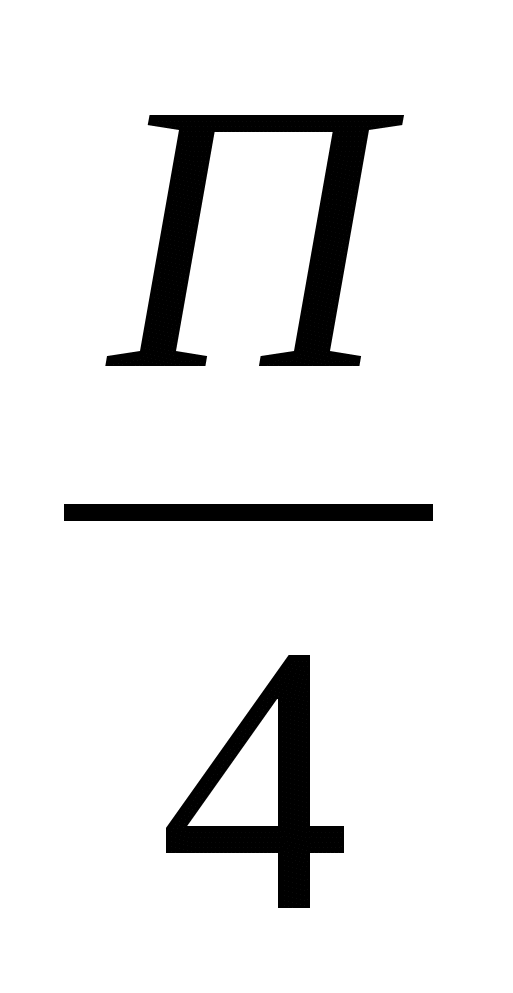
2. Найдите ƒ'(х), если:
а) ƒ(х)=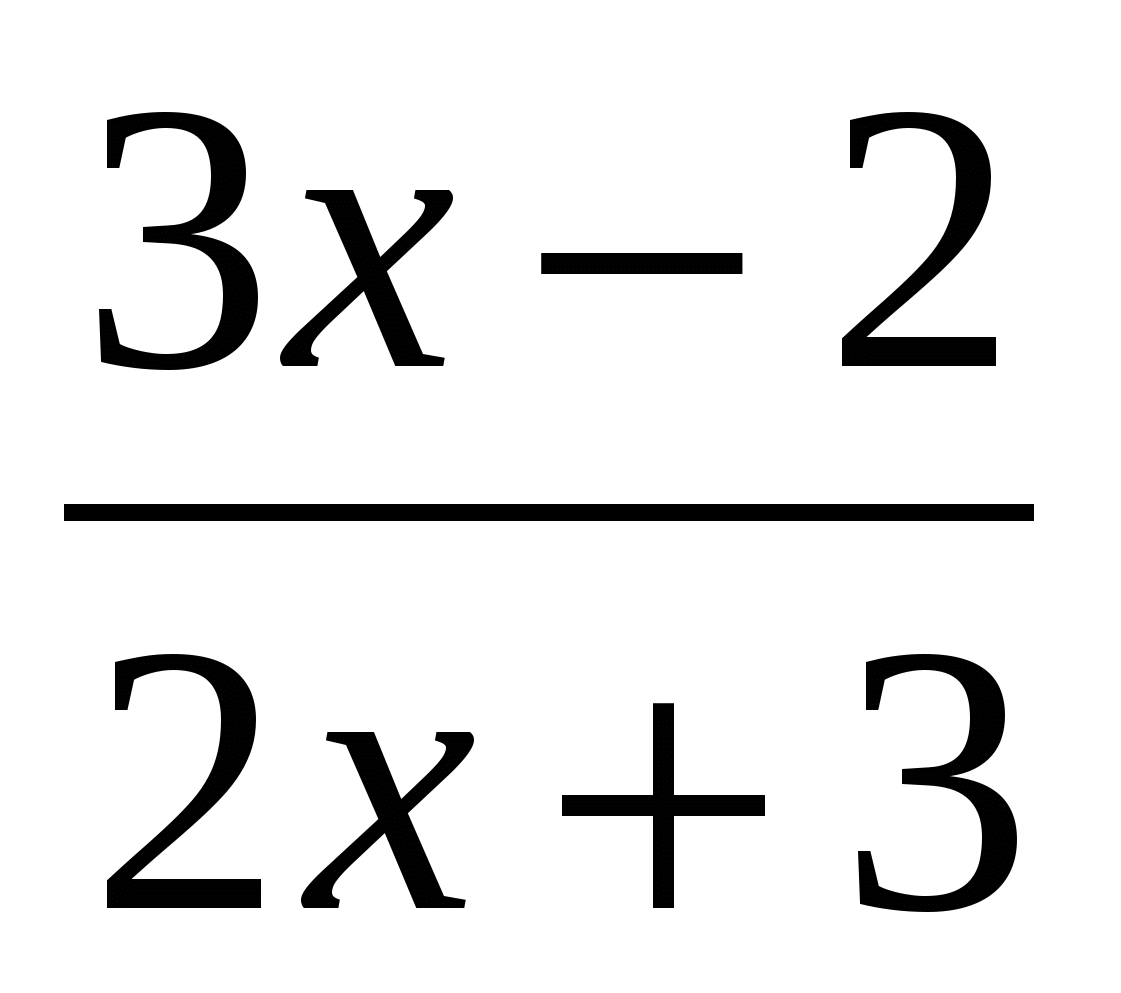 ; б) ƒ(х)=7 7
; б) ƒ(х)=7 7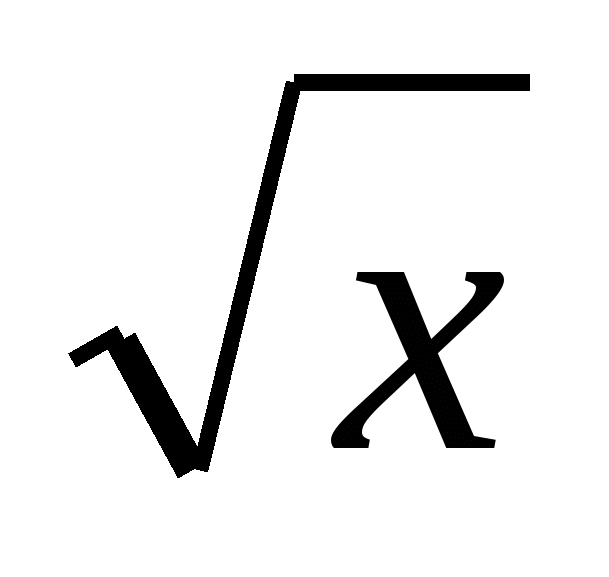 6 ; в) ƒ(х)=lg x; г) ƒ(х) =
6 ; в) ƒ(х)=lg x; г) ƒ(х) = 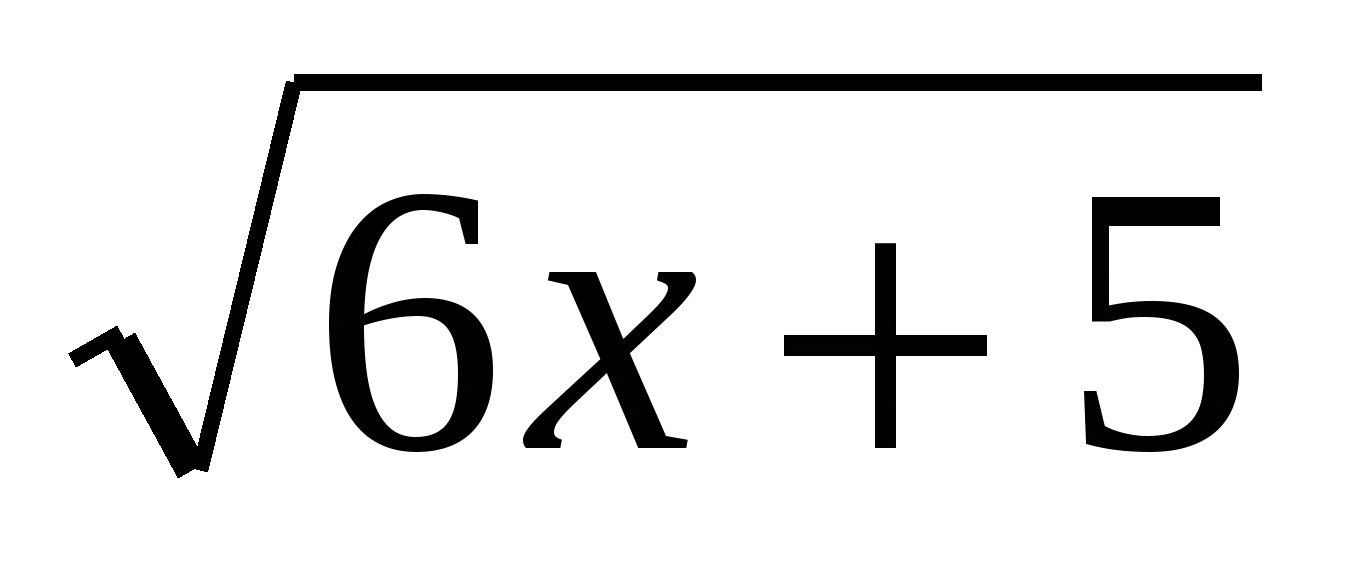
3.Вычислите значение производной функции у=sin 2x в точке х0=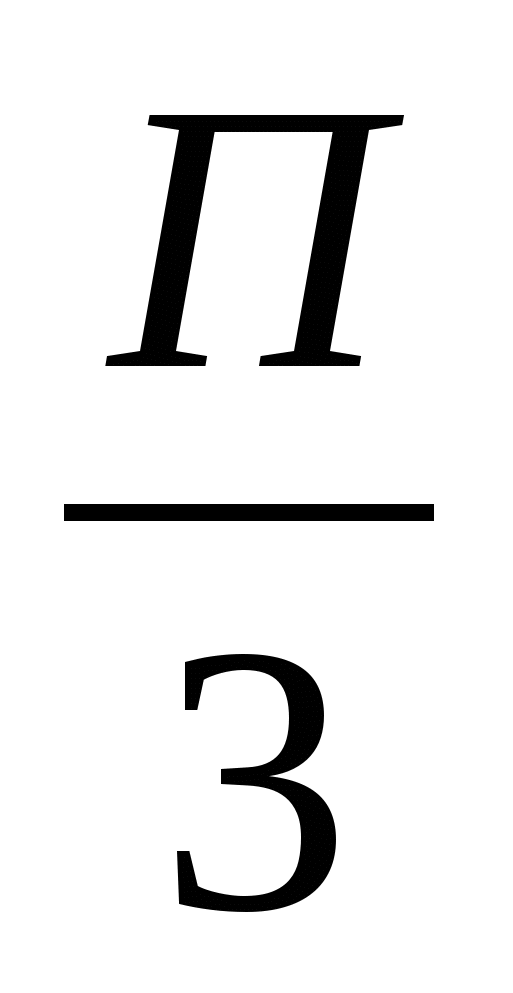
4. Найдите все значения х, при каждом из которых производная функции
а) ƒ(х)=х3+2х2-7х-13 равна нулю.
5. Найдите ƒ'(х), если:
а) ƒ(х)=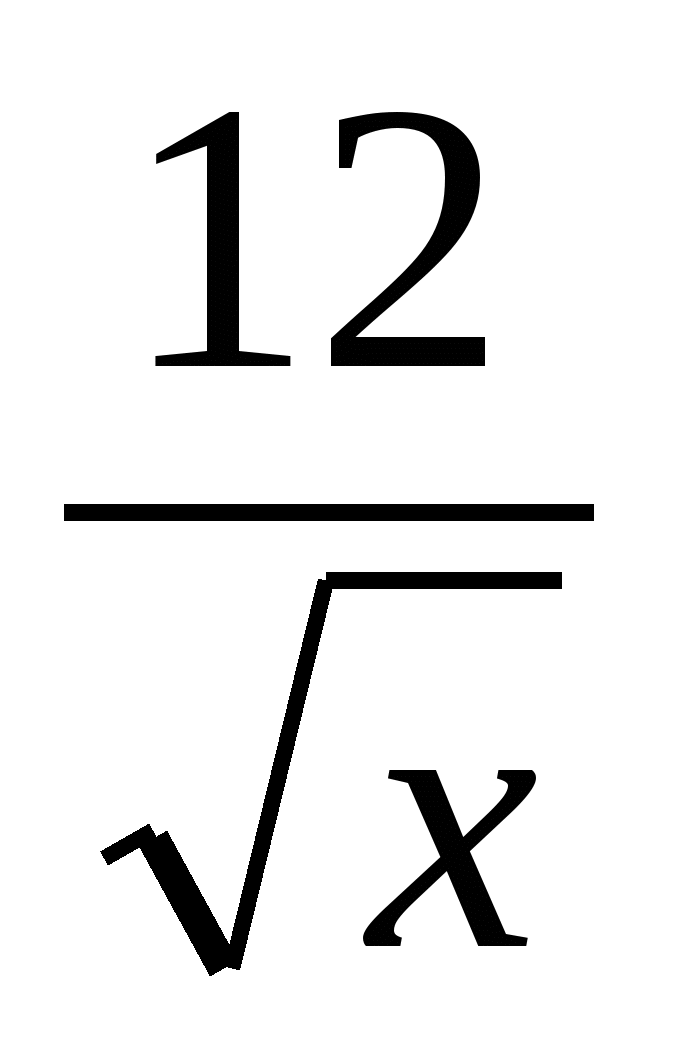 - 6 3
- 6 3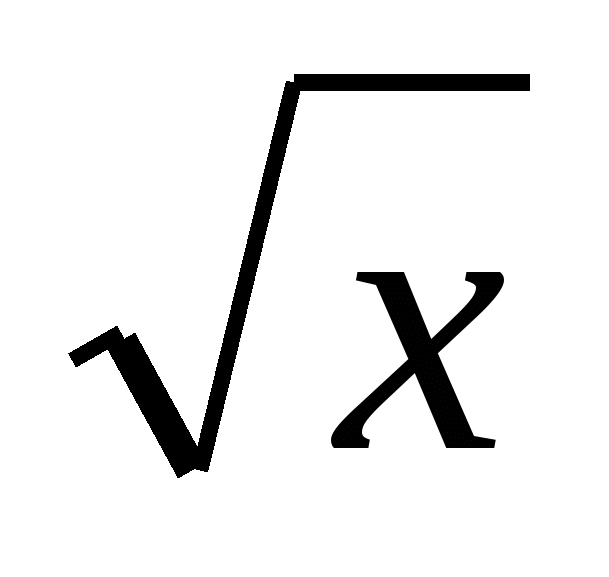 5; б) ƒ(х)=104x-3); в) ƒ(х)=4х√4х2-2х+1
5; б) ƒ(х)=104x-3); в) ƒ(х)=4х√4х2-2х+1
6. Точка движется по прямой. Зависимость ее координаты х от времени t задана формулой х=27+24t-2t2.Найдите момент времени t, когда точка остановится.
7. Найдите производную функции
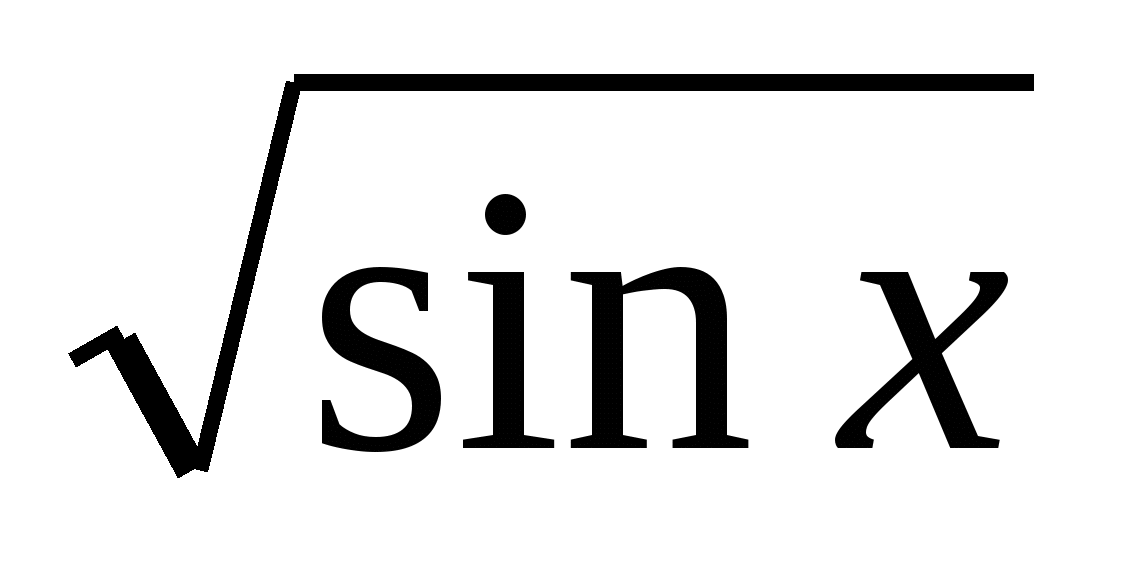
ƒ(х)=e
8. Найдите производную функции
а) у=х2 соs 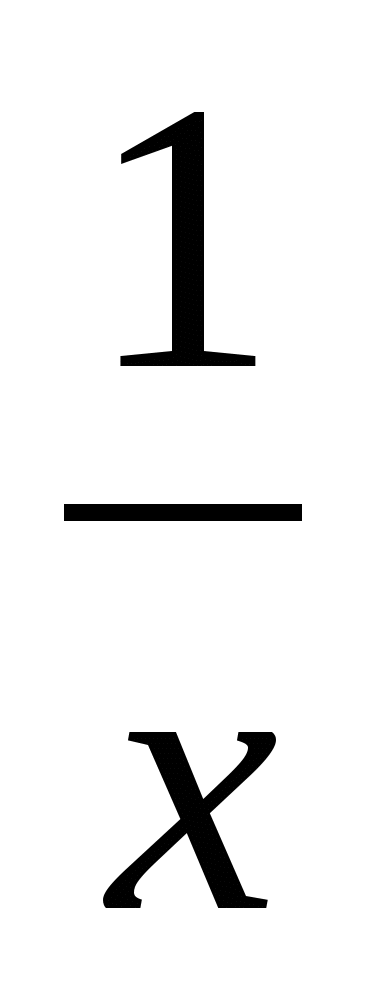 б) y=
б) y=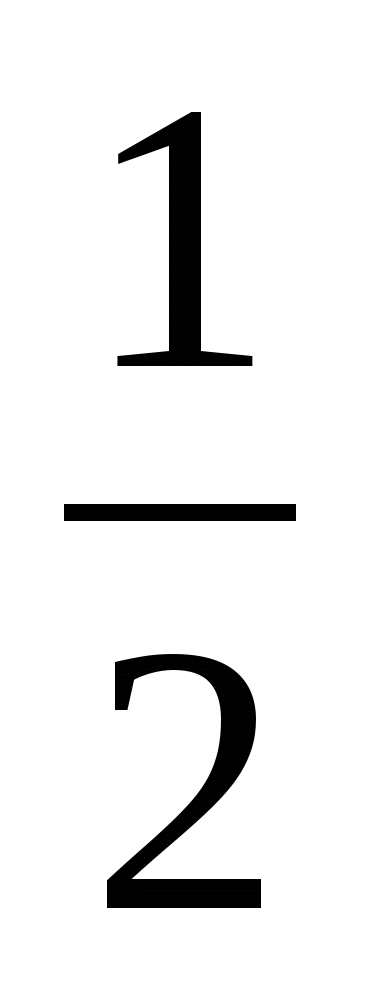 log3(9x+7)· arcctg2 x3
log3(9x+7)· arcctg2 x3
в) y=sin 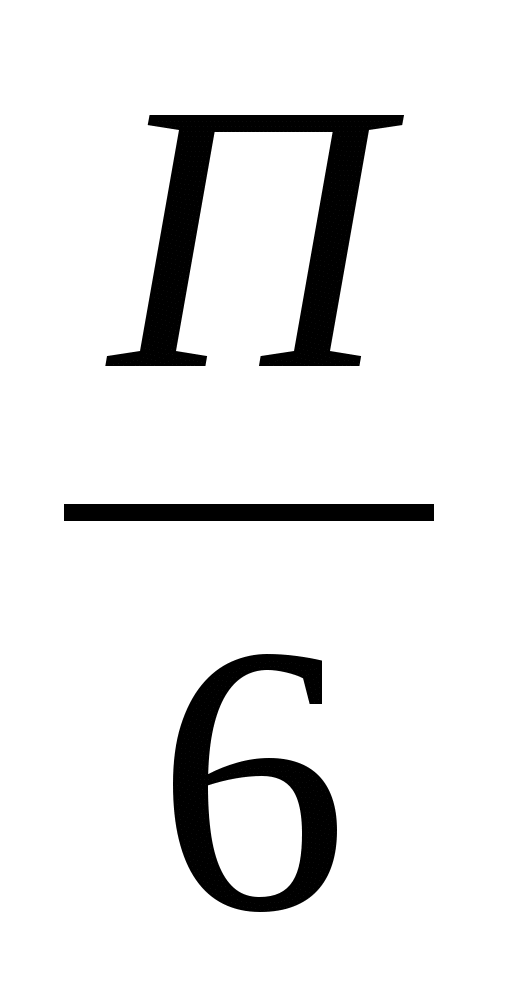 -
-