- Преподавателю
- Математика
- Математикадан олимпиадалық есептерді шығару
Математикадан олимпиадалық есептерді шығару
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Баймухашева Л.К. |
| Дата | 28.11.2013 |
| Формат | doc |
| Изображения | Есть |
Атырау облысы
Жылыой ауданы
«№23 жалпы орта білім беретін мектеп»
мемлекеттік мекемесі.

Математикалық индукция және теңсіздіктерді дәлелдеу.
Баймұхашева Лиза Қожантаевна.
математика пәні мұғалімі
Құлсары қаласы- 2013ж.
Жоспары:
1.Кіріспе ------------------------------------------------------------------2-3бет
2.Негізгі бөлім:
а)Математикалық индукция әдісіне берілген олимпиадалық есептерді шығару жолдары------------------------------------------3-10 бет
б)Теңсіздіктерді дәлелдеуге берілген олимпиадалық есептерді шығару жолдары-------------------------------------------------------11-23 бет
3.Қорытынды.----------------------------------------------------------23 бет.
4.Пайдаланылған әдебиеттер-----------------------------------------24 бет.
Қазіргі кезде ғылым мен техниканың даму деңгейі әрбір адамды сапалы және терең білім мен іскерліктің болуын, ойлау қабілетінің жоғары, шығармашылықпен жұмыс істеуін талап етеді. Оқушылардың математика-лық білімін жоғары деңгейде оқыту, яғни тереңдету әр ұстаздың алдындағы міндет.
Мұғалім шеберлігінің негізгі көрсеткіштерінің бірі-әдістеме саласындағы ғылыми жаңалықтар мен озық тәжірибені жетік игеру.
Оқушылардың білімділік және тәрбиелік деңгейі шешуші дәрежеде мұға-лімге байланысты, яғни мұғалім ізденісін қажет етеді. Дарынды балалардың қабілетін дамытудың жолдары көп. Соның ішінде олимпиадалардың ролі ерекше. Оқушылардың пәнге қызығушылығын оятатын, олардың математи-калық ой-өрісінің, шығармашылық қабілетінің дамуына дәнекер болатын қосымша тақырыптар көп әсерін тигізеді. Атап айтқанда,«Математикалық индукция әдісі», «Диофант теңдеулері», «Параметрлі теңдеулер мен теңсіз-діктер», «Комбинаторика», «Тригонометриялық өрнектерді түрлендіру», «Теңсіздіктерді дәлелдеу» және тағы да басқа тақырыптарды айтуға болады. Бұндай тақырыптар математикалық пән олимпиадаларында өз үлесін қосары сөзсіз.
Олимпиадаға дайындалу кезінде әрбір тараудың есептерін шешудің бірне-ше тәсілдерін қарастырамыз. Олимпиадалық есептерді алып қарайтын болсақ, қиындығы өте жоғары. Мұндай есептерді шығару оқушылардан терең ізденуді, терең ойлануды, еңбекқорлықты, шыдамдылықты талап етеді және соған тәрбиелейді. Олимпиадада кездесетін есептер мектеп көлемінде нақты оқылмайды, сондықтан оған қосымша ізденіп, еңбектену керек.
Қарастырғалы отырған тақырыптар: «Теңсіздіктерді дәлелдеу» және «Математикалық индукция әдісі» . Теңсіздіктерді дәлелдеу кезінде матема-тикалық индукция әдісін қолдануға болады. Математикалық индукция әдісін пайдаланып натурал сан немесе натурал санға байланысты ұғымдары бар математикалық негіздеуді қажет ететін сөйлемдер дәлелденеді. Теңбе-теңдік-терді дәлелдеуге, шектеулі қосындыларды есептеуге және теңсіздіктерді шешуге көптеген дәлелдеу жолымен көз жеткізуге болады. Математикалық индукция әдісіне және теңсіздіктерді дәлелдеу тақырыптарына қысқаша ғана тоқталып, мектепаралық, аудандық, облыстық, республикалық, халықаралық олимпиадаларда осы тақырыптар бойынша шығарылған қиын есептерге тоқталмақпын.
Математика индукция әдісі
Математикалық индукция принципінің мәнісі төмендегідей : егер қайсыбір тұжырым (формула) n=1 болғанда (немесе бұл ұйғарымның мағынасы бар n-нің басқа мәндерінде ) ақиқат болса және n=k қандай бір натурал мәні үшін ақиқат деп ұйғарылуынан келесі натурал n=k+1 үшін де тұжырымның ақиқаттығы шығатын болса, онда тұжырым n-нің барлық натурал мәнінде ақиқат. Математикалық индукция принципін қолдануға негізделген дәлелдеу әдісі математикалық индукция әдісі деп аталады.
Математикалық индукция әдісімен дәледеу тәсілі төмендегі келесі кезеңдерден тұрады:1) n=1 болғанда тұжырымның (формуланың) ақиқаттағы тікелей тексеріледі немесе дәлелденеді; 2) қайсыбір натурал n=k үшін тұжырым ақиқат, тура деп ұйғарылып, тұжырымның ақиқаттағы n=k+1 үшін дәлелденеді. Математикалық индукция әдісін , натурал n-ге тәуелді тұжырымдарды дәлелдеуге ғана қолдануға болатыны айқын. Негізінен ол есептің екі түрін шешуге қолданылады: 1)жекелеген бақылаулардан ой түйіп , кейбір заңдылықты тағайындайды және одан кейін оның дұрыстығын математикалық индукция әдісімен дәлелдейді; 2) кейбір формулалардың ақиқаттығын математикалық индукция әдісімен дәлелдейді.
Жалпы орта білім беретін мектептің 9- сыныбына арналған алгебра оқулы- ғында «математикалық индукция әдісі» қарастырылған. Оқулық авторлары: А.Е. Әбілқасымова , Н.П. Майкотов, Қ.И. Қаңлыбаев ,
Ә.С. Кенеш. Осы оқулықтың 162 бетіндегі қиынырақ есептерді мектепішілік олимпиадаларға алуға болады. Сол есептердің шығарылуына тоқталып өтейін.
Мектепішілік олимпиада:
№8 есеп.
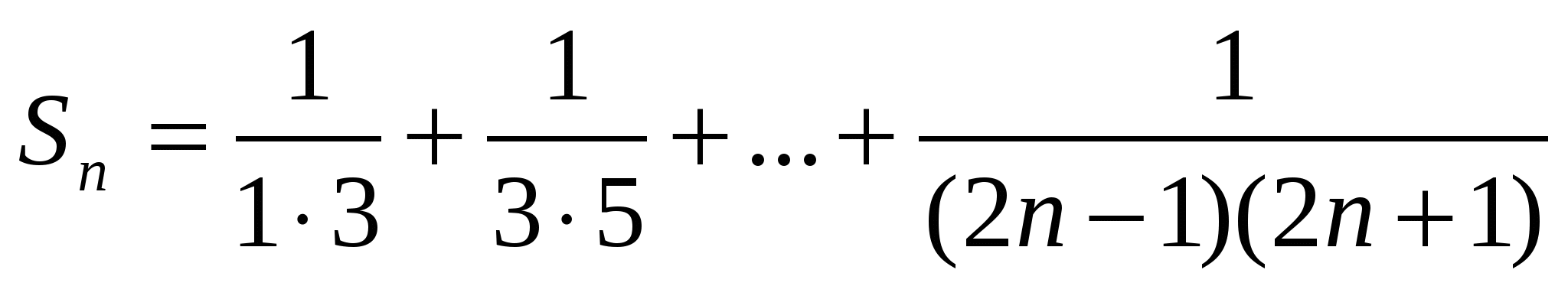 қосындысын табыңдар.
қосындысын табыңдар.
Шешуі: 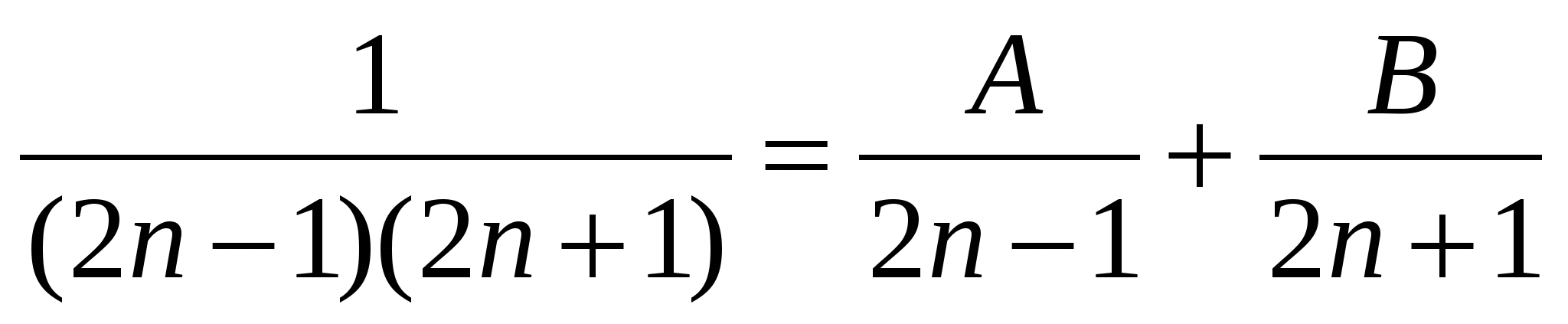
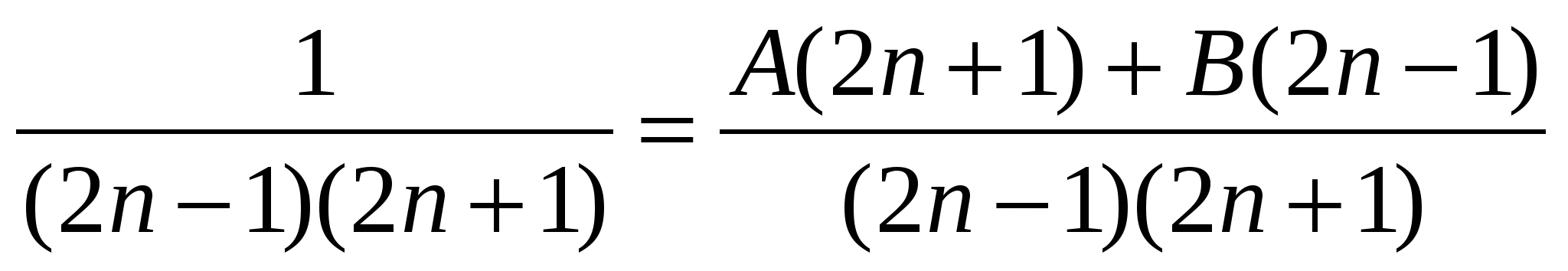

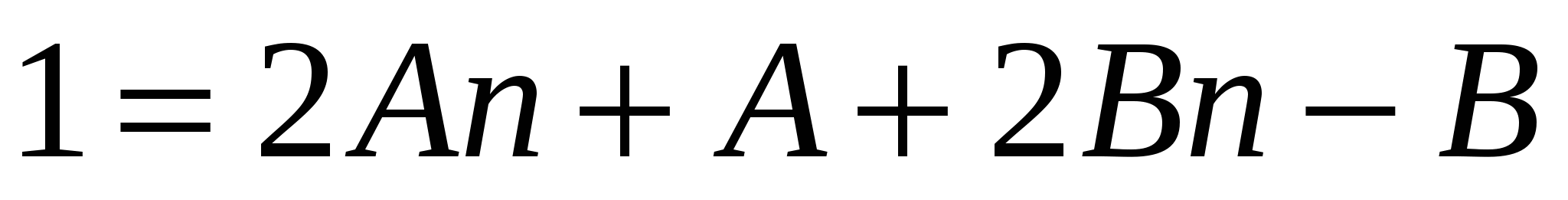
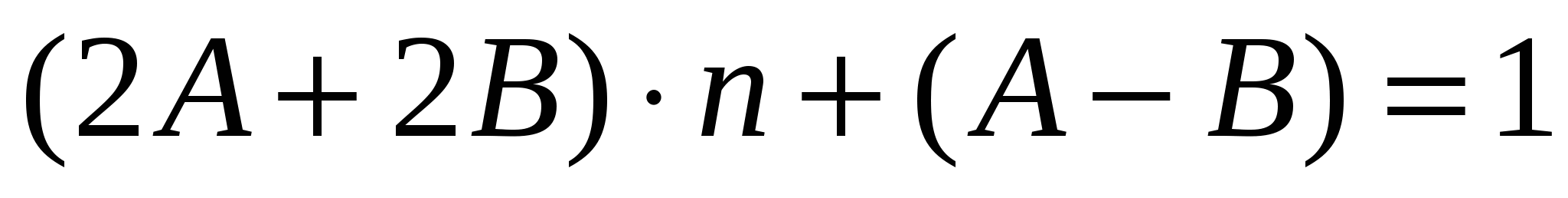
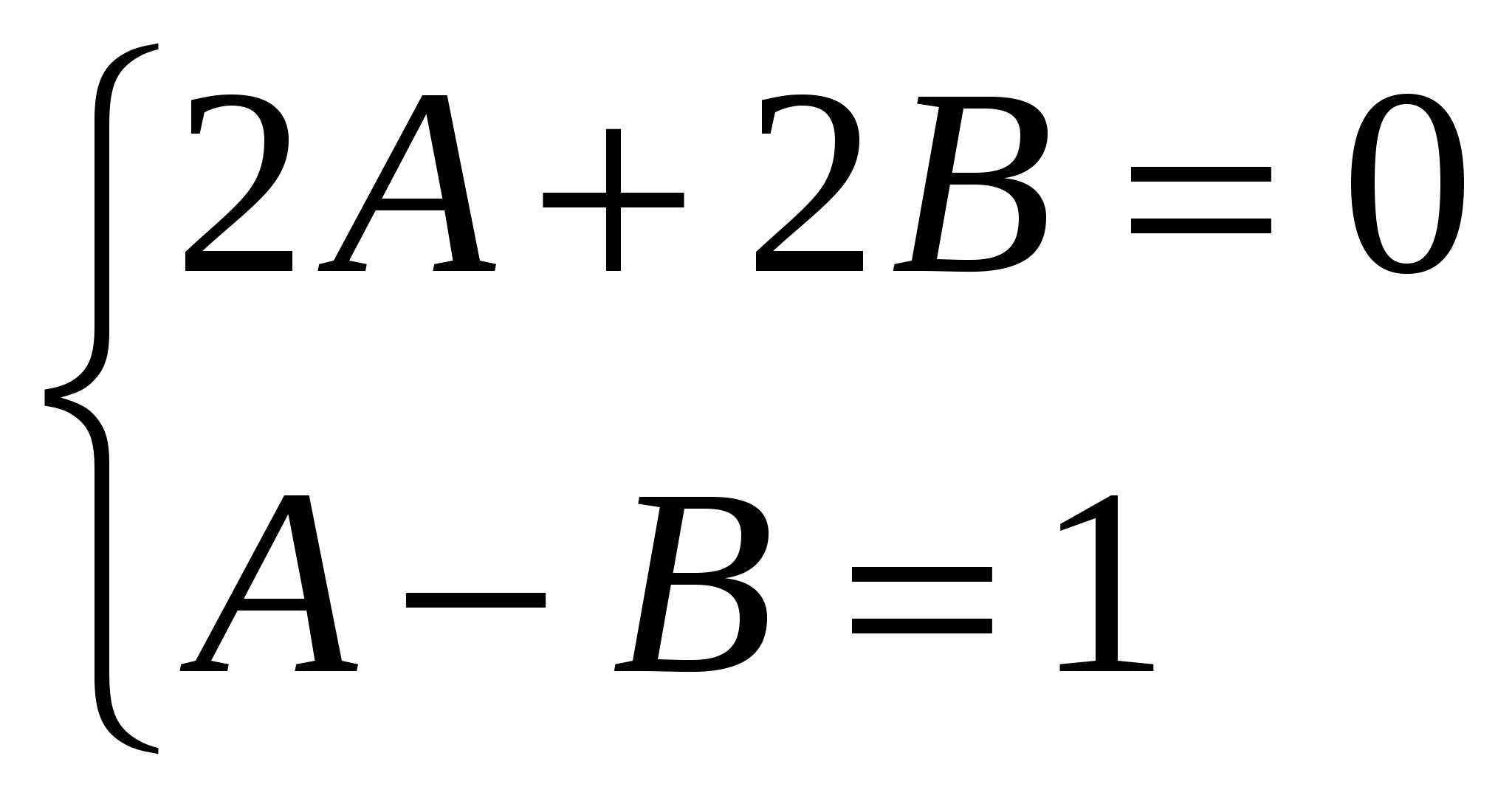

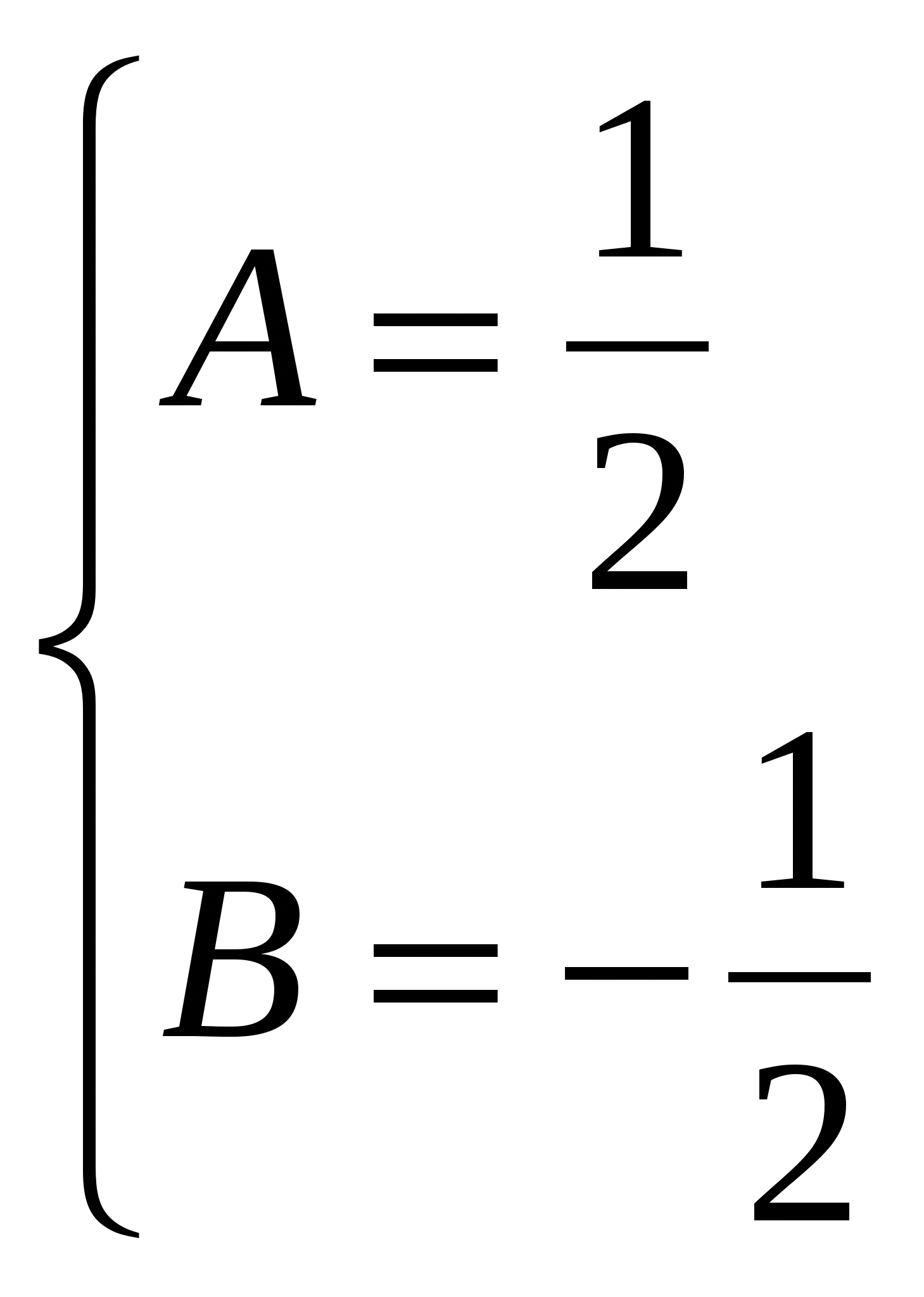
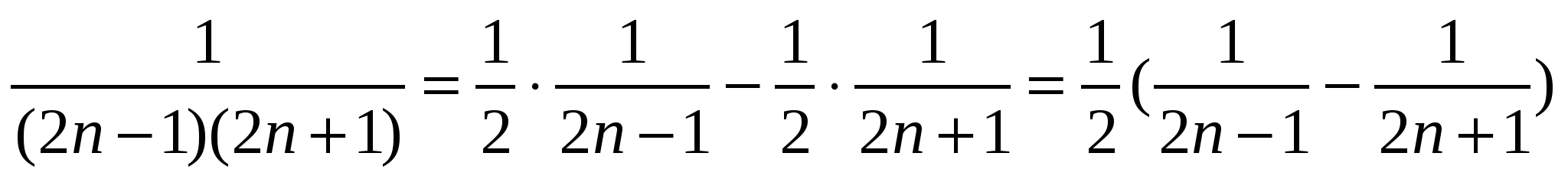
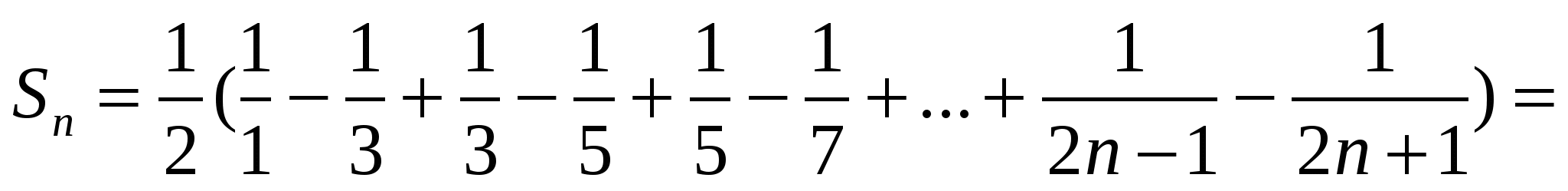
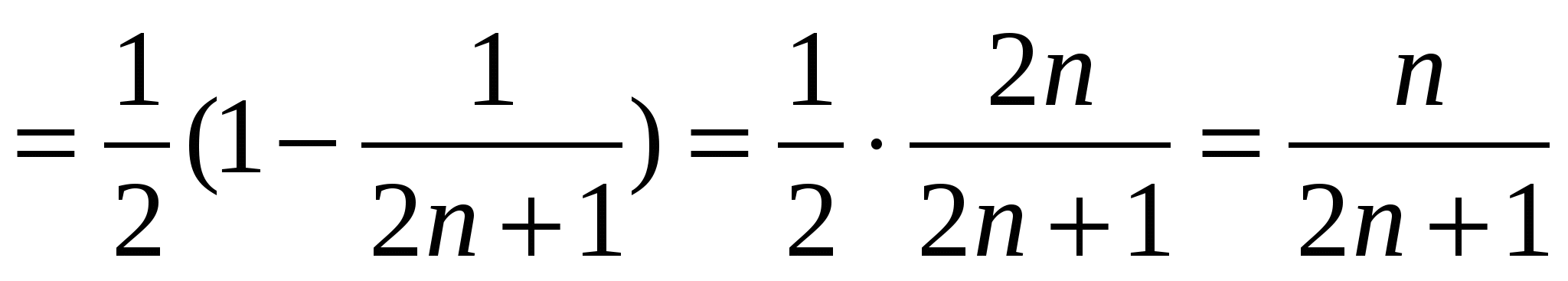 .
.
Жауабы: 
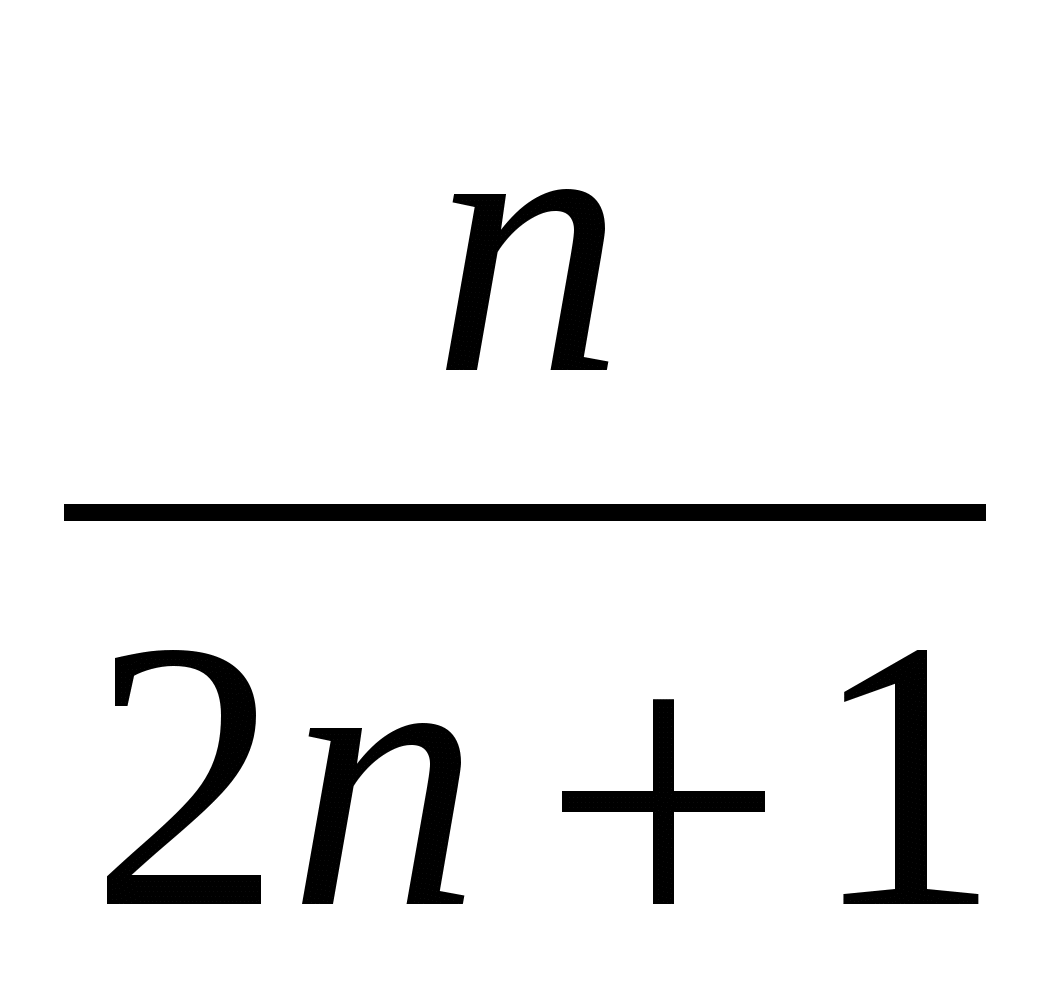 .
.
№9 есеп.
 қосындысын табыңдар.
қосындысын табыңдар.
Шешуі: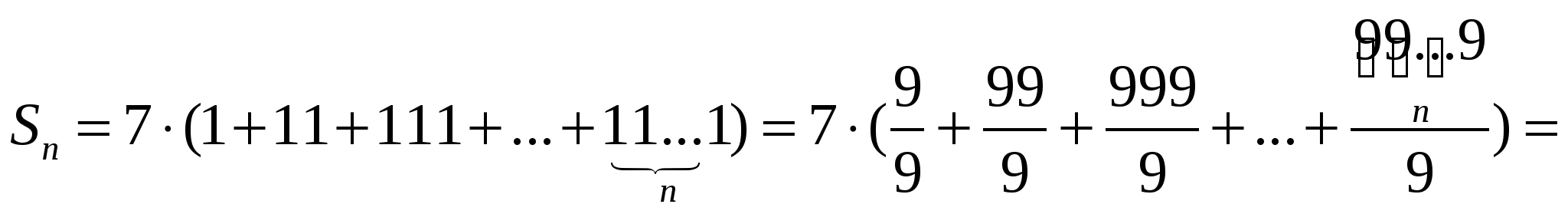
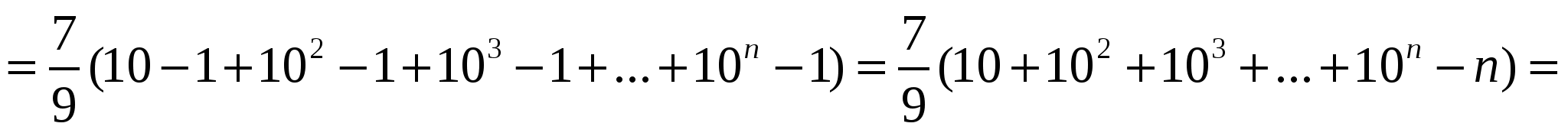
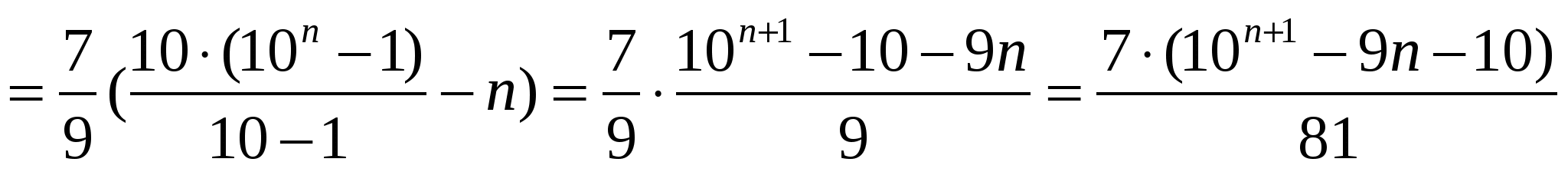
Жауабы: 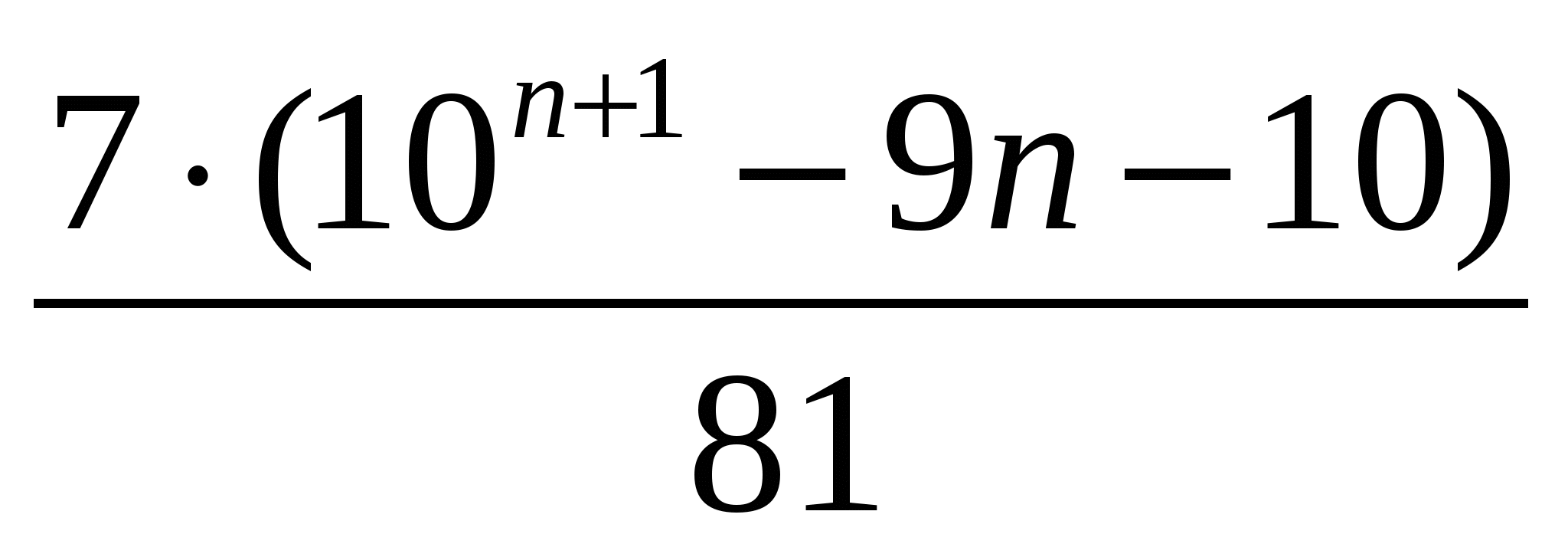 .
.
№10 есеп.
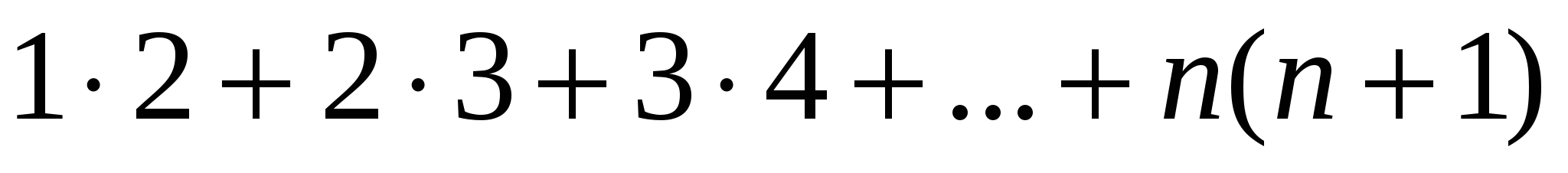 қосындысын табу керек.
қосындысын табу керек.
Шешуі: 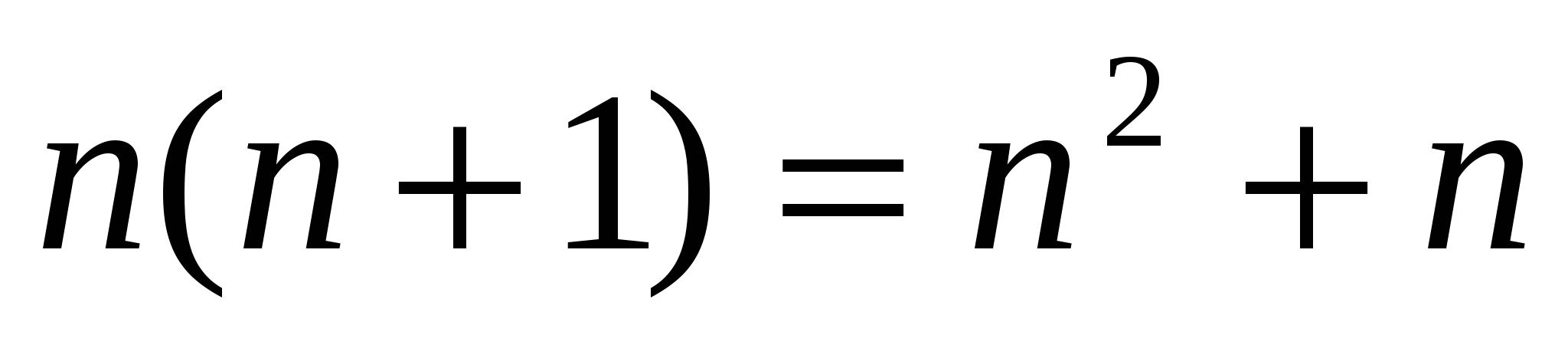 .
.
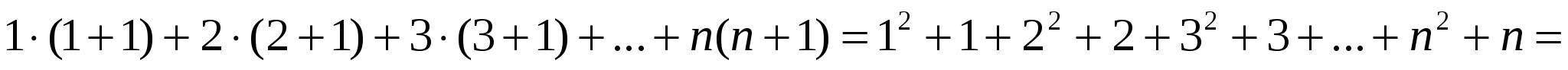
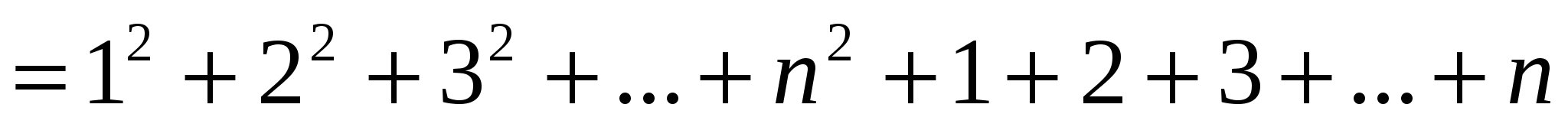 , мұнда
, мұнда
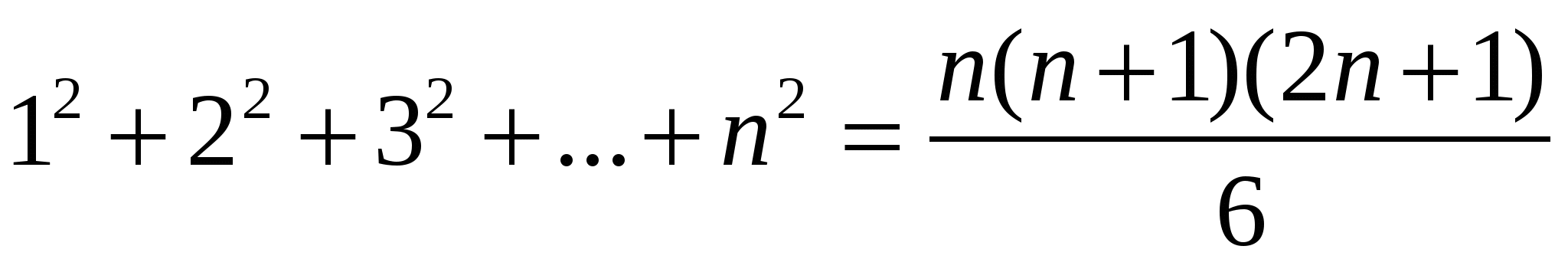 тепе-теңдігі математикалық индукция әдісімен дәлелденген (68 бет 2-мысал), ал
тепе-теңдігі математикалық индукция әдісімен дәлелденген (68 бет 2-мысал), ал 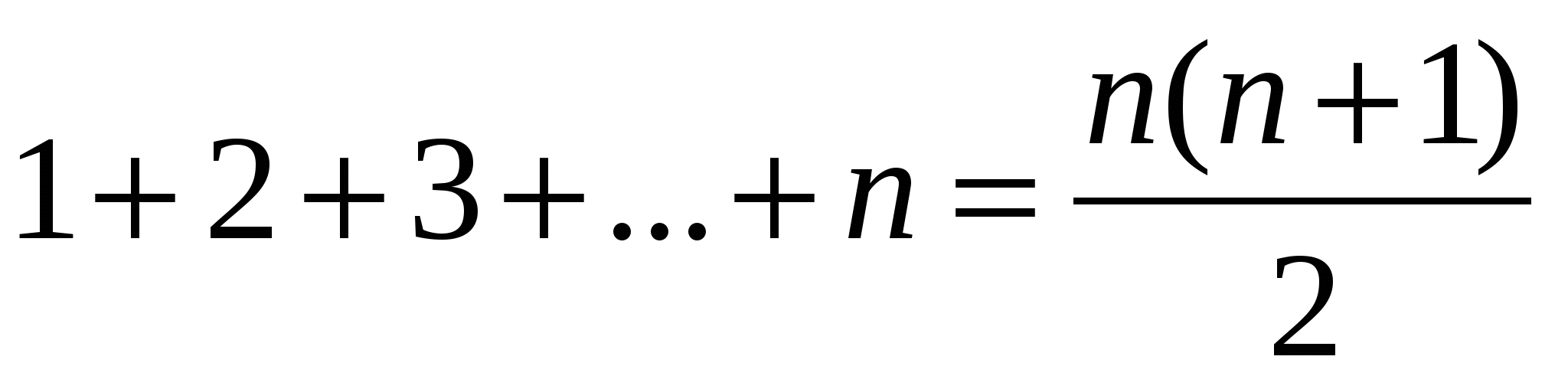 .
.
Сонда
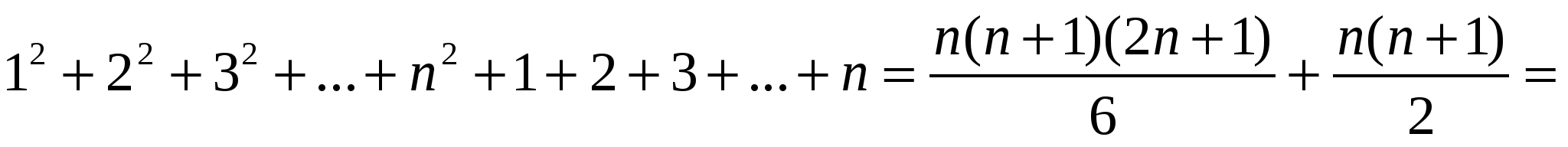
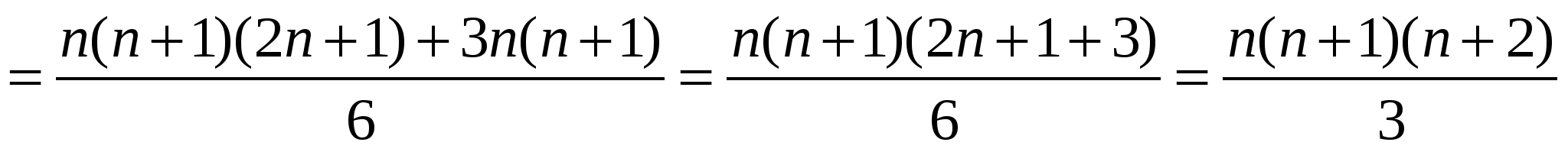 .
.
Жауабы: 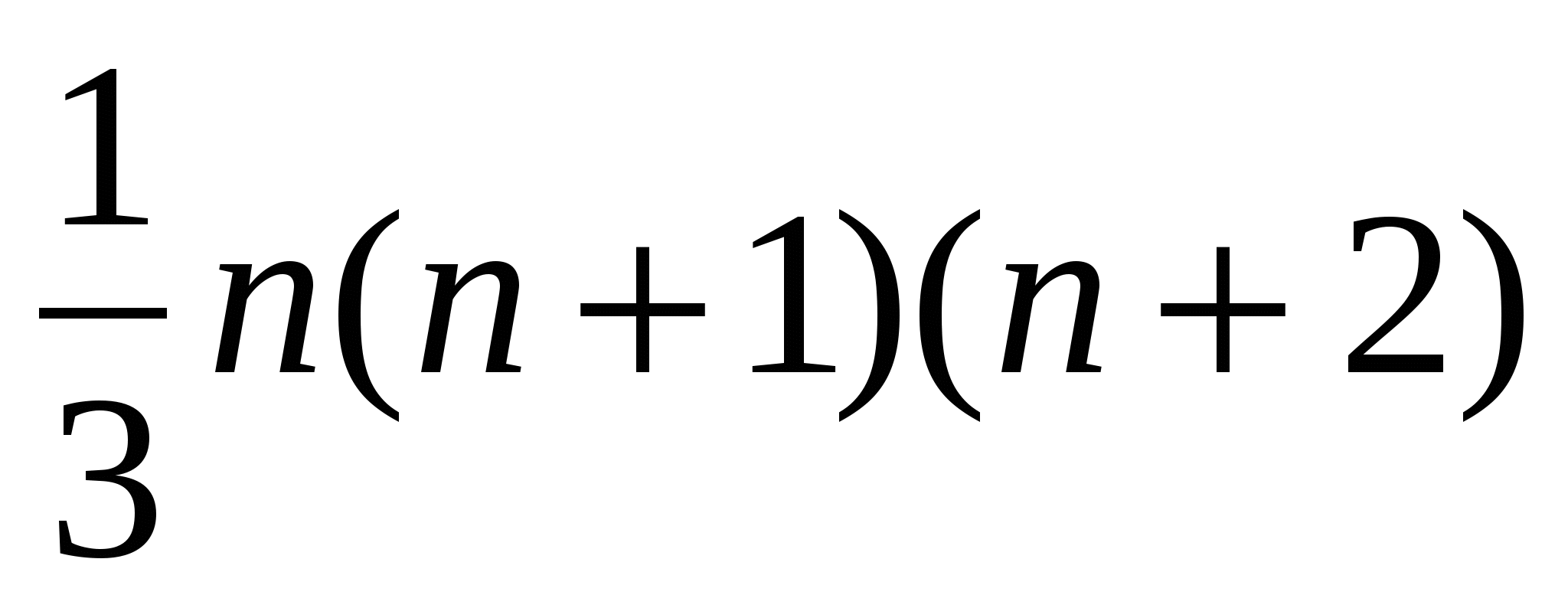 .
.
№11 есеп.
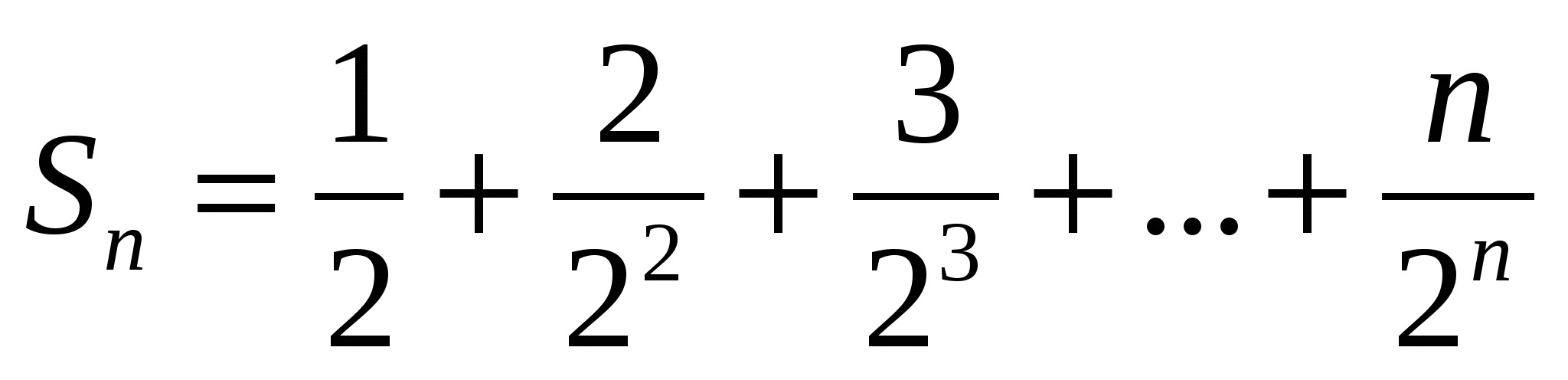 қосындысын табыңдар.
қосындысын табыңдар.
Шешуі:
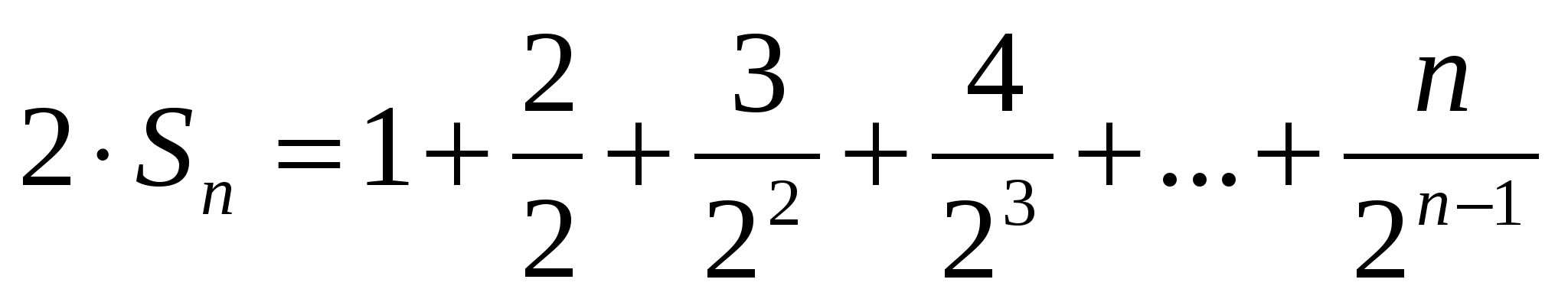
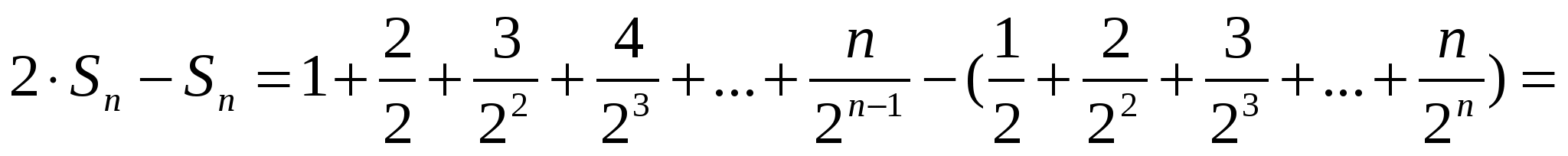
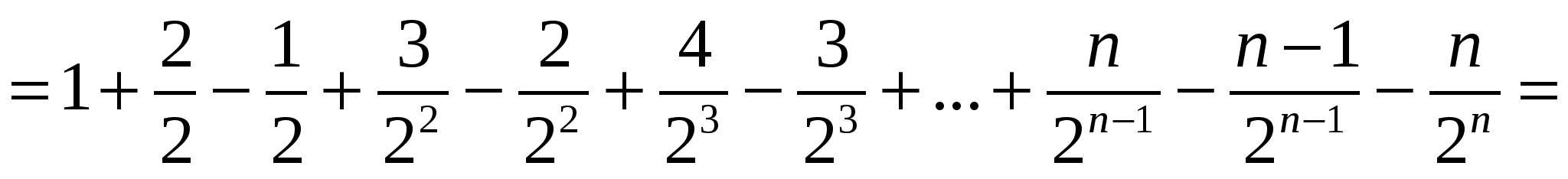
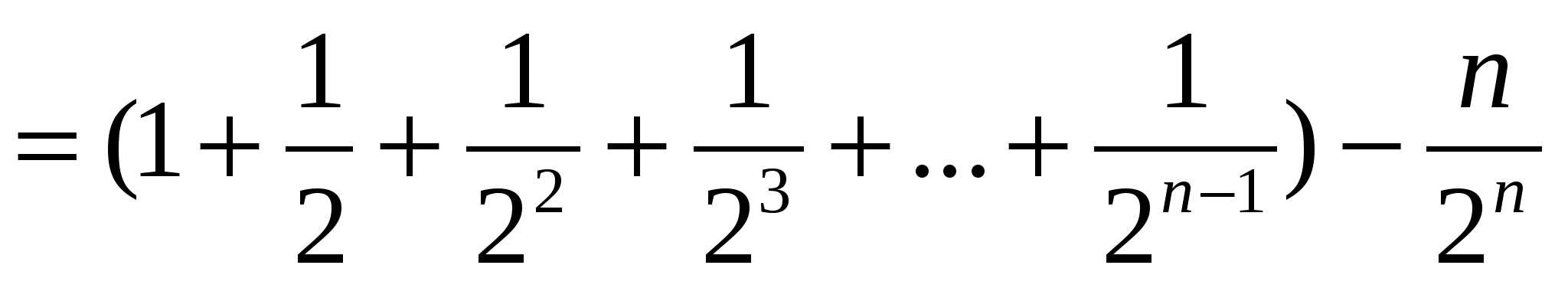
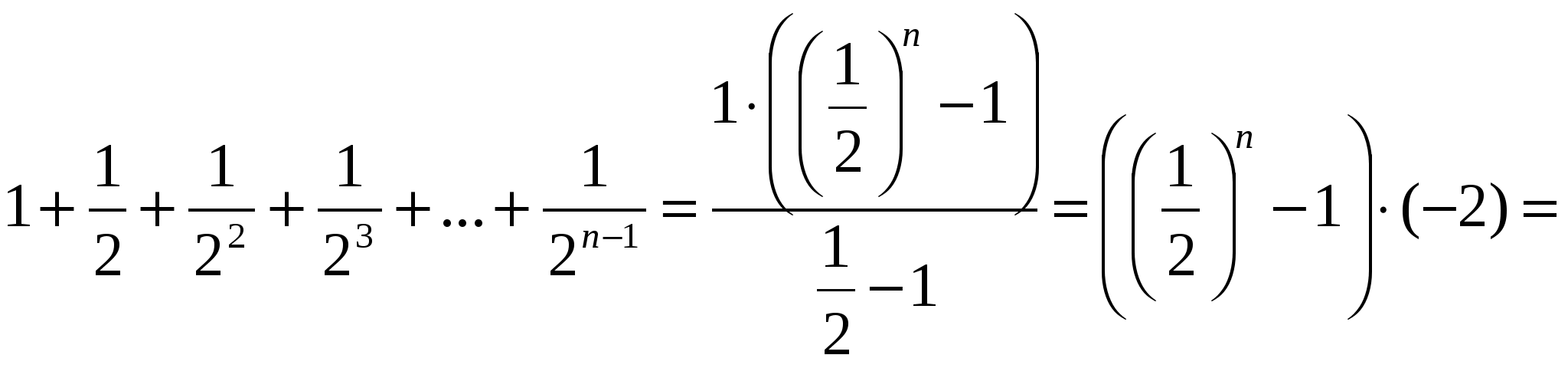
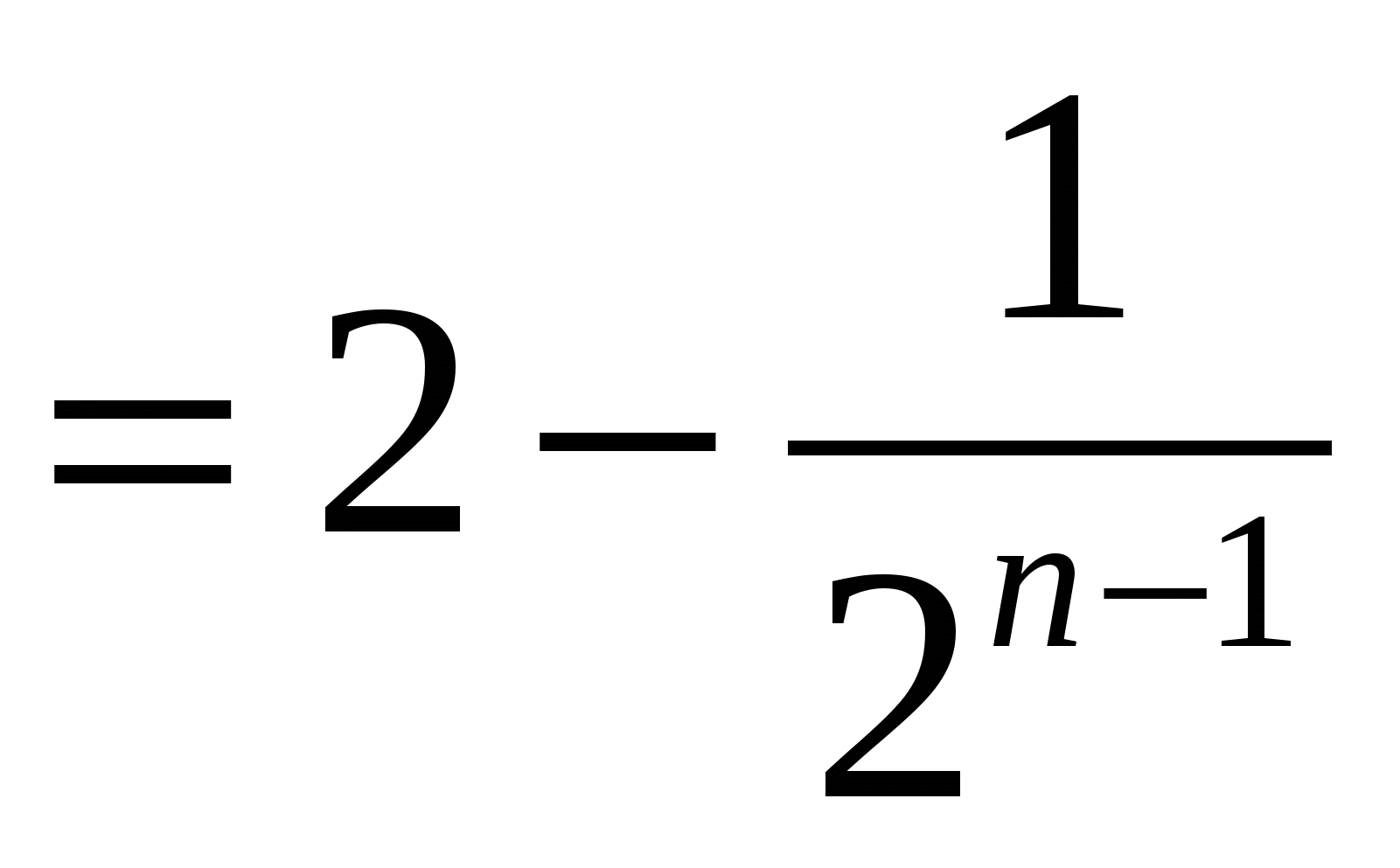 .
.
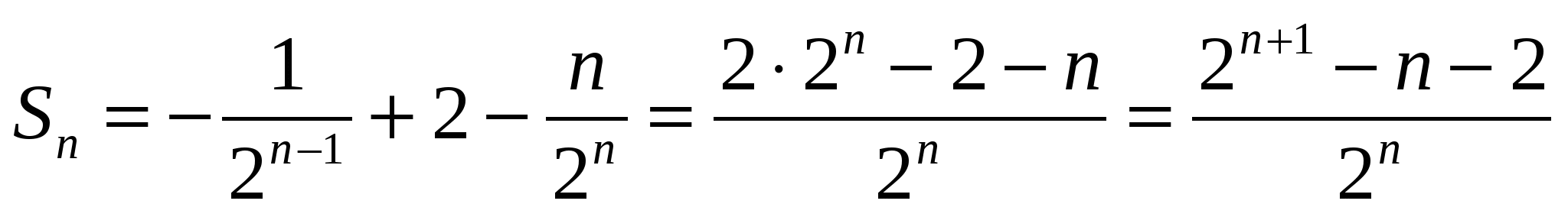
Жауабы: 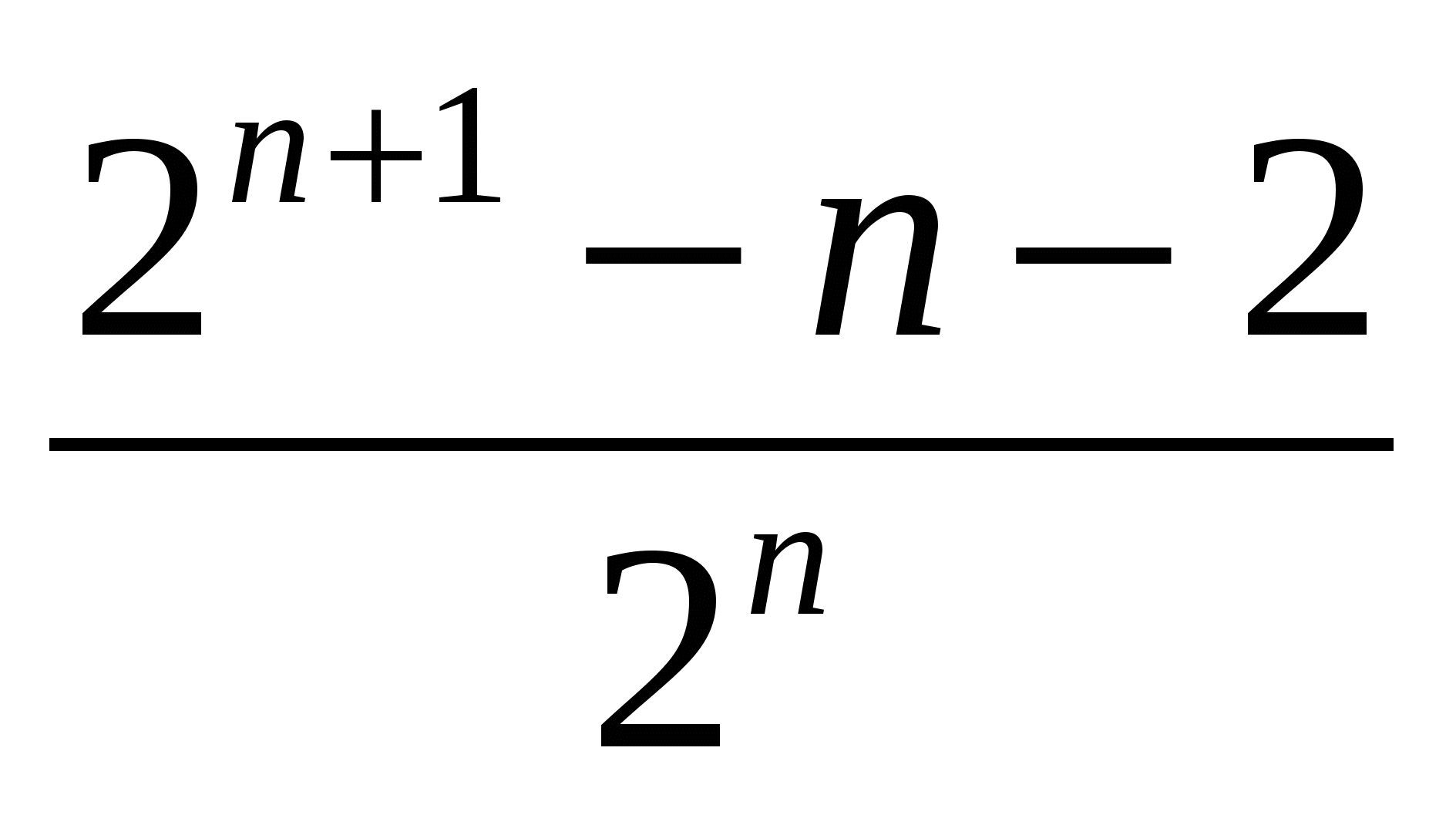 .
.
№19 есеп.
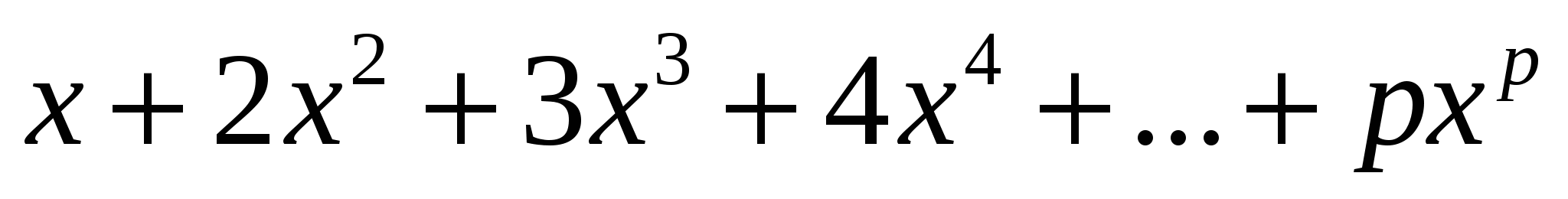 қосындысын есептеңдер,
қосындысын есептеңдер, 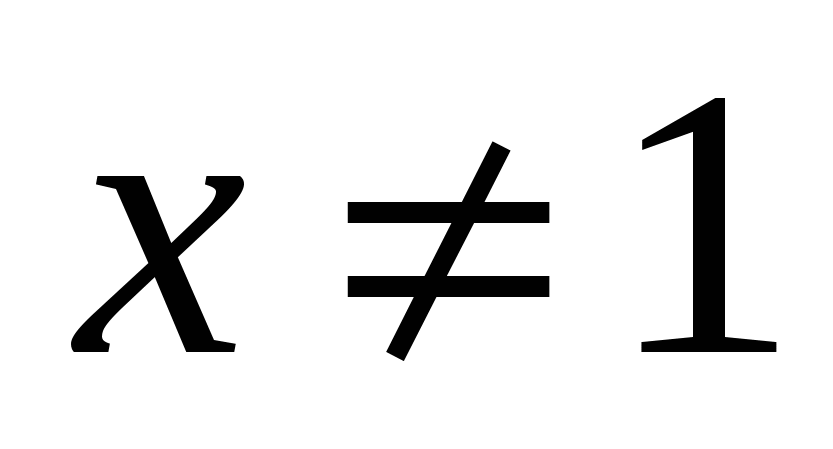 .
.
Шешуі:
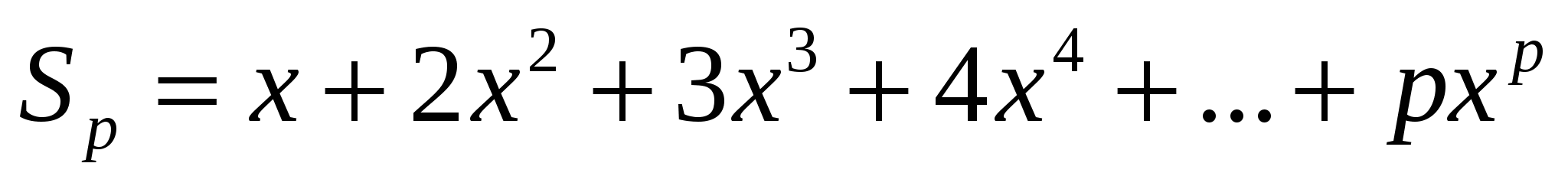
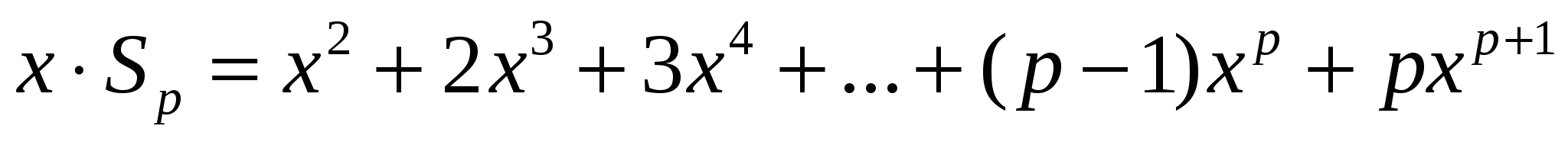
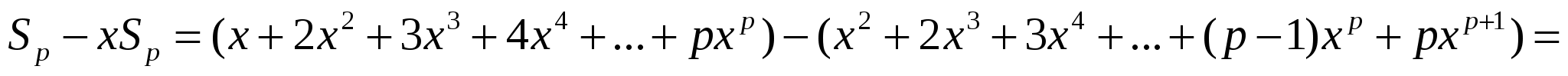
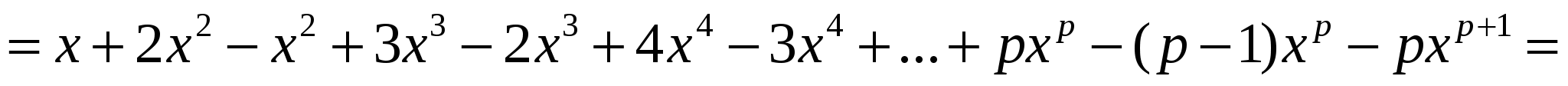
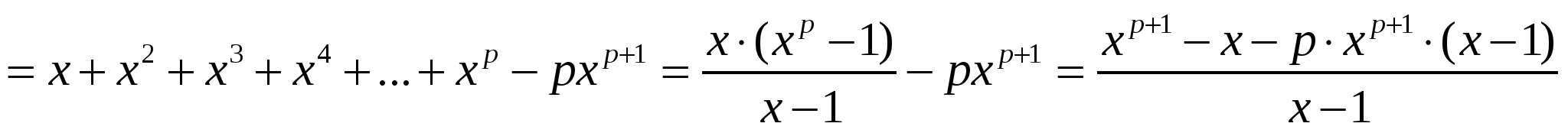
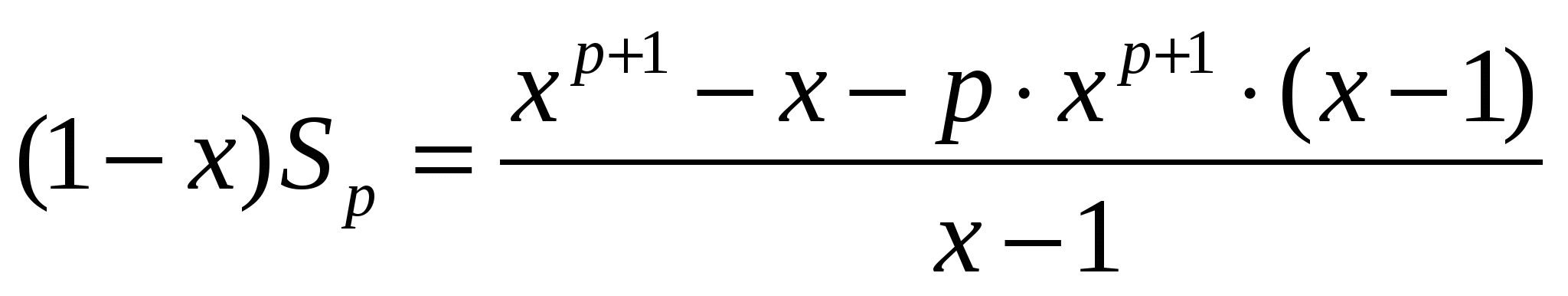
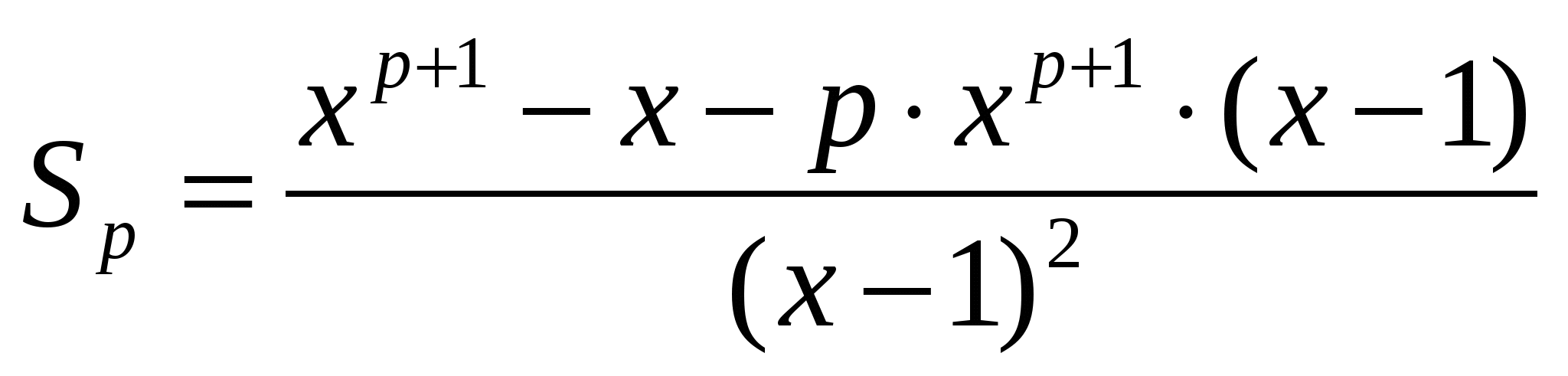 .
.
Жауабы: ![]() .
.
Аудандық олимпиадада берілген есептер:
9-сынып.
№1.Кез-келген n натурал саны үшін n(n2-1)(5n+2) өрнегінің 24-ке бөлінетіндігін дәлелдеңдер.
Дәлелдеуі: 5n+2=(5n+10)-8 теңдігін ескеріп өрнекті түрлендіріп жазайық:
n(n2-1)(5n+2)=5n(n2-1)(n+2)-8n(n2-1)= 5(n-1)n * (n+1)(n+2) -8 (n-1)n(n+1). (n-1)n(n+1)(n+2) өрнегі төрт тізбектес натурал санның көбейтіндісі болғандықтан , әрі 3-ке бөлінеді, әрі 8-ге бөлінеді. 8 бен 3 өзара жай сан болғандықтан бұл өрнек 24-ке бөлінеді.
8(n-1)n(n+1) өрнегі де 24-ке бөлінеді , себебі (n-1)n(n+1) көбейтіндісі 3-ке бөлінеді.
10-сынып.
№1. а мен в сандары х2-6х+1=0 теңдеуінің түбірлері.Кез-келген натурал саны үшін аn+вn өрнегінің бүтін сан болатындығын және 5-ке бөлінбейтіндігін дәлелдеңдер.
Дәлелдеуі:
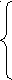 Математикалық индукция тәсілін қолданайық. Виет теоремасына сүйеніп жазайық:
Математикалық индукция тәсілін қолданайық. Виет теоремасына сүйеніп жазайық:
ав=1 Сонымен n=1 болғанда аn+вn өрнегі бүтін және 5-ке
а+в=6 бөлінбейді n=k болғанда
аk+вk өрнегі бүтін болып 5-ке бөлінбейтін болсын n=k+1 болғанда ak+1 +вk+1 өрнегінің бүтін болып және 5-ке бөлінбейтінін дәлелдейік.
(ak+вk)(а+в) = ak+1+авk+ ваk+ в k+1= (ak+1+вk+1 )+ав (вk-1+ ak-1)
Осыдан мынадай өрнекке келеміз.
ak+1+вk+1=(ak+вk)(а+в)- ав (вk-1+ ak-1)
Индукция болжамы бойынша ak+вk єZ; вk-1+ ak-1є z және ав=1 , а+в =6. Олай болса , ak+1 +вk+1 өрнегі бүтін және 5-ке бөлінбейді. Онда математикалық индукция принципі бойынша аn+вn өрнегінде кез-келген n натурал саны үшін бүтін болады және 5-ке бөлінбейді.
Республикалық олимпиада есептері:
9-сынып.
№1.(1+√2)1981 санының а+ в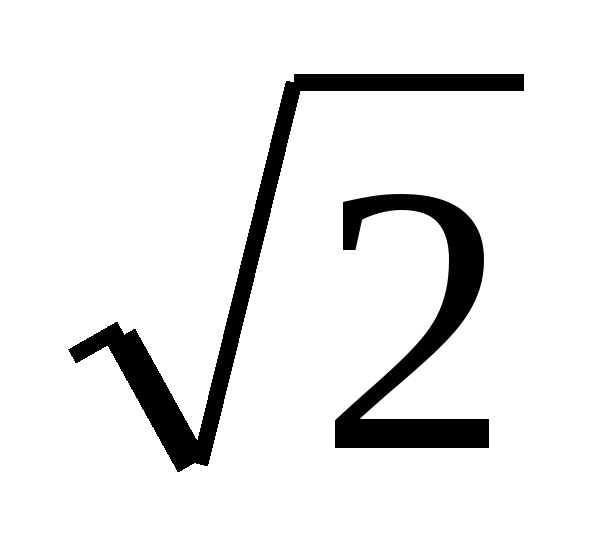 түрінде өрнектелетінін дәлелдеңдер, мұндағы a мен в өзара жай сандар
түрінде өрнектелетінін дәлелдеңдер, мұндағы a мен в өзара жай сандар
Шешуі: Индукция бойынша дәлелдейміз. Айталық, (1+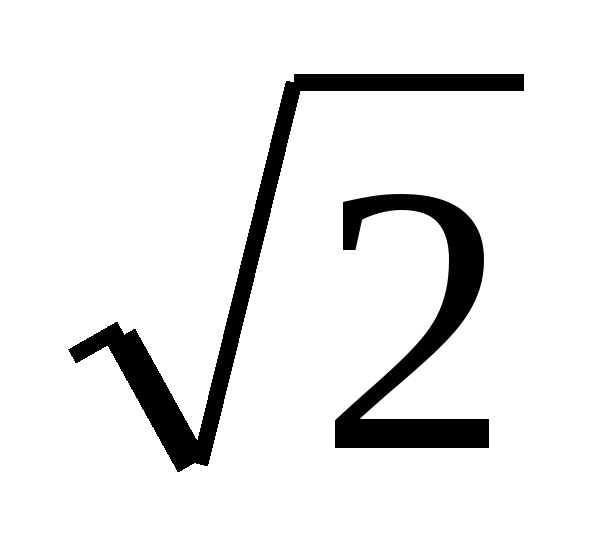 )n=a+в
)n=a+в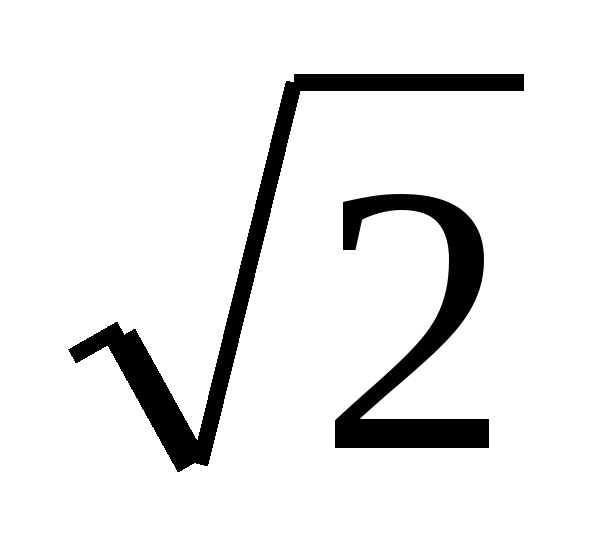
мұндағы а және в - өзара жай сандар. n=1 бұл тура болсын. Сонда (1+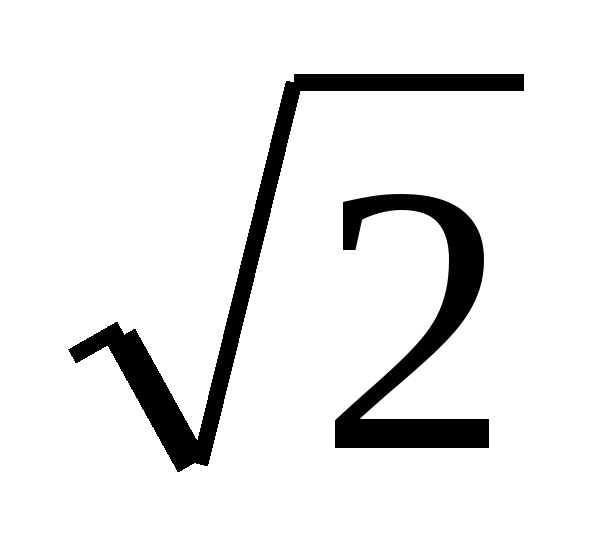 )n+1= (a+в
)n+1= (a+в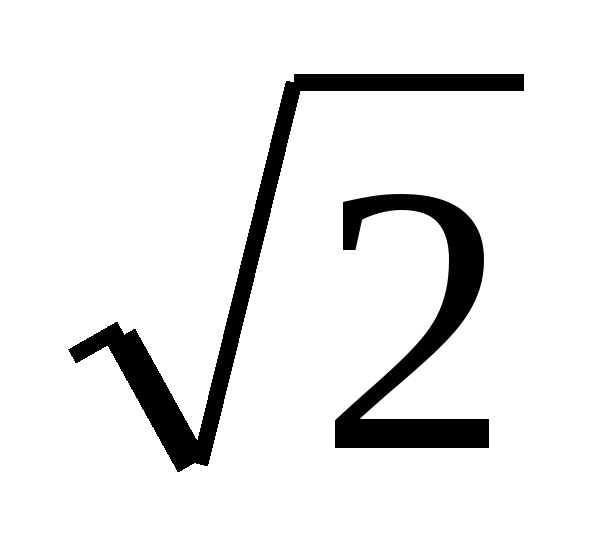 ) ∙(1+
) ∙(1+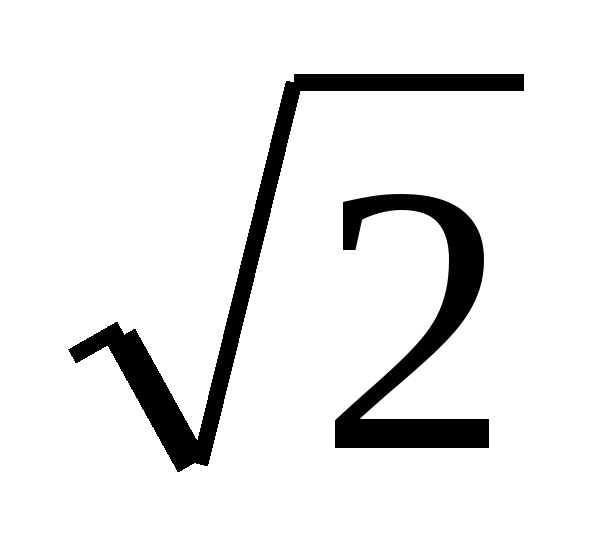 )= (a+2в)+(а+в)
)= (a+2в)+(а+в) 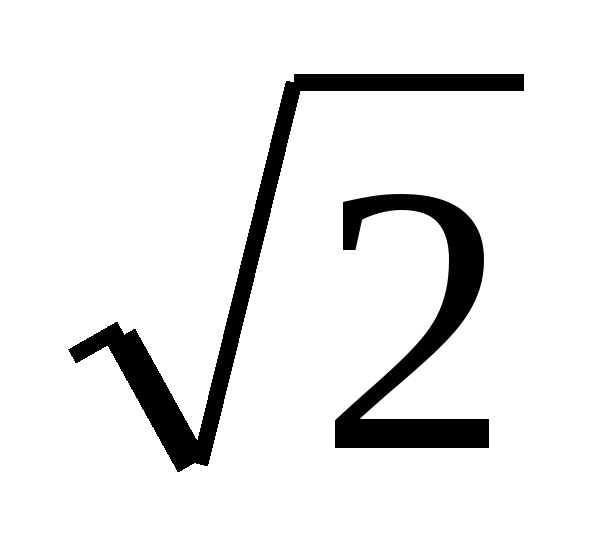
а+2в=а1және а+в=в1 сандары өзара жай, өйткені олай болмаса а=2 в1- а1 , в=а1-в1 сандарының да ортақ d>1 бөлгіші бар болар еді. Сонымен, есеп қортындысы кез-келген натурал n үшін тура , демек n=1981 үшін де тура.
№2.Екі бала мынандай ойын ойнайды. Бастаушы бірінші жүрісімен берілген n≥2 тастан тұратын үймені өзінің қалауынша 2 немесе 3 үймеге бөледі. Ары қарай кезектесіп жүреді және әрқайсысы өз жүріс кезеңінде кез-келген үймені таңдап алып, өз қалауынша оны 2 немесе 3 үймеге бөледі. Соңғы мүмкін жүрісті жасаған бала ұтады. Дұрыс ойнаса кім ұтады.
Шешуі:Дұрыс ойнаса әрқашанда бастаушы ұтады. Ол үшін ұту стратегиясын көрсетейік. Екі жағдайды қарастырамыз.
1)n- жұп сан. Бірінші жүрісімен бастаушы тастарды тең 2 үймеге бөледі. Сонан соң өз кезегінде қарсыласының жүрісіне симметриялы жүріс жасап отырады.
2)n=2m+1-тақ сан. Бірінші жүрісімен бастаушы тастарының саны m, m және 1 болатын үш үймеге бөледі. Бір тастан тұратын үймені қарастырмасақ та болады. Әры қарай «Симметриялық» әдісті қолданады.
Халықаралық олимпиада есептері:
11-сынып.
№1. Кез-келген n натурал сан үшін теңдеуді шешіңіздер: cosnx-sinnx=1
Шешуі: Үш жағдай қарастырамыз:
1)n жұп болсын, яғни n=2m.Онда cos2mx=1+sin2mx , cos2mx≤1≤1+sin2mx болғандықтан sinx=0 және cosx=±1, яғни x=kπ , kєZ.
2) n-тақ , яғни n=2m+1(m≥1). Онда cos2m+1x-sin2m+1x=1.Бұл жағдайда теңдеудің шешімі мынадай түрде жазылады: x=2kπ, не x=2 kπ-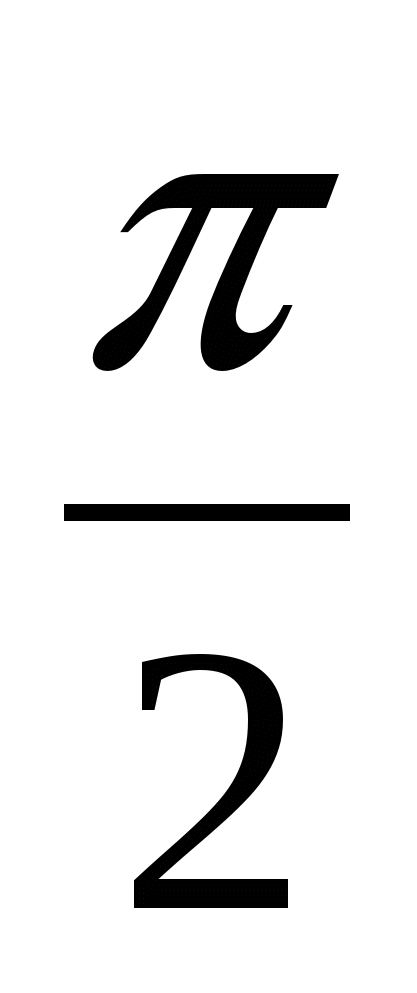 ,kєZ
,kєZ
3) n=1. Бұл жағдайда теңдеу cosx-sinx=1түрінде жазылады, немесе cos(x+![]() )=
)=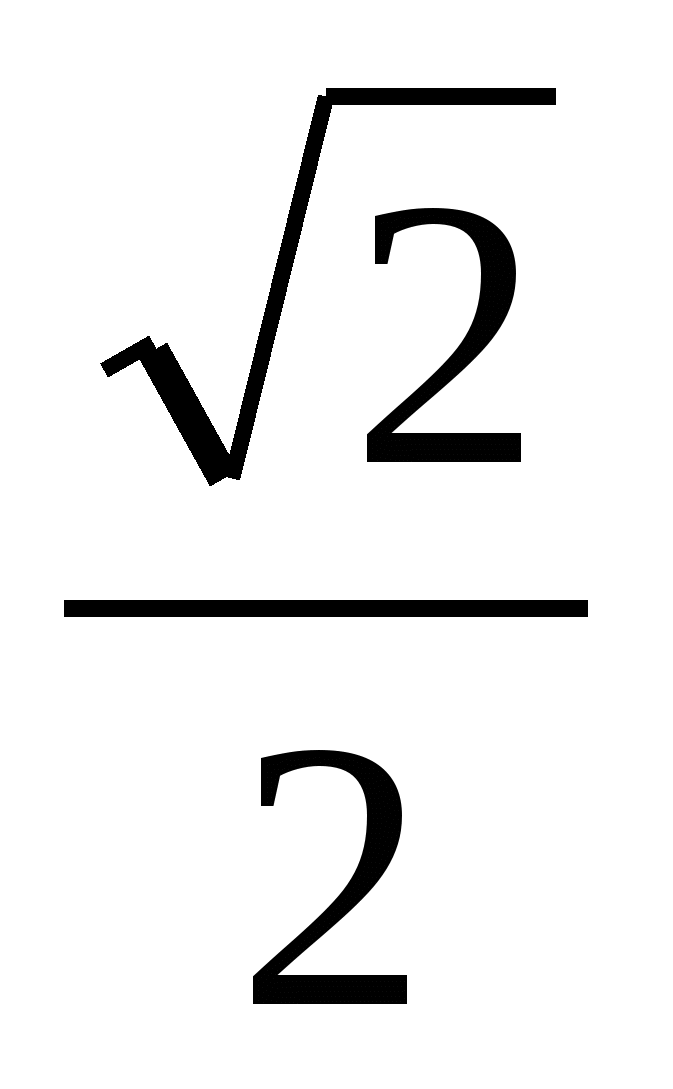 . Бұл жағдайдағы шешім екінші жағдайдағымен бірдей болады.
. Бұл жағдайдағы шешім екінші жағдайдағымен бірдей болады.
Теңсіздіктерді дәлелдеу.
І. Қарапайым теңсіздіктерді дәлелдеу
Мектеп көлемінде қарапайым теңсіздіктер дәлелденеді, сол теңсіздіктер арқылы күрделі теңсіздіктерде дәлелденеді.
№1 а2 + b2 ≥ 2ab.
Дәлелдеуі:
a2+ b2 - 2аb = (а - b)2 ≥ 0.
№2
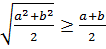 кез келген a және b үшін.
кез келген a және b үшін.
Дәлелдеуі:
Берілген теңсіздіктен 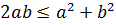 , біз мына теңсіздікті аламыз
, біз мына теңсіздікті аламыз 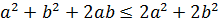 бұдан
бұдан 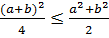 немесе
немесе 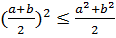 соны мына түрде жазамыз
соны мына түрде жазамыз 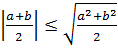 бұдан
бұдан 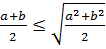
II. Штурм әдісін қолданып теңсіздікті дәлелдеу
Бұл әдісті неміс математигі Р.Штурм ұсынған. Бұл әдістің көмегімен бірнеше теңсіздікті дәлелдейік:
№3 Егер 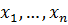 қосындысы 1-ге тең болса, онда
қосындысы 1-ге тең болса, онда 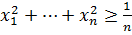 дәлелдеу керек
дәлелдеу керек
Дәлелдеуі:
Егер 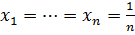 онда
онда 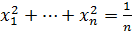 .
.
Қаралатын сандардың ішінде ең болмағанда екі сан бір-біріне тең болмаса, онда сандардың ішінен екі сан табылады, сонын біреуі  - нан үлкен болады, ал екіншісі
- нан үлкен болады, ал екіншісі  кіші болады. Осы сандар
кіші болады. Осы сандар 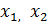 болсын, және де
болсын, және де ![]()
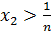 болсын, онда
болсын, онда 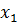 - ді
- ді 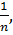
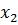 -ні
-ні 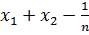 - мен алмастырып, мынандай теңсіздік аламыз
- мен алмастырып, мынандай теңсіздік аламыз 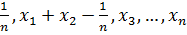 және олардың қосындысы 1-ге тең.
және олардың қосындысы 1-ге тең.
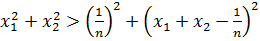 болғандықтан, осыдан
болғандықтан, осыдан
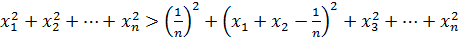 .
.
Осы амалды бірнеше рет қайталап, шыққан тізбектің кез келген мүшесі ![]() -ге тең, ал олардың квадраттарының қосындысы берілген
-ге тең, ал олардың квадраттарының қосындысы берілген 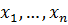 сандардың квадраттарының қосындысынан кіші болады.
сандардың квадраттарының қосындысынан кіші болады.
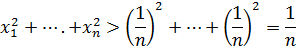
III. Арифметикалық, геометриялық, квадраттық, гармониялық орталардың ара қатынасын қолдану әдісі
Кейбір теңсіздіктерді дәлелдегенде, оң a және b сандары үшін арифметикалық, геометриялық, квадраттық, гармониялық орталардың ара қатынасын қолданады: 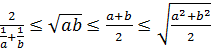 .
.
Мына өрнекте 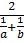 гармониялық орта,
гармониялық орта,
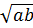 - геометриялық орта,
- геометриялық орта,
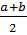 - арифметикалық орта,
- арифметикалық орта,
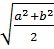 - квадраттық орта.
- квадраттық орта.
Бұл теңсіздікті дәлелдеу әдісі күрделі теңсіздіктерді дәлелдеуде көп қолданылады.
№4 теңсіздікті дәлелде 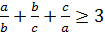 , мұндағы
, мұндағы 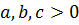
Дәлелдеуі: егер 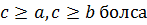 , онда
, онда 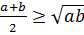 - ны қолданып,
- ны қолданып,
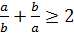 -ны (1) аламыз және
-ны (1) аламыз және 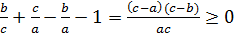 осыдан
осыдан 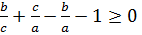 (2)
(2)
(1) және (2) қосып 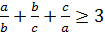 аламыз.
аламыз.
IV. Коши-Буняковский әдісін қолдану
Коши-Буняковский әдісін бірінші 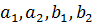 сандар үшін дәлелдейміз.
сандар үшін дәлелдейміз. 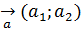 және
және 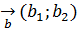 векторлары берілсін, мектеп көлемінде белгілі
векторлары берілсін, мектеп көлемінде белгілі 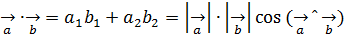
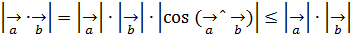
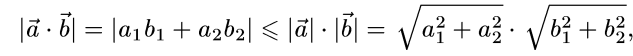
немесе
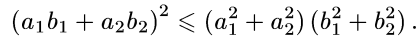
Бұл Коши-Буняковскийдің теңсіздігі 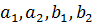 сандары үшін орындалатын дербес жағдайы болады.
сандары үшін орындалатын дербес жағдайы болады.
Коши-Буняковскийдің теңсіздігі 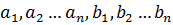 сандары үшін келесі жалпы түрде жазылады:
сандары үшін келесі жалпы түрде жазылады:
№5. Дәлелдеу керек :
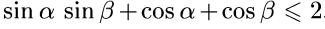
Дәлелдеуі:
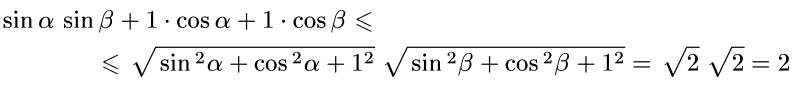
V. Жаңа айнымалы енгізу әдісі
Кейбір теңсіздіктерді дәлелдеу үшін жаңа айнымалы енгізу арқылы мақсатқа жетуге болады.
№6. Теңсіздікті дәлелде
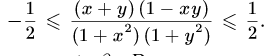
Дәлелдеуі:
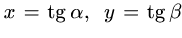
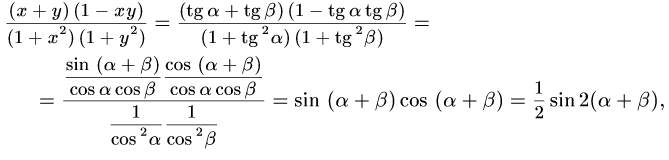
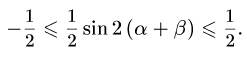
VI. Симметриялық және біртекті қасиеттерді қолдану
№7 Теңсіздікті дәлелде:
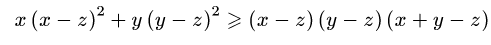
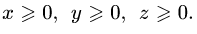
Дәлелдеуі:
Теңсіздікті түрлендіре отырып келесі түрге көшеміз
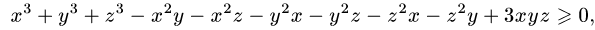
x, y, z айнымалы арқылы симметриялық теңсіздік аламыз, бұдан x y
y z
z 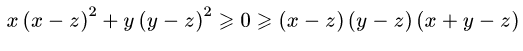
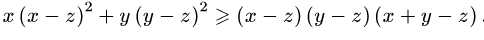
VII. Математикалық индукция тәсілін қолдану
Теңсіздіктерді дәлелдеуде математикалық индукция тәсілін қолдануға болады. Математикалық индукция принциптерін келесі берілген тұжырымдамада барлық натурал n сандары p-дан кіші емес үшін ақиқат, егер:
1) n=p үшін тұжырымдама ақиқат болса,
2) n=k(k p) тұжырымдама ақиқат деп, n=k+1 үшін тұжырымдама ақиқат екенін дәлелдеу керек.
p) тұжырымдама ақиқат деп, n=k+1 үшін тұжырымдама ақиқат екенін дәлелдеу керек.
№8. Дәлелдеу керек:
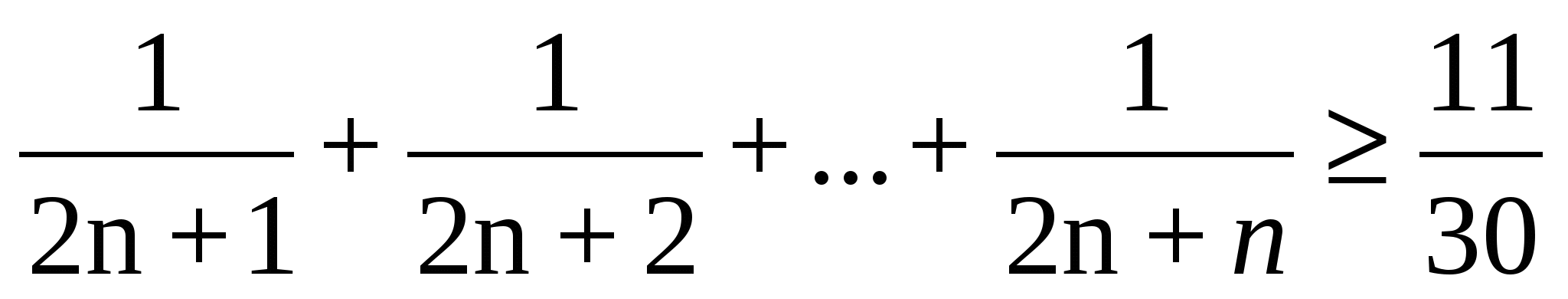 мұндағы n>1, n
мұндағы n>1, n N
N
Дәлелдеуі:
n=2 , 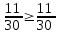 ақиқат
ақиқат
n=k тұжырымдама ақиқат деп алып
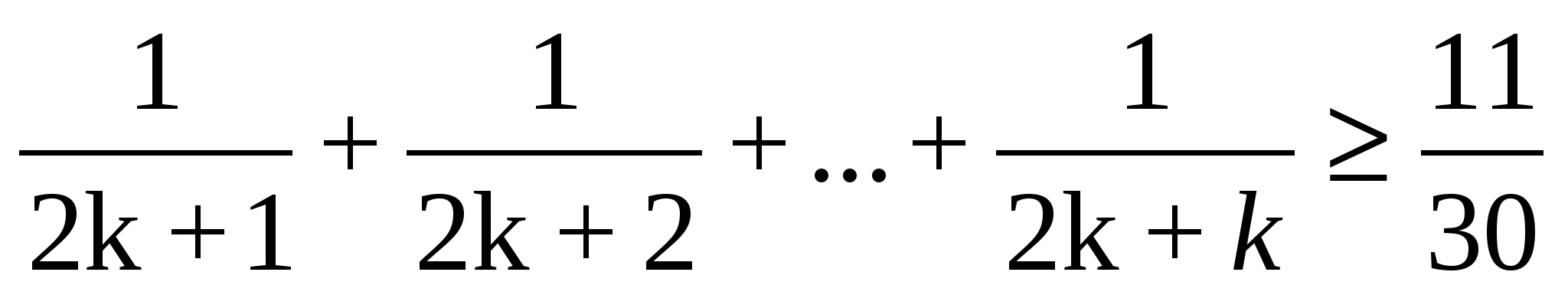
n=k+1 тұжырымдаманың ақиқат екенін дәлелдейміз
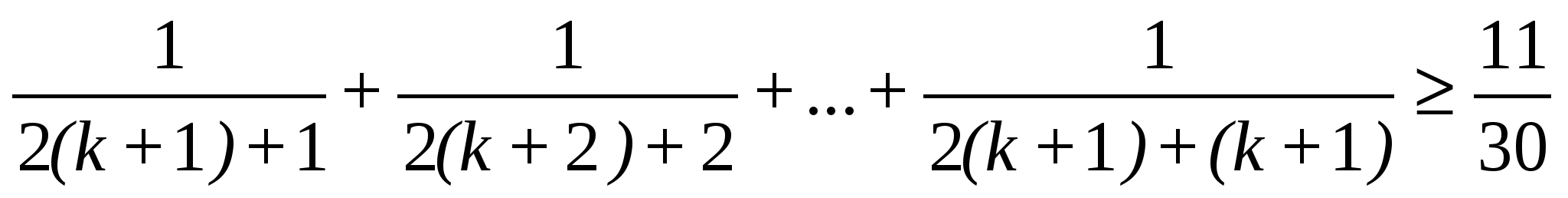
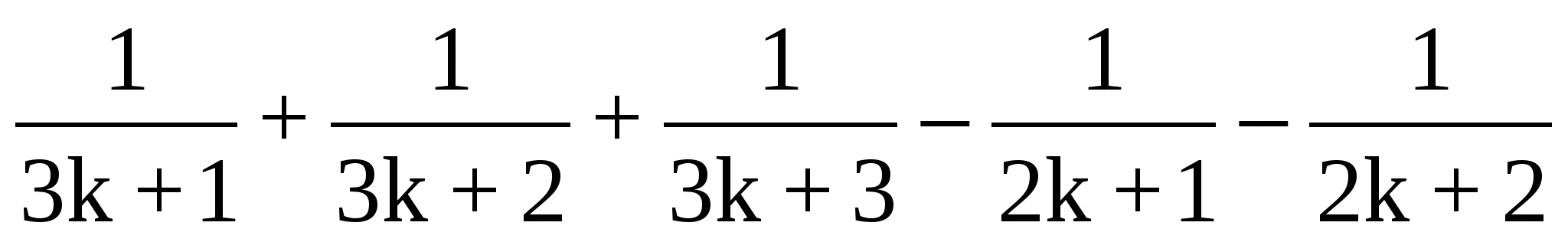
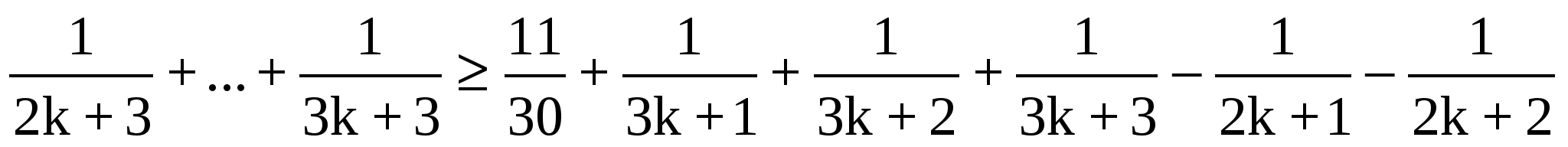
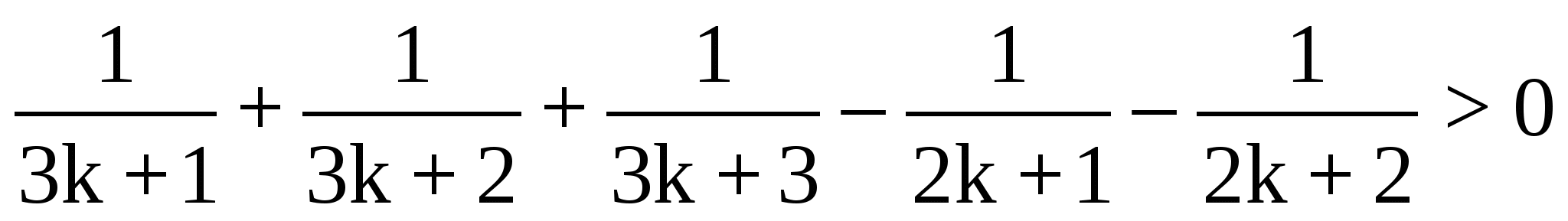
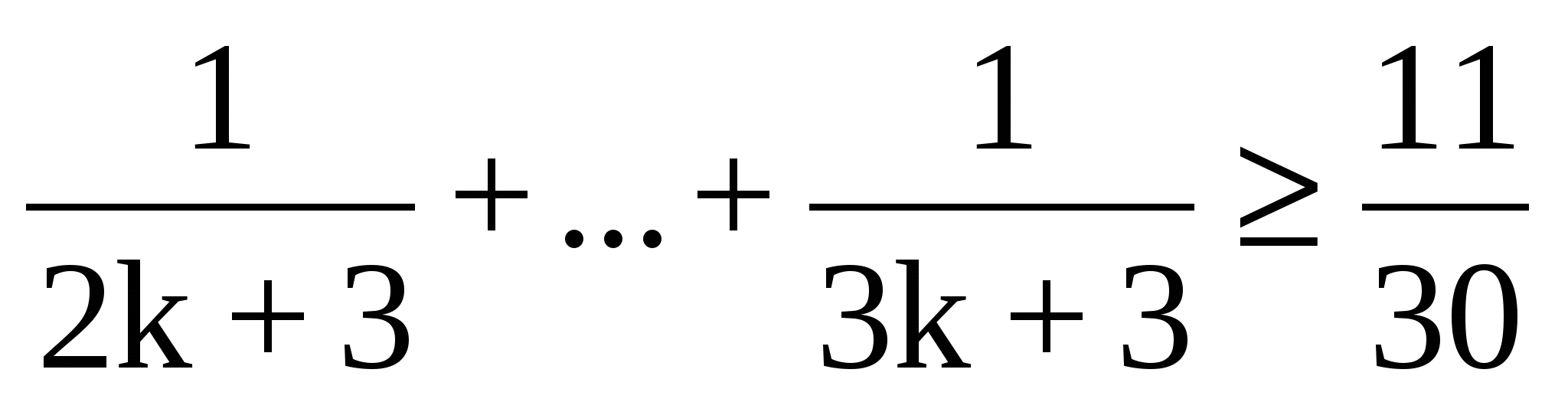
n(n>1)
VIII. Бір теңсіздікті бірнеше рет қолдану тәсілі
№9. Қос теңсіздікті дәлелдеу керек:
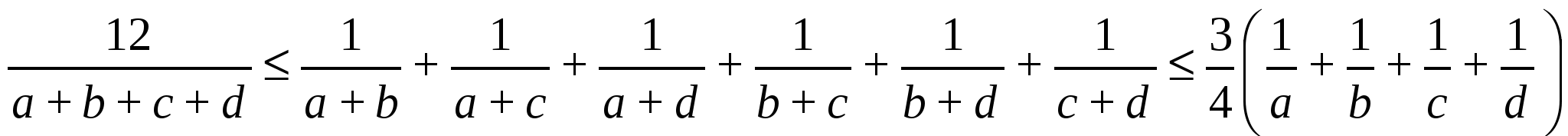 ,
,
a>0, b>0, c>0, d>0.
Дәлелдеуі:
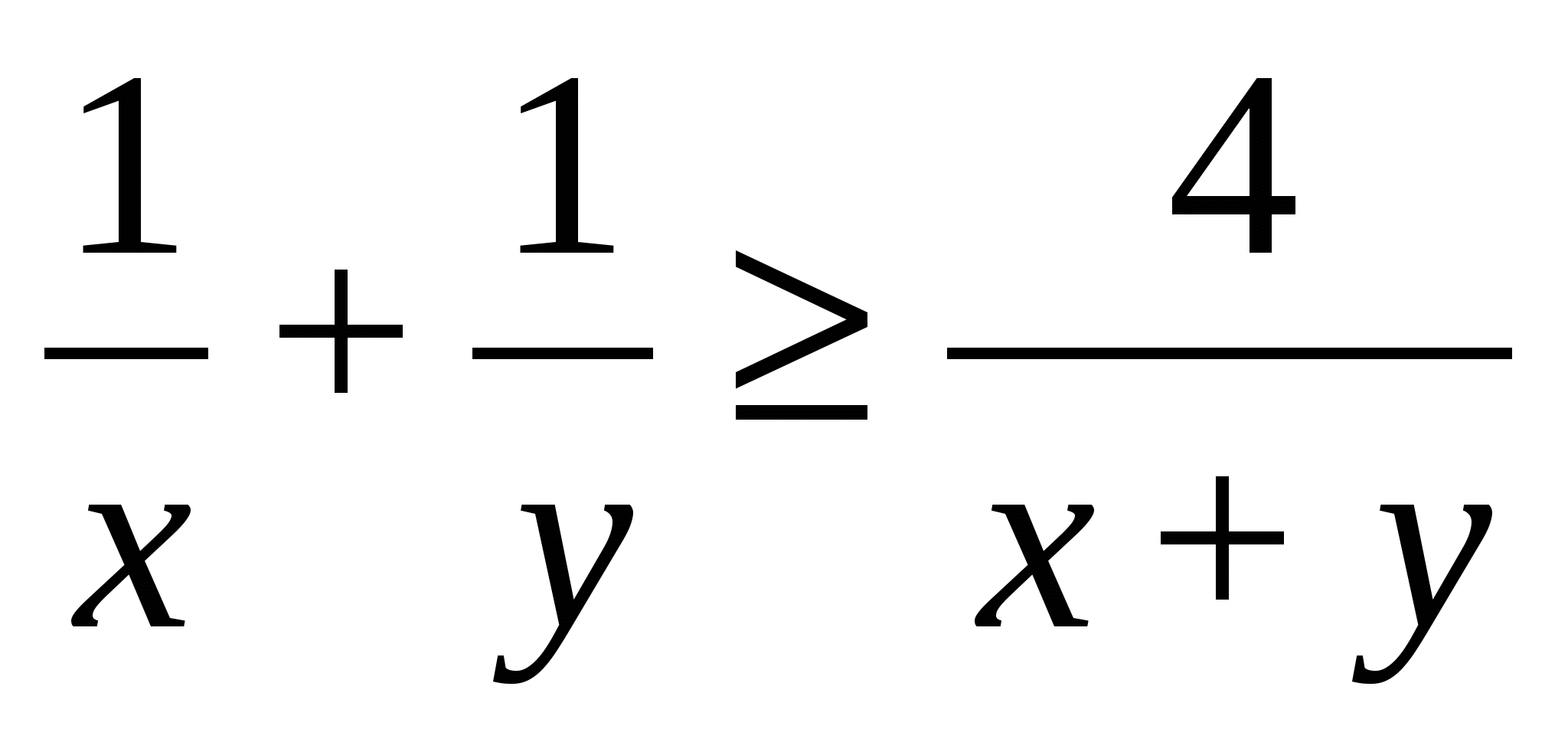
x>0, y>0
осы теңсіздікті бірнеше рет қолданып дәлелдейміз
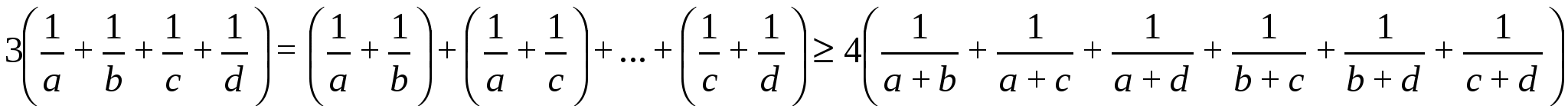
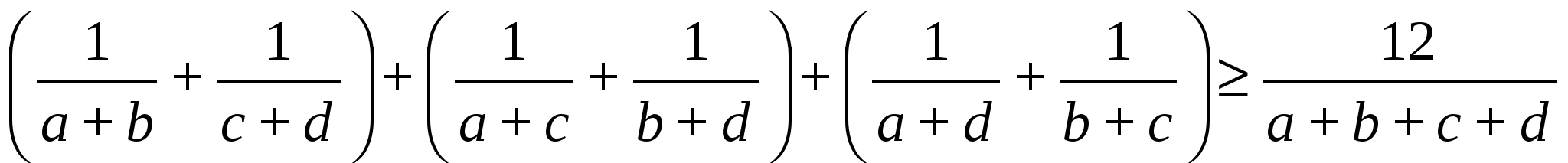
IX. Туынды мен интегралды қолданып дәлелдеу тәсілі
Егер функция f(x) және g(x) І аралығында анықталса, және үздіксіз болса, онда, f(x) g(x) теңсіздігін [a,b]=I немесе [a, +∞)=I аралығында дәлелдеу үшін, келесі теореманы қолдануға болады:
g(x) теңсіздігін [a,b]=I немесе [a, +∞)=I аралығында дәлелдеу үшін, келесі теореманы қолдануға болады:
Теорема: Егер f(x) және g(x) І аралығында дифференциалданса,
f(a) g(a) осы аралықта және h'(x)
g(a) осы аралықта және h'(x)  0, мұндағы h(x)= f(x) - g(x), онда
0, мұндағы h(x)= f(x) - g(x), онда
f(x) g(x) теңсіздігі осы аралықта орындалады.
g(x) теңсіздігі осы аралықта орындалады.
№1. 2x+1>x+2, x 1 теңсіздікті дәлелде.
1 теңсіздікті дәлелде.
Дәлелдеуі: функция h(x)=2x+1-x-2 [1,+∞) аралығындағы функцияны қарастырамыз.
h(1)=1 және h/(x)=2x+1ln2-1 функциясы y=2x [1, +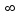 ) аралығында өспелі болады, ендеше h/(x)
) аралығында өспелі болады, ендеше h/(x)  4ln2-1>0 бұдан x
4ln2-1>0 бұдан x 1, h(x)
1, h(x) h(1) болса немесе
h(1) болса немесе
2x+1 x+3,
x+3,
2x+1>x+2 онда орындалады.
Мектепішілік олимпиада
№1.Теңсіздікті дәлелдеңдер.
(a+в+c)(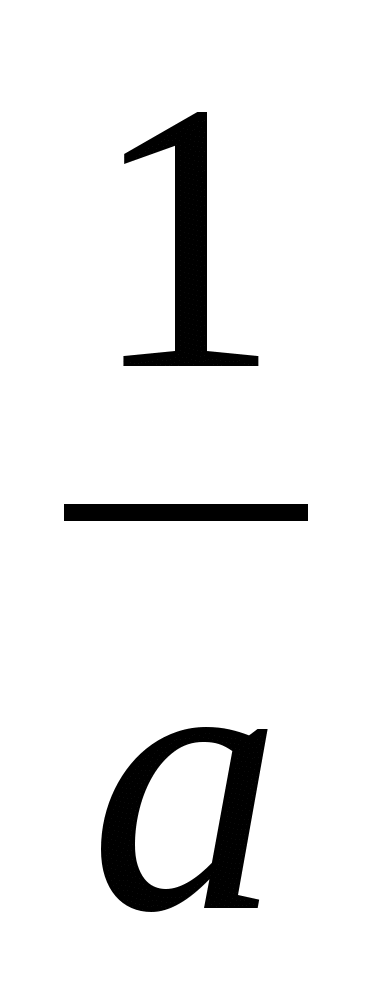 +
+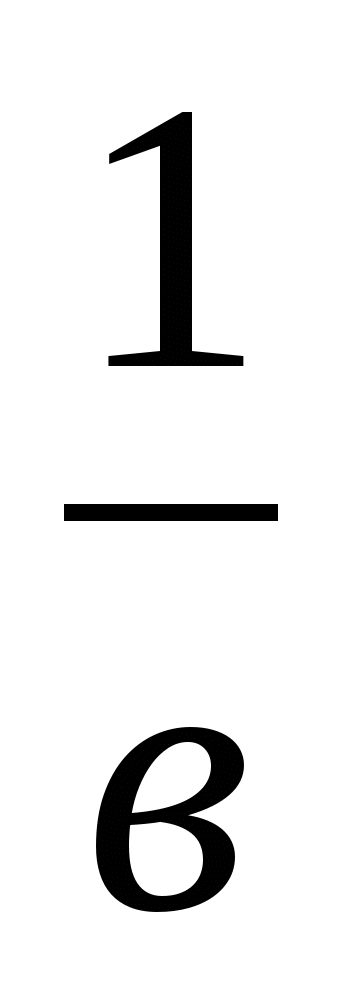 +
+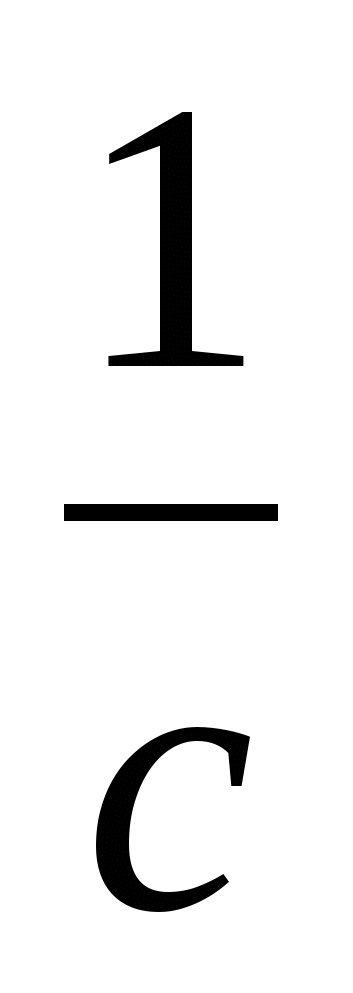 )≥9 (мұндағы а>0, в>0,с>0)
)≥9 (мұндағы а>0, в>0,с>0)
Теңсіздіктің сол бөлігін түрлендірейік:
(a+в+c)(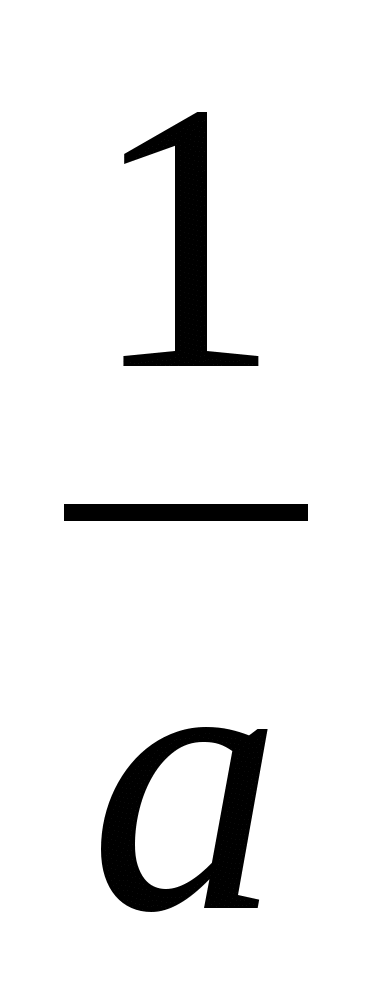 +
+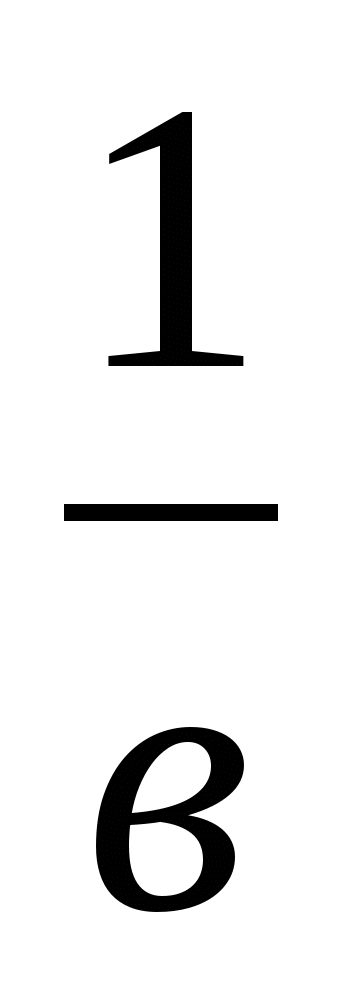 +
+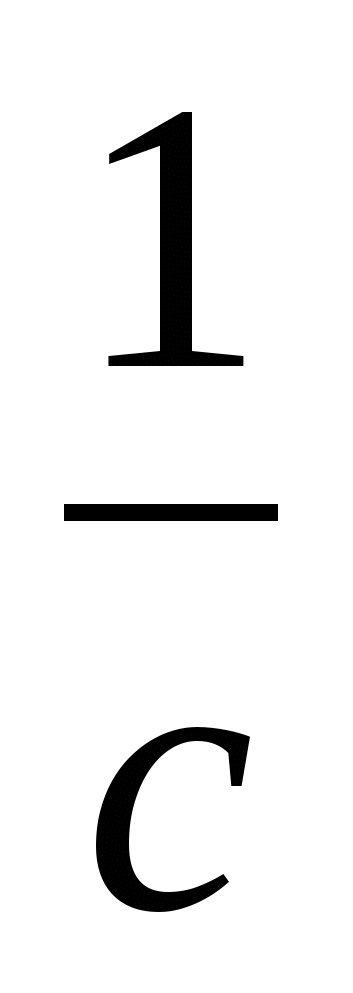 )=1+
)=1+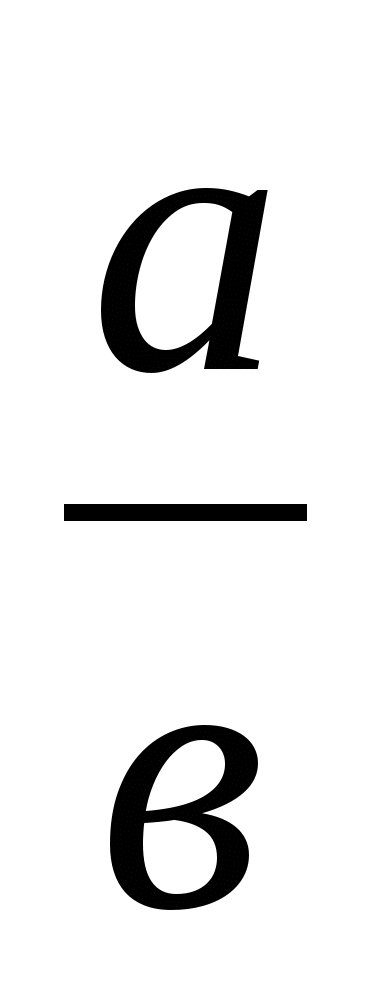 +
+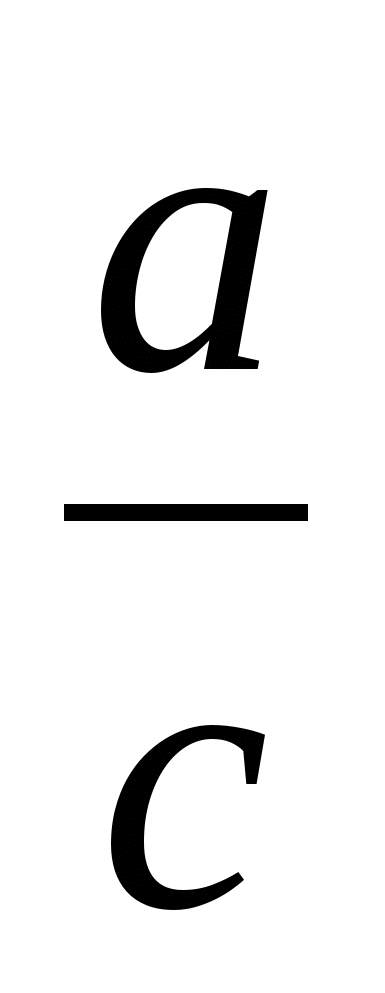 +1+
+1+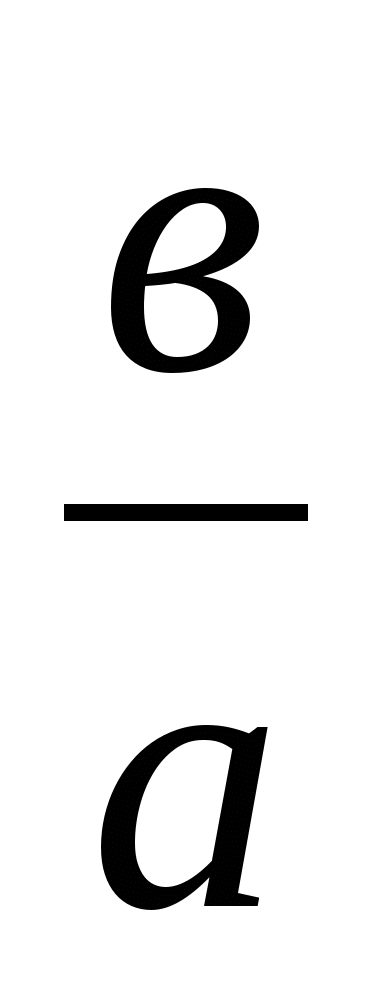 +
+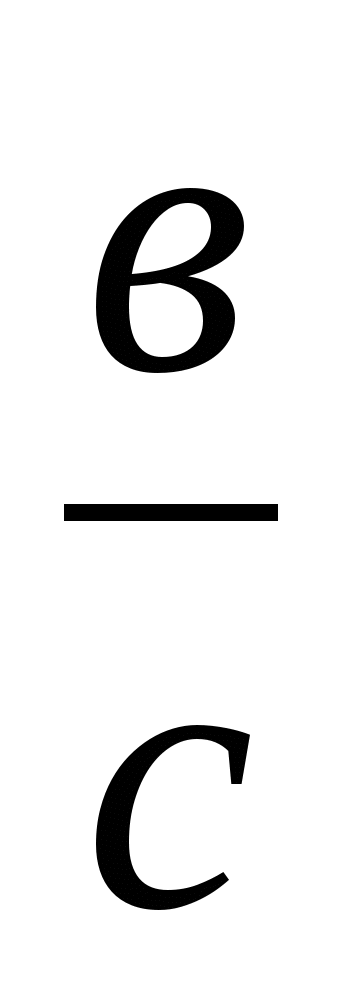 +
+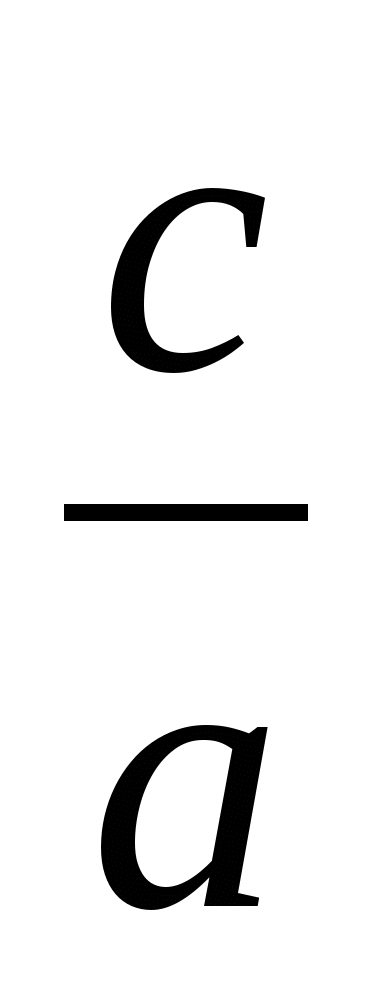 +
+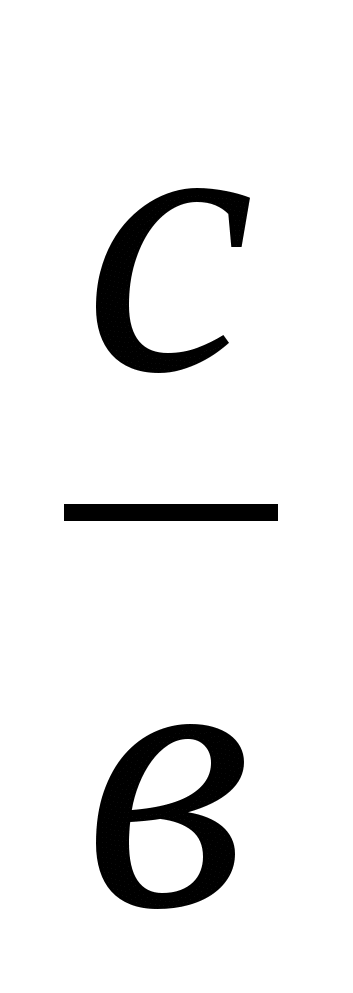 +1=3(
+1=3(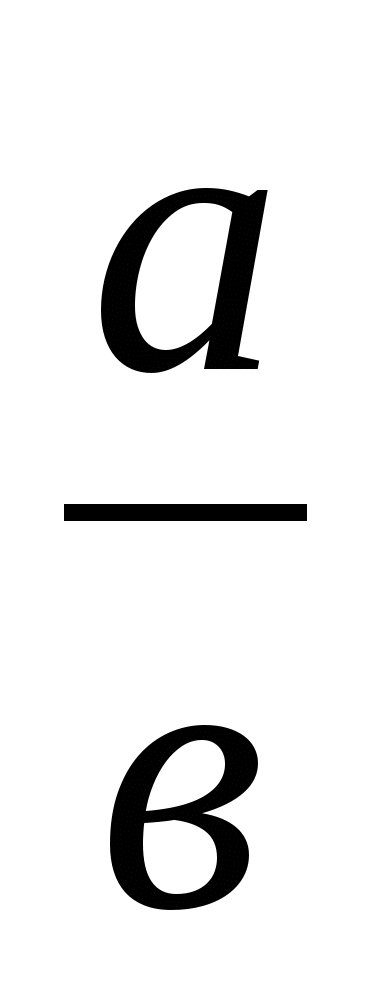 +
+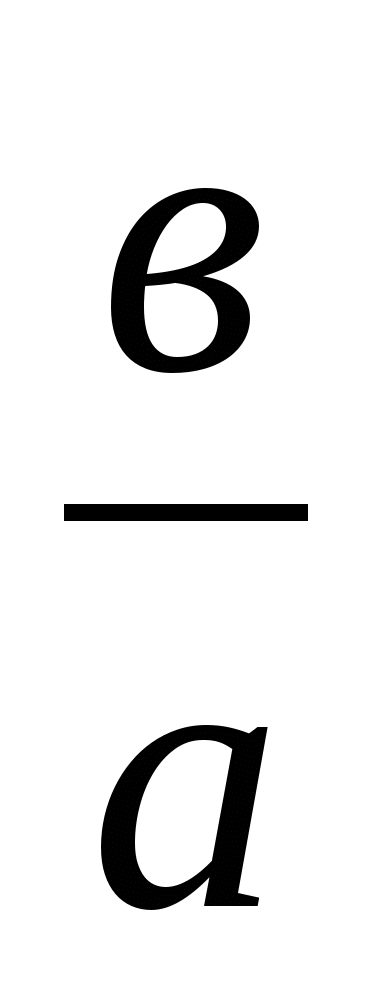 )+(
)+(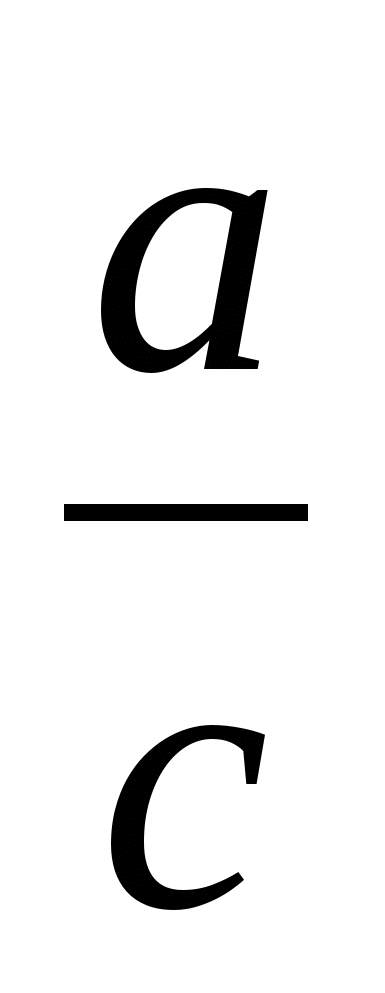 +
+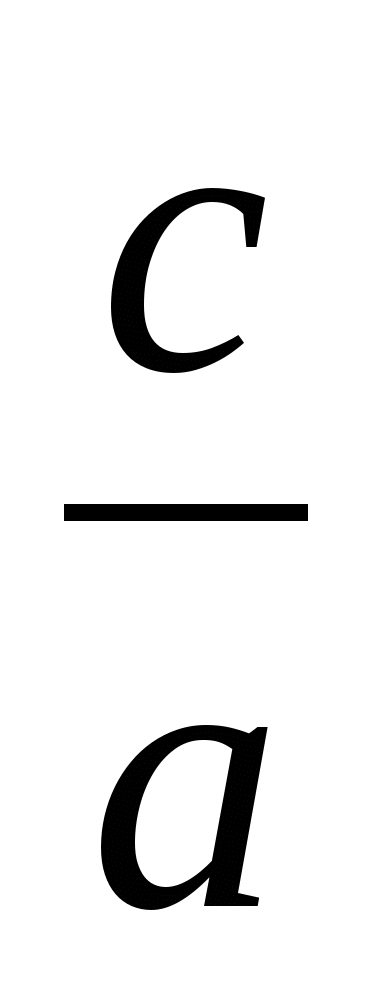 )+(
)+(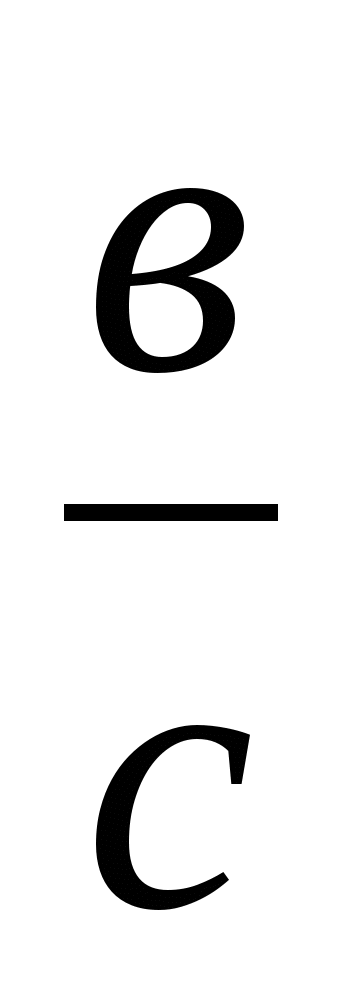 +
+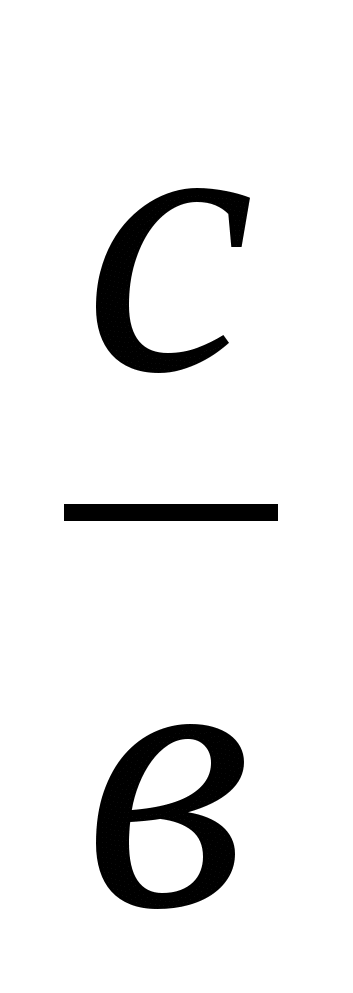 )≥
)≥
≥3+2+2+2=9 (себебі әр жақшаның ішіндегі қосынды 2-ге тең немесе одан үлкен).
№2.
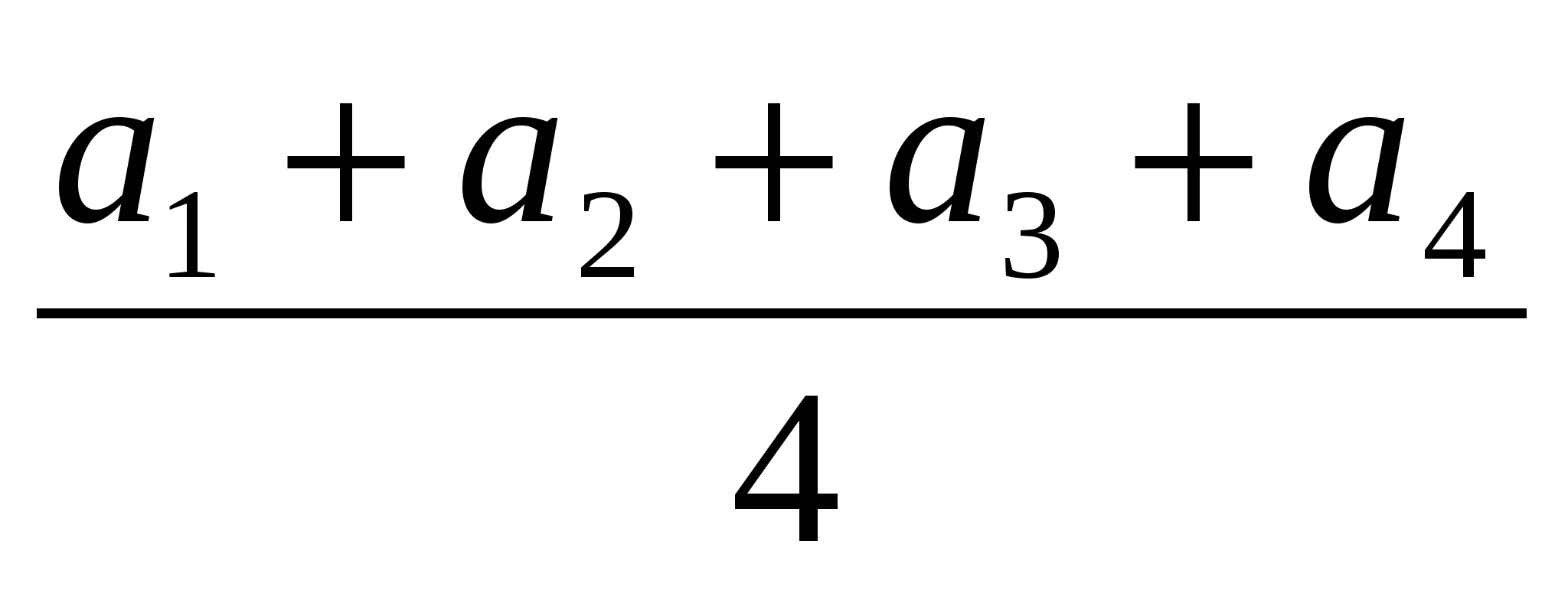 ≥а1 а2 а3 а4 (мұндағы а1 >0,а2>0,а3>0,а4 >0)
≥а1 а2 а3 а4 (мұндағы а1 >0,а2>0,а3>0,а4 >0)
Нұсқау.Екі оң санның арифметикалық орташасы мен геометриялық орташасын екі рет салыстыруды қолданамыз.
№3.Егер а2+в2 =1 болса , │а+в│≤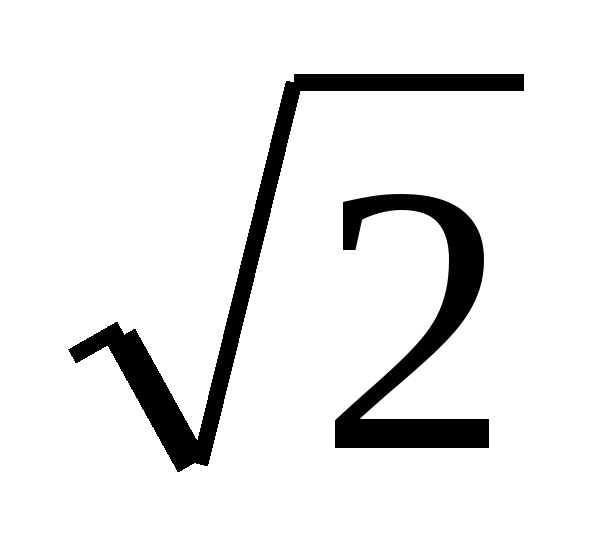 онда екенін дәлелдеңіздер.
онда екенін дәлелдеңіздер.
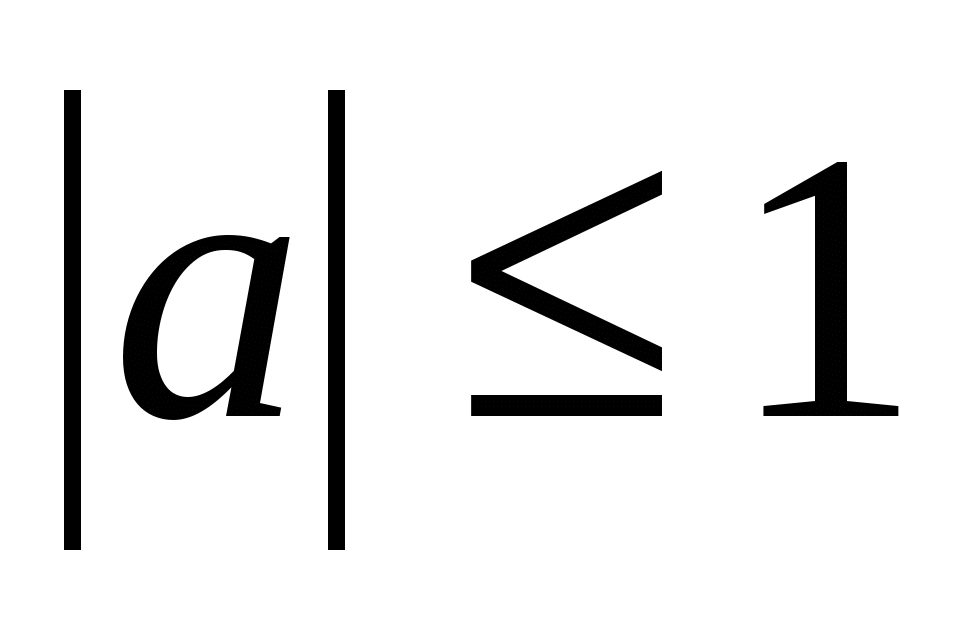 және
және 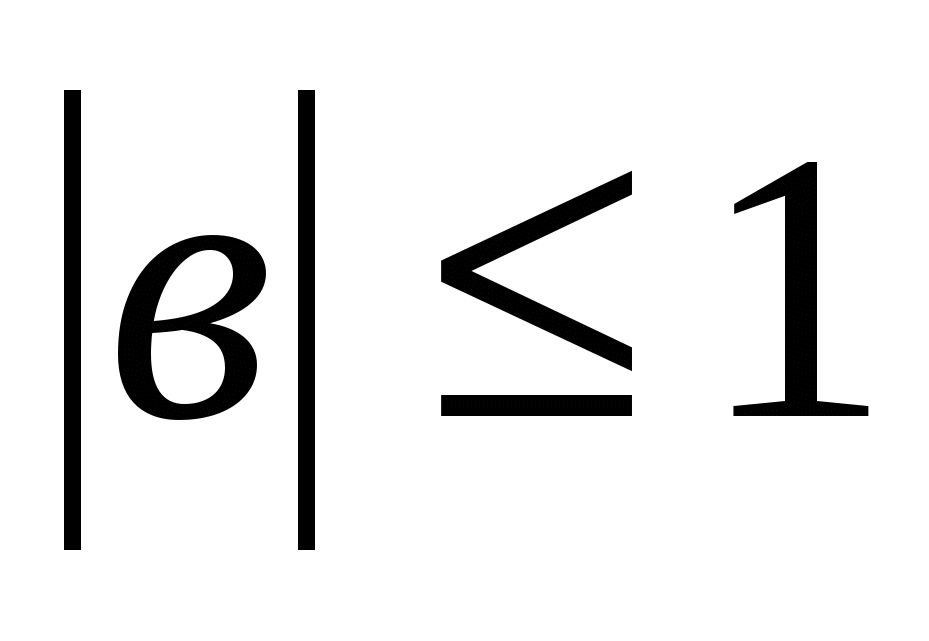 екені есептің шартынан шығады. Сондай -ақ а2+в2 =1 болғандықтан, а мен в-ны синуспен және косинуспен ауыстыруға болады: a=sinα , в=cosα. Онда а+в=sinα+cosα=sinα+sin
екені есептің шартынан шығады. Сондай -ақ а2+в2 =1 болғандықтан, а мен в-ны синуспен және косинуспен ауыстыруға болады: a=sinα , в=cosα. Онда а+в=sinα+cosα=sinα+sin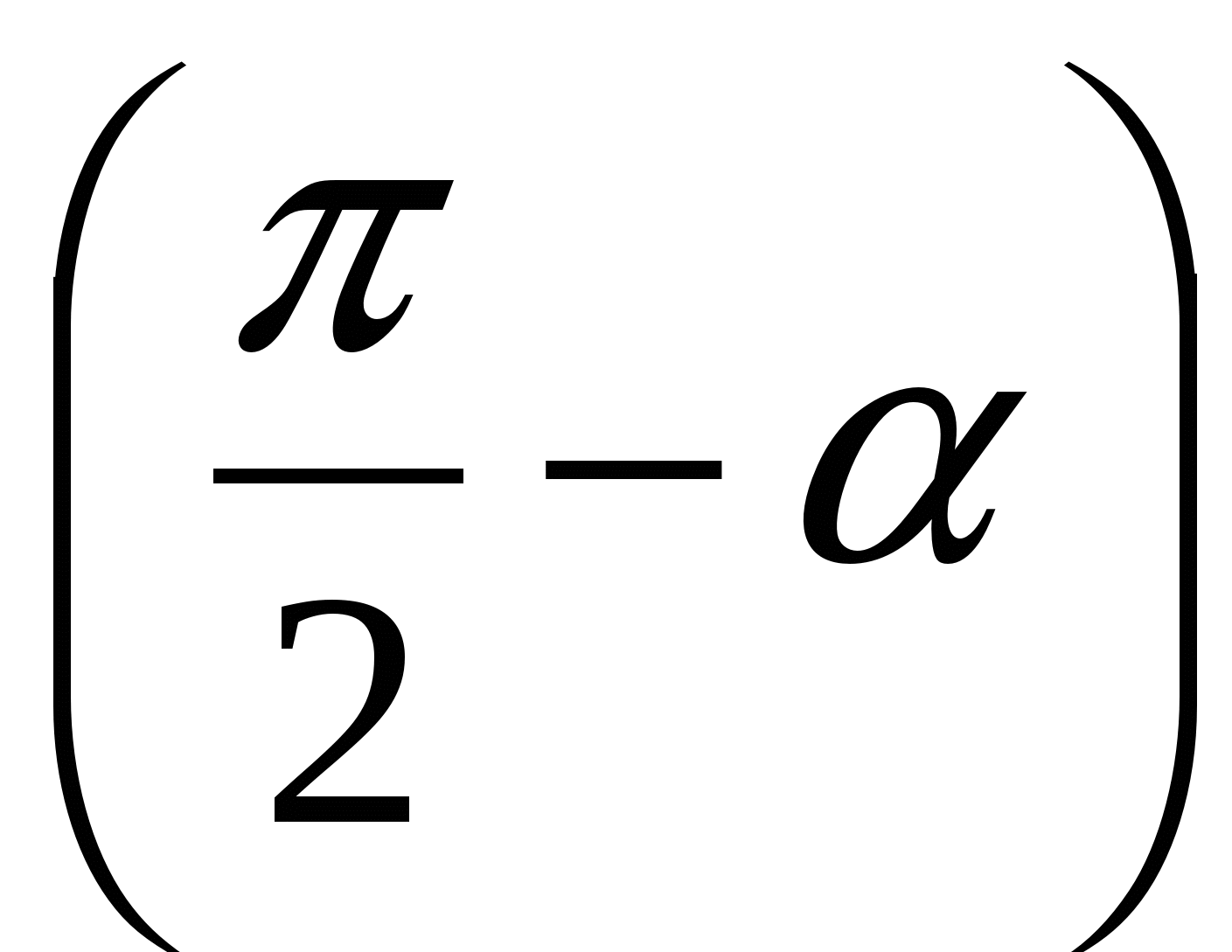 = =2sin
= =2sin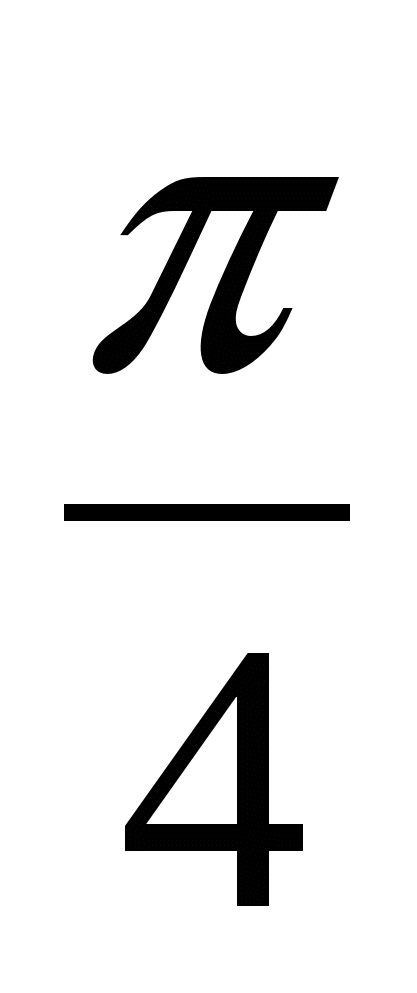 cos
cos 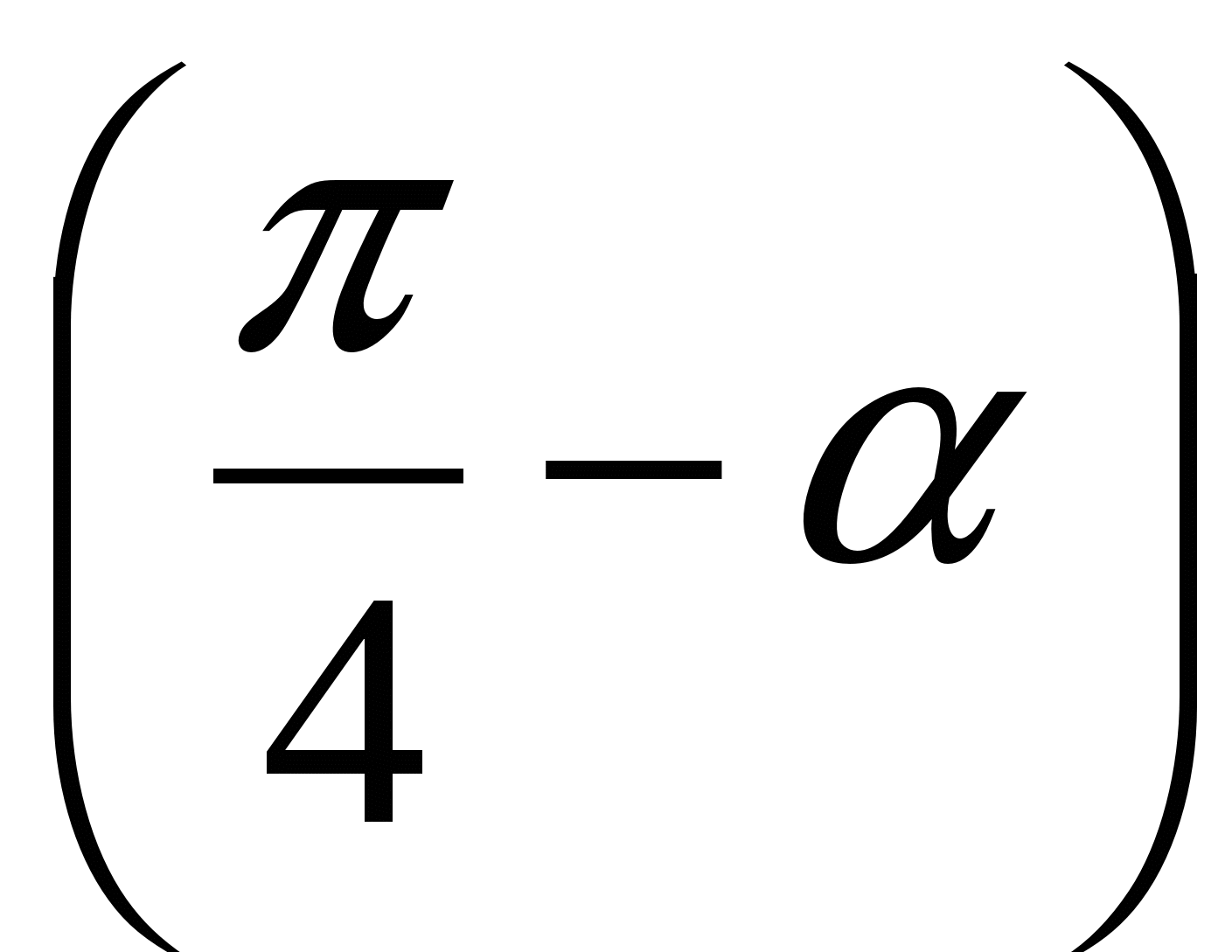 =
=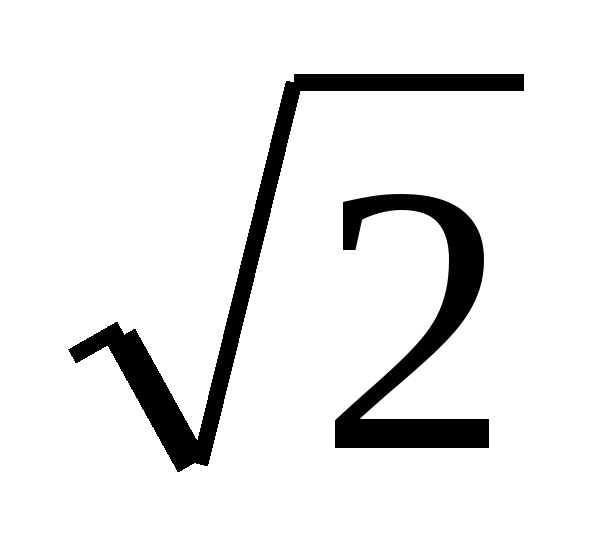 cos
cos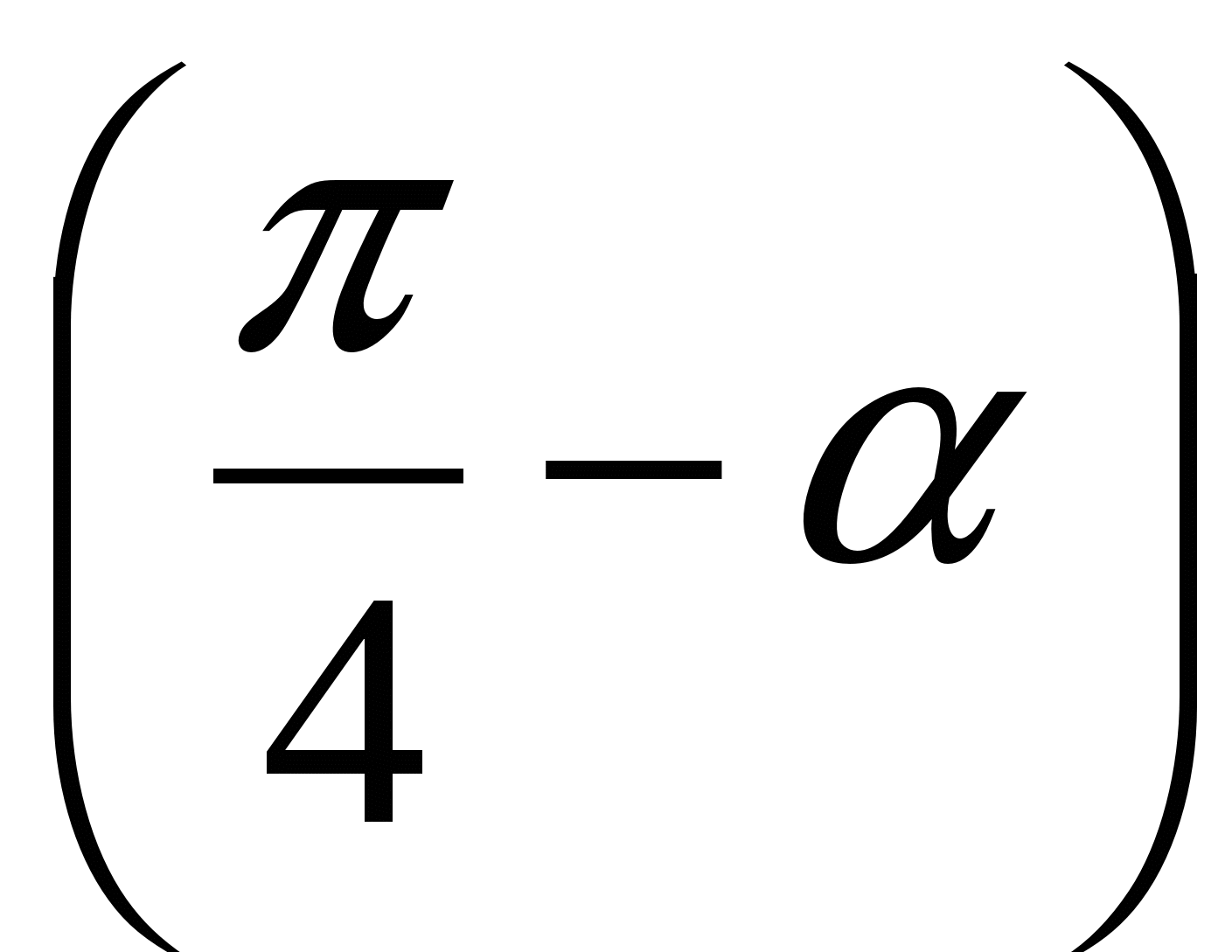 .
.
cos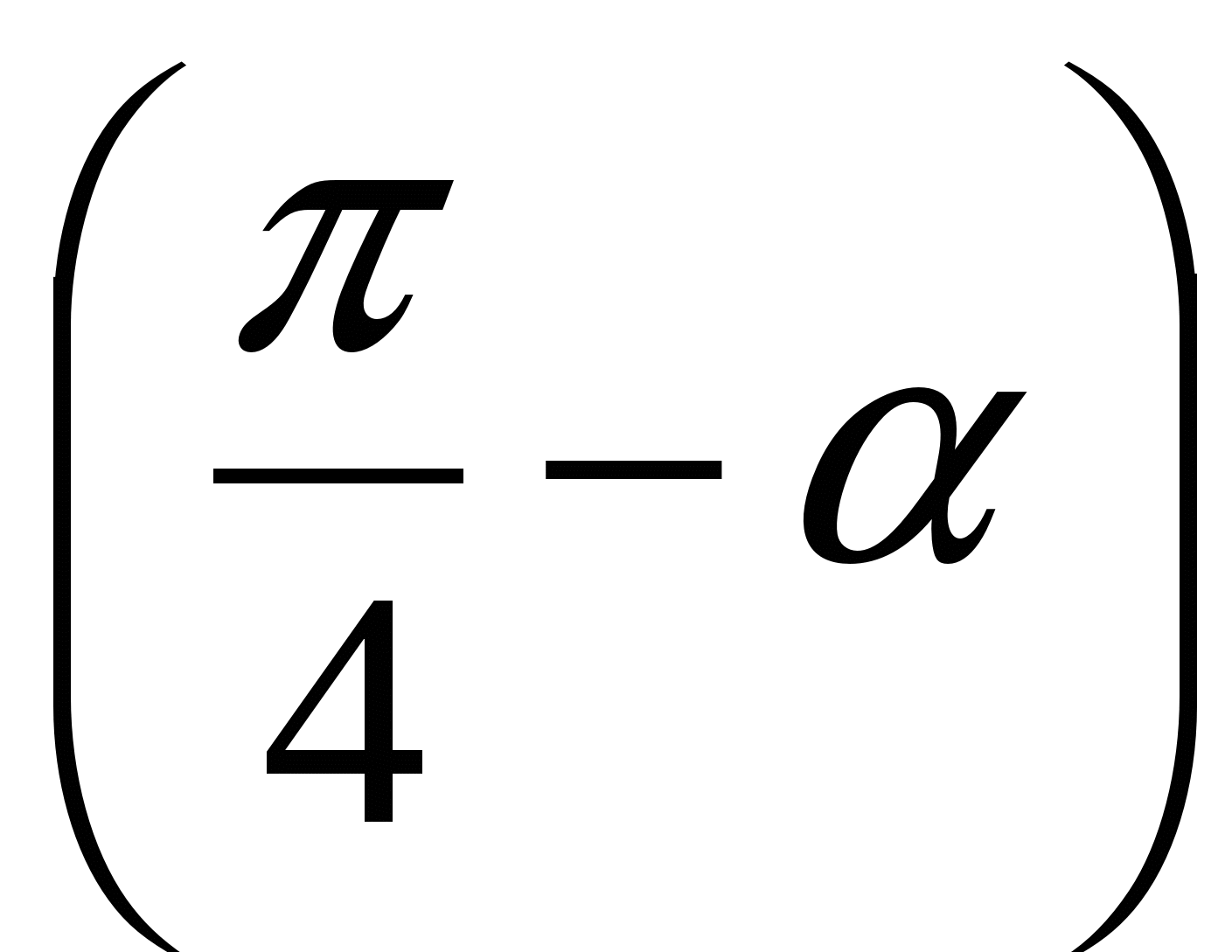 ≤1.Демек , │а+в│≤
≤1.Демек , │а+в│≤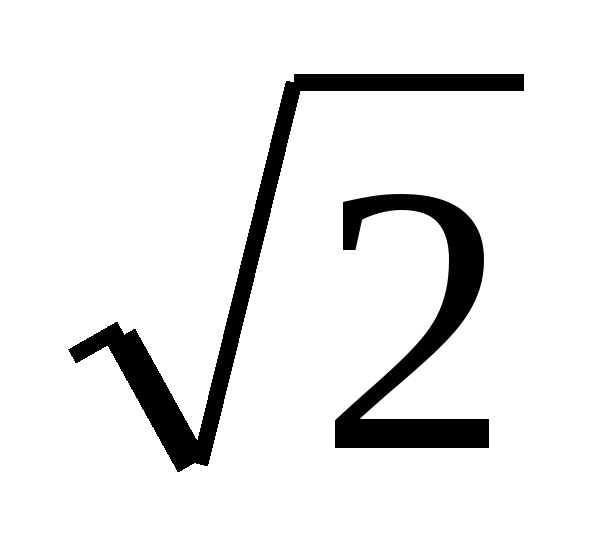 .
.
Басқаша талқылап көрелік: 1=а2+в2≥2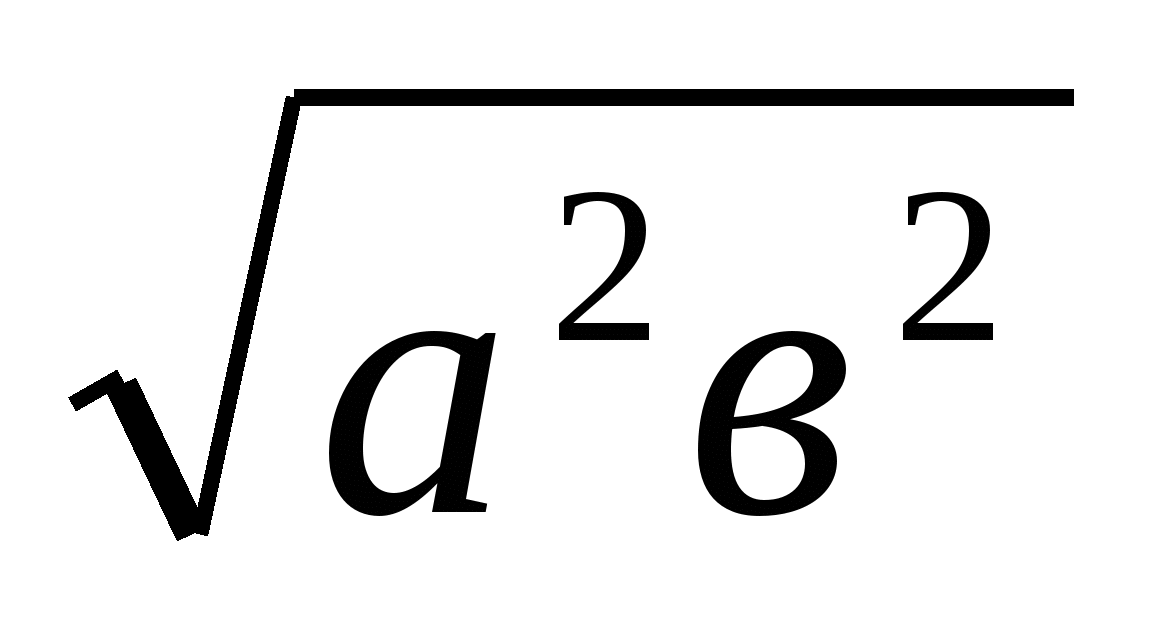 =2
=2 ; 2≥а2+в2+2
; 2≥а2+в2+2 =
=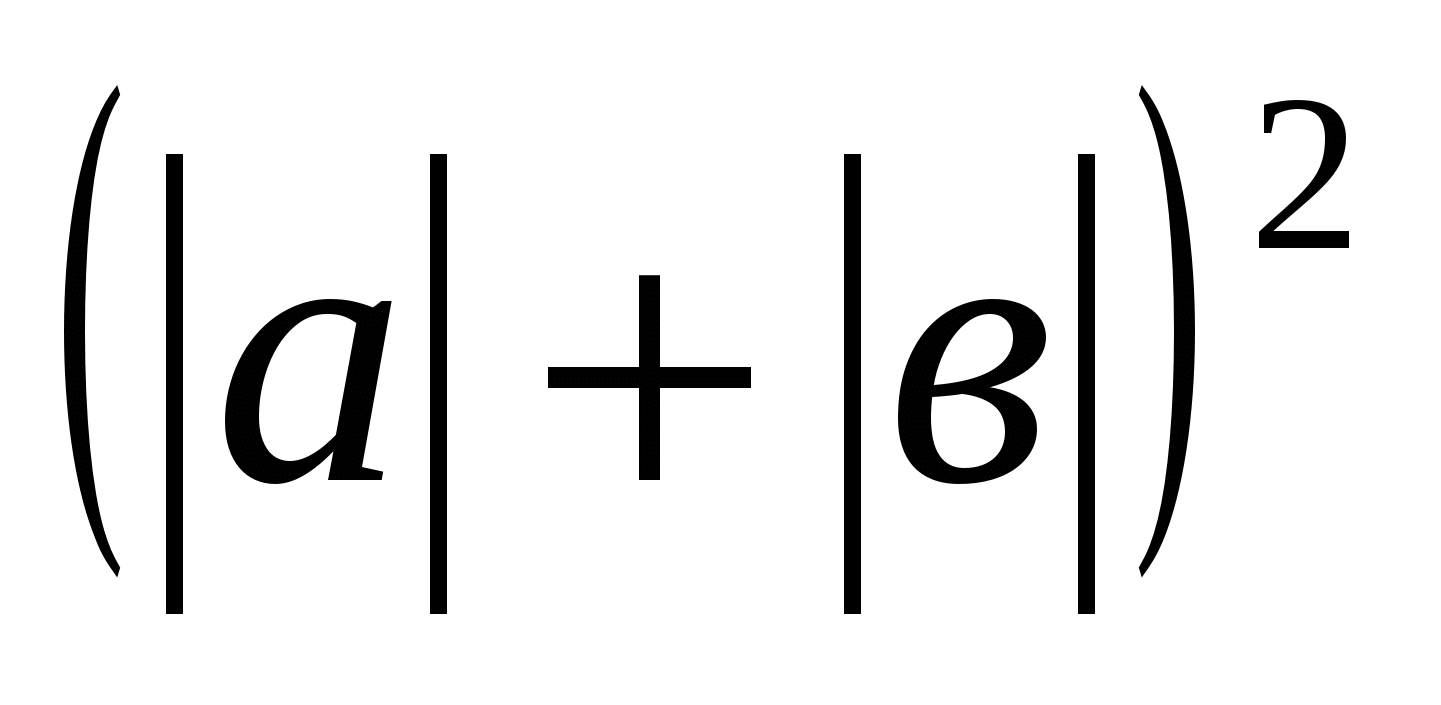 ;
;
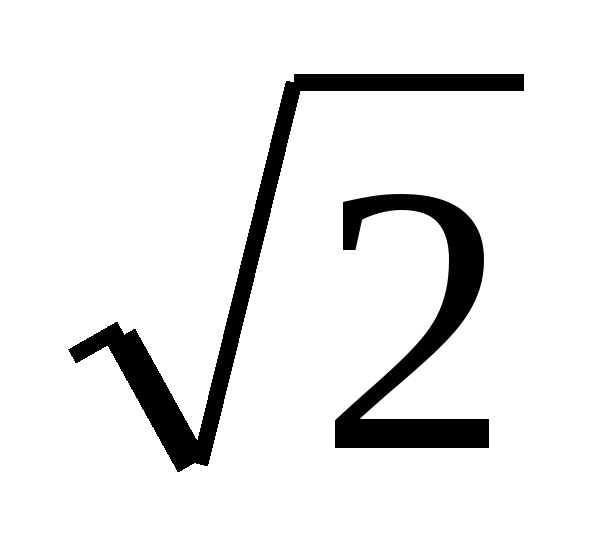 ≥
≥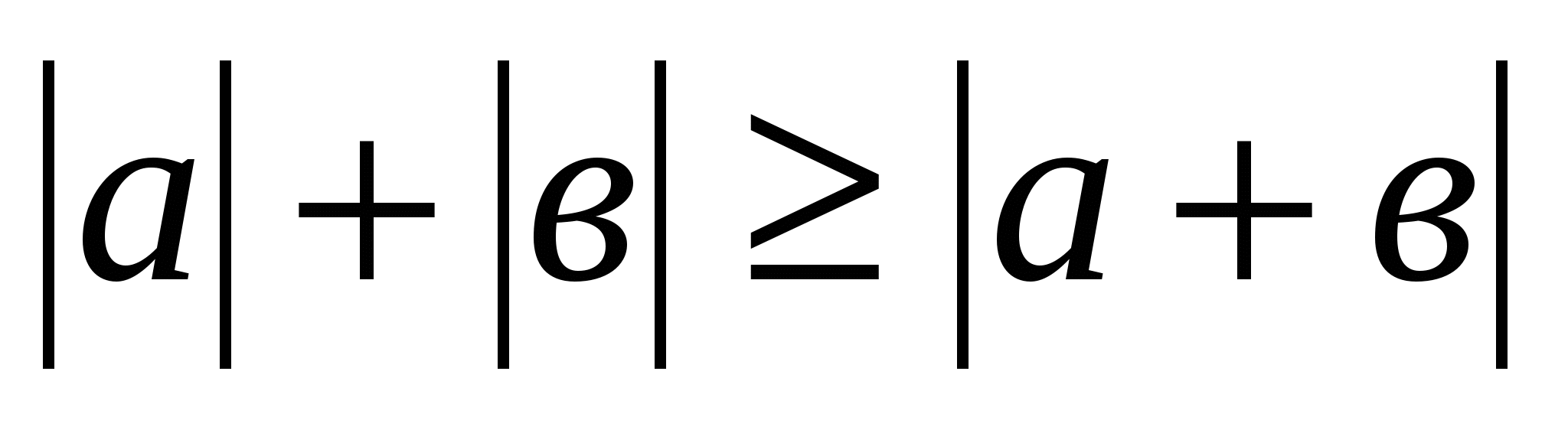 .
.
Аудандық олимпиада
11-сынып
№1.Теңсіздікті шеш:
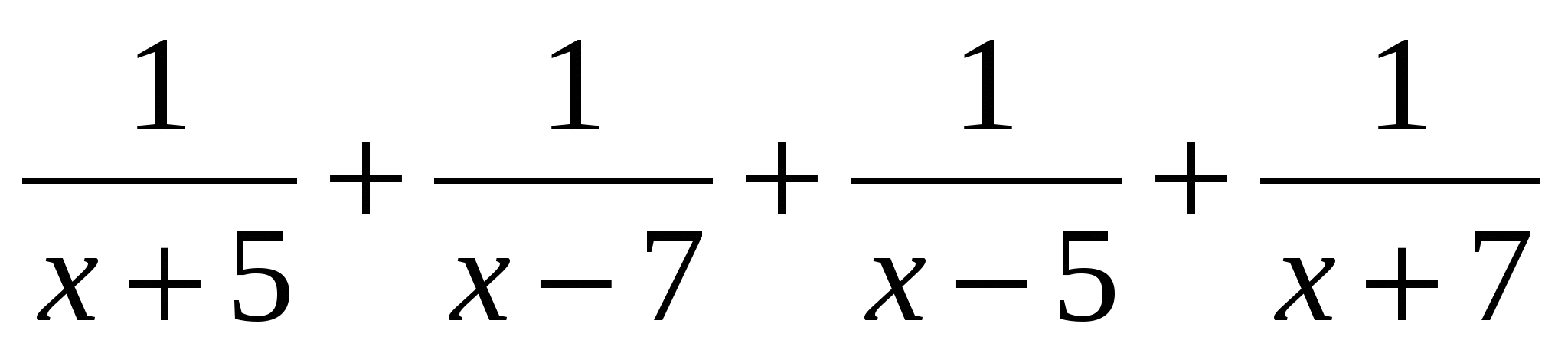 >0
>0
Теңсіздіктің сол жағын ортақ бөлімге келтіріп ықшамдап жазайық.
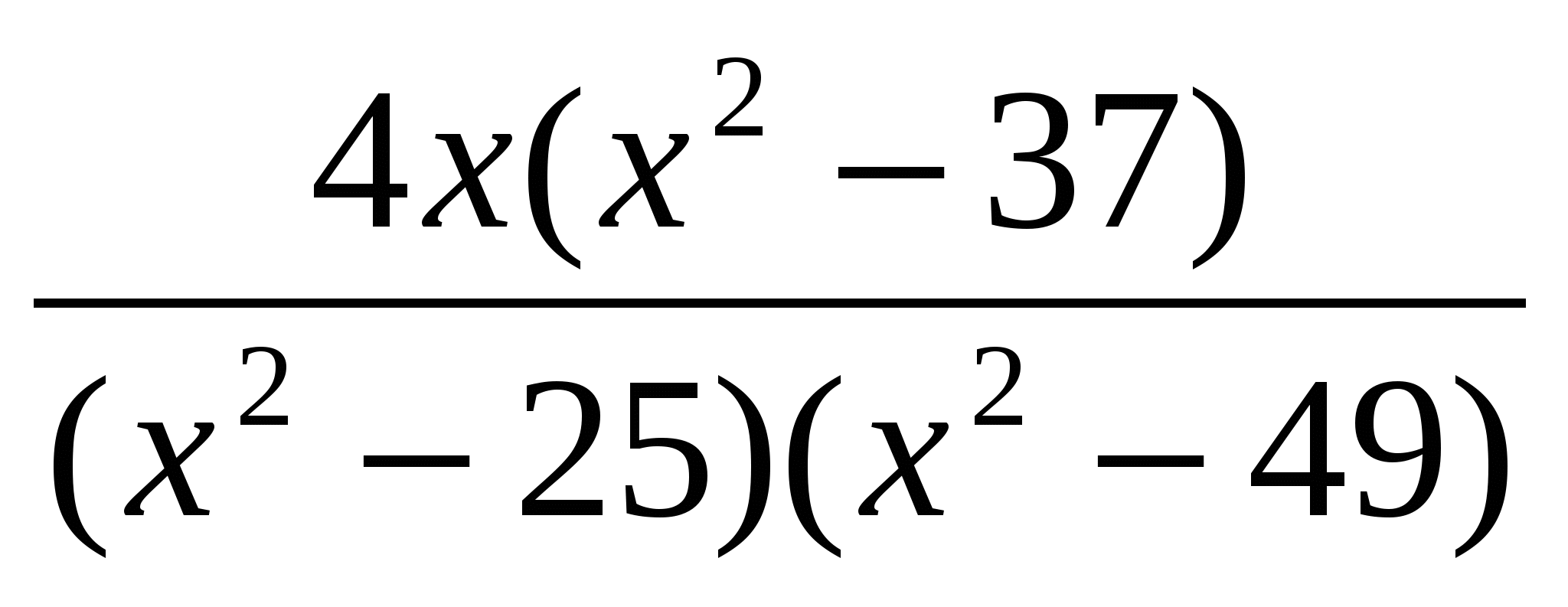 >0
>0
С






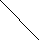 онда берілген теңсіздікке мәндес теңсіздік
онда берілген теңсіздікке мәндес теңсіздік 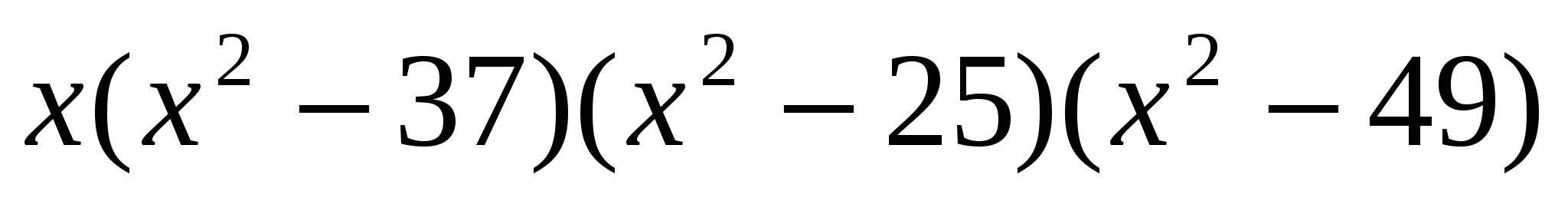 >0 болады.
>0 болады.

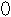
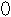
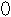
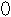 - + - + - + - +
- + - + - + - +
-7 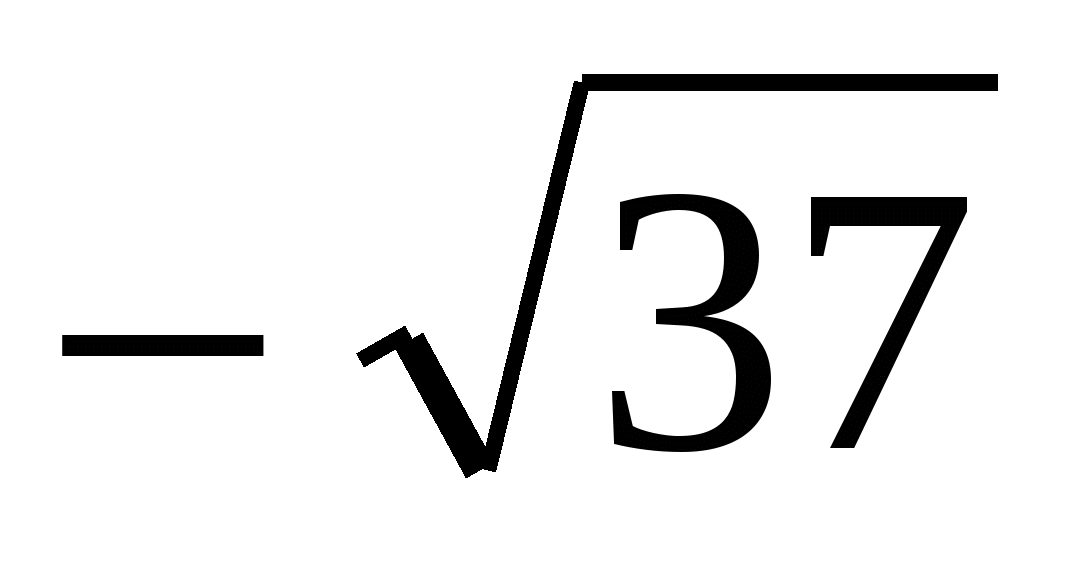 -5 0 5
-5 0 5 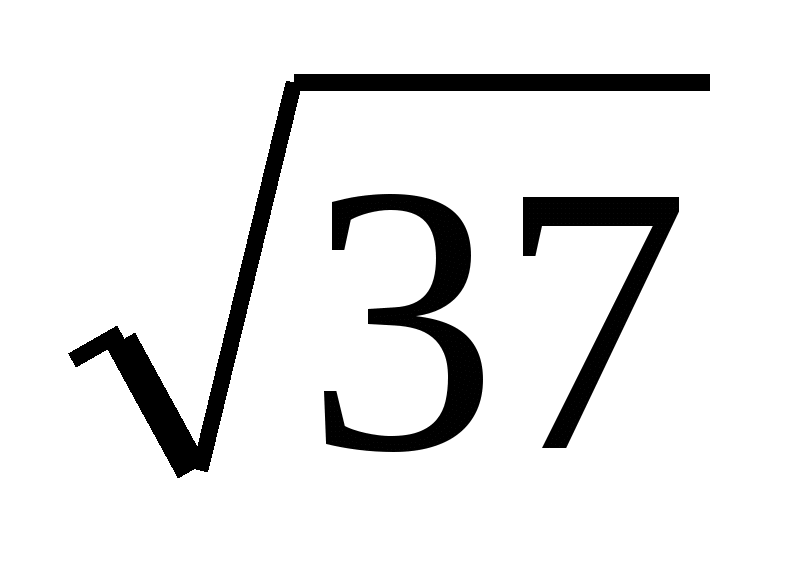 7
7
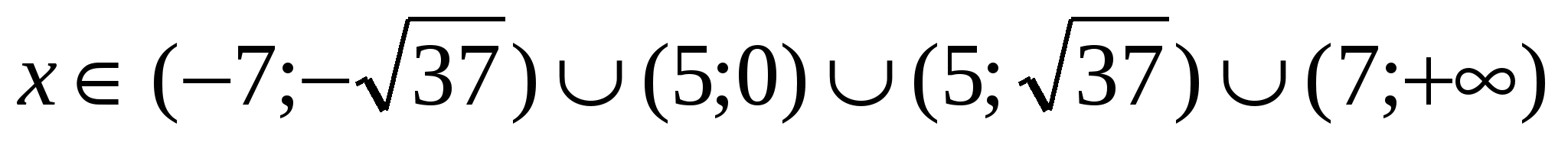 .
.
№2.Теріс емес, а,в,с сандары үшін теңсіздікті дәлелдеңдер: (а+в)(в+с)(с+а)≤8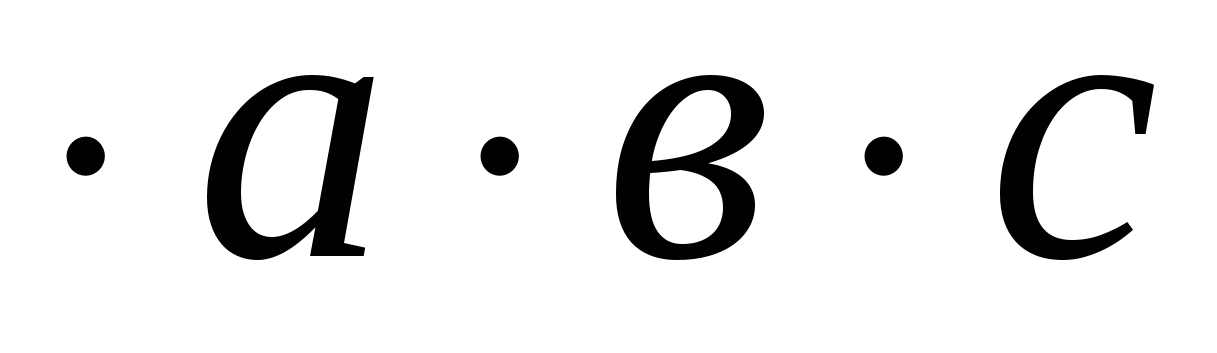
Нұсқау:Мынадай үш теңсіздікті көбейту керек 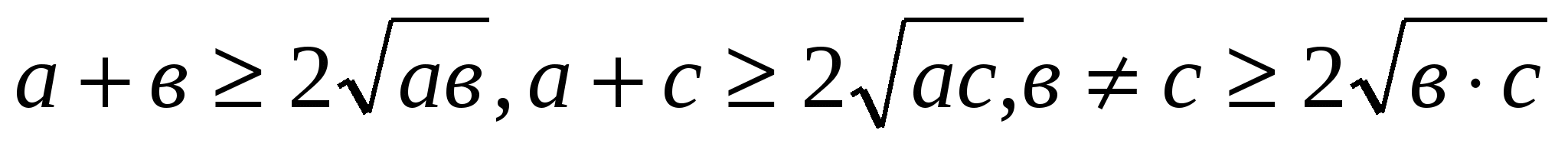 .
.
10-сынып.
№1.х-кез-келген сан болсын, дәлелдеңдер: 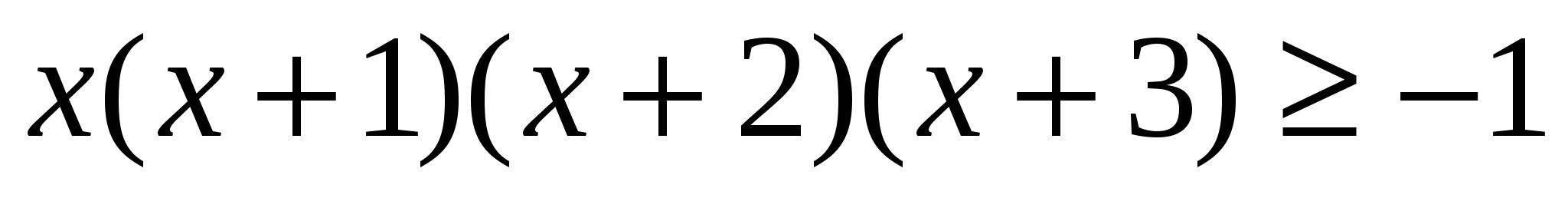
Дәлелдеуі: x(x+3)(x+1)(x+2)=(x2+3x)(x2+3x+2)=((x2+3x+1)-1)((x2+3x+1)+1)=(x2+3x+1)2-1≥-1
Облыстық олимпиада
10-сынып
№1.Теңсіздікті дәлелдеңдер.
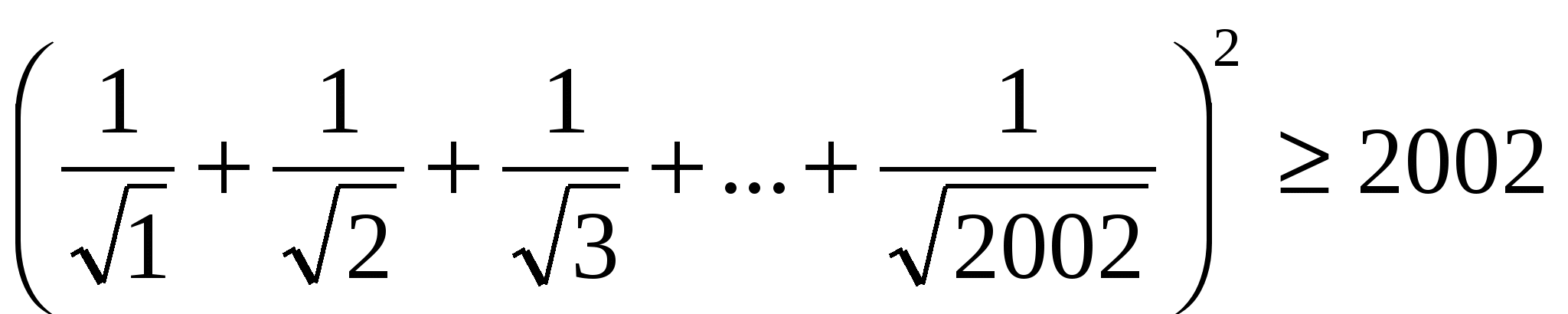
Шешуі: 
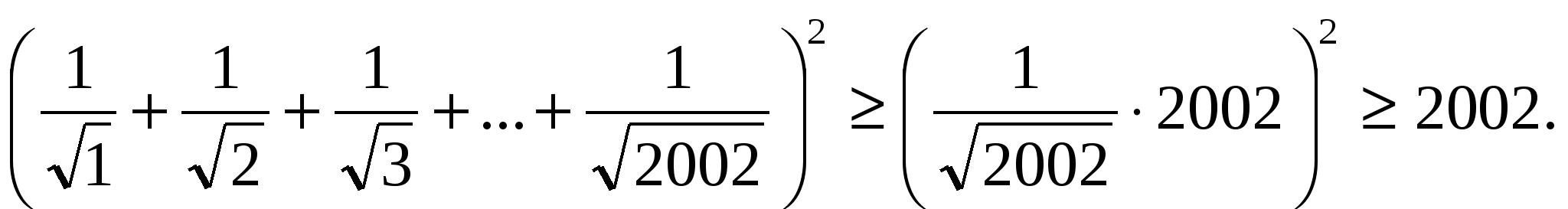
11-сынып
№2.Теңсіздікті дәлелдеңдер.
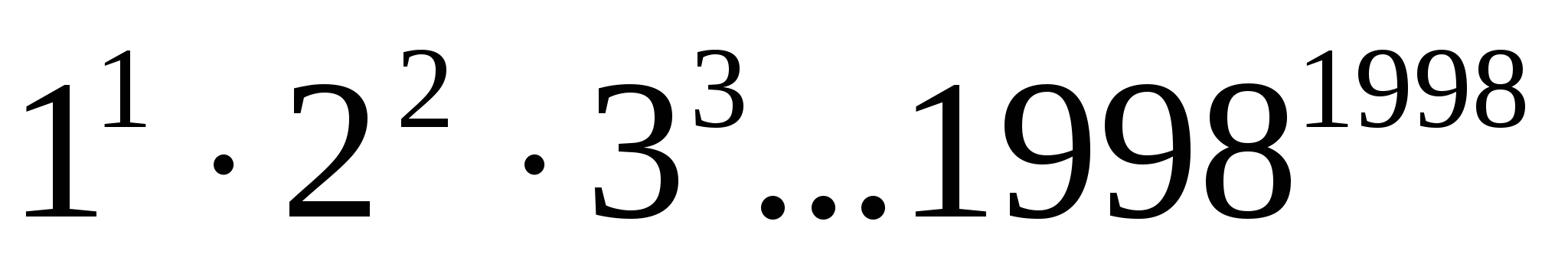 >
>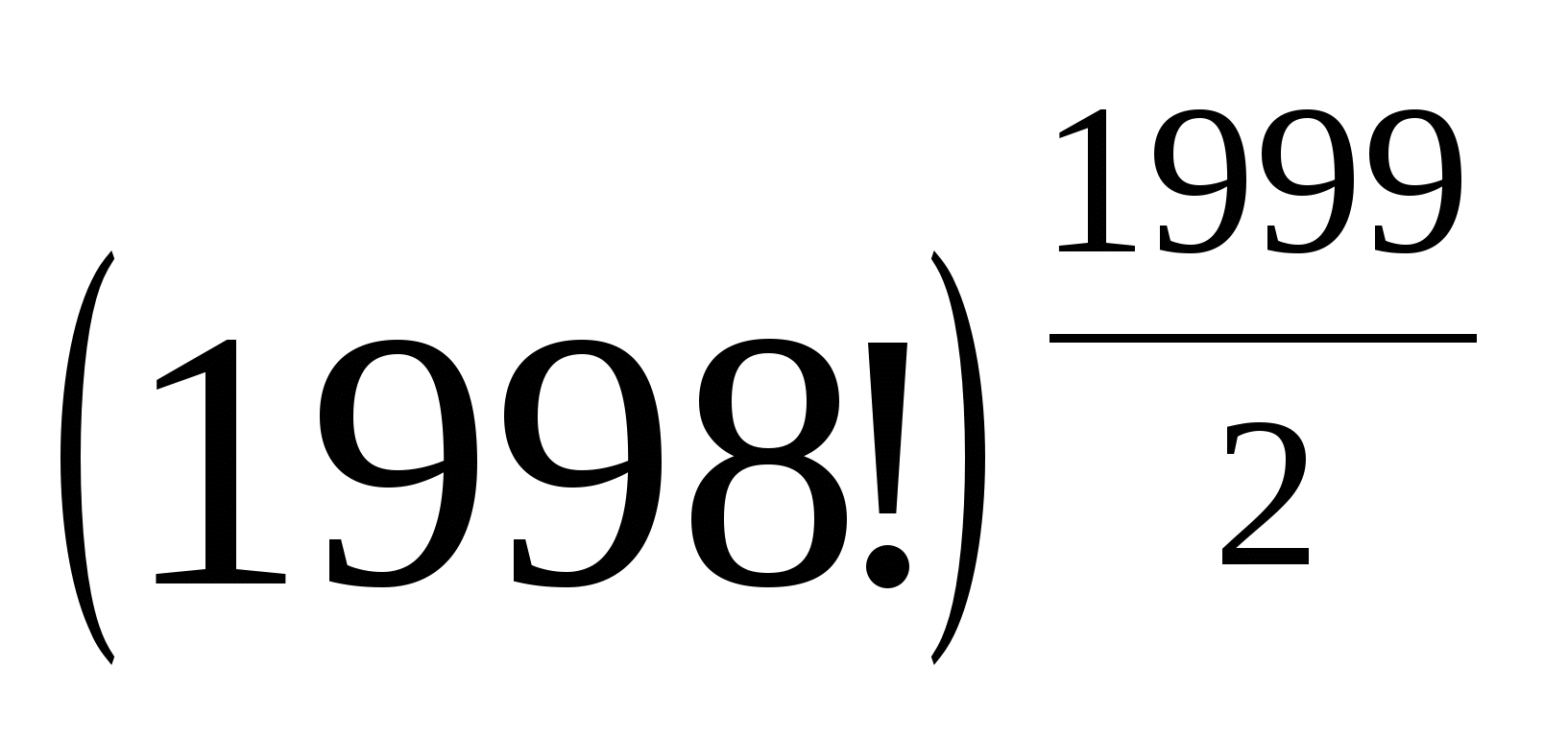
Дәлелдеуі:Теңсіздікті К≤999 натурал сандар үшін дәлелдейік:
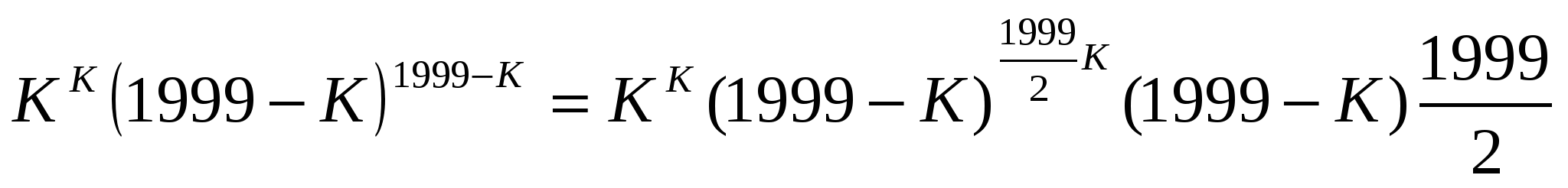 >
>
>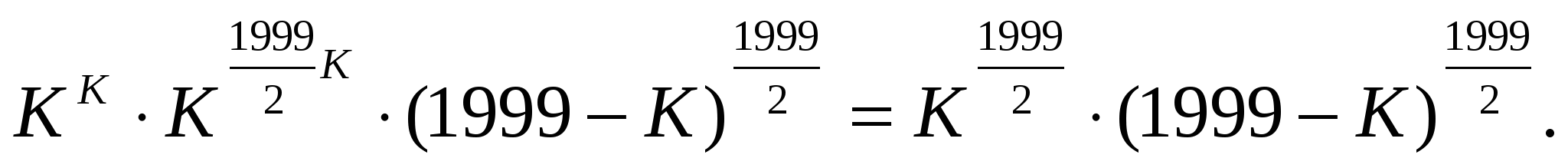
Сондықтан, 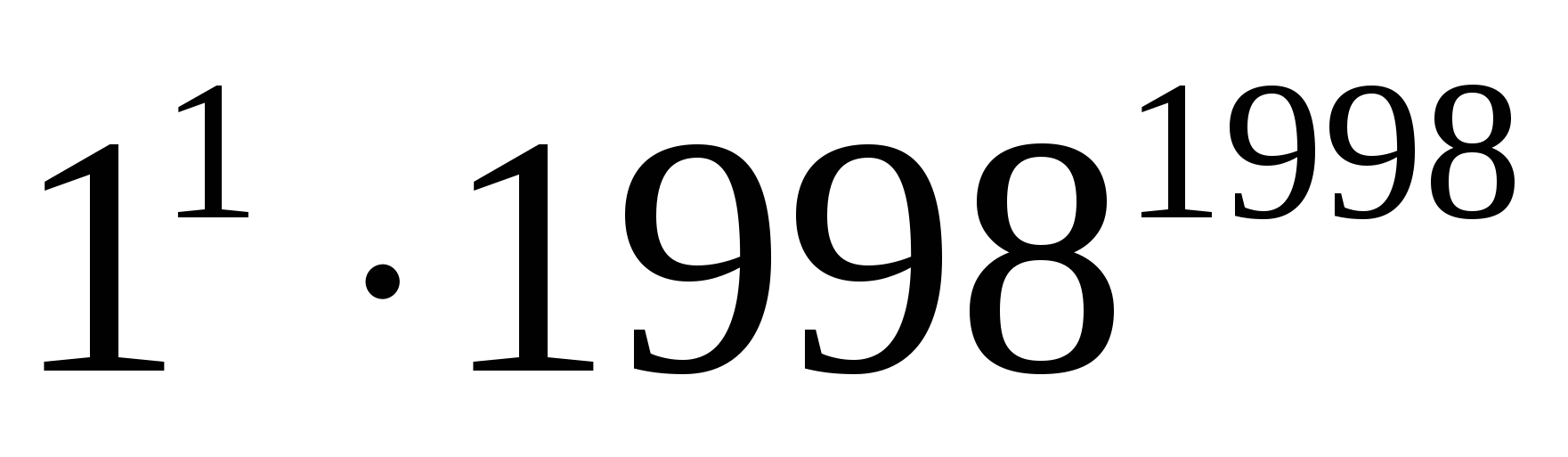 >
>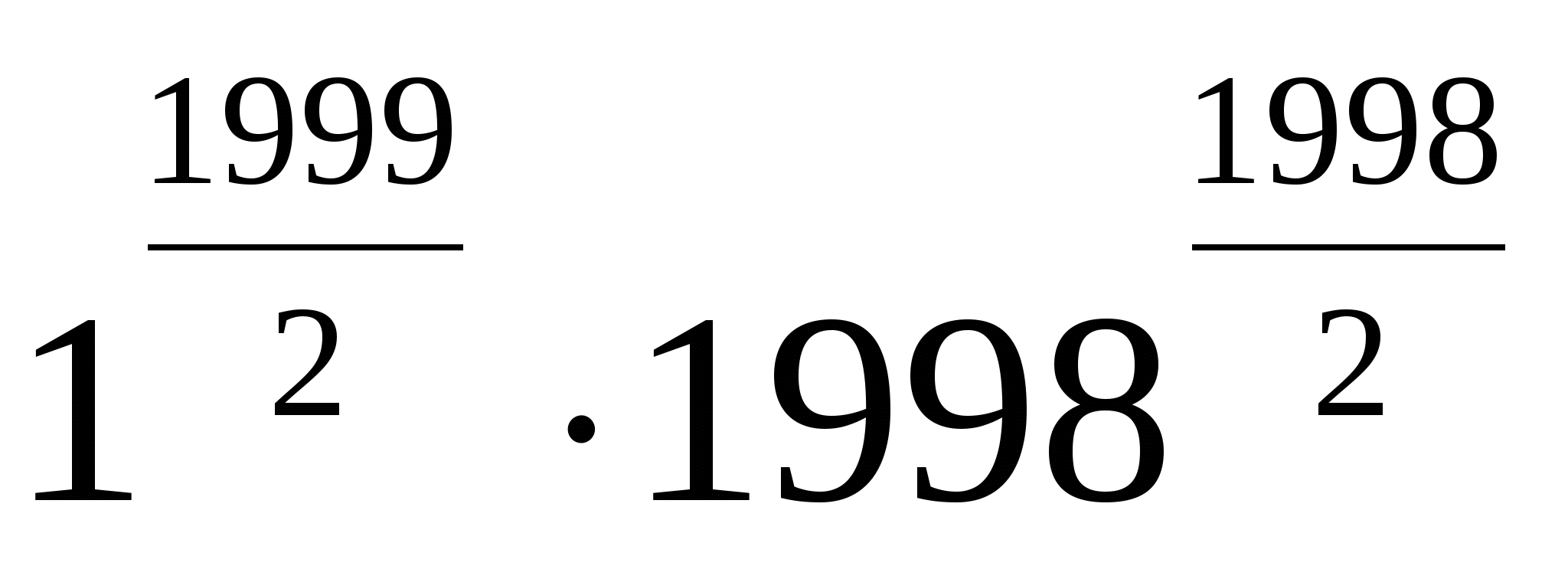 ;
;
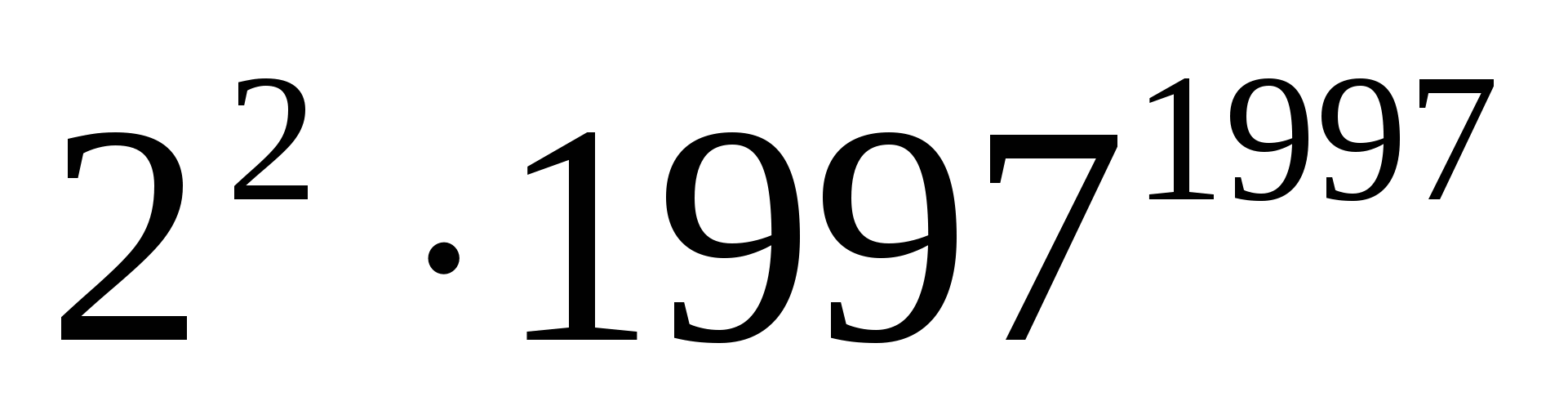 >
>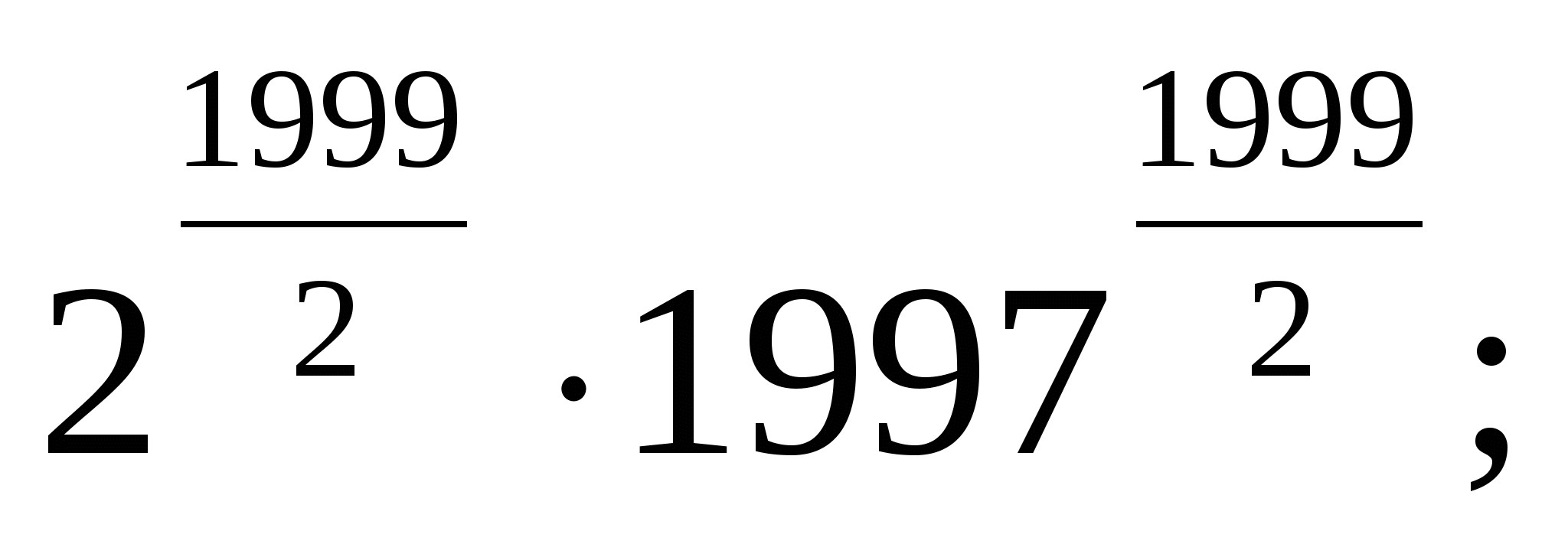 ...
... 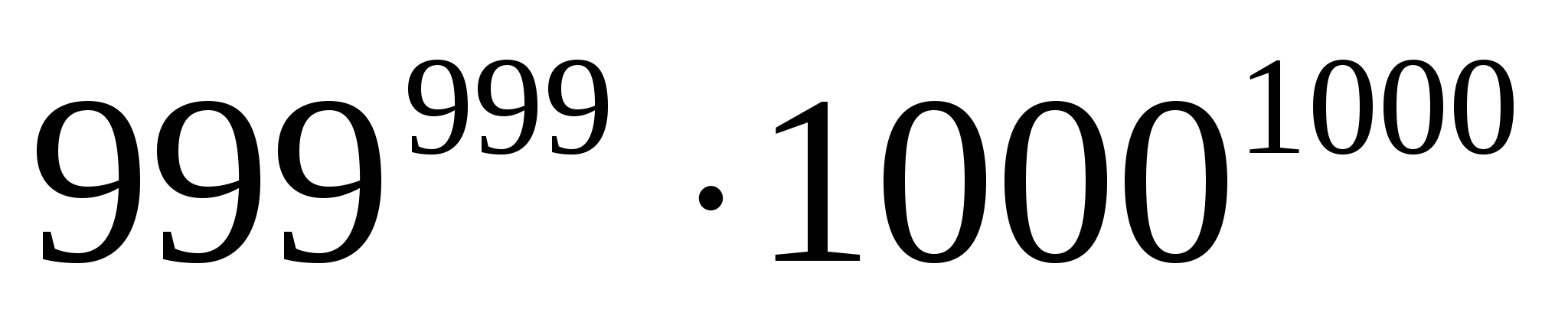
 >
>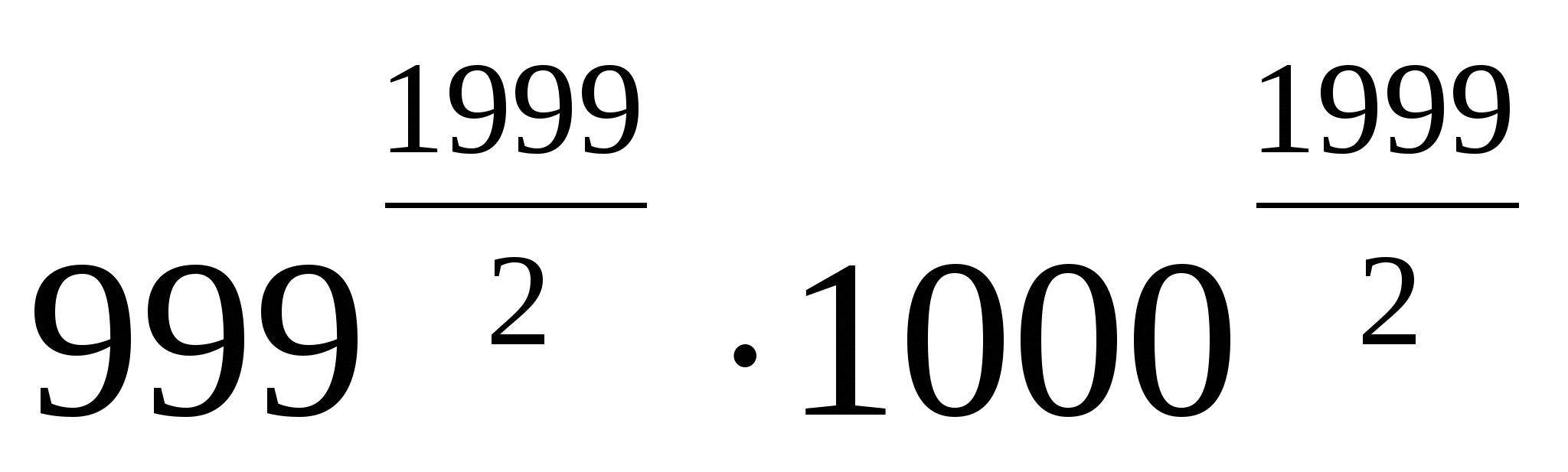
 Бұл теңсіздіктерді мүшелеп көбейтіп, дәлелденілген теңсіздікке келеміз.
Бұл теңсіздіктерді мүшелеп көбейтіп, дәлелденілген теңсіздікке келеміз.
9-сынып
№1. a>в>0 сандары үшін 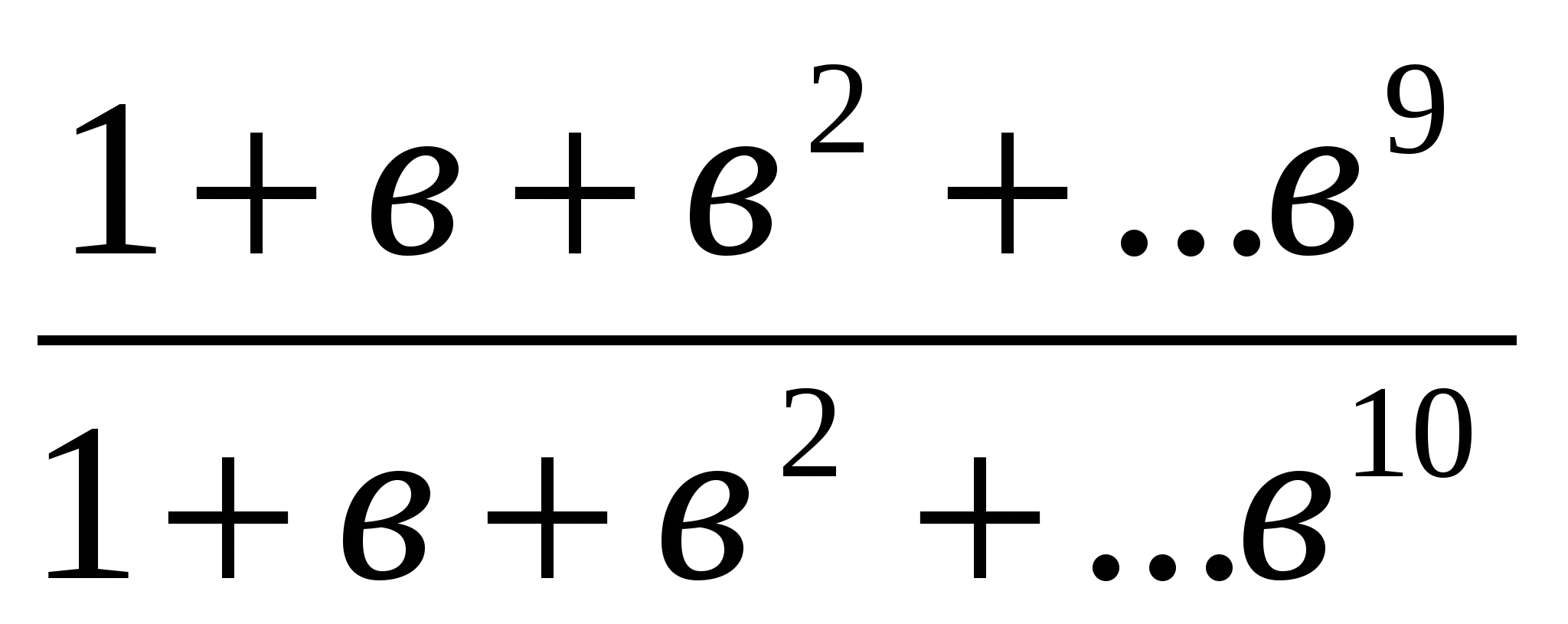 >
>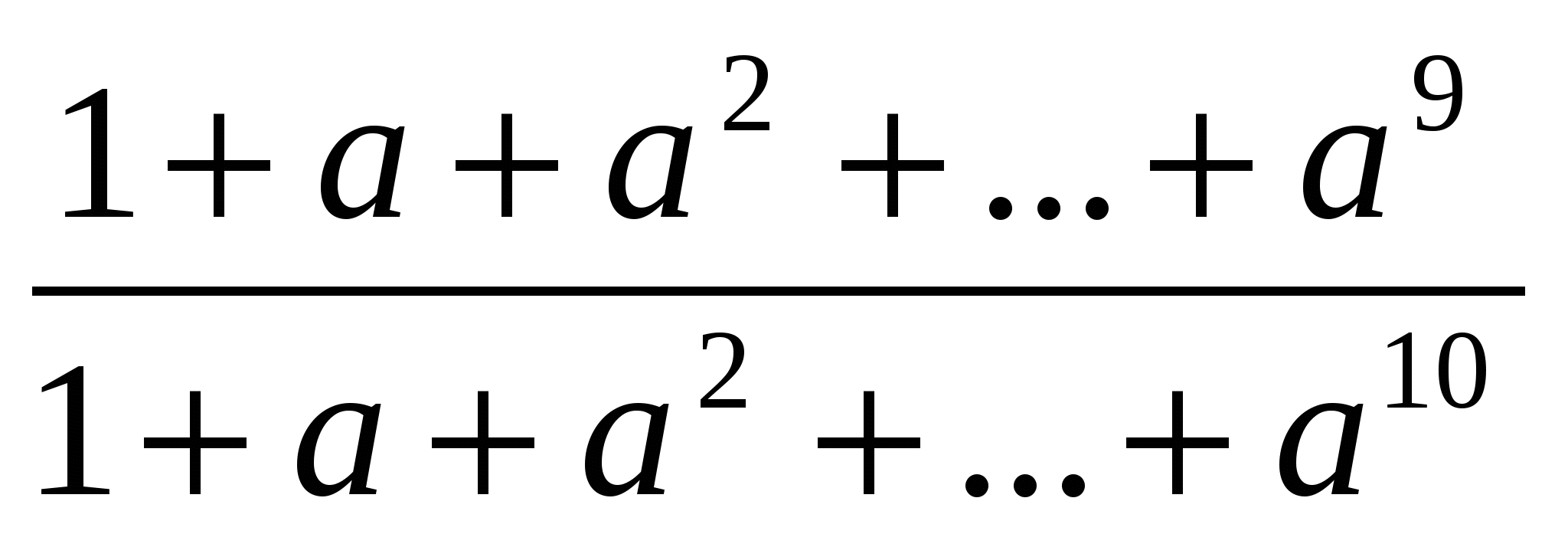 теңсіздігін дәлелдеңдер.
теңсіздігін дәлелдеңдер.
Дәлелдеуі: Дәлелденетін теңсіздік мынадай теңсіздікпен мәндес:
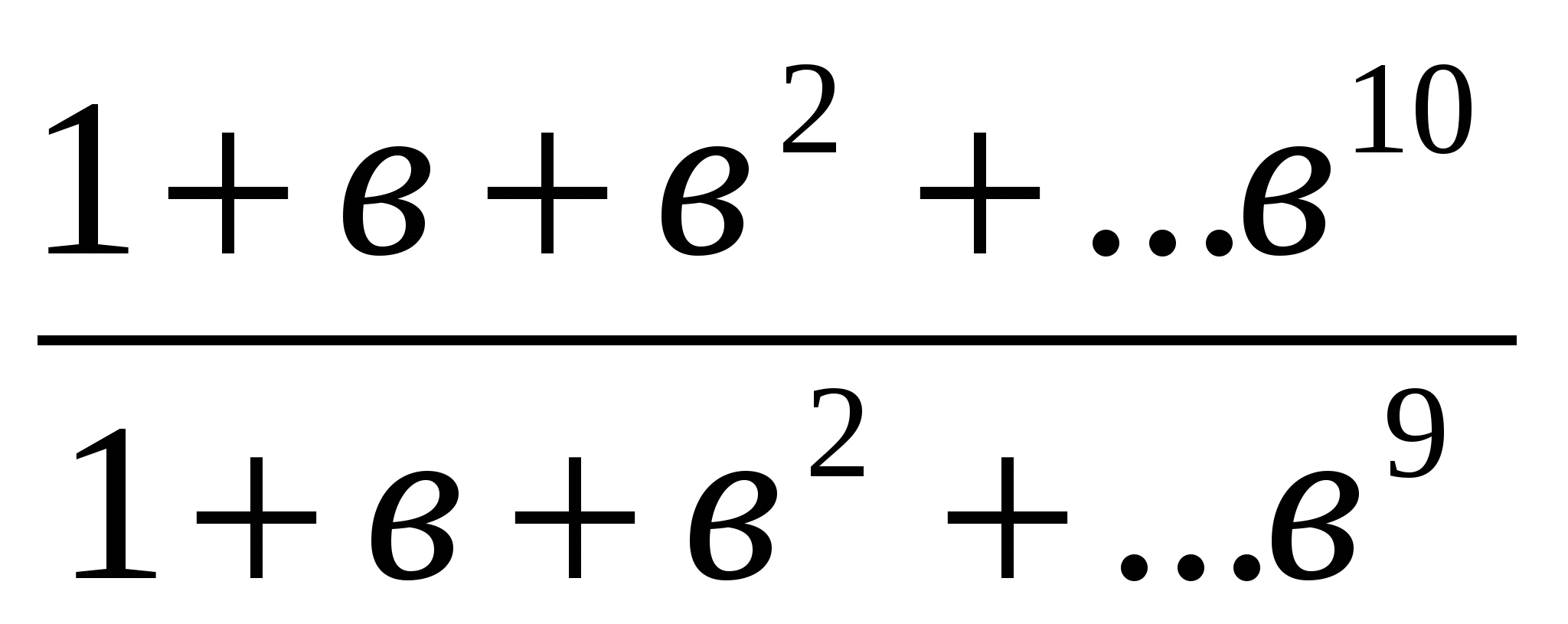 <
<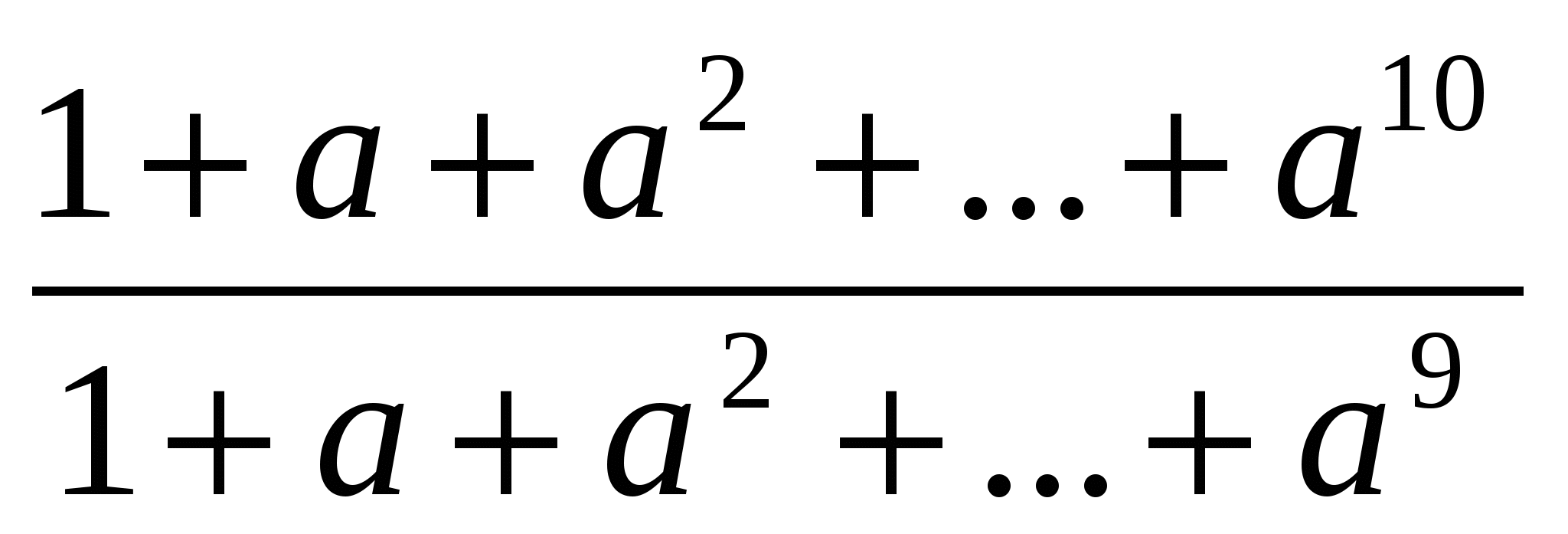
немесе 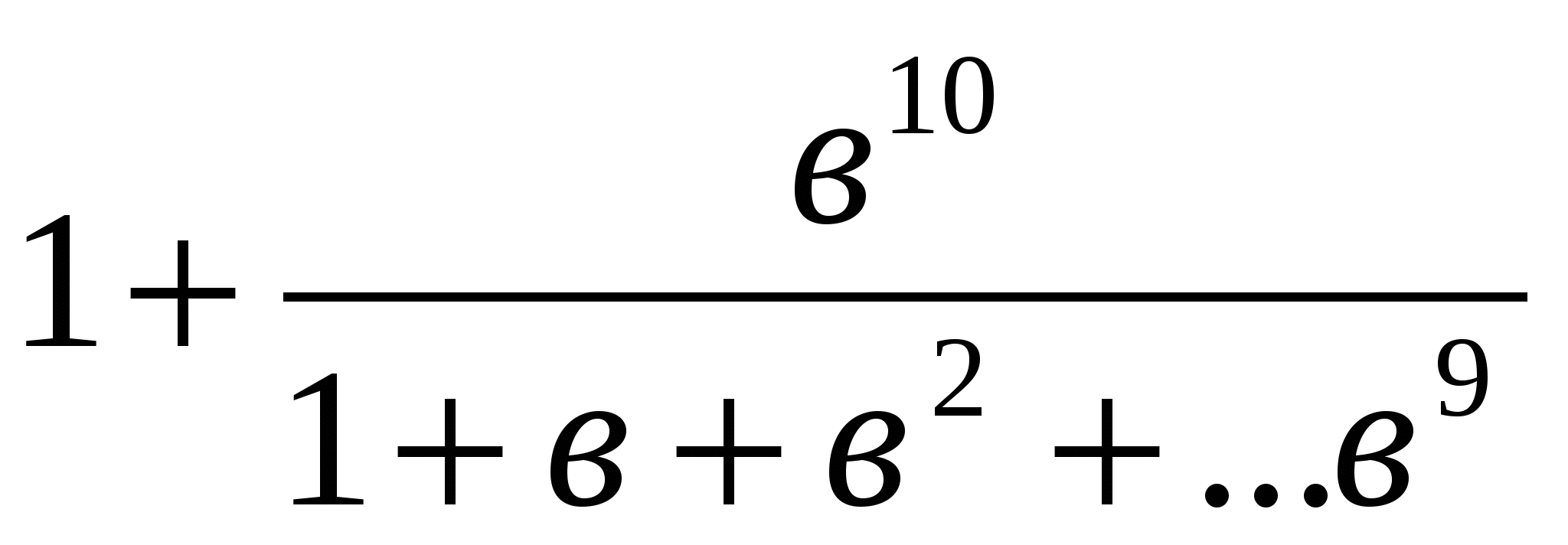 <
< 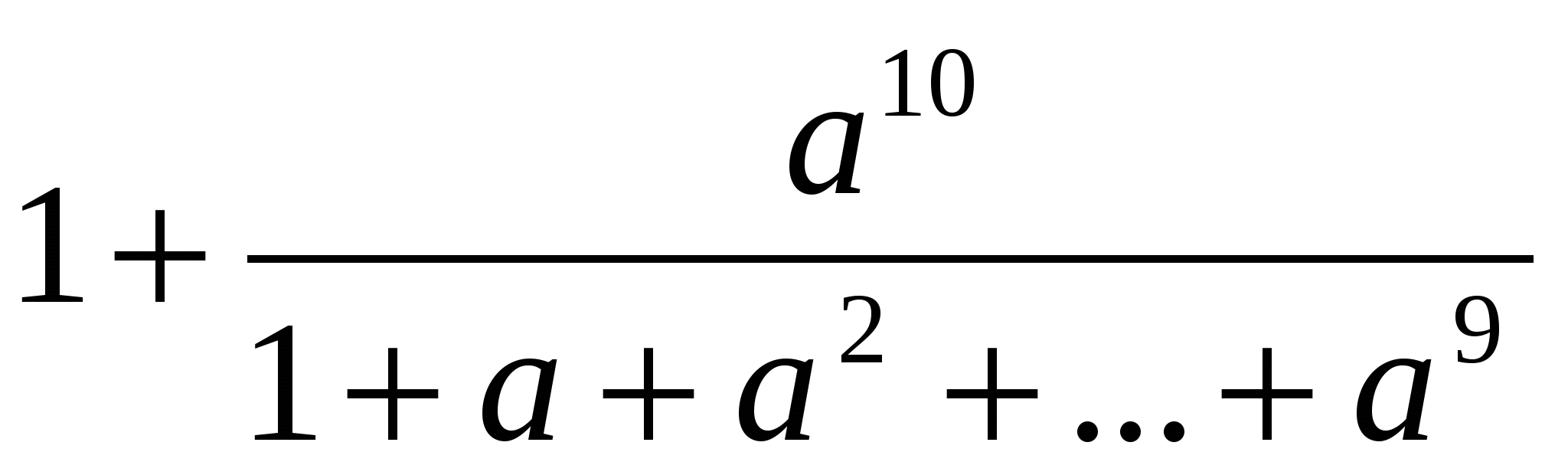
немесе 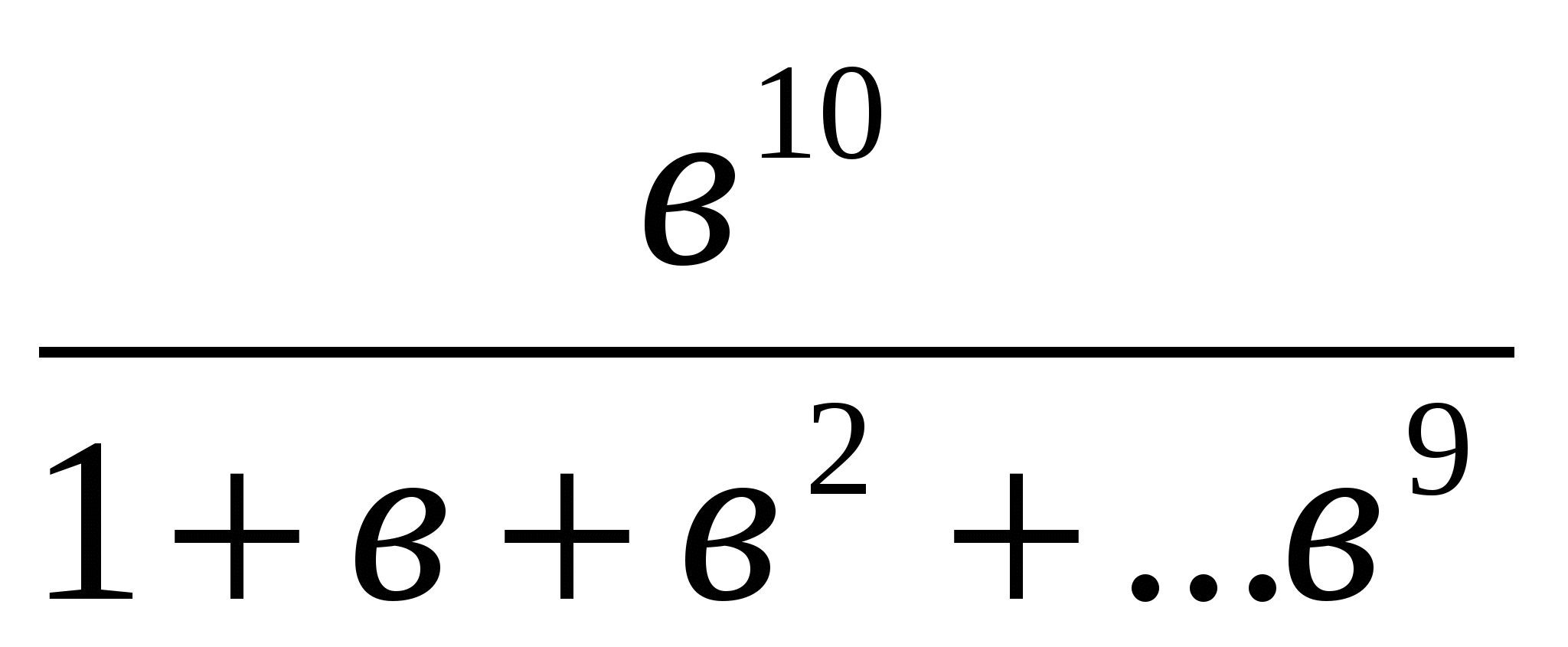 <
<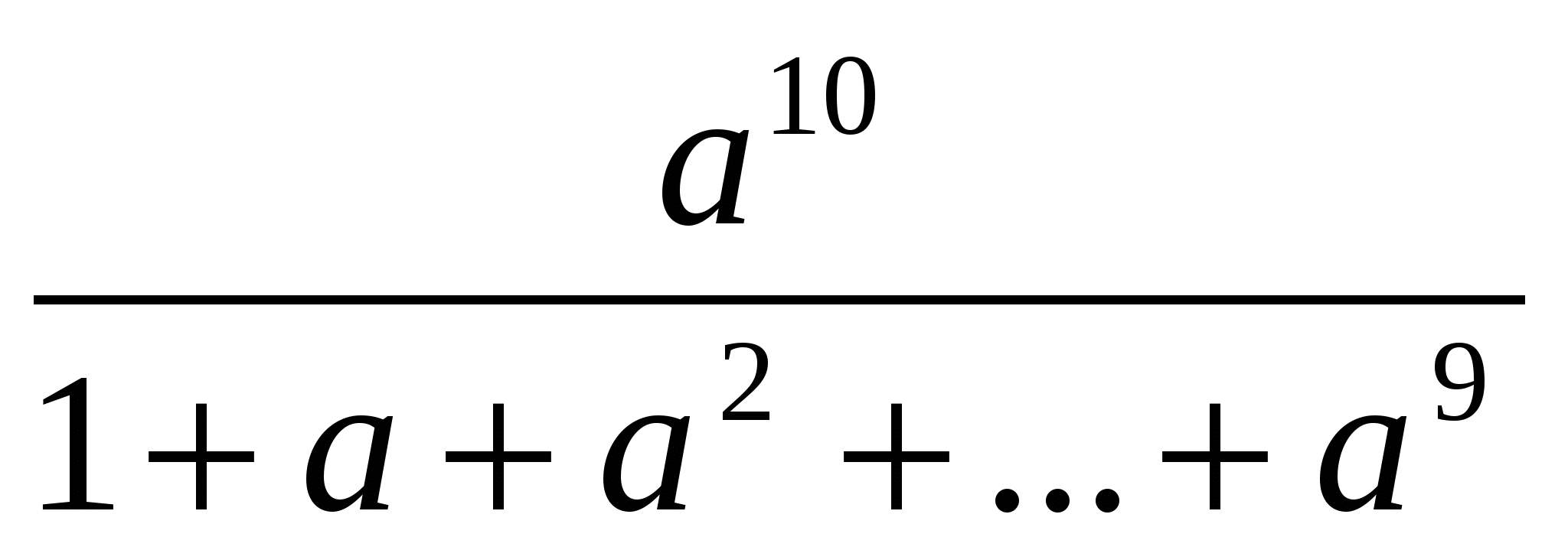
немесе 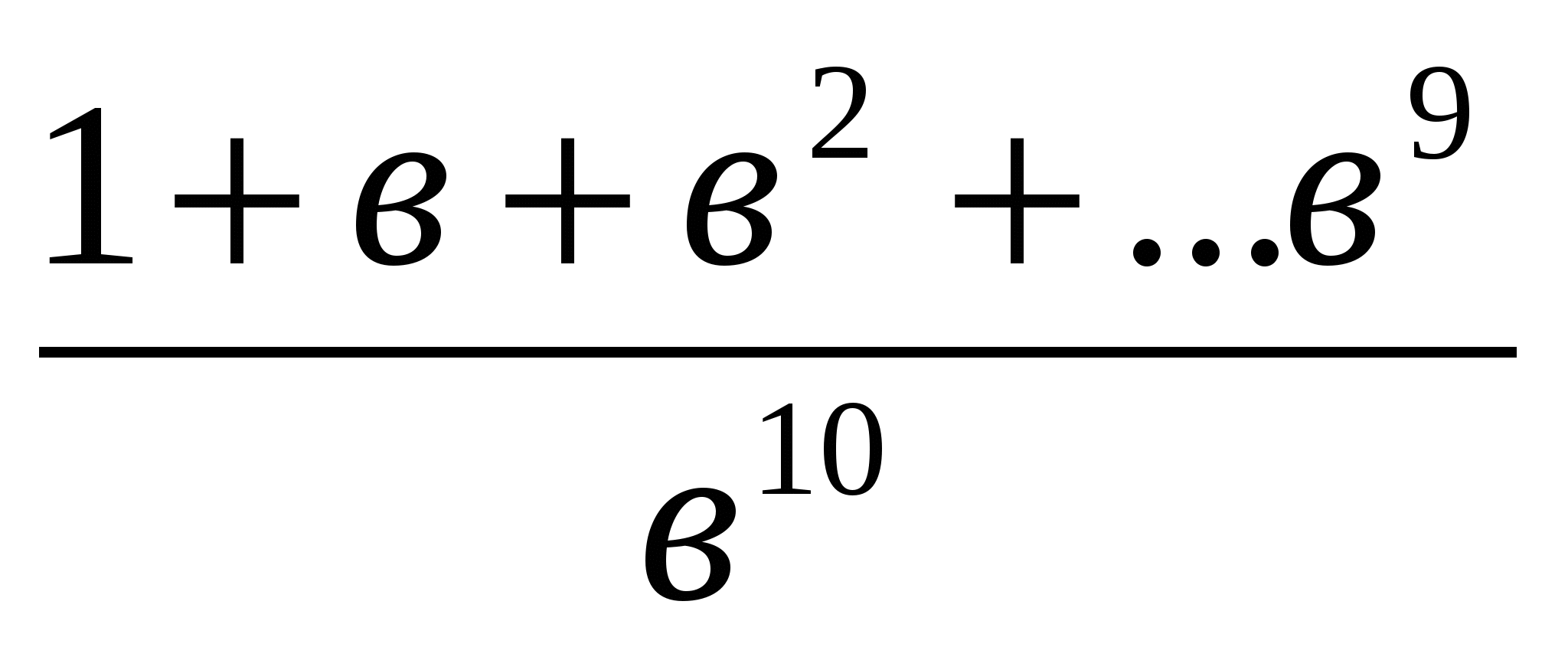 >
>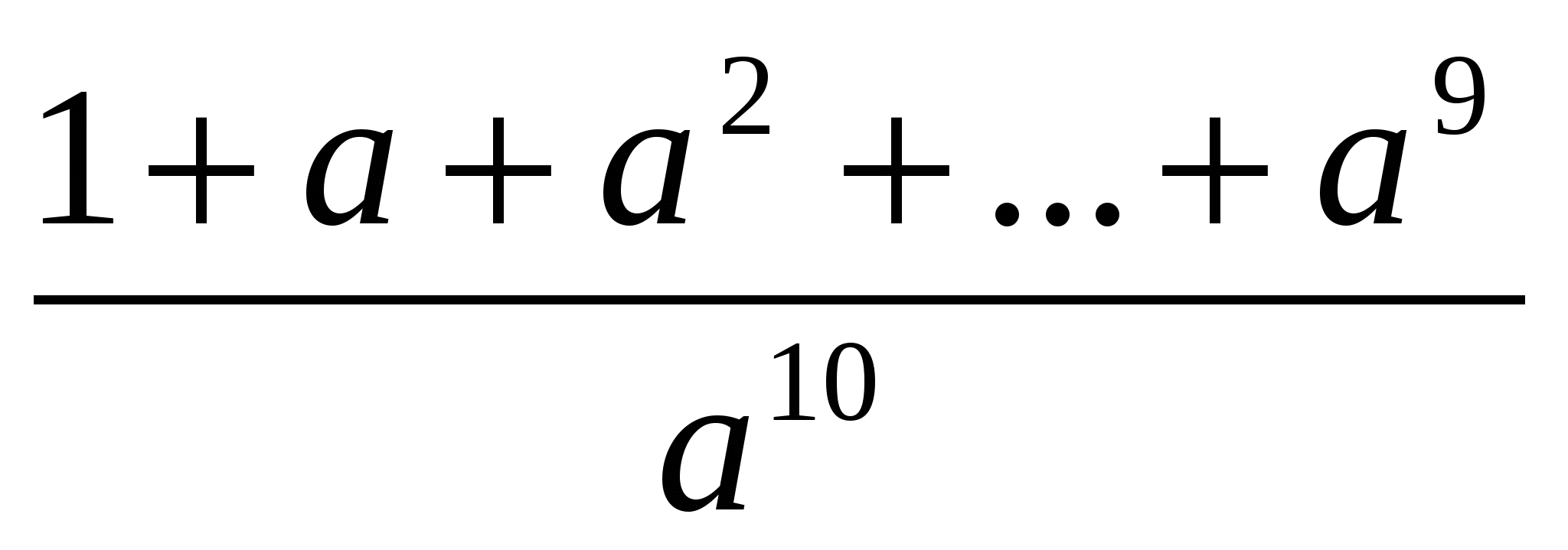
немесе 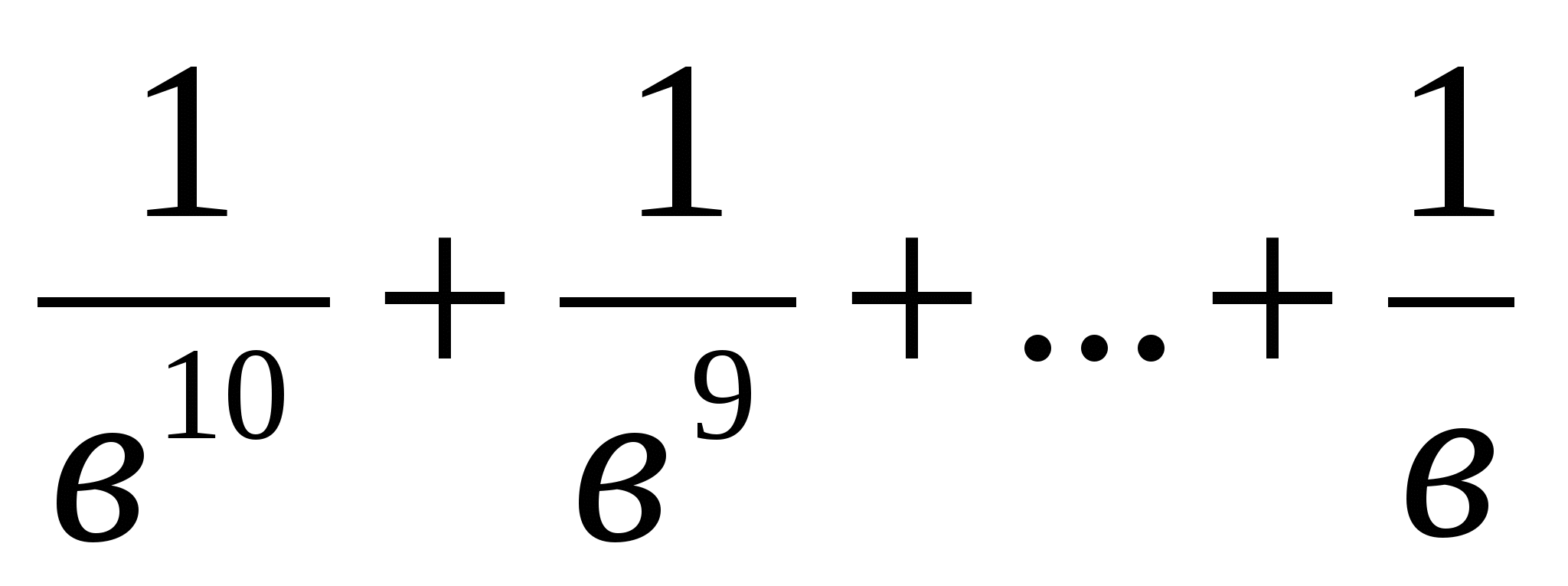 >
>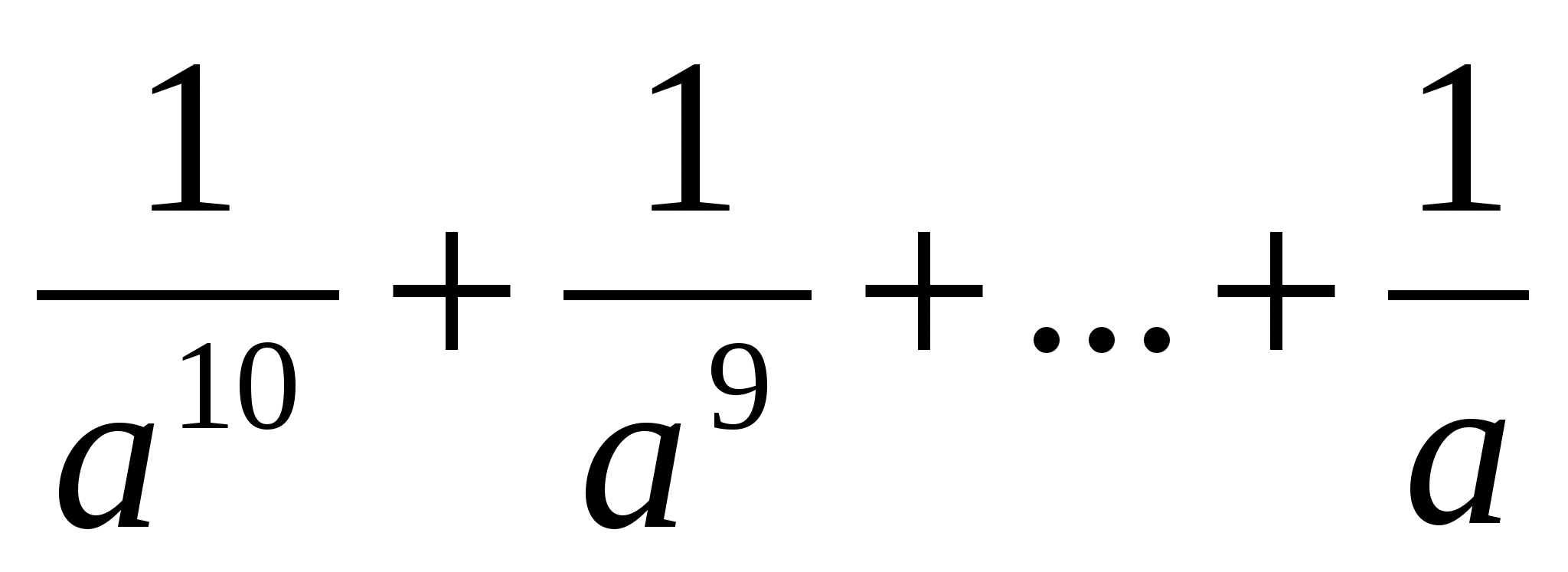
Соңғы теңсіздік тура болғандықтан дәлелденілетін теңсіздік те тура болады.
Республикалық олимпиада
11-сынып
№1.а+в+с=1, (a,в,с≥0) шарттарын қанағаттандыратын а,в,с сандары үшін теңсіздікті дәлелдеңіздер. (1+а)(1+в)(1+с)≥8(1-а)(1-в)(1-с).
Дәлелдеуі: 1+а=(1-в)+(1-с) онда 1+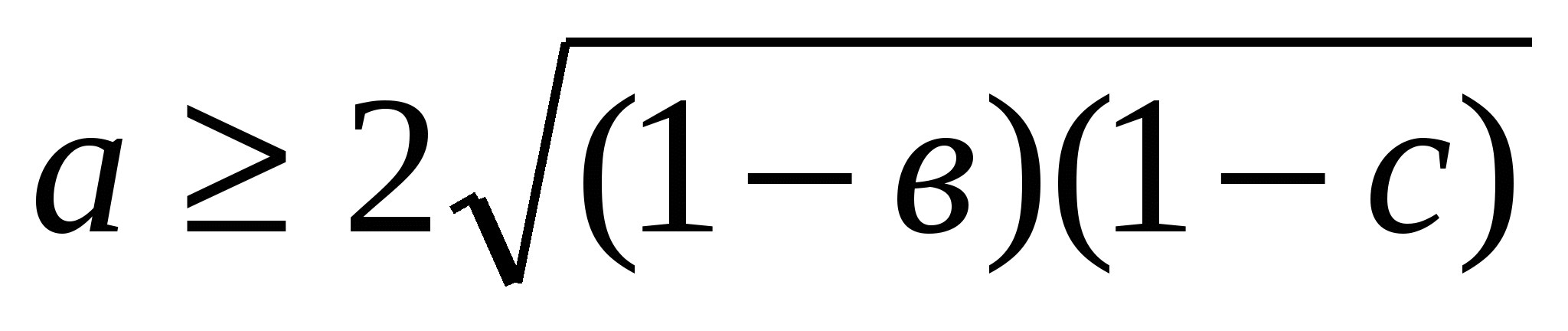 . Осы сияқты
. Осы сияқты 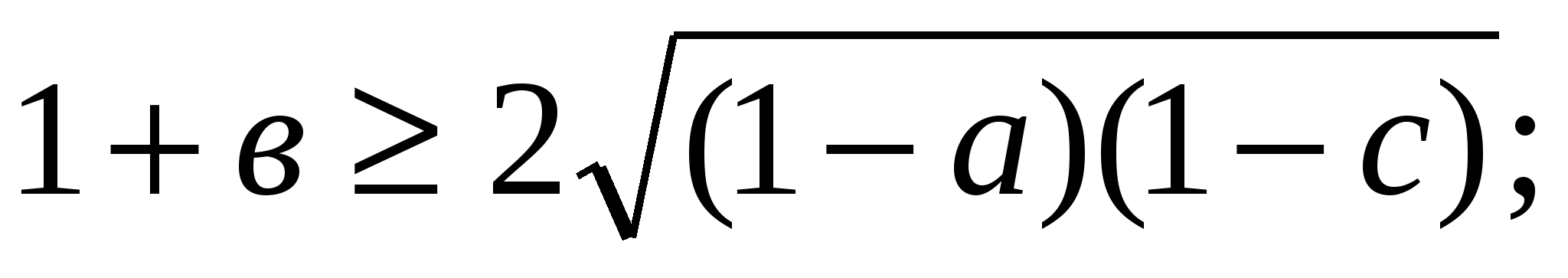
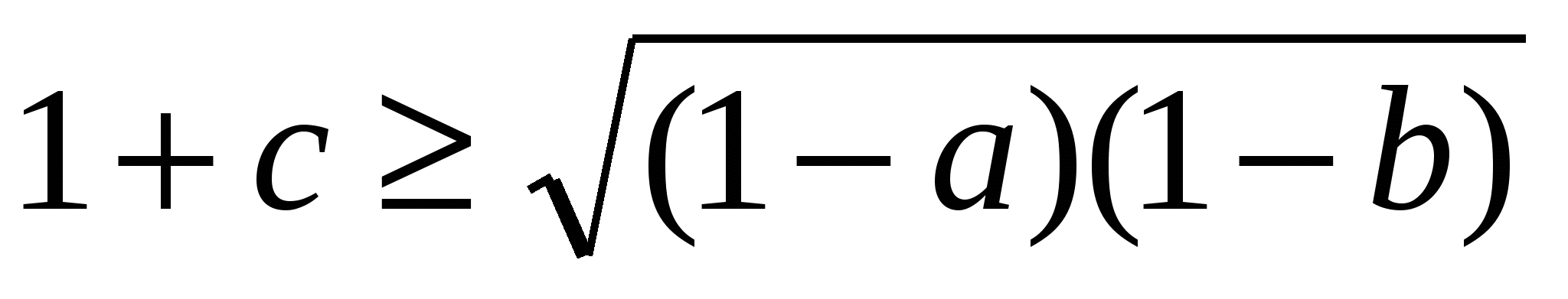 .Бұл теңсіздіктерді мүшелеп көбейтсек , дәлелденілетін теңсіздік шығады.
.Бұл теңсіздіктерді мүшелеп көбейтсек , дәлелденілетін теңсіздік шығады.
9-сынып
№1.Оң x,y,z сандары үшін теңсіздікті дәлелдеңдер:
x(1+y)+y(1+z)+z(1+x)≥6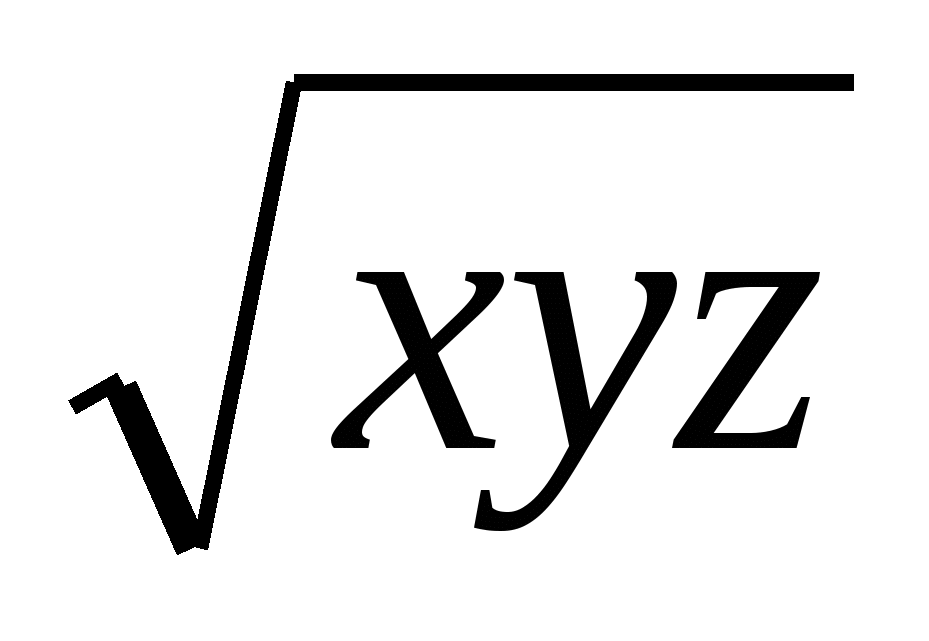
Дәлелдеуі:Белгілі а+в≥2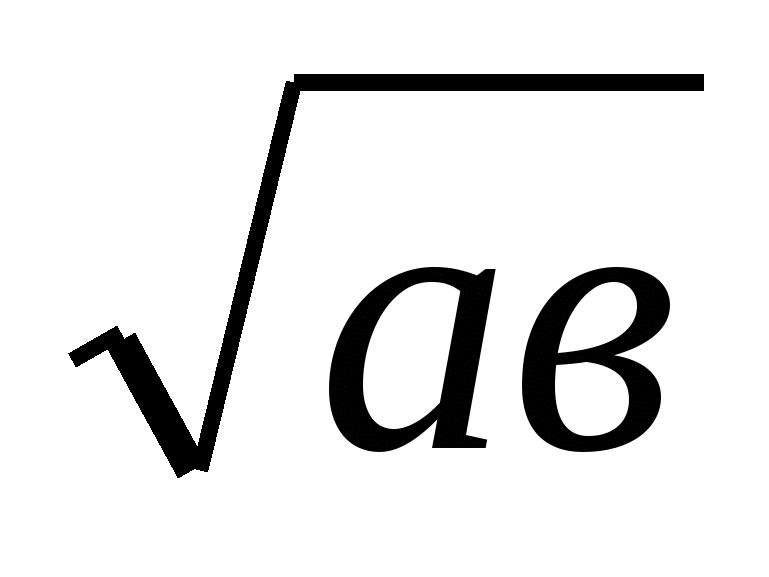 теңсіздігін (а,в, ≥0) пайдаланып x+yz≥2
теңсіздігін (а,в, ≥0) пайдаланып x+yz≥2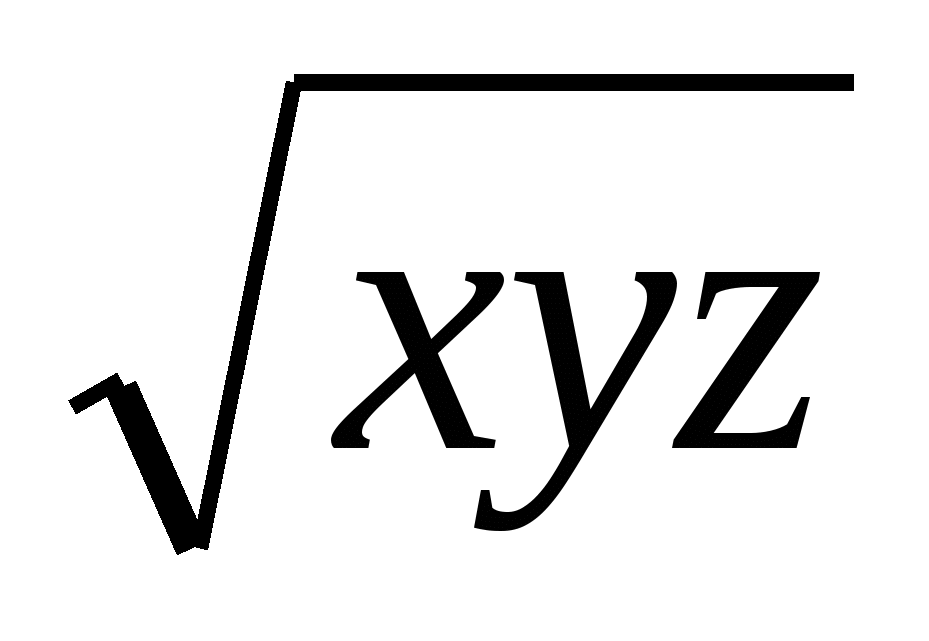 , y+xz≥2
, y+xz≥2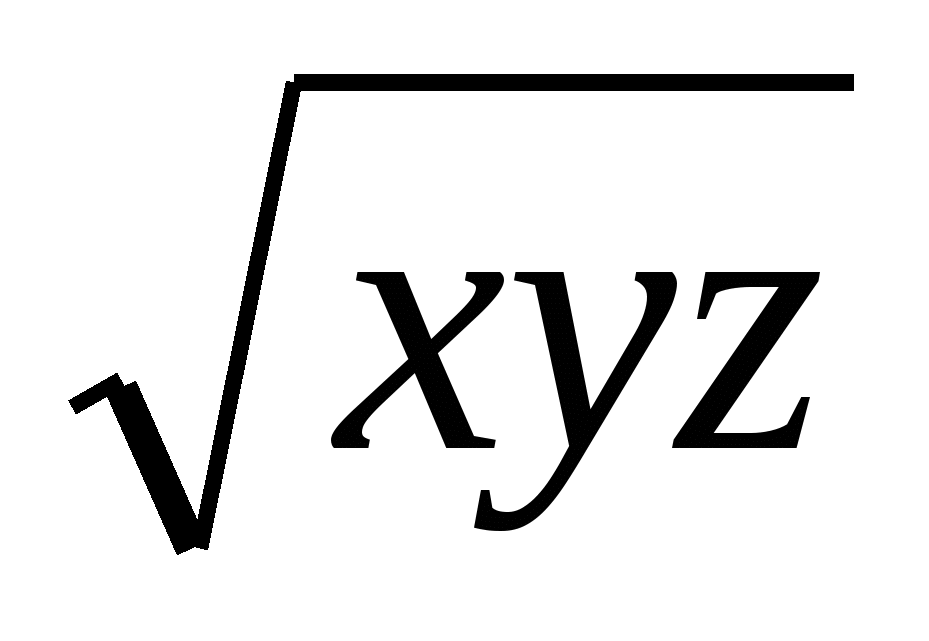 , z+xy≥2
, z+xy≥2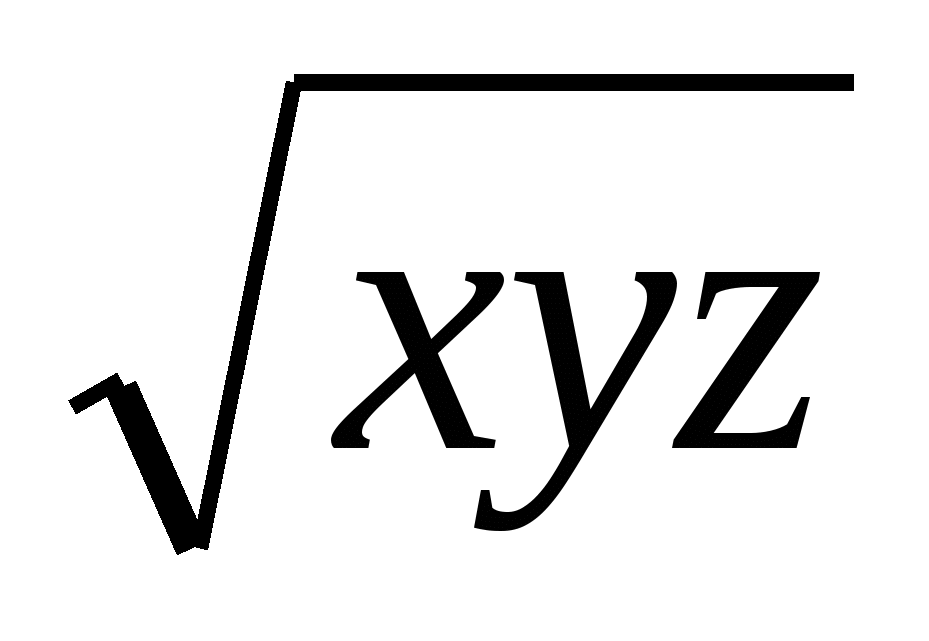 теңсіздіктерін аламыз. Осы үш теңсіздікті қосып
теңсіздіктерін аламыз. Осы үш теңсіздікті қосып
x+yz+y+xz+z+xy=x(1+y)+y(1+z)+z(1+x)>6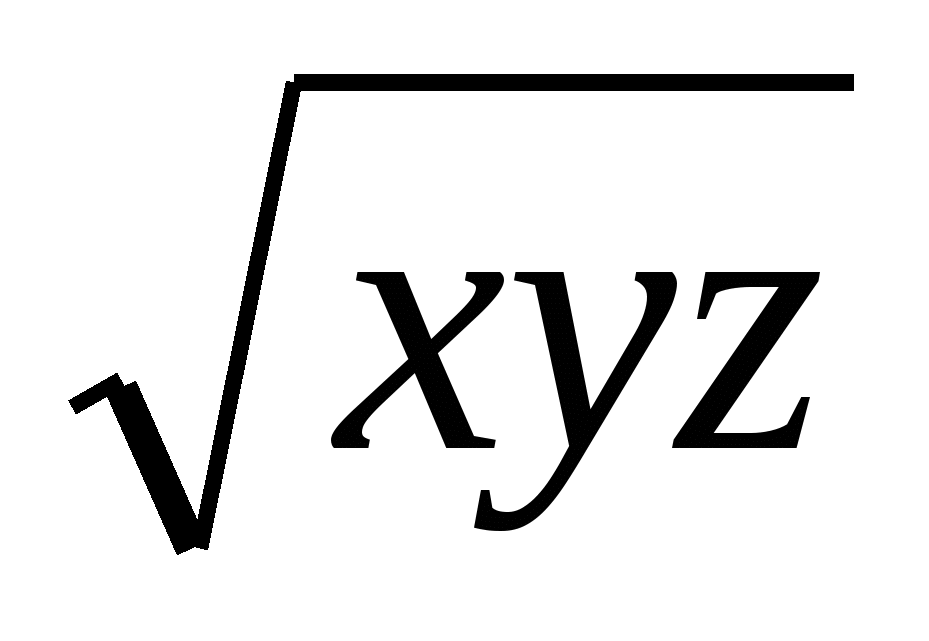 теңсіздігін аламыз.
теңсіздігін аламыз.
10-сынып.
№1.Теріс емес а,в үшін 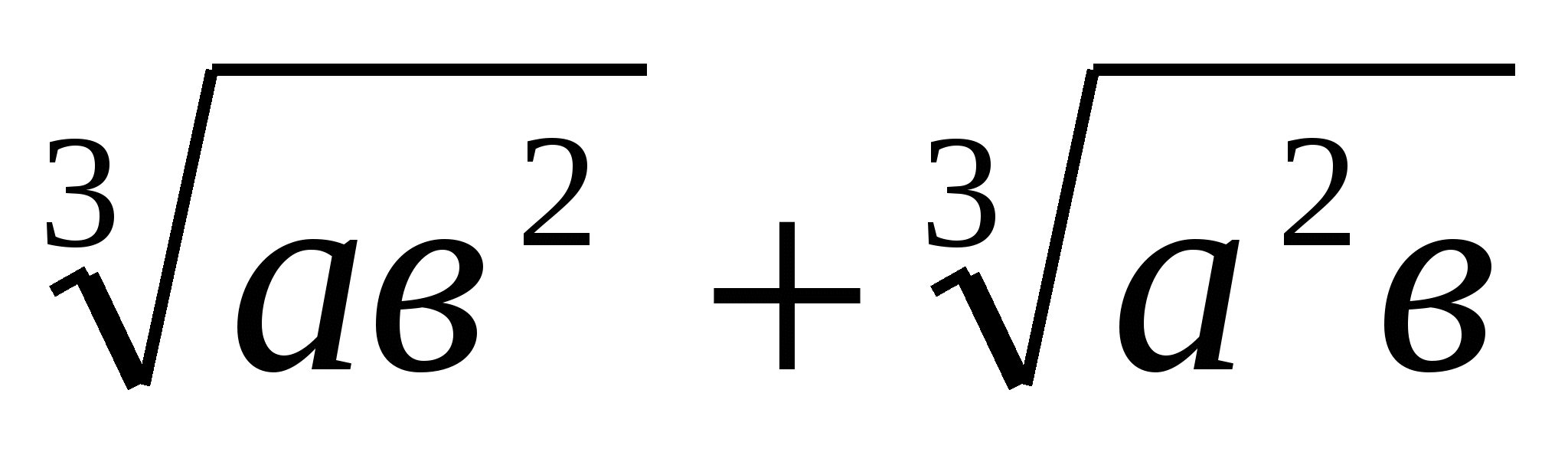 ≤а+в теңсіздігін дәлелдеңдер.
≤а+в теңсіздігін дәлелдеңдер.
Бізге 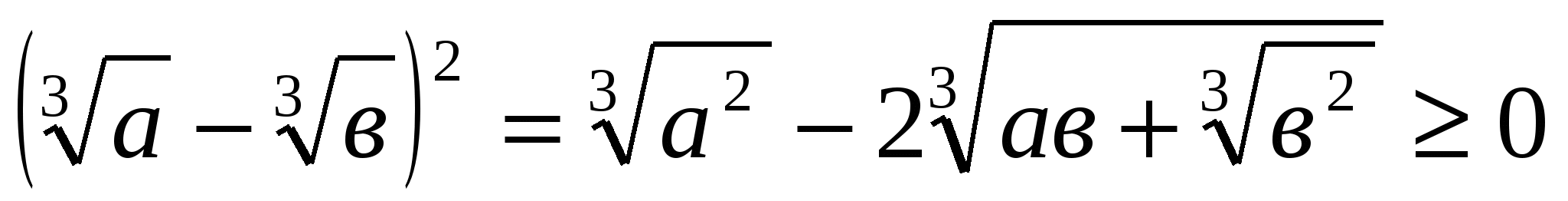 теңсіздігінен
теңсіздігінен 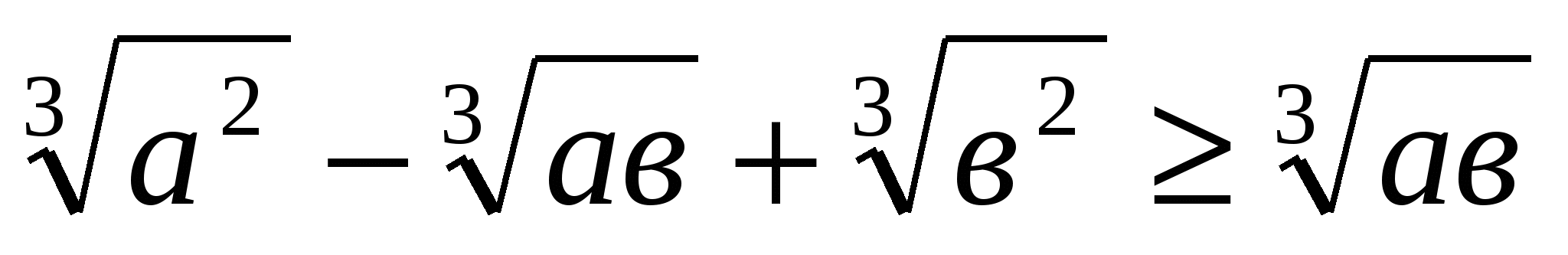
шығатыны анық.Соңғы теңсіздіктің екі жағын 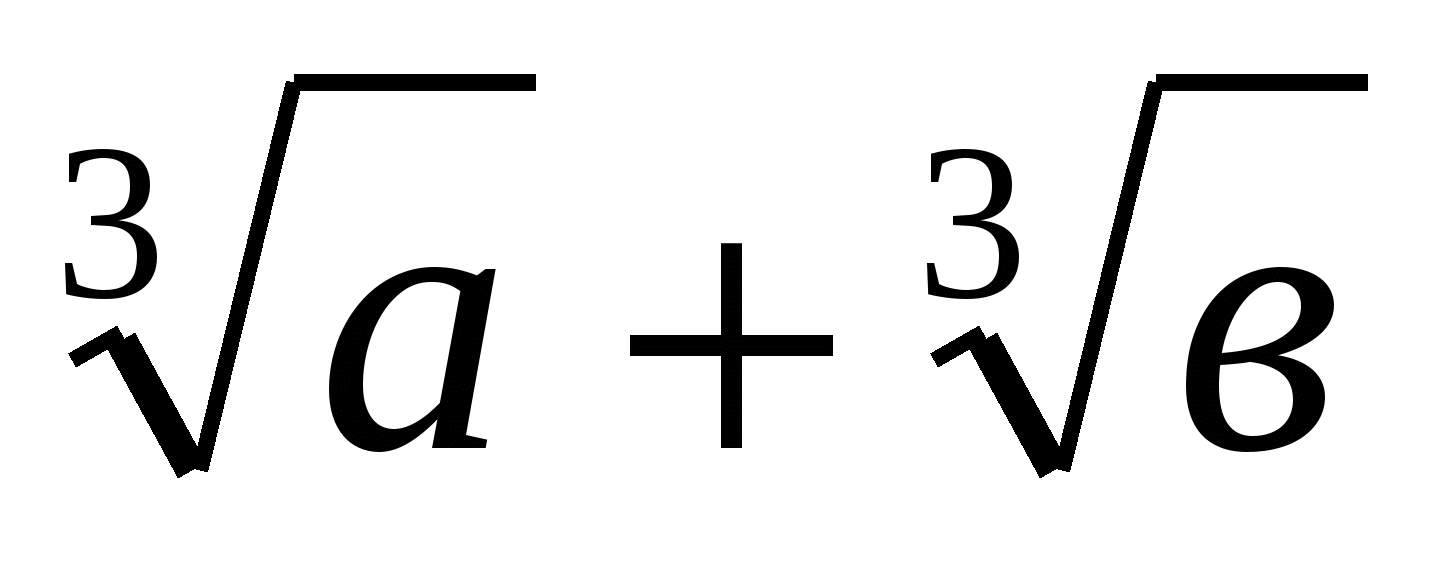 -қа көбейтсек, бізге керекті теңсіздік шыға келеді.
-қа көбейтсек, бізге керекті теңсіздік шыға келеді.
Халықаралық олимпиада
№1. а,в,с оң сандар болып және авс=1. Мынадай теңсіздікті дәлелдеңіздер:
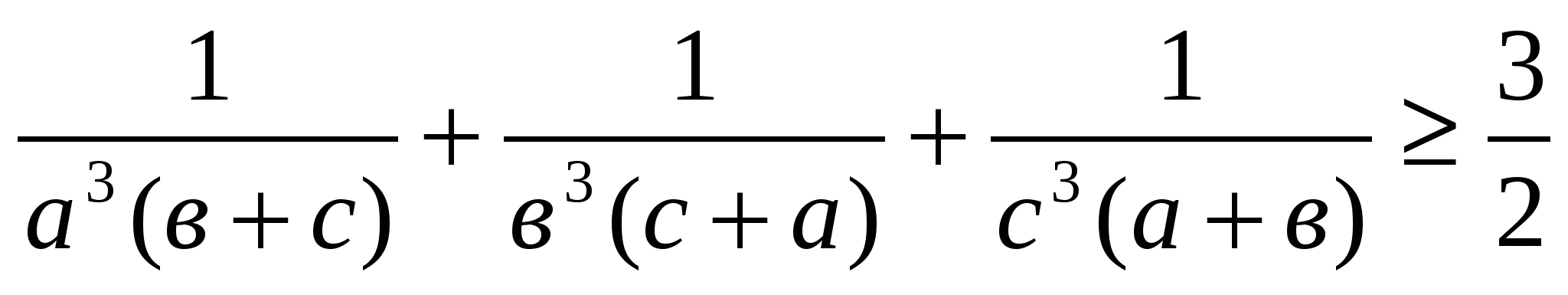
Дәлелдеуі:Жаңа белгілер енгізейік: 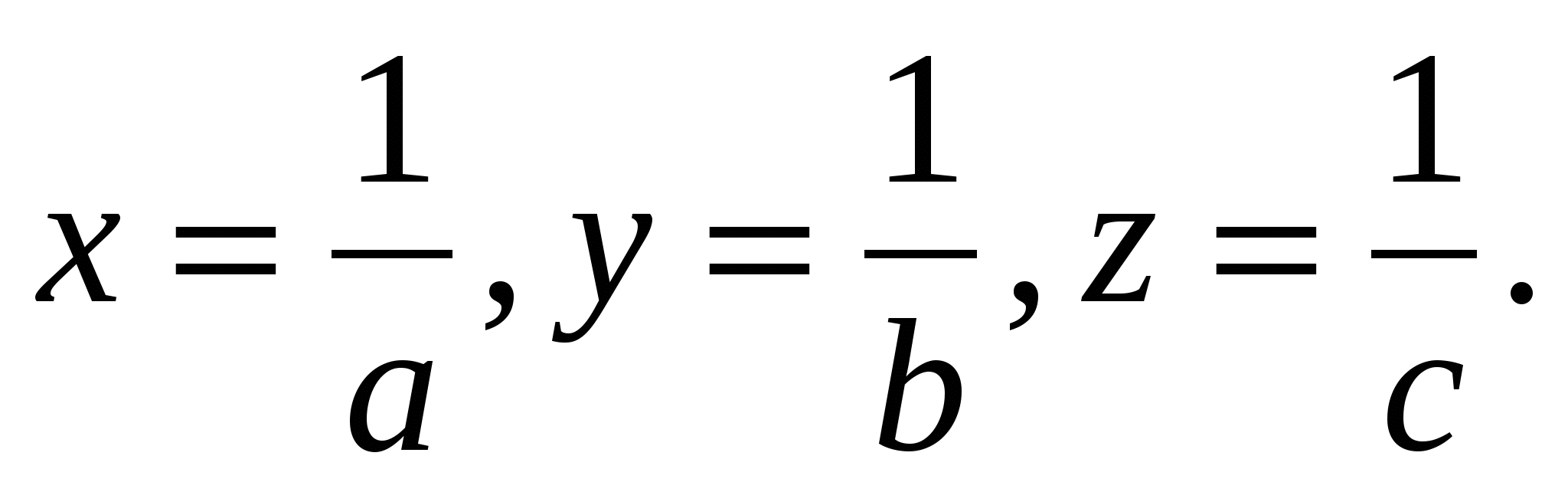
Есептің шарты бойынша xyz=1.Енді дәлелденілетін теңсіздік мынадай теңсіздікпен мәндес болады.
S=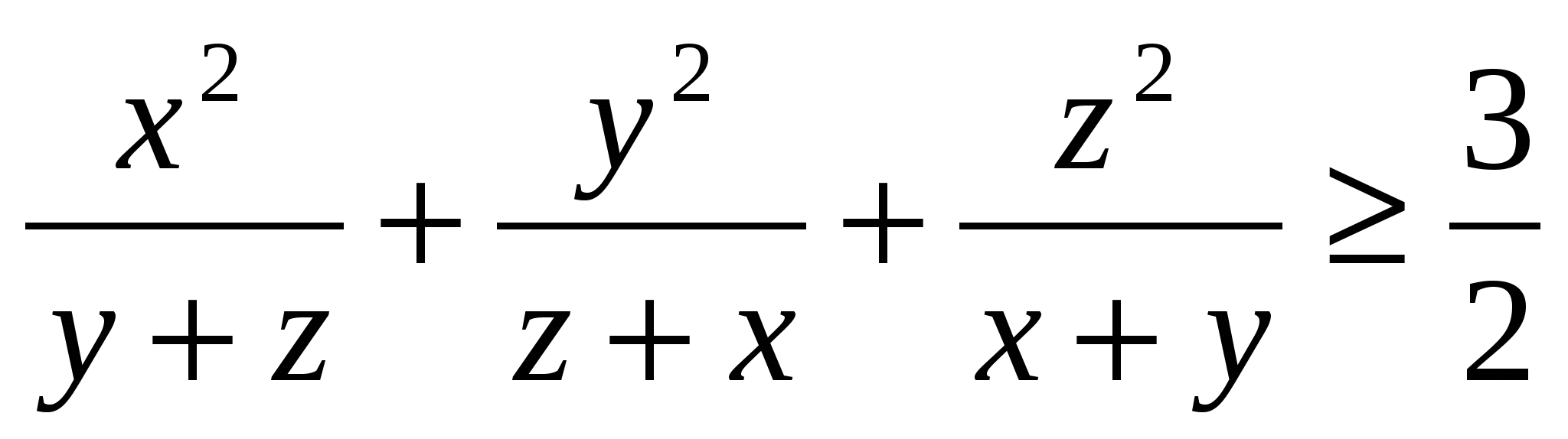 (1)
(1)
Біз оң сандардың арифметикалық ортасы мен геометриялық ортасының арасындағы байланысты қолданамыз: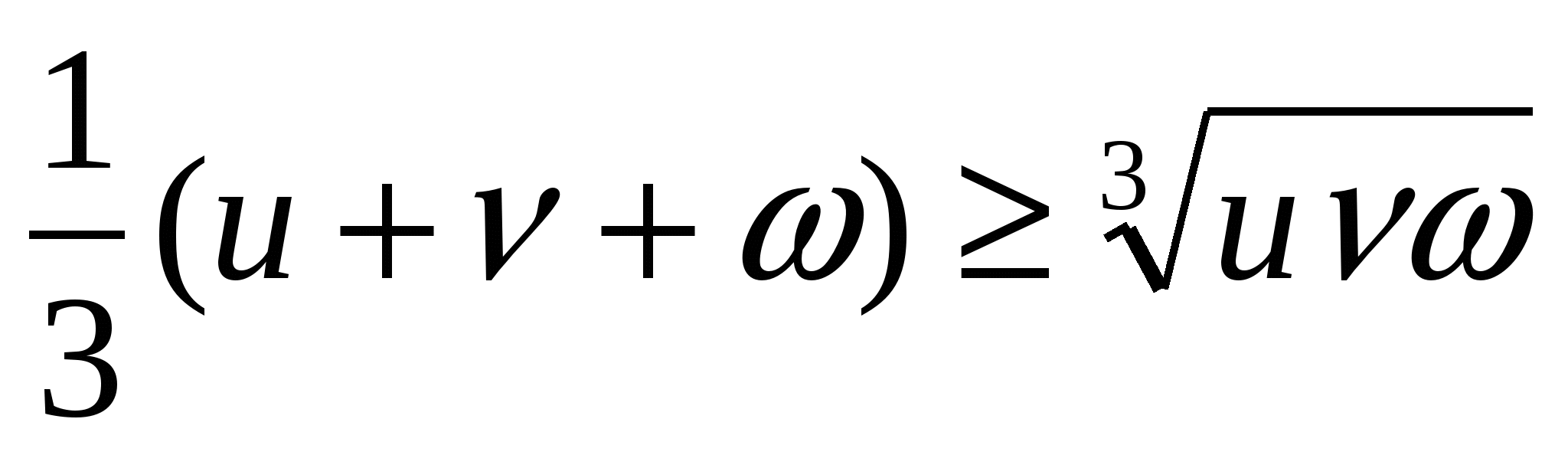 (2)
(2)
Енді Коши-Буняковский теңсіздігін қолданамыз:
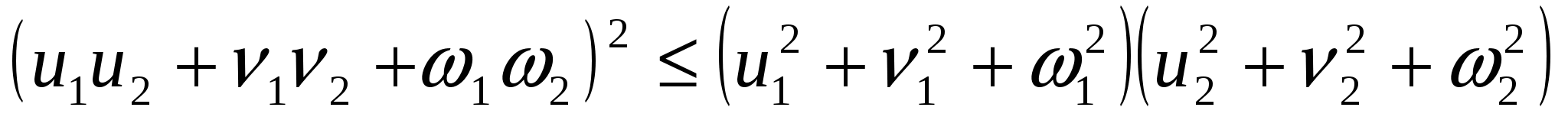
бұл теңсіздікті 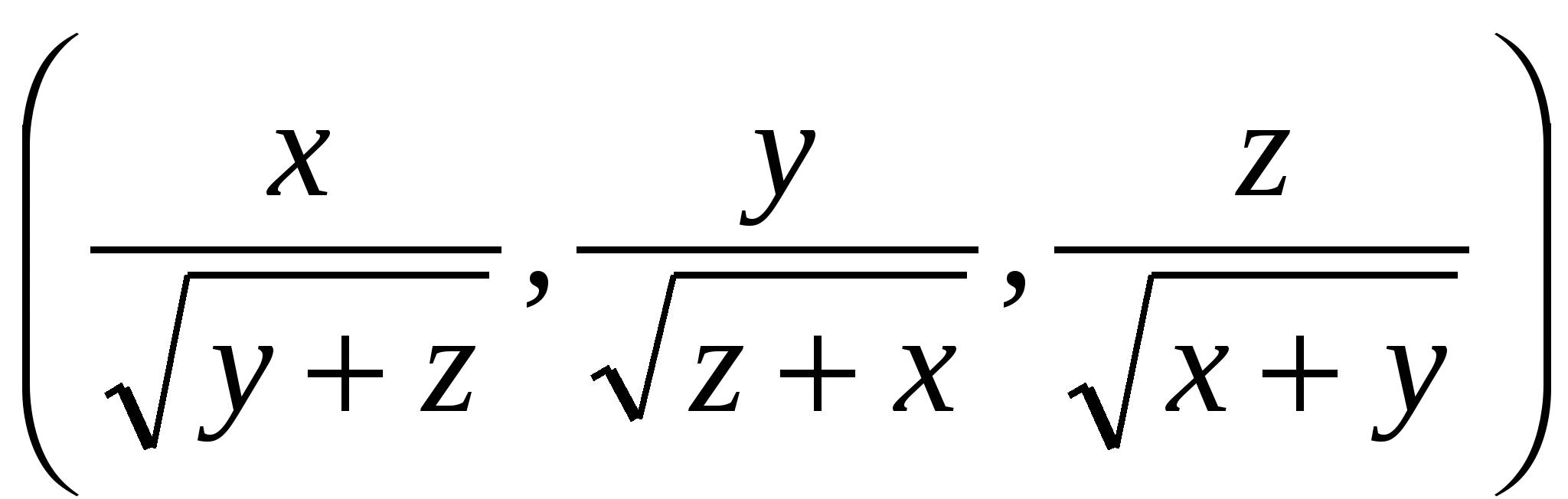 және
және 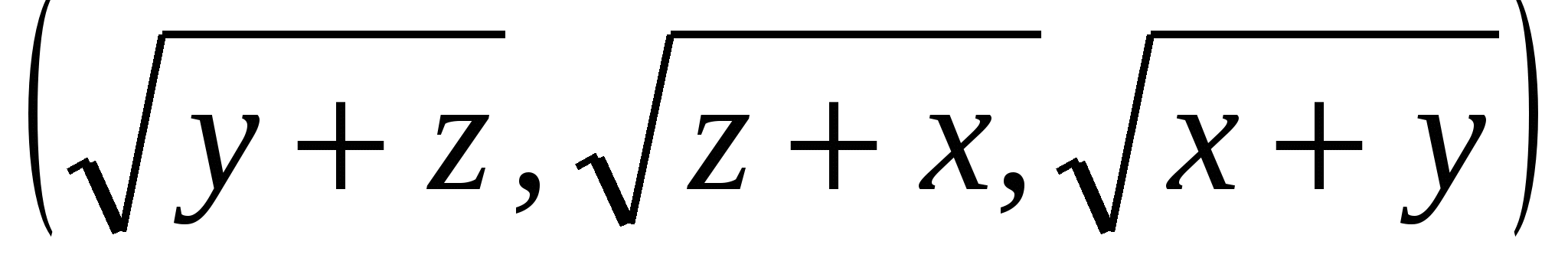 векторларына қолданып жазамыз:
векторларына қолданып жазамыз:![]() немесе
немесе 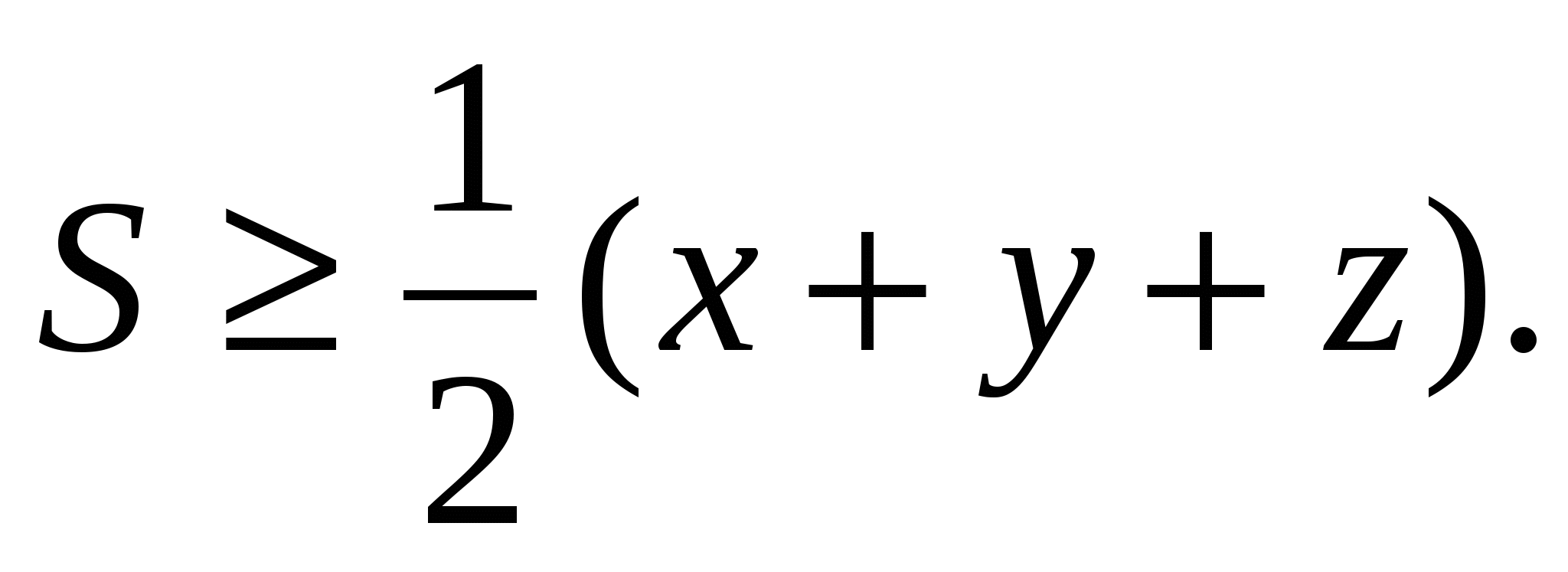
Енді 2) теңсіздікті қолданып табамыз
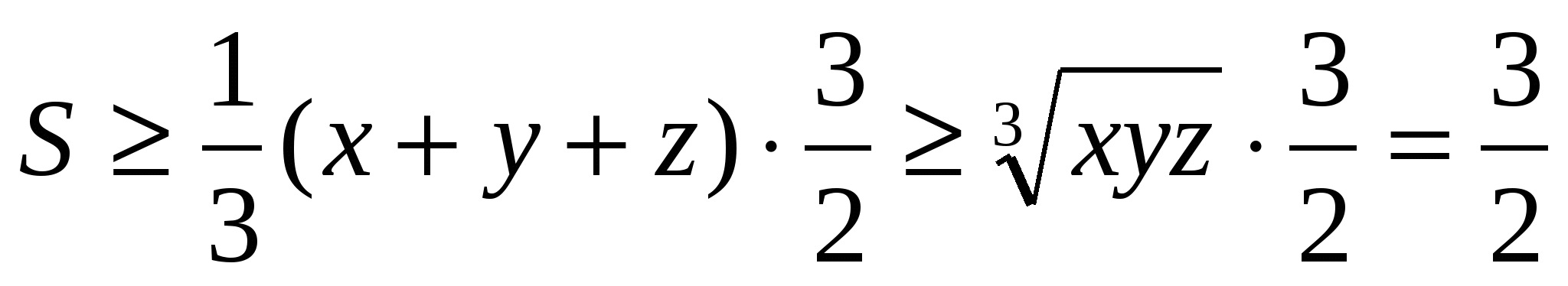
№2. Ауданы S келетін үшбұрыштың қабырғалары а,в,с болсын. Мынадай теңсіздікті дәлелдеңіздер: а2+в2+с2≥4S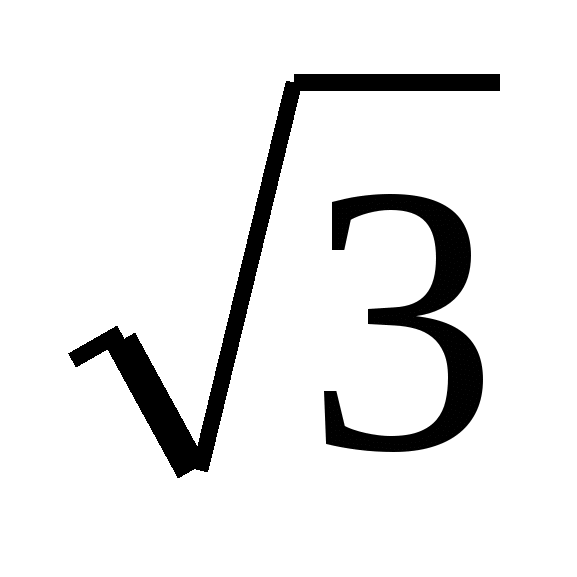 . Теңдік қашан болады?
. Теңдік қашан болады?
Дәлелдеуі: Герон формуласын жазайық.
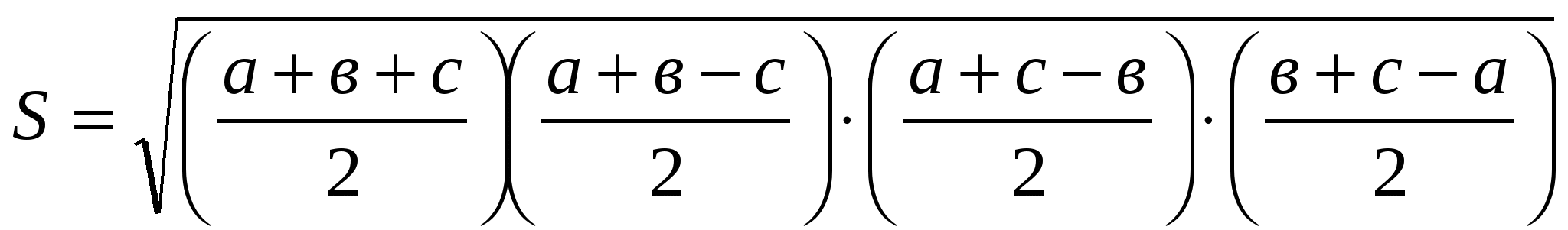
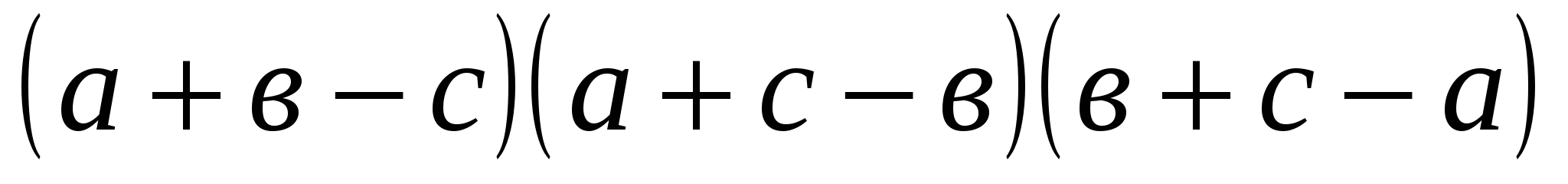 көбейтіндісын бағалау үшін мынадай теңсіздікті қолданайық
көбейтіндісын бағалау үшін мынадай теңсіздікті қолданайық 
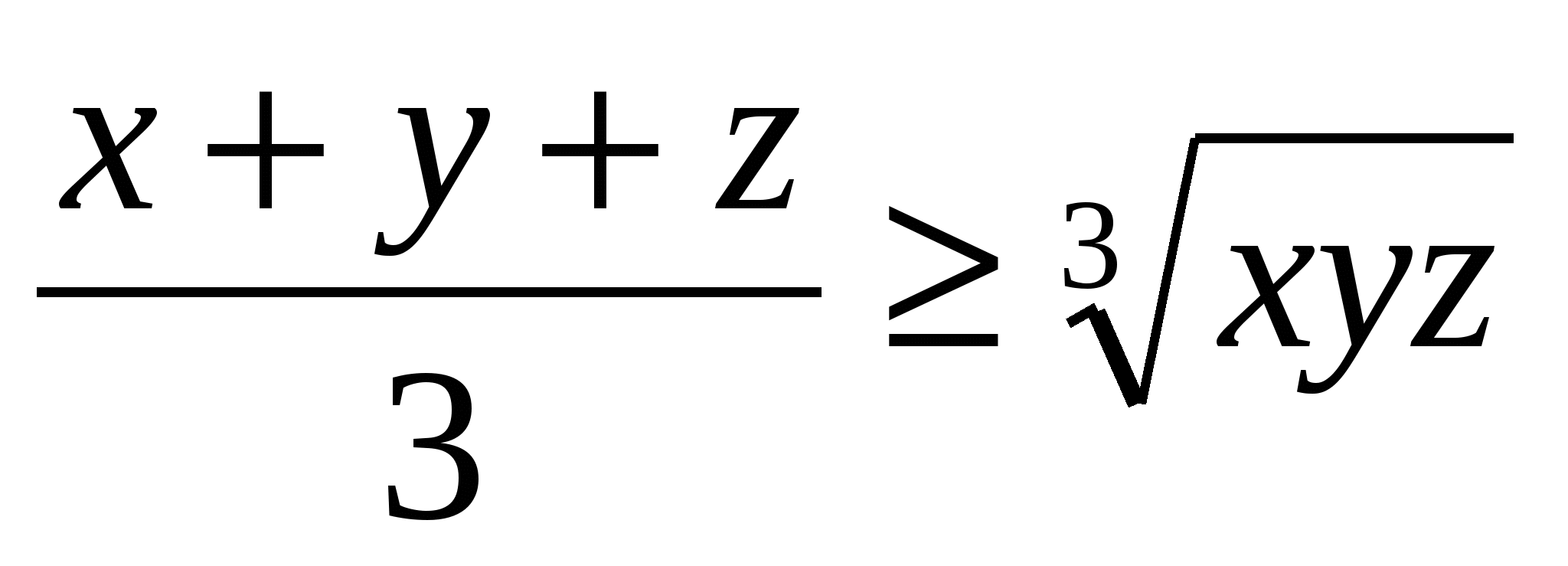 немесе xyz
немесе xyz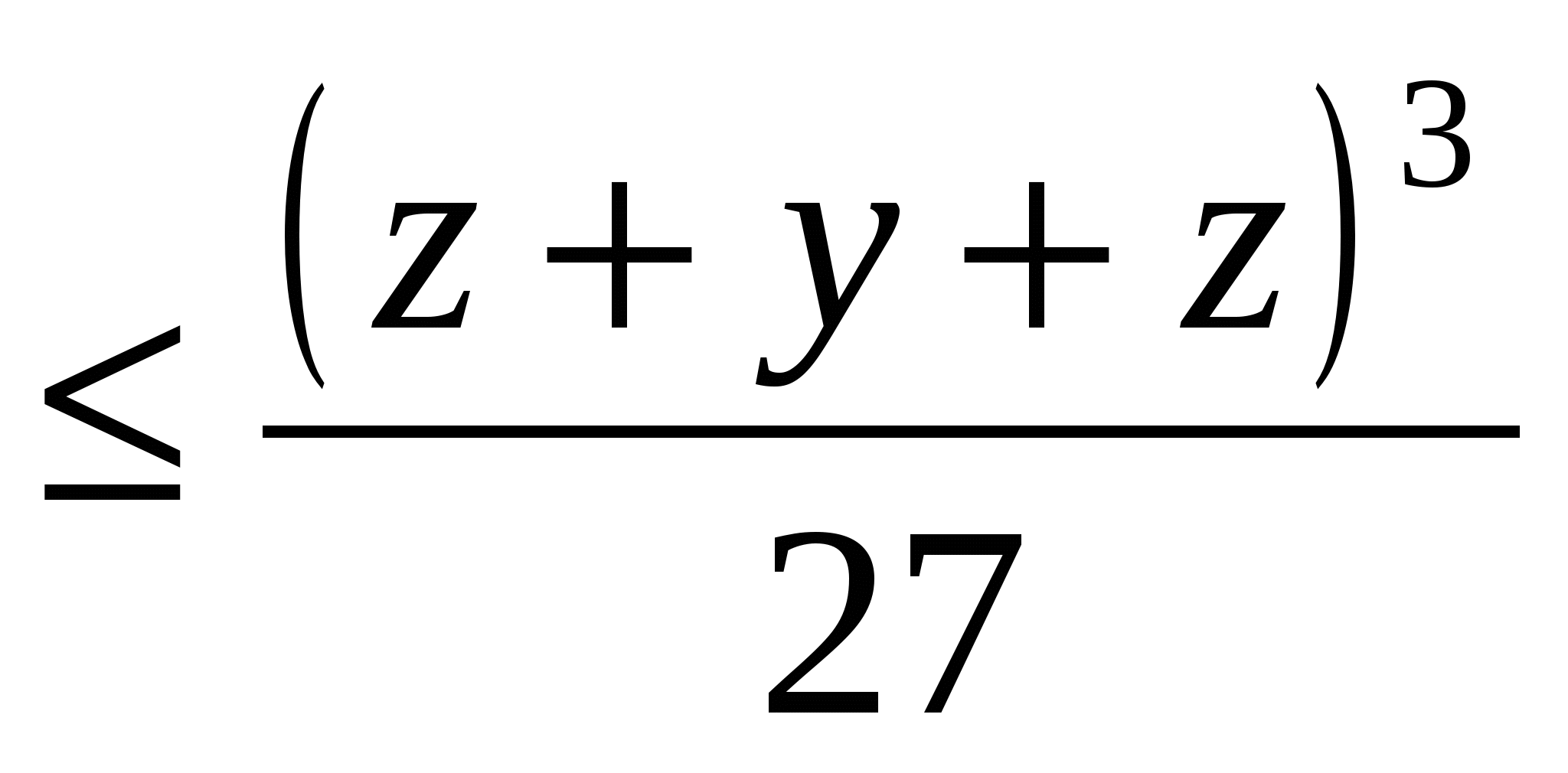 . Белгілеулер енгізейік:
. Белгілеулер енгізейік: 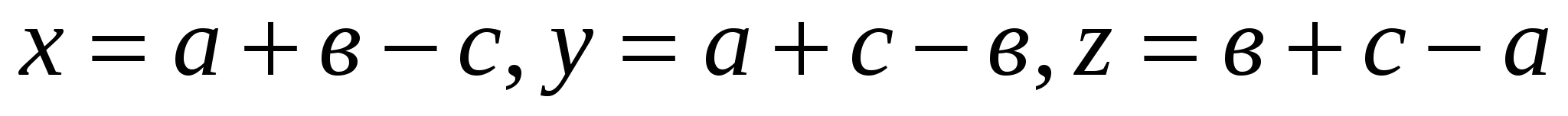 . Енді мынадай теңсіздіктерді жазуға болады:
. Енді мынадай теңсіздіктерді жазуға болады:
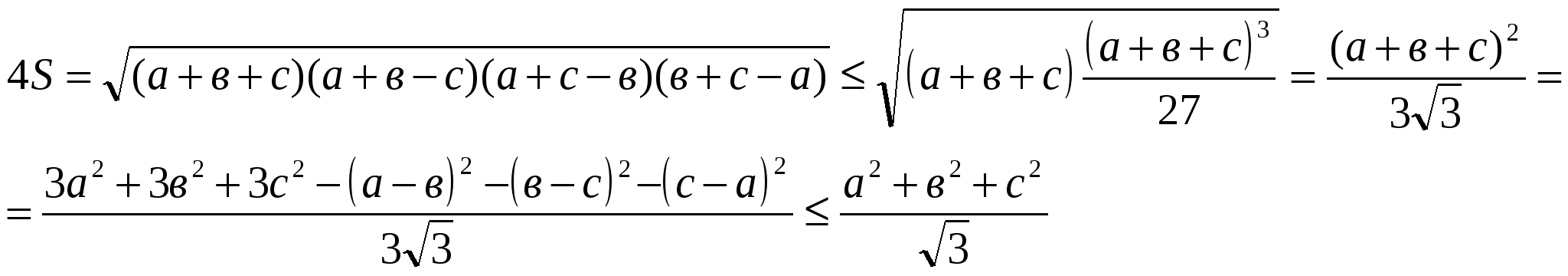
теңдік а=в=с болғанда орындалады.
Қорытындылай келе, қазіргі уақытта білім беру қызметкерлерінің алдында тұрған басты мақсат- еліміздегі білім беруді халықаралық деңгейге көтеру және білім сапасын көтеру, жеке тұлғаны қалыптастыру, қоғам қажеттілігін өтеу, оны әлемдік білім кеңістігіне кіріктіру болмақ. Сондықтан, математика пәнінен деңгейі жоғары оқушылармен олимпиадалық есептерді дайындық ретінде қарастыруға болады деп ойлаймын.
Пайдаланылған әдебиеттер.
1.Алгебра оқулығы 9-кл. А.Е. Әбілқасымова, Н.Р.Майкотов , Қ.И.Қаңлыбаев.
2. Т.Т.Абылайханов , Т.Т. Абылайханов «Математика есептері»
3. «Математика в школе» №3; 1991
4.Информатика, физика, математика №6; 1998
5.Информатика, физика, математика №3; 2001
6.Математика,физика №2; 2003

25


