- Преподавателю
- Математика
- Разработка урока по теме Применение метода интервалов для решения неравенств
Разработка урока по теме Применение метода интервалов для решения неравенств
| Раздел | Математика |
| Класс | 9 класс |
| Тип | Конспекты |
| Автор | Кублик Г.Е. |
| Дата | 08.11.2015 |
| Формат | docx |
| Изображения | Есть |
Урок № 34
Тема: Применение метода интервалов для решения неравенств
Цели:
-
Рассмотреть использование метода интервалов для решения неравенств других типов.
-
Развивать память, внимание и логическое мышление обучающихся.
-
Вырабатывать трудолюбие.
Ход урока.
I. Организационные моменты
Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала:
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Методом интервалов решите неравенство.
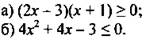
2. Найдите область определения функции 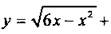
Вариант 2
1. Методом интервалов решите неравенство.
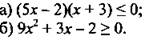
2. Найдите область определения функции 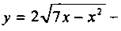
III. Изучение нового материала
Уже рассматривался метод интервалов. Применим тот же метод к решению неравенств высоких степеней. Рассмотрим схему решения на следующем примере.
Пример 1
Решим неравенство 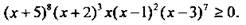
Прежде всего отметим, что если в разложение многочлена на множители входит сомножитель (х - х0)k, то говорят, что х0 - корень многочлена кратности k. Для решения неравенства важно знать, является ли k четным или нечетным числом, т. к. при четном k многочлен справа и слева от х0 имеет один и тот же знак (т. е. знак многочлена не меняется), а при нечетном k многочлен справа и слева от х0 имеет противоположные знаки (т. е. знак многочлена изменяется).
Вернувшись к данному неравенству, отметим, что многочлен имеет корни: х1 = -5 (кратности 8 - четная кратность), х2 = -2 (кратности 3 - нечетная), х3 = 0 (кратности 1 - нечетная), х4 = 1 (кратности 2 - четная), х5 = 3 (кратности 7 - нечетная). Нанесем эти корни на числовую ось и буквами «Н» и «Ч» отметим четность кратности этих корней.
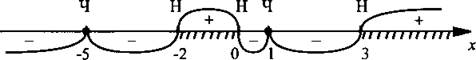
Определим знак многочлена, стоящего в левой части неравенства при любом х, не совпадающем с корнями (например, при х = -3 многочлен отрицательный). Рассмотрим теперь знаки многочлена, двигаясь в положительном направлении оси 0х. Так как х = -2 - корень нечетной кратности, то при этом значении х происходит изменение знака многочлена на противоположный и многочлен на промежутке (-2; 0) положительный. При х = 0 (корень нечетной кратности) опять происходит изменение знака многочлена и он на промежутке (0; 1) становится отрицательным. Так как х = 1 - корень четной кратности, то многочлен знака не меняет и на промежутке (1; 3) он по-прежнему отрицательный. Рассуждая подобным образом, нетрудно получить полную диаграмму знаков многочлена на всей числовой оси, приведенную на рисунке. После этого легко ответить на вопрос задачи: при каких х знак многочлена неотрицательный. Из рисунка видно, что такими х являются 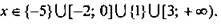
Разумеется, в тех случаях, когда неравенство не имеет вида, приведенного в примере 1, необходимо, используя те или иные приемы, привести это неравенство к указанному виду.
Пример 2
Решим неравенство х3 + 6 > 7х.
Запишем неравенство в виде х3 + 6 - 7х > 0 и разложим многочлен в левой части на множители. Для этого член -7х представим как сумму двух слагаемых: -6х и -х и сгруппируем члены многочлена: х3 - х + (6 - 6х) > 0, или х(х2 - 1) - 6(х - 1) > 0, или х(х - 1)(х + 1) - 6(х - 1) > 0, или (х - 1)(х2 + х - 6) > 0. Разложение х2 + х - 6 на множители проводим стандартным путем, зная его корни (х = -3, х = 2), и окончательно получаем: (х - 1)(х +3)(х - 2) > 0. Все корни этого многочлена первой кратности, и дальнейшее решение не вызывает трудностей. Построив диаграмму знаков многочлена, найдем х ∈ (-3; 1)U(2; +∞).

Остановимся теперь на решении рациональных неравенств методом интервалов.
Рациональные неравенства легко сводятся к решению неравенств высоких степеней. Действительно, после преобразований левая часть рационального неравенства может быть представлена в виде отношения многочленов Р(х) и Q(х), т. е. 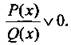 Умножим обе части такого неравенства на многочлен [Q(x)]2, который положителен при всех допустимых значениях х (т. к.Q(x) ≠ 0). Тогда знак неравенства не меняется и получаем неравенство Р(х) · Q(x) v 0, эквивалентное данному. То есть исходное неравенство
Умножим обе части такого неравенства на многочлен [Q(x)]2, который положителен при всех допустимых значениях х (т. к.Q(x) ≠ 0). Тогда знак неравенства не меняется и получаем неравенство Р(х) · Q(x) v 0, эквивалентное данному. То есть исходное неравенство 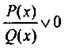 эквивалентно системе неравенств
эквивалентно системе неравенств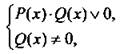 которая далее решается методом интервалов.
которая далее решается методом интервалов.
Пример 3
Решим неравенство 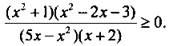
Отметим прежде всего, что (5х - х2)(х + 2) ≠ 0, или х(5 - х)(х + 2) ≠ 0, т. е. х ≠ -2, х ≠ 0, х ≠ 5 (ОДЗ неравенства). Сведем данное рациональное неравенство к алгебраическому (аналогичному примеру 1). Для этого умножим обе части неравенства на положительное выражение - квадрат знаменателя (5х - х2)2(х + 2)2. При этом знак неравенства не меняется и получаем: (х2 + 1)(х2 - 2х - 3)(5х - х2)(х + 2) ≥ 0. Разложив квадратные трехчлены на множители, имеем: (х2 + 1)(х - 3)(х + 1)х(5 - х)(х + 2) ≥ 0. Решаем это неравенство методом интервалов, учитывая, что все корни многочлена имеют первую кратность: х ∈ (-∞; -2]U[-1; 0]U[3; 5).

Теперь учтем ОДЗ исходного неравенства и окончательно найдем: х ∈ (-∞; -2)U[-1; 0)U[3; 5).
В более сложных случаях рациональные неравенства сначала сводятся к неравенствам, аналогичным примеру 3, а затем решаются методом интервалов.
Пример 4
Решим неравенство 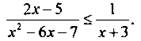
Чтобы свести пример к аналогичному предыдущему примеру, перенесем все члены неравенства в его левую часть: 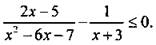 Приведя дроби к общему знаменателю, получим:
Приведя дроби к общему знаменателю, получим: 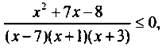 т. е. неравенство предыдущего типа. Решая его аналогично, найдем: х ∈ (-∞; -8]U(-3; -1)U[1; 7).
т. е. неравенство предыдущего типа. Решая его аналогично, найдем: х ∈ (-∞; -8]U(-3; -1)U[1; 7).
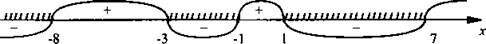
Для диаграммы знаков учтены корни числителя х2 + 7х - 8 (х = -8 и х = 1), первая кратность всех корней и ограничения на х (х ≠ -3, х ≠ -1, х ≠ 1).
Пример 5
Решить неравенство 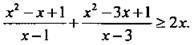
ОДЗ неравенства определяется условиями: х - 1 ≠ 0, х - 3 ≠ 0 (т. е. х ≠ 1, х ≠ 3). Почленно разделим дроби в левой части неравенства на знаменатели, сгруппировав слагаемые в числителях дробей: 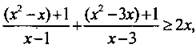 или
или 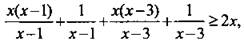 или
или 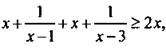 или
или 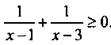 Приводим дроби к общему знаменателю и получаем:
Приводим дроби к общему знаменателю и получаем: 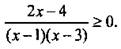 Далее решаем это неравенство по обычной схеме и находим: х ∈ (1; 2]U(3; +∞).
Далее решаем это неравенство по обычной схеме и находим: х ∈ (1; 2]U(3; +∞).

При наличии в рациональных неравенствах знаков модуля их надо раскрыть.
IV. Формирование умений и навыков обучающихся:
Задание на уроке:
№ 327 (а); 328 (б); 329 (а); 332 (б); 334 (в, г); 335 (а, г); 336 (а, б); 337 (в, г); 338 (а, г).
-
Подведение итогов урока
-
Задание на дом:
№ 327 (б); 328 (а); 329 (б, в); 333 (а); 334 (а, б); 335 (б, в); 36 (в, г); 337 (а, б); 338 (б, в).
5


