- Преподавателю
- Математика
- Методическое пособие Методы решения линейного уравнения с параметрами
Методическое пособие Методы решения линейного уравнения с параметрами
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Зевина Е.П. |
| Дата | 17.01.2015 |
| Формат | docx |
| Изображения | Есть |











































 Министерство обороны Российской Федерации
Министерство обороны Российской Федерации

Федеральное государственное общеобразовательное учреждение
«Оренбургское президентское кадетское училище»
МЕТОДЫ РЕШЕНИЯ
ЛИНЕЙНОГО УРАВНЕНИЯ С ПАРАМЕТРАМИ.
(Методические рекомендации для преподавателей и воспитанников)
Преподаватель
математики высшей категории
Зевина Елена Петровна
Оренбург
2011г.
УДК 372
Зевина Е.П.: Методы решения линейных уравнений с параметрами. Методическое пособие для воспитанников и преподавателей.
-Оренбург: ФГКОУ Оренбургское ПКУ,-20с.
Учебное пособие содержит линейные уравнения с параметрами, при решении которых возникают наибольшие затруднения во время изучения алгебры 7 класса. Методам решения таких уравнений в общеобразовательном учреждении уделяется мало внимания, и целью данного пособия является помочь воспитанникам в устранении этого пробела. Пособие может быть полезно преподавателям для работы на индивидуальных занятиях с воспитанниками.
Рассмотрено на заседании методического совета ФГКОУ Оренбургского ПКУ.
© ФГКОУ «Оренбургское президентское кадетское училище», 2012г.
Содержание
-
Введение…………………………………………………………... 4
-
Уравнения с параметром………………………………………….4
-
Простейшие уравнения с параметром…………………………….7
-
Графический способ решения линейного уравнения с параметром……………………………………………………… 10
-
Линейное уравнение, содержащее дробные коэффициенты…..13
-
Линейное уравнение, содержащее знак модуля……………… ..15
-
Алгоритм решения линейного уравнения с параметром………18
-
Примеры уравнений с параметрами из школьного учебника…18
-
Задачи для самостоятельного решения………………………….19
-
Литература ………………………………………………………..20
Введение
При изучении различных закономерностей часто приходим к решению уравнений. В школьном курсе математики в системе изучаются методы решения алгебраических уравнений, неравенств и их систем. Наибольшие затруднения вызывают уравнения с параметрами, поскольку наличие параметра предполагает решение не по аналогии и не по шаблону. Недостаточно механического применения формул, необходимо понимание логики решения, навыки анализа конкретного случая на основе известных общих свойств объекта, системность и последовательность в решении, умение объединить рассматриваемые частные случаи в единый результат. Решение уравнений с параметрами требует исследования. Этим обусловлены трудности, возникающие у учащихся при решении таких уравнений. В учебном процессе решение уравнений с параметрами предусматривается, но крайне редко, не в системе, и поэтому у учащихся зачастую не сформированы навыки их решения. Один из наиболее трудных разделов школьного курса математики рассматривается только на немногочисленных факультативных занятиях. В данном пособии будут предложены рекомендации, которые помогут понять логику решения линейных уравнений с параметрами. Данная статья может быть использована для самостоятельной подготовки к экзаменам при наличии хороших знаний школьного курса 7 класса, а также может быть полезной учителям для индивидуальной работы с учащимися, для работы на факультативных занятиях.
Уравнения с параметром.
Линейное уравнение - это уравнение вида: ах = b , где a и b - некоторые постоянные. При решении линейных уравнений, получаем различное количество корней уравнения. Чтобы понять логику решения линейного уравнения с параметрами рассмотрим решение следующих частных уравнений.
Пример 1. Решить уравнение 3х = - 15 .
Решение: Т.к. а = 3, а b = - 15, то х = - 15 : 3(деление возможно, 3≠0);
х = -5.
Проверка: 3 ( -5) = - 15 0; - 15 = - 15(верное), то -5 является корнем исходного уравнения
Ответ: -5
Пример 2. Решить уравнение 0х = 0
Решение: 0 = 0(верное при любом значении переменной х ), то корнем уравнения является любое число.
Ответ: х - любое число
Пример 3. Решить уравнение 0х= 7
Решение: 0 = 7 (не верно при любом значении х), уравнение корней не имеет.
Ответ: хЄ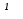
Вывод: 1) Если а≠0, то уравнение имеет единственный корень: х = 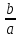 ( ах = b; ах = b; х = b : а; х=
( ах = b; ах = b; х = b : а; х=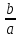 )
)
2) Если а = 0 и b = 0, то корнем уравнения ах= b является любое число.
3) Если а = 0, b≠0, то уравнение ах= b не имеет корней, хЄ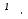
Если а и b не принимать конкретными значениями, то, говорят, что а и b - это параметры в уравнении ах=b, а само уравнение ах=b - уравнение с параметрами. Однако овладеть методикой решения уравнений с параметром мне кажется очень полезным: оно существенно повышает уровень логической подготовки учащихся, позволяет чуть по-новому, как бы изнутри взглянуть на линейную зависимость, подробно анализируемую школьной программой.
Многие учащиеся воспринимают параметр, как «обычное» число. Действительно, в некоторых уравнениях параметр можно считать постоянной величиной, но эта постоянная величина принимает неизвестные значения! Поэтому необходимо рассматривать уравнение при всех возможных значениях этой постоянной.
С параметрами семиклассники встречаются уже при введении некоторых понятий. В качестве примеров рассмотрим следующие объекты:
- функция прямая пропорциональность: y = kx (x и y переменные, k - параметр, k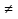 0);
0);
- линейная функция: y = kx+b (x и y - переменная, k и b - параметры);
- линейное уравнение: ax+b=0 (x - переменная, a и b - параметры, a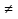 0).
0).
К уравнениям с параметрами, рассматриваемым в школьном курсе, можно отнести, например, поиск решений линейных уравнений в общем виде, исследование количества их корней в зависимости от значений параметров. Этот небольшой класс задач, конечно, многим не позволяет усвоить главное: параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойную природу. С одной стороны, с параметром работаем как с числом, с другой - это неизвестное. Так, деление на выражение, содержащее параметр, без предварительных исследований невозможно. Как правило, результаты этих исследований влияют и на решение, и на ответ.
Основное, что нужно усвоить при первом знакомстве с параметром, - это необходимость осторожного, даже деликатного обращения с фиксированным, но неизвестным числом. Определение уравнения с параметром: «Пусть дано равенство с переменными х, а: f (x; а) = 0. Если ставится задача для каждого действительного значения а решить это уравнение относительно х, то уравнение f (х; а) = 0 называется уравнением с переменной х и параметром а. Решить уравнение с параметром а - это значит, для каждого значения а найти значение х, удовлетворяющие этому уравнению». Назовем контрольными значения параметра те значения, при которых обращается в нуль коэффициент при х в линейном уравнении. Рассмотрим алгебраический способ решения линейного уравнения.
Простейшие уравнения с параметром.
-
Простейшие уравнения с параметром.
Рассмотрим решение линейных уравнений, если параметр является свободным членом.
Пример 4. Решить уравнение x - a = 0.
Ответ: x = a, при любом a
Пример 5. Решить уравнение 5x = a . Ответ: x = 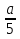 , при любом a.
, при любом a.
-
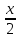 = a Ответ: x = 2a, при любом a.
= a Ответ: x = 2a, при любом a.
Вывод: если параметр является свободным членом в уравнении, то уравнение всегда имеет один корень.
Подобные упражнения помогают учащимся привыкнуть к параметру, к необычной форме ответов при решении уравнений. Замечу, что даже такие, казалось бы, совершенно элементарные уравнения часто требуют от учителя подробных комментариев и терпеливых объяснений.
2. В качестве второго шага, рассмотрим уравнения с параметром, где выделим уравнения с небольшим числом легко угадываемых ветвлений.
Пример 6. Решить уравнение 0•х = а.
Ответ: при а 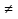 0, корней нет,
0, корней нет,
при а = 0, х - любое из множества R.
Пример 7. Решить уравнение. |x| = a.
Ответ: при а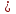 0, корней нет,
0, корней нет,
при а = 0, х = 0,
при а 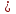 0, х =
0, х = 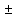 а.
а.
3.Рассмотрим уравнения с параметром, где параметр - это коэффициент линейного уравнения, и, он может имеет вид алгебраического выражения.
Пример 8. Решить уравнение ах = 1.
Решение: Найдем контрольные значения параметра для коэффициента при х, а=0. Решение данного уравнения сведем к одному из случаев примеры 1-3.
-
Если а=0, то уравнение примет вид: 0х=1, а это уравнение не имеет корней.
-
Если а≠0, то деление на а возможно и х =
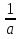
Ответ: Ø при а =0; 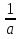 при
при 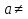 0.
0.
Пример 9. Решить уравнение (а -3)х=1.
Решение: Найдем контрольные значения параметра для коэффициента при х, т.е. а-3=0, то а=3. Решение данного уравнения сведем к одному из трех случаев. (примеры 1-3).
1)Если а=3, то а -3=0, и уравнение (а -3)х=1 примет вид 0х=1, а это уравнение корней не имеет.
2)Если а ≠3, то то деление на а возможно и х=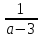
Ответ: Ø, при а =3; 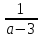 , при а ≠3.
, при а ≠3.
Рассмотрим уравнения с параметром, где коэффициент линейного уравнения и свободный член содержат параметр.
Пример 10. Решить уравнение (а -2)х= а -2.
Решение: Найдем контрольные значения параметра для коэффициента при х , т.е. а -2=0, то а =2.
-
Если а =2, то а -2=0, и уравнение (а -2)х= а -2 примет вид 0х=0, х - любое число.
-
Если а ≠2, то деление на а возможно х=
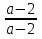 =1
=1
Ответ: любое число, при а =2; 1, при а ≠2
Пример 11. Решить уравнение b х + 1=2b + х.
Решение: Приведем данное уравнение b х + 1=2b + х к виду ах = b.
b х - x=2b - 1
(b - 1)х=2b - 1
Найдем контрольные значения параметра для коэффициента при х,
b - 1=0, b=1.
Если b=1,то b - 1=0, то уравнение (b - 1)х=2b - 1 примет вид 0х=1, корней нет
-
Если b≠1, то b - 1≠0 деление возможно на b - 1 и х=
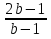
Ответ: Ø, при b=1; 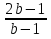 , при b≠1.
, при b≠1.
Пример 12. Решить уравнение (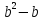 )х=
)х=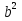 - 1.
- 1.
Решение: (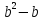 )х=
)х=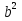 - 1
- 1
Найдем контрольные значения параметра для коэффициента при х, т.е.
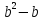 =0, b(b-1)=0, b=0 или b=1
=0, b(b-1)=0, b=0 или b=1
1)Если b=1,то 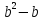 =0, уравнение(
=0, уравнение(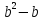 )х=
)х=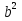 - 1 примет вид 0х=0, то х - любое.
- 1 примет вид 0х=0, то х - любое.
2)Если b=0,то 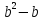 =0, уравнение примет вид 0х= - 1, корней нет
=0, уравнение примет вид 0х= - 1, корней нет
3)Если b≠1 и b≠0, то деление на b(b-1) возможно и х=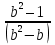 =
=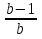
Ответ: любое число, при b=1;
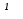 , при b=0;
, при b=0;
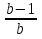 , при b≠1 и b≠0.
, при b≠1 и b≠0.
Пример 13. Решить уравнение 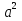 х=а(х+2) - 2
х=а(х+2) - 2
Решение: Приведем данное уравнение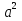 х=а(х+2) - 2 к виду ах = b.
х=а(х+2) - 2 к виду ах = b.
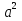 х=а(х+2) - 2
х=а(х+2) - 2
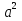 х=ах+2а-2
х=ах+2а-2
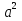 х-ах=2а-2
х-ах=2а-2
(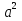 -а)х=2а-2
-а)х=2а-2
Найдем контрольные значения параметра для коэффициента при х,
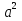 -а=0, а(а-1)=0, а=0 или а=1
-а=0, а(а-1)=0, а=0 или а=1
-
Если а=0, то
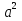 -а=0, и уравнение (
-а=0, и уравнение (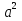 -а)х=2а-2примет вид ох= - 2, корней нет
-а)х=2а-2примет вид ох= - 2, корней нет -
Если а=1, то
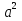 -а=0, и уравнение примет вид 0х=0, х - любое число
-а=0, и уравнение примет вид 0х=0, х - любое число -
Если а≠0 и а≠1, то х=
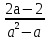 =
=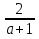
Ответ: 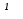 , при а=0;
, при а=0;
любое число, при а=1;
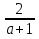 , при а≠0 и а≠1.
, при а≠0 и а≠1.
Данные выше примеры позволили увидеть, как изменяется вид рассматриваемого линейного уравнения с изменением значения параметра и влияние параметра как переменной на значение корней и их количество.
Графический способ решения линейного уравнения с параметром.
Рассмотрим геометрическую интерпретацию решения линейного уравнения с параметрами kx+b=0. Графический способ определения числа корней уравнения в зависимости от входящего в него параметра является более удобным, чем аналитический. Количество корней линейного уравнения kx+b=0 зависит от расположения прямых у= kx+b и у=0, но второе уравнение можно записать в виде у= 0x+0, где k=0, b=0. Две прямые на плоскости могут либо пересекаться (только в одной точке), либо быть параллельными, либо совпадать, а соответственно уравнение kx+b=0 может иметь 1 корень, не иметь корней, или иметь бесчисленное множество корней.
Решением уравнения kx+b=0 являются абсциссы точек пересечения прямых, заданных уравнениями у= kx+b и у= 0x+0.
Рассмотрим эти случаи расположения прямых, и подтвердим, от чего зависит решение уравнения.
1 случай:
Пусть в уравнении у= kx+b, параметр b - некоторое фиксированное число, k - любое, k≠0. Это уравнение на плоскости задает множество прямых, проходящих через точку (0; b). k - угловой коэффициент прямой и он один и тот же для данного множество прямых. Т.к. k≠0, то прямые, заданные уравнениями у= kx+b и у= 0x+0, пересекаются.
Вывод: уравнение kx+b=0 при k≠0 имеет один корень. ( рис.1)
Рис.1
0 у=0х+0 x
2 случай:
Пусть в уравнении у= kx+b, k - некоторое фиксированное число, k≠0, b - любое. Графиком данного уравнения является множество параллельных прямых, имеющих один и тот же угловой коэффициент. Построим в одной системе координат графики функций y=kx+b y=0x+0 (y=0) и найдем координаты точек пересечения: (х;0). Абсциссы этих точек являются решением уравнения kx+b=0.
Вывод: уравнение kx+b=0 при k≠0 имеет один корень.(рис. 2 и рис.3 )
Если k>0. Если k<0
Y Y
0 у=0х+0 x 0 x
3случай:
Пусть в уравнении kx+b=0 k=0, b≠0. Найдем координаты точек пересечения прямых, заданных уравнениями у= kx+b и у=0. Учитывая условия, уравнения примут вид у= 0x+b и у=0х+0. Так как угловые коэффициенты (k=0) равны, то прямые параллельны. (рис.4)
У у=0х+b
b 0 х
Вывод: уравнение kx+b=0 корней не имеет.
4случай:
Если в уравнении kx+b=0, k=0 и b=0, то уравнение примет вид 0х+0=0. Найдем координаты точек пересечения прямых, заданных уравнениями у=0х+0 и у=0 (что то же самое у=0х+0). Угловые коэффициенты прямых и свободные члены соответственно равны, то прямые совпадают (ось 0х). (рис.5)
у
у=0х+0
0 у=0 х
Вывод: уравнение kx+b=0, при k=0 и b=0 имеет бесчисленное множество корней.
Линейное уравнение, содержащее дробные коэффициенты.
Пример 14. Решить относительно х уравнение 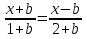 .
.
Решение: уравнение 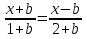 запишем в виде ах=в, для этого перенесем все в одну часть и приведем к общему знаменателю. Получим:
запишем в виде ах=в, для этого перенесем все в одну часть и приведем к общему знаменателю. Получим:
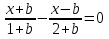
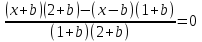 , выполним алгебраические преобразования числителя полученной дроби и сгруппируем слагаемые относительно х.
, выполним алгебраические преобразования числителя полученной дроби и сгруппируем слагаемые относительно х.
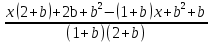 = 0
= 0
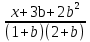 = 0
= 0
В числителе полученной дроби выражение линейное относительно х. найдем контрольные значения параметра для знаменателя дроби, т.е. 1+b=0, 2+b = 0; b = - 1, b = - 2.
-
Если b = - 1, b = - 2, то знаменатель дроби обращается в нуль, а следовательно уравнение корней не имеет.
-
Если b≠ - 1 и b≠ - 2, то
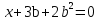 , х =
, х = 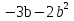
Ответ:1) 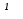 , при b = - 1, b = - 2;
, при b = - 1, b = - 2;
-
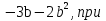 b≠ - 1 и b≠ - 2.
b≠ - 1 и b≠ - 2.
Пример 15. Решить относительно х уравнение 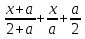 = 1.
= 1.
Решение: уравнение 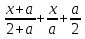 = 1 запишем в виде ах=в, для этого перенесем все в одну часть и приведем к общему знаменателю. Получим:
= 1 запишем в виде ах=в, для этого перенесем все в одну часть и приведем к общему знаменателю. Получим:
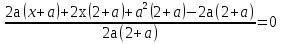
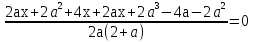
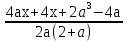 = 0
= 0
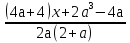 = 0
= 0
В числителе полученной дроби выражение линейное относительно х. Контрольными значениями параметра для знаменателя дроби, а = 0 и а=-2.
-
Если а = 0 и а = -2, то х Є
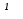 .
. -
Если а ≠ 0 и а ≠ -2, то
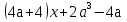 = 0
= 0
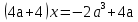
Найдем контрольные значения параметра для коэффициента при х, а = - 1
а) если а = - 1, то уравнение примет вид 0х = - 2, хЄ 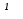 .
.
б) если а ≠ - 1, то х = 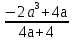 , х =
, х = 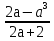 .
.
Ответ: 1) х Є 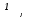 при а = 0, а = -2, а = - 1;
при а = 0, а = -2, а = - 1;
2) 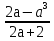 , при а ≠ 0, а ≠ -2 и а ≠ - 1.
, при а ≠ 0, а ≠ -2 и а ≠ - 1.
Линейное уравнение, содержащее знак модуля.
Пример 16. Найти число решений уравнения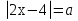
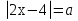
Решение: Запишем уравнение в виде системы
у = | 2x - 4|
у = а
Изобразим графически (рис.6)
у
4
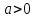
0 2 а=0 х
а 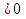
(рис. 6)
Ответ: если 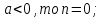
если a = 0, 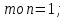
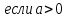 , то
, то 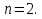
Пример 17.| х | = х - а
Решение: запишем данное уравнение в виде системы
у = | x |
y = x - a
у = х - а даёт множество прямых, параллельных биссектрисе I и II координатного угла. Изобразим графически (рис.9)
у
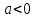
а = 0 а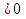
(рис. 9)
Ответ: если а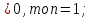
если а = 0, то 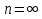 ;
;
если а 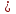 0, то
0, то 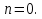
Рассмотрим более сложное задание.
Пример 18. Для каждого значения параметра решить уравнение.
| x+3|-а| x-1 |=4
-
Точки перегиба: х+3=0 и х-1=0
х=-3 х=1
Точки -3 и 1 разбивают всю числовую прямую на части
-3 1 х
х<-3, -3≤х≤1, х>1
-
Рассмотрим каждый из случаев.
Пусть х<-3, тогда х+3<0 и х-1<0, то уравнение примет вид
-х-3+ах-а=4
(а-1)х=4+а+3
(а-1)х=7+а
Найдем контрольные значения параметра для старшего коэффициента
а=1
-
Если а=1, то уравнение примет вид 0х=8, х - любое число.
-
Если а≠1, то х=
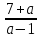
Проверим , при каких значениях параметра а выполняется условие 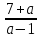 <-3, аЄ(-1;1)=>при х<-3 уравнение имеет корень х=
<-3, аЄ(-1;1)=>при х<-3 уравнение имеет корень х=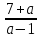 , при аЄ(-1;1).
, при аЄ(-1;1).
-
Если -3≤х≤1, то х+3≥0 и х-1≤0, и уравнение примет вид:
х+3+ах-а=4
(а+1)х=4-3+а
(а+1)х=1+а
Найдем контрольные значения параметра для старшего коэффициента
а=-1
а) если а=-1, то уравнение примет вид: 0х=0, -3≤х≤1
б) если а≠-1, то х=1, -3≤1≤1
3) х>1, то х+3≥0 и х-1>0, и уравнение примет вид:
х+3-ах+а=4
(1-а)х=1-а
Найдем контрольные значения параметра для старшего коэффициента
а=1.
а) если а=1, то 0х=0, х - любое, х>1
б) если а≠1, то х=1, 1 не является решением неравенства х>1, хЄØ
Изобразим решение уравнения на числовой прямой.
1 -3≤х≤1 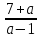 ; 1 х≥1 1 а
; 1 х≥1 1 а
-1 1
Ответ: 1) х=1, при а<-1 и а>1
2) х= 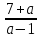 , х=1 при -1<а<1
, х=1 при -1<а<1
3) -3≤х≤1, при а=-1
4) х≥1, при а=1
Алгоритм решения линейного уравнения с параметром.
Рассмотрев решение линейных уравнений с параметром можно предложить следующий алгоритм решения.
1. Определить «контрольные» значения параметра при х в уравнении вида ах = b .
2. Рассмотреть случаи решения уравнения относительно х, при контрольных значениях параметра и отличных от «контрольных».
3. Записать ответ в виде:
1) уравнение корней не имеет, при значениях параметра ... .
2) уравнение имеет корни ... ; при значениях параметра ...
3) уравнение имеет корни ... ; при значениях параметра ... .
Примеры уравнений с параметрами из школьного учебника.
При каких значениях а корнем уравнения х(6 - а)+а(х+2)=26 является число 4? (А.Г. Мордкович Алгебра 7 класс. Часть 2. Задачник для общеобразовательных учреждений, стр. 33 домашняя контрольная работа №1, задание 8)
Решение: выполним алгебраические преобразования данного уравнения х(6 - а)+а(х+2)=26
6х - ах+ах+2а = 26
6х+2а = 26
6х = 26 - 2а число корней данного уравнения не зависит от значения │параметра а. По условию число 4 - корень уравнения, поэтому 26 - 2а=6•4, 26 - 2а=24, 2а = 2, а = 1.
Ответ: при а=1 число 4 - корень уравнения.
Задачи для самостоятельного решения
Решить относительно х уравнения:
-
ах = 5
-
ах = х+5
-
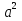 х = 4х+2+а
х = 4х+2+а -
(а - 1)х+2 = а+1
-
сх+2 = 2х+1
-
│x - 2│ = a
-
│x - a│ = a
-
│x - a│ = x - a
Ответы для самоконтроля:
-
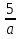 , при а≠0; Ø при а = 0
, при а≠0; Ø при а = 0 -
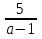 , при а≠ 1; Ø при а = 1
, при а≠ 1; Ø при а = 1 -
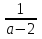 , при а≠2, а≠ -2; Ø при а = 2; х - любое при а = - 2
, при а≠2, а≠ -2; Ø при а = 2; х - любое при а = - 2 -
х - любое, при а = 1; 1, при а≠ 1.
-
хЄ
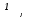 при с = 2;
при с = 2; 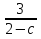 , при а ≠ 2.
, при а ≠ 2. -
а+2 и 2 - а, при а˃0; 2, при а = 0; Ø, при а˂0.
-
0 и 2а, при а ˃0; 0, при а = 0; Ø, при а˂0.
-
х≥а, при любом а.
Литература
-
Виленкин Н.Я., Виленкин А.Н. и др. Алгебра - 8 с углубленным изучением математики. М.Просвещение, 1995
-
Виленкин Н.Я., Виленкин А.Н. и др. Алгебра -9 с углубленным изучением математики. М.Просвещение, 1995
-
Галицкий М.Л, Гольфман А.М., Звавич Л.И. сборник задач по алгебре для 8 - 9 классов с углубленным изучением математики. М «Просвещение», 1994.
-
Горнштейн П.И., Полонский В.Б.. Задачи с параметрами, М: Илекса, Харьков, 1998.
-
Кузнецова Л.В., Суворова С.Б. Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе. Алгебра. Москва «Просвещение, 2009г.
-
Кострикина Н.П. Задачи повышенной трудности в курсе алгебры 7 - 9 классов. Просвещение, 1995.
-
Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начала анализа. Просвещение, 1990.
-
Макарычев Ю.Н., Миндюк Н.Г. Дополнительные главы к школьному учебнику. М.Просвещение, 2004.
-
Изучение сложных тем курса алгебры в средней школе: Учебно - методические материалы по математике /Под ред. Л.Я.Фалько. Изд. 3 - е.-М.: Народное образование, Илекса, 2005.


