- Преподавателю
- Математика
- Статья: Активизация мыслительной и познавательной деятельности учащихся на уроках математики
Статья: Активизация мыслительной и познавательной деятельности учащихся на уроках математики
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Ладонкина Е.Ю. |
| Дата | 26.07.2015 |
| Формат | docx |
| Изображения | Есть |
Активизация мыслительной и познавательной деятельности учащихся
Математику уже затем учить надо, что она ум в порядок приводит
М.В. Ломоносов
Страшная эта опасность - безделье за партой; безделье шесть часов ежедневно, безделье месяцы и годы. Это развращает, морально калечит человека, и ни школьная бригада, ни школьный участок, ни мастерская - ничто не может возместить того, что упущено в самой главной сфере, где человек должен быть тружеником, - в сфере мысли.
В.А. Сухомлинский
Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как поддержать интерес к изучаемому материалу у учащихся, их активность на протяжении всего урока. Творческая активность учащихся, успех урока целиком зависит от методических приемов, которые выбирает учитель. Как сформировать интерес к предмету у ребенка? Через самостоятельность и активность, через поисковую деятельность на уроке и дома, создание проблемной ситуации, разнообразие методов обучения, через новизну материала, эмоциональную окраску урока.
Традиционные методы обучения ориентированы главным образом на обучение готовым знаниям. Учитель объясняет учебный материал, привлекая различные средства наглядности, а ученики воспринимают информацию, заучивают её и по требованию учителя воспроизводят. Сообщить готовое быстрее, чем открывать его вместе с учениками. Но от "прослушанного", как известно, через две недели в памяти остается только 20%. Развивающий эффект таких методов обучения весьма низок, так как он не вызывает активной мыслительной деятельности ученика. Традиционные методы обучения вполне имеют право на существование, но мне бы хотелось поговорить о методах обучения направленных на активизацию мыслительной деятельности учащихся, на обучение их познавательной деятельности.
Методы проблемного обучения (исследовательский, эвристический и метод проблемного изложения). В качестве психологической основы проблемного обучения ставится тезис С.Л. Рубинштейна: «Мышление начинается с проблемной ситуации».
Важно сделать учащихся участниками поиска: рассуждая вслух, высказывая предположения, обсуждая их, доказывая истину. Учащиеся включаются в деятельность, которая носит исследовательский характер. В реализации проблемного обучения существенную роль играет создание на уроке учебной проблемной ситуации. Проблемная ситуация может создаваться на всех этапах процесса обучения: при объяснении, закреплении, контроле. Это оправдывающий себя дидактический прием, с помощью которого учитель держит в постоянном напряжении одну из внутренних пружин процесса обучения - детскую любознательность.
В качестве конкретного примера применения исследовательского метода в обучении рассмотрим изучение свойств средней линии трапеции.
1.Учащиеся уже знакомы со свойствами средней линии треугольника. На уроке вспоминаем эти свойства, делаем чертёж. Рядом с треугольником прошу начертить трапецию АВCD, M и N - середины боковых сторон трапеции. Прошу начертить отрезок MN - говорю, что этот отрезок называется средней линией трапеции. Задаю вопрос: «Как можно сформулировать определение средней линии трапеции?», ответ не вызывает затруднений (по аналогии с определением средней линии треугольника).
2. Возникает вопрос, какими свойствами обладает средняя линия трапеции? Для учащихся этот вопрос является проблемой. Так как рисунок трапеции со средней линией специально изображен рядом с рисунком треугольника, была выдвинута гипотеза о параллельности средней линии трапеции её основаниям. Доказываем это предложение (причём, два ученика догадались, что достаточно доказать параллельность средней линии одному из оснований). Второе свойство средней линии не лежит на поверхности и с помощью рисунка его не вывести. Опять обращаю внимание учеников на треугольник. Естественно, возникает вопрос, нет ли у средней линии трапеции свойства, аналогичного второму свойству средней линии треугольника. Прошу ребят образовать в трапеции какие-нибудь треугольники. Было несколько предложений - проводили высоту к основанию, чертили параллельные линии, проводили диагональ трапеции. Рассмотрели все предложенные случаи и сами сформулировали теорему, выражающую свойства средней линии трапеции. А вот доказательство я попросила сделать двумя способами - с помощью тех же треугольников и с помощью векторов. Оба доказательства разобрали на уроке, весь класс принимал активное участие, равнодушных не оказалось. В заключении урока я прочитала ребятам слова Фридриха Адольфа Дистервега «Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должны достигнуть этого собственной деятельностью, собственными силами, собственным напряжением»
Для того, чтобы знания учащихся были результатом их собственных поисков, управляемых учителем, их самостоятельной познавательной деятельности, необходимо организовать эти поиски, развивать познавательную деятельность учащихся, что намного сложнее, чем объяснение учебного материала традиционными методами.
Одним из средств активизации познавательной деятельности школьников является широкое использование их жизненного опыта. Большую роль в усвоении материала играют при этом практические работы. Часто дети запоминают только то, над чем потрудились их руки, если ученик что-то рисовал, чертил, вырезал или закрашивал, то это что-то само по себе становится опорой для его памяти. Такой вид работы как обучающее практическое занятие является творческим для учащихся. Выполнение задания и обобщение результатов приводит их к новому математическому знанию. При работе над темой «Координатная плоскость» мои ученики выполняют очень много творческих заданий - по координатам точек начерти животное, сам нарисуй в координатной плоскости что-то и найди координаты рисунка. Рисунки собираются и проводится выставка в классе, ребята принимают активное участие, домашние задания носят творческий характер. Материал прочно усваивается всеми учащимися, и когда в старших классах начинаем строить графики функций - с построением не возникает никаких трудностей.
При объяснении нового материала часто использую работу в группах по построению алгоритмов решений той или иной проблемы, составление опорных схем или памяток. Ребята сами предлагают рациональные способы решения, выстраивают их в виде алгоритма. Разбираем все предложенные схемы и выбираем наиболее рациональную. Роль таких опорных схем, алгоритмов в активизации познавательной деятельности учащихся велика. Они помогают при повторении материала, уменьшают нагрузку на память.
Во время обучения математике очень важно добиваться от учащихся сознательного и обоснованного решения задач, стремиться к тому, чтобы они опирались при решении на ранее изученные определения, законы, чтобы приобретенные ими знания неразрывно связывались с практическими навыками. Понимая важность этой проблемы, вызывая учеников к доске, как и многие учителя математики, прошу их обосновывать решаемые задачи. Остальные ученики класса слушают, но слушают не всегда внимательно, потому что чаще ребята не вникают в суть обоснований и решают задачи чисто механически, только по аналогии, а объясняют в большинстве случаев для учителя. Хотелось бы создать такие условия, чтобы у учащихся возникали внутренние потребности в обосновании, чтобы они понимали, что это очень важный момент в решении задач и упражнений. В чем же причина механического выполнения учащимися ряда действий при решении задач? Ответить на этот вопрос мне помогла книга П.А. Шеварева «Обобщенные ассоциации в учебной работе школьника». В своей книге он обнаружил закономерности:
Если при выполнении новой темы выполняются условия:
-
учащемуся предлагают задачи только одного типа,
-
их решение сводится к одной и той же операции, которая может быть и довольно сложной, состоящей из ряда элементарных операций,
-
эту операцию (её результат) учащемуся не надо выбирать среди других, которые возможны в сходных ситуациях,
-
данные задач не являются для учащегося непривычными,
-
он уверен в безошибочности своих действий,
то учащийся очень быстро (нередко при решении второй или третьей задачи) перестаёт применять изучаемые определения, законы, прекращает обосновывать решения задач.
Если хотя бы одно из перечисленных условий нарушается при решении какой-то задачи, то учащийся начинает обосновывать решения.
Подтверждением вышесказанного является изучение темы «Показательные уравнения и неравенства». Ученики без особых проблем решают показательные неравенства вида: 3х < 27; 8х > 1; 7х > 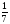 ;
; 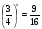
Это упражнения одного типа, их решение сводится к одной операции - переход к линейному неравенству с сохранением знака исходного неравенства, эту операцию не надо выбирать среди других, задание очень быстро становится привычным и решается механически, решение практически в каждом случае оказывается безошибочным и у учащихся не возникает сомнения по поводу своих действий. В результате ребята по своей инициативе перестают опираться на свойство монотонности функции .
Факт бездумного решения выявляют задания типа:
(0,1)х < (0,1)7; 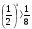 ;
; 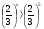 ; 7х > 7-2;
; 7х > 7-2; 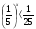
При решении появляются ошибки, и это заставляет учащихся работать более вдумчиво, проверять себя, рассуждать.
Если с самого начала изучения темы чередовать неравенства у которых основания степеней то больше, то меньше единицы (но больше нуля), то учащиеся вынуждены с самого начала выбирать операцию: менять знак неравенства на противоположный или сохранять его при переходе к линейному, т.е. постоянно опираться на свойство монотонности показательной функции. Это приводит к активизации мыслительной деятельности учащихся.
Активизация мыслительной деятельности ведёт к тому, что учащиеся осознанно обосновывают решение и ответ, делают аргументированные ссылки и всё это снижает возникновение формальных навыков.
Нарушение любого из условий (1 - 5) закономерности побуждает учащихся активизировать свою умственную деятельность. Учителю необходимо очень аккуратно подходить к выбору заданий, помнить об опасности однотипных упражнений (хотя и совсем от них отказываться нельзя, т.к. иначе у многих школьников не сформируются необходимые умения и навыки). Необходимо продумывать упражнения так, чтобы учащийся был поставлен перед выбором операции, особенно если упражнение сводится к одной операции.
Очень хорошо стимулируют активизацию мыслительной деятельности провоцирующие упражнения, наталкивающие учащихся на ошибку. Анализ ошибки ослабляет излишнюю самоуверенность школьников и последующую работу они делают внимательнее.
Пример: Ребятам при работе над темой «Линейные и квадратные неравенства» было предложено упражнение из учебника «Алгебра 9 класс» под редакцией А.Г. Мордковича № 1.7.
3х2 + х + 2 > 0
Ребята без проблем находят дискриминант квадратного трёхчлена 3х2 + х + 2
Получают: D = - 23 < 0. И сразу же допускают ошибку, по аналогии с решением квадратного уравнения они делают вывод, что если дискриминант меньше нуля, то неравенство решений не имеет. Предлагаю проверить для любого значения переменной это неравенство. Оказывается, что неравенство справедливо при любом значении переменной.
Следом решаем другое неравенство: 5х2 - 2х + 1 < 0
Находим дискриминант квадратно трёхчлена D = - 16 < 0. И опять ошибка - сразу же делается поспешный вывод - неравенство справедливо при любых значениях переменной. Прошу найти несколько таких значений, возникает заминка.
После решения этих упражнений вспоминаем утверждения, которые были доказаны в курсе алгебры 8-го класса.
1. Если D < 0, а > 0, то неравенство ах2 + bх + с > 0 выполняется при всех х; напротив, неравенство ах2 + bх + с < 0 в этом случае не имеет решений.
2. Если D < 0, а > 0, то неравенство ах2 + bх + с < 0 выполняется при всех х; напротив, неравенство ах2 + bх + с > 0 в этом случае не имеет решений.
И логично перейти к теореме: «Если квадратный трехчлен ах2 + bх + с имеет отрицательный дискриминант, то при любом х значение трёхчлена имеет знак старшего коэффициента а»
Подобные упражнения, чередования провоцирующих примеров, примеров, требующих осознанного применения выученных теорем, законов и свойств помогают активизировать мыслительную деятельность учащихся.
В зависимости от сложности и структуры изучаемого материала для развития мышления можно использовать и различные типы уроков:
1. Новый материал рациональнее подавать крупным блоком в виде урока-лекции - это экономит время для дальнейшей практической и творческой работы и помогает раскрыть тему;
2. Использование разноуровневых заданий на уроке контроля знаний;
3. Урок - повторения материала проводить в группах. Преимущество групповой работы в том, что ребята учатся высказываться, отстаивать собственное мнение, у них формируется критическое мышление. В результате совместного обсуждения активизируется мыслительная деятельность и поисковая активность.
Сегодня существует целый ряд способов и методов активизации мыслительной деятельности учащихся в процессе обучения. В зависимости от времени и места применения метода, особенностей сочетания в нем различных способов, приемов и средств один и тот же метод обучения может оказаться эффективным или неэффективным. Найти удачный метод обучения в каждом конкретном случае означает найти удачную комбинацию различных приемов и средств, позволяющих достичь поставленной заранее цели наиболее оптимальным в данных условиях путем. Важно лишь пробудить мыслительный процесс ученика, заинтересовать его.
Нельзя не сказать о том, что большую роль в развитии мышления учащихся играет система математических знаков.
Ещё Лейбниц говорил, что люди употребляют знаки не только для того, чтобы передавать свои мысли окружающим, но и для того, чтобы сделать более продуктивным сам процесс мышления.
Знак - это материальный, чувственно воспринимаемый объект, который символически, условно представляет обозначенный им предмет, явление, действие, свойство, связь или отношение. [1]
Возникновение математики как науки, её историческое становление нельзя представить без создания и использования символического языка. Система математических знаков давно стала неотъемлемой составной её частью. К сожалению, достаточно распространён среди учителей (и потому среди учеников) взгляд на знак как на формальный фиксатор понятий и операций. Учащиеся нечётко осознают математическое содержание знаков плюс и минус в буквенных выражениях, знаков равенства и неравенства, знака модуля рационального числа, обозначение понятий, а также смешению знаков логических операций с математическими знаками.
Такие же знаковые формы существуют и в геометрии. Геометрические рисунки (чертежи) возникли и используются наряду с числами. Чертежи также играют большую роль как при решении практических задач, так и при построении и доказательстве теоретических положений. Преобразование и построение чертежей дают новые знания о равенстве и отношении между фигурами, возникает идея подобия (теорема Фалеса, Пифагора и др.) с помощью которой осуществляются новые преобразования.
Математические знаки являются важным средством формирования математических понятий, являются новым, самостоятельным абстрактным объектом процесса мышления учащегося. Они позволяют перейти к новым обобщениям математических понятий , способствуют развитию мышления, дают наглядную картину при решении математических задач.
Между тем мышление в знаковых формах становится не только более компактным, но и более активным. Ведь не зря же существует математический язык. И у многих учащихся возникают проблемы при решении текстовых задач именно при переводе задачи с русского языка на язык математический. Это те же проблемы, что и учителей иностранных языков при переводе текстов. Необходимо постоянно помнить, что математический язык позволяет многие утверждения сделать ярче, прозрачнее и, наконец, короче.
«Говорят, что культурный человек, кроме родного языка, должен владеть хотя бы одним иностранным языком. Культурный человек должен ещё уметь говорить, писать, думать на математическом языке, поскольку это тот язык, на котором «говорит» окружающая действительность».
Вспомним концепцию учебника «Алгебры», Мордковича А.Г. - «Математика - гуманитарный предмет, который позволяет субъекту правильно ориентироваться в окружающей действительности, «Ум в порядок приводит» и оказывает существенное влияние на развитие речи обучаемых. Математика описывает реальные процессы на математическом языке в виде математических моделей. Поэтому - математический язык и математическая модель - ключевые слова в постепенном развертывании курса, его идейный стержень».
«Одной из основных целей математического образования должно быть воспитание умения математически исследовать явления реального мира. Значит, нужно научить школьников составлять математические модели реальных ситуаций, а для этого они должны владеть математическим языком, описывающим указанные модели» (Мордкович А.Г.)
Объясняя ребятам новые правила, давая новые определения, вводя новые математические символы иногда сталкиваешься с тем, что они либо просто не понимают того, о чем говорит учитель, либо очень быстро забывают то, что выучили, либо не могут применить это при решении задач, т.е. на практике.
Все дело в том, что школьники, как и все люди вообще, мыслят по-разному: у одних преобладает абстрактное, вербально-логическое мышление (в этом случае говорят об аналитическом, «мыслительном» складе ума), у других преобладает образное мышление (в этом случае говорят об образном, художественном типе мышления), у третьих образные и абстрактные компоненты мышления находятся в относительном равновесии (в этом случае говорят о гармоническом складе ума). По некоторым данным у 21 % людей один вид мышления резко преобладает над другим .[2 ].
Существуют специальные психологические тесты, которые проводятся психологом школы (а при необходимости и самим учителем), которые помогают определить, какой вид мышления преобладает у ребят в том или ином классе, это очень помогает в работе. Я в своей работе применяю тест Липпмана «Логические закономерности» для определения уровня развития логического мышления, тест «Художник - Мыслитель» для определения логического или художественного склада мышления, методику «Закономерности числового ряда» для оценки логического аспекта мышления, методику «Исключение понятий» для исследования способности к классификации и анализу.
Результаты тестирования учащихся 9 класса В этом году - при оценивании логического аспекта мышления 11 человек из 21 показали уровень ниже нормы, 10 человек - показали уровень нормы взрослого человека, при определении уровня развития логического мышления: 4 человек - хорошая норма большинства людей, 14 человека - средняя норма, 3 человека - низкая норма, 7 человек - ниже среднего уровня развития логического мышления и 6 человека - низкая скорость мышления. Логический тип мышления (по тесту «Художник - Мыслитель») у 8 учеников, 13 школьников являются людьми художественного склада. Подводя итоги тестирования, можно сделать вывод, что у учащихся 9 класса приблизительно 38 % обладают логическим типом мышления и 62 % - образным, художественным типом мышления. Для того, чтобы успешно работать с классом, необходимо это знать, т.к. т.к. одностороннее развитие ума неизбежно приводит к трудности в учебной работе и зачастую именно здесь и скрываются многие неудачи наших учеников.
Школьники с аналитическим складом ума страдают там, где успешность работы зависит от развития воображения. Геометрия таким детям дается труднее, чем алгебра.
Иные трудности характерны для школьников с наглядно-образным типом мышления. Трудности для этих учащихся возникают там, где им приходится работать без наглядной опоры. Как замечает В.А. Крутецкий, образность часто заменяет представителям этого типа мышления логичность. «Но если им не удается создать наглядные опоры, использовать предметную или схематическую наглядность при решении задач, то они с трудом оперируют отвлеченными схемами. Они упорно пытаются оперировать наглядными схемами. Образами и представлениями даже там, где задача легко решается рассуждением, а использование наглядных опор излишне затруднено».[3].
Гораздо легче усваивается ход решения, запоминается математическое понятие, если некоторые моменты связать с жизнью, сравнить с обыденными понятиями окружающего нас мира. В этом случае математические умозаключения ассоциируются с представлениями реальной действительности. Любая точная (знаковая) информация фиксируется в мозге в виде ассоциации. Дело в том, что в мыслительной деятельности мы широко пользуемся ассоциациями, поскольку они оказывают весьма существенную помощь в решении мыслительных задач.[2].
Хочу поделиться своими методическими находками, которые уже не первый год помогают мне и моим ученикам знать и любить математику. Причем метод наводящих ассоциаций применяется импровизационно, они как бы сами собой вспыхивают в мозгу.
В пятом классе при изучении темы: «Округление натуральных чисел», мы встречаемся с достаточно громоздким правилом. За большим количеством слов, которые содержатся в этом правиле, ребята теряют смысл. При автоматическом заучивании (зазубривании) тоже ничего хорошего не получается, т.к. они путаются, когда надо увеличить последнюю оставшуюся цифру на единицу, а когда оставить без изменения. Мы придумали свое правило и назвали его «правилом светофора». Смысл его очень прост, все цифры мы окрасили в два цвета: 0, 1, 2, 3, 4 - зеленые цифры, 5, 6, 7, 8. 9 - красные цифры. Зеленый цвет у ребят ассоциируется с зеленым цветом светофора, все спокойно, можно смело переходить дорогу (если первая отброшенная или замененная нулем цифра зеленая, то стоящую перед ней цифру оставляй без изменения). А красный - цвет опасности, будь внимателен, надо посмотреть по сторонам (внимание, если первая отброшенная или замененная нулем цифра - красная, то стоящую перед ней цифру увеличивай на 1). Мы преобразовали обычные цифры в яркие зрительные образы, которые рефлекторно запомнились. Кстати, мы еще раз повторяем и правила дорожного движения.
Характерная ошибка школьников при решении уравнений - решение в цепочку, идет из начальной школы. Ребята могут поставить знак равенства несколько раз (х = 15 - 5 = 10). От этой ошибки мы тоже очень быстро избавились с помощью ассоциации - уравнение сравниваем либо с чашечными весами, либо с перевесами. Попробуйте покататься на перевесах если доску положить не на один камень, а на два?
Когда мы изучали сравнение отрицательных чисел, ребята из слабого коррекционного класса долго не могли понять (у них просто не укладывалось в голове) почему - 5 < - 2. Вспомнив, что отрицательные числа были введены как долг, один из учеников объяснил это так: «Что лучше, иметь долг 5 рублей или 2 рубля? Конечно же 2 рубля, поэтому - 2 и больше». С точки зрения математики это объяснение, мягко говоря, не корректно, но ошибок при сравнении отрицательных чисел стало гораздо меньше!
Аббревиатуру НОД (наибольший общий делитель) можно раскрыть и так - необходимо отыскать друга. В этих трех словах содержится смысл правила по отысканию наибольшего общего делителя.
Иногда параллельно с правилом можно ребятам предложить небольшое стихотворение, которое поможет прочнее и лучше запомнить это правило. На уроках математики обычно нарушается баланс между знаково-цифровой и образной информацией. Поэтому я считаю, что полезно давать ребятам задачи в стихах и включать стихи в правила.
При изучении темы: «Умножение и деление обыкновенных дробей» мы решаем задачи на нахождение дроби от числа и на нахождение числа по его дроби. Ребята раньше часто путали, когда надо умножать, а когда делить на обыкновенную дробь, помог им в этом разобраться простой стишок:
Если часть узнать желаешь, то на дробь ты умножаешь.
Хочешь целое узнать, тут нельзя нам умножать,
Тут уж всем на удивление, делай действие - деление.
Может сложиться впечатление, что я пытаюсь четкий и лаконичный математический язык заменить каким-то суррогатом. Сразу хочу оговориться, на моих уроках ребята учатся красиво и правильно говорить, полно, математически грамотно аргументировать свои ответы. Но в то же время, мне хочется, чтобы математика стала им ближе и понятнее, а именно в этом нам и помогают такие «нематематические», образные ассоциации.
«Образы и понятия взаимно содержат друг друга, - писал французский психолог А. Валлон. - Потенциально они находятся одни в других. Движение мысли между ними - это не настоящее перемещение, это серия дополняющих ориентаций».[2].
Обучение, совсем не адресованное к образному мышлению, не только не способствует его развитию, но и в конечном счете подавляет его. Умственная работа, лишенная наглядной, образной опоры, в ряде случаев оказывается трудной не только для школьников.
Неумение привлечь зрительные образы или ассоциации к работе в нужный момент - одна из причин низкого качества умственной работы. Недостаток воображения сказывается отрицательно на усвоении не только математики, но и всех школьных предметов.
Если говорить о вопросе способных и неспособных к математике детей (не о вундеркиндах и не о детях умственно отсталых). Специально занимавшийся этим вопросом В.А. Крутецкий считает: «Абсолютной неспособности к изучению математики, своего рода «математической слепоты» не существует. Каждый нормальный и здоровый в психическом отношении школьник способен при правильном обучении более или менее успешно овладеть школьным курсом математики, приобрести знания и умения в объеме программы средней школы».[3].
Психологами было замечено, что обучение, направленное на активацию образного компонента мышления, выполняет также и важную психогигиеническую функцию. У школьников повышаются адаптивные возможности, он становится стессоустойчивым и устойчивым к возникновению различных заболеваний. Кроме того, такой тип обучения, как показал Ю.А. Грибов, меняет всю атмосферу в коллективе и помогает созданию благоприятного климата межличностных отношений.
Необходимо помнить, что обучение математике - это не цель, а средство на пути совершенствования личности ученика, ее развития. А вот это и является главной целью и обучения и воспитания в школе.
Литература:
-
Тесленко И.Ф. Формирование диалектико-материалистического мировоззрения учащихся при изучении математики. - М., Просвещение, 1979
-
Басов Н.В. Педагогика и практическая психология. - Ростов н/Д: «Феникс», 2000.
-
Труднев В.П. Внеклассная работа по математике в начальной школе. Пособие для учителей. - М.: Просвещение, 1975


