- Преподавателю
- Математика
- Занятие Окружность тринадцати точек
Занятие Окружность тринадцати точек
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Диамбекова А.Л. |
| Дата | 12.11.2015 |
| Формат | docx |
| Изображения | Есть |
 План занятия группы углубленного изучения математики
План занятия группы углубленного изучения математики
ТО «Пифагор» МКОУ ДОД ДДТ Дигорского района
Педагог: Диамбекова Алла Лазаровна
2014г.
Тема занятия: «Окружность тринадцати точек»
Цели:
Образовательные: познакомить учащихся с теоремами Эйлера и Фейербаха, рассмотреть нестандартные задачи, при решении которых применяются новые понятия.
Развивающие: развивать логическое мышление, наблюдательность, внимание, математическую речь обучающихся.
Воспитывающие: воспитывать самостоятельность, умение анализировать и применять имеющиеся знания в нестандартных ситуациях.
Оборудование: мультимедийный проектор, презентация по теме.
Ход занятия.
Организационный момент.
Подготовка к восприятию новых понятий:
- замечательные точки треугольника;
- признаки параллельности и перпендикулярности прямых.
Изучение новых теорем проходит в лекционной форме.
Первая теорема, связанная с окружностью тринадцати точек, была получена Эйлером в 1765 году. Он установил, что основания высот и середины сторон разностороннего треугольника лежат на одной окружности. Отсюда и название «окружность шести точек».
Впоследствии он обнаружил, что на этой же окружности лежат точки, принадлежащие высотам и расположенные от вершин на расстоянии одной треть длин самих высот. Так окружность стала «окружностью девяти точек».
Сформулируем её.
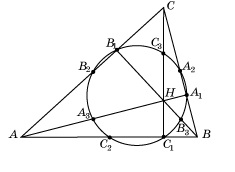
Теорема. Пусть в треугольнике ABC (рис. 1), H - точка пересечения высот треугольника; точки A1, B1, C1 - основания высот; A2, B2, C2 - середины соответствующих сторон; A3, B3, C3 - середины отрезков AH, BH и CH. Тогда точки A1, B1, C1, A2, B2, C2, A3, B3, C3 лежат на одной окружности. [1]
Действительно, A3B2 -средняя линия треугольника AHC и, следовательно, A3B2 || CC1. B2A2 - средняя линия треугольника ABC и, следовательно, B2A2 || AB. Так как CC1 ┴ AB, то
 A3B2A2 =90. Аналогично,
A3B2A2 =90. Аналогично,  A3C2A2 = 90. Поэтому точки A2, B2, C2, A3 лежат на одной окружности с диаметром A2A3. Так как AA1 перпендикулярна BC, то точка A1 также принадлежит этой окружности. Аналогичным образом показывается, что точки B1 и B3, C1 и C3 лежат на этой окружности. Значит, все девять точек лежат на одной окружности. Что и требовалось доказать. [3]
A3C2A2 = 90. Поэтому точки A2, B2, C2, A3 лежат на одной окружности с диаметром A2A3. Так как AA1 перпендикулярна BC, то точка A1 также принадлежит этой окружности. Аналогичным образом показывается, что точки B1 и B3, C1 и C3 лежат на этой окружности. Значит, все девять точек лежат на одной окружности. Что и требовалось доказать. [3]
Рис. 1.
Прямая, проходящая через центр описанной окружности О и ортоцентр Н данного треугольника называется прямой Эйлера.
Окружность девяти точек обладает рядом свойств.
1. Прямая Эйлера проходит через:
а) ортоцентр треугольника;
б) точку пересечения серединных перпендикуляров;
в) центроид М, который делит отрезок ОН в отношении ОМ:МН = 1:2;
г) центр N окружности Эйлера. [3]
2. Радиус  описанной около треугольника окружности в два раз больше радиуса
описанной около треугольника окружности в два раз больше радиуса 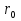 окружности девяти точек. [1]
окружности девяти точек. [1]
3. Описанная окружность есть образ окружности девяти точек относительно гомотетии с центром Н и коэффициентом 2. [1]
Докажем справедливость приведённых утверждений.
1. а) и б) верны по определению прямой Эйлера;
в). Требуется доказать, что точки O, M, H лежат на одной прямой.
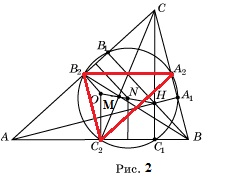
Рассмотрим гомотетию с центром в точке M и коэффициентом -0,5 (рис.2). Вершины A, B, C треугольника ABC перейдут соответственно в точки A2, B2, C2. Высоты треугольника ABC перейдут в высоты треугольника A2B2C2 и, следовательно, точка H перейдет в точку O. Поэтому точки O, M, H будут лежать на одной прямой. При этом ОМ в два раза меньше МН. Что и требовалось доказать. [3]
г). Покажем, что середина N отрезка OH является центром окружности девяти точек. Действительно, C1C2 - хорда окружности девяти точек. Поэтому серединный перпендикуляр к этой хорде является диаметром и пересекает OH в середине N. Аналогично, серединный перпендикуляр к хорде B1B2 является диаметром и пересекает OH в той же точке N. Значит N - центр окружности девяти точек. Что и требовалось доказать. [3]
2. Так как ОМ:МН=1:2 и N -середина ОН, то ОМ:МN = 2:1. При гомотетии относительно М с коэффициентом -2 N то есть радиус окружности Эйлера перейдёт в радиус описанной окружности и
то есть радиус окружности Эйлера перейдёт в радиус описанной окружности и  =2
=2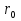 . Что и требовалось доказать.
. Что и требовалось доказать.
3. Так как A3, B3, C3 - середины отрезков AH, BH и CH, то они при гомотетии относительно Н с k=2 переходят соответственно в точки A, B, C, то есть окружность девяти точек отображается в окружность, описанную около треугольника (рис.1).
Что и требовалось доказать.
В 1821 году окружность Эйлера, выкладки о которой так и не были опубликованы учёным, была заново открыта учителем провинциальной гимназии в Германии. Звали этого учителя Карл Фейербах (он был родным братом известного философа Людвига Фейербаха).
Дополнительно Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это - точки ее касания с четырьмя окружностями специального вид (рис 3). Одна из этих окружностей вписанная, остальные три - вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон. Точки касания этих окружностей с окружностью девяти точек и называются точками Фейербаха.
Таким образом, окружность девяти точек является в действительности окружностью тринадцати точек. [2]
Но отдавая дань гению первооткрывателя, Карл указывает на первенство Эйлера в этом открытии и называет окружность его именем. Так в мире математиков она и называется «окружность Эйлера».

Рис. 3.
Приведём доказательство о десятой точке Фейербаха. Для этого решим следующую задачу.
ЗАДАЧА.
Проведём через основание биссектрисы угла A разностороннего треугольника ABC от- личную от стороны BC касательную к вписанной в треугольник окружности. Точку её касания с окружностью обозначим через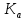 . Аналогично построим точки
. Аналогично построим точки 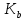 и
и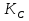 . Докажите, что три прямые, соединяющие точки
. Докажите, что три прямые, соединяющие точки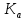 ,
, 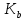 и
и 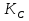 с серединами сторон BC,CA и AB соответственно, имеют общую точку, причём эта точка лежит на вписанной окружности (рис.4).
с серединами сторон BC,CA и AB соответственно, имеют общую точку, причём эта точка лежит на вписанной окружности (рис.4).
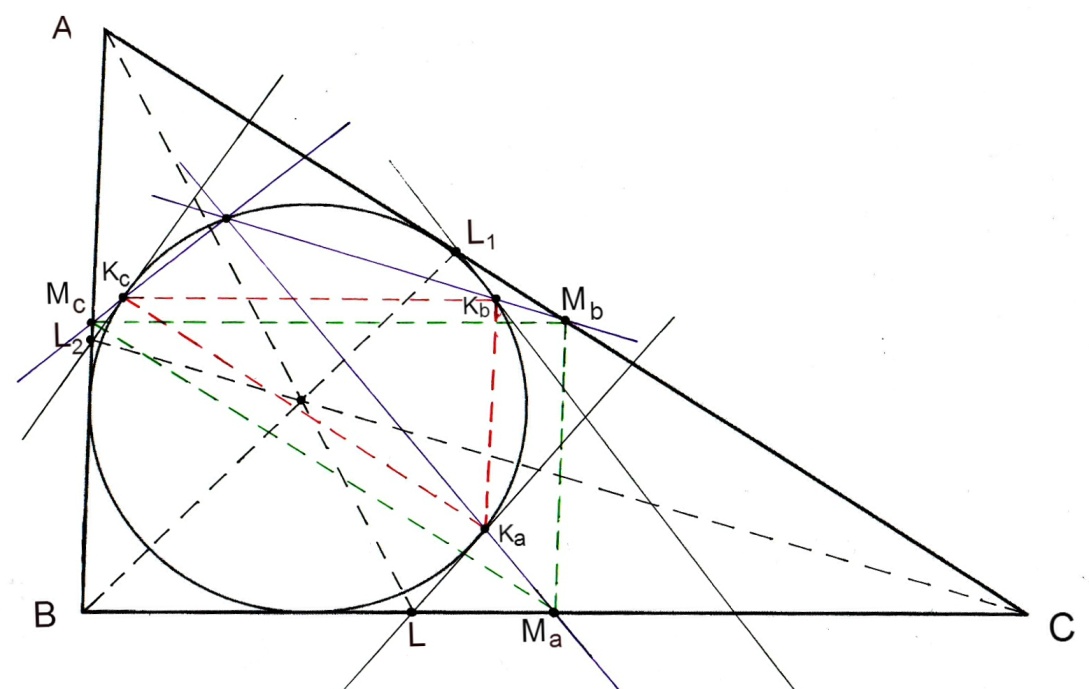
Рис.4
Решение в первоисточнике приводится к чертежу 4 и занимает полстранички. (см ниже)
Сначала докажем, что стороны треугольника 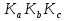 параллельны соответствующим сторонам треугольника ABC. Пусть AC>AB. Имеем равенства POL=
параллельны соответствующим сторонам треугольника ABC. Пусть AC>AB. Имеем равенства POL=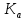 OL и POB=ROB, поэтому
OL и POB=ROB, поэтому 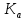 OR=2LOB. Угол LOB внешний в треугольнике AOB, значит
OR=2LOB. Угол LOB внешний в треугольнике AOB, значит 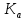 OR=α+β. Подобными же рассуждениями получаем, что
OR=α+β. Подобными же рассуждениями получаем, что 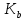 OR= α+β. Следовательно, точки
OR= α+β. Следовательно, точки 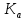 и
и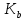 симметричны относительно прямой OR, поэтому
симметричны относительно прямой OR, поэтому 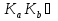 AB. Итак, соответствующие стороны треугольников
AB. Итак, соответствующие стороны треугольников 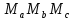 и
и 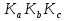 параллельны(
параллельны(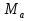 ,
, 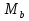 ,
,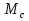 - середины сторон треугольника), поэтому эти треугольники гомотетичны. Центр этой гомотетии является общей точкой прямых
- середины сторон треугольника), поэтому эти треугольники гомотетичны. Центр этой гомотетии является общей точкой прямых 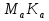 ,
, 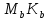 и
и 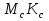 .
.
Пусть прямая 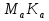 вторично пересекает вписанную в треугольник ABC окружность в точке А. Докажем, что описанная вокруг треугольника F
вторично пересекает вписанную в треугольник ABC окружность в точке А. Докажем, что описанная вокруг треугольника F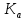 L окружность проходит через основание высоты H треугольника ABC. Для этого достаточно проверить выполнение равенства
L окружность проходит через основание высоты H треугольника ABC. Для этого достаточно проверить выполнение равенства 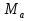 L·
L·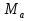 H =
H = 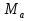 P2, так как
P2, так как 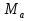 P2 =
P2 = 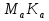 ·
·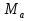 F.
F.
Пользуясь параллельностью прямых AH и OP, MaPʹ=MaP1(рис.7) и теоремой Фалеса, получаем: 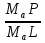 =
= 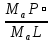 =
= 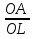 =
= 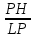 =
= 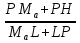 =
= 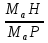 . Так как четырехугольник F
. Так как четырехугольник F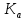 LH вписанный, углы
LH вписанный, углы 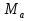 FH и
FH и 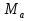 L
L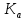 равны. Угол
равны. Угол 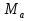 L
L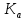 легко выражается через углы треугольника ABC:
легко выражается через углы треугольника ABC: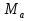 L
L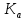 =
= 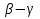 . Рассмотрим теперь четыругольник
. Рассмотрим теперь четыругольник 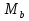 FH
FH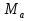 .
.
Заметим, что 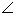 HCA =
HCA = 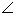 CH
CH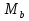 =
=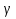 ,
, 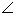 C
C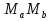 =
= 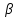 . Поэтому
. Поэтому 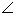
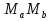 H = =
H = = 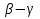 , значит
, значит 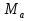 FH
FH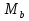 - вписанный и, следовательно,
- вписанный и, следовательно, ![]()
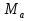 F
F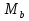 =
= 
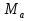 H
H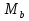 =
=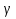 . Обозначим через K точку пересечения отрезка F
. Обозначим через K точку пересечения отрезка F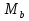 со вписанной окружностью(рис.8). Так как вписанный в окружность угол
со вписанной окружностью(рис.8). Так как вписанный в окружность угол 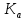 FK равен
FK равен 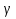 , а дуга R
, а дуга R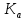 вписанной окружности равна
вписанной окружности равна 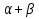 , точки
, точки 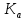 и K симметричны относительно этой прямой. Значит, точки K и
и K симметричны относительно этой прямой. Значит, точки K и 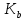 совпадают, что означает, что прямые
совпадают, что означает, что прямые 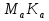 и
и 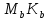 пересекаются в точке F вписанной окружности. ЧТД
пересекаются в точке F вписанной окружности. ЧТД
Таким образом, треугольник обладает неожиданными для нас свойствами, которые характеризуют глубину познаний в математике и бесконечность новых открытий. Дерзайте, молодые!!!
СПАСИБО ЗА ВНИМАНИЕ!!!


