- Преподавателю
- Информатика
- Учебное пособие Логические основы компьютера
Учебное пособие Логические основы компьютера
| Раздел | Информатика |
| Класс | 10 класс |
| Тип | Другие методич. материалы |
| Автор | Гардер С.А. |
| Дата | 21.08.2015 |
| Формат | doc |
| Изображения | Есть |
МОУ «Средняя общеобразовательная школа № 6
с углубленным изучением французского языка»
Логические основы компьютера
Учебное пособие по информатике
для 10 класса
Содержание
§1. Основы логики…………………………………..…….………3
§ 2. Логические операции……………………………..…..….…..5
§ 3. Логические формулы. Таблица истинности логической формулы……………………………………………..…..…...….….8
§ 4. Основные законы алгебры логики. Упрощение логических формул…………………….....……………....………11
§ 5. Решение логических задач…………………………...…….13
§ 6. Логическая функция…………………………...………..….18
§ 7. Логические основы ЭВМ. Базовые логические элементы………………………………..………………………….21
§ 8. Логические элементы компьютера. Триггер и сумматор...........................................................................................25
Вопросы для самоконтроля…………..……...…………….29
§ 1. Основы логики.
В процессе обработки двоичной информации компьютер выполняет арифметические и логические операции. Поэтому для получения представлений об устройстве компьютера необходимо познакомится с основными логическими элементами, лежащими в основе построения компьютера. Начнем это знакомство с основных начальных понятий логики.
Сам термин «логика» происходит от древнегреческого logos, означающего «слово, мысль, понятие, рассуждение, закон».
Логика - наука о законах и формах мышления.
Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Аристотель впервые отделил логические формы речи от ее содержания, исследовал терминологию логики, подробно разобрал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления.
К основным понятиям логики относятся следующие.
Логическое высказывание - это любое повествовательное предложение, в отношении кoтopoгo можно однoзначнo сказать, истинно oнo или лoжнo.
Так, например, предложение "6 - четное число" следует считать высказыванием, так как оно истинное. Предложение "Рим - столица Франции" тоже высказывание, так как оно ложное.
Утверждение - это суждение, которое требуется доказать или опровергнуть.
Например, любая теорема - это утверждение, требующее доказательства.
Рассуждение - это последовательность высказываний или утверждений, определенным образом связанных друг с другом.
Например, ход доказательства какой-либо теоремы можно назвать рассуждением.
Умозаключение - это форма мышления, посредством которой из одного или нескольких суждений выводится новое суждение. Умозаключения бывают дедуктивные, индуктивные и по аналогии.
В дедуктивных умозаключениях рассуждения ведутся от общего к частному. Например, из двух суждений: «Все металлы электропроводны» и «Ртуть является металлом» можно сделать вывод, что «Ртуть электропроводна».
В индуктивных умозаключениях рассуждения ведутся от частного к общему. Например, установив, что отдельные металлы - железо, медь, цинк, алюминий и др. - обладают свойством электропроводности, мы делаем вывод, что все металлы электропроводны.
Умозаключение по аналогии переносит знание об одних объектах на другие. Например, химический состав Солнца и Земли сходен по многим показателям. Поэтому, когда на солнце обнаружили неизвестный еще на Земле химический элемент гелий, то по аналогии заключили, что такой элемент есть и на Земле.
Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения "ученик десятого класса" и "информатика - интересный предмет". Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие "интересный предмет". Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.
Предложения типа "в городе A более миллиона жителей", "у него голубые глаза" не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются логическими выражениями.
Логическое выражение - это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Область знаний, которая изучает истинность или ложность высказываний, называется математической логикой.
Подобно тому, как для описания действий над переменными величинами был разработан раздел математики - алгебра, так и для обработки логических выражений в математической логике была создана алгебра высказываний или алгебра логики.
Алгебра логики - это раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Алгебра логики рассматривает любое высказывание только с одной точки зрения - является ли оно истинным или ложным. Заметим, что зачастую трудно установить истинность высказывания. Так, например, высказывание "площадь поверхности Индийского океана равна 75 млн. кв. км" в одной ситуации можно посчитать ложным, а в другой - истинным. Ложным - так как указанное значение неточное и вообще не является постоянным. Истинным - если рассматривать его как некоторое приближение, приемлемое на практике.
§ 2. Логические операции.
Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если..., то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Так, например, из элементарных высказываний "Петров - врач", "Петров - шахматист" при помощи связки "и" можно получить составное высказывание "Петров - врач и шахматист", понимаемое как "Петров - врач, хорошо играющий в шахматы".
При помощи связки "или" из этих же высказываний можно получить составное высказывание "Петров - врач или шахматист", понимаемое в алгебре логики как "Петров или врач, или шахматист, или и врач и шахматист одновременно".
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание "Тимур поедет летом на море", а через В - высказывание "Тимур летом отправится в горы". Тогда составное высказывание "Тимур летом побывает и на море, и в горах" можно кратко записать как А и В. Здесь "и" - логическая связка, А, В - логические переменные, которые могут принимать только два значения - "истина" или "ложь", обозначаемые, соответственно, "1" и "0".
Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio - соединение) или логическим умножением и обозначается точкой " . " (может также обозначаться знаками или &).
Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны.
Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" - ложны.
Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio - разделение) или логическим сложением и обозначается знаком v (или плюсом).
Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Например, высказывание "10 не делится на 2 или 5 не больше 3" ложно, а высказывания "10 делится на 2 или 5 больше 3", "10 делится на 2 или 5 не больше 3", "10 не делится на 2 или 5 больше 3" - истинны.
Операция, выражаемая словом "не", называется логическим отрицанием или инверсией и обозначается чертой над высказыванием (или знаком ).
Высказывание А истинно, когда A ложно, и ложно, когда A истинно.
Например, "Луна - спутник Земли" (А) - истинно; "Луна - не спутник Земли" ( А) - ложно.
Операция, выражаемая связками "если ..., то", "из ... следует", "... влечет ...", называется импликацией (лат. implico - тесно связаны) и обозначается знаком .
Высказывание А В ложно тогда и только тогда, когда А истинно, а В ложно.
Каким же образом импликация связывает два элементарных высказывания?
Покажем это на примере высказываний: "данный четырёхугольник - квадрат" (А) и "около данного четырёхугольника можно описать окружность"(В). Рассмотрим составное высказывание А В, понимаемое как "если данный четырёхугольник квадрат, то около него можно описать окружность".
Есть три варианта, когда высказывание А В истинно:
-
А истинно и В истинно, то есть данный четырёхугольник квадрат, и около него можно описать окружность;
-
А ложно и В истинно, то есть данный четырёхугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырёхугольника);
-
A ложно и B ложно, то есть данный четырёхугольник не является квадратом, и около него нельзя описать окружность.
Ложен только один вариант, когда А истинно, а В ложно, то есть данный четырёхугольник является квадратом, но около него нельзя описать окружность.
В обычной речи связка "если ..., то" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться "бессмысленностью" импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: "если президент США - демократ, то в Африке водятся жирафы", "если арбуз - ягода, то в бензоколонке есть бензин".
Операция, выражаемая связками "тогда и только тогда", "необходимо и достаточно", "...равносильно...", называется эквиваленцией или двойной импликацией и обозначается знаком или ~.
Высказывание А В истинно тогда и только тогда, когда значения А и В совпадают.
Например, высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 3", "23 делится на 6 тогда и только тогда, когда 23 делится на 3" истинны, а высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 5", "21 делится на 6 тогда и только тогда, когда 21 делится на 3" ложны.
Высказывания А и В, образующие составное высказывание А В, могут быть совершенно не связаны по содержанию, например: "три больше двух" (А), "пингвины живут в Антарктиде" (В). Отрицаниями этих высказываний являются высказывания "три не больше двух" (А), "пингвины не живут в Антарктиде" (В). Образованные из высказываний А и В составные высказывания A B и A B истинны, а высказывания A B и A B - ложны.
§ 3. Логические формулы. Таблица истинности логической
формулы.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.
Определение логической формулы:
-
Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") - формулы.
-
Если А и В - формулы, то A, А . В , А v В , А B , А В - формулы.
3. Никаких других формул в алгебре логики нет.
В п. 1 определены элементарные формулы; в п. 2 даны правила образования из любых данных формул новых формул.
В качестве примера рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог". Это высказывание формализуется в виде (A v B) C. Такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".
Как показывает анализ формулы (A v B) C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях - значение "ложь". Такие формулы называются выполнимыми.
Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Например, формула А v А, соответствующая высказыванию "Этот треугольник прямоугольный или непрямоугольный" истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
В качестве другого примера рассмотрим формулу А . А, которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо А обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом "=" Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
Нами рассмотрены пять логических операций: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
Импликацию можно выразить через дизъюнкцию и отрицание:
А В = Аv В.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А В = (А v В) . (Вv А).
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции - дизъюнкция ("или") и в последнюю очередь - импликация.
Таблица истинности логической формулы - таблица, выражающая соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0, 0), (0, 1), (1, 0), (1, 1).
Если формула содержит три переменные, то таких наборов восемь: (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д. Т.е., если N - количество переменных, то 2N - количество наборов значений переменных.
Таблица истинности элементарных логических формул
Конъюнкция
Дизъюнкция
Инверсия
Импликация
Эквиваленция
х
у
х · у
х
у
х у
х
х
х
у
х у
х
у
х у
0
0
0
0
0
0
0
1
0
0
1
0
0
1
0
1
0
0
1
1
1
0
0
1
1
0
1
0
1
0
0
1
0
1
1
0
0
1
0
0
1
1
1
1
1
1
1
1
1
1
1
1
Удобной формой записи при нахождении значений формулы, содержащей несколько логических операций, является таблица, в которой кроме значений переменных и значений формулы также указаны и значения
промежуточных формул.
Примеры.
1. Составим таблицу истинности для формулы х · у (х у) х, которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах - значения промежуточных формул и в последнем столбце - значение формулы.
Переменные
Промежуточные логические формулы
Формула
х
у
х
х · у
х у
(х у)
х · у (х у)
х · у (х у) х
0
0
1
0
0
1
1
1
0
1
1
1
1
0
1
1
1
0
0
0
1
0
0
1
1
1
0
0
1
0
0
1
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.
2. Таблица истинности для формулы:(х у) · (х · у)
Переменные
Промежуточные логические формулы
Формула
х
у
х у
(х у)
у
х · у
(х у) · (х · у)
0
0
0
1
1
0
0
0
1
1
0
0
0
0
1
0
1
0
1
1
0
1
1
1
0
0
0
0
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.
3. Таблица истинности для формулы: (х у) х · z
Переменные
Промежуточные логические формулы
Формула
x
y
z
у
х у
(х у)
х
х · z
(х у) х · z
0
0
0
1
1
0
1
0
0
0
0
1
1
1
0
1
1
1
0
1
0
0
0
1
1
0
1
0
1
1
0
0
1
1
1
1
1
0
0
1
1
0
0
0
0
1
0
1
1
1
0
0
0
0
1
1
0
0
1
0
0
0
0
1
1
1
0
1
0
0
0
0
Из таблицы видно, что формула в некоторых случаях принимает значение 1, а в некоторых - 0, то есть является выполнимой.
§ 4. Основные законы алгебры логики. Упрощение
логических формул.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений.
№
Закон
Представление
в алгебре логики
1
Переместительный (коммутативный)
a b = b a, a b = b a
2
Сочетательный (ассоциативный)
a (b c) = (a b) с,
a (b c) = (a b) c
3
Распределительный (дистрибутивный)
a (b c) = (a b) (a c),
a (b c) = (a b) (a c)
4
Правила де Моргана
(a b) = a b,
(a b) = a b
5
Закон двойного отрицания (инволюции)
а = а
6
Операции с переменной и ее инверсией
a a = 0, a a =1
7
Операции с константами
a 1 = 1, a 1 = a,
a 0 = a, a 0 = 0
8
Законы идемпотентности
a a = a, a a = a
9
Законы поглощения
x (x y) = x, x (x y) = x
10
Законы склеивания
(x y) ( x y) = y,
(x y) ( x y) = y
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Рассмотрим на примерах некоторые приемы и способы, применяемые при упрощении логических формул.
Пример 1.
(х у) · (х · у) = х · у · (х · у) = х · х · у · у = 0 · у · у = 0 · у = 0
(Законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами).
Пример 2.
х · у (х у) х = х · у х · у х = х · (у у ) х = х х = 1
(Применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией).
Пример 3.
(х у) · ( х у ) · ( х у) = (х у) · ( х у ) · ( х у ) · ( х у) = у · х
(Повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания).
Пример 4.
(х · у z) = (х · у) · z = (х · у) · z
(Сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого применяем правило де Моргана; затем используем закон двойного отрицания);
Пример 5.
х · у х · у · z х · р · z = х · (у у · z z · р) = х · (у · (1 z) z · р) =
= х · (у z · р)
(Выносятся за скобки общие множители; применяется правило операций с константами);
Пример 6.
x · y x · y · z x · y · z x ·(y · z ) = x · ( y y · z y · z (y · z )) =
= x · (( y y · z ) (y · z (y · z )) = x · ( y y · z 1) = x · 1 = x
(Общий множитель x выносится за скобки, комбинируются слагаемые в скобках - первое с третьим и второе с четвертым, к дизъюнкции применяется правило операции переменной с её инверсией);
Из этих примеров видно, что при упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге. Навыки приходят с опытом.
§ 5. Решение логических задач.
Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач:
-
средствами алгебры логики;
-
табличный;
-
с помощью рассуждений.
Познакомимся с ними поочередно.
I. Решение логических задач средствами алгебры логики
Обычно используется следующая схема решения:
-
изучается условие задачи;
-
вводится система обозначений для логических высказываний;
-
конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
-
определяются значения истинности этой логической формулы;
-
из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.
Пример 1. Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего этапа гонок.
- Вот увидишь, Шумахер не придет первым, - сказал Джон. Первым будет Хилл.
- Да нет же, победителем будет, как всегда, Шумахер, - воскликнул Ник. - А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
- Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение.
Введем обозначения для логических высказываний:
Ш - победит Шумахер; Х - победит Хилл; А - победит Алези.
Реплика Ника "Алези пилотирует самую мощную машину" не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Джон: Ш · Х, Ник: Ш · А, Питер: Х
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание
( Ш · Х)·(Ш · А) · Х ( Ш · Х)·(Ш · А)· Х ( Ш · Х)·(Ш · А)· Х = =( Ш · Х · Ш · А ·Х)( Ш · Х · (Ш · А) · Х ) (Ш Х) · Ш · А · Х = = 0 0 Ш · А · Х = Ш · А · Х
Высказывание Ш · А · Х истинно только при Ш=1, А=0, Х=0.
Ответ. Победителем этапа гонок стал Шумахер.
II. Решение логических задач с помощью таблиц истинности.
При использовании этого способа условия, которые содержит задача, и результаты рассуждений фиксируются с помощью специально составленных таблиц.
Пример 2. В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Виссона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
-
Смит самый высокий;
-
играющий на скрипке меньше ростом играющего на флейте;
-
играющие на скрипке и флейте и Браун любят пиццу;
-
когда между альтистом и трубачом возникает ссора, Смит мирит их;
-
Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Решение.
Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как музыкантов трое, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют.
Из условия 4 следует, что Смит не играет ни на альте, ни на трубе, а из условий 3 и 5, что Браун не умеет играть на скрипке, флейте, трубе и гобое. Следовательно, инструменты Брауна - альт и кларнет. Занесем это в таблицу, а оставшиеся клетки столбцов "альт" и "кларнет" заполним нулями:
скрипка
флейта
альт
кларнет
гобой
труба
Браун
0
0
1
1
0
0
Смит
0
0
0
Виссон
0
0
Из таблицы видно, что на трубе может играть только Виссон.
Из условий 1 и 2 следует, что Смит не скрипач. Так как на скрипке не играет ни Браун, ни Смит, то скрипачом является Виссон. Оба инструмента, на которых играет Виссон, теперь определены, поэтому остальные клетки строки "Виссон" можно заполнить нулями:
скрипка
флейта
альт
кларнет
гобой
труба
Браун
0
0
1
1
0
0
Смит
0
0
0
0
Виссон
0
0
0
0
0
1
Из таблицы видно, что играть на флейте и на гобое может только Смит.
скрипка
флейта
альт
кларнет
гобой
труба
Браун
0
0
1
1
0
0
Смит
0
1
0
0
1
0
Виссон
0
0
0
0
0
1
Ответ: Браун играет на альте и кларнете, Смит - на флейте и гобое, Виссон - на скрипке и трубе.
Пример 3. Три одноклассника - Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего - регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра - единственный врач в семье, заядлый турист.
Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Решение.
Здесь исходные данные разбиваются на тройки (имя - профессия - увлечение).
Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист.
-
Имя
Юра
Профессия
врач
Увлечение
туризм
Буква "а", присутствующая в слове "врач", указывает на то, что Влад тоже не врач, следовательно, врач - Тимур. В его имени есть буквы "т" и "р", встречающиеся в слове "туризм", следовательно второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени - Юра. Юра не юрист и не регбист, так как в его имени содержатся буквы "ю" и "р". Следовательно, окончательно имеем:
-
Имя
Юра
Тимур
Влад
Профессия
физик
врач
юрист
Увлечение
бег
туризм
регби
Ответ. Влад - юрист и регбист, Тимур - врач и турист, Юра - физик и бегун.
III. Решение логических задач с помощью рассуждений
Этим способом обычно решают несложные логические задачи.
Пример 4. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение. Имеется три утверждения:
-
Вадим изучает китайский;
-
Сергей не изучает китайский;
-
Михаил не изучает арабский.
Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно.
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
Остается считать верным третье утверждение, а первое и второе - ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил - японский, Вадим - арабский.
Пример 5. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты соглашения о полном разоружении, представленные каждой из стран. Отвечая затем на вопрос журналистов: "Чей именно проект был принят?", министры дали такие ответы:
Россия - "Проект не наш, проект не США";
США - "Проект не России, проект Китая";
Китай - "Проект не наш, проект России".
Один из них (самый откровенный) оба раза говорил правду; второй (самый скрытный) оба раза говорил неправду, третий (осторожный) один раз сказал правду, а другой раз - неправду.
Определите, представителями каких стран являются откровенный, скрытный и осторожный министры.
Решение. Для удобства записи пронумеруем высказывания дипломатов:
Россия - "Проект не наш" (1), "Проект не США" (2);
США - "Проект не России" (3), "Проект Китая" (4);
Китай - "Проект не наш" (5), "Проект России" (6).
Узнаем, кто из министров самый откровенный.
Если это российский министр, то из справедливости (1) и (2) следует, что победил китайский проект. Но тогда оба утверждения министра США тоже справедливы, чего не может быть по условию.
Если самый откровенный - министр США, то тогда вновь получаем, что победил китайский проект, значит, оба утверждения российского министра тоже верны, чего не может быть по условию.
Получается, что наиболее откровенным был китайский министр. Действительно, из того, что (5) и (6) справедливы, следует, что победил российский проект. А тогда получается, что из двух утверждений российского министра первое ложно, а второе верно. Оба же утверждения министра США неверны.
Ответ: Откровеннее был китайский министр, осторожнее - российский, скрытнее - министр США.
§ 6. Логическая функция.
В алгебре логики простые высказывания заменяют логическими переменными, прочем значения переменных могут быть только 0 и 1. Логические связки заменяют соответствующими им математическими символами. При этом сложное высказывание превращается в логическую функцию.
Логической функцией F от набора логических переменных (a, b, c, …) называется функция, которая может принимать только два значения: 0 и 1.
F(a, b) = a b - логическое умножение (конъюнкция).
F(a, b) = a v b - логическое сложение (дизъюнкция).
F(a) = a - отрицание (инверсия).
F(a, b) = a b - импликация.
F(a, b) = a b - эквиваленция.
Логические функции можно вычислять с помощью таблиц истинности.
Таблица истинности логической функции зависит от количества логических переменных и содержит 2n наборов переменных.
Пример 1. Вычисление значения логической функции
F(a, b) = (a v b) (a b)
Выделим промежуточные логические функции и заполним таблицу истинности для соответствующих наборов логических переменных.
a
b
a v b
(a v b)
b
a b
F(a, b)
0
0
0
1
1
0
0
0
1
1
0
0
0
0
1
0
1
0
1
1
0
1
1
1
0
0
0
0
Из таблицы видно, что при любых наборах логических переменных функция F(a, b) тождественно равна нулю.
Пример 2. Вычисление значения логической функции при заданных значениях переменных.
F (a, b, c) = a v b (a с b).
Вычислите: F (1, 0, 1).
Решение:
F (1, 0, 1) = 1 v 0 (1 1 0)
Значение выражения в скобках можно не вычислять, т.к. затем выполняется конъюнкция 0 и выражения в скобках. Тогда имеем:
F (1, 0, 1) = 1 v 0 = 1.
Ответ: F (1, 0, 1) = 1.
Метод построения таблиц истинности используется и для доказательства логического равенства различных по записи логических функций. При этом если на всех одинаковых наборах логических переменных значения функций совпадают, они называются эквивалентными.
Две логические функции называются эквивалентными, если на всех одинаковых наборах логических переменных значения функций совпадают.
Пример 3. Доказательство равенства двух логических функций.
Докажем, что функции F1(a, b) = a v b и F2(a, b) = a b эквивалентны.
a
b
a
a v b
a b
0
0
1
1
1
0
1
1
1
1
1
0
0
0
0
1
1
1
1
1
По таблице определяем, что на всех одинаковых наборах логических переменных значения функций совпадают, следовательно, они эквивалентны.
Применение законов логики позволяет сокращать количество переменных в логических выражениях и упрощать логические функции.
Законы логики также применяются для построения логических функций по таблицам истинности. При этом нужно руководствоваться следующим правилом:
-
Для каждой строки таблицы истинности с единичным значением построить минтерм (конъюнкцию переменных), при этом переменная должна встретиться один раз (без отрицания или с отрицанием). Если в таблице истинности переменные имеют нулевые значения в строке, то в минтерм они входят с отрицанием, а переменные, имеющие значение единица, входят в минтерм без отрицания.
-
Объединить все минтермы операцией дизъюнкции.
-
Упростить, если возможно, полученную логическую формулу.
Пример 4. Построение логической функции по заданной таблице истинности.
a
c
F(a, b, c)
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
0
Выберем строки, в которых функция равна 1 и построим для них минтермы:
строка 1: a b c;
строка 2: a b c.
Объединим минтермы: F(a, b, c) = a b c a b c.
Упростим логическую функцию: F(a, b, c) = a b c a b c = {3} = a b ( c c) = {6} = a b 1= {7} = a b = {4} = (a b)
Итак, мы получили логическую функцию F(a, b, c) = (a b).
§ 7. Логические основы ЭВМ. Базовые логические элементы.
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: "1" и "0".
Из этого следует два вывода:
-
Одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
-
На этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации. В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули.
Логический элемент компьютера - это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Базовыми логическими элементами компьютеров для реализации логических функций являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ (называемые также вентилями).
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от одного до восьми входов и один или два выхода.
Чтобы представить два логических состояния - "1" и "0" в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт. Высокий уровень обычно соответствует значению "истина" ("1"), а низкий - значению "ложь" ("0").
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов также описывают с помощью таблиц истинности.
И (конъюнктор)
Схема И реализует конъюнкцию двух или более логических значений.
x
y
x . y
0
0
0
0
1
0
1
0
0
1
1
1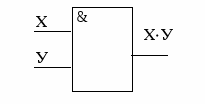
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x . y
Операция конъюнкции на структурных схемах обозначается знаком "&" (читается как "амперсэнд"), являющимся сокращенной записью английского слова and.
ИЛИ (дизъюнктор)
Схема ИЛИ реализует дизъюнкцию двух или более логических значений.
x
y
x y
0
0
0
0
1
1
1
0
1
1
1
1
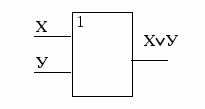
Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y
Знак "1" на схеме - от устаревшего обозначения дизъюнкции как ">=1" (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1).
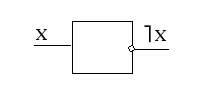
НЕ (инвертор)
Схема НЕ реализует операцию отрицания (инверсию).
x
х
0
1
1
0
Связь между входом x этой схемы и выходом z можно записать соотношением z = х (читается как "не x" или "инверсия х").
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0.
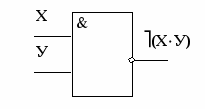
И-НЕ (элемент Шеффера)
x
y
(x . y)
0
0
1
0
1
1
1
0
1
1
1
0
Схема И-НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И.
Связь между выходом z и входами x и y схемы записывают следующим образом: z = (x . y), где x . y читается как "инверсия x и y".
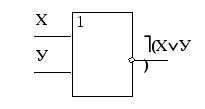
ИЛИ-НЕ (элемент Пирса)
Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.
Связь между выходом z и входами x и y схемы записывают следующим образом: z = (x y), (читается как "инверсия x или y ").
x
y
(xy)
0
0
1
0
1
0
1
0
0
1
1
0
Пример:
Построить схему, реализующую данную функцию:
F(a, b, c) = a · (b c) ( b · c)
Р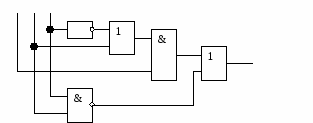 ешение: а в с
ешение: а в с
F(a, в, c)
Упражнение:
Упростите логические формулы и постройте соответствующие им схемы:
-
F = a · (b c) a · b a · c
-
F = ( a · b a · (b c)
-
F = (a b c) · ( a b c) · (a b c)
-
F = a · ( b c) (a e · d) · ( a b · c)
-
F = a · b · c a · b · c a · b · c · d
-
F = a a · (b c) ( a d g) · (b d) · (c d g · h)
§ 8. Логические элементы компьютера. Триггер и сумматор.
Триггер - это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое - двоичному нулю
Термин триггер происходит от английского слова trigger - защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает "хлопанье". Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить ("перебрасываться") из одного электрического состояния в другое и наоборот.
Самый распространённый тип триггера - так называемый RS-триггер (S и R, соответственно, от английских set - установка, и reset - сброс).
S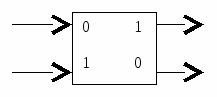 Q
Q
R Q
Он имеет два симметричных входа S и R и два симметричных выхода Q и Q, причем выходной сигнал Q является логическим отрицанием сигнала Q.
На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов.
Наличие импульса на входе будем считать единицей, а его отсутствие - нулем.
Реализация триггера с помощью вентилей ИЛИ-НЕ и соответствующая таблица истинности.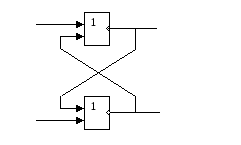
S
R
Q
Q
0
0
запрещено
0
1
1
0
1
0
0
1
1
1
хранение битаS Q
R Q
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ-НЕ
-
Если на входы триггера подать S="1", R="0", то (независимо от состояния) на выходе Q верхнего вентиля появится "0". После этого на входах нижнего вентиля окажется R="0", Q="0" и выход Q станет равным "1".
-
Точно так же при подаче "0" на вход S и "1" на вход R на выходе Q появится "0", а на Q - "1".
-
Если на входы R и S подана логическая "1", то состояние Q и Q не меняется.
-
Подача на оба входа R и S логического "0" может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена.
Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 х 210 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
В целях максимального упрощения работы компьютера все многообразие математических операций сводится к сложению двоичных чисел.
Вспомним, что при сложении двоичных чисел образуется сумма в данном разряде, а также возможен перенос в старший разряд.
Слагаемые
Перенос
Сумма
A
B
P
S
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
Из этой таблицы видно, что перенос реализуется с помощью логического элемента «И».
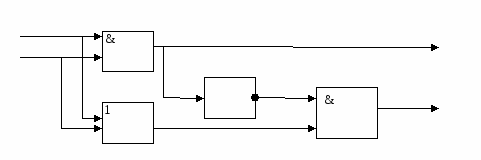
Что касается суммы, то наиболее подходящим логическим элементом является элемент «ИЛИ». Однако при сложении четвертой пары чисел в результате должен получаться 0, а не 1. Для того чтобы достичь необходимого результата, можно подать сигнал переноса на логический элемент «НЕ», а затем с его выхода и выхода элемента «ИЛИ» подать сигнал на элемент «И». На выходе элемента «И» мы получим требуемый сигнал.
A (0,0,1,1) P (0,0,0,1)
B(0,1,0,1)
0,0,0,1 1,1,1,0 S(0,1,1,0)
0,1,1,1
Данная схема называется полусумматором, т.к. реализует суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.
Сумматор - это электронная логическая схема, выполняющая суммирование двоичных чисел
Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.
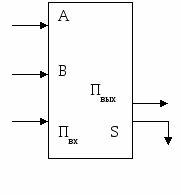 ai
ai
bi
pi
pi-1
ci
При сложении чисел A и B в одном i-ом разряде приходится иметь дело с тремя цифрами:
1. цифра ai первого слагаемого;
2. цифра bi второго слагаемого;
3. перенос pi-1 из младшего разряда.
В результате сложения получаются две цифры: цифра ci для суммы; перенос pi из данного разряда в старший.
Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности:
Входы
Выходы
Первое слагаемое
Второе слагаемое
Перенос
Сумма
Перенос
ai
bi
pi-1
ci
pi
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.
Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров.
Например, схема вычисления суммы C = (с3 c2 c1 c0) двух двоичных трехразрядных чисел A = (a2 a1 a0) и B = (b2 b1 b0), где с0 - младший разряд суммы, с3 - старший разряд суммы, может иметь вид:
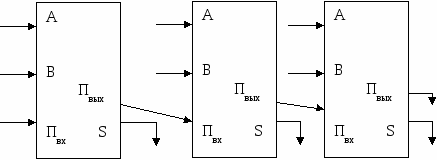
a0 a1 a2
b0b1 b2
0с3
с0 с1 с2
Таким образом, можно сделать вывод, что логические элементы являются строительными «кирпичиками», из которых путем конструирования логических схем строится «здание» любого современного компьютера.
Вопросы для самоконтроля:
-
Что изучает логика, математическая логика, алгебра логики?
-
Дайте определение следующих понятий: высказывание, утверждение, рассуждение, умозаключение, логическое выражение.
-
Основные логические связки, элементарное и составное высказывания.
-
Перечислите основные логические операции и способы их записи.
-
Дайте определение логической формулы.
-
Объясните смысл следующих понятий: выполнимая логическая формула, тавтология, противоречие, равносильное преобразование формулы.
-
Запишите формулы замены импликации и эквиваленции на комбинацию остальных основных логических операций.
-
Понятие таблицы истинности логической формулы. Таблицы истинности элементарных формул.
-
Что такое упрощение формулы?
-
Основные законы алгебры логики.
-
Перечислите и охарактеризуйте основные способы решения логических задач.
-
Дайте определение логической функции.
-
Понятие эквивалентных логических функций.
-
Правило построения логической функции по таблицам истинности.
-
Определение логического элемента компьютера. Базовые логические элементы.
-
Триггер и сумматор. Соответствующие таблицы истинности и логические схемы.
25