- Преподавателю
- Информатика
- Научно-исследовательская работа «Применение компьютерных технологий к решению задач методом графов»
Научно-исследовательская работа «Применение компьютерных технологий к решению задач методом графов»
| Раздел | Информатика |
| Класс | 11 класс |
| Тип | Другие методич. материалы |
| Автор | Мамастина Е.В. |
| Дата | 19.09.2015 |
| Формат | doc |
| Изображения | Есть |
«Применение компьютерных технологий к решению задач методом графов»
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №25
г. Пензы им. В.П. Квышко»
Научно-исследовательская ученическая работа
«Применение компьютерных технологий
к решению задач методом графов»
Выполнили:
Борисов Никита,
Елистратова Анастасия,
ученики 11 «А» класса
Руководитель:
Мамастина Е.В.
Пенза, 2015 год
Содержание
Вступление……………………………………………………….2
Задача про молоковоз и школы…………………………………
Понятие графа, простейшие свойства……………………….....3
Способы представления графов………………………………...5
Алгоритмы обхода связного графа…………………………......8
Заключение……………………………………………………….15
Приложение 1…………………………………………………….16
Литература ……………………………………………………….20
Вступление
Кто может с уверенностью сказать, с чего началась теория чисел? С алгоритма, предложенного Евклидом (IV-III вв. до н.э.), или принадлежащего ему же доказательства теоремы о бесконечности множества простых чисел? Или с работ Диофанта (III в. н.э.) о решении уравнений в целых числах? Или с исследований Пьера Ферма (XVII в. н.э.), в которых изучение свойств целых чисел было основной и, самое важное, осознанной целью?
Кто может с уверенностью сказать, когда возникло понятие функции и кем оно было введено? Тоже никто.
Теория графов - одна из тех немногих математических теорий, для которых точно известен ее создатель, время и место создания: Леонард Эйлер, 1736 г., г. Петербург. Именно в этом году Л.Эйлером в "Записках Петербургской академии наук" была опубликована статья, в которой приводилось решение широко теперь известной задачи о Кёнигсбергских мостах. Разумеется, работа Л.Эйлера содержала не только отрицательный ответ на вопрос о возможности обойти все семь мостов г. Кенигсберга так, чтобы по каждому из них пройти ровно один раз. В ней великий математик сформулировал и обосновал критерий, позволяющий отвечать на данный вопрос для любого графа. Однако эта статья была единственной в течение почти столетия. Лишь в середине XIX века возродился интерес к теории графов. Исследование электрических сетей, структур молекул и строения кристаллов, применения к решению проблем в биологии и психологии послужили мощным катализатором в становлении данного раздела математики. Графы оказались удобным средством для описания самых разнообразных систем и явились эффективным инструментом структурного анализа. Графы успешно применяются для решения разнообразных задач планирования - выбор оптимального маршрута (транспортная задача), построение сетевого графика, исследование потоков в сетях и т.п. Одной из самых знаменитых задач, которая вызвала фейерверк остроумных работ в области теории графов, была предложенная де Морганом (около 1850 г.) проблема четырех красок: верно ли, что для раскраски любой карты так, чтобы граничащие между собой страны ' были раскрашены в разные цвета, достаточно четырех красок?
С некоторыми задачами, апеллирующими к понятию графа, и алгоритмами их решения мы познакомимся в этой работе.
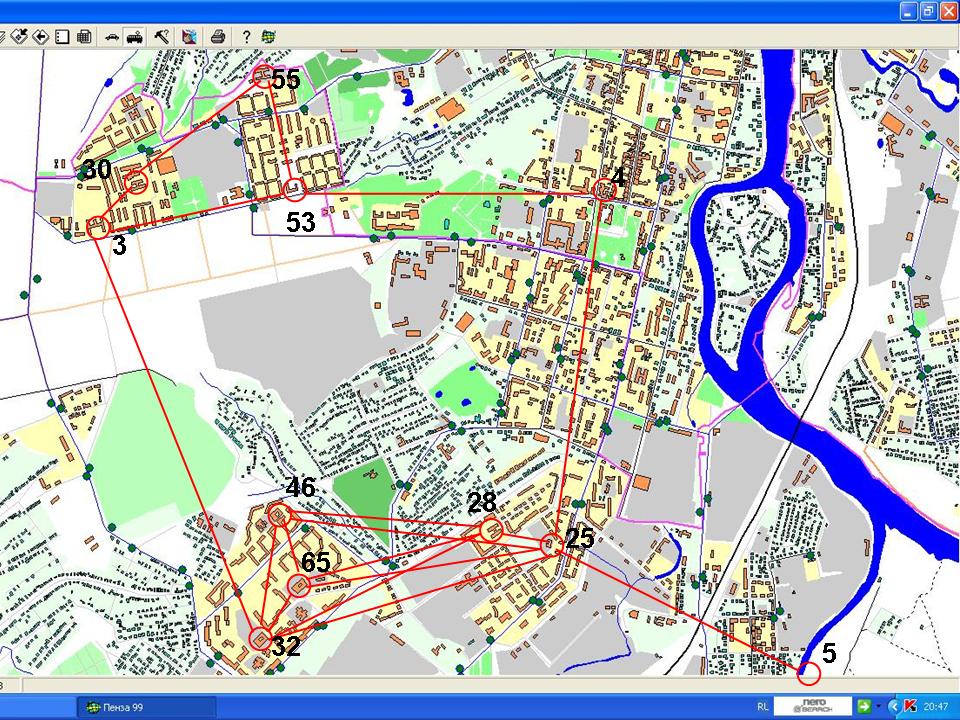
Рассмотрим актуальную задачу. В настоящее время во все школы города доставляется молочная продукция. Имеется карта города. Спрашивается: как молоковоз может развести молоко по всем школам?
В городе Пензе около 70 школ. Чтобы посчитать все варианты доставки, потребуется немалое количество времени. Поручим это задание компьютеру. Составим алгоритм объезда молоковозом школ города.
Удобнее всего решать эту задачу методом графов. Нужно только представить школы как вершины графа, а соединяющие их дороги - как ребра графа.
Прежде чем составить алгоритм обхода графа, необходимо рассмотреть некоторые вопросы теории графов.
1. Понятие графа. Простейшие свойства
Напомним, что граф - это конечная совокупность вершин, некоторые из которых соединены ребрами. Мы будем рассматривать только такие графы, у которых две вершины могут быть соединены только одним ребром. Иногда, конечно, возникает необходимость рассматривать конфигурации, когда пара вершин соединена несколькими ребрами, - в этом случае говорят, что задан мультиграф, а ребра, соединяющие одну и ту же пару вершин, называют кратными. Отметим еще, что ребро не обязано соединять разные вершины. Если ребро соединяет вершину саму с собой, то такое ребро называют петлей.
Если две различные вершины графа соединены ребром, то такие вершины называются смежными. Количество ребер, выходящих из одной вершины, называется степенью этой вершины. Для петли будем считать, что это ребро выходит из вершины дважды. Степень вершины а будем обозначать v(a).
Сформулируем свойство, относящееся к любым графам.
Теорема 1. Сумма степеней всех вершин графа равна удвоенному числу его ребер.
Эта теорема доказывается совсем просто: легко видеть, что, когда подсчитывается сумма степеней всех вершин, каждое ребро в этой сумме фигурирует ровно два раза.
Из этого свойства есть следствие, которое принято называть "леммой о рукопожатиях".
Теорема 2. Количество вершин нечетной степени любого графа всегда четно.
А "леммой о рукопожатиях" это утверждение называют из-за следующей интерпретации: в любой момент времени количество людей, сделавших нечетное число рукопожатий, четно. Действительно, если вершины графа - это люди, и вершины соединены ребром, если соответствующие два человека обменялись рукопожатием, то это одно и то же утверждение о получившемся графе.
А вот еще одно свойство.
Теорема 3. В любом графе есть по крайней мере две вершины, имеющие одинаковую степень.
Доказательство. Пусть в графе п вершин. Ясно, что степень каждой вершины может иметь значение от 0 до п - 1. Если степени всех вершин различны, то каждое из указанных значений должно реализоваться ровно для одной вершины. Рассмотрим вершины степени 0 и степени п - 1. Степень 0 означает, что эта вершина не соединена ни с какой другой; степень п - 1 означает, что эта вершина соединена со всеми другими вершинами. Но одновременно так быть не может.
Граф обычно изображают так, как сказано в определении: рисуют множество точек, изображающих вершины, и соединяют линией те из них, которые являются смежными. Линии при этом вовсе не обязаны быть отрезками прямых.
Ясно, что один и тот же граф может оказаться изображенным по-разному. Например, на рис. 1a и 1б изображен один и тот же граф - легко понять, какие вершины в изображении графа на рис. 1a соответствуют вершинам изображения графа на рис. 1б так, что смежные вершины при этом соответствии остаются смежными, а не смежные - не смежными.
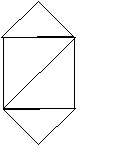
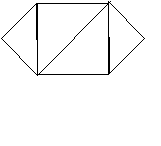
а) б)
Рис. 1. Разные изображения одного графа
М
e2аршрутом на графе называется последовательность ребер e1, e2, ..., ek , в которой конец одного ребра служит началом следующего. Если при этом конец последнего ребра последовательности совпал с началом первого ребра, то маршрут называется циклическим. Для графа, изображенного на рис. 2, последовательности e1, е2, е4, е5, е2, е3 и е2, е4, е5 являются маршрутами, причем второй из них - циклический. А последовательность e1, e2, e5 маршрутом не является.
e1
e3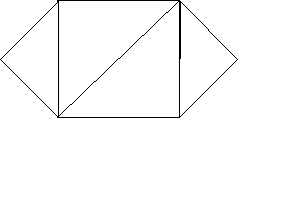
e4
e6
e5
e7
e8
e9
Рис. 2
Если вершина является концом какого-либо ребра, принадлежащего маршруту, то будем говорить, что данный маршрут проходит через эту вершину.
Маршрут называется цепью, если каждое ребро содержится в нем не более одного раза. Цепь, являющаяся циклическим маршрутом, называется циклом. Цепь, проходящая через каждую свою вершину ровно один раз, называется простой. Если цикл является простой цепью, то он тоже называется простым.
Поскольку в рассматриваемых нами графах нет кратных ребер, то маршрут можно задавать и последовательным перечислением вершин, через которые он проходит. Мы будем иногда этим пользоваться.
Вершины а и b называют связанными, если существует цепь, начинающаяся в вершине а и заканчивающаяся в вершине b. Договариваются также считать, что каждая вершина связана сама с собой.
Граф называется связным, если любые две его вершины связаны. Если же граф несвязен, то в нем можно выделить так называемые связные компоненты (или компоненты связности), т.е. такие множества вершин, соединенных ребрами исходного графа, каждое из которых является связным графом, но вершины из разных множеств уже не связаны. Легко убедиться в справедливости следующей теоремы.
Теорема 4. Если в связном графе удалить ребро, принадлежащее циклу, то граф останется связным.
2. Способы представления графов
Изображение графа рисунком удобно для восприятия человеком. Однако если для решения задачи, связанной с графом, надо применить компьютер, такой способ представления уже малопригоден. Поэтому используют другие способы представления графов.
Граф называется нагруженным (взвешенным), если каждому ребру сопоставлено некоторое число (вес ребра). В зависимости от рассматриваемой задачи это число может обозначать расстояние между вершинами или время перехода от одной вершины к другой (если, например, графом изображена какая-либо транспортная схема), или пропускную способность канала, соединяющего две данные вершины (если в виде графа изображена какая-либо коммуникационная сеть), или еще что-либо. Иногда бывает удобно рассматривать ненагруженный граф как нагруженный, у которого каждому ребру поставлено в соответствие число 1.
Обычно граф задают одним из двух способов: перечислением всех его ребер или таблицей, где в клетке на пересечении строки и столбца, соответствующих данным вершинам, указано, соединены эти вершины ребром или нет. Такая таблица называется таблицей смежности. Если граф нагруженный, то для каждого ребра в соответствующей клетке указывается нагрузка. Ниже для нагруженного графа, изображенного на рис. 3, приведены его задания списком ребер и таблицей смежности.
Список ребер: (AA; 2), (АВ; 3), (АС; 6), (ВС; 2), (AD; 4), (BD; 3), (CD; 5).
Таблица смежности 2.1
Вершина
А
В
С
D
А
2
3
6
4
В
3
0
2
3
С
6
2
0
5
D
4
3
5
0
В
2таблице смежности ненагруженного графа везде вместо чисел, указывающих нагрузку (т.е. отличных от 0), стояло бы число 1. А в списке ребер ненагруженного графа просто не нужна числовая характеристика

3
A
2
6
4
3
C
D
5
Рис. 3
Надо, конечно, уметь переходить от одного способа описания графа к другому. Но работа такая совершенно формальна и, следовательно, может быть поручена компьютеру - нужно только составить соответствующий алгоритм.
В дальнейшем в заданиях на составление алгоритма, тем или иным образом обрабатывающего граф, мы для простоты будем считать вершины графа перенумерованными натуральными числами от 1 до n (без пропусков и повторений). Список ребер для нагруженного графа будем задавать как двумерный массив А [1 : n, 1 : 3], где в первой строке соответствующей этому массиву таблице указывается один конец ребра, во второй - другой его конец, а в третьей - величина нагрузки (здесь п - число ребер в графе). Для ненагруженного графа соответствующий массив содержит только первые две строки. Если граф задается таблицей смежности, то договоримся считать значение первого индекса номером первой вершины, а второго индекса - номером второй вершины; сами номера вершин в массиве не присутствуют. В частности, для графа на рис. 3 при естественной нумерации вершин А - 1, В - 2, С - 3 и D - 4 список ребер в силу нашей договоренности задается массивом, который можно изобразить табл. 2.2, а таблица смежности выглядит так, как показано в табл. 2.3.
Таблица 2.2 Таблица 2.3
1
1
1
1
2
2
3
2
3
6
4
1
2
3
4
3
4
4
3
0
2
3
2
3
6
4
2
3.
5
6
2
0
5
4
3
5
0
3. Алгоритмы обхода связного графа
Пусть имеется связный граф. Это означает, что из любой вершины можно, двигаясь по ребрам, добраться до любой другой его вершины. Скажем сразу: алгоритма, позволяющего по двум заданным вершинам построить путь из одной вершины в определенную другую, нет. Но можно указать алгоритм, позволяющий из заданной вершины совершить обход всех остальных вершин и, значит, заведомо добраться до нужной второй вершины. Скажем сразу, что алгоритмов таких существует несколько; мы рассмотрим два из них - наиболее популярных.
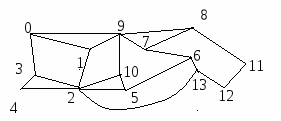
О дин из них называется поиском в глубину. Идея алгоритма такова. Пусть зафиксирована начальная вершина v0. Выберем смежную с ней вершину v1. Затем для v1 поступаем так же: выбираем смежную с ней вершину из числа еще невыбранных вершин. И так далее: если мы уже выбрали вершины v0, v1,…,vk , то следующая вершина выбирается смежной с vk из числа невыбранных. Если для вершины vk такой вершины не нашлось, то возвращаемся к вершине vk-1 и для нее ищем смежную среди невыбранных. При необходимости возвращаемся еще на шаг назад и т.д. Ясно, что так будут перебраны все вершины графа, и поиск закончится. На рис. 5 показаны две реализации поиска в глубину для одного и того же графа (при одинаковом выборе начальной вершины): около каждой вершины написан присвоенный ей порядковый номер при исполнении поиска в глубину. Свое название этот метод получил за то, что при его реализации мы стремимся как можно дальше уйти от исходной вершины, а когда идти уже некуда, возвращаемся в ту вершину, откуда идет хотя бы одно ребро в непройденные еще вершины.
дин из них называется поиском в глубину. Идея алгоритма такова. Пусть зафиксирована начальная вершина v0. Выберем смежную с ней вершину v1. Затем для v1 поступаем так же: выбираем смежную с ней вершину из числа еще невыбранных вершин. И так далее: если мы уже выбрали вершины v0, v1,…,vk , то следующая вершина выбирается смежной с vk из числа невыбранных. Если для вершины vk такой вершины не нашлось, то возвращаемся к вершине vk-1 и для нее ищем смежную среди невыбранных. При необходимости возвращаемся еще на шаг назад и т.д. Ясно, что так будут перебраны все вершины графа, и поиск закончится. На рис. 5 показаны две реализации поиска в глубину для одного и того же графа (при одинаковом выборе начальной вершины): около каждой вершины написан присвоенный ей порядковый номер при исполнении поиска в глубину. Свое название этот метод получил за то, что при его реализации мы стремимся как можно дальше уйти от исходной вершины, а когда идти уже некуда, возвращаемся в ту вершину, откуда идет хотя бы одно ребро в непройденные еще вершины.
а)
б)
Рис. 5. Два варианта применения поиска в глубину
Однако от идеи до алгоритма путь неблизкий. Во-первых, надо договориться, как задан граф. Во-вторых, надо как-то помечать вершины, которые уже просмотрены. В-третьих, надо уметь каждый раз решать, какую из нескольких вершин, смежных с той, где мы находимся, выбрать следующей. В-четвертых, когда уже некуда двигаться из вершины, где мы находимся, уметь вернуться в ту вершину, для которой еще есть хотя бы одна непройденная смежная вершина. Текст данного алгоритма на языке Visual Basic приводится в приложении 1.
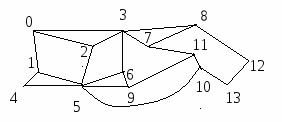
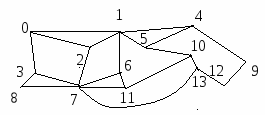
Другой алгоритм называется поиском в ширину. Суть этого подхода состоит в том, чтобы рассматривать все вершины, смежные с уже рассмотренными. На рис. 6 показаны две реализации поиска в ширину для одного и того же графа (при одинаковом выборе начальной вершины).
а)
б
)
Рис. 6. Два варианта применения поиска в ширину
Как и для поиска в глубину, прежде чем написать алгоритм, надо ответить на те же вопросы: каким способом представлен граф, как помечать просмотренные вершины, как выбирать очередную вершину из нескольких еще непросмотренных, но смежных с уже просмотренными. Текст алгоритма поиска в ширину на языке Visual Basic приводится в приложении 1.
А сейчас рассмотрим одну из часто встречающихся задач: найти длину кратчайшей цепи от заданной вершины до любой другой. Длиной цепи при этом называют количество содержащихся в ней ребер.
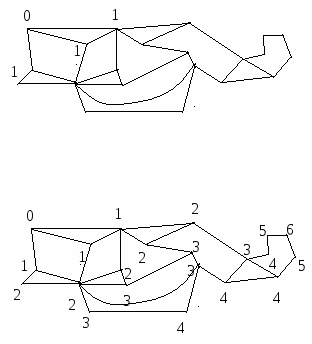
Идея решения этой задачи состоит в следующем. Исходной вершине припишем число 0. Каждой смежной с ней вершине припишем число 1. Каждой вершине, смежной с той, которая уже помечена числом 1 и не была помечена раньше, приписываем число 2. Каждой вершине, смежной с той, которая уже помечена числом 2 и не была помечена раньше, приписываем число 3. И так далее, до тех пор, пока такое действие можно будет производить. Конечно, при этом могут оказаться вершины, добраться до которых так и не удастся. На рис. 7 приведен результат обработки указанным образом конкретного графа. Действие этого алгоритма напоминает распространение волны, и потому он получил название "волнового алгоритма".
а) После первого шага
б) Окончательный вид
Рис. 7. Результат обработки графа волновым алгоритмом
Легко понять, что число, написанное около вершины, показывает длину кратчайшей цепи, ведущей к ней от заданной вершины.
Алгоритм нахождения кратчайшего пути с помощью волнового алгоритма на языке Visual Basic приводится в приложении 1.
Можно показать применение алгоритмов «Поиск в глубину» и «Поиск в ширину» для графов, заданных таблицами 2.4-2.6.
Задача
У путешественника есть карта, на которой отмечены города и дороги между некоторыми из них. Все дороги допускают двустороннее движение, и для каждой дороги, соединяющей два города, указана ее длина. Путешественник хочет из одного города добраться в другой кратчайшим путем. Предложите алгоритм, позволяющий найти нужный путешественнику маршрут или сообщить, что такого маршрута нет.
Представим себе путь молоковоза в виде конечной системы объектов (школ), от которых расходятся дороги, причем каждая дорога соединяет два объекта (такие объекты будем называть смежными), но не исключается существование таких объектов, из которых можно проехать только по одной дороге (такие объекты будем называть тупиками). Геометрически путь молоковоза можно представить в виде системы точек А, В, С, ... (изображающих школы) и совокупности отрезков АВ, ВС, ... (изображающих дороги), соединяющих некоторые пары этих
точек (рис. 8) и вернутся к ним.
Р
Hис.8
С
I
N
M

В
E
D
K
L
А
F
Будем говорить, что объект Y достижим из объекта X, если существует путь, ведущий от X к Y через промежуточные дороги и объекты. Точнее, это означает, что либо X и Y - смежные объекты, либо существует последовательность объектов X1, X 2, Х3 ..., Хп, таких, что пары объектов X и X1, X 1 и Х2, X 2 и Х3, ..., Хп и У смежны. Например, на приведенном рисунке объект Н достижим из тупика А посредством пути , АВ, ВС, CD, DE, EF, FD, DH, в то время как объект К не достижим из А. Вместе с тем, если Y вообще достижим из X, то он достижим и посредством простого пути, т.е. такого пути, в котором каждый объект (а тем более и каждая дорога) проходится лишь один раз. В предыдущем примере путь не был простым, но, срезав петлю DE, EF, FD, мы получаем простой путь АВ, ВС, CD, DH.
Поскольку мы хотим облегчить мыслительную деятельность не только одному водителю одного молоковоза города Пенза, то решение поставленной задачи мыслится в виде общего метода поисков, пригодного при любых дорогах и при любом расположении в городе объектов А и М. Иными словами, решение мыслится в виде алгоритма, решающего любую из задач данного типа (именно в этом, как известно, заключается такое свойство алгоритма, как массовость).
Легко заметить, что в данной задаче можно применить волновой алгоритм обхода связного графа, приведенный в приложении 1, если задать представление совокупности школ и связывающих их дорог в виде таблицы смежности.
Заключение
Теория графов в настоящее время является интенсивно развивающимся разделом дискретной математики. Это объясняется тем, что в виде графовых моделей описываются многие объекты и ситуации: коммуникационные сети, схемы электрических и электронных приборов, химические молекулы, отношение между людьми и многое другое.
Графовые задачи обладают рядом достоинств, позволяющих использовать их для развития соображения и улучшения логического мышления детей, начиная с детского сада и заканчивая старшими классами средней школы. Язык графов прост, понятен и нагляден. Графовые задачи допускают изложение в занимательной, игровой форме. С другой стороны, графовые задачи труднее поддаются формализации, чем, например, школьные задачи по алгебре, для их решения часто не требуется глубоких знаний, а следует применить смекалку.
Описанные выше приемы позволяют использовать элементы теории графов для одновременного решения нескольких важных задач школьного образования. С их помощью можно обеспечивать учеников новыми знаниями, которые облегчат ему в дальнейшем изучение информатики; повышать логическое и умственное развитие школьников; приучать их к самостоятельной работе; развивать их воображение и повышать культуру общения.
Приложение 1.
Алгоритм, реализующий алгоритм поиска в глубину и волновой алгоритм.
Dim g(10, 10), b(10), st(10), p(10), n, j As Integer
Private Sub Command1_Click()
'алгоритм реализует ввод таблицы смежности'
n = Val(txt(0))
For j = 0 To n - 1
For i = j * 10 + 1 To j * 10 + n
Text1(i).Visible = True
Next i, j
For j = 0 To n - 1
For i = j * 10 + 1 To j * 10 + n
g(i - j * 10, j + 1) = Val(Text1(i).Text)
Next i, j
End Sub
Private Sub Command2_Click()
'алгоритм реализует поиск в глубину'
m = Val(Text2.Text)
Label3.Caption = ""
For t = 1 To n
b(t) = 0
st(t) = 0
Next t
b(m) = 1
st(1) = m
u = 1
While u > 0
t = 1 : s = 1
While ((t <= n) And (g(st(u), t) = 0) Or (b(t) = 1))
t = t + 1
Wend
If t < n + 1 Then u = u + 1: b(t) = 1: st(u) = t: Label3.Caption = Label3.Caption + Str(t) Else st(u) = 0: u = u - 1
Wend
End Sub
Private Sub Command3_Click()
'волновой алгоритм реализует поиск кратчайшего пути'
Label6.Caption = ""
m = Val(Text2.Text)
For i = 1 To n
p(i) = -1
Next i
p(m) = 0
For k = 0 To n - 1
For i = 1 To n
If p(i) = k Then
For j = 1 To n
If ((p(j) = -1) And (g(i, j) = 1)) Then p(j) = k + 1
Next j
End If
Next i
Next k
For i = 1 To n
If p(i) = -1 Then Label6.Caption = Label6.Caption + "Вершина" + Str(i) + "Недостижима из вершины" + Str(m) Else Label6.Caption = Label6.Caption + " кратчайший путь до вершины" + Str(i) + "от вершины" + Str(m) + "равен" + Str(p(i))
Next
End Sub
Private Sub Command4_Click()
End
End Sub
Private Sub Command5_Click()
'алгоритм реализует поиск в ширину'
m = Val(Text2.Text)
Label3.Caption = ""
For t = 1 To n
b(t) = 0
st(t) = 0
Next t
b(m) = 1
st(1) = m
u = 1
k = 0
While u > 0
t = 1
s = 1
1: While ((t <= n) And (g(st(u), t) = 0) Or (b(t) = 1))
t = t + 1
Wend
If t < n + 1 Then u = u + k - 1: b(t) = 1: st(u) = t: k = k + 1: Label3.Caption = Label3.Caption + Str(t): GoTo 1 Else st(u) = 0: u = u - k + 1
Wend
End Sub
Литература.
-
М.Г. Кац «О плоских правильных графах»,1975;
-
Б.А. Трахтенброт «Алгоритмы и вычислительные автоматы»,1974;
-
О. Оре "Графы и их применения",1965;
-
К. Берж "Теория графов и ее применение",1962;
-
А. Г. Гейн. «Математические основы информатики. Графы», Информатика - Приложение к газете «Первое сентября», № 20, 2007
-
Нить Ариадны, или алгоритм поиска выхода из лабиринта, Информатика - Приложение к газете «Первое сентября», № 7, 2007
-
http:/algolist.manual.ru/maths/graphs/.
-
tisbi.ru/resource/lib/graph/
3


